Analysis of Nearshore Near-Inertial Oscillations Using Numerical Simulation with Data Assimilation in the Pearl River Estuary of the South China Sea
Abstract
1. Introduction
2. Data, Model and Methods
2.1. High-Frequency Radar Data
2.2. Mooring Data
2.3. Model and Design of the Experiments
2.4. Empirical Orthogonal Function (EOF) Analysis
2.5. Filtering and Frequency Band Selection
2.6. Evaluation of HF Radar Data
3. Results
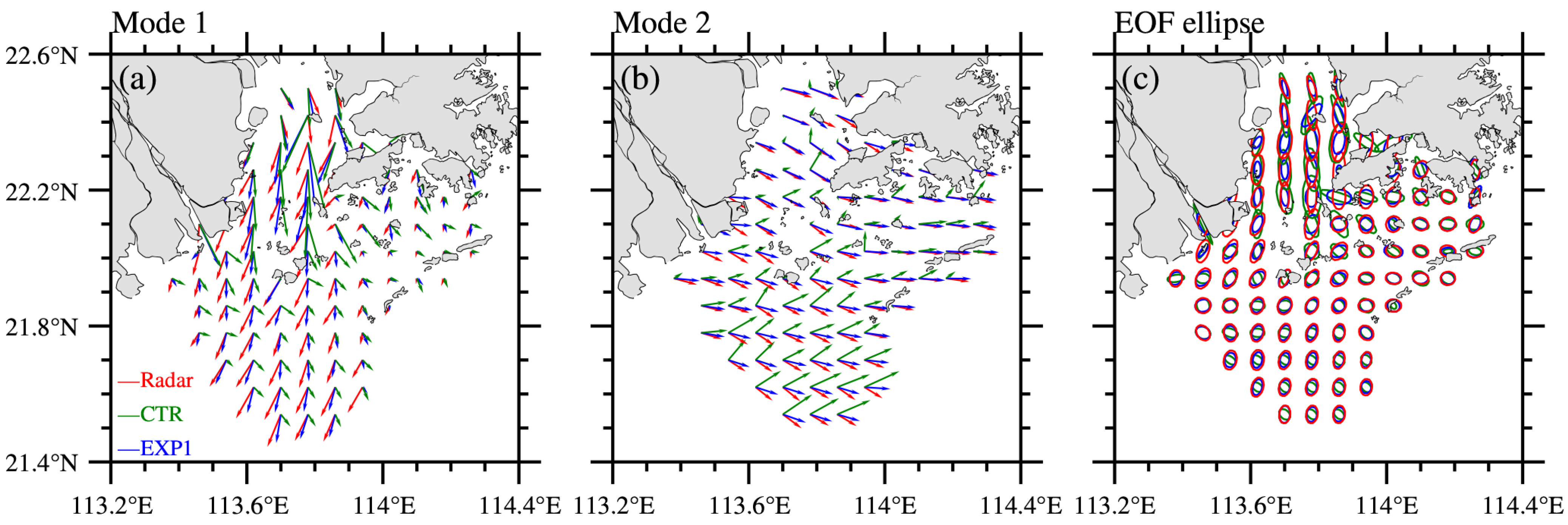
3.1. EOF Analysis of Model and Radar Data
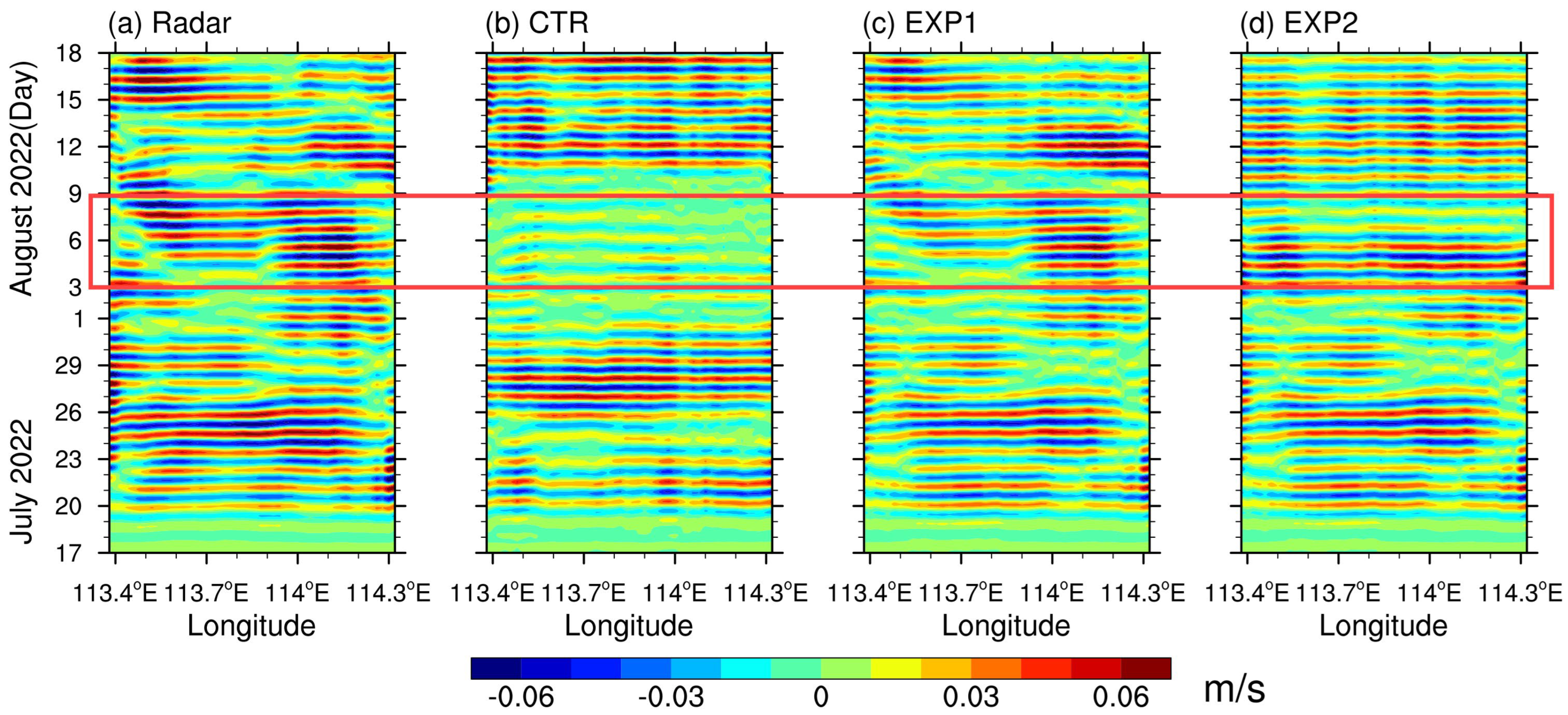
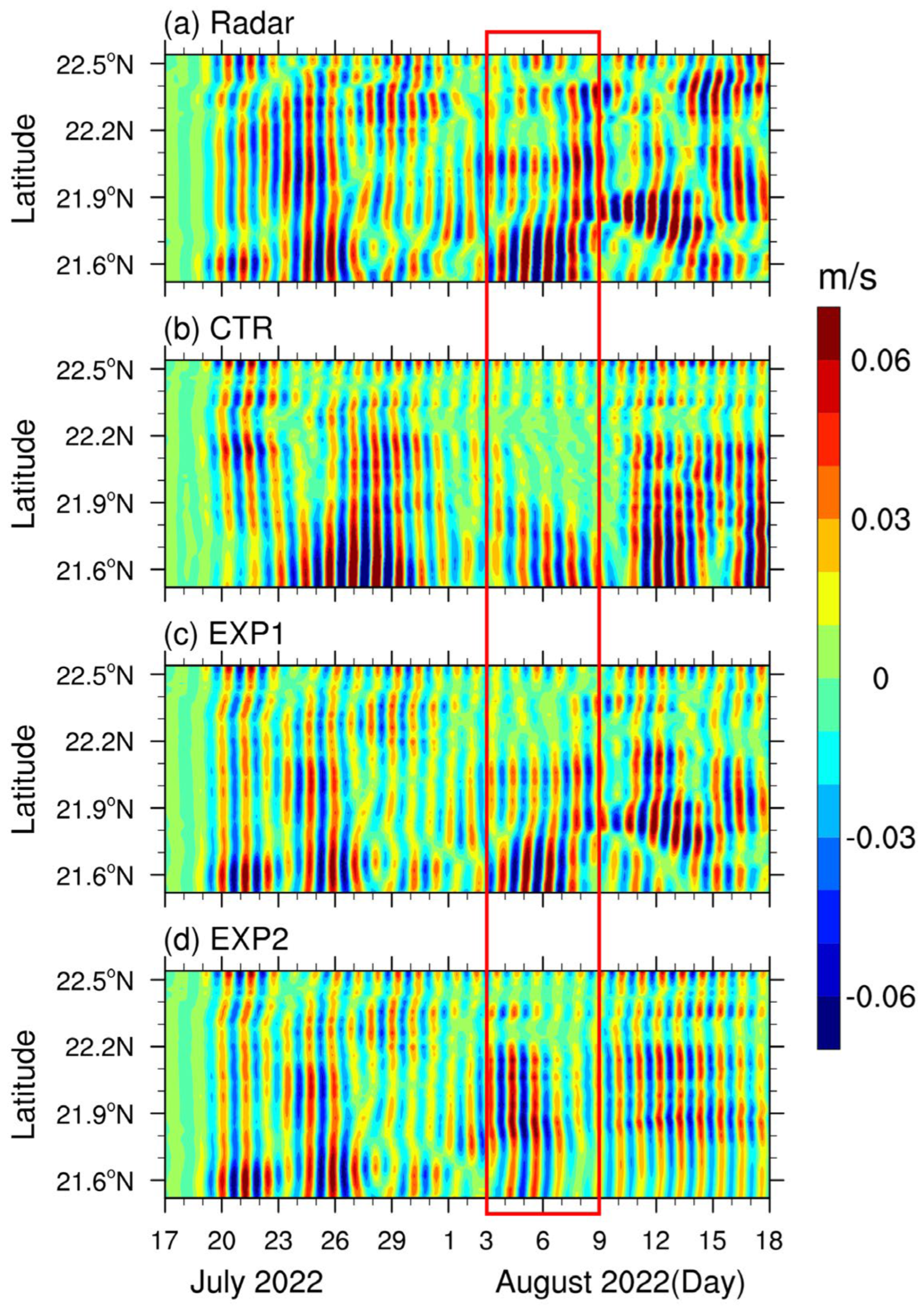
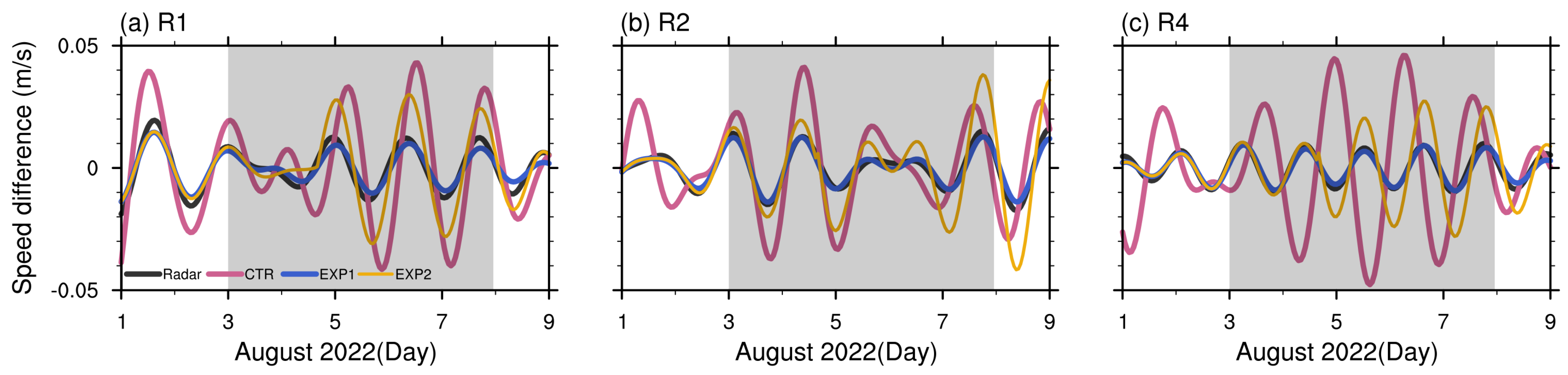
3.2. Sensitivity Experiments for Near-Inertial Oscillations Using FVCOM
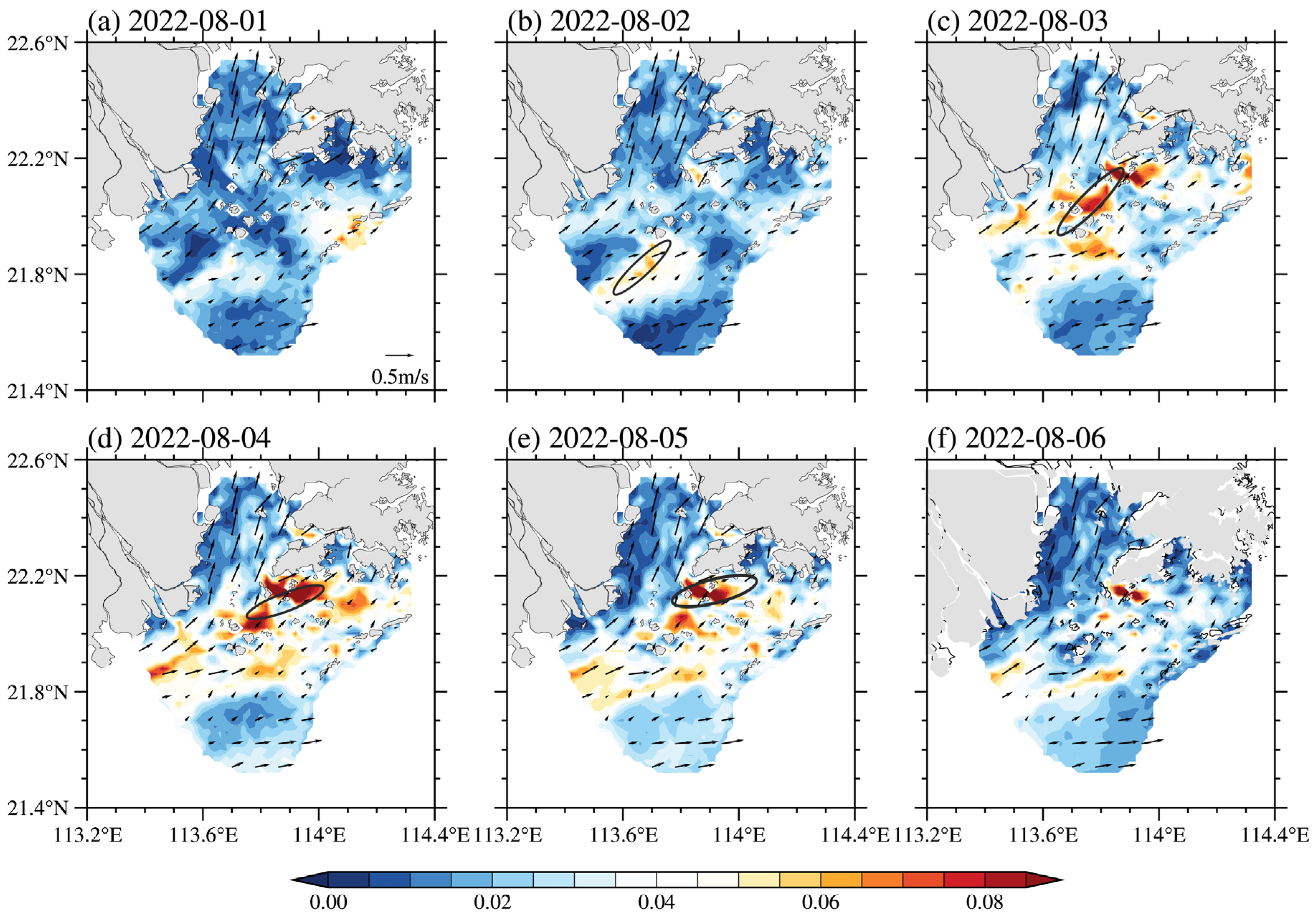
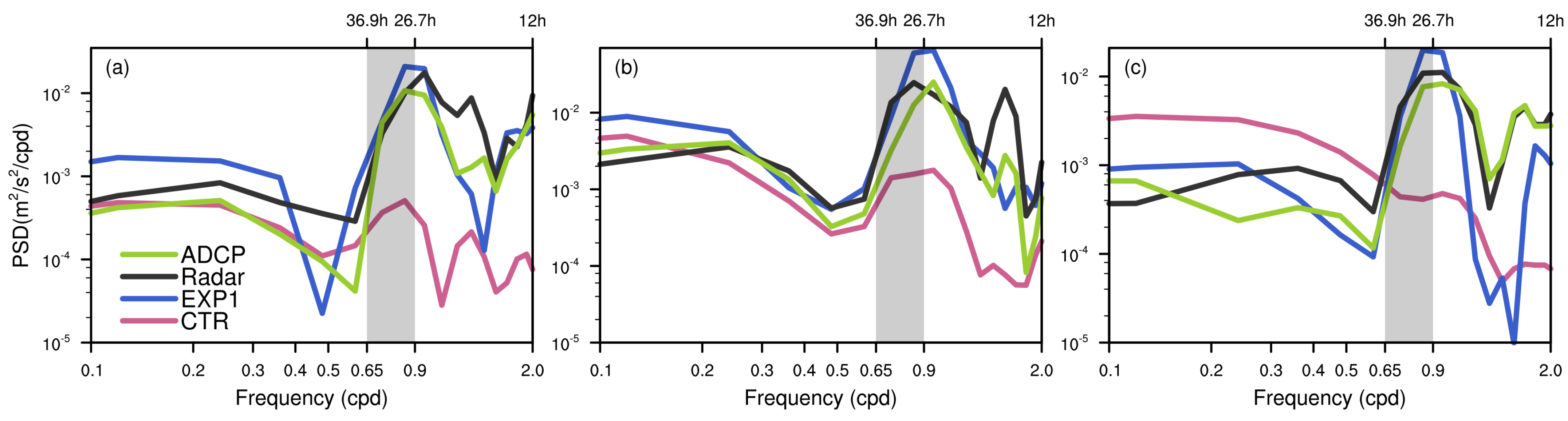
3.3. Near Inertial Kinetic Energy (NIKE) Analysis
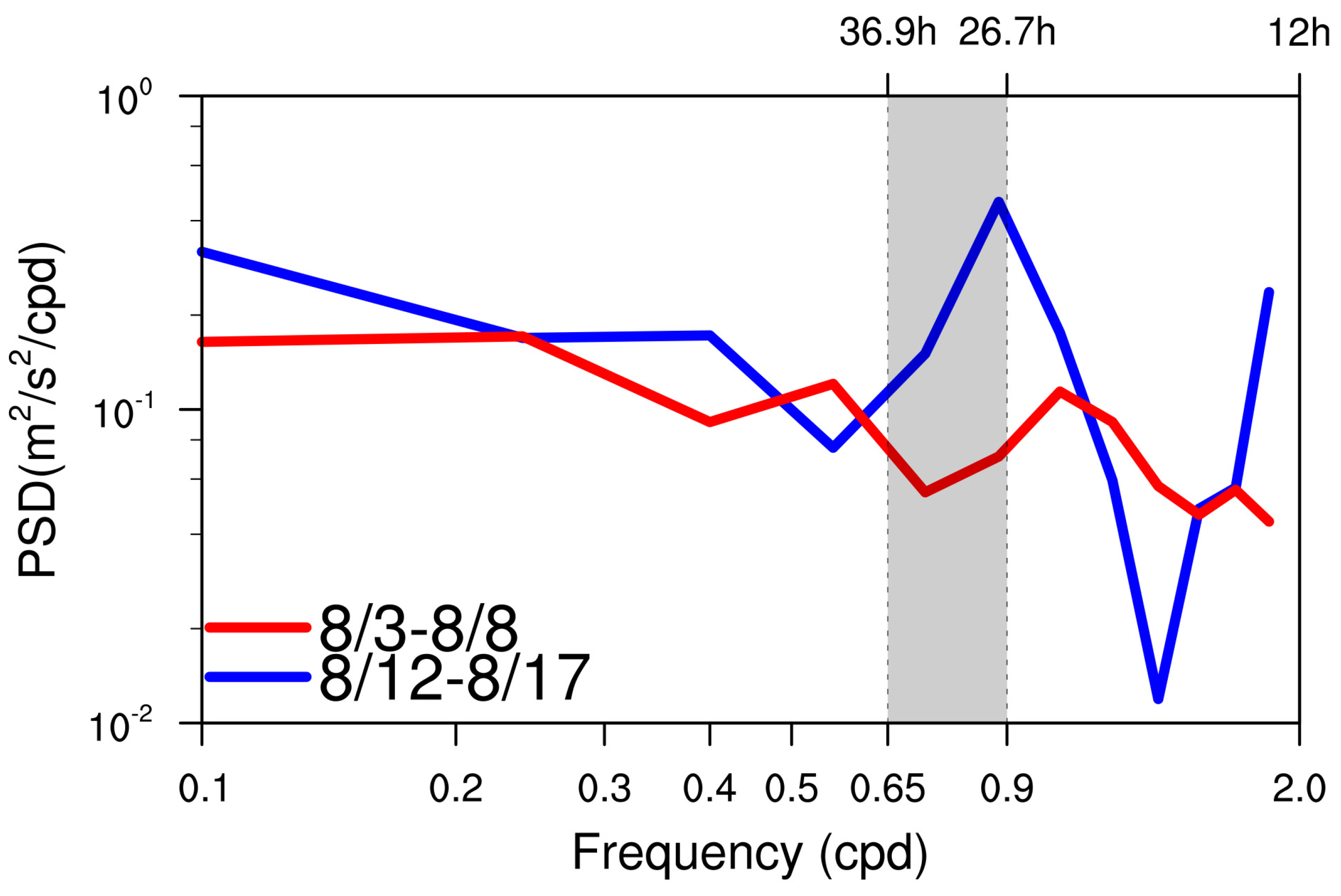
3.4. Vertical Diffusion Items of Near-Inertial Oscillations
4. Discussions
5. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vagn Walfrid, E. On the influence of the earth’s rotaion on ocean-currents. Ark. Mat. Astron. Fys. 1905, 2, 1–53. [Google Scholar]
- Webster, F. Observations of inertial-period motions in the deep sea. Rev. Geophys. 1968, 6, 473–490. [Google Scholar] [CrossRef]
- Munk, W.; Phillips, N. Coherence and band structure of inertial motion in the sea. Rev. Geophys. 1968, 6, 447. [Google Scholar] [CrossRef]
- Pollard, R.T.; Millard, R.C. Comparison between observed and simulated wind-generated inertial oscillations. Deep Sea Res. Oceanogr. Abstr. 1970, 17, 813–821. [Google Scholar] [CrossRef]
- D’Asaro, E.A. The Energy Flux from the Wind to Near-Inertial Motions in the Surface Mixed Layer. J. Phys. Oceanogr. 1985, 15, 1043–1059. [Google Scholar] [CrossRef]
- Rimac, A.; Storch, J.-S.; von Eden, C.; Haak, H. The influence of high-resolution wind stress field on the power input to near-inertial motions in the ocean. Geophys. Res. Lett. 2013, 40, 4882–4886. [Google Scholar] [CrossRef]
- Löb, J.; Köhler, J.; Walter, M.; Mertens, C.; Rhein, M. Time series of near-inertial gravity wave energy fluxes: The effect of a strong wind event. J. Geophys. Res. Ocean. 2021, 126, e2021JC017472. [Google Scholar] [CrossRef]
- Salat, J.; Tintore, J.; Font, J.; Wang, D.-P.; Vieira, M. Near-inertial motion on the shelf-slope front off northeast Spain. J. Geophys. Res. 1992, 97, 7277–7281. [Google Scholar] [CrossRef]
- Anderson, I.; Huyer, A.; Smith, R.L. Near-inertial motions off the Oregon Coast. J. Geophys. Res. 1983, 88, 5960–5972. [Google Scholar] [CrossRef]
- Yang, B.; Hou, Y.; Hu, P.; Liu, Z.; Liu, Y. Shallow ocean response to tropical cyclones observed on the continental shelf of the northwestern South China Sea. J. Geophys. Res. Ocean. 2015, 120, 3817–3836. [Google Scholar] [CrossRef]
- Thomson, R.E.; Huggett, W.S. Wind-driven inertial oscillations of large spatial coherence. Atmos. Ocean 1981, 19, 281–306. [Google Scholar] [CrossRef]
- Mukherjee, A.; Shankar, D.; Aparna, S.G.; Amol, P.; Fernando, V.; Fernandes, R.; Khalap, S.; Narayan, S.; Agarvadekar, Y.; Gaonkar, M.; et al. Near-inertial currents off the east coast of India. Cont. Shelf Res. 2013, 55, 29–39. [Google Scholar] [CrossRef]
- Xing, J.; Davies, A.M. On the influence of a surface coastal front on near-inertial wind-induced internal wave generation. J. Geophys. Res. 2004, 109, C01023. [Google Scholar] [CrossRef]
- Pettigrew, N.R. The Dynamics and Kinematics of the Coastal Boundary Layer off Long Island. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 15 July 2024. Available online: http://hdl.handle.net/1721.1/27913 (accessed on 15 July 2024.).
- Kim, S.Y.; Kurapov, A.L.; Michael Kosro, P. Influence of varying upper ocean stratification on coastal near-inertial currents. J. Geophys. Res. Ocean. 2015, 120, 8504–8527. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, D.; Shu, Y.; Chen, J.; He, Y.; Xie, Q. Bottom-reached near-inertial waves induced by the tropical cyclones, Conson and Mindulle, in the South China Sea. J. Geophys. Res. Oceans 2022, 127, e2021JC018162. [Google Scholar] [CrossRef]
- Pan, J.; Gu, Y.; Wang, D. Observations and numerical modeling of the Pearl River plume in summer season. J. Geophys. Res. Ocean. 2014, 119, 2480–2500. [Google Scholar] [CrossRef]
- Chen, Z.; Pan, J.; Jiang, Y. Role of pulsed winds on detachment of low salinity water from the Pearl River Plume: Upwelling and mixing processes. J. Geophys. Res. Ocean. 2016, 121, 2769–2788. [Google Scholar] [CrossRef]
- Old, C.P.; Vennell, R. Acoustic Doppler current profiler measurements of the velocity field of an ebb tidal jet. J. Geophys. Res. 2001, 106, 7037–7049. [Google Scholar] [CrossRef]
- Simpson, J.H.; Mitchelson-Jacob, E.G.; Hill, A.E. Flow structure in a channel from an acoustic Doppler current profiler. Cont. Shelf Res. 1990, 10, 589–603. [Google Scholar] [CrossRef]
- Vennell, R. Acoustic Doppler Current Profiler measurements of tidal phase and amplitude in Cook Strait, New Zealand. Cont. Shelf Res. 1994, 14, 353–364. [Google Scholar] [CrossRef]
- Teague, C.; Vesecky, J.; Fernandez, D. HF radar instruments, past to present. Oceanography 1997, 10, 40–44. [Google Scholar] [CrossRef]
- Paduan, J.D.; Washburn, L. High-Frequency Radar Observations of Ocean Surface Currents. Annu. Rev. Mar. Sci. 2013, 5, 115–136. [Google Scholar] [CrossRef] [PubMed]
- Crombie, D. Doppler Spectrum of Sea Echo at 13.56 Mc./s. Nature 1955, 175, 681–682. [Google Scholar] [CrossRef]
- Lipa, B.J.; Barrick, D.E. Least-squares methods for the extraction of surface currents from CODAR crossed-loop data: Application at ARSLOE. IEEE J. Ocean. Eng. 1983, 8, 226–253. [Google Scholar] [CrossRef]
- Liu, Y.; Weisberg, R.H.; Merz, C.R.; Lichtenwalner, S.; Kirkpatrick, G.J. HF Radar Performance in a Low-Energy Environment: CODAR SeaSonde Experience on the West Florida Shelf. J. Atmos. Ocean. Technol. 2010, 27, 1689–1710. [Google Scholar] [CrossRef]
- Liu, Y.; Weisberg, R.H.; Merz, C.R. Assessment of CODAR SeaSonde and WERA HF Radars in Mapping Surface Currents on the West Florida Shelf. J. Atmos. Ocean. Technol. 2014, 31, 1363–1382. [Google Scholar] [CrossRef]
- Liu, Y.; Merz, C.R.; Weisberg, R.H.; O’Loughlin, B.K.; Subramanian, V. Data Return Aspects of CODAR and WERA High-Frequency Radars in Mapping Currents. In Observing the Oceans in Real Time; Springer Oceanography: Cham, Switzerland, 2018; pp. 227–240. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, C.; Beardsley, R.C.; Ullman, D.; Butman, B.; Lin, H. Surface circulation in Block Island Sound and adjacent coastal and shelf regions: A FVCOM-CODAR comparison. Prog. Oceanogr. 2016, 143, 26–45. [Google Scholar] [CrossRef]
- Kaplan, D.M.; Largier, J.; Botsford, L.W. HF radar observations of surface circulation off Bodega Bay (northern California, USA). J. Geophys. Res. 2005, 110, C10020. [Google Scholar] [CrossRef]
- Gough, M.K.; Reniers, A.J.H.M.; MacMahan, J.H.; Howden, S.D. Resonant near-surface inertial oscillations in the northeastern Gulf of Mexico. J. Geophys. Res. Ocean. 2016, 121, 2163–2182. [Google Scholar] [CrossRef]
- Zhang, F.; Li, M.; Miles, T. Generation of near-inertial currents on the Mid-Atlantic Bight by Hurricane Arthur (2014). J. Geophys. Res. Ocean. 2018, 123, 3100–3116. [Google Scholar] [CrossRef]
- Shrira, V.I.; Forget, P. On the Nature of Near-Inertial Oscillations in the Uppermost Part of the Ocean and a Possible Route toward HF Radar Probing of Stratification. J. Phys. Oceanogr. 2015, 45, 2660–2678. [Google Scholar] [CrossRef]
- Chant, R.J. Evolution of Near-Inertial Waves during an Upwelling Event on the New Jersey Inner Shelf. J. Phys. Oceanogr. 2001, 31, 746–764. [Google Scholar] [CrossRef]
- Rubio, A.; Reverdin, G.; Fontán, A.; González, M.; Mader, J. Mapping near-inertial variability in the SE Bay of Biscay from HF radar data and two offshore moored buoys. Geophys. Res. Lett. 2011, 38, L19607. [Google Scholar] [CrossRef]
- Hisaki, Y.; Naruke, T. Horizontal variability of near-inertial oscillations associated with the passage of a typhoon. J. Geophys. Res. 2003, 108, 3382. [Google Scholar] [CrossRef]
- Glenn, S.M.; Boicourt, W.; Parker, B.; Dickey, T.D. Operational observation networks for ports, a large estuary and an open shelf. Oceanography 2000, 13, 12–23. [Google Scholar] [CrossRef]
- Chen, C.; Liu, H.; Beardsley, R.C. An Unstructured Grid, Finite-Volume, Three-Dimensional, Primitive Equations Ocean Model: Application to Coastal Ocean and Estuaries. J. Atmos. Ocean. Technol. 2003, 20, 159–186. [Google Scholar] [CrossRef]
- Verron, J. Nudging satellite altimeter data into quasi-geostrophic ocean models. J. Geophys. Res. 1992, 97, 7479–7491. [Google Scholar] [CrossRef]
- Chen, X.; Liu, C.; O’Driscoll, K.; Mayer, B.; Su, J.; Pohlmann, T. On the nudging terms at open boundaries in regional ocean models. Ocean Model 2013, 66, 14–25. [Google Scholar] [CrossRef]
- Li, H.; Kanamitsu, M.; Hong, S.-Y. California reanalysis downscaling at 10 km using an ocean-atmosphere coupled regional model system. J. Geophys. Res. 2012, 117, D12118. [Google Scholar] [CrossRef]
- Ruggiero, G.A.; Ourmières, Y.; Cosme, E.; Blum, J.; Auroux, D.; Verron, J. Data assimilation experiments using diffusive back-and-forth nudging for the NEMO ocean model. Nonlinear Process. Geophys. 2015, 22, 233–248. [Google Scholar] [CrossRef]
- Shulman, I.; Wu, C.-R.; Lewis, J.; Paduan, J.; Rosenfeld, L.; Kindle, J.; Ramp, S.; Collins, C. High resolution modeling and data assimilation in the Monterey Bay area. Cont. Shelf Res. 2002, 22, 1129–1151. [Google Scholar] [CrossRef]
- Lewis, J.K.; Shulman, I.; Blumberg, A.F. Assimilation of Doppler radar current data into numerical ocean models. Cont. Shelf Res. 1998, 18, 541–559. [Google Scholar] [CrossRef]
- Paduan, J.D.; Shulman, I. HF radar data assimilation in the Monterey Bay area. J. Geophys. Res. 2004, 109, C07S09. [Google Scholar] [CrossRef]
- Vandenbulcke, L.; Beckers, J.M.; Barth, A. Correction of inertial oscillations by assimilation of HF radar data in a model of the Ligurian Sea. Ocean Dyn. 2017, 67, 117–135. [Google Scholar] [CrossRef]
- Zhu, L.; Lu, T.; Yang, F.; Liu, B.; Wu, L.; Wei, J. Comparisons of Tidal Currents in the Pearl River Estuary between High-Frequency Radar Data and Model Simulations. Appl. Sci. 2022, 12, 6509. [Google Scholar] [CrossRef]
- Yang, Y.; Wei, C.; Yang, F.; Lu, T.; Zhu, L.; Wei, J. A Machine Learning-Based Correction Method for High-Frequency Surface Wave Radar Current Measurements. Appl. Sci. 2022, 12, 12980. [Google Scholar] [CrossRef]
- Zhu, L.; Yang, F.; Yang, Y.; Xiong, Z.; Wei, J. Designing Theoretical Shipborne ADCP Survey Trajectories for High-Frequency Radar Based on a Machine Learning Neural Network. Appl. Sci. 2023, 13, 7208. [Google Scholar] [CrossRef]
- Verron, J. Altimeter data assimilation into an ocean circulation model: Sensitivity to orbital parameters. J. Geophys. Res. 1990, 95, 11443. [Google Scholar] [CrossRef]
- Preisendorfer, R.W.; Mobley, C.D.; Barnett, T.P. The principal discriminant method of prediction: Theory and evaluation. J. Geophys. Res. 1988, 93, 10815–10830. [Google Scholar] [CrossRef]
- Qian, S.; Zhang, L.; Yang, B.; Huang, A.; Zhang, Y. Analysis of intraseasonal oscillation characteristics of Arctic summer sea ice. Geophys. Res. Lett. 2020, 47, e2019GL086555. [Google Scholar] [CrossRef]
- Matthews, A.J. Propagation mechanisms for the Madden–Julian Oscillation. Q. J. R. Meteorol. Soc. 2000, 126, 2637–2651. [Google Scholar] [CrossRef]
- Lin, X.-H.; Oey, L.-Y.; Wang, D.-P. Altimetry and drifter data assimilations of loop current and eddies. J. Geophys. Res. 2007, 112, C05046. [Google Scholar] [CrossRef]
- Liu, Z.-J.; Nakamura, H.; Zhu, X.-H.; Nishina, A.; Dong, M. Tidal and residual currents across the northern Ryukyu Island chain observed by ferryboat ADCP. J. Geophys. Res. Ocean. 2017, 122, 7198–7217. [Google Scholar] [CrossRef]
- Mau, J.-C.; Wang, D.-P.; Ullman, D.S.; Codiga, D.L. Model of the Long Island Sound outflow: Comparison with year-long HF radar and Doppler current observations. Cont. Shelf Res. 2008, 28, 1791–1799. [Google Scholar] [CrossRef]
- Xu, Z.; Yin, B.; Hou, Y.; Xu, Y. Variability of internal tides and near-inertial waves on the continental slope of the northwestern South China Sea. J. Geophys. Res. Ocean. 2013, 118, 197–211. [Google Scholar] [CrossRef]


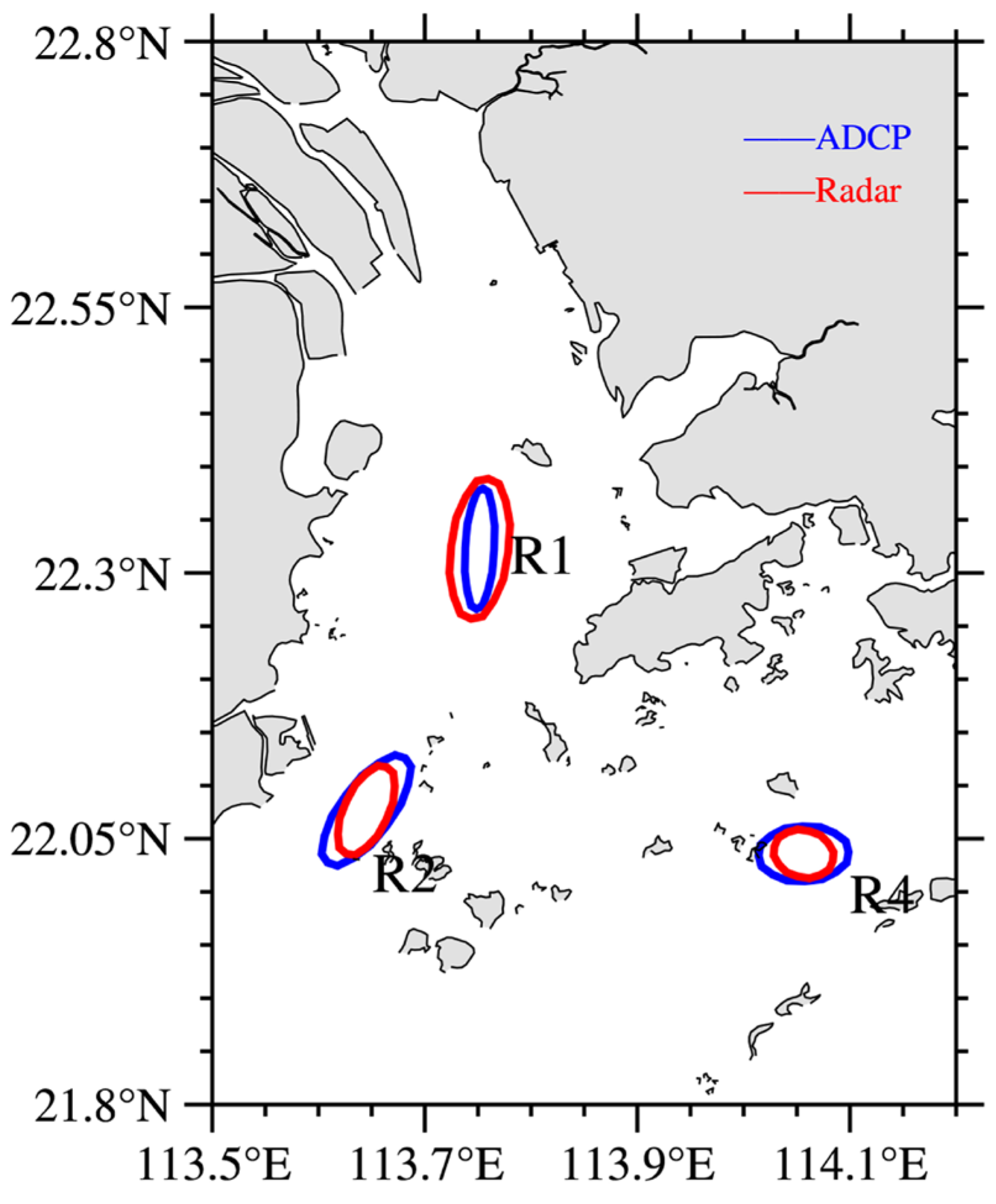
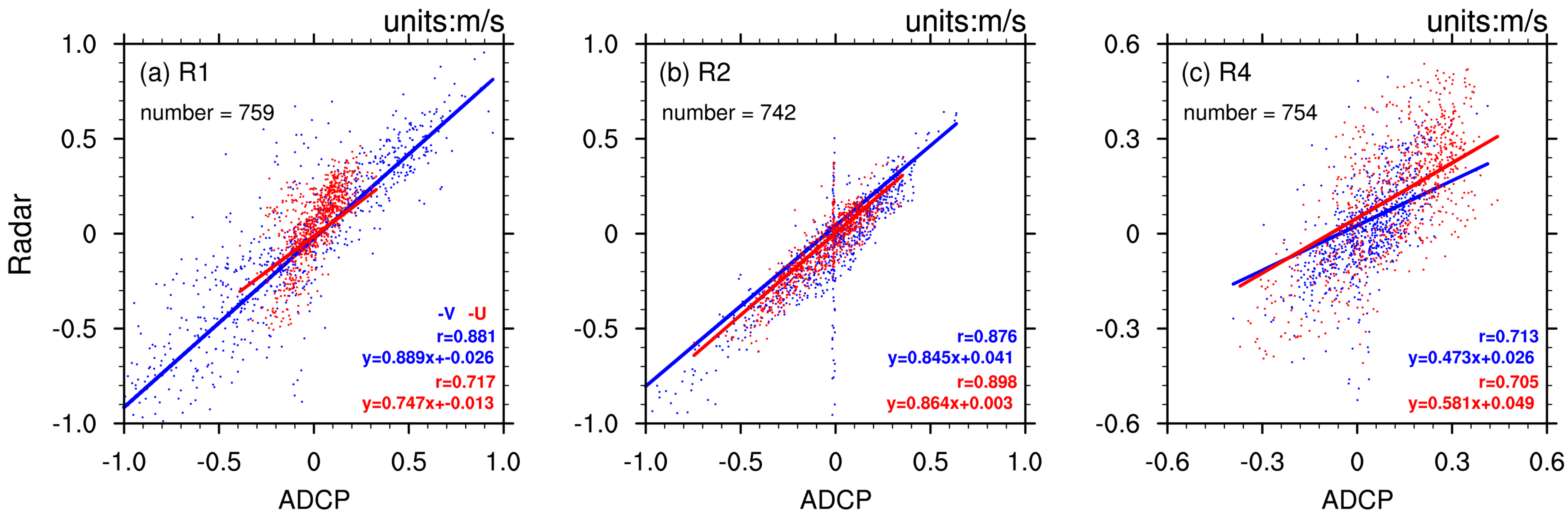
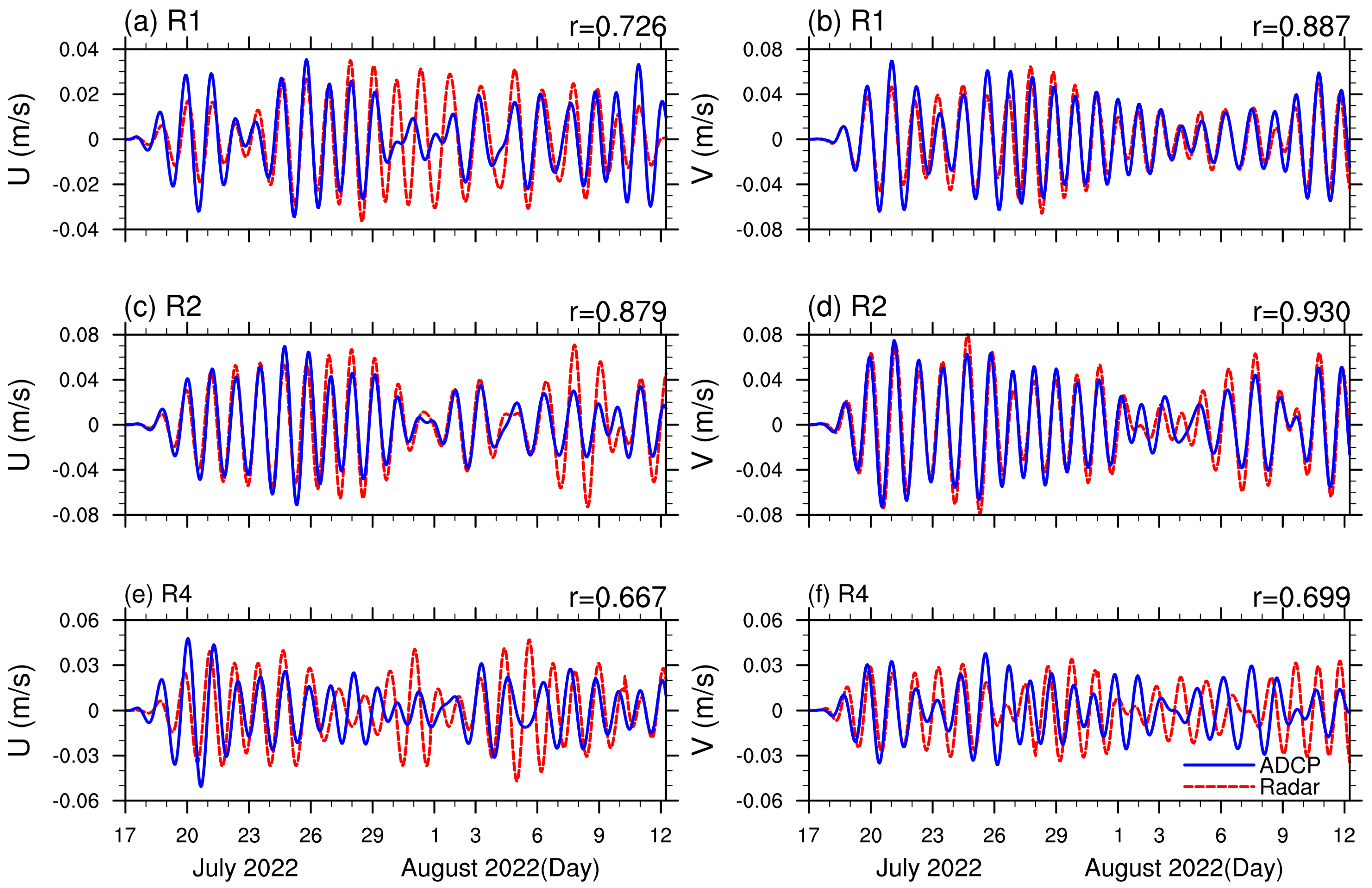


| Site | R1 | R2 | R4 |
|---|---|---|---|
| Location | 113.75°E, 22.32°N | 113.65°E, 22.08°N | 114.06°E, 22.04°N |
| Frequency | 1200 kHz | 600 kHz | 600 kHz |
| Time interval | 20 min | ||
| Top layer depth | 1.61 m | 2.11 m | 2.12 m |
| Vertical resolution | 0.5 m | 1 m | 1 m |
| Max profiling range | 20 m | 70 m | 70 m |
| Standard sensors | Temperature, Tilt, Compass | ||
| Beam angle | 20° | ||
| Experiment Name | Time | Wind | Tide | River Discharge | Assimilation | Assimilation Time | Assimilation Data |
|---|---|---|---|---|---|---|---|
| CTR | 17 July to 17 August 2022 | √ | √ | √ | |||
| EXP1 | √ | √ | √ | √ | 17 July to 17 August 2022 | radar | |
| EXP2 | √ | √ | √ | √ | 17 July to 30 July 2022 | radar |
| EOF Ellipse | R1 | R2 | R4 | |
|---|---|---|---|---|
| major axis | ADCP | 0.378 | 0.408 | 0.423 |
| HF radar | 0.442 | 0.300 | 0.189 | |
| minor axis | ADCP | 0.091 | 0.160 | 0.259 |
| HF radar | 0.180 | 0.138 | 0.147 | |
| rotation | ADCP | 86.962 | 53.427 | 177.822 |
| HF radar | 83.006 | 65.006 | 165.611 | |
| RMSE | 0.110 | 0.110 | 0.259 |
| Correlation Coefficient | R1 | R2 | R4 |
|---|---|---|---|
| HF radar | 0.853 | 0.967 | 0.955 |
| CTR | −0.416 | 0.776 | 0.915 |
| EXP1 | 0.829 | 0.969 | 0.951 |
| EXP2 | −0.385 | 0.121 | 0.878 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Z.; Wei, C.; Yang, F.; Wei, J. Analysis of Nearshore Near-Inertial Oscillations Using Numerical Simulation with Data Assimilation in the Pearl River Estuary of the South China Sea. Remote Sens. 2024, 16, 3276. https://doi.org/10.3390/rs16173276
Jiang Z, Wei C, Yang F, Wei J. Analysis of Nearshore Near-Inertial Oscillations Using Numerical Simulation with Data Assimilation in the Pearl River Estuary of the South China Sea. Remote Sensing. 2024; 16(17):3276. https://doi.org/10.3390/rs16173276
Chicago/Turabian StyleJiang, Zihao, Chunlei Wei, Fan Yang, and Jun Wei. 2024. "Analysis of Nearshore Near-Inertial Oscillations Using Numerical Simulation with Data Assimilation in the Pearl River Estuary of the South China Sea" Remote Sensing 16, no. 17: 3276. https://doi.org/10.3390/rs16173276
APA StyleJiang, Z., Wei, C., Yang, F., & Wei, J. (2024). Analysis of Nearshore Near-Inertial Oscillations Using Numerical Simulation with Data Assimilation in the Pearl River Estuary of the South China Sea. Remote Sensing, 16(17), 3276. https://doi.org/10.3390/rs16173276





