Abstract
As an effective physical field feature to perceive ferromagnetic targets, magnetic anomaly is widely used in covert marine surveillance tasks. However, its practical usability is affected by the complex marine magnetic noise interference, making robust magnetic anomaly detection (MAD) quite a challenging task. Recently, learning-based detectors have been widely studied for the discrimination of magnetic anomaly signal and achieve superior performance than traditional rule-based detectors. Nevertheless, learning-based detectors require abundant data for model parameter training, which are difficult to access in practical marine applications. In practice, target magnetic anomaly data are usually expensive to acquire, while rich marine magnetic noise data are readily available. Thus, there is an urgent need to develop effective models to learn discriminative features from the abundant marine magnetic noise data for newly appearing target anomaly detection. Motivated by this, in this paper we formulate MAD as a single-edge detection problem and develop a self-supervised marine noise learning approach for target anomaly classification. Specifically, a sparse autoencoder network is designed to model the marine noise and restore basis geomagnetic field from the collected noisy magnetic data. Subsequently, reconstruction error of the network is used as a statistical decision criterion to discriminate target magnetic anomaly from cluttered noise. Finally, we verify the effectiveness of the proposed approach on real sea trial data and compare it with seven state-of-the-art MAD methods on four numerical indexes. Experimental results indicate that it achieves a detection accuracy of 93.61% and has a running time of 21.06 s on the test dataset, showing superior MAD performance over its counterparts.
1. Introduction
The earth can be considered as a huge magnetic field in which ferromagnetic targets are magnetized to form a distorted anomaly field in the surrounding geomagnetic environment. This magnetic anomaly field can be described with the magnetic dipole model and has been widely used in transboundary target detection [,], localization [,] and recognition tasks []. Meanwhile, physical parameters of the ferromagnetic targets can be effectively estimated from the magnetic anomaly data for accurate target motion state prediction []. Due to its passive detection property, magnetic anomaly signal is quite suitable for marine target detection under covert application scenarios like underwater mines [,]. However, the magnetic anomaly field attenuates rapidly along with distance and is prone to disturbances from complex marine environmental magnetic noise []. Since the marine magnetic noise is the coupling interaction result of multiple random processes, it is difficult to achieve accurate noise modeling under dynamic observation scenes. Therefore, accurate target magnetic anomaly detection (MAD) in complex marine noise environment remains a significant challenge.
So far, the detection methods for magnetic anomaly can be generally classified into two major categories, i.e., unsupervised domain transformation (UDT) methods [,,] and supervised feature mapping (SFM) methods [,,]. Methods in the former category mainly focus on developing feature transformation techniques to convert the original time-domain magnetic data to the other information domains, where the anomaly signal component could be amplified for threshold discrimination []. This kind of method is based on prior knowledge of target and background and does not require extra labelled data for model supervision. Methods in the latter category turn to extract handcrafted features [,] or learn latent representations [] from the magnetic data, and build mapping relationship between the extracted features and data labels for automatic anomaly classification. This kind of method mostly adopts supervised learning mechanisms and is dependent on massive labelled data for model parameter training. In general, SFM methods can achieve better detection performance than UDT methods at the expense of extra data collection and annotation work.
For UDT methods, the most commonly used are orthogonal basis function (OBF) [,], minimum entropy detector (MED) [], wavelet transform (WT) [], Hilbert Huang transform (HHT) [], etc. The OBF detector is suitable for data with Gaussian white noise and may lose its efficiency in the face of complex marine magnetic noise. Moreover, the difficulty in estimating the closest proximity approach (CPA) further limits its practical applications []. The MED detector is based on the difference in information entropy between target and background for anomaly signal discrimination. It lacks adaptability to strong background noise in practice and tends to suffer from poor detection performance under low signal-to-noise ratio (SNR) []. In addition, the selection of model parameters in the WT method depends largely on experience and there is a relatively high false-alarm rate (FAR) in the detection results []. The HHT approach has high computational complexity and poor real-time performance, and the contamination of the background noise will reduce the signal parsing effect []. Despite their solid theory basis, there are specific application conditions and performance restrictions for the basic UDT methods.
Concerning the SFM methods, signal feature engineering is commonly combined with machine learning models for automatic magnetic anomaly classification [,]. Recently, there is a research trend to use deep learning models to perform simultaneous feature extraction and anomaly classification with guidance from labelled samples []. These intelligent methods usually require a large amount of labelled data for model training, which however are not easily accessible in many real-world problems. In fact, the small sample and sample imbalance problems are quite common in practical application scenarios, where the acquisition and annotation of real target samples are expensive but there are plenty of cheap and unlabeled background noise samples available. This is quite common for underwater passive magnetic detection platforms for long-term marine surveillance tasks []. In order to adapt to the complex real marine conditions, there is an urgent need to develop advanced algorithms that can perform self-supervised learning on the massive unlabeled magnetic noise data for target magnetic anomaly detection.
In recent years, the cross integration of deep learning techniques with many disciplinary fields has demonstrated great potential and received widespread attention. Among the various deep neural network structures, denoising autoencoder (DAE) can be used for the automatic denoising and intrinsic feature learning of one-dimensional data. Through hierarchical encoding and decoding processes, DAE can learn complex noise distributions for robust data denoising and recovery. For the marine magnetic sensing environment, geomagnetic field is the fundamental data observation source and marine magnetic interference field can be considered as superimposed noise. Correspondingly, the appearance of ferromagnetic targets near the measurement site will change the distribution characteristic of original marine magnetic interference noise. Thus, it is possible to design a DAE network for marine magnetic noise learning and geomagnetic field recovery under idle measurement periods. When ferromagnetic targets appear during the monitoring stage, denoising and recovery capability of the above learned network will be severely degraded. In this way, the learned network is equipped with denoising capability for marine magnetic noise, but lacks modeling capability for target magnetic anomaly signal. Meanwhile, sparse constraint is imposed on the hidden layer of the network to learn compact feature representations for the marine magnetic noise data. Redundancy existing in marine magnetic noise data is effectively compressed to avoid overfitting of the network and learn a more discriminative feature space. Towards this end, we can perform anomaly signal discrimination based on the reconstruction error of the network for online ferromagnetic target detection. The entire detection process works in a self-supervised manner with no need for labelled data and thus is more suited for practical marine application scenarios. The overall implementation process of the proposed marine target magnetic anomaly detection scheme is shown in Figure 1.
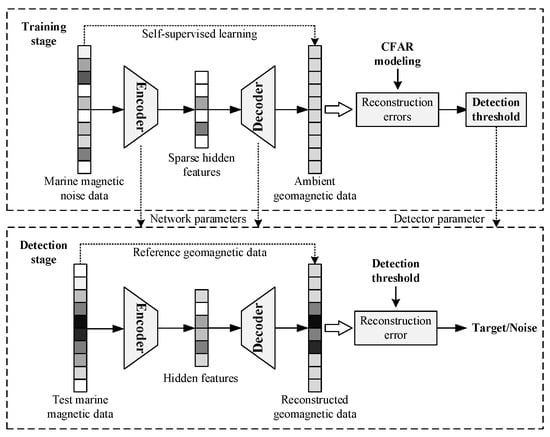
Figure 1.
Overall implementation process of the proposed marine target magnetic anomaly detection scheme. The different colored boxes in the data represent sample points with different magnetic intensities.
The main innovations and contributions of this paper are summarized as follows. First, we change our focus from target signal to background noise and propose to explore the abundant and fully realistic marine magnetic noise for target magnetic anomaly detection. A sparse denoising autoencoder (SDAE) network is specifically designed for self-supervised marine magnetic noise learning and generative target anomaly signal discrimination. Different from previous detection paradigms, the proposed method is a single-edge detector, which only requires unlabeled noise samples for model training. Second, the redundant property of marine magnetic noise data is theoretically modeled by applying sparse constraint to the hidden layer neurons of the SDAE network. A generalized loss function is designed for simultaneous output reconstruction error and hidden activation degree minimization, through which compact semantic features can be learned for reliable target detection. Compared with traditional feature engineering, our learned sparse deep features are more representative and discriminative, favoring weak anomaly signal detection. Third, different from previous discriminative detection models, reconstruction error of this designed generative deep neural network is naturally used as the statistical decision criteria to distinguish targets from noise with constant false alarm rate (CFAR) based optimal thresholding segmentation algorithm. The overall decision process is driven by background noise and physical rule, which is free from manual interference and data annotation, and thus more suited for the marine magnetic surveillance task here. Finally, we conducted experimental tests on real sea trial datasets to verify the effectiveness of the proposed method and compared it with seven state-of-the-art MAD methods on four numerical indexes. Our method achieves superior detection performance over the other seven state-of-the-art MAD methods in terms of both speed and accuracy.
2. Self-Supervised Marine Noise Learning Method
2.1. Self-Supervised Noise Learning Network Design
Marine magnetic field noise is affected both by the natural environment and human activities, such as the tide, geomagnetic diurnal change, maritime shipping, etc. Meanwhile, there are complex nonlinear interactions and coupling effects among the various random interference factors. As a result of this, magnetic noise in real marine environment is a complex random process superimposed with many random subprocesses, which is difficult to accurately describe with traditional probabilistic models. The complex distribution of time-varying marine magnetic noise brings severe challenges for their mathematical modeling and limits the target magnetic anomaly detection performance under cluttered marine environment []. Therefore, it is of great significance to explore an effective marine magnetic noise learning scheme for dynamic environmental anomaly sensing.
In practice, the marine observation data collected by the magnetometers are the compound result of different magnetic field components, including the ambient geomagnetic (AG) field, target anomaly (TA) field, and the background noise (BN) field []. For the underwater stationary observation platforms, the AG component can be approximately considered as a steady process during a very short time interval. The BN component is superimposed on the basic AG component to form the measured magnetic field when in the absence of targets. Also, the presence of ferromagnetic targets near the magnetometers will introduce extra TA component into the measured results. Thus, the collected data by the magnetometers in practice can be expressed in the following form.
where, is the collected magnetic data, , , and are, respectively, the data components from ambient geomagnetic, background noise, and target anomaly fields. An intuitive illustration of the magnetic fields measured by an underwater stationary sensor platform in presence of a ferromagnetic target is shown in Figure 2.
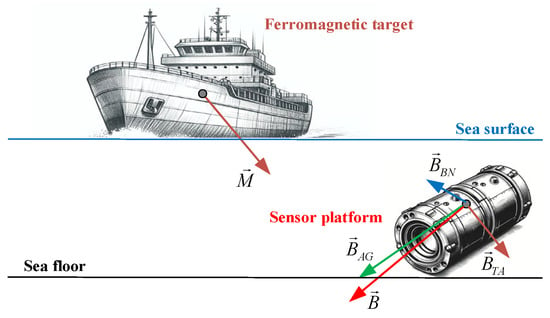
Figure 2.
Illustration of the magnetic fields measured by an underwater stationary sensor platform in the presence of a ferromagnetic target.
For most of the observation periods, the magnetometer data reveal the quiet marine environment without target activities, and thus are the composite results of and components. Denoting the collected magnetic data in this situation as , we can derive the follow mathematical expression.
where, is the norm of data vector, represents the vector inner product operation, and is the unit directional vector (direction cosine) of the geomagnetic field []. The second term on the right side of the equation represents the projection component of along the geomagnetic field direction, which in practice is much smaller than the first term. It can be viewed as superimposed interference noise on the overall geomagnetic trend and may be eliminated by effective denoising algorithms for ambient geomagnetic component recovery [].
As mentioned above, probabilistic distribution of the time-varying marine magnetic noise is quite complicated and cannot be accurately described with explicit linear analytical models. In practice, it is desired that the denoising models should possess nonlinear representation and adaptive learning capability to the constantly changing marine physical field environment. In recent years, deep learning (DL) theories have shown great advantages and potentials for many complex real-world problems modeling. Among the various deep neural network structures, denoising autoencoder is specifically designed for complex noise learning and corrupted signal recovery. Through encoding and decoding processes, the dependency relationship between stable network structure and data distribution property can be effectively learned for adaptive noise removal. Inspired by this, in this paper we propose to learn the marine magnetic noise with denoising autoencoder for target magnetic anomaly detection in a self-supervised manner. Meanwhile, to reduce the redundancy of marine magnetic noise data for intrinsic feature mining, sparse learning mechanism is incorporated into the hidden layer of the network. The general structure of the designed sparse denoising autoencoder network for marine magnetic noise learning is shown in Figure 3.
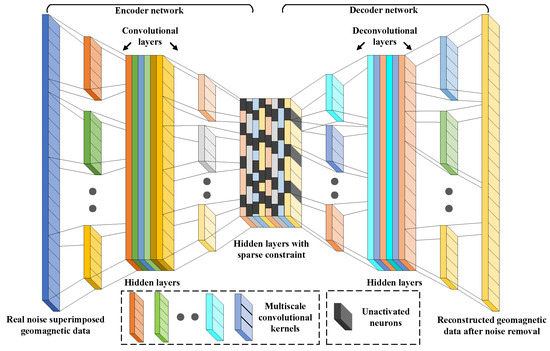
Figure 3.
General network structure of the designed sparse denoising autoencoder for marine magnetic noise learning.
From the feature learning perspective, there is huge redundancy in the marine magnetic noise data, which should be compressed for compact cognitive feature extraction. Towards this end, we force part of the neurons in the last layer of the encoder network not to be activated by introducing sparse constraint condition into the learning process. Through this sparse coding process, the high-dimensional time series data from the magnetometer can be projected into a compact low-dimensional subspace for intrinsic feature mining. The designed lightweight sparse denoising autoencoder network takes noisy marine magnetic data as its input and intends to recover the ambient geomagnetic data as its output. For an underwater stationary sensor platform, the geomagnetic field around it possesses short-time invariance property and can be approximately estimated from the observed noisy magnetic data. Therefore, the designed SDAE network can learn denoising capacity from the noisy marine magnetic data without external supervision information. It possesses both redundancy reduction and noise perception capabilities, and thus is well suited for this specific application scenario. Specifically, the complex distribution of real marine magnetic noise can be accurately learned for efficient noise removal and target anomaly detection.
Given an original noisy marine magnetic data (n is the number of sampling points), it successively passes through the hierarchical and multiscale convolutional kernels for intrinsic feature extraction. The corresponding encoder network output (h is the number of neurons in the last layer of the encoder network) is a sparse feature vector with a few nonzero elements in it. During this forward feature mapping stage, the redundancy in marine magnetic noise data is effectively compressed by the enforced sparse constraint. Followed by this, the sparse hidden representation is used as the input of the decoder network for ambient geomagnetic data reconstruction through the hierarchical and multiscale deconvolutional kernels. Accordingly, the final decoder network output is the recovered ambient geomagnetic data that shares the same size with that of the original input. In the designed network structure, the one-dimensional convolution operation can capture the dependency relationship of temporal data, and adopting rectified linear unit (ReLU) activation function in the neurons can better learn the nonlinear patterns of marine magnetic noise. The overall feature learning and data reconstruction process is fully data driven and does not require manual interference or external knowledge.
To better illustrate the internal working mechanism of the designed SDAE network, we show the output waveforms of the various layers on a typical marine magnetic noise sequence in Figure 4. It can be observed that the multiscale convolution kernels can achieve the extraction of signal features at multiple scales, and the addition of sparse constraint helps to retain only the key feature information in the hidden layer. Also, through hierarchical asymmetric feature transformations, noise in the input marine magnetic data can be effectively filtered for ambient geomagnetic data recovery. The complex distribution of marine magnetic noise can be learned in an implicit manner to obtain environmental adaptability of the network model. Compared with supervised MAD methods that require a large amount of labelled data for model training, the proposed method works in a self-supervised manner, which avoids the need for expensive data labeling and removes the barrier towards practical use. Only a large amount of unlabeled noisy data is needed for network training, which can be easily available in real-world marine applications. It is also worth mentioning that the designed network can learn the intrinsic law of real marine magnetic noise and has good generalization capability and environmental adaptability.
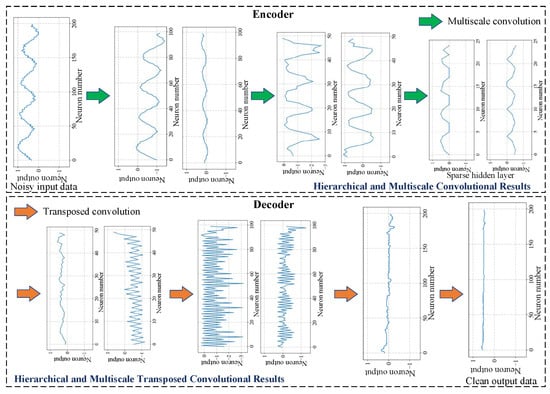
Figure 4.
Illustration of the output waveforms of various layers in the designed network on a typical marine magnetic noise sequence.
2.2. Sparsity Constrained Optimization Algorithm Design
Due to the randomness of interference sources, the marine magnetic noise data contain redundant and repetitive patterns that do not carry truly meaningful information. If the data are directly fitted with deep neural network (DNN), the resulting model easily tends to capture the local patterns of the redundant random noise. As a result of this, it is unlikely for the DNN to learn meaningful and discriminative features for robust marine magnetic noise data modeling. From the machine learning perspective, this situation may lead to serious overfitting problem and poor generalization ability of the model. As an important biological cognitive rule, sparsity is considered as an effective way to compress data redundancy for compact feature extraction. By enforcing sparse constraint, we can force the feature extraction units of the network to be sensitive only to a small proportion of the data, avoiding the handling of massive redundancy. It is therefore introduced here to help the DAE network to focus on meaningful feature patterns and prevent overfitting for repeated random noise.
Following the principles of reconstruction and generalization, we first build the augmented loss function for the designed SDAE network. The overall loss function is composed of two independent parts, i.e., the reconstruction error (RE) term and sparsity penalty (SP) term. Specifically, the former is used to evaluate the closeness degree between the reconstructed data and the expected output data, and the latter is used to quantize the sparsity degree of the network latent representations. The above two terms are combined through weighted summation to form the final augmented loss function for network parameter optimization. Given the weight and bias parameters in the network and , we use the following objective function for network parameter learning.
where, and are, respectively, the reconstruction error and sparsity penalty terms, and is the weighting coefficient used to balance between the two terms. Specifically, the RE term is used to evaluate the network denoising effect by calculating the mean square error (MSE) between the decoder output and expected output.
where, m is the number of data samples used for network training, and are respectively the i-th elements of the decoder output and expected output on the j-th data sample. Meanwhile, the SP term is designed to measure the compactness of the learned network latent features, which has the following expression form.
where, is the Kullback–Leibler (KL) divergence. It is used to penalize network parameters with corresponding activation degrees deviating from the given sparsity ratio . is the average activation degree of the i-th neuron in the last layer of encoder network, which is defined as follows.
where, is the output of the i-th neuron on the j-th data sample and is the sigmoid function used to project the neuron output into (0, 1). The closer the output value of the sigmoid function is to 0.5, the closer the corresponding neuron output is to 0 (indicating an unactivated neuron). Thus, the sparsity ratio is set to be 0.5 in practice for compact and concise feature learning of marine magnetic noise data.
In the above formulas, KL divergence can be used to effectively measure the distance between the given sparsity ratio and average activation degree distribution of the encoder output layer. Since there is a definite theoretical upper bound for its range of values, it is beneficial for loss function design and network parameter learning. Meanwhile, using KL divergence as the penalty function is numerically stable and not prone to gradient vanishing and exploding, which is quite crucial for the optimization of hidden layer sparsity. By introducing sparsity penalty into the optimization objective, we can prevent the designed network from over parameterization and overfitting. Intrinsic features of the marine magnetic noise data can be extracted with fewer hidden units to accurately reconstruct the ambient geomagnetic data. Solutions with excessive complexity can be suppressed in the parameter space so as to improve the model generalization capability for newly emerging data. As a result of this, more discriminative feature patterns can be learned from the noisy marine magnetic data for the denoising and detection tasks under complex interference environment.
Till now, we can train the designed SDAE network by minimizing the objective function with iterative optimization algorithm. Specifically, the adaptive moment (Adam) estimation is used as the optimizer for efficient network structure and parameter learning. Finally, to observe the algorithm convergence property and model generalization capability, we evaluate the learning effect of our method on the built training and validation datasets. Real marine magnetic noise data are used for this purpose and the number of samples in the training and validation datasets is sufficient for the network learning and evaluation. Loss curves of the designed network model on the above two datasets during the learning processes are shown in Figure 5 for intuitive performance analysis. As can be seen from the results, loss values of the designed network decrease gradually along with the iteration process and finally converge to stable states on both datasets. This sufficiently confirms the good convergence and generalization capability of the designed network model on marine magnetic noise datasets. Therefore, it can be expected to get satisfactory noise learning effect to facilitate the denoising and target anomaly detection of marine magnetic data. Below, we will introduce how to use the trained network model for generative target magnetic anomaly detection.
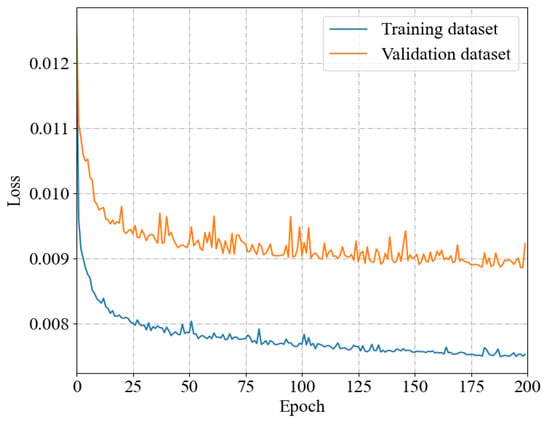
Figure 5.
Loss curves of the designed network model on the training and validation datasets.
2.3. Reconstruction-Error-Based Anomaly Discrimination
After the training stage, we can obtain a deep generative network model for the recovery of ambient geomagnetic data from the collected noisy marine magnetic data. However, this generative network model does not yet possess the ability to directly discriminate target magnetic anomaly signal from background noise. Since we develop a self-supervised way to build a single-edge detector, only the distribution characteristic of marine magnetic noise (rather than the target magnetic anomaly signal) is learned by the network model. Therefore, it is reasonable to believe that reconstruction error of the network model for target signal will be much greater than that of the marine noise. Based on this unique property, we further propose to use the network reconstruction error as a statistical decision criteria for generative target magnetic anomaly detection. In this paper, we adopt the idea of constant false alarm rate (CFAR) to find a theoretically optimal detection threshold for the discrimination of target signal and marine noise.
Given the trained network model, we first calculate the reconstruction errors of the samples in the validation dataset, which are denoted as ( is the sample number in the validation dataset). Under a preset false alarm rate , the optimal detection threshold can be determined from the following integral upper limit equation.
where, and are, respectively, the mean and standard deviation of the elements in . Since the integral upper limit function on the right side of the equation is monotonically increasing, in practice we use the bisection method to search for the optimal solution in an efficient manner. By modeling the reconstruction error of the generative network as a statistical variable, we may estimate its distribution parameters with respect to marine magnetic noise from the validation dataset. Based on the estimated distribution parameters, we can deduce an optimal detection threshold to discriminate target magnetic anomaly signal under a constant false alarm rate. For a newly collected test sample , we can determine whether there exists a target anomaly signal in it according to the following rule.
where, is the reconstruction error of on the trained generative network model.
Due to its single-edge characteristic, the trained generative network is only responsible for the denoising and recovery of ambient geomagnetic data in the absence of targets. The emergence of targets in the surrounding will destroy the data distribution and correspondingly the network may lose denoising and recovery capability. Reconstruction error of the network is a natural reflection of this degradation process and thus can be used as a reliable statistical variable for weak target magnetic anomaly perception. It is worth mentioning that the above data-driven anomaly discrimination scheme is adaptive to the complex marine noise environment and therefore has much stronger practicability. In the following, we will give experimental results of the proposed method on real marine magnetic data for comprehensive performance analysis and evaluation.
3. Experimental Results and Discussion
In this section, we will first describe the marine experimental scene and magnetic data acquisition process in detail. Followed by this, detection results of the proposed approach along with other 7 state-of-the-art MAD methods on the collected marine magnetic dataset will be given for comprehensive performance comparison and analysis. Meanwhile, we will conduct ablation study to verify the effectiveness of the designed sparse deep learning mechanism for massive redundant marine magnetic data modeling. The differences in reconstruction effect and feature extraction will be specifically investigated to gain deeper understanding of the model performance. Finally, we will build simulation datasets to test the target detection performance of the various MAD methods under different SNRs.
3.1. Experimental Scene and Data Acquisition
To verify the effectiveness of the proposed approach, we conducted real sea trials near Sanya in the South China Sea. Experimental scenario of the sea trial is shown in Figure 6 for intuitive spatial layout observation. A watertight platform was deployed at the sea floor (with a water depth of about 40 m) in advance, which carried a fluxgate sensor in it for marine magnetic data collection. In practice, sampling frequency of the fluxgate sensor was set to 1 Hz, and its sensitivity and measurement noise are, respectively, 10 μT/V and 0.1 nT. Meanwhile, a surface ferromagnetic ship sailed through the underwater measurement platform from different abeam distances at a speed of 8 knots, with navigation routes along the east–west direction. Each navigation route corresponds to a specific abeam distance ranging from −100 m to 100 m, which constitutes a certain CPA under this measurement scene. During the experiments, the test sea area was relatively quiet with no interference from other ferromagnetic objects. Both target magnetic anomaly data during navigation processes and a large amount of marine magnetic noise data during idle measurement periods were collected for model performance evaluation and analysis.
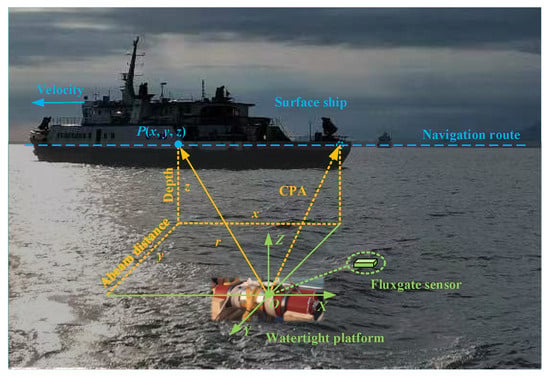
Figure 6.
Illustration of the experimental scenario for real sea trials. A fluxgate sensor is carried on the underwater watertight platform for transboundary detection of surface ship magnetic anomaly.
Under the above settings, we conducted voyage experiments to collect target magnetic anomaly data as well as marine magnetic noise data for performance verification of the proposed method. Due to the varying target abeam distances and marine noise interferences as well as the underwater platform sway, the obtained target magnetic anomaly data are with different SNRs. This provides a relatively complete dataset for target detection performance evaluation under practical application conditions. Some of the collected typical target samples with different SNRs are shown in Figure 7 for visual observation. As can be seen, the quality of the collected data in practice is severely affected by target magnetic field attenuation and complex marine environmental noise. It is thus required that advanced models be designed that are robust to marine magnetic noise for accurate target anomaly detection.
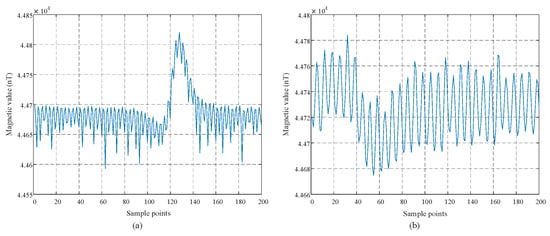
Figure 7.
Typical target samples with different SNRs collected by the underwater platform during the voyage experiments. (a,b) are two real target samples collected under different conditions.
As mentioned above, real target samples are quite rare compared with the massive noise samples, leading to a small sample and sample imbalance problem in practice. It is therefore a challenging problem to design advanced learning models in this situation to achieve satisfactory target magnetic anomaly detection performance. In this paper, the massive marine magnetic noise data are fully explored to train a self-supervised learning-based deep generative model for adaptive noise filtering and target anomaly detection. Specifically, the trained deep generative model can be used to discriminate target anomaly signal from cluttered background noise for detection performance test. Towards this end, we established a marine magnetic detection dataset that contains real noise samples for model training and target anomaly samples for model performance verification. Detailed information on the composition of the marine magnetic detection dataset is summarized in Table 1.

Table 1.
Composition of the marine magnetic detection dataset.
3.2. Denoising and Detection Performance Evaluation
Since the proposed method adopts a denoising and reconstruction idea to detect the target magnetic anomaly signal, both the denoising and detection results are obtained for comprehensive performance evaluation. Specifically, the aforementioned validation and test datasets are, respectively, used to check the model denoising and detection performance. Both the qualitative visualization results and quantitative numerical indexes are given for thorough performance analysis. Also, we compare our approach with seven other state-of-the-art MAD methods in terms of both accuracy and speed to verify its superiority. Through this, we wish to show the advantages and potentials of self-supervised noise learning for magnetic anomaly detection under real marine application scenarios. The experiments below are conducted on a laptop computer with Windows 11 operating system (version 23H2) and an Intel i7-13700H CPU with 16 GB RAM (Intel Corporation, Santa Clara, CA, USA).
In practice, the designed network model is built with Python 3.8 under the PyTorch 2.0.1 framework. We first segment the collected magnetic data sequence into fragments and save all the samples (each with 200 sampling points) in CSV format. We traverse the saved CSV files and read them as Pandas DataFrame, and then call the data preprocessing function to transform the samples into PyTorch tensor form. Followed by this, we instantiate the dataset class and encapsulate the dataset for later network training. Till now, we can set learning parameters like batch size to form an iterator for the model to perform batch data training. Finally, the trained model is saved as .pth format file for the next step of reconstruction error based magnetic anomaly detection task. Concerning the two parameters and in our model, they are, respectively, set to be 0.9 and 4.6% during the experiments for achieving satisfactory detection performance. Note that we conducted controlled experiments by, respectively, varying the above two parameters within their reasonable value ranges, and choose the values with the best detection performance as the final parameter settings.
Figure 8 shows the typical denoising reconstruction results of the trained SDAE network on the validation dataset. The two groups of marine magnetic data are, respectively, collected by the aforementioned underwater fluxgate sensor platform. As can be seen from the results, the marine background noise can be greatly suppressed to well reconstruct the ambient geomagnetic field with the trained network. By learning from massive noise data, the designed network is able to accurately model the complex distributions of marine magnetic noise for adaptive environmental anomaly sensing. It provides a stable background prior support for the enhanced sensing of weak target magnetic anomaly signal under noisy conditions. Since the noise learning process is performed in a self-supervised manner with no label information needed, the proposed method is quite suitable for practical underwater surveillance applications. To quantitatively evaluate the noise suppression effect, we calculate the average peak-to-peak value (VPP) of the samples before and after the denoising on the validation dataset. According to the statistical results, the average VPP on the validation dataset after denoising with SDAE is reduced by 85.2%, showing a significant improvement in data quality.
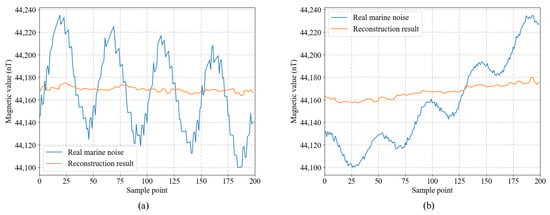
Figure 8.
Denoising reconstruction results of the trained SDAE network on the validation dataset. (a) and (b) are, respectively, the marine magnetic data collected by the underwater fluxgate sensor platform.
Figure 9 shows the typical denoising reconstruction results of the trained SDAE network for target samples on the test dataset. The two groups of target magnetic data are, respectively, collected by the aforementioned underwater fluxgate sensor platform. As can be seen from the results, the trained network has degraded noise suppression and ambient geomagnetic field reconstruction effects for the target magnetic data. This is consistent with our previous assumption on the problem that the existence of target signals in the data will destroy the data distribution and lead to large reconstruction errors. As we see, this unique property of our designed network model is crucial for accomplishing self-supervised marine noise learning based generative target magnetic anomaly detection tasks.
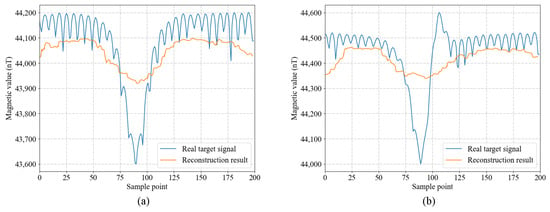
Figure 9.
Denoising reconstruction results of the trained SDAE network for target samples on the test dataset. (a) and (b) are, respectively, the target magnetic data collected by the underwater fluxgate sensor platform.
After the end-to-end self-supervised learning, the designed SDAE network successfully learns the global and local distribution characteristics of marine magnetic noise. It can effectively suppress the complex marine background noise in the collected magnetic data for enhanced target anomaly detection. Based on this, we adopt a reconstruction error based decision criterion to accomplish the discrimination of target anomaly signals from cluttered background noise. Meanwhile, 7 classical MAD methods, including OBF, MED, SVM [], DeepMAD [], IForest [], SR [], and 1D CNN [], are implemented and used for performance comparison with our method on the test dataset. As commonly used evaluation metrics, probability of detection (Pd), FAR, and accuracy are used for quantitative analysis of the detection performance. For the samples in the test dataset, they are successively fed into the trained SDAE network for denoising reconstruction and their reconstruction errors are compared with the CFAR detection threshold to obtain the corresponding classification labels. In addition, the running times of all the detectors on the test dataset are calculated for detection efficiency analysis.
In Table 2, we show the numerical evaluation results of all the eight MAD detectors on the test dataset for performance comparison. It is worth noting that the OBF and MED detectors project the original data into the energy and entropy domains and further interpretation is needed to obtain the final detection results. Also, OBF is a target-oriented detector that requires knowledge of the target distance information in advance, and thus it is only applicable to performance evaluation of target samples. As can be seen from the results, our method achieves higher Pd and accuracy as well as much lower FAR than the other seven detectors. In terms of the running speed, it is much faster than the other counterparts. This further confirms the performance advantages and application potentials of our method for target MAD under cluttered marine environment.

Table 2.
Numerical evaluation results of the magnetic anomaly detectors on the test dataset.
In addition, to gain deeper understanding for the UDT methods, we observe the projection results of OBF and MED for marine magnetic data in the energy and entropy domains. Shown in Figure 10 and Figure 11 are, respectively, the domain transformation results of OBF and MED for the collected noisy target and pure noise samples.
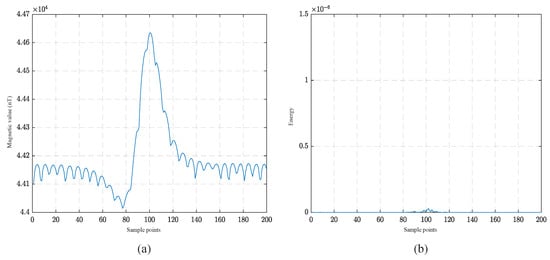
Figure 10.
Projection result of OBF for a noisy target sample in the energy domain. (a) is the noisy target sample data to be detected and (b) is its energy function result obtained by OBF.
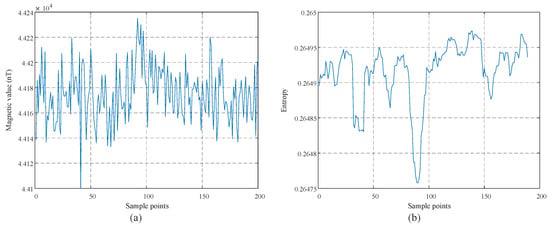
Figure 11.
Projection result of MED for a pure noise sample in the entropy domain. (a,b) are, respectively, the pure noise sample and its projection result in the entropy domain.
As can be seen, the transformed energy domain feature of OBF detector for the noisy target sample is relatively weak, which may cause missing detections in practice. This is mainly due to the reason that OBF detector tends to lack robustness to the non-Gaussian distributed marine magnetic noise. Also, spike fragments in the pure noise sample are unexpectedly amplified in the transformed entropy domain feature of MED, which may induce false alarms in practice. The reason for this issue is that MED is quite likely to lose its efficiency when facing strong marine magnetic noise. Thus, the UDT methods like OBF and MED may not fully capture the intrinsic features of strong non-Gaussian marine magnetic noise for reliable target MAD. Since our method adopts sparse deep modeling scheme, it is able to learn the complex distributions of marine magnetic noise for efficient target magnetic anomaly sensing.
3.3. Ablation Study and Model Verification
Since sparsity is introduced as a key element for redundant marine magnetic noise learning in our model, here we conduct ablation study experiments to further verify its effectiveness. Specifically, we remove the sparsity penalty term in the original objective function and retrain the network to get a simplified model called DAE. On the basis of this, we use DAE to perform denoising and detection tasks on the validation and test datasets, and compare its performance with that of the original SDAE. Moreover, to gain deeper insights into the model behavior, we draw the learned channel features in the output layer of the encoder network for visual analysis. Figure 12 shows the output channel features of the DAE and SDAE encoder networks on a typical marine magnetic noise sample.
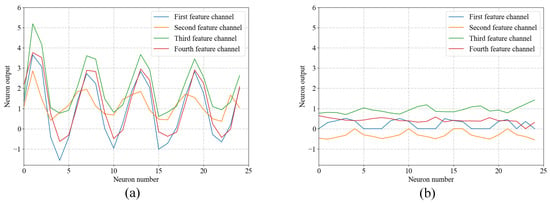
Figure 12.
Output channel features of the encoder networks on a marine magnetic noise sample. (a) and (b) are, respectively, the results of DAE and SDAE networks.
It can be observed that outputs of some neurons in the last layer of encoder network tend to approach zero after enforcing sparse constraint to the network. These neurons can be considered as unactivated during the feature extraction process and thus reduce the latent feature space dimension. On the contrary, there is a high correlation among the feature channels of DAE, indicating a large redundancy in the learned features. As a result of this, the learned features in different channels of SDAE are more informative than that of DAE. Therefore, better feature learning effects can be achieved by SDAE for the compact representation of redundant marine magnetic noise data, which will contribute to the improvement of model denoising and detection capability in practice.
Concerning the denoising result, the average VPP on the validation dataset after denoising with DAE is reduced by 81.6%, which is lower than that of SDAE as mentioned above. This implies that sparse feature learning can lead to better denoising effect for marine magnetic data. Besides, we show the numerical evaluation results of DAE and SDAE on the test dataset in Table 3 for detection performance comparison. As can be seen, SDAE achieves higher target detection accuracy with less time consumption, showing better adaptability to this problem. The meaning of sparse constraint mainly comes from two aspects, i.e., finding a discriminative feature space and building a compact network structure. For this reason, the SDAE network model is better suited to be a MAD detector for real-time target detection from marine magnetic data. In general, we provide a novel noise learning perspective for magnetic anomaly detector design under sample deficiency situations, which has broad application prospects in related fields.

Table 3.
Numerical evaluation results of DAE and SDAE networks on the test dataset.
In addition, we can find that there are obvious noises with certain frequency bands in the typical target samples of Figure 7. As a part of real measurement noises, these kinds of periodic noises may distort the target signal waveforms and bring extra challenges to the various detectors. Therefore, we conduct ablation study experiments to further observe their influence on the detector performance. Specifically, we first analyze their frequency bands and then remove them from the data through filtering techniques. The spectrum diagrams of the typical target samples are shown in Figure 13. As can be seen from the results, the frequency bands of the noises are not necessarily the same, but are all much higher than that of the target anomaly signals. Towards this end, we design a low-pass filter to remove these noises from the original data and the filtered results are shown in Figure 14 for visual observation. We can see that the quality of the data after filtering is improved, which may favor the succeeding detection task.
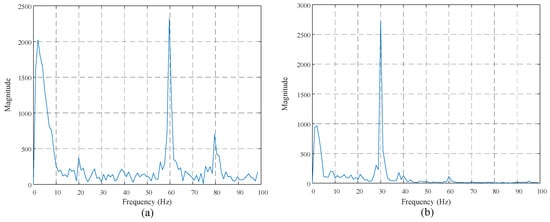
Figure 13.
Spectrum diagrams of the typical target samples in Figure 7. (a) and (b) are respectively the spectrum diagrams of the two real target samples.
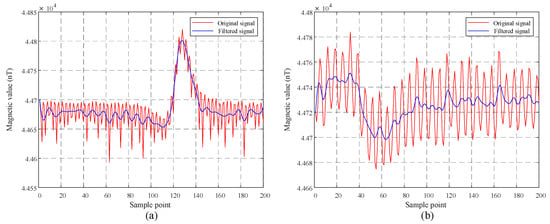
Figure 14.
Low-pass filtered results of the typical target samples in Figure 7. (a) and (b) are respectively the low-pass filtered results of the two real target samples.
Till now, the filtered real target samples in the test dataset are used to evaluate the detection performance of the various detectors. According to the experimental results, the Pd indexes of OBF, SVM, and DeepMAD are, respectively, increased to 87.01%, 84.42%, and 89.61% after filter processing, while no change is observed for the Pd indexes of the other 5 detectors. This means that removing these kinds of periodic noises will help to improve the magnetic anomaly detection performance of noise-sensitive detectors like OBF, SVM, and DeepMAD in practice.
3.4. Performance Assessment under Different SNRs
Since the SNRs of the real collected noisy target magnetic data are not fully controllable and readily known in practice, it is therefore necessary to construct simulated noisy target magnetic dataset for performance assessment of the various detectors under different SNRs. Towards this end, we use simulated target anomaly signal and real marine magnetic noise to compose noisy target magnetic data of different SNRs. Given the peak-to-peak values of target anomaly signal and marine magnetic noise , the SNR of their composited noisy target magnetic data can be determined as follows.
where, k is the amplification factor for the marine magnetic noise. To control the SNR of the composited noisy target magnetic data, we first amplify the marine magnetic noise by an appropriate factor and then add the amplified marine magnetic noise to the simulated target anomaly signal. The amplification factor k is chosen such that the above equation should be strictly satisfied under a given SNR value.
In practice, we use magnetic dipole model to generate simulated target anomaly signal according to the experimental settings in the aforementioned real sea trial. By varying the abeam distance from −100 m to 100 m with a span of 10 m, we can generate a set of 21 simulated target magnetic anomaly signals. Meanwhile, we randomly select a set of 30 real marine magnetic noise samples collected from the sea trial for noise addition. Under a given SNR value, we generate a total of 630 composited noisy target magnetic data by combining every two data from the two sets with an appropriate amplification factor. Meanwhile, 16 typical SNR values between −10 dB and 5 dB are designed to assess the detector behaviors in relatively challenging situations. In this way, we build a simulated noisy target magnetic dataset containing 16 subsets for comprehensive detection performance evaluation of the various detectors.
In Figure 15, we show a typical simulated target anomaly signal and a real marine magnetic noise, and their composited noisy target magnetic data under 4 different SNR values (5 dB, 0 dB, −5 dB, and −10 dB). As can be observed from the results, target anomaly signal is gradually buried in marine magnetic noise along with the decrease in data SNR. This degradation in data quality will bring severe challenges to the MAD methods. To observe the detection performance of the various detectors under different SNRs, we show their Pd indexes on the built simulated noisy target magnetic dataset in Figure 16. Note that the numerical indexes in each line of Figure 16 are the statistical results of the corresponding detector on the various subsets. We can see that all the methods see a performance drop with the decrease in data SNR, indicating a relatively high dependency of detection performance on the data quality. In general, UDT methods are more sensitive to data SNR than SFM methods, which further proves that SFM methods are more robust to noise. Compared with the other counterparts, our method achieves higher Pd indexes on all the 16 subsets, showing more robust marine target MAD performance under low data SNRs. With the designed sparse deep representation learning model, more intrinsic features of marine magnetic noise can be extracted for reliable target MAD under complex interference environment.
Figure 15.
Composited noisy target magnetic data under 4 different SNR values. (a) is a typical simulated target anomaly signal, (b) is a real marine magnetic noise, and from (c–f) are their composited noisy target magnetic data with SNRs being, respectively, 5 dB, 0 dB, −5 dB, and −10 dB.
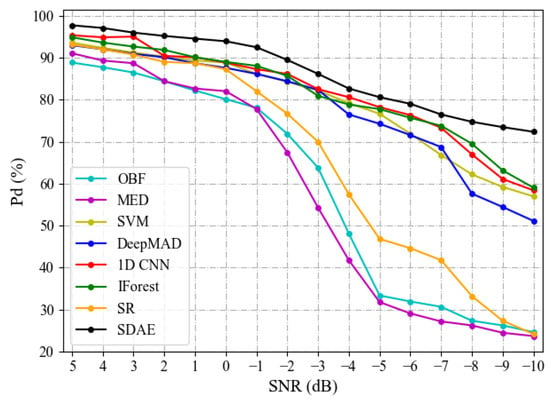
Figure 16.
Probability of detection indexes of the various detectors under different SNRs.
4. Conclusions
For covert underwater application scenarios, marine magnetic noise interference forms the background bases for target anomaly signal discovery and presents an inevitable obstructive factor for the accurate sensing of a target magnetic anomaly signal. Therefore, there is an urgent need to learn from the massive collected marine magnetic noise data for intrinsic feature extraction and noise interference suppression, so as to facilitate long-distance target magnetic anomaly detection tasks. However, the complex properties of marine magnetic noise limit the usability of traditional mathematical or signal analysis tools and make the design of learning-based detection models even more difficult. Motivated by this, in this paper we propose a self-supervised learning based sparse denoising autoencoder network for marine magnetic noise modeling and target anomaly signal detection. Different from previous target-oriented or data-driven methods, the proposed approach only uses the massive unlabeled marine magnetic noise data for model construction and is not dependent on target data or manual labeling. Specifically, the trained network model can learn the complex distributions of marine magnetic noise for robust geomagnetic field recovery from collected noisy magnetic data. On the basis of this, the network reconstruction error is used as a reliable cue for target anomaly signal discrimination from cluttered marine background noise. Finally, we conduct real sea trial experiments to collect marine magnetic data for performance verification of the proposed approach. It achieves superior performance over the other seven state-of-the-art MAD methods in terms of both detection accuracy and speed, showing great potential for real-world marine applications.
Author Contributions
Conceptualization, S.W. and X.Z.; methodology, S.W., X.Z. and B.L.; software, X.Z.; validation, S.W. and B.L.; formal analysis, X.Z.; investigation, S.W. and X.Z.; resources, B.L. and S.W.; data curation, Y.Z. and H.Y.; writing—original draft preparation, S.W. and X.Z.; writing—review and editing, S.W., X.Z., Y.Z., H.Y. and B.L.; visualization, Y.Z. and H.Y.; supervision, S.W. and B.L.; project administration, B.L.; funding acquisition, S.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (61906157), the China Postdoctoral Science Foundation (BX20190282; 2020M673490), the Young Talent Fund of Xi’an Association for Science and Technology (095920221371), and the Fundamental Research Funds for the Central Universities (31020180QD094).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Liu, H.; Zhang, X.L.; Dong, H.B.; Liu, Z.; Hu, X.Y. Theories, applications, and expectations for magnetic anomaly detection technology: A review. IEEE Sens. J. 2023, 23, 17868–17882. [Google Scholar] [CrossRef]
- Jin, H.H.; Guo, J.; Wang, H.B.; Zhuang, Z.H.; Qin, J.; Wang, T.L. Magnetic anomaly detection and localization using orthogonal basis of magnetic tensor contraction. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5944–5954. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, S.W.; Guo, Y.G.; Wu, Y.P.; Wang, Y.; Zhao, J. Joint use of scalar and vector magnetometers for underwater magnetic target localization. IEEE Geosci. Remote Sens. Lett. 2023, 20, 7505305. [Google Scholar] [CrossRef]
- Liu, G.G.; Zhang, Y.Z.; Wang, C.; Li, Q.; Li, F.; Liu, W.Y. A new magnetic target localization method based on two-point magnetic gradient tensor. Remote Sens. 2022, 14, 6088. [Google Scholar] [CrossRef]
- Ou, J.D.; Qiu, J.; Xie, D.; Wang, Z.; Du, J.Z.; Chang, Q.J. Research on the moving magnetic object recognition method based on magnetic signature waveform. IEEE Trans. Magn. 2022, 58, 6500108. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Chen, R.; Deng, T.Y.; Wang, Y.H.; Di, W.N.; Luo, H.S.; Han, T. Magnetic anomaly detection using three-axis magnetoelectric sensors based on the hybridization of particle swarm optimization and simulated annealing algorithm. IEEE Sens. J. 2022, 22, 3686–3694. [Google Scholar] [CrossRef]
- Liu, W.D.; Li, L.F.; Li, L.; Jiao, H.F.; Qu, J.Q.; Sun, G.W. Velocity estimation of underwater vehicle based on abnormal magnetic field waveform. IEEE Sens. J. 2024, 24, 367–376. [Google Scholar] [CrossRef]
- Sithiravel, R.; Balaji, B.; Nelson, B.; Mcdonald, M.K.; Tharmarasa, R.; Kirubarajan, T. Airborne maritime surveillance using magnetic anomaly detection signature. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 3476–3490. [Google Scholar] [CrossRef]
- Qin, T.; Zhou, L.Y.; Chen, S.; Chen, Z.X. The novel method of magnetic anomaly recognition based on the fourth order aperiodic stochastic resonance. IEEE Sens. J. 2022, 22, 17043–17053. [Google Scholar] [CrossRef]
- Wan, C.B.; Pang, H.F.; Mou, S.F.; Li, H.; Pan, M.C.; Zhang, Q.; Yang, D.N. Magnetic anomaly detection using a parallel stochastic resonance system. IEEE Trans. Instrum. Meas. 2022, 71, 9502208. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, X.L.; Dong, H.B.; Liu, Z.; Hu, X.Y. Magnetic anomaly detection based on energy-concentrated discrete cosine wavelet transform. IEEE Trans. Instrum. Meas. 2023, 72, 9700210. [Google Scholar] [CrossRef]
- Wang, J.Z.; Jiang, Z.K.; Gao, J.Q.; Zhao, S.X.; Zhai, W.M.; Shen, Y. Frequency characteristics analysis for magnetic anomaly detection. IEEE Geosci. Remote Sens. Lett. 2022, 19, 8007505. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Han, Q.; Zhan, D.C.; Li, Q. Magnetic anomaly detection network with adaptive time-frequency feature expression. IEEE Sens. J. 2023, 23, 21620–21630. [Google Scholar] [CrossRef]
- Xu, Y.J.; Wang, Z.; Liu, S.C.; Zhang, Q.; Pan, M.C.; Hu, J.F.; Chen, D.X.; Liu, Z.Y. Magnetic anomaly detection using multifeature fusion-based neural network. IEEE Geosci. Remote Sens. Lett. 2022, 19, 8020905. [Google Scholar] [CrossRef]
- Hu, M.K.; Jing, S.; Du, C.P.; Xia, M.Y.; Peng, X.; Guo, H. Magnetic dipole target signal detection via convolutional neural network. IEEE Geosci. Remote Sens. Lett. 2022, 19, 8003005. [Google Scholar] [CrossRef]
- Liu, X.G.; Yuan, Z.F.; Du, C.P.; Peng, X.; Guo, H.; Xia, M.Y. Adaptive basis function method for the detection of an undersurface magnetic anomaly target. Remote Sens. 2024, 16, 363. [Google Scholar] [CrossRef]
- Wang, T.; Li, J.T.; Liu, N.Z.; Peng, S.L.; Li, Y.D.; Fang, G.Y. A new data processing method for magnetic anomaly detection and localization based on 2-D orthonormal basis functions. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5912011. [Google Scholar] [CrossRef]
- Tang, Y.; Liu, Z.Y.; Pan, M.C.; Zhang, Q.; Wan, C.B.; Guan, F.; Wu, F.H.; Chen, D.X. Detection of magnetic anomaly signal based on information entropy of differential signal. IEEE Geosci. Remote Sens. Lett. 2018, 15, 512–516. [Google Scholar] [CrossRef]
- Zhao, J.W.; Zeng, Z.F.; Zhou, S.; Guo, H.; Yan, J.H.; Liu, T.Y. CWT-based magnetic anomaly data denoising method combing stochastic resonance system and pixel connectivity thresholding. IEEE Trans. Instrum. Meas. 2024, 73, 9500610. [Google Scholar]
- Fan, L.M.; Hu, H.; Zhang, X.J.; Wang, H.G.; Kang, C. Magnetic anomaly detection using one-dimensional convolutional neural network with multi-feature fusion. IEEE Sens. J. 2022, 22, 11637–11643. [Google Scholar] [CrossRef]
- Sheinker, A.; Frumkis, L.; Ginzburg, B.; Salomonski, N.; Kaplan, B.Z. Magnetic anomaly detection using a three-axis magnetometer. IEEE Trans. Magn. 2009, 45, 160–167. [Google Scholar] [CrossRef]
- Zhou, J.Q.; Wang, C.D.; Peng, G.Z.; Yan, H.; Zhang, Z.H.; Chen, Y. Magnetic anomaly detection via a combination approach of minimum entropy and gradient orthogonal functions. ISA Trans. 2023, 134, 548–560. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.K.; Huang, G.; Zhang, X.Y. Geomagnetic sensor noise reduction for improving calibration compensation accuracy based on improved HHT algorithm. IEEE Sens. J. 2019, 19, 12096–12104. [Google Scholar] [CrossRef]
- Liu, R.P.; Chang, Q.; Wang, Y.L.; Wang, L.P. Feature entropy adaptive network for weak magnetic signal classification. IEEE Sens. J. 2024, 24, 1322–1332. [Google Scholar] [CrossRef]
- Gunes, H.; Bicakci, S.; Citak, H.; Coramik, M.; Ege, Y. Buried magnetic material detection system: An SVM algorithm application. IEEE Trans. Magn. 2021, 57, 6500509. [Google Scholar] [CrossRef]
- Chang, Q.; Liu, R.P.; Wang, Y.L.; Wang, L.P. High-precision magnetic field reconstruction and anomaly classification. IEEE Sens. J. 2023, 23, 19163–19175. [Google Scholar] [CrossRef]
- Wang, S.G.; Zhang, X.Y.; Qin, Y.Q.; Song, W.H.; Li, B. Marine target magnetic anomaly detection based on multitask deep transfer learning. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1501705. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, J.Z.; Gao, J.Q. Noise suppression for vector magnetic anomaly detection by noise spatial characteristics investigation. IEEE Geosci. Remote Sens. Lett. 2022, 19, 7503104. [Google Scholar] [CrossRef]
- Chen, L.Z.; Feng, Y.Q.; Wu, P.L.; Zhu, W.H.; Fang, G.Y. An innovative magnetic anomaly detection algorithm based on signal modulation. IEEE Trans. Magn. 2020, 56, 6200609. [Google Scholar] [CrossRef]
- Birsan, M. Inversion of magnetic dipole parameters using a scalar field gradiometer. IEEE Sens. J. 2021, 21, 7434–7438. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, X.L.; Liao, C.Y.; Dong, H.B.; Liu, Z.; Hu, X.Y. Synergistic Hankel structured low-rank approximation with total variation regularization for complex magnetic anomaly detection. IEEE Trans. Instrum. Meas. 2023, 72, 6003710. [Google Scholar] [CrossRef]
- Fan, L.M.; Kang, C.; Wang, H.G.; Hu, H.; Zhang, X.J.; Liu, X. Adaptive magnetic anomaly detection method using support vector machine. IEEE Geosci. Remote Sens. Lett. 2022, 19, 8001705. [Google Scholar] [CrossRef]
- Xu, X.; Huang, L.; Liu, X.J.; Fang, G.Y. DeepMAD: Deep learning for magnetic anomaly detection and denoising. IEEE Access 2020, 8, 121257–121266. [Google Scholar] [CrossRef]
- Zhang, N.; Liu, Y.F.; Xu, L.; Lin, P.F.; Zhao, H.D.; Chang, M. Magnetic anomaly detection method based on feature fusion and isolation forest algorithm. IEEE Access 2022, 10, 84444–84457. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).