Abstract
This study focused on improving the clustering performance of hyperspectral imaging (HSI) by employing the Generalized Orthogonal Matching Pursuit (GOMP) algorithm for feature extraction. Hyperspectral remote sensing imaging technology, which is crucial in various fields like environmental monitoring and agriculture, faces challenges due to its high dimensionality and complexity. Supervised learning methods require extensive data and computational resources, while clustering, an unsupervised method, offers a more efficient alternative. This research presents a novel approach using GOMP to enhance clustering performance in HSI. The GOMP algorithm iteratively selects multiple dictionary elements for sparse representation, which makes it well-suited for handling complex HSI data. The proposed method was tested on two publicly available HSI datasets and evaluated in comparison with other methods to demonstrate its effectiveness in enhancing clustering performance.
1. Introduction
In the field of remote sensing, hyperspectral imaging (HSI) technology plays a crucial role in various domains such as environmental monitoring, resource management, and agriculture [1,2,3]. This technology provides rich spectral information by capturing images across numerous contiguous spectral bands, enabling a detailed analysis and identification of materials based on their spectral signatures. However, the complexity and high-dimensionality of hyperspectral data present significant challenges for effective data processing and analysis [4]. Despite the advances in deep learning techniques that have improved feature extraction from HSI data, these methods often require large amounts of labeled data and substantial computational resources, which can be limiting factors in practical applications [5,6]. In this context, clustering, an unsupervised learning technique, holds a pivotal place in HSI processing. By grouping data based on the similarity of features, clustering reveals the intrinsic structure of the data without the need for labeled training samples. This makes it particularly valuable for tasks such as land cover detection, mineral mapping, and vegetation analysis in HSI [7,8,9].
However, the high-dimensionality of HSI data poses several challenges. These include a high computational complexity, the presence of redundant information, and noise, all of which complicate the process of effective feature extraction and clustering [10,11]. While graph-based feature extraction techniques, such as graph signal processing and graph learning [12,13,14], have been introduced to address these challenges by modeling the relationships between pixels as graphs [15], they often require complex computations and rely on labeled data for training [16,17]. These graph-based methods have demonstrated effectiveness in HSI segmentation, where they capture both spatial and spectral information in a structured way [18]. However, their complexity may limit their applicability, especially in unsupervised learning tasks like clustering, where the lack of labels makes it difficult to leverage the full potential of graph-based approaches.
Orthogonal Matching Pursuit (OMP) is a classical sparse representation algorithm that has shown promise in handling high-dimensional data and extracting salient features [19]. OMP works by iteratively selecting dictionary elements that are most correlated with the residuals of the data, effectively reducing complexity while preserving essential features. However, traditional OMP has limitations when dealing with complex, correlated features, as it selects only one dictionary element per iteration. This can result in inadequate representation of the data structure.
To address these limitations, this paper introduces the Generalized Orthogonal Matching Pursuit (GOMP), an advanced variant of the OMP. Compared to previous methods, the GOMP offers a simpler and more computationally efficient approach by focusing on sparse representations. The GOMP enhances the flexibility and adaptability of the algorithm by allowing for the selection of multiple dictionary elements in each iteration, making it particularly suitable for complex datasets such as HSI, where multiple features may be highly correlated [20,21,22]. By maintaining sparsity, the GOMP improves the feature combination process in hyperspectral data, thereby enhancing clustering performance.
In this study, we employed the GOMP and dictionary learning techniques to achieve a sparse representation of HSI data, which is then used to improve clustering performance. We validated our approach using two publicly available HSI datasets: the Pavia University dataset [23] and the Salinas dataset [24]. Additionally, we explored the integration of the GOMP with various clustering techniques, including K-means, hierarchical clustering, and spectral clustering. This comparative analysis allowed us to identify the most effective strategies for applying these algorithms in different HSI scenarios. For each clustering algorithm, we conducted three sets of experiments: (1) clustering using raw data, (2) clustering after preprocessing with Principal Component Analysis (PCA), and (3) clustering after preprocessing with the GOMP. By comparing the results of these experiments on standard HSI datasets, we not only demonstrated the effectiveness of the GOMP algorithm in enhancing clustering performance but also assessed the suitability and efficiency of different clustering techniques for HSI processing [25,26]. The findings of this study provide deeper insights into HSI clustering analysis and showcase the applicability of the GOMP for sparse representation, ultimately contributing to the advancement of remote sensing technology and its practical applications.
2. Materials and Methods
In this section, we provide an overview of the experimental datasets, methodology, evaluation metrics, and experimental setup.
2.1. Dataset
This study utilized two publicly available hyperspectral image datasets: Pavia University and Salinas Datasets. The two datasets are extensively used in various fields related to HSI experiments, such as classification and clustering [27,28,29,30]. The scene images of the two datasets are depicted in Figure 1.
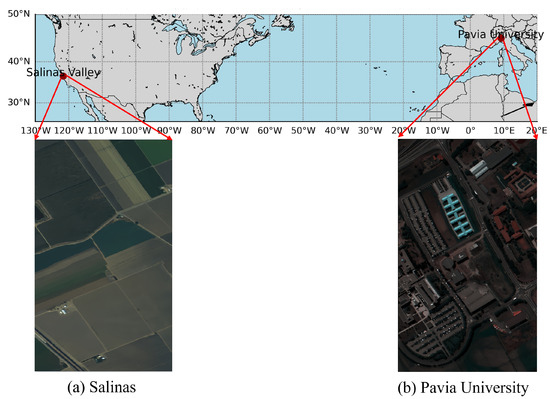
Figure 1.
The scene images of two datasets used in our experiment.
2.1.1. Pavia University Dataset
The Pavia University Dataset was acquired by the German Reflective Optics Spectrographic Imaging System (ROSIS-03) in 2003, covering a portion of Pavia, Italy. This imager captures images in 115 continuous bands within the wavelength range of 0.43–0.86 μm. Due to noise in some bands, 103 spectral bands are typically used after removing 12 noise-affected bands. The dataset has a spatial resolution of 1.3 m, with image dimensions of 610 × 340 pixels, encompassing 2,207,400 pixels. In reality, the total number of pixels containing ground object information is 42,776, distributed across 9 categories, including trees, asphalt roads, bricks, meadows, etc.
2.1.2. Salinas Dataset
The Salinas Dataset was obtained by the AVIRIS imaging spectrometer, covering the Salinas Valley region in California, USA. The dataset has a high spatial resolution of 3.7 m and consists of 224 bands. The image size of this dataset is 512 × 217 pixels, totaling 111,104 pixels, of which 56,975 are background pixels and 54,129 are usable for classification, divided into 16 categories, including fallow, celery, etc.
Table 1 shows the distribution and sample count for both datasets. The Pavia University dataset has a diverse urban coverage, with varying sample sizes across categories. The Salinas dataset, with its focus on agriculture, includes 16 categories showcasing spectral changes in plants. Using the two datasets, we aimed to provide a comprehensive evaluation of the GOMP algorithm in different settings.

Table 1.
Class information for the two datasets.
2.2. GOMP for Sparse Representation of HSI
In this section, we introduce the application of the GOMP algorithm for sparse representation in HSI clustering. As shown in Figure 2, the overall process consists of three main stages: dictionary learning, GOMP sparse coding, and clustering analysis. First, in the dictionary learning stage, a dictionary is trained using HSI data. The goal is to minimize the reconstruction error, resulting in a dictionary that compactly represents the key features of the data. This dictionary is then used in the subsequent sparse coding step. In the GOMP sparse coding stage, the GOMP algorithm iteratively selects dictionary atoms in a greedy manner to reduce residuals, thus achieving a sparse representation of the data. This process involves initializing the sparse matrix, selecting a sample, setting up the residual and support set, and updating the sparse matrix, repeating these steps until all pixels are processed. Finally, the sparsely coded data are applied to various clustering methods, such as K-means clustering, hierarchical clustering, and spectral clustering, to evaluate the enhancement in clustering performance achieved by the GOMP. This approach, by integrating dictionary learning and sparse representation, simplifies the dimensionality of data while preserving important global structural information, which significantly enhances the effectiveness of clustering analysis.
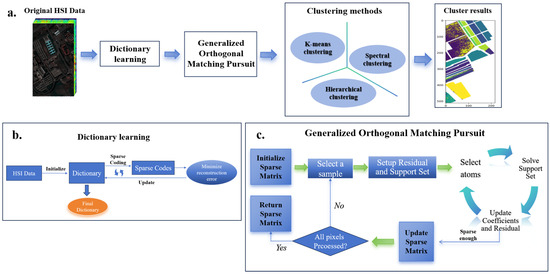
Figure 2.
GOMP-based sparse representation and clustering workflow for hyperspectral images. The process involves three main stages: (a) Dictionary learning stage, where the goal is to minimize reconstruction error and produce a compact representation of hyperspectral data. (b) GOMP sparse coding stage, where dictionary atoms are greedily selected during each iteration to reduce residuals and achieve sparse data representation. (c) Clustering analysis stage, where the sparsely coded data are applied to clustering methods such as K-means, hierarchical clustering, and spectral clustering to evaluate the enhancement in clustering performance achieved by the GOMP.
2.2.1. Online Dictionary Learning
Dictionary learning is pivotal for effectively employing the GOMP algorithm [31,32]. Its goal is to create a set of atoms that accurately represent HSI features. This step involves identifying a dictionary that can efficiently capture the diverse characteristics present in HSI data. Our method is initiated by learning a dictionary from the hyperspectral data , where m denotes the number of features for each pixel, and k is the number of dictionary atoms. In our method, the process involves iteratively optimizing the sparse code A and updating the dictionary D as follows:
- Sparse Coding: For a fixed D, the sparse representation for each data sample is computed by solvingwhere controls the sparsity.
- Dictionary Update: With a fixed A, dictionary D is updated by minimizing the reconstruction error over the batch:
2.2.2. Generalized Orthogonal Matching Pursuit (GOMP)
After dictionary learning, the next phase is applying the GOMP algorithm. The entire algorithmic process is depicted in Algorithm 1. It uses the learned dictionary to achieve a sparse representation of HSI data. The GOMP algorithm iteratively builds sparse representations for each pixel sample y using the learned dictionary D, which is instrumental in reducing dimensionality and accentuating vital features. In Algorithm 1, the input data matrix represents the hyperspectral image pixel data, where m denotes the number of features for each pixel, and n denotes the number of samples. The dictionary matrix is used to represent the sparse dictionary, where k indicates the number of dictionary atoms. The support set S is utilized to track the dictionary atoms selected in each iteration for constructing the sparse representation. The residual vector r represents the difference between the current signal and the selected dictionary atoms, while the correlation vector c computes the correlation between the dictionary atoms and the residual, allowing for the most correlated atoms to be selected. Lastly, the sparse coefficient a is solved via least squares and used to update the sparse representation.
The GOMP process begins by initializing the residual , where y represents the input signal or pixel sample, and setting the support set to empty. During each iteration t, the following steps are performed: first, the correlation between the current residual and all atoms in the learned dictionary D (where , with m representing the number of features and k being the number of dictionary atoms) is computed. Next, the top L correlated atoms are selected to update the support set . Then, the algorithm solves a constrained least squares problem, which is framed as follows:
where is the sparse coefficient vector, and the non- elements of x are set to zero, ensuring that only the coefficients corresponding to the selected atoms are updated. Finally, the residual is updated:
where represents the updated residual after subtracting the contribution of the selected atoms from the input signal, effectively reducing the approximation error with each iteration.
This process is repeated until the sparsity of the representation aligns with a predefined threshold. The combination of online dictionary learning with the GOMP is essential for efficient feature extraction in HSI analysis.
| Algorithm 1 Generalized Orthogonal Matching Pursuit (GOMP) |
| Require: The dataset ; Dictionary ; Sparsity level L. Ensure: Sparse coefficient matrix .
|
2.2.3. Clustering Methods
In hyperspectral data analysis, the selection of an effective clustering algorithm is pivotal. This study examined three prevalent clustering techniques—K-means, hierarchical, and spectral clustering—and evaluated their performance after feature extraction via the GOMP algorithm.
- a.
- K-means Clustering
K-means clustering, a well-known partitioning method, aims to segregate the dataset into K distinct clusters by minimizing the variance within each cluster [33]. The objective function is defined as
where K denotes the number of clusters, represents the set of points in the i-th cluster, and is the centroid of the points in , with d representing the dimensionality of the data points. Although K-means is efficient for large datasets, its performance may deteriorate with increasing data dimensionality. This is because, in higher dimensions, the distance metric used by K-means becomes less effective, leading to potential inaccuracies in clustering results. We hypothesize that the dimensionality reduction capabilities of the GOMP will enhance K-means clustering by simplifying the data structure, thereby improving clustering accuracy.
- b.
- Hierarchical Clustering
Hierarchical clustering organizes data into a tree-like structure without requiring a predetermined number of clusters [34]. It constructs a dendrogram that iteratively merges the closest pairs of clusters. This method is particularly advantageous for datasets with inherent hierarchical relationships, such as land cover classification, where broad categories like vegetation, water bodies, and urban areas can be further subdivided into more specific classes (e.g., different types of vegetation such as trees, grasslands, or shrubs, or different types of urban areas such as residential, commercial, or industrial zones). In hyperspectral data, hierarchical relationships can manifest as subtle variations within these broad categories, such as distinguishing between species of trees or different soil types, which have distinct spectral signatures. These multi-level structures reflect the natural hierarchies present in the data, and hierarchical clustering is well-suited to reveal them. With the integration of the GOMP, which simplifies the feature space while preserving essential structural details, hierarchical clustering is expected to provide more precise clustering by effectively capturing the subtle hierarchies within HSI data.
- c.
- Spectral Clustering
Spectral clustering approaches data partitioning through the lens of graph theory. It constructs a graph reflecting the relationships between data points and partitions the graph by minimizing the cut across different clusters [35]. The associated Laplacian matrix L is given by the following:
where W is the affinity matrix and D is the diagonal degree matrix with . Spectral clustering aims to solve
where A and B are disjoint subsets of the dataset V, represents the sum of the weights of the edges between A and B, and indicates the total edge weights connected to A. We anticipate that GOMP’s feature extraction will enable spectral clustering to better exploit global structural information, thus significantly enhancing its clustering capability.
To ensure a balanced evaluation, all clustering experiments were conducted under identical initialization conditions. Additionally, comparative analyses included PCA-reduced data to assess the relative effectiveness of dimensionality reduction techniques. These experiments were aimed to deepen our understanding of how the feature extraction of the GOMP influences the performance of various clustering methods, providing valuable insights for optimizing HSI analysis.
2.3. Cluster Evaluation Metrics
To assess clustering effectiveness, we utilized Normalized Mutual Information (NMI) and Rand Index (RI) [36,37], which are primarily used to measure the consistency between clustering results and true labels.
- Normalized Mutual Information (NMI): NMI is an extension of the mutual information metric, normalized to compare the amount of information shared between two clusters relative to a chance alignment. It is particularly valuable in scenarios where the cluster sizes vary significantly. The metric normalizes the mutual information score to a range between 0 and 1, where 0 indicates no mutual information and 1 denotes perfect correlation between the clusters. NMI is calculated with the following formula:U and V represent the true labels and the clustering results, respectively. is the mutual information between the two clusterings, and and are their respective entropies.
- Rand Index (RI): The RI quantifies the accuracy of a clustering result by considering all pairs of samples and counting pairs that are assigned in the same or different clusters in the predicted and true labels. RI values range from 0 to 1, where 0 signifies no agreement between the two clusterings beyond what would be expected by chance, and 1 indicates complete agreement. The RI is particularly useful for measuring the performance of a clustering algorithm without the influence of the number of clusters. It is defined as follows:where (true positives) and (true negatives) are the counts of sample pairs correctly identified as belonging to the same or different clusters, respectively. (false positives) and (false negatives) are the counts of sample pairs wrongly identified as belonging to the same or different clusters, respectively.
2.4. Experimental Design
The original HSI are initially standardized to ensure comparability across different spectral bands [38]. To examine the enhancement of the GOMP on clustering performance, this study utilized three widely employed clustering algorithms: K-means, hierarchical clustering, and spectral clustering. For these experiments, the number of cluster centers was set to match the category count of the dataset, and a fixed random seed of 42 was utilized to ensure reproducibility. All algorithms were implemented using the scikit-learn library in Python [39].
- Original Data: Clustering was performed on the standardized original data without additional feature extraction or dimensionality reduction. All three clustering methods were implemented in their most conventional form. This experiment was programmatically executed using the sklearn library to ensure robust and reproducible clustering results.
- PCA: Dimensionality reduction via Principal Component Analysis (PCA) precedes clustering:where W represents the principal components extracted from the data. In our experiments, PCA was implemented using the FAISS library, and the number of principal components was set to match the number of atoms selected in the GOMP process, ensuring a direct comparison of dimensionality reduction effects between PCA and GOMP.
- GOMP: Key parameters for the GOMP algorithm included a dictionary size of , a regularization parameter , 200 iterations, and a batch size of 128. The number of selected atoms L was also set to 5. Depending on the dataset and clustering method used, adjustments to the value and the number of iterations may be necessary to optimize performance. After feature extraction via the GOMP, the data underwent clustering analysis using K-means, hierarchical, and spectral clustering methods. This approach allowed us to evaluate and compare the performance enhancements attributed to the sparse representation provided by the GOMP, thus facilitating a thorough assessment of its impact on clustering efficiency and effectiveness.
3. Result and Analysis
In this section, we thoroughly evaluate the performance of the GOMP and compare it with other methods in clustering HSI. Our analysis includes a detailed examination of feature distributions using t-distributed Stochastic Neighbor Embedding (t-SNE) technology [40,41], a comprehensive review of cluster evaluation metrics, and the use of visualization techniques to create maps of clustering result. These visualizations not only demonstrate the potential of the GOMP to improve clustering quality but also highlight its superiority over other methods.
3.1. T-SNE Feature Analysis
We employ t-SNE to visually assess the impact of the GOMP on clustering via feature extraction on the both datasets.
Figure 3 presents the t-SNE visualization results for the Pavia dataset, from which we can observe the impact of different feature extraction techniques on clustering outcomes. The distribution of data with original features displays blurred class boundaries, reflecting the intrinsic complexity and overlap among categories in high-dimensional data. This blurriness makes accurate clustering challenging, as closely related categories may be difficult to distinguish in the feature space. When PCA is applied for feature extraction, an improvement in the differentiation between categories is observed, although many boundaries remain ambiguous. This indicates that while PCA can reduce the dimensionality of data and remove noise to some extent, its capacity is limited in handling highly overlapping categories. In contrast, the feature extraction process of the GOMP demonstrates a significant advantage. Data processed by the GOMP shows a more distinct and separated category distribution in the t-SNE visualization, suggesting that the GOMP not only effectively reduces the dimensionality of the data but also enhances the separability between categories. This is a key attribute for an effective clustering analysis, as good class separation aids clustering algorithms in more accurately identifying different categories.
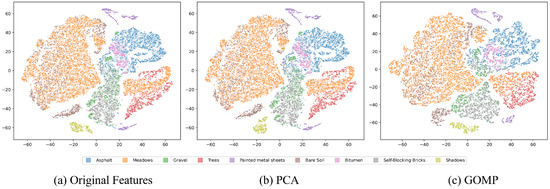
Figure 3.
T-SNE visualization of features from the Pavia University dataset, where different colors indicate ground truth classes: (a) Original features. (b) PCA-processed features. (c) GOMP-processed features.
As depicted in Figure 4, the t-SNE visualization of the Salinas dataset demonstrates a similar trend with the Pavia University dataset. Both the original and PCA-processed data exhibit widespread and indistinct category distributions, which pose challenges for accurate clustering. However, preprocessing with the GOMP results in more clearly defined and concentrated clusters for each category, showcasing its superiority in enhancing category differentiation compared to the original and PCA features.
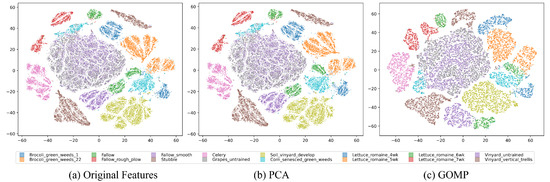
Figure 4.
T-SNE visualization of features from the Salinas Dataset, where different colors indicate ground truth classes: (a) Original features. (b) PCA-processed features. (c) GOMP-processed features.
These visualizations highlight the significant advantage of using the GOMP in the feature extraction of HSI. The GOMP substantially improves category separation compared to the original and PCA features, offering clearer clustering decision boundaries. This advantage is consistent across various datasets, emphasizing the robustness and critical importance of the GOMP in enhancing HSI clustering analysis.
3.2. Cluster Evaluation Metrics Analysis
Table 2 presents a detailed clustering accuracy table that thoroughly compares three clustering algorithm—K-means, hierarchical, and spectral clustering—across the Pavia University and Salinas datasets. These comparisons are based on data processed using original features, PCA, and GOMP. The main evaluation metrics are the RI and NMI, which provide measures of the clustering quality by assessing the similarity of the clustering outcomes to the ground truth and quantifying the mutual information between the clustering results and the actual labels, respectively.

Table 2.
Clustering accuracy for Pavia University and Salinas datasets using different methods and feature processing techniques.
The data reveal that GOMP processing significantly enhances performance across all algorithms and datasets. Specifically, the spectral clustering algorithm using GOMP-processed features achieved an RI of 0.823 and an NMI of 0.648 on the Pavia University dataset, significantly outperforming other feature processing methods. This indicates that the GOMP can generate sparse yet information-rich feature representations, emphasizing characteristics crucial for clustering. Compared to the significant effects of the GOMP, PCA, although effective in reducing dimensionality, only shows moderate improvements in clustering accuracy and may even reduce performance in some cases. This suggests that the linear transformation properties of PCA might not effectively capture the nonlinear structures essential for precise clustering. In contrast, the GOMP preserves and accentuates these critical structures, thereby enhancing the clustering performance significantly.
Moreover, Table 2 also details the performance differences of each clustering algorithm under various feature processing types. For K-means clustering, the GOMP’s sparse representation significantly improves its clustering accuracy. On the Salinas dataset, RI increased from 0.921 to 0.924, and NMI from 0.757 to 0.794 using GOMP-processed features. This indicates that the GOMP reduces overlap between clusters and enhances the prominence of cluster centroids, providing more accurate and robust clustering results for K-means.
In hierarchical clustering, the data showed the most significant increase in NMI, particularly on the Salinas dataset, where it jumped from 0.748 to 0.813, an 8.7% increase. This improvement is attributed to the GOMP’s excellent performance in maintaining and highlighting hierarchical relationships within the data. By capturing these relationships, the GOMP allows for hierarchical clustering to merge clusters more precisely based on true similarities.
For spectral clustering, the data in the table indicate that using GOMP-processed features on the Pavia University dataset improved RI from 0.787 to 0.823, a 4.6% increase. This boost stems from the GOMP’s enhancement of data spectral features, thus optimizing edge definitions in the similarity graph used by spectral clustering. By improving these edge definitions, the GOMP helps spectral clustering more effectively separate the commonly non-contiguous clusters in hyperspectral images.
By enhancing feature selectivity and reducing redundancy, the GOMP not only improves the quality of the resulting clusters but also makes clustering algorithms more efficient in handling complex data structures. These quantified improvements highlight the GOMP’s key role in enhancing the interpretability and accuracy of clustering outcomes, which is particularly important for hyperspectral data analysis.
Overall, the data presented in the table clearly demonstrate the effectiveness of the GOMP as a preprocessing step in enhancing clustering accuracy. By enhancing feature selectivity and reducing redundancy, the GOMP does not only improve the quality of clustering performance in managing complex data structures. These quantified improvements highlight the pivotal role of the GOMP in enhancing both the interpretability and accuracy of clustering outcomes.
3.3. Clustering Map Analysis
In this section, the visualization maps of the clustering results demonstrate the superiority of the GOMP algorithm. It is essential to understand the key distinction between category identification in clustering analysis [42]. Unlike supervised learning, clustering does not rely on predefined labels and cannot directly map data points to specific labels. Therefore, in a clustering map, pixels of the same color only represent their classification into the same group, and it does not imply that these pixels correspond to specific labels.
3.4. The Clustering Map of Salinas Dataset
Figure 5 illustrates the clustering maps of the Salinas dataset processed through different clustering algorithms and feature extraction techniques. In this figure, we observe the effectiveness of three clustering algorithms: K-means clustering in the first row, hierarchical clustering in the second row, and spectral clustering in the third row. Each clustering method is applied with three types of feature extraction techniques: original features, PCA, and GOMP. The maps display the ability of algorithms to capture complex crop distribution patterns in the agricultural fields, such as Broccoli and Fallow areas, achieving significant separation between classes. The use of colors cleverly enhances the visual representation, delineating the classification of different regions by the algorithms. For instance, in the hierarchical clustering maps, a deep purple region distinctly marks a specific crop type. Upon referencing the ground truth, this area is identified as Broccoli, illustrating the algorithm’s precision in accurately identifying and classifying distinct agricultural zones. However, there are also areas with mixed colors, indicating challenges that clustering algorithms might face on adjacent land cover types with similar spectral features.
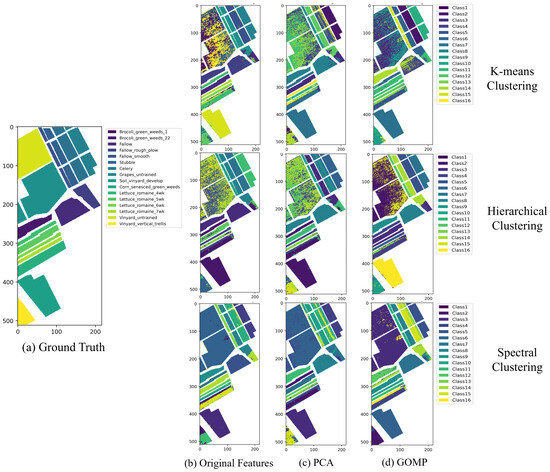
Figure 5.
The clustering maps of Salinas dataset by different clustering algorithms under different feature extraction techniques.
Notably, the sparsity-inducing technique of the GOMP exhibits unique advantages in this context. By extracting rich spectral features, the GOMP significantly enhances the accuracy of spectral clustering, resulting in clearer and more coherent agricultural plots on the map. This technique reduces spectral overlap between different crops and improves the precision of clustering. Next, we delve into a detailed analysis of the clustering maps generated by different methods on the Salinas dataset, focusing on their specific impacts and areas for improvement.
As illustrated in Figure 6, the performance of K-means clustering on original features reveals moderately blurred clustering boundaries for certain crops, particularly between spectrally similar crop types such as “Stubble”, “Celery”, and “Vineyard” (the red frames in Figure 6). This suggests that the original features might contain substantial noise and redundancy. However, the boundaries between these categories become clearer after applying PCA for dimensionality reduction, indicating that PCA effectively reduces information redundancy. Moreover, the GOMP refines key spectral features crucial for distinguishing different agricultural categories. By reducing variance within clusters and sharpening the centroids in the feature space, the GOMP significantly enhances the performance of K-means clustering. Notably, in categories such as “Vineyard” and “Lettuce”, intra-class consistency is notably improved, and the separation between classes is more distinct.
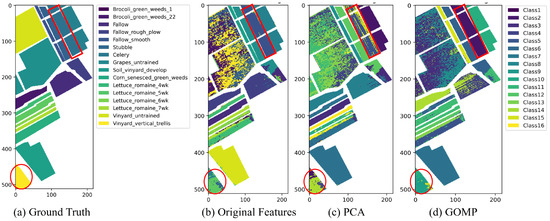
Figure 6.
The clustering map of Salinas dataset by K-means clustering algorithm under different feature extraction techniques.
In the case of hierarchical clustering, the results are similar to those of K-means clustering. Directly using original features for clustering within the “Vineyard” category does not yield ideal results, possibly due to the inherent hierarchical decomposition properties of this method. While the use of PCA features slightly improves the clustering shape, some confusion still persists. However, when the GOMP is integrated for feature extraction, hierarchical clustering performs excellently in terms of category compactness and distinction, especially in regions with strong color contrasts between classes. The GOMP is able to highlight the hierarchical data structure, revealing more detailed clustering layers, which helps to accurately capture nested patterns of approximate categories in agricultural data, enabling effective separation at different granularity levels in hierarchical clustering.
As for spectral clustering, as shown in Figure 7, the results with original features already demonstrate relatively clear class boundaries. Compared to the first two methods, spectral clustering better utilizes the structural information of the original spectral data in regions like “Vineyard” (the red frames in Figure 7). While PCA moderately enhances the delineation of specific categories and improves clustering outcomes, the enhancements achieved through the GOMP are substantially more pronounced. This improvement is primarily due to the feature selection strategy of the GOMP, which focuses on identifying and prioritizing the key attributes that distinguish each category. The GOMP preserves non-linear relationships and diverse spectral characteristics, leading to the creation of a more precise similarity matrix. This matrix is critical for effective spectral clustering, enhancing the accuracy of the clustering results.
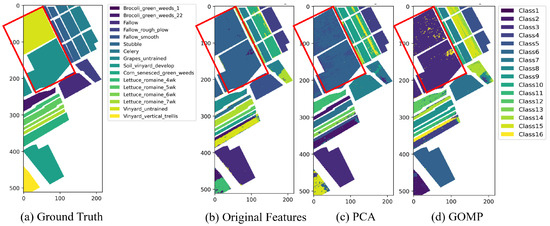
Figure 7.
The clustering map of Salinas dataset by spectral clustering algorithm under different feature extraction techniques.
3.5. The Clustering Map of Pavia University Dataset
Figure 8 presents the clustering maps of the Pavia University dataset processed with different clustering algorithms and feature extraction methods. From this figure, it is evident that features processed by the GOMP yield effective clustering results. For example, in spectral clustering combined with the GOMP, categories such as “trees” and “asphalt” exhibit high spatial consistency and class separability. This demonstrates the robust capability of the GOMP to enhance the distinctiveness and accuracy of clustering outcomes, particularly in distinguishing between complex environmental textures.
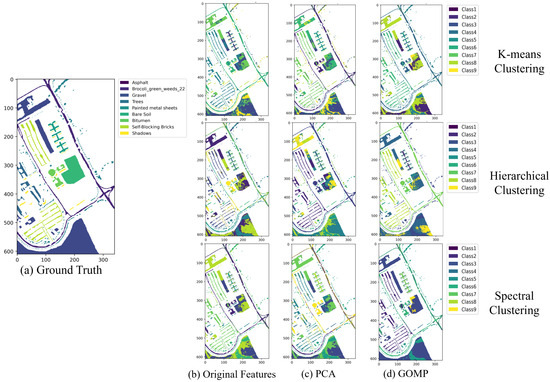
Figure 8.
The clustering maps of Pavia University dataset by different clustering algorithms under different feature extraction techniques.
Figure 9 details the effects of K-means clustering on the Pavia University dataset. K-means clustering can initially differentiate various land cover types based on original features, but the boundaries of some categories, such as “gravel” (the red frames in Figure 9), are not clearly defined in the clustering results. Using PCA for feature extraction slightly improves the distinction between categories, especially in enhancing the boundaries of certain land covers. Furthermore, the feature extraction of the GOMP is superior, enhancing the accuracy of clustering, particularly when dealing with complex materials such as “painted metal sheets” and “gravel”.
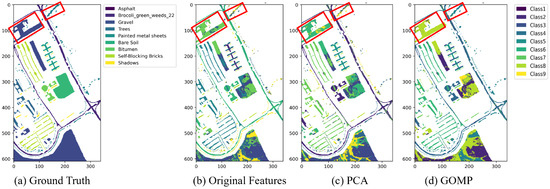
Figure 9.
The clustering maps of Pavia University dataset by K-means clustering algorithm under different feature extraction techniques.
Figure 10 presents the clustering maps generated by hierarchical clustering. Hierarchical clustering with original features reveals a fragmented distribution of categories such as “asphalt” and “block bricks” (the red frames in Figure 10). This fragmentation may be attributed to the high sensitivity of the method to intra-class variations. PCA enhances the consistency of these categories to some extent, and the improvement of the GOMP is more pronounced. Considering the structured nature of urban environments, the hierarchical data representation capability of the GOMP significantly enhances the performance of hierarchical clustering. This is particularly effective in capturing the complexity of urban structures, where different building materials and types of vegetation are precisely separated into distinct and coherent clusters. This precise segmentation accurately reflects the actual layout of the city, demonstrating the strength of the GOMP in dealing with multifaceted urban data.
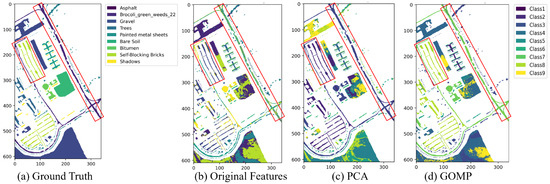
Figure 10.
The clustering maps of Pavia University dataset by hierarchical clustering algorithm under different feature extraction techniques.
The results of spectral clustering enhance the advantages of hierarchical clustering. Clustering with original features provides a more precise delineation of land cover boundaries than K-means and hierarchical clustering, particularly in categories such as “trees”. When combined with the GOMP, the performance of spectral clustering is further enhanced. The GOMP enhances the spectral features of various urban characteristics to improve clustering performance, exhibiting excellent spatial coherence and category consistency. Overall, on the Pavia University dataset, the GOMP significantly enhances the performance of various clustering algorithms, demonstrating considerable advantages.
In summary, the feature extraction by the GOMP significantly enhances the performance of clustering algorithms such as K-means, hierarchical clustering, and spectral clustering. By iteratively selecting multiple dictionary elements, the GOMP enriches and sparsifies the feature space, focusing on key spectral features crucial for distinguishing various types of land cover. This improves class differentiation, exhibiting superior performance in the complex environment of hyperspectral imaging. Furthermore, while enhancing the precision of feature selection, the GOMP preserves the data structure, aligning clustering results more closely with the intricate realities of hyperspectral data. The extraction of key information boosts the discriminative power of clustering algorithms, resulting in superior visual and statistical clustering outcomes.
4. Discussion
4.1. Time Efficiency Analysis of GOMP
In this section, we explore the computational efficiency of various clustering methods applied to the Pavia University and Salinas datasets using different feature extraction techniques. Table 3 provides a detailed comparison of computational times for K-means, hierarchical, and spectral clustering using original features, PCA-processed features, and GOMP-processed features.

Table 3.
The execution times efficiency for each clustering method combined with three types of feature extraction techniques. The times are measured in seconds and highlight the performance differences across datasets and methodologies.
The scale, dimensionality, and intrinsic structure of datasets significantly influence the computational efficiency of clustering algorithms and feature extraction techniques. For instance, large, high-dimensional datasets may require more computational resources and could impact the runtime of algorithms. Different clustering algorithms exhibit various levels of computational complexity. Simpler algorithms like K-means generally run faster, while more complex methods may require longer computation times. Additionally, the sensitivity of algorithms to initial parameters and data distributions can affect their efficiency and accuracy.
One of the main reasons for the increased computational time in the GOMP is the dictionary learning process, which requires iterative optimization to select the most relevant dictionary elements for sparse representation. This process, while beneficial for improving clustering accuracy, adds computational overhead, especially for datasets with diverse and complex spectral features. Although the GOMP occasionally increases computation time, it significantly improves clustering outcomes by providing features with a high discriminative power. Therefore, in practical applications, a balance between time efficiency and accuracy needs to be considered. For large datasets or applications requiring high-speed processing, PCA may be a more suitable option, while the GOMP offers superior results in situations where a higher clustering accuracy is the priority.
4.2. Evaluation of GOMP on the Botswana Dataset for Supervised and Unsupervised Tasks
To further validate the universality and effectiveness of the GOMP-based feature extraction method, we conducted additional experiments using the Botswana dataset. This dataset is a widely recognized benchmark in hyperspectral imaging (HSI) research, frequently used for remote sensing tasks. It contains 145 spectral bands with a spatial resolution of 30 m and covers the Okavango Delta region of Botswana. Due to its diversity and complexity, the Botswana dataset serves as an ideal testbed for evaluating feature extraction methods across different HSI analysis tasks.
We performed two sets of experiments on the Botswana dataset: unsupervised clustering and supervised classification. The primary objective was to assess whether GOMP-processed features can enhance performance in both tasks and to compare the effectiveness of the GOMP with other commonly used feature extraction techniques, such as PCA and directly using the original features.
4.2.1. Clustering Performance Evaluation
In the clustering experiments, we also applied three common clustering algorithms—K-means, hierarchical, and spectral clustering—to the Botswana dataset. We evaluated the clustering performance using original features, PCA-processed features, and GOMP-processed features. The performance was quantified using NMI and RI, which are standard metrics for clustering accuracy.
As shown in Table 4, GOMP-processed features consistently outperform both PCA and original features across all clustering methods. For example, spectral clustering with GOMP-processed features achieved the highest performance, with an NMI of 0.812 and an RI of 0.937. These results demonstrate the superior ability of the GOMP to reduce the dimensionality of hyperspectral data while preserving critical structural information. This results in more accurate and robust clustering outcomes compared to PCA, which primarily focuses on linear transformations. The strength of the GOMP lies in its capacity to capture complex, non-linear relationships within hyperspectral data, making it particularly effective for clustering tasks.

Table 4.
Clustering performance metrics for different clustering methods combined with three types of feature extraction techniques on the Botswana Dataset.
4.2.2. Supervised Classification Evaluation and Analysis of Classification Results
For the supervised classification experiments, we assessed the performance of GOMP-processed features using several widely adopted classifiers: Support Vector Machine (SVM), k-Nearest Neighbors (KNN), Multi-Layer Perceptron (MLP), and Random Forest (RF). The classification accuracy was evaluated and compared across three feature extraction methods: original features, PCA-processed features, and GOMP-processed features. These classifiers were implemented using the scikit-learn library.
The classification accuracy results, illustrated in Figure 11, show that GOMP-processed features consistently lead to higher classification accuracy compared to the original features. Additionally, GOMP-processed features are competitive with, or even outperform, PCA-processed features across all classifiers. For instance, the SVM classifier achieves an accuracy of 0.951 with GOMP-processed features, a significant improvement over the 0.841 accuracy with original features. The KNN and MLP classifiers similarly show strong performance, with accuracies of 0.950 and 0.952, respectively, when using GOMP-processed features.
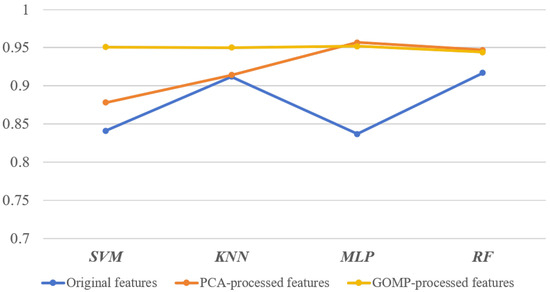
Figure 11.
Classification accuracy comparison across different classifiers and feature extraction methods.
Upon analyzing the classification results, it is evident that the GOMP significantly enhances the performance of machine learning models by producing more informative and sparse feature representations. The KNN classifier, for example, exhibits a noticeable improvement when using GOMP-processed features, with accuracy increasing from 0.912 (original features) to 0.950. Similarly, the MLP classifier benefits from the feature extraction of the GOMP, achieving an accuracy of 0.952, further confirming the effectiveness of the proposed method in capturing key feature representations while mitigating noise. In contrast, PCA-processed features perform well but exhibit a slightly lower accuracy, particularly in the KNN classifier.
However, as the complexity of the learning network increases, we observe that the advantages of feature extraction methods like the GOMP can become more limited. In some cases, the use of original features yields better results, particularly with more complex deep learning models. This is primarily because such models have enhanced learning capabilities, allowing them to directly learn from raw data and capture intricate patterns that may be diminished or lost through preprocessing. As a result, the utility of convenient feature extraction methods like the GOMP and PCA may diminish when the model itself has sufficient capacity to extract relevant features autonomously. Future research on how to better integrate the GOMP with advanced classification algorithms would be highly valuable.
4.3. Prospects of GOMP in Clustering HSI
Although the GOMP demonstrates significant advantages in this study, its limitations must be considered. First, the experimental scope is confined to two HSI datasets, so future research should further validate the GOMP algorithm across a more diverse and extensive array of datasets. Second, a characteristic of the GOMP algorithm is its relatively high computational complexity, which may impose constraints in scenarios requiring real-time processing or in handling large-scale data. Third, the performance of the GOMP may be highly sensitive to dictionary and parameter selection. Future research should focus on enhancing the computational efficiency and robustness of the GOMP algorithm to accommodate a broader range of application settings.
5. Conclusions
This study demonstrates the significant efficacy of the GOMP algorithm in enhancing the clustering performance of HSI. Exhaustive experiments were conducted on two publicly available HSI datasets and clearly showed the superiority of the GOMP over other feature extraction techniques, such as PCA. The core of the GOMP algorithm lies in its iterative approach, which involves selecting multiple dictionary elements for sparse representation. This unique processing method enables the GOMP to efficiently handle complex and information-rich HSI data. It not only effectively reduces redundancy and noise in the data but also precisely captures key features, significantly improving the accuracy and clarity of clustering. Notably, the application of the GOMP in the sparse representation of HSI greatly improves the consistency and similarity of clustering. This means that after processing with the GOMP, data points within the same category are more tightly clustered together, while the distinction between different categories is markedly increased. This is not only visually evident but also objectively verified through quantitative metrics such as NMI and RI.
Overall, this study not only delves into the application of the GOMP algorithm in HSI clustering but also confirms its tremendous potential in enhancing feature extraction and improving the accuracy of clustering analysis from both theoretical and practical perspectives. This undoubtedly provides new insights and directions for the future unsupervised processing and analysis of HSI. Future research could focus on further optimizing the computational efficiency of the GOMP, particularly for large-scale or real-time applications. Moreover, applying the GOMP to a wider range of HSI datasets and exploring different dictionary and parameter selection strategies will help establish a more robust and adaptable framework.
Author Contributions
Conceptualization, W.G. and X.X. (Xu Xu); methodology, W.G.; software, W.G.; data curation, W.G. and X.X. (Xu Xu); writing—original draft preparation, W.G.; writing—review and editing, S.G. and X.X. (Xiaoqiang Xu); visualization, W.G. and X.X. (Xu Xu); supervision, W.G.; Validation, Z.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The datasets used in this study are publicly available. The Pavia University dataset can be accessed at https://paperswithcode.com/dataset/pavia-university (accessed on 11 June 2024), and the Salinas dataset can be accessed at https://paperswithcode.com/dataset/salinas (accessed on 11 June 2024). The code used in this research is available upon request by contacting the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lassalle, G. Monitoring natural and anthropogenic plant stressors by hyperspectral remote sensing: Recommendations and guidelines based on a meta-review. Sci. Total Environ. 2021, 788, 147758. [Google Scholar] [CrossRef]
- Lu, B.; Dao, P.D.; Liu, J.; He, Y.; Shang, J. Recent Advances of Hyperspectral Imaging Technology and Applications in Agriculture. Remote Sens. 2020, 12, 2659. [Google Scholar] [CrossRef]
- Mayra, J.; Keski-Saari, S.; Kivinen, S.; Tanhuanpää, T.; Hurskainen, P.; Kullberg, P.; Poikolainen, L.; Viinikka, A.; Tuominen, S.; Kumpula, T.; et al. Tree species classification from airborne hyperspectral and LiDAR data using 3D convolutional neural networks. Remote Sens. Environ. 2021, 256, 112322. [Google Scholar] [CrossRef]
- Pour, A.B.; Guha, A.; Crispini, L.; Chatterjee, S. Editorial for the Special Issue Entitled Hyperspectral Remote Sensing from Spaceborne and Low-Altitude Aerial/Drone-Based Platforms—Differences in Approaches, Data Processing Methods, and Applications. Remote Sens. 2023, 15, 5119. [Google Scholar] [CrossRef]
- Hong, D.; Han, Z.; Yao, J.; Gao, L.; Zhang, B.; Plaza, A.; Chanussot, J. SpectralFormer: Rethinking Hyperspectral Image Classification With Transformers. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5518615. [Google Scholar] [CrossRef]
- Vaddi, R.; Kumar, B.L.N.P.; Manoharan, P.; Agilandeeswari, L.; Sangeetha, V. Strategies for dimensionality reduction in hyperspectral remote sensing: A comprehensive overview. Egypt. J. Remote Sens. Space Sci. 2024, 27, 82–92. [Google Scholar] [CrossRef]
- Sun, W.; Peng, J.; Yang, G.; Du, Q. Correntropy-Based Sparse Spectral Clustering for Hyperspectral Band Selection. IEEE Geosci. Remote Sens. Lett. 2020, 17, 484–488. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Du, B.; You, J.; Tao, D. Hyperspectral image unsupervised classification by robust manifold matrix factorization. Inf. Sci. 2019, 485, 154–169. [Google Scholar] [CrossRef]
- Kong, X.; Fu, M.; Zhao, X.; Wang, J.; Jiang, P. Ecological effects of land-use change on two sides of the Hu Huanyong Line in China. Land Use Policy 2021. [Google Scholar] [CrossRef]
- Li, Q.; Mu, T.; Gong, H.; Dai, H.; Li, C.; He, Z.; Wang, W.; Han, F.; Tuniyazi, A.; Li, H.; et al. A Superpixel-by-Superpixel Clustering Framework for Hyperspectral Change Detection. Remote Sens. 2022, 14, 2838. [Google Scholar] [CrossRef]
- Rasti, B.; Hong, D.; Hang, R.; Ghamisi, P.; Kang, X.; Chanussot, J.; Benediktsson, J.A. Feature Extraction for Hyperspectral Imagery: The Evolution From Shallow to Deep: Overview and Toolbox. IEEE Geosci. Remote Sens. Mag. 2020, 8, 60–88. [Google Scholar] [CrossRef]
- Zhang, S.; Deng, Q.; Ding, Z. Multilayer graph spectral analysis for hyperspectral images. EURASIP J. Adv. Signal Process. 2022, 2022, 92. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X.; Jiang, X.; Zhou, Y. Marginalized Graph Self-Representation for Unsupervised Hyperspectral Band Selection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5516712. [Google Scholar] [CrossRef]
- Liu, Q.; Xue, D.; Tang, Y.; Zhao, Y.; Ren, J.; Sun, H. PSSA: PCA-Domain Superpixelwise Singular Spectral Analysis for Unsupervised Hyperspectral Image Classification. Remote Sens. 2023, 15, 890. [Google Scholar] [CrossRef]
- Zhang, H.; Zou, J.; Zhang, L. EMS-GCN: An End-to-End Mixhop Superpixel-Based Graph Convolutional Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5526116. [Google Scholar] [CrossRef]
- Shi, C.; Liao, Q.; Li, X.; Zhao, L.; Li, W. Graph Guided Transformer: An Image-Based Global Learning Framework for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2023, 20, 3509105. [Google Scholar] [CrossRef]
- Wu, K.; Zhan, Y.; An, Y.; Li, S. Multiscale Feature Search-Based Graph Convolutional Network for Hyperspectral Image Classification. Remote Sens. 2024, 16, 2328. [Google Scholar] [CrossRef]
- Kotzagiannidis, M.S.; Schonlieb, C.-B. Semi-Supervised Superpixel-Based Multi-Feature Graph Learning for Hyperspectral Image Data. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4703612. [Google Scholar] [CrossRef]
- Tropp, J.A.; Gilbert, A.C. Signal Recovery From Random Measurements Via Orthogonal Matching Pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Zong, Z.; Fu, T.; Yin, X. High-Dimensional Generalized Orthogonal Matching Pursuit With Singular Value Decomposition. IEEE Geosci. Remote Sens. Lett. 2023, 20, 7502205. [Google Scholar] [CrossRef]
- Justo, J.A.; Orlandić, M. Study of the gOMP Algorithm for Recovery of Compressed Sensed Hyperspectral Images. In Proceedings of the 2022 12th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS), Rome, Italy, 13–16 September 2022; pp. 1–5. [Google Scholar]
- Fu, T.; Zong, Z.; Yin, X. Generalized Orthogonal Matching Pursuit With Singular Value Decomposition. IEEE Geosci. Remote Sens. Lett. 2022, 19, 8013405. [Google Scholar] [CrossRef]
- Zhu, M.; Fan, J.; Yang, Q.; Chen, T. SC-EADNet: A Self-Supervised Contrastive Efficient Asymmetric Dilated Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–17. [Google Scholar] [CrossRef]
- Alkhatib, M.Q.; Al-Saad, M.; Aburaed, N.; Almansoori, S.; Zabalza, J.; Marshall, S.; Al-Ahmad, H. Tri-CNN: A Three Branch Model for Hyperspectral Image Classification. Remote Sens. 2023, 15, 316. [Google Scholar] [CrossRef]
- Celik, T. Unsupervised Change Detection in Satellite Images Using Principal Component Analysis and k-Means Clustering. IEEE Geosci. Remote Sens. Lett. 2009, 6, 772–776. [Google Scholar] [CrossRef]
- Johnson, J.; Douze, M.; Jégou, H. Billion-Scale Similarity Search with GPUs. IEEE Trans. Big Data 2021, 7, 535–547. [Google Scholar] [CrossRef]
- Liu, S.; Shi, Q.; Zhang, L. Few-Shot Hyperspectral Image Classification With Unknown Classes Using Multitask Deep Learning. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5085–5102. [Google Scholar] [CrossRef]
- Zhai, H.; Zhang, H.; Xu, X.; Zhang, L.; Li, P. Kernel Sparse Subspace Clustering with a Spatial Max Pooling Operation for Hyperspectral Remote Sensing Data Interpretation. Remote Sens. 2017, 9, 335. [Google Scholar] [CrossRef]
- Roy, S.K.; Krishna, G.; Dubey, S.R.; Chaudhuri, B.B. HybridSN: Exploring 3-D–2-D CNN Feature Hierarchy for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2020, 17, 277–281. [Google Scholar] [CrossRef]
- Vaddi, R.; Manoharan, P. Hyperspectral image classification using CNN with spectral and spatial features integration. Infrared Phys. Technol. 2020, 107, 103296. [Google Scholar] [CrossRef]
- Sun, R.; Yang, Z.; Zhai, Z.; Chen, X. Sparse representation based on parametric impulsive dictionary design for bearing fault diagnosis. Mech. Syst. Signal Process. 2019, 122, 737–753. [Google Scholar] [CrossRef]
- Qin, Y.; Zou, J.; Tang, B.; Wang, Y.; Chen, H. Transient Feature Extraction by the Improved Orthogonal Matching Pursuit and K-SVD Algorithm With Adaptive Transient Dictionary. IEEE Trans. Ind. Informa. 2020, 16, 215–227. [Google Scholar] [CrossRef]
- Celebi, M.E.; Kingravi, H.A.; Vela, P.A. A Comparative Study of Efficient Initialization Methods for the K-Means Clustering Algorithm. ArXiv 2012, arXiv:1209.1960. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. A Universal density profile from hierarchical clustering. Astrophys. J. 1997, 490, 493–508. [Google Scholar] [CrossRef]
- Elhamifar, E.; Vidal, R. Sparse Subspace Clustering: Algorithm, Theory, and Applications. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2765–2781. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, M.; Seraj, R.; Islam, S.M.S. The k-means Algorithm: A Comprehensive Survey and Performance Evaluation. Electronics 2020, 9, 1295. [Google Scholar] [CrossRef]
- Estevez, P.A.; Tesmer, M.; Perez, C.A.; Zurada, J.M. Normalized Mutual Information Feature Selection. IEEE Trans. Neural Netw. 2009, 20, 189–201. [Google Scholar] [CrossRef]
- Castaldi, F.; Chabrillat, S.; Jones, A.; Vreys, K.; Bomans, B.; Van Wesemael, B. Soil Organic Carbon Estimation in Croplands by Hyperspectral Remote APEX Data Using the LUCAS Topsoil Database. Remote Sens. 2018, 10, 153. [Google Scholar] [CrossRef]
- Gomez, S.; Van Der Walt, S.; Schönberger, J.L.; Nunez-Iglesias, J.; Boulogne, F.; Warner, J.D. Scikit-image: Image Processing in Python. PeerJ 2014, 2, e453. [Google Scholar]
- Van der Maaten, L.; Hinton, G.E. Visualizing Data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Linderman, G.C.; Rachh, M.; Hoskins, J.G.; Steinerberger, S.; Kluger, Y. Fast Interpolation-based t-SNE for Improved Visualization of Single-Cell RNA-Seq Data. Nat. Methods 2017, 16, 243–245. [Google Scholar] [CrossRef]
- Guo, W.; Zhang, W.; Zhang, Z.; Tang, P.; Gao, S. Deep Temporal Iterative Clustering for Satellite Image Time Series Land Cover Analysis. Remote Sens. 2022, 14, 3635. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).