Auroral Image Classification Based on Second-Order Convolutional Network and Channel Attention Awareness

Abstract

Accurate classification of ground-based auroral images is essential for studying variations in auroral morphology and uncovering magnetospheric mechanisms. However, distinguishing subtle morphological differences among different categories of auroral images presents a significant challenge. To excavate more discriminative information from ground-based auroral images, a novel method named learning representative channel attention information from second-order statistics (LRCAISS) is proposed. The LRCAISS is highlighted with two innovative techniques: a second-order convolutional network and a novel second-order channel attention block. The LRCAISS extends from Resnet50 architecture by incorporating a second-order convolutional network to capture more detailed statistical representation. Meanwhile, the novel second-order channel attention block effectively recalibrates these features. LACAISS is evaluated on two public ground-based auroral image datasets, and the experimental results demonstrate that LRCAISS achieves competitive performance compared to existing methods.

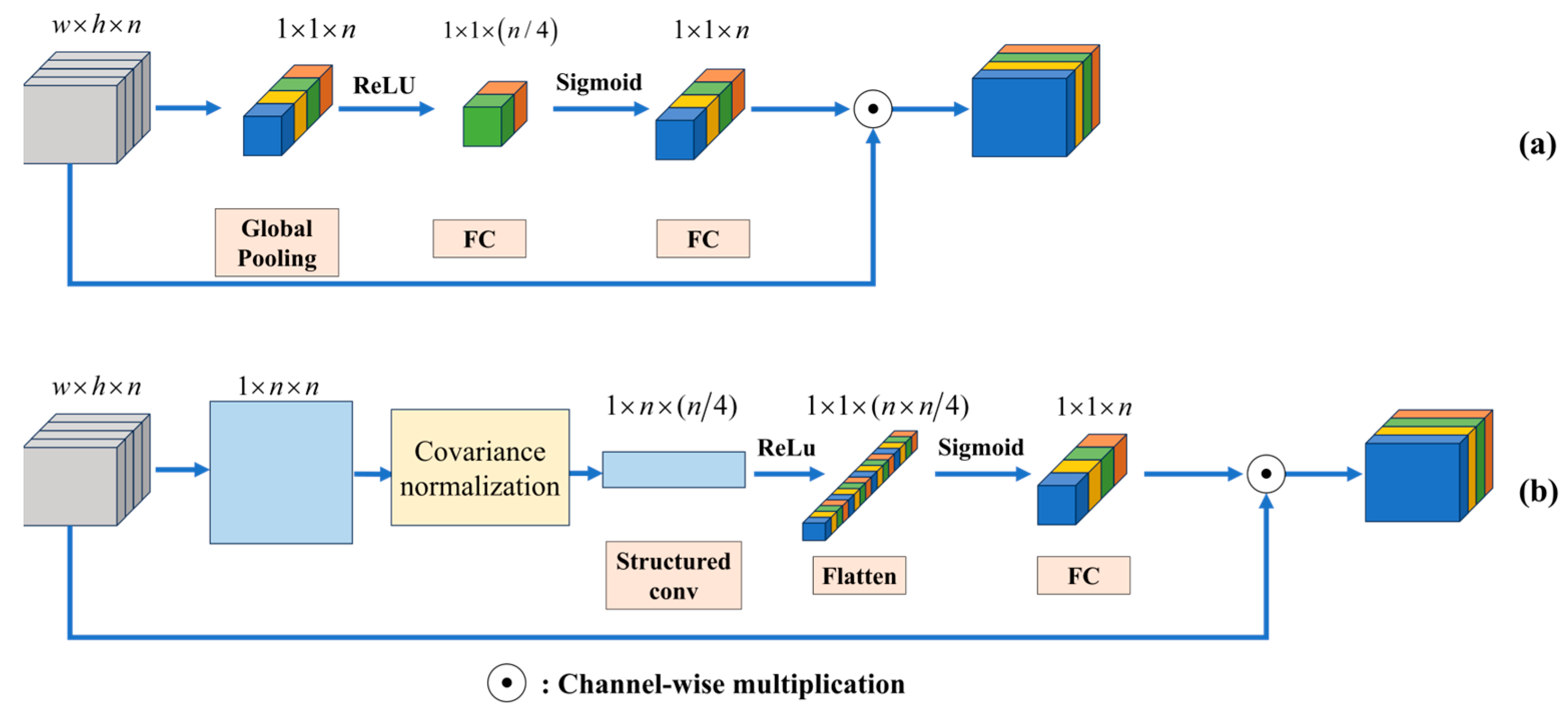
1. Introduction

Auroras are the most captivating manifestations of solar winds, which arise from the collision of charged particles ejected from the solar and molecules in the Earth’s upper atmosphere [1]. Different shapes or colors of auroras are linked to the physical characteristics of the Earth’s atmosphere, and a variation in auroral morphology indicates the development of an auroral substorm. Akasofu [2] modeled the development of an auroral substorm by different auroral morphology. Sado et al. [3] attempted to predict magnetometer value with the integration of magnetometer data and auroral image. Therefore, classifying auroral images specifically by shape or color helps in discovering physical messages in near-Earth space and understanding the mechanisms of the phenomena caused by disturbances in the magnetosphere [4]. All-sky imagers are the main source of auroral images, and they provide continuous observation of auroras with high resolution, which are conducive to analyzing auroral variation and morphology [5].

Initially, auroral images are manually labeled [6], which is not capable of leveraging an enormous number of auroral images. Traditional auroral image classification methods design features to correspond to different tasks and then feed classifiers with the extracted features [7,8]. Since it is difficult to distinguish complex auroral structures by using only a single feature to represent the image, methods are devised to model the correlation among different features [9,10]. Recently, deep learning networks for automatic feature extraction have rapidly evolved as handcraft feature-based aurora image classification methods relying on expert knowledge. Convolutional neural networks (CNN) are widely used in image classification tasks [11,12,13,14,15,16,17,18,19], and several effective CNN architectures are utilized to classify auroral images [15,16]. In addition, CNNs can be considered feature extractors, and the features generated based on CNNs can be used to train classifiers [17]. Yang et al. [19] integrated multiwavelength information from auroral images to enhance classification performance. A CNN automatically extracts features in the local receptive field and aggregates all channels using the same weights. But the human visual system tends to focus more on essential and differential features. To apply such a mechanism in the computer vision domain, attention methods are introduced into different models.

Channel attention methods calculate attention scores for every channel and then rescale the input features. A large attention score means its corresponding component plays a crucial role in classification, and a small attention score indicates that the information needs to be suppressed. Squeeze-and-excitation networks (SENets) [20] adaptively assign attention scores by simple operations: the SE block first applies global average pooling (GAP) to initialize each attention score, and two multi-layer perceptron (MLP) layers with nonlinear activation functions are followed to learn the interdependency among channels. Finally, attention scores are imposed on each channel to rescale the input features. Subsequently, the convolutional block attention module (CBAM) [21] demonstrates the information loss during global pooling and addresses this issue by adding global max pooling (GMP) information. To better understand this problem, frequency channel attention (FcaNet) views channel compression as a discrete cosine transform (DCT) [22] and points out that all frequency components still contain discriminative information, creating the need for a better way to initialize attention scores. Paralleling this channel attention strategy, the self-attention mechanism also advances image representation. It encodes the internal correlations within an image by assessing the mutual alignment of features via their query, key, and value representations. Transformer was originally proposed for natural language processing (NLP) problems by Vaswani et al. [23], which is based on a pure self-attention mechanism. Hence, the Transformer architecture is adapted for image processing, giving rise to a multitude of Transformer variants tailored for visual tasks [24,25,26,27,28]. While Transformers show superior performance on large datasets, their efficacy on smaller datasets is comparatively limited, as they possess less inductive bias than CNNs [26]. Furthermore, the existing deep learning networks rarely explore feature distribution higher than first-order statistics.

Second-order statistics encapsulate the feature interdependencies, contributing to more discriminative representations than first-order statistics. These statistics, exemplified by covariance matrices, inhabit a curved manifold space as opposed to the flat Euclidean space, which presents challenges in exploring the geometric properties of the covariance matrix space. Aided by two pivotal metrics, the Log-Euclidean (Log-E) metric [29] and Power-Euclidean (Pow-E) metric [30], a multitude of methodologies are introduced to delve into the geometry of second-order statistics space [29,30,31,32,33,34]. Huang et al. [32] built a deep Riemannian network for a symmetric positive definite (SPD) matrix involving the Log-E metric. Li et al. [33] proposed matrix power normalized covariance (MPN-COV) by changing the way to calculate covariance and utilizing the Pow-E metric. Hu et al. [34] exploited the manifold geometry by Log-E metric and adopted Riemannian manifold learning to obtain more compact and separatable CovDs. These methods successfully embed second-order statistics into deep networks, and MPN-COV presents slight differences between Log-E and Pow-E: the Log-E metric measures geodesic distance precisely, and the Pow-E metric measures it in a proximate way. They demonstrate that Pow-E acquires competitive results on large-scale datasets, but the efficiency of the above two metrics on task-specific datasets, like the auroral image dataset, is still unknown. Both second-order statistics and channel attention explore the feature correlation among channels; to learn more representative feature expression, second-order attention methods are proposed [35,36,37,38]. However, a limited number of methods are specifically designed for auroral image classification within this paradigm.

In conclusion, the main challenges in existing auroral image classification methods are summarized as follows: (1) existing CNN-based methods cannot directly exploit second-order statistics; (2) the interdependencies are not considered in feature representations. To address these two problems, a novel method named learning representative channel attention information from second-order statistics (LRCAISS) is proposed. Extensive experiments are conducted on two public auroral image datasets. The main contributions are as follows:

(1)

A second-order convolutional network is built. The second-order statistics are exploited by calculating covariance matrices from CNN-based features. Experimental results demonstrate that the Log-E metric explores the geometry of covariance matrix space better than the Pow-E metric for auroral image classification.

(2)

A novel second-order attention block is designed. LRCAISS learns attention scores from second-order statistics rather than first-order statistics and replaces covariance pooling with a trainable 1D convolutional layer to adaptively inherit more information from second-order statistics.

(3)

Experimental results on two public datasets show the superiority of LRCAISS over existing auroral image classification and attention-based image classification methods.

2. Proposed Method

2.1. Overview of the Proposed Method

This section exhibits the workflow of the proposed LRCAISS. As shown in Figure 1, auroral images are input into the backbone to extract low-level features. And then a second-order convolutional network exploits the second-order statistics from the extracted low-level features, which outputs discriminative tensor features. Finally, two MLP layers are used as classifiers. The second-order convolutional network contains an encoding block, a second-order channel attention (SCA) block, and operations for leveraging the discriminative ability of extracted features. Each part of LRCAISS is detailed below.

2.2. Backbone Network

Resnet-50 is an efficient CNN architecture and is involved in many successful networks [39]. The output feature map dimension from the last convolutional layer of Resnet-50 is $7\times 7\times 2048$, whose channel dimension is much larger than the sample size. Directly using a pretrained CNN by cutting off the fully connected (FC) layers encounters the HDSS challenge, which hinders robust covariance estimation [40,41]. To effectively compute second-order statistics, it is essential that the spatial dimensions of the feature maps exceed the number of channels. The backbone in LRCAISS is modified from Resnet-50, and its detailed parameter settings are provided in

Table 1. The backbone network settings.

Layer Name	Output Size	Modified Resnet-50
Conv 1	(112, 112, 64)	$7\times 7$, 64, Stride = 2
Stage 1	(56, 56, 256)	$\left[\begin{array}{c}1\times 1,64\\ 3\times 3,64\\ 1\times 1,256\end{array}\right]\times 3$, Stride = 2
Stage 2	(28, 28, 512)	$\left[\begin{array}{c}1\times 1,128\\ 3\times 3,128\\ 1\times 1,512\end{array}\right]\times 4$, Stride = 2
Stage 3	(28, 28, 1024)	$\left[\begin{array}{c}1\times 1,256\\ 3\times 3,256\\ 1\times 1,1024\end{array}\right]\times 6$, Stride = 1
Stage 4	(28, 28, 2048)	$\left[\begin{array}{c}1\times 1,512\\ 3\times 3,512\\ 1\times 1,2048\end{array}\right]\times 3$, Stride = 1
Conv 2	(28, 28, $n$)	$1\times 1,256$, Stride = 1

. The changes of backbone network from Resnet-50 include the removal of down sampling in Stage 3 and Stage 4 [42,43], and the addition of an $1\times 1$ convolutional layer (Conv 2) to the last convolutional layer of the modified Resnet-50, resulting in the size of the output of the backbone network being $w\times h\times n$.

2.3. Second-Order Convolutional Network

The second-order convolutional network is designed to better extract and fully utilize the second-order statistics. Starting with an encoding block, the CovD is calculated to capture high-order information from the CNN-based features. The SCA block is followed to excavate the potential correlations between channels, and assign different weights to rescale feature maps. And then the CovD is calculated with the rescaled feature map, and finally the CovD is flattened to a vector feature. By exploiting the symmetry of CovD, the upper triangular elements of CovD are retained. Then, diagonal and non-diagonal elements are attributed different weights and finally flattened into vector features for FC layers:

$$V=\left[e_{1,1},\dots ,e_{n,n},\sqrt{2}{e}_{1,2},\dots ,\sqrt{2}{e}_{n-1,n}\right],$$

(1)

where $E=\left[e_{1,1},\dots ,e_{n,n},e_{1,2},\dots ,\sqrt{2}{e}_{n-1,n}\right]$ is the output of covariance normalization block, and $V$ is the vectorized $E$ with the length of $n\left(n+1\right)/2$.

2.3.1. Encoding Block

The CNN-based feature $F\in {ℝ}^{w\times h\times n}$, extracted from the auroral image $I$ via the backbone network, is reshaped into $G=\left[g_1,\dots ,g_s\right]$, where $s=w\times h$ and $g_k$ is a $n$-dimensional feature. CovD $X$ encapsulates feature correlation between channels [44,45], which is calculated as:

$$\mu ={\displaystyle \frac{1}{s}}{\displaystyle \sum _{k=1}^s{g}_k},$$

(2)

$$X={\displaystyle \frac{1}{s-1}}{\displaystyle \sum _{k=1}^s\left(g_k-\mu \right)}{\left(g_k-\mu \right)}^T,$$

(3)

$\mu$ denotes the mean vector of the input feature maps over channel, and they are subtracted to suppress the noise in an auroral image. CovD is a common form of second-order statistics, whose diagonal elements are the variances of each channel, and the off-diagonal components stand for the covariances between channels. If all the channel-wise features are independent, the off-diagonal elements in CovD are zero, and the second-order statistics are equivalent to first-order statistics. The condition $s>n$ is ensured and thus the CovD $X$ is a symmetric positive definite (SPD) matrix which resides on the SPD manifold.

2.3.2. Covariance Normalization

Since CovD $X$ lies on the SPD manifold, covariance normalization should be involved to better exploit the geometry of the covariance matrix space. The Log-E metric and the Pow-E metric are two widely used metrics [33]. For both metrics, singular value decomposition (SVD) is implemented on $X$:

$$X=U\Lambda U^T,$$

(4)

where $\Lambda$ is a diagonal matrix with all eigenvalues in order, and $U$ is an orthogonal matrix. Occasionally, some eigenvalues are extremely small, which wakens the robustness of extracted features. The gate function is utilized to exclude small eigenvalues:

$${\Lambda }_P=\left\{\begin{array}{c}\Lambda ,\Lambda \ge \epsilon \\ \epsilon ,\Lambda <\epsilon \end{array}\right.,$$

(5)

where $\epsilon$ is a preset positive constant and ${\Lambda }_P=diag\left({\lambda }_1,\dots ,{\lambda }_n\right)$ contains the normalized eigenvalues. Following [32], $\epsilon$ is set as 0.0001. And the Log-E metric is defined as:

$$E_L=U\log \left({\Lambda }_P\right)U^T=Udiag\left(\log \left({\lambda }_1\right),\dots ,\log \left({\lambda }_n\right)\right)U^T,$$

(6)

where $E_L$ denotes the normalized CovD $X$. Logarithm operation is imposed on eigenvalues and $E_L$ is obtained with orthogonal matrix $U$. Different from Log-E, the Pow-E metric is imposed by covariance matrix power operation:

$$E_P=U{\Lambda }_P^{\alpha }{U}^T=Udiag\left({\lambda }_1^{\alpha },\dots ,{\lambda }_n^{\alpha }\right)U^T,$$

(7)

where $E_P$ represents the CovD normalized by Pow-E metric and $\alpha$ is a positive real number. The Pow-E metric is evaluated with $\alpha =0.5$ since in large-scale visual recognition tasks, this setting obtains the best performance [33]. In the rest of the article, for brevity, $E$ is used to denote $E_L$ or $E_P$.

2.3.3. SCA Block

Figure 2a depicts the framework of the SE block which is a classic structure, and existing channel attention methods are adapted on this foundation. The SE block contains global pooling and two FC layers with ReLU and Sigmoid activation functions. ReLU and Sigmoid are used to provide non-linearity; furthermore, Sigmoid is inserted at the end of channel attention block to map the attention values between 0 and 1.

Figure 2b details the SCA block, which is computed as:

$$\mathit{w}={\delta }_s\left(W_{2}reshape\left({\delta }_r\left(W_1\ast E\right)\right)\right),$$

(8)

where $\mathit{w}$ is the output of the SCA block, which represents the attention scores with the size $1\times 1\times n$, $\ast$ symbolizes 1D convolution, $reshape\left(•\right)$ represents the flattened operation, ${\delta }_s\left(•\right)$ and ${\delta }_r\left(•\right)$ correspond to the Sigmoid and ReLU activation functions, $W_1\in {ℝ}^{\left(n/4\right)\times n}$ and $W_2\in {ℝ}^{n\times \left(n^2/4\right)}$ encompass the weight sets of the 1D convolutional layer and the FC layer. To derive the channel correlation from $E$, a previous method like SOCA (the block for extracting second-order statistics in SAN) utilizes global covariance average pooling. The SCA block replaces the global covariance average pooling with a 1D convolutional layer of $n/4$ filters of $n\times 1$ kernel, which reduces the feature map dimension to $n\times n/4$. The 1D convolution layer performs row-wise convolution on CovD, where the row-wise element in CovD represents the correlation between one channel and all channels. Different from global covariance pooling, which only preserves the average value, the 1D convolution dynamically outputs a better transformation of the CovD. And then the ReLU activation follows the 1D convolutional layer for nonlinearity. Finally, one FC layer is adopted to rescale the feature length to $1\times 1\times n$ and a Sigmoid is used to turn the attention scores into positive values. The output of the SCA block is a vector feature that signifies the importance of each channel, which is used to rescale the feature maps:

$$F_{scale}=\mathit{w}F=\left[w_1{f}_1^{\prime },\dots ,w_n{f}_n^{\prime }\right],$$

(9)

where $f^{\prime }$ denotes one 2D feature map from $F$ with the size of $w\times h$ and $F_{scale}$ is the rescaled feature map. $F_{scale}$ is acquired by channel-wise multiplication of attention scores $w$ and the CNN-based feature $F$.

The training stage of LRCAISS is summarized in Algorithm 1; $N$ is the number of auroral images for training and $c$ is the number of auroral image categories.

Algorithm 1: Training of LRCAISS

$\mathbf{Input}\mathbf{:}\mathrm{Auroral} \mathrm{images} {\left\{I_i\right\}}_{i=1}^N$$, \mathrm{the} \mathrm{corresponding} \mathrm{labels} {\left\{l_i\right\}}_{i=1}^N,l_i\in \left\{1,2,\dots ,c\right\}$, the parameters of network $W$$, \mathrm{the} \mathrm{learning} \mathrm{rate} \gamma =0.0001$, the maximum epoch 100, the number of SCA blocks $t$ $\mathbf{Output}\mathbf{:}\mathrm{The} \mathrm{optimized} \mathrm{network} \mathrm{parameters} W^{\ast }$

$\mathbf{For} Ite{r}_1\to$100 do $\mathrm{Extract} \mathrm{the} \text{CNN-based} \mathrm{features} {\left\{F_i\right\}}_{i=1}^N,F_i\in {ℝ}^{w\times h\times n}$ $\mathrm{Calculate} \mathrm{CovDs} \mathrm{as} {\left\{X_i\right\}}_{i=1}^N$$\mathrm{with} {\left\{F_i\right\}}_{i=1}^N$ by Equations (2) and (3). $\mathrm{Applying} \mathrm{covariance} \mathrm{normalization} \mathrm{on} {\left\{X_i\right\}}_{i=1}^N$$\mathrm{to} \mathrm{obtain} {\left\{E_i\right\}}_{i=1}^N$ via Equations (6)–(8). $\mathbf{For} Ite{r}_2\to$$t$ do       $\mathrm{Learning} \mathrm{attention} \mathrm{scores} {\left\{w\right\}}_i^N$$\mathrm{with} {\left\{E_i\right\}}_{i=1}^N$ by Equation (8).       $\mathrm{Rescale} \mathrm{the} \text{CNN-based} \mathrm{features} {\left\{F_i\right\}}_{i=1}^N$$\mathrm{with} {\left\{w\right\}}_i^N$ by Equation (9). End for $\mathrm{Calculate} \mathrm{new} \mathrm{CovDs} {\left\{X_i^{\ast }\right\}}_{i=1}^N$$\mathrm{with} {\left\{F_{scale,i}\right\}}_{i=1}^N$ by Equations (2) and (3). $\mathrm{Applying} \mathrm{covariance} \mathrm{normalization} \mathrm{on} {\left\{X_i^{\ast }\right\}}_{i=1}^N$$\mathrm{to} \mathrm{obtain} {\left\{E_i^{\ast }\right\}}_{i=1}^N$ via Equations (4)–(6). $\mathrm{Preserve} \mathrm{the} \mathrm{upper} \mathrm{triangular} \mathrm{elements} \mathrm{and} \mathrm{flatten} \mathrm{them} \mathrm{with} {\left\{E_i^{\ast }\right\}}_{i=1}^N$$\mathrm{to} \mathrm{acquire} {\left\{V_i^{\ast }\right\}}_{i=1}^N$ by Equation (1). $\mathrm{After} \mathrm{processing} \mathrm{of} {\left\{V_i^{\ast }\right\}}_{i=1}^N$ through two MPL layers, the predicted labels are derived. Update the model parameters W$\mathrm{by} \mathrm{minimizing} \mathrm{the} \text{cross-entropy} \mathrm{loss} \mathrm{between} {\left\{l_i\right\}}_{i=1}^N$ and predicted labels, adjusting for the learning rate $\gamma$. End for

3. Datasets and Experimental Settings

To ensure the reproducibility of the experiments, this section provides detailed information on the two auroral image datasets and the experimental settings.

3.1. Dataset Description

Two public auroral image datasets are utilized to evaluate the proposed methods. In this paper, the names of all auroral categories are italicized to make the expression clear. Dataset 1 [15] was collected by the all-sky camera from 2010 to 2019, deployed at Kiruna, Sweden. The latitude and longitude location of the camera is 67.84°N, 20.42°E. This all-sky camera archives images in JPEG with a resolution of $720\times 479$ pixels. All images were preprocessed by rotation, filtering, and cropping, resulting in a resolution of $128\times 128$ pixels. The images were then manually labeled, and finally, 3864 images were selected from 14,030 images to constitute Dataset 1. Seven categories are involved, including breakup, colored, arcs, discrete, patchy, edge, and faint. The representative samples from each category are displayed in Figure 3, and the sample distribution of different types is listed in

Table 2. Number of images in different categories.

No	Class	Number
1	Arcs	831
2	Discrete	194
3	Colored	133
4	Edge	217
5	Breakup	146
6	Faint	175
7	Patchy	2150

.

Dataset 2 [17] originates from the Time History of Events and Macroscale Interactions during Substorms (THEMIS) all-sky imagers system [46], which contains 5824 images with the resolution of $256\times 256$ pixels. Their classification criterion is adapted from [47], which divides the images into four classes: no aurora, arcs, patchy aurora, and omega-band. Novock et al. [17] use similar types, namely diffuse as patchy and discrete as omega-band aurora, and classify no aurora into three subclasses: cloudy, moon, and clear. The examples of each class are exhibited in Figure 4, and the sample distribution is provided in

Table 3. The number of sample distributions of Dataset 2.

No	Class	Number
1	Arcs	774
2	Discrete	1400
3	Diffuse	1102
4	Cloudy	852
5	Moon	614
6	Clear	1082

.

The difference between Dataset 1 and Dataset 2 is that the number of images in each category in Dataset 1 is not evenly distributed, which may cause the model to perform poorly in certain categories. The classification criteria of the two datasets are also not quite the same; Dataset 1 dispatches images without auroras and classifies aurora images into seven categories in a more detailed manner, with some unique categories added, such as taking into account the position of the aurora in the image and the color of the auroras by classifying them into edge and colored. On the other hand, Dataset 2 not only categorizes auroras but also subdivides the non-aurora images into three categories, which helps to determine the presence of auroras. Different categories have corresponding physical meanings, e.g., arcs represents a steady state of auroras [11], which is generated by the acceleration of quasi-static particles [48]. Discrete represents a mixed representation of multiple physical processes that generate auroras, and patchy consists of several pulsating structures [49]. Collisions between different energetic particles produce auroras of different colors, so colored is related to the altitude and excited atmosphere component. The detailed classification criteria of the two datasets are in [15,17].

3.2. Experimental Settings

3.2.1. Implementation Details

Experiments were conducted on a high-performance platform, utilizing an 11th Gen Intel^® Core™ i9-11980HK @ 2.60 GHz 3.30 GHz, complemented by an NVIDIA GeForce GTX 3070 Laptop GPU. The computational environment was established using Python 3.7.0 and PyTorch 1.11.0.

To bolster the credibility of experiments and assess the generalization capability of the LRCAISS method, a rigorous approach was employed to dataset partitioning. The datasets were split using four random seeds: 42, 306, 3406, and 114,514, ensuring variability and robustness in results. Specifically, Dataset 1 is apportioned into training and testing sets in a ratio of 3000:846, following the precedent set by [15]. Similarly, Dataset 2 is divided with a ratio of 7:3, aligning with the methodology described in [17].

For the backbone network, the Resnet-50 model pretrained on the Image-1K dataset was utilized, ensuring a strong foundation for feature extraction. Within the network’s architecture, the feature dimension $n$ at the Conv 2 layer was set to 256. The learning process is meticulously tuned with a learning rate of 0.0001, employing the Adam optimizer over 100 training epochs to achieve convergence. The cross-entropy loss function was employed to facilitate the training process, providing a reliable measure of performance and guiding the optimization towards the most discriminative features.

3.2.2. Evaluation Metric

To better understand the experimental results, four evaluation metrics are involved, including accuracy, precision, recall, and F1-score. The true positive (TP) represents the number of samples correctly classified as a specific category, false positive (FP) is the number of samples erroneously predicted as a specific category, true negative (TN) means the number of samples accurately classified for the rest of the categories, and false negative (FN) represents the number of images incorrectly predicted as the remaining categories. Four evaluation metrics are computed as in [50]:

$$Accuracy={\displaystyle \frac{TP+TN}{TP+TN+FP+FN}},$$

(10)

$$Precision={\displaystyle \frac{TP}{TP+FP}},$$

(11)

$$Recall={\displaystyle \frac{TP}{TP+FN}},$$

(12)

$$F1\_score=2{\displaystyle \frac{Precision\times Recall}{Precision+Recall}}.$$

(13)

4. Experiments

In this section, extensive experiments are conducted on the two datasets. The experiments are employed to find out the best configuration and then compare LRCAISS with other methods based on attention mechanisms and second-order statistics. The best results are bolded.

4.1. Effectiveness of Different Configurations

Several configurations in LRCAISS, namely, the backbone network settings, the attention blocks, and the metrics, that seem to have an impact on the results, and a series of experiments are employed on two ground-based auroral image datasets to analyze their performance. In this subsection, two datasets are divided into training sets and testing sets by four random seeds 42, 306, 3406, 114,514, to identify better configurations in a more generalized context.

Previous research only provides the difference between the two metrics theoretically but does not analyze them on specific tasks [33]. The performances of two second-order channel attention methods with different metrics are shown in

Table 4. The overall accuracy of different metrics (in %, mean ± standard deviation).

Datasets	Methods	Accuracy
Dataset 1	SOCA + Log	94.60 ± 0.42
	SOCA + Pow	94.39 ± 0.81
	SCA + Log	98.05 ± 0.18
	SCA + Pow	97.14 ± 0.32
Dataset 2	SOCA + Log	92.92 ± 0.40
	SOCA + Pow	92.11 ± 0.83
	SCA + Log	94.11 ± 0.72
	SCA + Pow	92.99 ± 0.50

. Generally, SCA + Log obtains the best results, and the Log-E metric outperforms the Pow-E metric. This demonstrates that the Log-E metric explores the geometric properties of covariance matrix space geometry better in the context of the second-order channel attention mechanism approach, and the Log-E metric is adopted in the subsequent experiments.

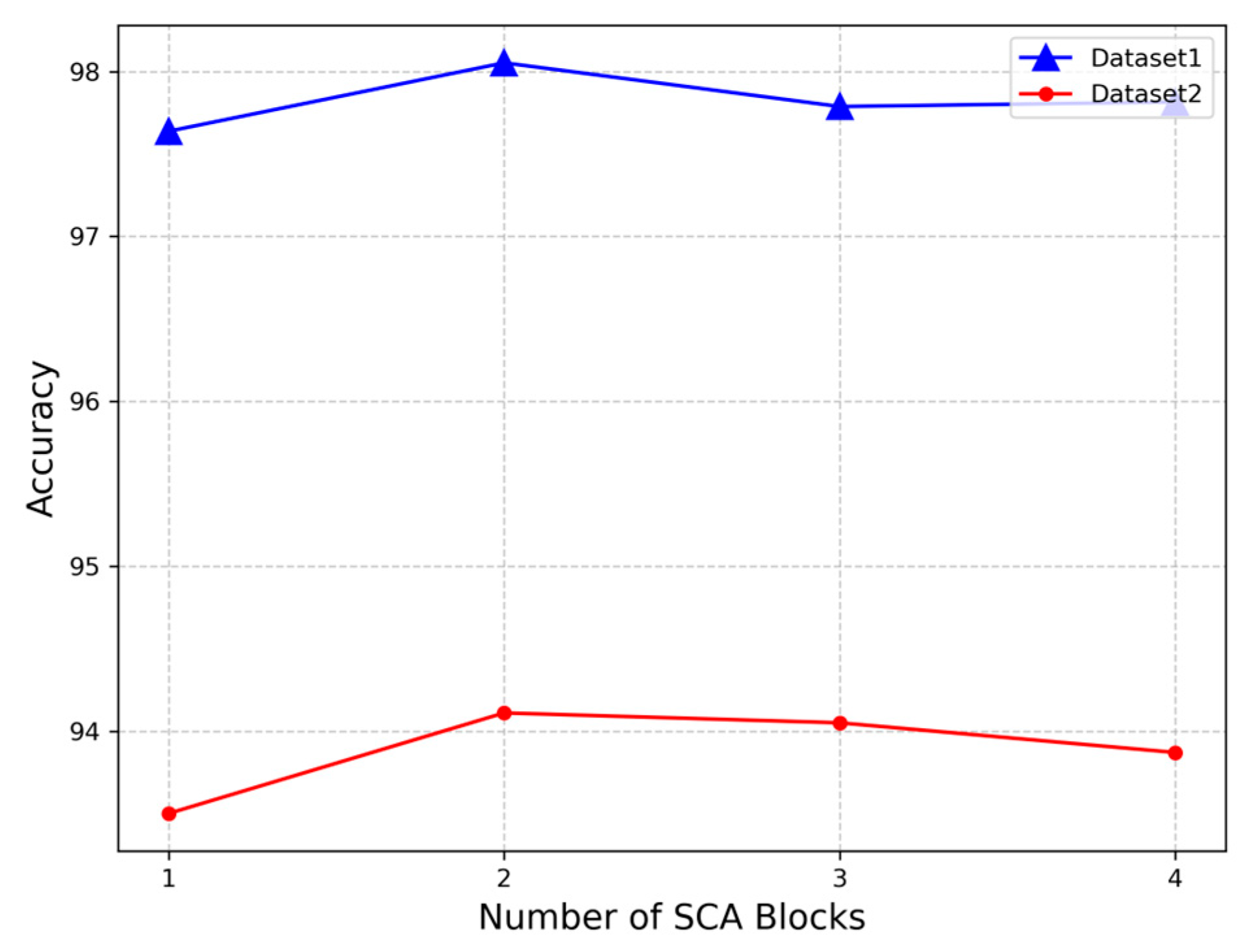
The SCA block can be cascaded multiple times to comprehensively capture channel attention information, and the optimal number of SCA blocks for aurora image classification is needed. Figure 5 illustrates how accuracy varies with the number of SCA blocks ranging from one to four. The trend in classification accuracy change is similar across both datasets. Specifically, the accuracy peaks when there are two SCA blocks. However, deviating from this optimal number, either increasing or decreasing the count, leads to diminished classification accuracy. Hence, LRCAISS is designed with two SCA blocks.

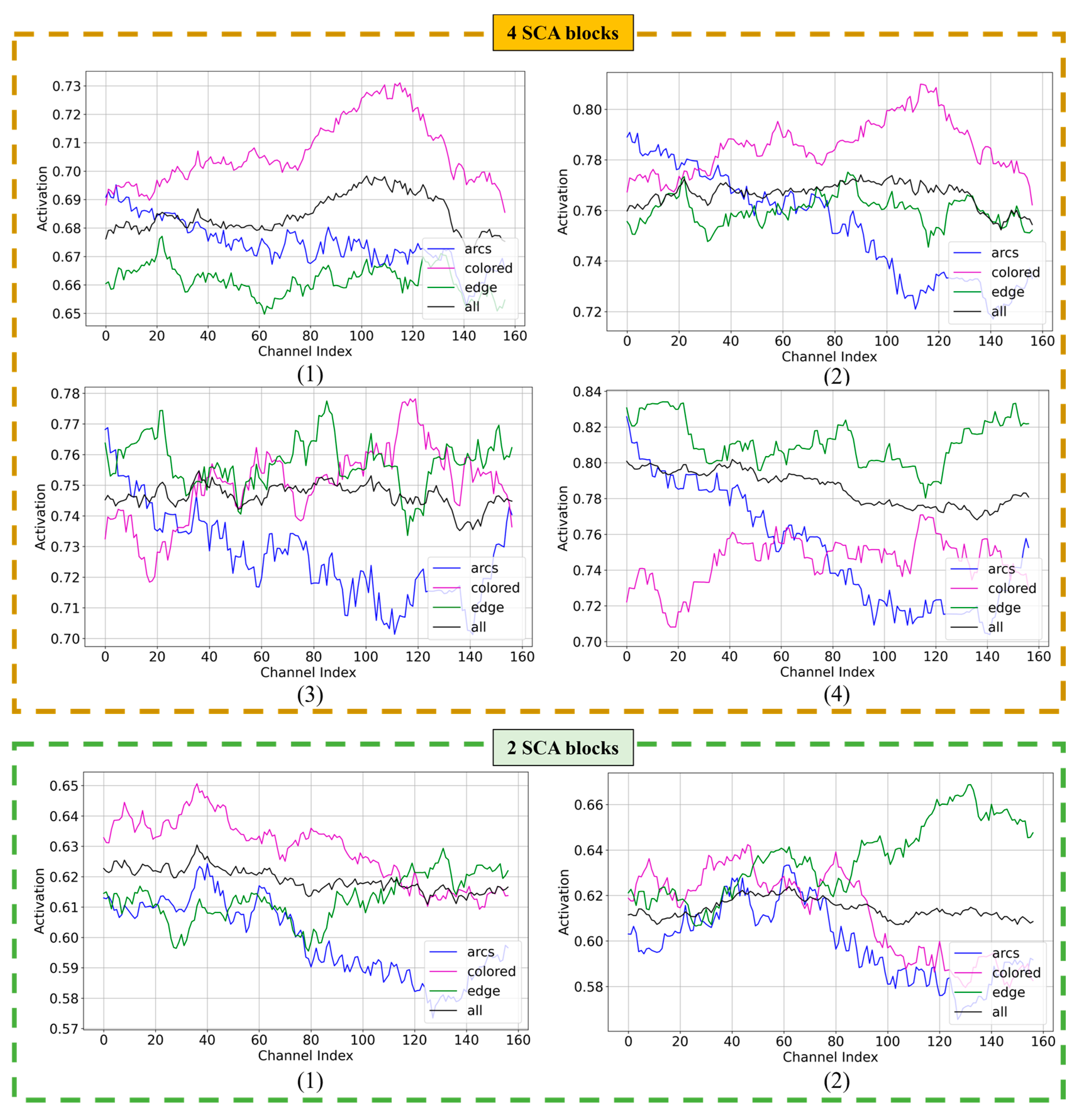
To further understand the second-order channel attention mechanism operating in LRCAISS, three classes of auroral images are sampled in Dataset 1, and the distribution of average channel attention activation is shown in Figure 6. And the distribution of average activation over all classes is provided for comparison. Directly drawing the activation of each channel would result in an irregular graph, so shift smoothing is applied to enhance its clarity, and the horizontal coordinate is less than 256, the number of channels. The number below each graph denotes the distribution output by the corresponding SCA block, and larger activation values mean the channel plays a more important role in classification. As for the LRCAISS with four SCA blocks, the activation distributions of each SCA block are provided in the upper part of Figure 6. From the first to the fourth block, the activation values become more class-specific. For LRCAISS with two SCA blocks, a consistent pattern is observed, which is that the variation in attentional values between channels increases progressively from the first to the second block. This suggests that the blocks help the network to better discern differences between classes. Furthermore, according to the results in Figure 5, two blocks achieved the best performance. This may be because two blocks are sufficient to learn the necessary differences, while more blocks led to overfitting and fewer blocks did not capture enough distinctions. This phenomenon also suggests that directly cascading the SCA block may not significantly enhance the network’s representational capacity.

Generally, features extracted from the shallow layer contain basic information like texture and edge, and features from the deep layer concentrate more on the semantic representation, such as the holistic concept [16]. Moreover, to better explore the discriminative ability of features extracted from different layers, the results are obtained by different configurations of the backbone network in

Table 5. The classification accuracy of different backbone network settings (in %, mean ± standard deviation).

Datasets	Stage 1	Stage 2	Stage 3	Stage 4	Accuracy
Dataset 1	✓				98.05 ± 0.18
	✓	✓			98.01 ± 0.05
	✓	✓	✓		97.79 ± 0.29
	✓	✓	✓	✓	97.52 ± 0.22
Dataset 2	✓				94.11 ± 0.75
	✓	✓			93.29 ± 0.24
	✓	✓	✓		93.95 ± 0.53
	✓	✓	✓	✓	93.50 ± 0.37

. The application of the backbone network, using the backbone ticked in Stage 1 of Table 5 as an example, consists of Conv 1, Stage 1, and Conv 2. Obviously, the backbone with only Stage 1 achieves the best results on both datasets. The reason behind this is that second-order information may be more abundant in low-level features. Additionally, the classification accuracy on training sets with the four backbone configurations approaches 100%. However, with increasingly complex backbones, accuracy on the testing sets decreases, suggesting that complexity in the backbone architecture leads to overfitting.

Finally, the effectiveness of each component in LRCAISS is evaluated in

Table 6. The effectiveness of different components in LRCAISS (in %, mean ± standard deviation).

Datasets	Component
	Attention	Second-Order	Accuracy
Dataset 1			94.54 ± 0.48
	✓		93.08 ± 0.64
		✓	96.81 ± 0.34
	✓	✓	98.05 ± 0.18
Dataset 2			91.46 ± 0.66
	✓		88.32 ± 0.74
		✓	93.32 ± 1.06
	✓	✓	94.11 ± 0.72

. The network with attention or second-order methods acquires higher classification accuracy than the network structure without either technique, which validates the effectiveness of the two mechanisms in auroral image classification. LRCAISS obtains the best results on the two datasets since the CovD captures more representative information from the feature map, and the channel attention mechanism allows the network to focus on vital features.

Following the aforementioned ablation study, the main component of LRCAISS for auroral image classification consists of the first stage of Resnet50, two SCA blocks, and a Log metric. Additionally, the two-layer MLP is configured, with the first layer having a dimension of 256 and the second layer’s dimension corresponding to the number of aurora image categories.

4.2. Main Results

To address the effectiveness of the LRCAISS, a series of auroral image classification methods [16,17], attention methods [20,27], and second-order statistics methods [32,34,35] were evaluated. Novock et al. [17] utilized pretrained inception-v4 to extract features by cutting off the FC layers and training ridge classifier, which is a concise and effective solution to auroral image classification. Zhong et al. [16] utilized a pretrained CNN, which achieves competitive performance. Huang et al. [32] opened the direction of SPD matrix non-linear learning in deep learning models by solving the backpropagation on the Stiefel manifold. SE network [20] is a classic channel attention method, and SOCA [35] mines the channel attention scores from second-order statistics. CrossVIT [27] learns self-attention information, which is an improved version of VIT for more efficient and effective training. Hu et al. [34] proposed a method named learning deep tensor feature representation (LDTFR) on the Riemannian manifold to improve auroral image classification performance on a small sample set.

Table 7. The accuracy of different methods on two datasets (in %, mean ± standard deviation).

Datasets	Methods	Accuracy
Dataset 1	Novock et al. [17]	86.02 ± 1.07
	Zhong et al. [10]	94.61 ± 0.30
	Huang et al. [32]	96.18 ± 0.78
	SENet [20]	97.14 ± 0.09
	SOCA [35]	94.39 ± 0.81
	CrossVIT [27]	93.02 ± 0.86
	LDTFR [34]	96.98 ± 0.24
	LRCAISS	98.05 ± 0.18
Dataset 2	Novock et al. [17]	83.18 ± 1.19
	Zhong et al. [10]	91.46 ± 0.66
	Huang et al. [32]	86.94 ± 0.27
	SENet [20]	93.58 ± 0.34
	SOCA [35]	92.11 ± 0.83
	CrossVIT [27]	80.56 ± 1.57
	LDTFR [34]	91.71 ± 0.47
	LRCAISS	94.11 ± 0.72

shows the classification accuracy of different methods on the two datasets. Obviously, LRCAISS outperforms the channel attention method and second-order convolutional networks, demonstrating the effectiveness of the integration of the two mechanisms. Moreover, LRCAISS also acquires better results than SOCA block since the proposed method improves the calculation of second-order statistics and utilizes a 1D convolutional layer to substitute the global covariance pooling to inherit more information.

Figure 7a exhibits the confusion matrix of predictions with Dataset 1. Except for discrete and faint, the classification accuracies of the other types are higher than 90%. The reason for the high rate of misclassification of discrete is due to the small number of discrete in Dataset 1, which makes it difficult for the model to capture its characteristic, and any misclassification will lead to a significant decrease in the accuracy of this category. Figure 7b illustrates the confusion matrix of LRCAISS predictions of Dataset 2. Obviously, the proposed method recognizes the image types without auroral well, achieving precise detection of auroras. Misclassification occurs mostly among the three image types containing auroras since the classification criteria are occasionally ambiguous. Examples of misclassification are provided in the following section.

Table 8. Performance evaluation (%) of each category in Dataset 1.

Categories	Metrics
	Precision	Recall	F1 Score
Arcs	98.11	99.36	98.73
Breakup	96.77	93.75	95.24
Colored	84.85	90.32	87.50
Discrete	93.94	86.11	89.86
Edge	95.92	94.00	94.95
Faint	96.55	87.50	91.80
Patchy	99.22	100	99.61

shows the detailed performance assessment of Dataset 1. Colored has the lowest precision of 84.85% and F1 score of 87.50%, and the rest of the categories show scores ranging from 89% to 100%. Therefore, LRCAISS achieves near-perfect performance for most classes of auroral images. Discrete appears in various shapes and orientations of auroral arcs [15], which makes the boundary between discrete and other auroral images unclear, resulting in the largest misclassification.

Table 9. Performance evaluation (%) of each category in Dataset 2.

Categories	Metrics
	Precision	Recall	F1 Score
Arcs	93.58	77.78	84.95
Diffuse	90.77	95.02	92.85
Discrete	88.56	94.16	91.27
Cloudy	99.94	100	99.82
Moon	100	98.95	99.47
Clear	97.52	96.91	97.21

provides the results of each class in three evaluation metrics. The category discrete also has the lowest precision of 88.56%, and arcs has the lowest recall of 77.78%. Note that although some categories, like discrete, are presented in both datasets, they are defined slightly differently. Discrete is characterized by distinct auroras and sharp edges, but the auroras are not arc-shaped according to [17]. There are times when the arc is incomplete, or the combination of multiple arcs makes the boundaries of the arcs not obvious, making it difficult to distinguish between discrete and arcs.

Figure 8a is derived from Dataset 1. The difference between discrete and arcs is in whether the auroral arc is complete in an image. Figure 8a shows two discrete shapes connected in the middle of the image, which looks like an auroral arc with bright edges and a dark center, resulting in the misclassification from discrete to arcs. Figure 8b–d are misclassified samples selected from Dataset 2. The bottom of Figure 8b is arc-shaped, and it is incorrectly predicted as arcs. The classification model recognizes a bright and well-defined auroral arc in Figure 8c, but ignoring the boundary is ambiguous, and large patches of auroras are covered. Consequently, it is misclassified from discrete to arcs. Figure 8d depicts multiple auroras in an image, but the shapes are not strictly arced.

5. Discussion

The LRCAISS method is distinguished from existing approaches to auroral image classification in several notable ways. In contrast to methods such as those used by Zhong et al. [10] and Novock et al. [17], which apply deep learning models to the domain of auroral image classification with minimal adaptation, LRCAISS modifies the Resnet50 backbone for more effective feature extraction. By integrating the SCA block to capture channel interdependencies and rescale feature maps, LRCAISS achieves significant accuracy improvements of at least 3.44% and 2.55% on the two datasets, respectively.

While Huang et al. [32] concentrate on the dimension reduction of second-order statistics on the manifold, LRCAISS opts to control the size of second-order statistics by adjusting the dimensions of the final convolutional layer. Furthermore, by incorporating channel attention blocks, LRCAISS enhances the computation of second-order statistics, resulting in accuracy gains of 1.87% and 7.17% on the two datasets.

When compared to existing attention mechanisms, such as channel attention [20] and self-attention methods [27], LRCAISS demonstrates its superiority on auroral imager datasets. For instance, SENet [20] derives attention scores from first-order statistics, namely the mean values of each feature map. In contrast, LRCAISS derives attention values from second-order statistics, considering the variances of each channel and the covariances between channels. This approach allows the SCA block to extract richer discriminative information, leading to higher accuracy improvements of 0.89% and 0.53% on the two datasets. One plausible explanation for this enhancement is that LRCAISS not only replicates SENet’s strategy of capturing channel interdependencies but also expands upon it by calculating second-order statistics, thereby acquiring a more detailed understanding of channel relationships. CrossVIT [27] may necessitate larger datasets to achieve satisfactory results, indicating that LRCAISS could be more efficient in scenarios with limited data availability.

The SOCA [35] method diverges from LRCAISS in two key respects: LRCAISS subtracts the mean vector of features when calculating second-order statistics, boosting feature robustness, which SOCA does not perform subtraction operation. Additionally, the initialization of the channel attention scores differs; while SOCA uses global covariance pooling, LRCAISS employs a learnable 1D convolutional layer to better assimilate information from second-order statistics. This distinction results in LRCAISS achieving higher accuracy increases of 3.66% and 2% on the two datasets.

6. Conclusions

This paper introduces a second-order channel attention network named LRCAISS for auroral image classification. Experimental results on two auroral image datasets demonstrate the generalization ability of the proposed method, underscoring the effectiveness of LRCAISS. It is superior to the traditional channel attention methods based on first-order statistics, showing the advantage of learning attention scores from second-order statistics over first-order counterparts. Moreover, LRCAISS outperforms methods relying solely on second-order convolutional networks, indicating that integrating an attention mechanism improves auroral representation learning. Thus, the dual mechanism approach enhances performance, facilitating more effective auroral analysis. However, the current implementation of LRCAISS runs with a long computation time, which could be a limitation when processing large-scale image datasets. Future research should concentrate on refining the computational efficiency and incorporating the latest deep learning models into LRCAISS for better effectiveness. Additionally, diverse attention mechanisms, such as spatial attention, are proven effective in the domain of image classification. Therefore, exploring their relationships and integrating their strengths holds promise for advancing auroral image processing.