Abstract
Satellite imagery has become a widespread resource for modeling variability in lake surfaces. However, the extended monitoring of a lake’s perimeter faces significant challenges due to atmospheric obstacles that cannot be rectified. Due to the atmosphere’s everchanging opacity, only half of the acquired satellite images have reliable qualitative accuracy making it possible to identify a lake’s contour. Consequently, approximately 50% of the monthly lake outline values can be determined using remote sensing methods, leaving the remaining 50% unknown. This situation is applicable to three lakes in Morocco (Abakhan, Ouiouan, and Tiglmanine), the subjects of the current research for the period between 1984 and 2022. What can we do if, during a period of time in which we monitored the evolution of the surface of a lake by satellite means, we obtain only about 50% of the possible images? Shall we just settle for this and stop the analysis? Although it may be challenging to believe, the present study introduces two statistical methods for interpolating and validating the monthly values of the lake outline: the iterative ratio method based on the autocorrelation of the monthly water balance and the Kalman filter. We estimated the reconstruction errors of the missing values and validated the methodology using an inverse philosophy, reconstructing the initial data from the table of the simulation results. Given that the difference between the initial values and the reconstructed initial values resembles white noise or an AR (1) process with a low coefficient, we deemed the methodological approach acceptable. Several comparison criteria between the two interpolation methods were employed, yet determining the more appropriate one remains challenging. Based on our surface reconstruction method, Lake Abakhan, with an average area of 22 hectares, experienced significant fluctuations, ranging from a maximum of 34 hectares in 2010 to a minimum of 0.8 hectares in 2022. Lake Ouiouan, with an average area of 14 hectares, displayed much lower variation, with a maximum of 17 hectares in 2020 and a minimum of 6.5 hectares in 1988. Lake Tiglmanine showed a pattern similar to that of Lake Abakhan but with less pronounced fluctuations. With an average area of 6.1 hectares, its maximum was 9.2 hectares in 2011 and its minimum was 4.1 hectares in 1984.
Keywords:
RS application; Landsat; limited images; lakes; interpolation; Kalman filter; ratio method; water resources; Morocco 1. Introduction
Lakes, as vital freshwater resources, are directly usable [1]; however, climate change and human activities, such as converting wetlands into meadows or pastures, are damaging wetlands, causing soil drying, and reducing biodiversity [2]. Therefore, effective water resource management and ensuring water security are crucial for developing responsible policies [3]. Scientific efforts to determine the areas of lakes as correctly as possible are necessary as recent scientific studies have shown a clear correlation between the decreasing surface area of Morocco’s lakes and the intensifying effects of climate change. [4] Rising temperatures are leading to increased evaporation, while altered rainfall patterns result in reduced water inflow. This delicate balance, once tilted in favor of replenishment, now leans towards depletion.
The water surface area derived from remote sensing imagery is commonly used as a proxy for monitoring lake changes [5]. Recently, various remotely sensed images, including radar altimeters [6], Synthetic Aperture Radar (SAR) [7], and optical remote sensing images [8], have facilitated surface change monitoring. Among these, Landsat satellite sensors are preferred for lake monitoring [9,10,11,12,13,14]. The cloud cover during the monsoon season particularly presents significant challenges for extracting lake area using optical remote sensing [15], which limits hydrological studies of lakes with smaller surface areas.
Missing data is a complex problem in many research fields. In data mining, missing values not only result in the loss of useful information but also make it difficult for prediction models to identify underlying patterns in datasets [16]. To address this issue and predict future values, interpolation methods are often used [17]. Interpolation solves the problem of temporal and spatial gaps in data [18]. There are three main types of interpolation methods: temporal, spatial, and spatiotemporal [19]. Generally, interpolation techniques rely on the principles of spatial autocorrelation, which assumes that closer points are more similar than distant ones [20]. Interpolating remote sensing data is a well-researched area, often using statistical approaches to estimate missing values based on nearby data points [21]. In our study, we propose using the iterative ratio method and the Kalman filter to fill gaps in Landsat data for three lakes in Morocco.
The Moroccan Atlas contains about 40 modest and permanent lakes, known as “Daya or Aguelamam” [22,23,24]. The origin of the Middle Atlas lakes can be attributed either to topographic hollows of dissolution in the limestone, as exemplified by Aguelmam Azigza, or to basins formed by volcanic activity, as seen in the case of Aguelmam Sidi Ali [22]. In the upper Oued Oum Er Rbia watershed “UpB-OER”, the combination of highly karstified liasic carbonate formations and tectonic activity has led to the formation of basins of various sizes and important geological lineaments [24,25], which have hydrological consequences. These hydrosystems play crucial socio-economic and ecological roles across the country [26], especially in Khenifra province, which has the largest number of lakes in the Oum Er Rbia Water Basin Agency action area [27]. This article will focus on studying three lakes that we consider among the most representative of the Middle Atlas (Figure 1): Lake Ouiouane “LaO”, the central lake of Tiglmamine “c-LaT”, and Lake Abekhane “LaB”.
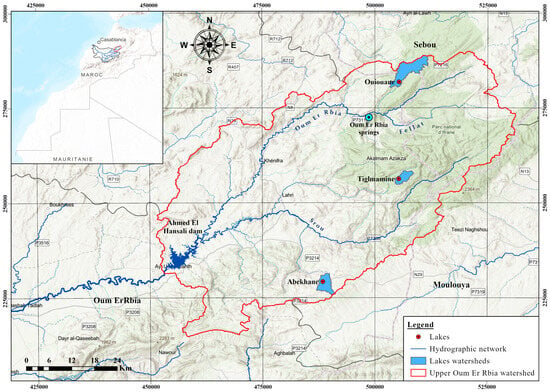
Figure 1.
Location of the three lakes at the upper Oued Oum Er Rbia watershed “UpB-OER”.
To the north of the UpB-OER lies the LaO (33°07′N, 5°20′W, 1620 m). This semi-artificial lake covers an area of 13 ha, with a catchment area of 26.7 km². It is shallow, relatively silted-up and home to an abundance of planktonic and benthic fauna. To the south, the LaB (32°40′N, 5°31′W, 1670 m) is a natural endoreic lake of karstic origin. With a catchment area of 12.6 km2, this mountain lake has an average surface area of 23 ha and a maximum depth of around 4 m. According to the plan of the Moroccan Protected Areas Directorate, the LaO and LaB are classified as sites of biological and ecological interest, with a protection priority level of 3 [28]. In the center of the UpB-OER, the Tiglmamine lakes “LaT” (32°54′N, 5°20′W, 1640 m) form a group of three juxtaposed lakes, not communicating at the surface and dug into the dolomites of the Lower Lias. The LaT form a part of a small catchment area of around 8 km2. The lake to the south is the deepest (20 m), the lake in the center has a deep (18 m) and a marshy part, and the lake to the north is the smallest [26]. The c-LaT is considered the most significant lake [29].
Modifications in lake surface area indicate changes in lake storage and provide insights into hydrological processes and water resource management [30]. Most studies rely on single-date imagery, overlooking seasonal variations. To overcome this limitation, time series from satellite imagery like Landsat are used to capture seasonal changes [31], though challenges persist with persistent cloud cover and small lake identification [32]. Ideally, higher temporal resolution data are preferred [33]. This article addresses the challenge of incomplete satellite imagery, with only about 50% of possible images available. Despite this limitation, we propose using interpolation and validation procedures to analyze and capture the monthly evolution of lake surfaces. Our contribution includes employing optimal interpolation, the newly developed iterative ratio method, and the Kalman filter to enhance the understanding of seasonal variability in the surface areas of three selected lakes through a seamless Landsat time series.
2. Data
The increasing availability of remote sensing data with appropriate spatiotemporal resolutions facilitates effective monitoring of lake changes [34] and provides synoptic and spatiotemporal views for a better understanding of lakes [35]. For the purpose of green and sustainable regional development, it is crucial to utilize remote sensing data to study the long-term changes and influencing factors of lakes [36]. To reconstruct a monthly pattern of the lakes’ variations, Landsat images were acquired, calibrated, and corrected. The extensions of the three lakes were then extracted, and two interpolation methods were applied to produce a complete data series (Figure 2).
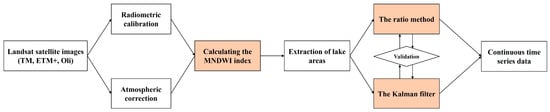
Figure 2.
Flowchart of this study.
More than 230 images (Path: 201, Row: 037) from the Thematic Mapper (TM), Enhanced Thematic Mapper Plus (ETM+), and Landsat Operational Land Imager (OLI) satellites were downloaded between 1984 and 2022, all with good quality and a 30 m resolution. Among the many techniques to extract water surfaces from satellite imagery, we chose water body indices that identify water bodies by determining the optimal threshold from the histogram of multiple bands [37]. The Modified Normalized Difference Water Index (MNDWI), proposed in [38], is one of the most popular methods widely used to produce water body maps at different scales (Equation (1)). Many researchers have demonstrated that MNDWI is more suitable for accurately delineating water bodies [38,39,40,41,42,43].
: reflectance in the green and short-wave infrared bands.
The remote sensing data used to monitor the three lakes are not continuous due to cloud cover. Clouds and their shadows are unavoidable issues in high-resolution remote sensing images [44]. Globally, cloud cover averages around 66% annually, frequently obscuring Earth’s surface and complicating data processing and analysis [45,46]. In our study, covering September 1984 to August 2022, out of 456 potential observations, we recorded only 272, 252, and 232 values for LaB, LaO, and c-LaT, respectively, resulting in 40%, 45%, and 50% missing data (Figure 3). Given the prevalence of cloud cover and its impact, employing suitable methods to fill data gaps is essential.
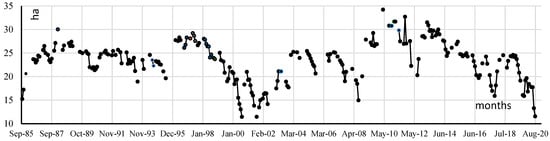
Figure 3.
Only 272/456 observed values for LaB from September of 1984 to August of 2022.
3. Interpolation Methodology
3.1. The Iterative Ratio Method
The normal ratio method was initially proposed by Paulhus and Kohler [47] to interpolate missing precipitation records. It is widely used to interpolate missing rainfall [48], flow [49] or discharge data [50] but it has also been used for temperature data [51]. The normal ratio method is based upon the temporal and spatial correlation of data. Revised variants of the method use weights to show the importance of distance and/or time to the spatial and temporal location with the missing value [52].
The core idea of the method is that the ratio between two data series remains constant over time and space. In our research, the base method was used, which determines the ratio for the joint period (Equation (2)) and applies it for the missing values (Equation (3)) without using any weights.
where
- N—joint period length;
- xi, yi—values at reference at missing location.
- NR—calculated normal ratio;
- yk—missing value;
- xk—existing value at a different location.
The above equations were implemented in Excel (Figure 4). A column is designated to hold the reference data, which, in this implementation, are allowed to have gaps. The second column is for the missing data. The functions determine the joint period and the normal ratio. Using the normal ratio value, the results’ column’s data are calculated following three rules (Figure 5a): (1) if the data are present in the missing column, these are kept in the result column; (2) if the reference data are present but there is a gap in missing data, these are calculated using the normal ratio; (3) if the data in both of the columns are missing, then the result will have a missing value too.

Figure 4.
Excel functions for implementing the normal ratio method.
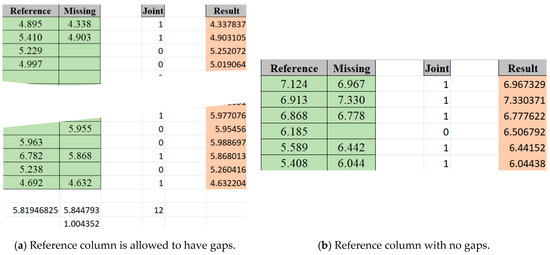
Figure 5.
Excel work interface with the four involved columns.
The Excel table can be used for longer data series but can also be applied to shorter periods, e.g., selecting a reference dataset with no gaps and a missing dataset with only one missing value. Also, in this case, the Excel formula conforms to the situation, using the correct length in calculations (Figure 5b). The ratio method will hereafter be called R-Interpolation.
The normal (original) ratio method was extended in our research, introducing a new approach to its practical application. Each gap was filled individually in a step-by-step manner, developing a separate equation for each. Using a data table with years as rows and months as columns, the calculations were applied iteratively. In the first iteration, only gaps bounded at the top and/or bottom and on one side by measured values were calculated using the longest possible bounding series (until reaching a gap). This considered the autocorrelation between subsequent months and years. From the second iteration onward, the same approach was applied, but the calculated cells from the first iteration were incorporated into the gap value calculation. Iterations continued until all gaps were filled. The iterative ratio method was implemented in RStudio by developing the necessary R functions.
3.2. Kalman Filter
The Kalman Filter “KF” [53] is a sequential filtering method utilized for linear systems, where the residuals conform to a Gaussian distribution [54]. The KF is highly popular and robust in practical applications due to the ease of coding and testing [55]; moreover, the KF has more derivative variants than any other method [56]. Some of these methods were developed to overcome the limitations of linearity and the challenge of objectively estimating the error statistics required for applying the KF [57]. The frequently employed adaptations of the original algorithm encompass the Extended Kalman Filter “EKF” [58], the Unscented Kalman Filter [59], and the Ensemble Kalman Filter “EnKF” [60]. A variant of the EnKF is the Ensemble Kalman Smoother “EnKS” [61], which can be sequentially applied in highly nonlinear systems.
The implementation of the KF is relatively simple, it is extensively applied in hydrological datasets, and it exhibits great flexibility for integration with hydrological models [56]. The KF concurrently incorporates the data from the previous time step, system noise statistics, measurement errors, and uncertainty in the model description to optimally estimate the current state of the relevant variables [62]. The algorithm operates in two steps: predicting, in the first step, the current state of variables under uncertainty conditions, and, in the second step, updating the previous estimation with a weighted arithmetic mean after obtaining measurements [63].
Our analysis utilized the Kalman filter for data gap input in R. The imputeTS package [64] provided the necessary functionality through its na_kalman function. Before applying na_kalman, the original data series needed conversion into a time series format. This is shown in Figure 6, where d represents the original data series with gaps marked as NAs (not a number), dt is the obtained time series with gaps, and gap_filled is the resulting gap-filled time series.

Figure 6.
Applying the Kalman filter in R.
To the best of our knowledge, the application of the iterative ratio method and the Kalman filter in filling gaps in time series data for lake extensions is introduced for the first time in this context. This novel approach marks the initial utilization of these methods for such purposes in our knowledge.
The Kalman filter method for interpolation will be called K-Interpolation for the remainder of this study.
To validate our methodology for reconstructing the data of missing surface area, we applied an “inverse philosophy”. We estimated reconstruction errors and subsequently meticulously reconstructed the original data based on simulated results (Figure 7), as will be discussed in the following sections.
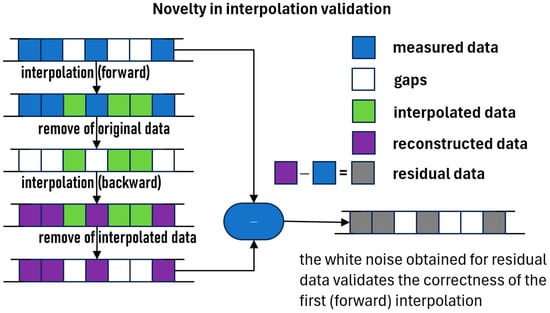
Figure 7.
Flowchart of interpolated data validation.
4. Results
The methodology enabled us to fill in the data gaps concerning the three lakes studied, by using satellite imagery, and thus produce a complete dataset for the period from 1984 to 2022. The analysis of the results revealed changes in lake areas, indicating declining trends, which could be due to natural factors or human intervention. The accuracy of the reconstruction depends on the quality of the satellite data and the suitability of the interpolation models used to characterize these data.
The results that follow below are illustrated in the form of two types of procedures and corresponding graphs, called “forward” and “backward”. In the case of the “forward” procedure, we performed the interpolation based on the observed data. For example, in the case of the Abekhame lake, starting from 272 observed dispersed values (Figure 3), we generated 456–272 = 182 values. In the case of the “backward” procedure, we took into account the 182 generated values resulting from the “forward” procedure and generated 456–182 = 272 values. These 272 interpolated values correspond exactly to the moments of time in which the 272 values were recorded through Landsat procedures. We were still interested in finding the extent to which the generation of new values is acceptable or not. We made the difference between the entire series of values interpolated by the “forward” procedure and the “backward” series, and the series of resulting errors was called “residual”.
4.1. LaB Case
On monthly time steps, the LaB area showed significant variations over the study period, marked by a standard deviation of the lake surface of 6.7 ha and a coefficient of variation of 31%. The average surface area is 22 ha, with a maximum of 34 ha recorded in 2010 and a minimum of 0.8 ha in 2022. Regarding the terms of LaB’s surface area evolution, there was a notable increase in 2008, reaching its peak in 2010, followed by a decrease in recent years, marked by the smallest surface areas ever recorded. In contrast to other lakes, a steep drop in LaB’s surface area can be observed after 2018.
With regard to the interpolation results, it is observable that the data generated by the two methods, “the iterative ratio method” and “Kalman filter”, seemed to closely follow those obtained by remote sensing, thus revealing a certain symmetry between the two datasets. The results obtained by the K-Interpolation method presented data that appeared more regular and consistent than those derived from R-Interpolation, suggesting that the Kalman filter may offer a more stable interpolation (Figure 8).
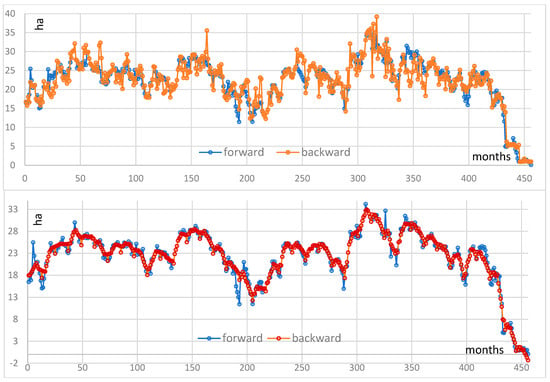
Figure 8.
R-Interpolation (top graph) and K-Interpolation (bottom graph) for the LaB case.
For both interpolation methods, the residuals were generally distributed around the 0 value, indicating that both methods predicted satellite values with satisfactory accuracy (Figure 9). However, it should be noted that the K-Interpolation method showed a slight improvement in accuracy over the R-Interpolation method, with mean residual values of −0.01 and 0.06, respectively.
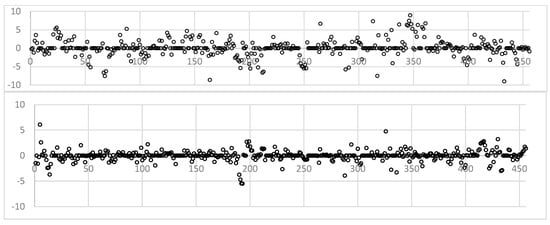
Figure 9.
Residual series of R-Interpolation (top graph) and of K-Interpolation (bottom graph) for the LaB case.
It is important to also interpret the results in consideration of the fact that the values interpolated by the “backward” procedure are able, or not, to reconstitute the values generated by the “forward” procedure. Because of this, we chose to compare the main descriptive statistical characteristics of the respective series. Table 1 shows that, in the case of “forward” and “backward”, the average, the standard deviation, the median, the Cv, the Cs and the Ck are very similar in both R-Interpolation and K-Interpolation. Obviously, there were differences between the two groups of minimums and between the two groups of maximums, considering that it was about mathematical generation of values and such differences in results frequently appear when it comes to simulated values.

Table 1.
Descriptive statistics of R-Interpolation and K-Interpolation for the LaB case.
Second, visible in the tabular comparison, from a descriptive statistics point of view, R-Interpolation and K-Interpolation were almost equivalent. The results of the R-Interpolation procedure led to a greater dispersion of the resulting values compared to K-Interpolation. There were some differences between the residual series, i.e., the series of interpolation errors, which prompted us to look for a validation method (more about this in Section 5).
4.2. LaO Case
In contrast to the other lakes, LaO’s surface area was virtually constant due to its semi-artificial nature. This stability was reflected in a standard deviation of 0.8 ha and a coefficient of variation of 6%. The average surface area is 14 ha, with a peak of 17 ha recorded in 2020 and a minimum of 6.5 ha recorded in 1988.
As in the case of the LaB, the data generated by the two methods followed the same trend as the satellite data for Lake Ouiouan. Thus, both interpolation methods were equally suitable for filling the gaps in satellite data for the surface area of LaO (Figure 10). The K-Interpolation method proves more accurate in reconstructing Lake Ouiouan data than the R-Interpolation method. This superiority is reflected in an average residual of −0.009 for the former method and 0.03 for the latter (Figure 11).
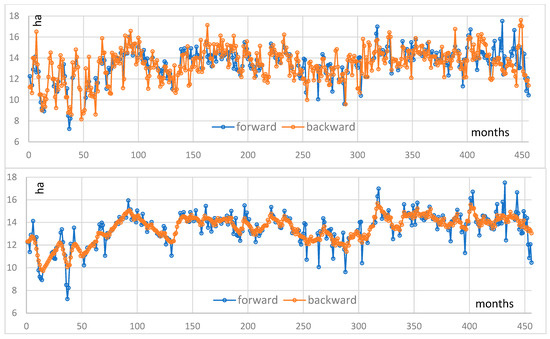
Figure 10.
R-Interpolation (top graph) and K-Interpolation (bottom graph) for the LaO case.
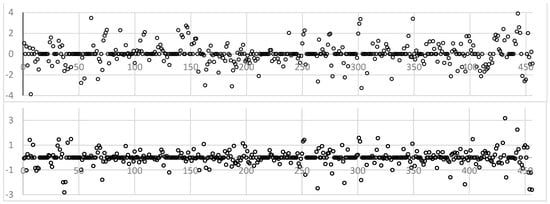
Figure 11.
Residual series of R-Interpolation (top graph) and of K-Interpolation (bottom graph) for the LaO case.
From a descriptive statistics point of view (Table 2), the results regarding the interpolations for the LaO case were broadly similar to those from the LaB case. There were some differences between Cv, Cs and Ck between “forward” and “backward” but they were not too big. However, the smaller dispersion in the case of K-Interpolation, places this method in a more advantageous position in relation to R-Interpolation.

Table 2.
Descriptive statistics of R-Interpolation and K-Interpolation for the LaO case.
4.3. c-LaT Case
The evolution of the surface area of lake c-LaT follows a similar trend to that of lake LaB. However, variability was less marked, with a standard deviation of 0.8 ha and a coefficient of variation of 13%. The average surface area was 6.1 ha, reaching a maximum of 9.2 ha in 2011 and a minimum of 4.1 ha in 1984. A notable increase was recorded in 2008, reaching its peak in 2011, followed by a steady decline in recent years.
It should be remembered that the application of the R-Interpolation method aimed to fill the gaps in the satellite data, thus generating a more complete data series covering the period from 1984 to 2022. It is important to note that this method introduced some distortion, particularly in the first third of the time series (Figure 12). As with the first two lakes, the K-Interpolation method also offered the possibility of filling the gaps in the satellite data with greater precision, thus promoting a more faithful representation of the actual trend in lake area. The average residual value is −0.01 for both methods (Figure 13).
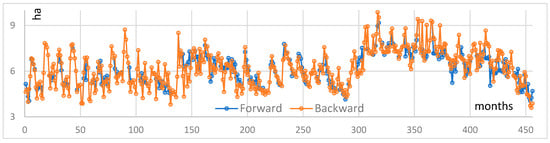
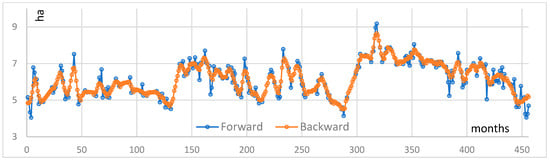
Figure 12.
R-Interpolation (top graph) and K-Interpolation (bottom graph) for the c-LaT case.
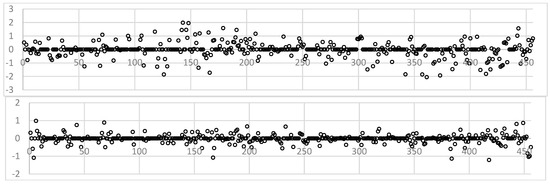
Figure 13.
Residual series of R-Interpolation (top graph) and of K-Interpolation (bottom graph) for the c-LaT case.
From a descriptive statistics perspective (Table 3), we obtained similar results in the c-LaT, LaB and LaO cases, although very minor differences appeared in “forward” and “backward” Cv, Cs and Ck. Similar to when comparing with LaO and LaB, utilizing K-Interpolation rather than R-Interpolation provided a more advantageous position.

Table 3.
Descriptive statistics of R-Interpolation and K-Interpolation for the c-LaT case.
Comparing the results of the interpolations for the three lakes according to the number of values needed to be interpolated, we could say that the best fitting “forward” interpolation was in the case of LaB because only 182 values had to be generated, but we must remember that in the “backward” case, based on the 182 theoretical values, 272 values had to be generated for the LaB case. At the other extreme was the case of c-LaT, where 224 values were generated by “forward”, and, based on them, by the “backward” procedure, 232 values were generated. Obviously, the “forward” procedure generated better values because of the smaller number of values to be interpolated. “Backward” as the reciprocal of “forward” respects the same feature in the sense that the best interpolation was in the case of c-LaT because only 232 values were generated by backward.
It is important to emphasize that, although both methods contribute to more complete data, their use requires careful evaluation, particularly at times when satellite data are less abundant. This critical analysis will ensure accurate interpretation of lake area variations over time.
5. Discussion
5.1. Discussion on the Interpolation Validation
The difference between original data and simulated series is the residual series or error series, whose statistical characteristics are visible in the last columns of Table 1, Table 2 and Table 3. The validation of the interpolation results could be accepted if the residual series has characteristics such as “white noise”. That is why, in the following, we performed error analysis based on ACF (autocorrelation function) and PACF (partial autocorrelation function).
The model’s success is indicated by white noise residuals that capture all original data information. The absence of a significant correlation in the ACF and PACF plots for these residuals is crucial [65].
AR models with appropriate orders are employed to capture correlated errors [66]. The order of AR models is typically determined by analyzing the ACF and PACF of the errors [67]. These AR models can be discrete [68] or continuous [69] depending on error characteristics. In hydrological modeling, the AR (1) model, representing a first-order autoregressive model, is commonly used to address correlated errors [70]. Consequently, the literature provides mathematical formulations of the likelihood function based on the AR (1) model [67].
The residual of the Kalman filter (K-Interpolation) is white noise for all three lakes (an example for the c-LaT case is shown in Figure 14).
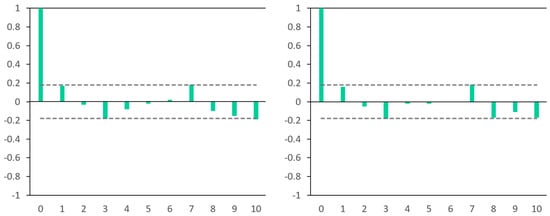
Figure 14.
The ACF (left) and the PACF (right) of residual series generated by K-Interpolation (the case c-LaT) indicates white noise.
Beyond lag 0, the autocorrelations are within the bounds, suggesting that there is no significant autocorrelation at these lags. The PACF plot shows the partial correlation of the time series with itself at various lags, and the result is the same as in the case of ACF, which is the white noise of the error series.
In the case of R-Interpolation, the residual series for each of the three lakes tested with ACF and PACF indicate an ARMA (1, 1) structure. The coefficients corresponding to the AR (1) order exhibit low values. For example, the residuals from the R-Interpolation method (Figure 15) exhibit a low AR (1) coefficient = 0.23, just over the bounds (0.14).
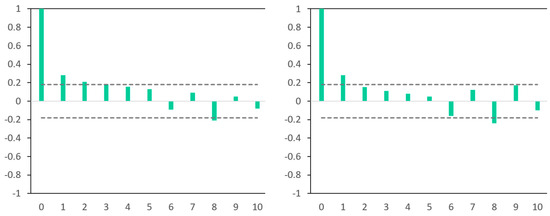
Figure 15.
The ACF (left) and the PACF (right) of residual series generated by R-Interpolation (the case c-LaT) indicates ARMA (1,1) structure but the AR (1) coefficient is very low.
Therefore, we can say that the iterative ratio method, R-Interpolation, can be accepted due to its simplicity of calculation, even if it is not as accurate as K-Interpolation. Low autocorrelation in the residuals suggests that the R-Interpolation model effectively captures and explains the underlying patterns in the data. This aspect is critical in statistical analysis and prediction because it implies that the low model’s errors, or residuals, do not demonstrate a systematic pattern over time.
5.2. Discussion on the Obtained Results
On a monthly scale, in both the R-Interpolation and K-Interpolation plots, the trends for the three lakes appear to be consistent across both methods (Figure 16). In the case of c-LaT, there were 232 monthly values and it was necessary to generate 224 values; in the case of LaB, there were 272 monthly values and 182 values were generated; and in the case of LaO, there were 252 monthly values and 204 values were generated. LaB exhibits the highest surface area, LaO shows moderate surface areas, and both display a similar seasonal trend, with surface areas generally peaking during the winter and spring months and declining in the summer and autumn months (October to March). The c-LaT, the smallest lake, maintains a consistent surface area throughout the months, likely due to its characteristic of being an isolated body of water dug into limestone and not communicating at the surface with the other lakes. When comparing the two interpolation methods, the overall patterns for each lake’s surface area are remarkably similar, indicating that both the R-Interpolation and K-Interpolation methods yield consistent results for this specific dataset.
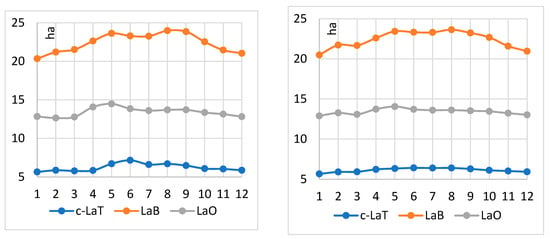
Figure 16.
The monthly variation in the surface of the lakes: values completed by R-Interpolation (left) and values completed by K-Interpolation (right).
On an annual scale, the overall trends of the lakes’ surface areas appear consistent between the two interpolation methods, indicating that R-Interpolation (Figure 17) and K-Interpolation (Figure 18) yield similar macrotrends for the dataset in question. The c-LaT and the LaO shows a moderate variation throughout the studied period in both graphs. It is the LaB that displays the most pronounced rate of decrease, particularly evident in the latter years due to a major anthropogenic effect, as seen in both the R-Interpolation and K-Interpolation graphs.
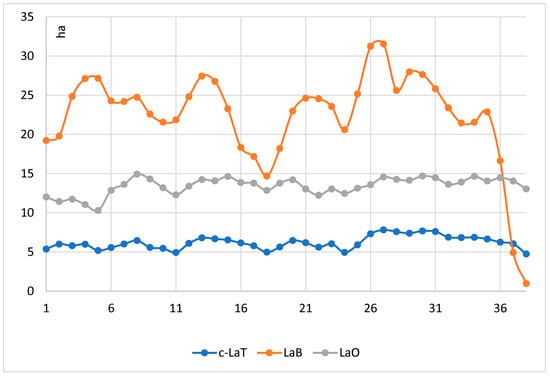
Figure 17.
The annual variation in the lake surface between 1984/85 and 2021/22 (R-Interpolation).
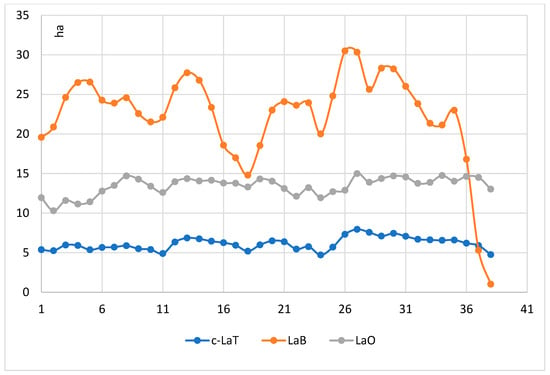
Figure 18.
The annual variation in the lake surface between 1984/85 and 2021/22 (K-Interpolation).
Combining remote sensing data and interpolated data harnesses the best of both worlds: remote sensing data anchor predictions, while interpolated data fill gaps. This complete picture empowers more accurate forecasting, extends prediction horizons, and unlocks deeper insights, making it a powerful tool for diverse fields like hydrological modeling.
6. Conclusions
The limited availability of freshwater resources, exacerbated by climate change and human activities, underscores the necessity for effective water resource management strategies. This study highlights the importance of remote sensing in monitoring global water resources, particularly in regions where traditional gauging methods are impractical. The focus on the Middle Atlas lakes in Morocco serves as an illustration of the socio-economic and ecological roles played by such hydrosystems.
The methodology employed in this study, incorporating the iterative ratio method and Kalman filter for filling gaps in time series data, represents a novel approach in the context of lake extension monitoring. The idea of assuming the existence of seasonality in monthly hydrological or climate data series is not new. It is not new either to assume that if seasonality in a monthly data series exists, then there is an autocorrelation between the successive months of the same year or between the same month in successive years. The novelty in our paper is the linking of the two ideas mentioned above, and the original way in which we realized the Excel algorithm for ratio method and developed an iterative ratio method in R to fill multiple sporadic or scattered gaps with plausible data.
The results obtained from the application of these methods to three specific lakes in the Middle Atlas region demonstrate their efficacy in providing accurate reconstructions of surface areas. The analysis of the reconstructed data reveals significant variations in lake areas, offering insights into hydrological processes, water resource management, and potential environmental changes. The data produced by both methods align with the trend observed in the satellite data, indicating that both interpolation methods are equally effective in filling gaps for the surface area of the three lakes. The accuracy of the obtained results depends both on the appropriate methodology and on the level of detail of the primary data. Thus, using high-resolution satellite images, the obtained results will improve the prediction and forecasting models that can be developed.
This research contributes to the evolving field of hydroclimatic dynamics and establishes a precedent for the application of innovative interpolation techniques in lake-monitoring studies.
Our study shows that although we only had a limited number of Landsat images, about 50% of what would have been possible if the meteorological conditions had not been restrictive, we generated complete seasonal and annual series for the period of 1984–2022. Based on these series, in subsequent research, it will be possible to develop predictions and forecasting for the purpose of efficient allocation of water resources in a semi-arid region.
Author Contributions
Conceptualization, I.H.; methodology, T.E.O., Z.M.-S. and I.H.; software, Z.M.-S. and I.H.; validation, I.H. and Z.M.-S.; formal analysis, S.L. and M.E.G.; investigation, T.E.O. and I.H.; resources, S.L. and M.E.G.; data curation, T.E.O. and Z.M.-S.; writing—original draft preparation, I.H. and T.E.O.; writing—review and editing, I.H. and T.E.O.; visualization, S.L. and M.E.G.; supervision, I.H., S.L. and M.E.G.; project administration, S.L. and M.E.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The recorded data can be obtained from TEO and the data generated by interpolation can be obtained from IH.
Acknowledgments
The corresponding author thanks the Remote Sensing Editorial Office for the invitation to publish an article in this journal.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Everhardt, B.A. Great Lakes Water Resources: Planning for the Nation’s Future. Toledo J. Gt. Lakes Law Sci. Policy 2001, 3, 90–111. [Google Scholar]
- Mleczko, M.; Mróz, M. Wetland Mapping Using SAR Data from the Sentinel-1A and TanDEM-X Missions: A Comparative Study in the Biebrza Floodplain (Poland). Remote Sens. 2018, 10, 78. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. A Review of Drought Concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- El-Bouhali, A.; Amyay, M.; Ech-Chahdi, K.E.O. Changes in water surface area of the Middle Atlas-Morocco lakes: A response to climate and human effects. IJEG 2024, 9, 221–232. [Google Scholar] [CrossRef]
- Bai, M.; Mo, X.; Liu, S.; Hu, S. Detection and Attribution of Lake Water Loss in the Semi-Arid Mongolian Plateau-A Case Study in the Lake Dalinor. Ecohydrology 2021, 14, e2251. [Google Scholar] [CrossRef]
- Duan, Z.; Bastiaanssen, W.G.M. Estimating Water Volume Variations in Lakes and Reservoirs from Four Operational Satellite Altimetry Databases and Satellite Imagery Data. Remote Sens. Environ. 2013, 134, 403–416. [Google Scholar] [CrossRef]
- White, L.; Brisco, B.; Dabboor, M.; Schmitt, A.; Pratt, A. A Collection of SAR Methodologies for Monitoring Wetlands. Remote Sens. 2015, 7, 7615–7645. [Google Scholar] [CrossRef]
- Zhao, Z.; Liu, F.; Zhang, Y.; Liu, L.; Qi, W. The Dynamic Response of Lakes in the Tuohepingco Basin of the Tibetan Plateau to Climate Change. Environ. Earth Sci. 2017, 76, 137. [Google Scholar] [CrossRef]
- Yao, F.; Wang, J.; Wang, C.; Crétaux, J.-F. Constructing Long-Term High-Frequency Time Series of Global Lake and Reservoir Areas Using Landsat Imagery. Remote Sens. Environ. 2019, 232, 111210. [Google Scholar] [CrossRef]
- Liu, K.; Song, C.; Wang, J.; Ke, L.; Zhu, Y.; Zhu, J.; Ma, R.; Luo, Z. Remote Sensing-Based Modeling of the Bathymetry and Water Storage for Channel-Type Reservoirs Worldwide. Water Resour. Res. 2020, 56, e2020WR027147. [Google Scholar] [CrossRef]
- Chen, T.; Song, C.; Ke, L.; Wang, J.; Liu, K.; Wu, Q. Estimating Seasonal Water Budgets in Global Lakes by Using Multi-Source Remote Sensing Measurements. J. Hydrol. 2021, 593, 125781. [Google Scholar] [CrossRef]
- Ahmed, I.A.; Shahfahad, S.; Baig, M.R.I.; Talukdar, S.; Asgher, M.S.; Usmani, T.M.; Ahmed, S.; Rahman, A. Lake Water Volume Calculation Using Time Series LANDSAT Satellite Data: A Geospatial Analysis of Deepor Beel Lake, Guwahati. Front. Eng. Built Environ. 2021, 1, 107–130. [Google Scholar] [CrossRef]
- Pi, X.; Luo, Q.; Feng, L.; Xu, Y.; Tang, J.; Liang, X.; Ma, E.; Cheng, R.; Fensholt, R.; Brandt, M.; et al. Mapping Global Lake Dynamics Reveals the Emerging Roles of Small Lakes. Nat. Commun. 2022, 13, 5777. [Google Scholar] [CrossRef]
- Zhao, G.; Li, Y.; Zhou, L.; Gao, H. Evaporative Water Loss of 1.42 Million Global Lakes. Nat. Commun. 2022, 13, 3686. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; Xiong, D.; Wen, F.; Wang, X. Lake Area Monitoring Based on Land Surface Temperature in the Tibetan Plateau from 2000 to 2018. Environ. Res. Lett. 2020, 15, 084033. [Google Scholar] [CrossRef]
- Gao, S.; He, D.; Zhang, Z.; Tang, X.; Zhao, Z. A novel dynamic interpolation method based on both temporal and spatial correlations. Appl Intell. 2023, 53, 5100–5125. [Google Scholar] [CrossRef]
- Lepot, M.; Aubin, J.B.; Clemens, F.H. Clemens, Interpolation in Time Series: An Introductive Overview of Existing Methods, Their Performance Criteria and Uncertainty Assessment. Water 2017, 9, 10. [Google Scholar] [CrossRef]
- Qin, R.; Chen, G.; Zhang, H.; Liu, L.; Long, S. A Kalman Filter-Based Method for Reconstructing GMS-5 Land Surface Temperature Time Series. Appl. Sci. 2022, 12, 15. [Google Scholar] [CrossRef]
- Shi, Q.; Dai, W.; Santerre, R.; Liu, N. A Modified Spatiotemporal Mixed-Effects Model for Interpolating Missing Values in Spatiotemporal Observation Data Series. Math. Probl. Eng. 2020, 2020, 1070831. [Google Scholar] [CrossRef]
- Arun, P.V. A comparative analysis of different DEM interpolation methods. Egypt J. Remote Sens. Space Sci. 2013, 16, 133–139. [Google Scholar] [CrossRef]
- Huber, F.; Schulz, S.; Steinhage, V. Deep Interpolation of Remote Sensing Land Surface Temperature Data with Partial Convolutions. Sensors 2024, 24, 5. [Google Scholar] [CrossRef] [PubMed]
- Martin, J.; Jover, H.; Le Coz, J.; Maurer, J.; Noin, D. Géographie du Maroc; Hatier: Paris, France, 1964. [Google Scholar]
- Baali, A. Genèse et Évolution Au Plio-Quaternaire de Deux Bassins Intram-Ontagneux en Domaine Carbonaté Méditerranéen. Les Bassins Versants Des Dayets (Lacs) Afourgagh et Agoulmam (Moyen Atlas, Maroc). Thesis, Université Sidi Mohamed Ben Abdellah, Fès, Morocco, 1998. [Google Scholar]
- Detriche, S. Evolution D’un Système Lacustre Karstique au Cours de la Période Historique D’après L’étude des Archives Sédimentaires: La Dayet Afourgagh (Moyen-Atlas, Maroc). Ph.D. Thesis, Université François Rabelais de Tours, Tours, France, 2007. [Google Scholar]
- Gouiss, A.; Taybi, Y.; Gharmane, Y.; M’Rabet, S. Contribution of Space Remote Sensing and New Gis Tools for Mapping Geological Structures in the Mekkam Region of Northeast Morocco. Geogr. Tech. 2023, 18, 149–157. [Google Scholar] [CrossRef]
- Chillasse, L.; Dakki, M.; Abbassi, M. Valeurs et fonctions écologiques des Zones humides du Moyen Atlas (Maroc). Humed. Mediterráneos 2001, 1, 139–146. [Google Scholar]
- ABHOER. Atlas des Sources et Lacs; Agence du Bassin Hydraulique de l’Oum Er Rbia: Beni Mellal, Morocco, 2019; p. 119. [Google Scholar]
- Chillasse, L.; Dakki, M. Potentialités et Statuts de Conservation Des Zones Humides Du Moyen-Atlas (Maroc), Avec Référence Aux Influences de La Sécheresse. Sci. Chang. Planétaires Sécher. 2004, 15, 337–345. [Google Scholar]
- Benkaddour, A. Changements Hydrologiques et Climatiques Dans Le Moyen-Atlas Marocain, Chronologie, Minéralogie, Géochimie Isotopique et Élémentaire Des Sédiments Lacustres de Tigalmamine. Ph.D. Thesis, Université Paris-Sud, Orsay, France, 1993. [Google Scholar]
- Bonnema, M.; Hossain, F. Inferring Reservoir Operating Patterns across the Mekong Basin Using Only Space Observations. WATER Resour. Res. 2017, 53, 3791–3810. [Google Scholar] [CrossRef]
- Xing, L.; Tang, X.; Wang, H.; Fan, W.; Gao, X. Mapping Wetlands of Dongting Lake in China Using Landsat and Sentinel-1 Time Series at 30 M. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 42, 1971–1976. [Google Scholar] [CrossRef]
- Slagter, B.; Tsendbazar, N.-E.; Vollrath, A.; Reiche, J. Mapping Wetland Characteristics Using Temporally Dense Sentinel-1 and Sentinel-2 Data: A Case Study in the St. Lucia Wetlands, South Africa. Int. J. Appl. Earth Obs. Geoinf. 2020, 86, 102009. [Google Scholar] [CrossRef]
- Han, X.; Chen, X.; Feng, L. Four Decades of Winter Wetland Changes in Poyang Lake Based on Landsat Observations between 1973 and 2013. Remote Sens. Environ. 2015, 156, 426–437. [Google Scholar] [CrossRef]
- Song, C.; Huang, B.; Ke, L.; Richards, K.S. Remote Sensing of Alpine Lake Water Environment Changes on the Tibetan Plateau and Surroundings: A Review. ISPRS J. Photogramm. Remote Sens. 2014, 92, 26–37. [Google Scholar] [CrossRef]
- Dörnhöfer, K.; Oppelt, N. Remote Sensing for Lake Research and Monitoring—Recent Advances. Ecol. Indic. 2016, 64, 105–122. [Google Scholar] [CrossRef]
- Lin, Y.; Li, X.; Zhang, T.; Chao, N.; Yu, J.; Cai, J.; Sneeuw, N. Water Volume Variations Estimation and Analysis Using Multisource Satellite Data: A Case Study of Lake Victoria. Remote Sens. 2020, 12, 3052. [Google Scholar] [CrossRef]
- Kang, J.; Guan, H.; Peng, D.; Chen, Z. Multi-Scale Context Extractor Network for Water-Body Extraction from High-Resolution Optical Remotely Sensed Images. Int. J. Appl. Earth Obs. Geoinf. 2021, 103, 102499. [Google Scholar] [CrossRef]
- Xu, H. Modification of Normalised Difference Water Index (NDWI) to Enhance Open Water Features in Remotely Sensed Imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Li, W.; Du, Z.; Ling, F.; Zhou, D.; Wang, H.; Gui, Y.; Sun, B.; Zhang, X. A Comparison of Land Surface Water Mapping Using the Normalized Difference Water Index from TM, ETM+ and ALI. Remote Sens. 2013, 5, 5530–5549. [Google Scholar] [CrossRef]
- Du, Z.; Li, W.; Zhou, D.; Tian, L.; Ling, F.; Wang, H.; Gul, Y.; Sun, B. Analysis of Landsat-8 OLI Imagery for Land Surface Water Mapping. Remote Sens. Lett. 2014, 5, 672–681. [Google Scholar] [CrossRef]
- Singh, K.V.; Setia, R.; Sahoo, S.; Prasad, A.; Pateriya, B. Evaluation of NDWI and MNDWI for Assessment of Waterlogging by Integrating Digital Elevation Model and Groundwater Level. Geocarto Int. 2015, 30, 650–661. [Google Scholar] [CrossRef]
- Du, Y.; Zhang, Y.; Ling, F.; Wang, Q.; Li, W.; Li, X. Water Bodies’ Mapping from Sentinel-2 Imagery with Modified Normalized Difference Water Index at 10-m Spatial Resolution Produced by Sharpening the SWIR Band. Remote Sens. 2016, 8, 354. [Google Scholar] [CrossRef]
- Sarp, G.; Ozcelik, M. Water Body Extraction and Change Detection Using Time Series: A Case Study of Lake Burdur, Turkey. J. Taibah Univ. Sci. 2017, 11, 381–391. [Google Scholar] [CrossRef]
- Inglada, J.; Vincent, A.; Arias, M.; Tardy, B.; Morin, D.; Rodes, I. Operational High Resolution Land Cover Map Production at the Country Scale Using Satellite Image Time Series. Remote Sens. 2017, 9, 95. [Google Scholar] [CrossRef]
- Li, Z.; Shen, H.; Cheng, Q.; Li, W.; Zhang, L. Thick Cloud Removal in High-Resolution Satellite Images Using Stepwise Radiometric Adjustment and Residual Correction. Remote Sens. 2019, 11, 1925. [Google Scholar] [CrossRef]
- Duan, C.; Pan, J.; Li, R. Thick Cloud Removal of Remote Sensing Images Using Temporal Smoothness and Sparsity Regularized Tensor Optimization. Remote Sens. 2020, 12, 3446. [Google Scholar] [CrossRef]
- Paulhus, J.L.H.; Kohler, M.A. Interpolation of missing precipitation records. Mon. Weather Rev. 1952, 80, 129–133. [Google Scholar] [CrossRef]
- Sattari, M.-T.; Rezazadeh-Joudi, A.; Kusiak, A. Assessment of Different Methods for Estimation of Missing Data in Precipitation Studies. Hydrol. Res. 2017, 48, 1032–1044. [Google Scholar] [CrossRef]
- Rugumayo, A.; Kayondo, D. Flood Analysis and Mitigation on Lake Albert, Uganda; Advances in Geosciences. Volume 4: Hydrological Science (HS); World Scientific: Singapore, 2006; pp. 31–45. ISBN 978-981-2707-20-8. [Google Scholar]
- Hedayatizade, M.; Reza Kavianpour, M.; Golestani, M.; Shahrokh Abdi, M. Estimation of Missing Annual Discharge. In Proceedings of the 2010 International Conference on Environmental Engineering and Applications, Singapore, 10–12 September 2010; pp. 38–43. [Google Scholar]
- Xia, Y.; Fabian, P.; Stohl, A.; Winterhalter, M. Forest Climatology: Estimation of Missing Values for Bavaria, Germany. Agric. For. Meteorol. 1999, 96, 131–144. [Google Scholar] [CrossRef]
- Amin Burhanuddin, S.N.Z.; Mohd Deni, S.; Mohamed Ramli, N. Revised Normal Ratio Methods for Imputation of Missing Rainfall Data. Sci. Res. J. 2016, 13, 83. [Google Scholar] [CrossRef]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Meinhold, R.J.; Singpurwalla, N.D. Understanding the Kalman Filter. Am. Stat. 1983, 37, 123–127. [Google Scholar] [CrossRef]
- Daum, F.E. Kalman Filters. In Encyclopedia of Systems and Control; Springer: Cham, Switzerland, 2021; pp. 1067–1070. ISBN 978-3-030-44184-5. [Google Scholar]
- Sun, L.; Seidou, O.; Nistor, I.; Liu, K. Review of the Kalman-Type Hydrological Data Assimilation. Hydrol. Sci. J. 2016, 61, 2348–2366. [Google Scholar] [CrossRef]
- Oikonomou, P.D.; Alzraiee, A.H.; Karavitis, C.A.; Waskom, R.M. A Novel Framework for Filling Data Gaps in Groundwater Level Observations. Adv. Water Resour. 2018, 119, 111–124. [Google Scholar] [CrossRef]
- Gelb, A. Applied Optimal Estimation; MIT Press: Cambridge, MA, USA, 1974; ISBN 0-262-57048-3. [Google Scholar]
- Julier, S.J.; Uhlmann, J.K. New Extension of the Kalman Filter to Nonlinear Systems. In Proceedings of the Signal processing, sensor fusion, and target recognition VI. SPIE 1997, 3068, 182–193. [Google Scholar]
- Evensen, G. Sequential Data Assimilation with a Nonlinear Quasi-geostrophic Model Using Monte Carlo Methods to Forecast Error Statistics. J. Geophys. Res. Oceans 1994, 99, 10143–10162. [Google Scholar] [CrossRef]
- Evensen, G.; Van Leeuwen, P.J. An Ensemble Kalman Smoother for Nonlinear Dynamics. Mon. Weather Rev. 2000, 128, 1852–1867. [Google Scholar] [CrossRef]
- Maybeck, P.S. Stochastic Models, Estimation, and Control; Academic Press: Cambridge, MA, USA, 1982; ISBN 978-0-08-096003-6. [Google Scholar]
- Khodarahmi, M.; Maihami, V. A Review on Kalman Filter Models. Arch. Comput. Methods Eng. 2023, 30, 727–747. [Google Scholar] [CrossRef]
- Moritz, S.; Bartz-Beielstein, T. imputeTS: Time Series Missing Value Imputation in R. R J. 2017, 9, 207. [Google Scholar] [CrossRef]
- Liu, Q.; Li, Z.; Ji, Y.; Martinez, L.; Ul Haq, Z.; Javaid, A.; Lu, W.; Wang, J. Forecasting the Seasonality and Trend of Pulmonary Tuberculosis in Jiangsu Province of China Using Advanced Statistical Time-Series Analyses. Infect. Drug Resist. 2019, 12, 2311–2322. [Google Scholar] [CrossRef]
- Schoups, G.; Vrugt, J.A. A Formal Likelihood Function for Parameter and Predictive Inference of Hydrologic Models with Correlated, Heteroscedastic, and Non-Gaussian Errors. Water Resour. Res. 2010, 46, W10531. [Google Scholar] [CrossRef]
- Datta, A.R. Evaluation of Implicit and Explicit Methods of Uncertainty Analysis on a Hydrological Modeling. Ph.D. Thesis, University of Windsor, Windsor, ON, Canada, 2011; p. 233. [Google Scholar]
- Laloy, E.; Fasbender, D.; Bielders, C.L. Parameter Optimization and Uncertainty Analysis for Plot-Scale Continuous Modeling of Runoff Using a Formal Bayesian Approach. J. Hydrol. 2010, 380, 82–93. [Google Scholar] [CrossRef]
- Yang, J.; Reichert, P.; Abbaspour, K.C.; Yang, H. Hydrological Modelling of the Chaohe Basin in China: Statistical Model Formulation and Bayesian Inference. J. Hydrol. 2007, 340, 167–182. [Google Scholar] [CrossRef]
- Bates, B.C.; Campbell, E.P. A Markov Chain Monte Carlo Scheme for Parameter Estimation and Inference in Conceptual Rainfall-Runoff Modeling. Water Resour. Res. 2001, 37, 937–947. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).