Rational Polynomial Coefficient Estimation via Adaptive Sparse PCA-Based Method
Abstract
:1. Introduction
- (1)
- We incorporate SPCA into the RPC estimation problem to automatically eliminate unnecessary and noise-related variables during PC computation.
- (2)
- We propose an adaptive regularization parameter approach to dynamically adjust the regularization parameters based on the explained variance of PCs and degrees of freedom, enhancing the method’s robustness in different scenarios.
- (3)
- We conduct extensive experiments to evaluate the performance of the proposed method, and the results show that our method demonstrates improved performance compared to existing competing methods.
2. Theoretical Background
2.1. Rational Function Model
2.2. PCA-Based RFM Optimization
3. Methodology
3.1. SPCA-Based RFM Method via NIPALS
| Algorithm 1 |
|
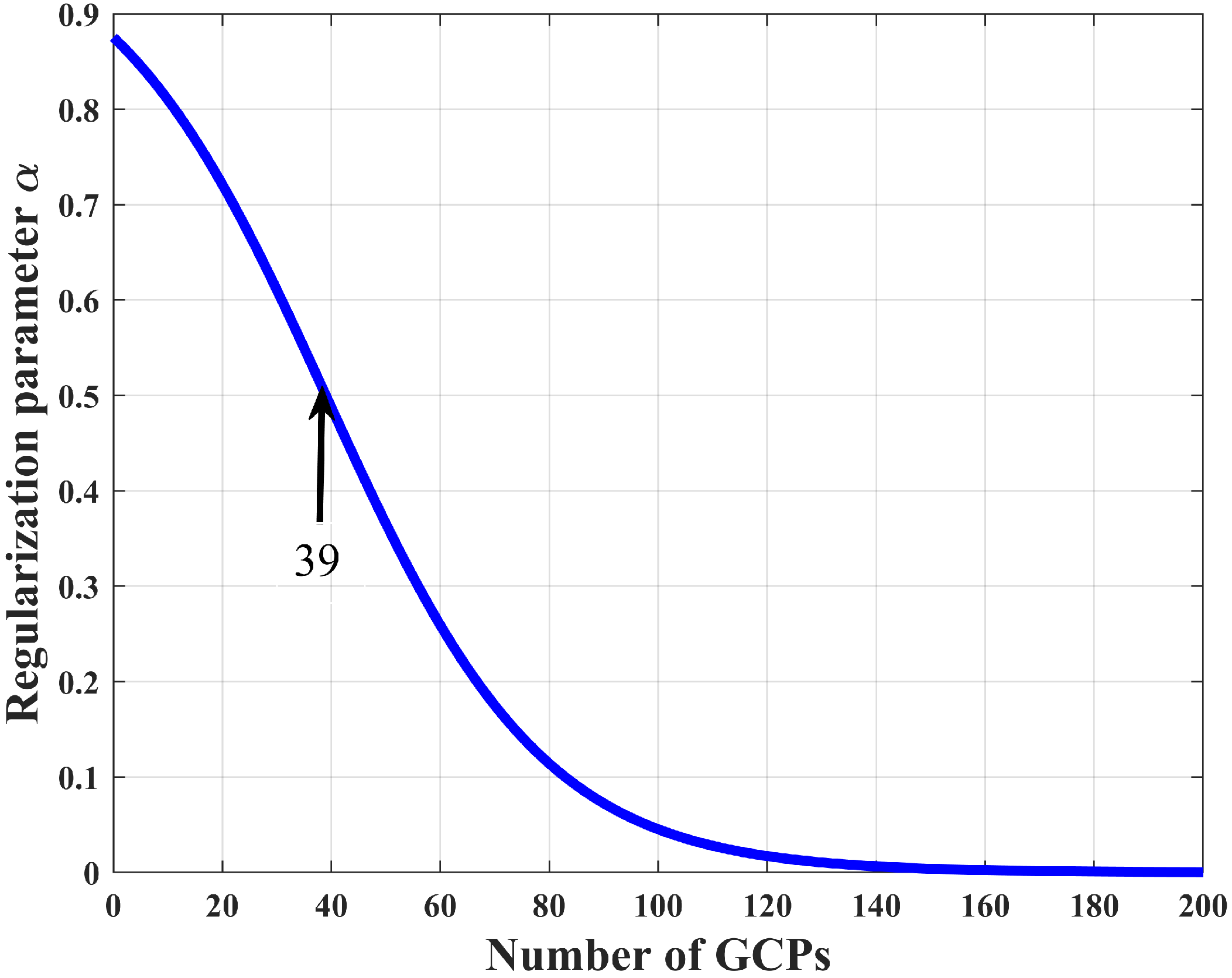
3.2. Adaptive Regularization Parameter Approach
| Algorithm 2 |
|
4. Experiments
4.1. Datasets and Metrics
4.2. Parameter Setting of the Methods in Comparison
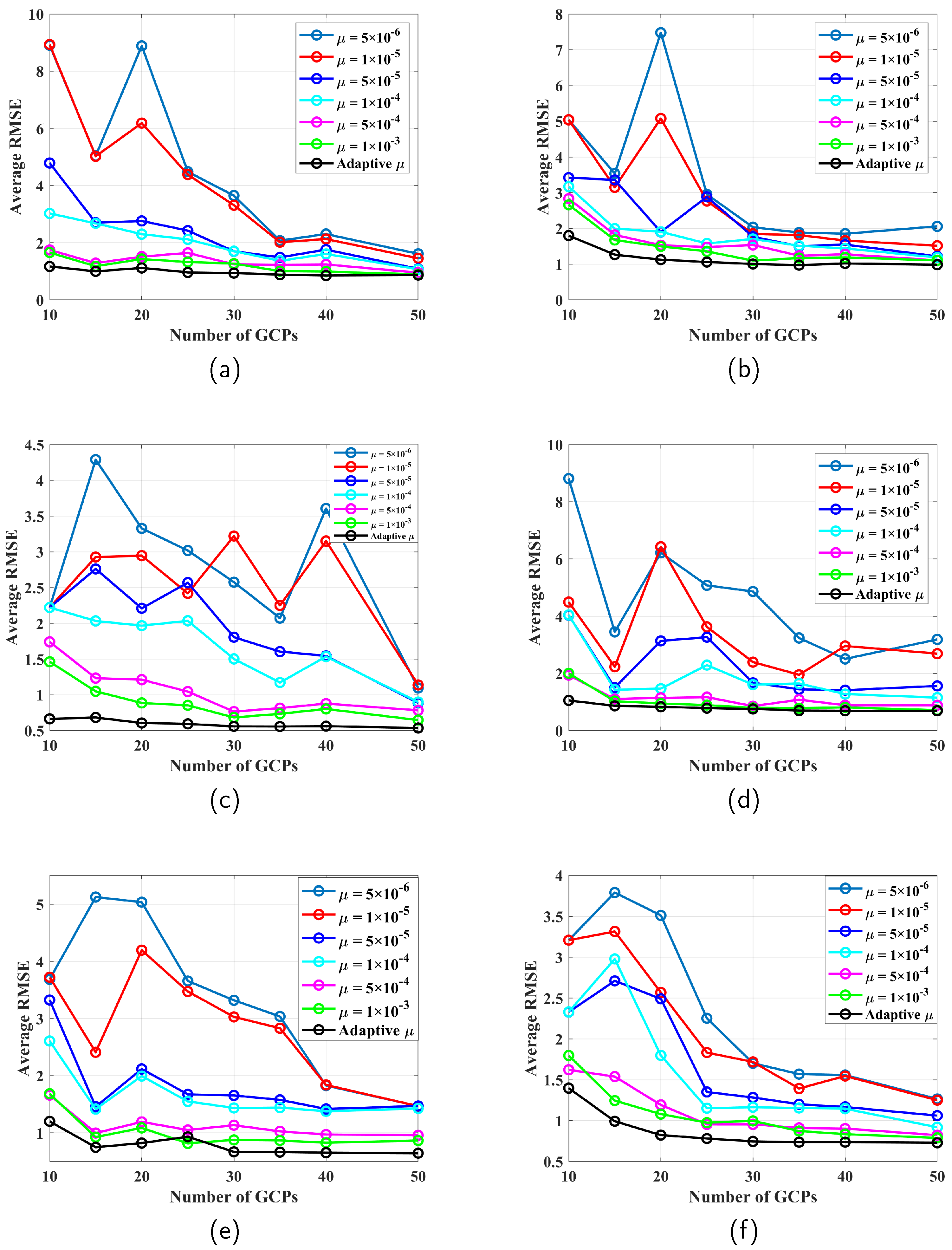
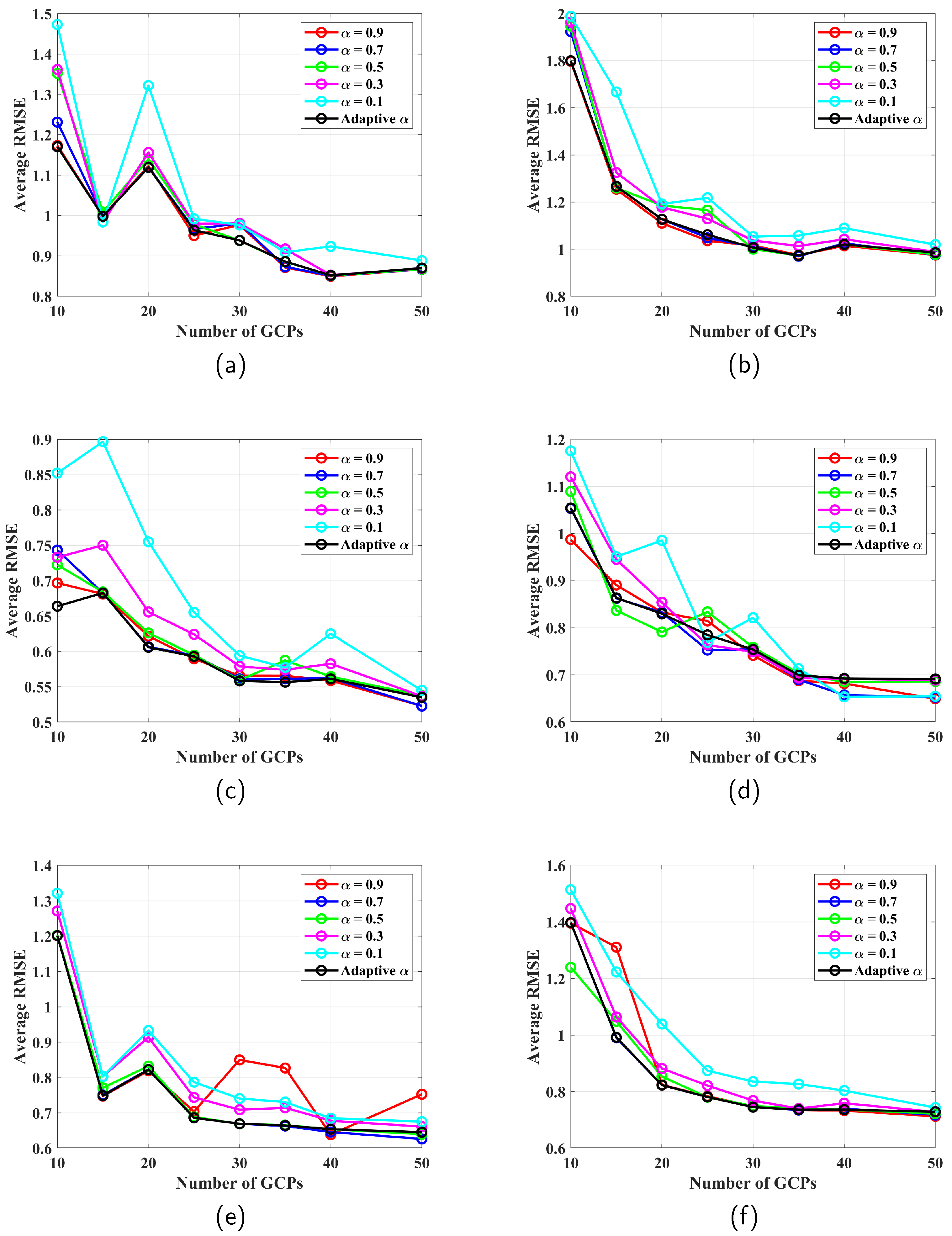
4.3. Comparative Results
4.4. Model Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Shen, X.; Li, Q.; Wu, G.; Zhu, J. Bias compensation for rational polynomial coefficients of high-resolution satellite imagery by local polynomial modeling. Remote Sens. 2017, 9, 200. [Google Scholar] [CrossRef]
- Toutin, T. Geometric processing of remote sensing images: Models, algorithms and methods. Int. J. Remote Sens. 2004, 25, 1893–1924. [Google Scholar] [CrossRef]
- Zhang, L.; He, X.; Balz, T.; Wei, X.; Liao, M. Rational function modeling for spaceborne SAR datasets. ISPRS J. Photogramm. Remote Sens. 2011, 66, 133–145. [Google Scholar] [CrossRef]
- Zhou, G.; Liu, X. Orthorectification model for extra-length linear array imagery. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–10. [Google Scholar] [CrossRef]
- Tao, C.V.; Hu, Y. A comprehensive study of the rational function model for photogrammetric processing. Photogramm. Eng. Remote Sens. 2001, 67, 1347–1358. [Google Scholar]
- Gholinejad, S.; Amiri-Simkooei, A.; Moghaddam, S.H.A.; Naeini, A.A. An automated PCA-based approach towards optimization of the rational function model. ISPRS J. Photogramm. Remote Sens. 2020, 165, 133–139. [Google Scholar] [CrossRef]
- Yuan, X.; Lin, X. A method for solving rational polynomial coefficients based on ridge estimation. Geomat. Inf. Sci. Wuhan Univ. 2008, 33, 1130–1133. [Google Scholar]
- Wu, Y.; Ming, Y. A fast and robust method of calculating RFM parameters for satellite imagery. Remote Sens. Lett. 2016, 7, 1112–1120. [Google Scholar] [CrossRef]
- Long, T.; Jiao, W.; He, G. Rpc estimation via L1-norm-regularized least squares (l1ls). IEEE Trans. Geosci. Remote Sens. 2015, 53, 4554–4567. [Google Scholar] [CrossRef]
- Gholinejad, S.; Naeini, A.A.; Amiri-Simkooei, A. Optimization of RFM Problem Using Linearly Programed l1-Regularization. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–9. [Google Scholar] [CrossRef]
- Zhao, L.; Liu, F.; Li, J.; Wang, W. Research on reducing term of higher order in RFM model. Sci. Surv. Mapp. 2007, 32, 14–17. [Google Scholar]
- Zhang, Y.; Lu, Y.; Wang, L.; Huang, X. A new approach on optimization of the rational function model of high-resolution satellite imagery. IEEE Trans. Geosci. Remote Sens. 2011, 50, 2758–2764. [Google Scholar] [CrossRef]
- Moghaddam, S.H.A.; Mokhtarzade, M.; Moghaddam, S.A.A. Optimization of RFM’s structure based on PSO algorithm and figure condition analysis. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1179–1183. [Google Scholar] [CrossRef]
- Tengfei, L.; Weili, J.; Guojin, H. Nested regression based optimal selection (NRBOS) of rational polynomial coefficients. Photogramm. Eng. Remote Sens. 2014, 80, 261–269. [Google Scholar] [CrossRef]
- Moghaddam, S.H.A.; Mokhtarzade, M.; Naeini, A.A.; Amiri-Simkooei, A. A statistical variable selection solution for RFM ill-posedness and overparameterization problems. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3990–4001. [Google Scholar]
- Zoej, M.V.; Mokhtarzade, M.; Mansourian, A.; Ebadi, H.; Sadeghian, S. Rational function optimization using genetic algorithms. Int. J. Appl. Earth Obs. Geoinf. 2007, 9, 403–413. [Google Scholar]
- Zhou, G. On-Board Processing for Satellite Remote Sensing Images; CRC Press: Boca Raton, FL, USA, 2023. [Google Scholar]
- Cavallaro, G.; Heras, D.B.; Wu, Z.; Maskey, M.; Lopez, S.; Gawron, P.; Coca, M.; Datcu, M. High-Performance and Disruptive Computing in Remote Sensing: HDCRS—A new Working Group of the GRSS Earth Science Informatics Technical Committee [Technical Committees]. IEEE Geosci. Remote Sens. Mag. 2022, 10, 329–345. [Google Scholar] [CrossRef]
- Zhang, R.; Zhou, G.; Zhang, G.; Zhou, X.; Huang, J. RPC-based orthorectification for satellite images using FPGA. Sensors 2018, 18, 2511. [Google Scholar] [CrossRef]
- Naeini, A.A.; Moghaddam, S.H.A.; Sheikholeslami, M.M.; Amiri-Simkooei, A. Application of PCA Analysis and QR Decomposition to Address RFM’s Ill-Posedness. Photogramm. Eng. Remote Sens. 2020, 86, 17–21. [Google Scholar] [CrossRef]
- Golub, G.H.; Van Loan, C.F. Matrix Computations; JHU Press: Baltimore, MD, USA, 2013. [Google Scholar]
- Hao, L.; Pan, C.; Liu, P.; Zhou, D.; Zhang, L.; Xiong, Z.; Liu, Y.; Sun, G. Detection of the coupling between vegetation leaf area and climate in a multifunctional watershed, Northwestern China. Remote Sens. 2016, 8, 1032. [Google Scholar] [CrossRef]
- Li, J.; Fan, K.; Zhou, L. Satellite observations of El Niño impacts on Eurasian spring vegetation greenness during the period 1982–2015. Remote Sens. 2017, 9, 628. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T.; Tibshirani, R. Sparse principal component analysis. J. Comput. Graph. Stat. 2006, 15, 265–286. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B Stat. Methodol. 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Wold, H.O.A. Nonlinear Estimation by Iterative Least Square Procedures. In Research Papers in Statistics: Festschrift for J. Neyman; David, F.N., Ed.; Wiley: New York, NY, USA, 1966. [Google Scholar]
- Zhou, G.; Yuan, M.; Li, X.; Sha, H.; Xu, J.; Song, B.; Wang, F. Optimal regularization method based on the L-curve for solving rational function model parameters. Photogramm. Eng. Remote Sens. 2021, 87, 661–668. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B Stat. Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Kincaid, D.R.; Cheney, E.W. Numerical Analysis: Mathematics of Scientific Computing; American Mathematical Society: Providence, RI, USA, 2009; Volume 2. [Google Scholar]
- Hotelling, H. Analysis of a complex of statistical variables into principal components. J. Educ. Psychol. 1933, 24, 417. [Google Scholar] [CrossRef]
- Zhang, G.; Xu, K.; Huang, W. Auto-calibration of GF-1 WFV images using flat terrain. ISPRS J. Photogramm. Remote Sens. 2017, 134, 59–69. [Google Scholar] [CrossRef]
- Fan, Z.; Liu, Y.; Liu, Y.; Zhang, L.; Zhang, J.; Sun, Y.; Ai, H. 3MRS: An effective coarse-to-fine matching method for multimodal remote sensing imagery. Remote Sens. 2022, 14, 478. [Google Scholar] [CrossRef]
- Ungar, S.G.; Pearlman, J.S.; Mendenhall, J.A.; Reuter, D. Overview of the earth observing one (EO-1) mission. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1149–1159. [Google Scholar] [CrossRef]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s optical high-resolution mission for GMES operational services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Shan, X.; Zhang, J. Does the Rational Function Model’s Accuracy for GF1 and GF6 WFV Images Satisfy Practical Requirements? Remote Sens. 2023, 15, 2820. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. Regularization paths for generalized linear models via coordinate descent. J. Stat. Softw. 2010, 33, 1. [Google Scholar] [CrossRef] [PubMed]



| Dataset | Satellite | Area Type | GSD (m) | Coverage (km2) | Elevation Range (m) | No. of GCPs |
|---|---|---|---|---|---|---|
| GF1-A | GF-1 | Mountain | 16 | 40 × 40 | 403∼917 | 200 |
| GF1-B | GF-1 | Urban | 16 | 20 × 20 | −22∼280 | 100 |
| EO1-A | EO-1 | Mountain, Lake | 30 | 30 × 30 | 4907∼5361 | 250 |
| EO1-B | EO-1 | Rural | 30 | 27 × 27 | 331∼437 | 120 |
| S2-A | Sentinel-2 | Urban, River | 60 | 110 × 110 | −55∼1257 | 80 |
| S2-B | Sentinel-2 | Rural | 60 | 110 × 110 | 847∼1272 | 300 |
| Dataset | GCPs/ICPs | Ridge Estimation | L1LS | PCA-RFM | APCA-RFM | ASPCA-RFM |
|---|---|---|---|---|---|---|
| GF1-A | 10/190 | 286.52 ± 115.44 | 3.8254 ± 2.5172 | 2.6414 ± 3.0570 | 2.5632 ± 3.0873 | 1.1704 ± 0.1413 |
| 15/185 | 69.087 ± 23.892 | 1.7546 ± 0.6008 | 1.0119 ± 0.1279 | 1.0017 ± 0.1106 | 0.9980 ± 0.0958 | |
| 20/180 | 48.835 ± 37.972 | 1.7815 ± 0.3979 | 1.1274 ± 0.2124 | 1.2313 ± 0.3530 | 1.1193 ± 0.2361 | |
| 40/160 | 4.4347 ± 1.6321 | 1.5912 ± 0.3304 | 0.8598 ± 0.0322 | 0.8382 ± 0.0289 | 0.8519 ± 0.0265 | |
| 50/150 | 3.0036 ± 1.4762 | 1.3455 ± 0.1606 | 0.8629 ± 0.0430 | 0.8489 ± 0.0394 | 0.8699 ± 0.0387 | |
| GF1-B | 10/90 | 83.932 ± 21.314 | 3.1493 ± 4.2251 | 1.9714 ± 0.4728 | 1.8910 ± 0.6624 | 1.7997 ± 0.5219 |
| 15/85 | 44.755 ± 22.098 | 4.2002 ± 4.2721 | 1.3033 ± 0.2391 | 1.5418 ± 0.6608 | 1.2666 ± 0.2015 | |
| 20/80 | 12.587 ± 5.5499 | 1.2065 ± 0.2709 | 1.1808 ± 0.0900 | 1.1688 ± 0.1349 | 1.1266 ± 0.0586 | |
| 40/60 | 7.8813 ± 8.3771 | 3.0036 ± 3.9359 | 1.0754 ± 0.1423 | 0.9914 ± 0.0511 | 1.0201 ± 0.0472 | |
| 50/50 | 7.3447 ± 10.400 | 3.3032 ± 4.2816 | 0.9870 ± 0.0583 | 0.9836 ± 0.0730 | 0.9850 ± 0.0578 | |
| EO1-A | 10/240 | 109.31 ± 33.435 | 1.5254 ± 1.0866 | 0.7464 ± 0.1207 | 0.7741 ± 0.1235 | 0.6639 ± 0.0747 |
| 15/235 | 58.242 ± 24.074 | 0.8955 ± 0.2221 | 0.6998 ± 0.1110 | 0.6995 ± 0.1325 | 0.6827 ± 0.0991 | |
| 20/230 | 24.292 ± 12.448 | 0.8026 ± 0.1566 | 0.6768 ± 0.0831 | 0.6152 ± 0.0834 | 0.6059 ± 0.0261 | |
| 40/210 | 4.0333 ± 1.7325 | 0.7326 ± 0.0876 | 0.5615 ± 0.0314 | 0.5622 ± 0.0664 | 0.5612 ± 0.0403 | |
| 50/200 | 1.4546 ± 0.5880 | 0.6847 ± 0.0407 | 0.5384 ± 0.0342 | 0.5172 ± 0.0163 | 0.5351 ± 0.0396 | |
| EO1-B | 10/110 | 145.15 ± 51.848 | 3.6538 ± 4.1398 | 1.1291 ± 0.3580 | 1.2531 ± 0.9818 | 1.0544 ± 0.3865 |
| 15/105 | 44.734 ± 14.071 | 1.3268 ± 0.2681 | 0.9563 ± 0.1560 | 0.9571 ± 0.2341 | 0.8635 ± 0.0599 | |
| 20/100 | 27.488 ± 10.997 | 1.1318 ± 0.3017 | 0.8690 ± 0.1708 | 0.8970 ± 0.1278 | 0.8299 ± 0.0847 | |
| 40/80 | 4.4904 ± 3.5525 | 0.9986 ± 0.1542 | 0.6987 ± 0.1015 | 0.7515 ± 0.1123 | 0.6927 ± 0.0565 | |
| 50/70 | 2.2041 ± 0.6681 | 0.9495 ± 0.1838 | 0.6770 ± 0.0823 | 0.6518 ± 0.0542 | 0.6915 ± 0.1411 | |
| S2-A | 10/70 | 168.88 ± 74.618 | 6.0041 ± 2.7493 | 1.2099 ± 0.4341 | 1.4811 ± 0.4198 | 1.2015 ± 0.4081 |
| 15/65 | 107.80 ± 93.904 | 4.6899 ± 3.2891 | 0.7706 ± 0.1451 | 0.8446 ± 0.2767 | 0.7485 ± 0.1598 | |
| 20/60 | 107.84 ± 106.98 | 4.8182 ± 3.7693 | 0.8929 ± 0.3100 | 1.0044 ± 0.2442 | 0.8224 ± 0.2362 | |
| 40/40 | 36.784 ± 34.181 | 2.0378 ± 0.7463 | 0.6694 ± 0.0356 | 0.7820 ± 0.2396 | 0.6538 ± 0.0277 | |
| 50/30 | 20.586 ± 21.144 | 1.5930 ± 0.8513 | 0.6606 ± 0.0694 | 0.8995 ± 0.3331 | 0.6452 ± 0.0418 | |
| S2-B | 10/290 | 107.13 ± 32.422 | 2.1641 ± 0.5022 | 1.2462 ± 0.3278 | 1.3315 ± 0.5066 | 1.3981 ± 0.5374 |
| 15/285 | 59.161 ± 31.510 | 2.1688 ± 0.5086 | 1.0541 ± 0.3425 | 1.5211 ± 0.7938 | 0.9921 ± 0.3166 | |
| 20/280 | 22.722 ± 18.665 | 1.6835 ± 0.3464 | 0.9005 ± 0.1483 | 0.9135 ± 0.2239 | 0.8233 ± 0.0686 | |
| 40/260 | 2.9398 ± 1.5114 | 1.7074 ± 0.3256 | 0.7457 ± 0.0193 | 1.0462 ± 0.7065 | 0.7366 ± 0.0065 | |
| 50/250 | 1.9344 ± 0.5927 | 1.6297 ± 0.1987 | 0.7217 ± 0.0103 | 0.7177 ± 0.0082 | 0.7290 ± 0.0252 |
| Ridge Estimation | L1LS | PCA-RFM | APCA-RFM | ASPCA-RFM-EVD | ASPCA-RFM (Ours) |
|---|---|---|---|---|---|
| 0.0008 s | 0.0013 s | 0.0009 s | 0.0021 s | 0.0845 s | 0.0454 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, T.; Wang, Y.; Wang, P. Rational Polynomial Coefficient Estimation via Adaptive Sparse PCA-Based Method. Remote Sens. 2024, 16, 3018. https://doi.org/10.3390/rs16163018
Yan T, Wang Y, Wang P. Rational Polynomial Coefficient Estimation via Adaptive Sparse PCA-Based Method. Remote Sensing. 2024; 16(16):3018. https://doi.org/10.3390/rs16163018
Chicago/Turabian StyleYan, Tianyu, Yingqian Wang, and Pu Wang. 2024. "Rational Polynomial Coefficient Estimation via Adaptive Sparse PCA-Based Method" Remote Sensing 16, no. 16: 3018. https://doi.org/10.3390/rs16163018
APA StyleYan, T., Wang, Y., & Wang, P. (2024). Rational Polynomial Coefficient Estimation via Adaptive Sparse PCA-Based Method. Remote Sensing, 16(16), 3018. https://doi.org/10.3390/rs16163018







