Temporal Dynamics of Fractional Vegetation Cover in the Yellow River Basin: A Comprehensive Analysis
Abstract
1. Introduction
2. Materials and Methods
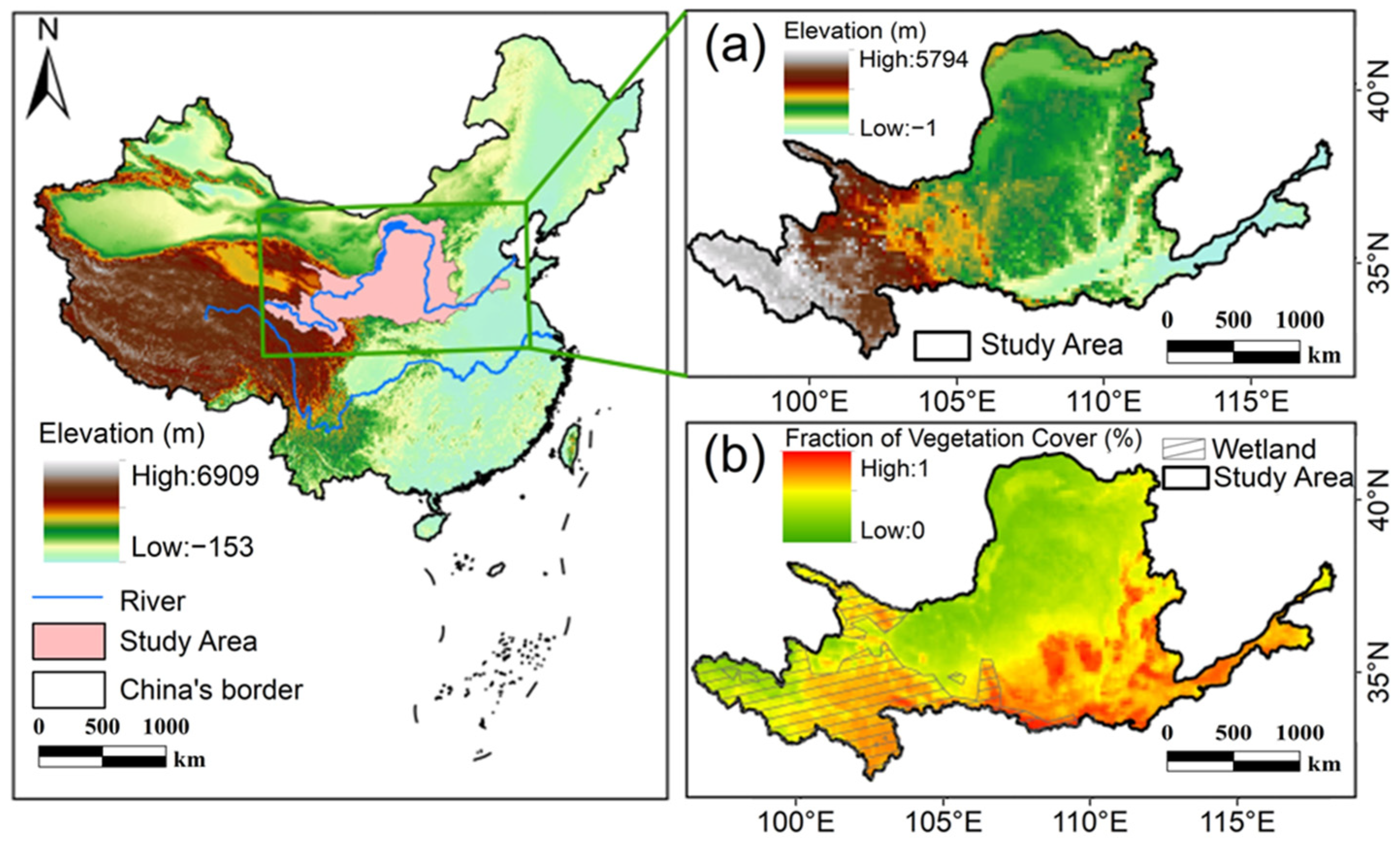
2.1. Study Area
2.2. Data Sources
2.3. Research Method
2.3.1. Preprocessing and Calculation of Fractional Vegetation Cover (FVC)
2.3.2. Trend Analysis
2.3.3. Mann–Kendall Trend Test
2.3.4. Grey Relational Analysis
2.3.5. Path Analysis
2.3.6. Time-Lag and -Accumulation Analysis
3. Results
3.1. Spatial Pattern and Trends in Meteorological Variables
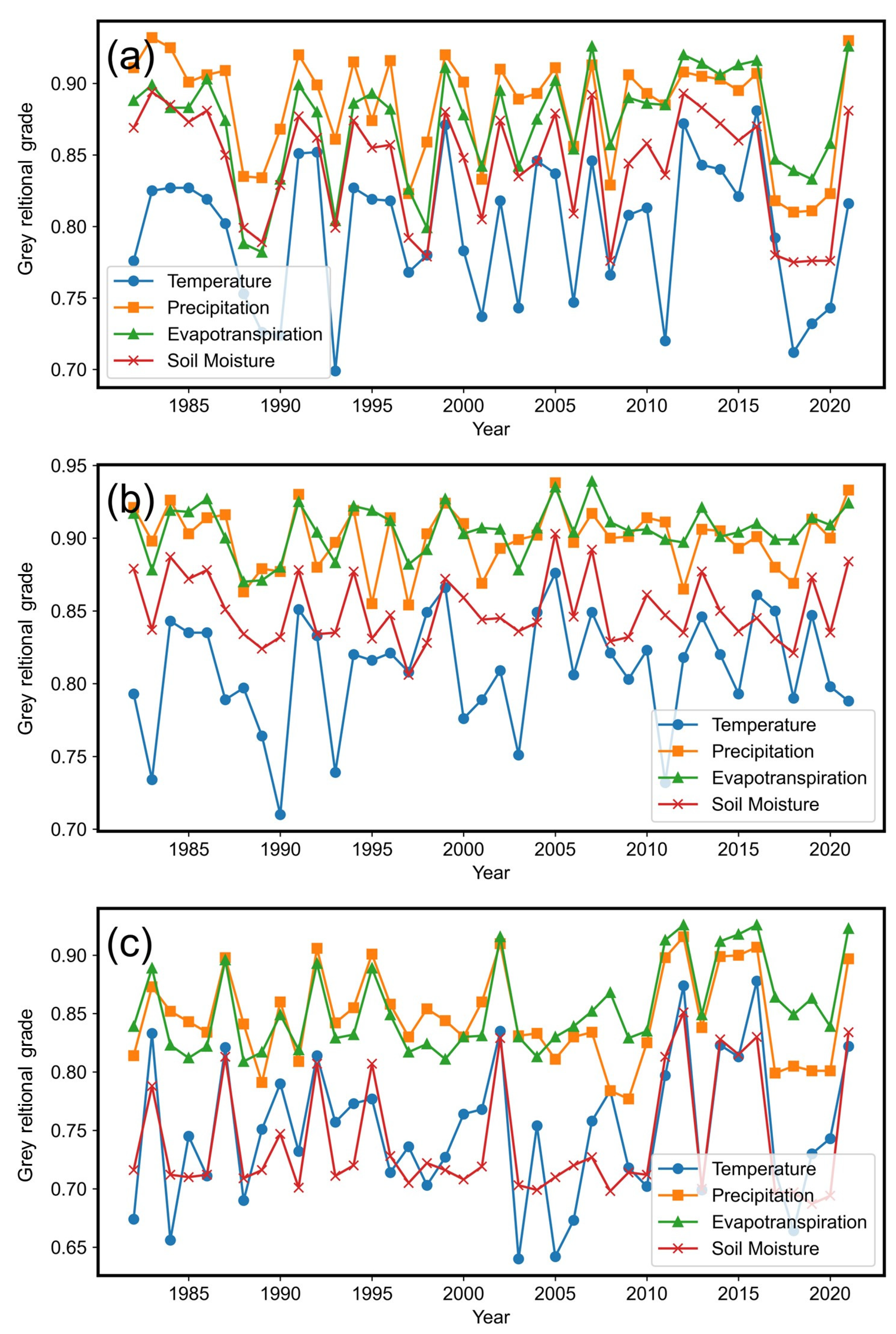
3.2. Grey Relation Analysis
3.3. Path Analysis of Meteorological Factors and FVC in Spatial and Temporal Dimensions
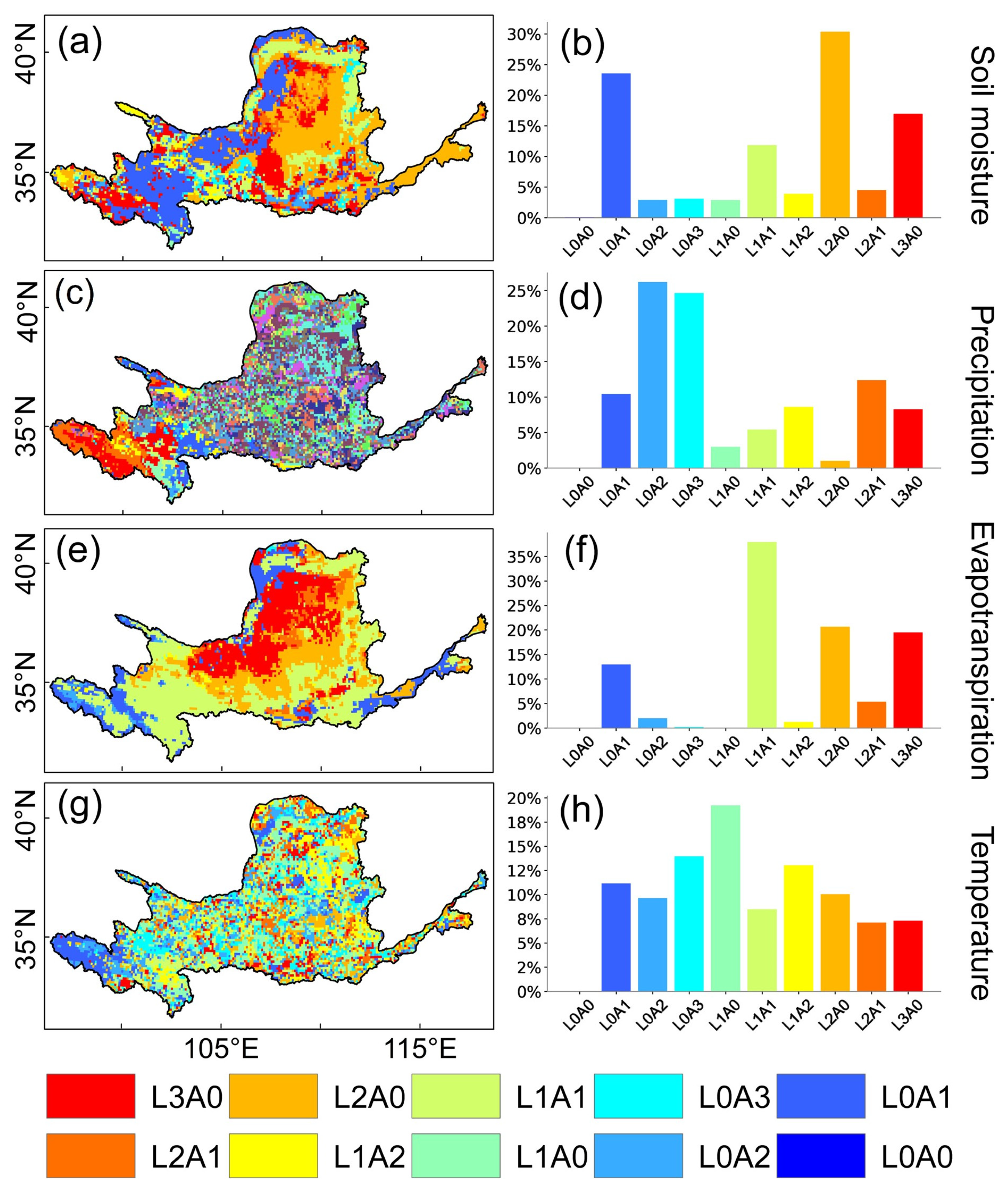
3.4. The Time-Lag and -Accumulation Effects of Meteorological Factors on FVC Changes
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Year | Temperature | Precipitation | Evapotranspiration | Soil Moisture |
|---|---|---|---|---|
| 1982 | 0.776 | 0.911 | 0.888 | 0.869 |
| 1983 | 0.825 | 0.932 | 0.899 | 0.894 |
| 1984 | 0.827 | 0.925 | 0.883 | 0.885 |
| 1985 | 0.827 | 0.901 | 0.883 | 0.873 |
| 1986 | 0.819 | 0.906 | 0.903 | 0.881 |
| 1987 | 0.802 | 0.909 | 0.874 | 0.850 |
| 1988 | 0.753 | 0.835 | 0.788 | 0.799 |
| 1989 | 0.726 | 0.834 | 0.782 | 0.789 |
| 1990 | 0.724 | 0.868 | 0.833 | 0.829 |
| 1991 | 0.851 | 0.920 | 0.899 | 0.877 |
| 1992 | 0.852 | 0.899 | 0.880 | 0.862 |
| 1993 | 0.699 | 0.861 | 0.804 | 0.799 |
| 1994 | 0.827 | 0.915 | 0.886 | 0.874 |
| 1995 | 0.819 | 0.874 | 0.893 | 0.855 |
| 1996 | 0.818 | 0.916 | 0.882 | 0.857 |
| 1997 | 0.768 | 0.823 | 0.826 | 0.792 |
| 1998 | 0.780 | 0.859 | 0.799 | 0.779 |
| 1999 | 0.871 | 0.920 | 0.911 | 0.880 |
| 2000 | 0.783 | 0.901 | 0.878 | 0.848 |
| 2001 | 0.737 | 0.833 | 0.842 | 0.805 |
| 2002 | 0.818 | 0.910 | 0.895 | 0.874 |
| 2003 | 0.743 | 0.889 | 0.842 | 0.835 |
| 2004 | 0.846 | 0.893 | 0.875 | 0.845 |
| 2005 | 0.837 | 0.911 | 0.902 | 0.879 |
| 2006 | 0.747 | 0.856 | 0.854 | 0.809 |
| 2007 | 0.846 | 0.913 | 0.926 | 0.892 |
| 2008 | 0.766 | 0.829 | 0.857 | 0.776 |
| 2009 | 0.808 | 0.887 | 0.890 | 0.844 |
| 2010 | 0.813 | 0.906 | 0.886 | 0.858 |
| 2011 | 0.720 | 0.893 | 0.885 | 0.836 |
| 2012 | 0.872 | 0.908 | 0.920 | 0.893 |
| 2013 | 0.843 | 0.905 | 0.914 | 0.883 |
| 2014 | 0.840 | 0.903 | 0.906 | 0.872 |
| 2015 | 0.821 | 0.895 | 0.913 | 0.860 |
| 2016 | 0.881 | 0.907 | 0.916 | 0.870 |
| 2017 | 0.792 | 0.818 | 0.847 | 0.780 |
| 2018 | 0.712 | 0.810 | 0.839 | 0.775 |
| 2019 | 0.732 | 0.811 | 0.833 | 0.776 |
| 2020 | 0.743 | 0.823 | 0.858 | 0.776 |
| 2021 | 0.816 | 0.930 | 0.926 | 0.881 |
| average | 0.797 | 0.883 | 0.873 | 0.843 |
| GRA order | 4 | 1 | 2 | 3 |
| Year | Temperature | Precipitation | Evapotranspiration | Soil Moisture |
|---|---|---|---|---|
| 1982 | 0.793 | 0.921 | 0.917 | 0.879 |
| 1983 | 0.734 | 0.898 | 0.878 | 0.837 |
| 1984 | 0.843 | 0.926 | 0.919 | 0.887 |
| 1985 | 0.835 | 0.903 | 0.918 | 0.872 |
| 1986 | 0.835 | 0.914 | 0.927 | 0.878 |
| 1987 | 0.789 | 0.916 | 0.900 | 0.851 |
| 1988 | 0.797 | 0.863 | 0.870 | 0.834 |
| 1989 | 0.764 | 0.879 | 0.871 | 0.824 |
| 1990 | 0.710 | 0.877 | 0.880 | 0.832 |
| 1991 | 0.851 | 0.930 | 0.925 | 0.878 |
| 1992 | 0.833 | 0.880 | 0.904 | 0.834 |
| 1993 | 0.739 | 0.897 | 0.883 | 0.835 |
| 1994 | 0.820 | 0.919 | 0.922 | 0.877 |
| 1995 | 0.816 | 0.855 | 0.919 | 0.831 |
| 1996 | 0.821 | 0.914 | 0.912 | 0.847 |
| 1997 | 0.808 | 0.854 | 0.882 | 0.806 |
| 1998 | 0.849 | 0.903 | 0.892 | 0.828 |
| 1999 | 0.866 | 0.924 | 0.927 | 0.872 |
| 2000 | 0.776 | 0.910 | 0.903 | 0.859 |
| 2001 | 0.789 | 0.869 | 0.907 | 0.844 |
| 2002 | 0.809 | 0.893 | 0.906 | 0.845 |
| 2003 | 0.751 | 0.899 | 0.878 | 0.836 |
| 2004 | 0.849 | 0.902 | 0.907 | 0.842 |
| 2005 | 0.876 | 0.938 | 0.935 | 0.903 |
| 2006 | 0.806 | 0.897 | 0.904 | 0.846 |
| 2007 | 0.849 | 0.917 | 0.939 | 0.892 |
| 2008 | 0.821 | 0.900 | 0.911 | 0.829 |
| 2009 | 0.803 | 0.901 | 0.905 | 0.832 |
| 2010 | 0.823 | 0.914 | 0.906 | 0.861 |
| 2011 | 0.732 | 0.911 | 0.899 | 0.847 |
| 2012 | 0.818 | 0.865 | 0.897 | 0.835 |
| 2013 | 0.846 | 0.906 | 0.921 | 0.877 |
| 2014 | 0.820 | 0.905 | 0.901 | 0.850 |
| 2015 | 0.793 | 0.893 | 0.904 | 0.836 |
| 2016 | 0.861 | 0.901 | 0.910 | 0.845 |
| 2017 | 0.850 | 0.880 | 0.899 | 0.831 |
| 2018 | 0.790 | 0.869 | 0.899 | 0.821 |
| 2019 | 0.847 | 0.913 | 0.914 | 0.873 |
| 2020 | 0.798 | 0.900 | 0.909 | 0.835 |
| 2021 | 0.788 | 0.933 | 0.924 | 0.884 |
| average | 0.810 | 0.900 | 0.906 | 0.851 |
| GRA order | 4 | 2 | 1 | 3 |
| Year | Temperature | Precipitation | Evapotranspiration | Soil Moisture |
|---|---|---|---|---|
| 1982 | 0.674 | 0.814 | 0.839 | 0.716 |
| 1983 | 0.833 | 0.873 | 0.889 | 0.788 |
| 1984 | 0.656 | 0.852 | 0.823 | 0.712 |
| 1985 | 0.745 | 0.843 | 0.812 | 0.710 |
| 1986 | 0.711 | 0.834 | 0.822 | 0.712 |
| 1987 | 0.821 | 0.898 | 0.896 | 0.813 |
| 1988 | 0.690 | 0.841 | 0.809 | 0.709 |
| 1989 | 0.751 | 0.791 | 0.817 | 0.716 |
| 1990 | 0.790 | 0.860 | 0.849 | 0.747 |
| 1991 | 0.732 | 0.809 | 0.819 | 0.701 |
| 1992 | 0.814 | 0.906 | 0.893 | 0.807 |
| 1993 | 0.757 | 0.842 | 0.829 | 0.711 |
| 1994 | 0.773 | 0.855 | 0.832 | 0.720 |
| 1995 | 0.777 | 0.901 | 0.889 | 0.807 |
| 1996 | 0.714 | 0.858 | 0.849 | 0.728 |
| 1997 | 0.736 | 0.830 | 0.817 | 0.705 |
| 1998 | 0.703 | 0.854 | 0.824 | 0.722 |
| 1999 | 0.727 | 0.844 | 0.811 | 0.716 |
| 2000 | 0.764 | 0.830 | 0.830 | 0.708 |
| 2001 | 0.768 | 0.860 | 0.831 | 0.719 |
| 2002 | 0.835 | 0.910 | 0.916 | 0.829 |
| 2003 | 0.640 | 0.831 | 0.830 | 0.703 |
| 2004 | 0.754 | 0.833 | 0.813 | 0.699 |
| 2005 | 0.642 | 0.811 | 0.830 | 0.710 |
| 2006 | 0.673 | 0.830 | 0.839 | 0.720 |
| 2007 | 0.758 | 0.834 | 0.852 | 0.727 |
| 2008 | 0.784 | 0.784 | 0.868 | 0.698 |
| 2009 | 0.718 | 0.777 | 0.829 | 0.714 |
| 2010 | 0.702 | 0.825 | 0.835 | 0.712 |
| 2011 | 0.797 | 0.898 | 0.913 | 0.813 |
| 2012 | 0.874 | 0.916 | 0.926 | 0.851 |
| 2013 | 0.699 | 0.838 | 0.849 | 0.700 |
| 2014 | 0.823 | 0.899 | 0.912 | 0.828 |
| 2015 | 0.813 | 0.900 | 0.918 | 0.815 |
| 2016 | 0.878 | 0.907 | 0.926 | 0.830 |
| 2017 | 0.715 | 0.799 | 0.864 | 0.697 |
| 2018 | 0.664 | 0.805 | 0.849 | 0.697 |
| 2019 | 0.730 | 0.801 | 0.863 | 0.687 |
| 2020 | 0.743 | 0.801 | 0.839 | 0.694 |
| 2021 | 0.822 | 0.897 | 0.923 | 0.834 |
| average | 0.750 | 0.847 | 0.854 | 0.741 |
| GRA order | 3 | 2 | 1 | 4 |
References
- Hill, M.J.; Guerschman, J.P. The MODIS global vegetation fractional cover product 2001–2018: Characteristics of vegetation fractional cover in grasslands and savanna woodlands. Remote Sens. 2020, 12, 406. [Google Scholar] [CrossRef]
- Huang, C.; Huang, X.; Peng, C.; Zhou, Z.; Teng, M.; Wang, P. Land use/cover change in the Three Gorges Reservoir area, China: Reconciling the land use conflicts between development and protection. Catena 2019, 175, 388–399. [Google Scholar] [CrossRef]
- Liu, H.; Li, X.; Mao, F.; Zhang, M.; Zhu, D.; He, S.; Huang, Z.; Du, H. Spatiotemporal evolution of fractional vegetation cover and its response to climate change based on MODIS data in the subtropical region of China. Remote Sens. 2021, 13, 913. [Google Scholar] [CrossRef]
- Agele, S.; Adejobi, K.; Charles, F.; Ogunleye, A.; Olayemi, L. Impacts and feedbacks of land use and land cover patterns in landscapes on ecosystem processes and microclimate: Case of a cacao-based agroforestry landscape. Curr. J. Appl. Sci. Technol. 2017, 22, 1–11. [Google Scholar]
- Filipponi, F.; Valentini, E.; Nguyen Xuan, A.; Guerra, C.A.; Wolf, F.; Andrzejak, M.; Taramelli, A. Global MODIS fraction of green vegetation cover for monitoring abrupt and gradual vegetation changes. Remote Sens. 2018, 10, 653. [Google Scholar] [CrossRef]
- Huang, S.; Zheng, X.; Ma, L.; Wang, H.; Huang, Q.; Leng, G.; Meng, E.; Guo, Y. Quantitative contribution of climate change and human activities to vegetation cover variations based on GA-SVM model. J. Hydrol. 2020, 584, 124687. [Google Scholar] [CrossRef]
- Kaye, J.P.; Quemada, M.J. Using cover crops to mitigate and adapt to climate change. A review. Agron. Sustain. Dev. 2017, 37, 4. [Google Scholar] [CrossRef]
- Wu, D.; Wu, H.; Zhao, X.; Zhou, T.; Tang, B.; Zhao, W.; Jia, K. Evaluation of spatiotemporal variations of global fractional vegetation cover based on GIMMS NDVI data from 1982 to 2011. Remote Sens. 2014, 6, 4217–4239. [Google Scholar] [CrossRef]
- Tang, L.; He, M.; Li, X. Verification of fractional vegetation coverage and NDVI of desert vegetation via UAVRS technology. Remote Sens. 2020, 12, 1742. [Google Scholar] [CrossRef]
- Wan, L.; Zhu, J.; Du, X.; Zhang, J.; Han, X.; Zhou, W.; Li, X.; Liu, J.; Liang, F.; He, Y.; et al. A model for phenotyping crop fractional vegetation cover using imagery from unmanned aerial vehicles. J. Exp. Bot. 2021, 72, 4691–4707. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Z.; Chen, J.; Chen, H.; Jin, J.; Han, J.; Wang, X.; Song, Z.; Wei, G. Development. Estimating soil salinity with different fractional vegetation cover using remote sensing. Land Degrad. Dev. 2021, 32, 597–612. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, B.; Zhao, J.; Ye, C.; Wei, L.; Sun, J.; Chu, C.; Ming Lee, T. Global patterns and abiotic drivers of ecosystem multifunctionality in dominant natural ecosystems. Environ. Int. 2022, 168, 107480. [Google Scholar] [CrossRef]
- Han, H.; Yin, Y.; Zhao, Y.; Qin, F. Spatiotemporal Variations in Fractional Vegetation Cover and Their Responses to Climatic Changes on the Qinghai–Tibet Plateau. Remote Sens. 2023, 15, 2662. [Google Scholar] [CrossRef]
- Li, P.; He, Z.; He, D.; Xue, D.; Wang, Y.; Cao, S. Fractional vegetation coverage response to climatic factors based on grey relational analysis during the 2000–2017 growing season in Sichuan Province, China. Int. J. Remote Sens. 2020, 41, 1170–1190. [Google Scholar] [CrossRef]
- Zhuang, Q.; Wu, S.; Feng, X.; Niu, Y. Analysis and prediction of vegetation dynamics under the background of climate change in Xinjiang, China. PeerJ 2020, 8, e8282. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Zhang, Q.; Li, T.; Zhang, K. Dynamic Vegetation Responses to Climate and Land Use Changes over the Inner Mongolia Reach of the Yellow River Basin, China. Remote Sens. 2023, 15, 3531. [Google Scholar] [CrossRef]
- Zhu, X.; He, H.S.; Zhang, S.; Dijak, W.D.; Fu, Y. Interactive effects of climatic factors on seasonal vegetation dynamics in the Central Loess Plateau, China. Forests 2019, 10, 1071. [Google Scholar] [CrossRef]
- Knapp, A.K.; Ciais, P.; Smith, M.D. Reconciling inconsistencies in precipitation–productivity relationships: Implications for climate change. New Phytologist 2017, 214, 41–47. [Google Scholar] [CrossRef]
- Yongyong, Z.; Jinjin, H.; Guoxia, M.; Xiaoyan, Z.; Aifeng, L.; Wei, W.; Zhonggen, W. Regional differences of water regulation services of terrestrial ecosystem in the Tibetan Plateau: Insights from multiple land covers. J. Clean. Prod. 2021, 283, 125216. [Google Scholar] [CrossRef]
- Maia, A.G.; Miyamoto, B.C.B.; Garcia, J.R. Climate change and agriculture: Do environmental preservation and ecosystem services matter? Ecol. Econ. 2018, 152, 27–39. [Google Scholar] [CrossRef]
- Mo, X.-G.; Hu, S.; Lin, Z.-H.; Liu, S.-X.; Xia, J. Impacts of climate change on agricultural water resources and adaptation on the North China Plain. Adv. Clim. Chang. Res. 2017, 8, 93–98. [Google Scholar] [CrossRef]
- Zeng, Y.; Yang, X.; Fang, N.; Shi, Z. Large-scale afforestation significantly increases permanent surface water in China’s vegetation restoration regions. Agric. For. Meteorol. 2020, 290, 108001. [Google Scholar] [CrossRef]
- Wang, J.; Wang, K.; Zhang, M.; Zhang, C. Impacts of climate change and human activities on vegetation cover in hilly southern China. Ecol. Eng. 2015, 81, 451–461. [Google Scholar] [CrossRef]
- Li, L.; Zha, Y.; Zhang, J.; Li, Y.; Lyu, H. Effect of terrestrial vegetation growth on climate change in China. J. Environ. Manag. 2020, 262, 110321. [Google Scholar] [CrossRef]
- Li, L.; Zhu, L.; Xu, N.; Liang, Y.; Zhang, Z.; Liu, J.; Li, X. Climate Change and Diurnal Warming: Impacts on the Growth of Different Vegetation Types in the North–South Transition Zone of China. Land 2022, 12, 13. [Google Scholar] [CrossRef]
- Running, S.W.; Nemani, R.R.; Heinsch, F.A.; Zhao, M.; Reeves, M.; Hashimoto, H. A continuous satellite-derived measure of global terrestrial primary production. Bioscience 2004, 54, 547–560. [Google Scholar] [CrossRef]
- de Jong, R.; Schaepman, M.E.; Furrer, R.; De Bruin, S.; Verburg, P.H. Spatial relationship between climatologies and changes in global vegetation activity. Glob. Chang. Biol. 2013, 19, 1953–1964. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Guan, Q.; Sun, Y.; Zhang, J.; Yang, L.; Yang, E.; Li, H.; Du, Q. Three-dimensional dynamic characteristics of vegetation and its response to climatic factors in the Qilian Mountains. Catena 2022, 208, 105694. [Google Scholar] [CrossRef]
- Zhu, J.; Zeng, X.; Zhang, M.; Dai, Y.; Ji, D.; Li, F.; Zhang, Q.; Zhang, H.; Song, X. Evaluation of the new dynamic global vegetation model in CAS-ESM. Adv. Atmos. Sci. 2018, 35, 659–670. [Google Scholar] [CrossRef]
- Sa, R.; Yin, S.; Bao, Y.; Bao, H. Change of Desertification based on MODIS Data in the Mongolia Border Region. In Proceedings of the 7th Annual Meeting of Risk Analysis Council of China Association for Disaster Prevention (RAC-2016), Changsha, China, 4–6 November 2016; pp. 837–843. [Google Scholar]
- Zhang, Q.; Wang, G.; Yuan, R.; Singh, V.P.; Wu, W.; Wang, D. Dynamic responses of ecological vulnerability to land cover shifts over the Yellow River Basin, China. Ecol. Indic. 2022, 144, 109554. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, J.; Singh, V.P.; Shi, P.; Sun, P. Hydrological responses to climatic changes in the Yellow River basin, China: Climatic elasticity and streamflow prediction. J. Hydrol. 2017, 554, 635–645. [Google Scholar] [CrossRef]
- Li, T.; Zhang, Q.; Singh, V.P.; Zhao, J.; Song, J.; Sun, S.; Wang, G.; Shen, Z.; Wu, W. Identification of degradation areas of ecological environment and degradation intensity assessment in the Yellow River Basin. Front. Earth Sci. 2022, 10, 922013. [Google Scholar] [CrossRef]
- Feng, Y.; Zhu, A.; Liu, P.; Liu, Z. Coupling and coordinated relationship of water utilization, industrial development and ecological welfare in the Yellow River Basin, China. J. Clean. Prod. 2022, 379, 134824. [Google Scholar] [CrossRef]
- Yang, T.; Zhang, Q.; Chen, Y.D.; Tao, X.; Xu, C.y.; Chen, X. A spatial assessment of hydrologic alteration caused by dam construction in the middle and lower Yellow River, China. Hydrol. Process. Int. J. 2008, 22, 3829–3843. [Google Scholar] [CrossRef]
- Yang, Y.; Tian, F. Abrupt change of runoff and its major driving factors in Haihe River Catchment, China. J. Hydrol. 2009, 374, 373–383. [Google Scholar] [CrossRef]
- Zhou, S.; Williams, A.P.; Lintner, B.R.; Berg, A.M.; Zhang, Y.; Keenan, T.F.; Cook, B.I.; Hagemann, S.; Seneviratne, S.I.; Gentine, P. Soil moisture–atmosphere feedbacks mitigate declining water availability in drylands. Nat. Clim. Chang. 2021, 11, 38–44. [Google Scholar] [CrossRef]
- Li, M.; Cao, S.; Zhu, Z.; Wang, Z.; Myneni, R.; Piao, S. Spatiotemporally consistent global dataset of the GIMMS Normalized Difference Vegetation Index (PKU GIMMS NDVI) from 1982 to 2022. Earth Syst. Sci. Data 2023, 15, 4181–4203. [Google Scholar] [CrossRef]
- Viovy, N.; Arino, O.; Belward, A.S. The Best Index Slope Extraction (BISE): A method for reducing noise in NDVI time-series. Int. J. Remote Sens. 1992, 13, 1585–1590. [Google Scholar] [CrossRef]
- Forkel, M.; Carvalhais, N.; Verbesselt, J.; Mahecha, M.D.; Neigh, C.S.; Reichstein, M. Trend change detection in NDVI time series: Effects of inter-annual variability and methodology. Remote Sens. 2013, 5, 2113–2144. [Google Scholar] [CrossRef]
- Hamed, K.H.; Rao, A.R. A modified Mann-Kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Fu, C.; Zheng, J.; Zhao, J.; Xu, W. Application of grey relational analysis for corrosion failure of oil tubes. Corros. Sci. 2001, 43, 881–889. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, J.; Luo, X.; Hu, C. Railway freight demand forecasting based on multiple factors: Grey relational analysis and deep autoencoder neural networks. Sustainability 2023, 15, 9652. [Google Scholar] [CrossRef]
- Werts, C.E.; Linn, R.L. Path analysis: Psychological examples. Corros. Sci. 1970, 74, 193. [Google Scholar] [CrossRef]
- Fei, N.; Gao, Y.; Lu, Z.; Xiang, T. Z-score normalization, hubness, and few-shot learning. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 142–151. [Google Scholar]
- Ding, Y.; Li, Z.; Peng, S. Geoinformation. Global analysis of time-lag and-accumulation effects of climate on vegetation growth. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102179. [Google Scholar]
- Wu, D.; Zhao, X.; Liang, S.; Zhou, T.; Huang, K.; Tang, B.; Zhao, W. Time—lag effects of global vegetation responses to climate change. Glob. Chang. Biol. 2015, 21, 3520–3531. [Google Scholar] [CrossRef]
- Schwinning, S.; Sala, O.E. Hierarchy of responses to resource pulses in arid and semi-arid ecosystems. Oecologia 2004, 141, 211–220. [Google Scholar] [CrossRef] [PubMed]
- Sala, O.E.; Gherardi, L.A.; Reichmann, L.; Jobbágy, E.; Peters, D. Legacies of precipitation fluctuations on primary production: Theory and data synthesis. Philos. Trans. R. Soc. B Biol. Sci. 2012, 367, 3135–3144. [Google Scholar] [CrossRef]
- Rodriguez-Iturbe, I.; Rinaldo, A. Fractal River Basins: Chance and Self-Organization; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Rodríguez-Iturbe, I.; Porporato, A. Ecohydrology of Water-Controlled Ecosystems: Soil Moisture and Plant Dynamics; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Wang, Y.; Zhao, J.; Fu, J.; Wei, W. Effects of the Grain for Green Program on the water ecosystem services in an arid area of China—Using the Shiyang River Basin as an example. Ecol. Indic. 2019, 104, 659–668. [Google Scholar] [CrossRef]
- Jian, S.; Zhang, Q.; Wang, H. Spatial–temporal trends in and attribution analysis of vegetation change in the yellow river basin, China. Remote Sens. 2022, 14, 4607. [Google Scholar] [CrossRef]
- Yang, L.; Jia, K.; Liang, S.; Liu, M.; Wei, X.; Yao, Y.; Zhang, X.; Liu, D. Spatio-temporal analysis and uncertainty of fractional vegetation cover change over northern China during 2001–2012 based on multiple vegetation data sets. Remote Sens. 2018, 10, 549. [Google Scholar] [CrossRef]
- Yu, X.; Xie, J.; Jiang, R.; Zhao, Y.; Li, F.; Liang, J.; Wang, Y. Spatiotemporal variation and predictability of vegetation coverage in the Beijing–Tianjin–Hebei metropolitan region, China. Theor. Appl. Climatol. 2021, 145, 47–62. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, T.; Yi, G.; He, D.; Zhou, X.; Li, J.; Bie, X.; Miao, J. Dynamic changes of NDVI in the growing season of the Tibetan Plateau during the past 17 years and its response to climate change. Int. J. Environ. Res. Public Health 2019, 16, 3452. [Google Scholar] [CrossRef] [PubMed]
- Gerus-Gościewska, M.; Gościewski, D. Grey systems theory as an effective method for analyzing scarce, incomplete and uncertain data on the example of a survey of public perceptions of safety in urban spaces. Land 2021, 10, 73. [Google Scholar] [CrossRef]
- Rosenberg, D.E. Shades of grey: A critical review of grey-number optimization. Eng. Optim. 2009, 41, 573–592. [Google Scholar] [CrossRef]
- Crockford, R.; Richardson, D.P. Partitioning of rainfall into throughfall, stemflow and interception: Effect of forest type, ground cover and climate. Hydrol. Process. 2000, 14, 2903–2920. [Google Scholar] [CrossRef]
- Senay, G.; Leake, S.; Nagler, P.; Artan, G.; Dickinson, J.; Cordova, J.; Glenn, E.P. Estimating basin scale evapotranspiration (ET) by water balance and remote sensing methods. Hydrol. Process. 2011, 25, 4037–4049. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture–climate interactions in a changing climate: A review. Earth-Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- Wang, S.; Fu, B.; Gao, G.; Yao, X.; Zhou, J. Soil moisture and evapotranspiration of different land cover types in the Loess Plateau, China. Hydrol. Earth Syst. Sci. 2012, 16, 2883–2892. [Google Scholar] [CrossRef]
- Wei, J.; Su, H.; Yang, Z.-L. Impact of moisture flux convergence and soil moisture on precipitation: A case study for the southern United States with implications for the globe. Clim. Dyn. 2016, 46, 467–481. [Google Scholar] [CrossRef]
- Spracklen, D.V.; Arnold, S.R.; Taylor, C.M. Observations of increased tropical rainfall preceded by air passage over forests. Nature 2012, 489, 282–285. [Google Scholar] [CrossRef]
- Cavanaugh, M.L.; Kurc, S.A.; Scott, R.L. Evapotranspiration partitioning in semiarid shrubland ecosystems: A two-site evaluation of soil moisture control on transpiration. Ecohydrology 2011, 4, 671–681. [Google Scholar] [CrossRef]
- Taylor, C.M.; de Jeu, R.A.; Guichard, F.; Harris, P.P.; Dorigo, W.A. Afternoon rain more likely over drier soils. Nature 2012, 489, 423–426. [Google Scholar] [CrossRef] [PubMed]
- Zeppel, M.; Wilks, J.V.; Lewis, J.D. Impacts of extreme precipitation and seasonal changes in precipitation on plants. Biogeosciences 2014, 11, 3083–3093. [Google Scholar] [CrossRef]
- Holdrege, M.C.; Beard, K.H.; Kulmatiski, A. Woody plant growth increases with precipitation intensity in a cold semiarid system. Ecology 2021, 102, e03212. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Liu, J.; Liu, H.; Sun, B.; Zhang, Z.; Shi, Z.; Ren, F.; Li, J. Effects of hillslope aspect on erosion rate of alpine meadows in the Three-River Headwater Region, China. Catena 2024, 239, 107971. [Google Scholar] [CrossRef]
- Wright, S. The method of path coefficients. Ann. Math. Stat. 1934, 5, 161–215. [Google Scholar] [CrossRef]
- Keenan, T.F.; Riley, W.J. Greening of the land surface in the world’s cold regions consistent with recent warming. Nat. Clim. Change 2018, 8, 825–828. [Google Scholar] [CrossRef] [PubMed]
- Piao, S.; Liu, Z.; Wang, T.; Peng, S.; Ciais, P.; Huang, M.; Ahlström, A.; Burkhart, J.F.; Chevallier, F.; Janssens, I.A.; et al. Weakening temperature control on the interannual variations of spring carbon uptake across northern lands. Nat. Clim. Chang. 2017, 7, 359–363. [Google Scholar] [CrossRef]
- Seddon, A.W.; Macias-Fauria, M.; Long, P.R.; Benz, D.; Willis, K.J. Sensitivity of global terrestrial ecosystems to climate variability. Nature 2016, 531, 229–232. [Google Scholar] [CrossRef]
- Forkel, M.; Carvalhais, N.; Rödenbeck, C.; Keeling, R.F.; Heimann, M.; Thonicke, K.; Zaehle, S.; Reichstein, M. Enhanced seasonal CO2 exchange caused by amplified plant productivity in northern ecosystems. Science 2016, 351, 696–699. [Google Scholar] [CrossRef]


| Variable Name | Short Name | Dimension | Variable Name in Product | Temporal Resolution | Horizontal Resolution |
|---|---|---|---|---|---|
| Precipitation | P | 3 | Total precipitation | Monthly | 0.1° × 0.1° |
| Evapotranspiration | E | 3 | Evaporation | Monthly | 0.1° × 0.1° |
| 2 m temperature | 2 mT | 3 | 2 m temperature | Monthly | 0.1° × 0.1° |
| Soil moisture | SM | 3 | Volumetric soil moisture layer | Monthly | 0.1° × 0.1° |
| Vegetation Coverage Value | Categories | YRB | Dryland | Wetland |
|---|---|---|---|---|
| 0.00 ≤ FVC < 0.30 | Extremely low coverage | 21.46% | 25.63% | 5.44% |
| 0.03 ≤ FVC < 0.45 | Low coverage | 27.78% | 30.37% | 18.32% |
| 0.45 ≤ FVC < 0.60 | Medium coverage | 21.24% | 18.74% | 31.54% |
| 0.60 ≤ FVC < 0.75 | Medium–high coverage | 21.93% | 16.91% | 38.10% |
| 0.75 ≤ FVC < 1.00 | High coverage | 7.58% | 8.34% | 6.61% |
| Category | Values | Soil Moisture | Precipitation | Evapotranspiration | Temperature |
|---|---|---|---|---|---|
| Immediate impacts (II) | Min | −0.372 | −0.513 | −0.407 | −0.151 |
| Mean | 0.401 | 0.204 | 0.075 | 0.003 | |
| Max | 0.981 | 0.616 | 0.585 | 0.133 | |
| STD | 0.202 | 0.176 | 0.151 | 0.026 | |
| Indirect impacts (DI) | Min | −0.380 | −0.103 | −0.251 | −0.107 |
| Mean | 0.217 | −0.001 | 0.145 | −0.003 | |
| Max | 0.724 | 0.074 | 0.794 | 0.099 | |
| STD | 0.150 | 0.019 | 0.206 | 0.025 | |
| Combined impacts (CI) | Min | −0.312 | −0.522 | −0.390 | −0.154 |
| Mean | 0.617 | 0.204 | 0.220 | 0.000 | |
| Max | 1.044 | 0.628 | 0.899 | 0.141 | |
| STD | 0.192 | 0.175 | 0.282 | 0.036 | |
| Min | −0.312 | −0.522 | −0.390 | −0.154 |
| Category | Values | Soil Moisture | Precipitation | Evapotranspiration | Temperature |
|---|---|---|---|---|---|
| Immediate impacts (II) | Min | −0.372 | −0.513 | −0.407 | −0.151 |
| Mean | 0.401 | 0.204 | 0.075 | 0.003 | |
| Max | 0.981 | 0.616 | 0.585 | 0.133 | |
| STD | 0.202 | 0.176 | 0.151 | 0.026 | |
| Indirect impacts (DI) | Min | −0.380 | −0.103 | −0.251 | −0.107 |
| Mean | 0.217 | −0.001 | 0.145 | −0.003 | |
| Max | 0.724 | 0.074 | 0.794 | 0.099 | |
| STD | 0.150 | 0.019 | 0.206 | 0.025 | |
| Combined impacts (CI) | Min | −0.312 | −0.522 | −0.390 | −0.154 |
| Mean | 0.617 | 0.204 | 0.220 | 0.000 | |
| Max | 1.044 | 0.628 | 0.899 | 0.141 | |
| STD | 0.192 | 0.175 | 0.282 | 0.036 | |
| Min | −0.312 | −0.522 | −0.390 | −0.154 |
| Category | Values | Soil Moisture | Precipitation | Evapotranspiration | Temperature |
|---|---|---|---|---|---|
| Immediate impacts (II) | Min | −0.372 | −0.513 | −0.407 | −0.151 |
| Mean | 0.401 | 0.204 | 0.075 | 0.003 | |
| Max | 0.981 | 0.616 | 0.585 | 0.133 | |
| STD | 0.202 | 0.176 | 0.151 | 0.026 | |
| Indirect impacts (DI) | Min | −0.380 | −0.103 | −0.251 | −0.107 |
| Mean | 0.217 | −0.001 | 0.145 | −0.003 | |
| Max | 0.724 | 0.074 | 0.794 | 0.099 | |
| STD | 0.150 | 0.019 | 0.206 | 0.025 | |
| Combined impacts (CI) | Min | −0.312 | −0.522 | −0.390 | −0.154 |
| Mean | 0.617 | 0.204 | 0.220 | 0.000 | |
| Max | 1.044 | 0.628 | 0.899 | 0.141 | |
| STD | 0.192 | 0.175 | 0.282 | 0.036 | |
| Min | −0.312 | −0.522 | −0.390 | −0.154 |
| Category | Soil Moisture | Precipitation | Evapotranspiration | Temperature |
|---|---|---|---|---|
| L0A0 | 0.05 | 0.02 | 0.02 | 0.02 |
| L0A1 | 23.57 | 10.42 | 12.96 | 11.16 |
| L0A2 | 2.88 | 26.20 | 2.00 | 9.63 |
| L0A3 | 3.09 | 24.67 | 0.20 | 13.96 |
| L1A0 | 2.87 | 2.98 | 0.05 | 19.23 |
| L1A1 | 11.84 | 5.43 | 37.96 | 8.49 |
| L1A2 | 3.88 | 8.60 | 1.25 | 13.05 |
| L2A0 | 30.37 | 1.00 | 20.66 | 10.04 |
| L2A1 | 4.51 | 12.38 | 5.37 | 7.10 |
| L3A0 | 16.95 | 8.29 | 19.54 | 7.31 |
| Category | Soil Moisture | Precipitation | Evapotranspiration | Temperature |
|---|---|---|---|---|
| L0A0 | 0.05 | 0.02 | 0.02 | 0.02 |
| L0A1 | 18.35 | 7.53 | 10.44 | 7.35 |
| L0A2 | 2.82 | 32.24 | 0.14 | 8.54 |
| L0A3 | 3.40 | 31.15 | 0.24 | 14.91 |
| L1A0 | 2.07 | 1.48 | 0.06 | 20.54 |
| L1A1 | 13.68 | 5.46 | 29.23 | 6.59 |
| L1A2 | 2.13 | 7.75 | 1.53 | 14.61 |
| L2A0 | 36.90 | 1.23 | 26.38 | 10.68 |
| L2A1 | 5.47 | 9.90 | 6.83 | 8.70 |
| L3A0 | 15.13 | 3.26 | 25.14 | 8.07 |
| Category | Soil Moisture | Precipitation | Evapotranspiration | Temperature |
|---|---|---|---|---|
| L0A0 | 0.05 | 0.05 | 0.05 | 0.05 |
| L0A1 | 41.03 | 20.12 | 21.39 | 23.88 |
| L0A2 | 3.09 | 6.01 | 8.20 | 13.24 |
| L0A3 | 2.02 | 2.98 | 0.05 | 10.80 |
| L1A0 | 5.53 | 7.98 | 0.00 | 14.84 |
| L1A1 | 5.69 | 5.32 | 67.16 | 14.84 |
| L1A2 | 9.74 | 11.44 | 0.32 | 7.82 |
| L2A0 | 8.52 | 0.27 | 1.54 | 7.93 |
| L2A1 | 1.28 | 20.70 | 0.48 | 1.76 |
| L3A0 | 23.04 | 25.12 | 0.80 | 4.79 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, K.; Zhang, Q.; Singh, V.P. Temporal Dynamics of Fractional Vegetation Cover in the Yellow River Basin: A Comprehensive Analysis. Remote Sens. 2024, 16, 2991. https://doi.org/10.3390/rs16162991
Zhang K, Zhang Q, Singh VP. Temporal Dynamics of Fractional Vegetation Cover in the Yellow River Basin: A Comprehensive Analysis. Remote Sensing. 2024; 16(16):2991. https://doi.org/10.3390/rs16162991
Chicago/Turabian StyleZhang, Kaiwen, Qiang Zhang, and Vijay P. Singh. 2024. "Temporal Dynamics of Fractional Vegetation Cover in the Yellow River Basin: A Comprehensive Analysis" Remote Sensing 16, no. 16: 2991. https://doi.org/10.3390/rs16162991
APA StyleZhang, K., Zhang, Q., & Singh, V. P. (2024). Temporal Dynamics of Fractional Vegetation Cover in the Yellow River Basin: A Comprehensive Analysis. Remote Sensing, 16(16), 2991. https://doi.org/10.3390/rs16162991









