Statistical Analysis of the Correlation between Geomagnetic Storm Intensity and Solar Wind Parameters from 1996 to 2023
Abstract
1. Introduction
2. Dataset and Methods
3. Results
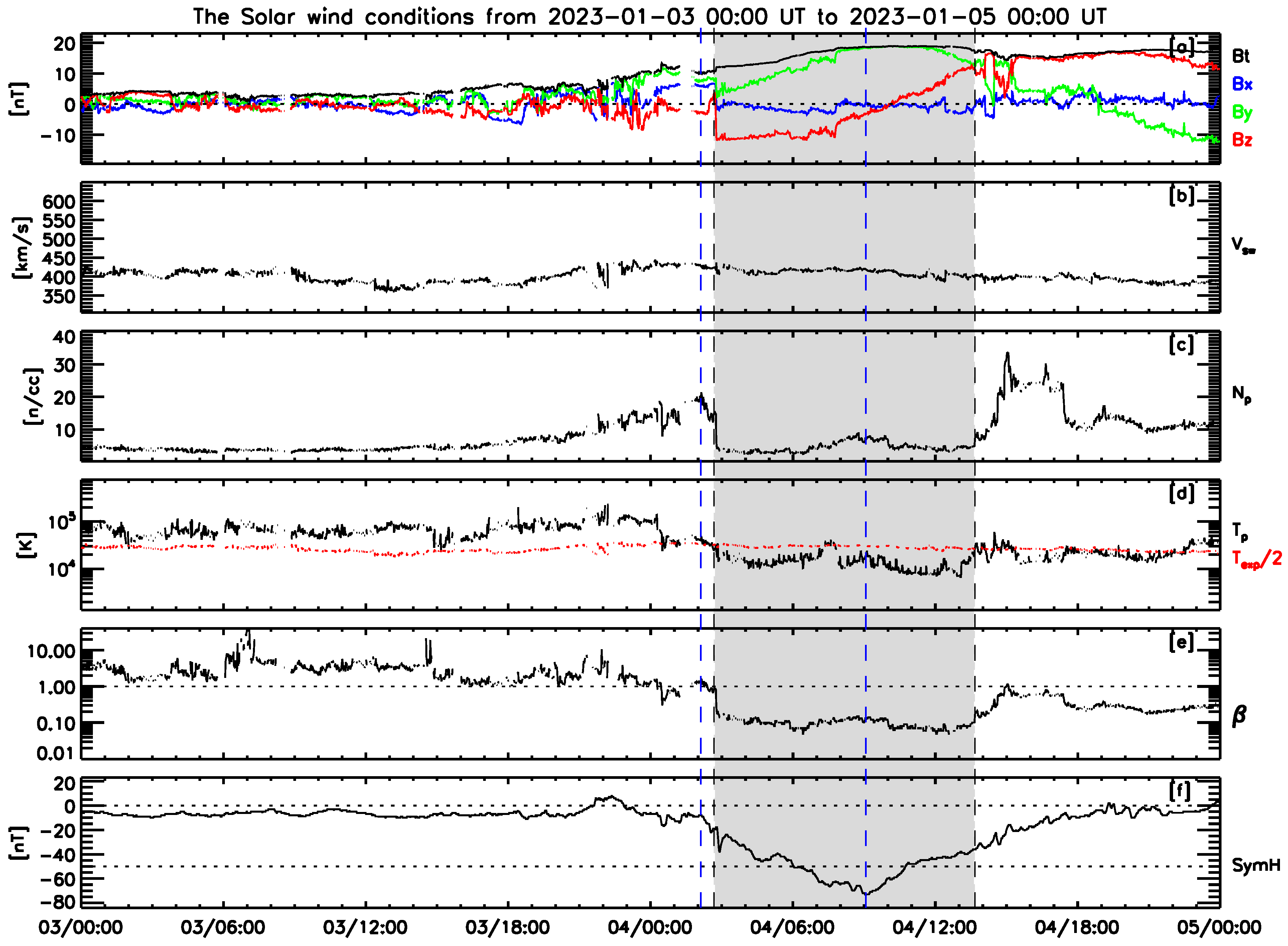
3.1. Examples of the Geomagnetic Storms
3.2. Statistics of the Geomagnetic Storms
3.3. Correlation Analysis
4. Discussion
5. Conclusions
- (1)
- The solar activity level in the 23rd solar cycle was the highest, while the 25th cycle’s first four years showed intermediate activity, compared to the initial four years of the 23rd and 24th cycles, a trend similar to geomagnetic storm occurrences;
- (2)
- ICME-related structures were the primary drivers of strong storms, causing approximately 88% of strong storms over the study period. This dominance was consistent but varied across different solar cycle phases, accounting for 88.5%, 100%, and 80% of strong storms in the first four years of the 23rd, 24th, and 25th solar cycles, respectively. The influence on moderate storms was more variable: over the entire period, they contributed to 40.2% of moderate storms overall, with 48.9%, 68%, and 34% in the initial four years of the 23rd, 24th, and 25th cycles, respectively;
- (3)
- For the all-384-storms, strong storm intensities showed higher CCs compared to moderate storms. ICME-related storms had a high negative correlation with (−0.827), a moderate positive correlation with IMF (~0.788), moderate negative correlations with (−0.776) and (−0.669), a moderate negative correlation with (~−0.512), a low negative correlation with (~−0.485), and a very low negative correlation with (~−0.274);
- (4)
- Compared to the 71 storms that occurred from the initial four years of the 23rd solar cycle and the all-384-storms from 1996-09 to 2023-12, there are 58 storms that occurred during the same phase of the 25th solar cycle that had lower correlations with the IMF and but higher correlations with , , , and ;
- (5)
- During approximately 66.7% of moderate storms and 51.5% of strong storms among the cont.-174/384-storms, the southward IMF lasted for a duration of ≤ 13 h. Continuous southward IMF enhanced solar wind–magnetosphere coupling, resulting in more effective energy transfer and stronger storms. This direct and efficient energy coupling strengthened the correlation between peak values of SWPs and storm intensity but weakened the influence of cumulative effects. Notably, the longer-duration of southward IMF (e.g., 13 h) further enhanced the correlations of storm intensity with both peak and integral values of SWPs. Contrarily, multiple or even frequent north–south directional changes in the IMF during the storm’s main phase weakened the reliance of storm intensity on the IMF . The results illustrated the complex interplay between immediate and cumulative influences on geomagnetic storm dynamics.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gonzalez, W.D.; Joselyn, J.A.C.; Kamide, Y.; Kroehl, H.W.; Rostoker, G.; Tsurutani, B.T.; Vasyliūnas, V.M. What is a geomagnetic storm? J. Geophys. Res. 1994, 99, 5771–5792. [Google Scholar] [CrossRef]
- Kamide, Y.; Maltsev, Y.-P. Geomagnetic Storms. In Handbook of the Solar-Terrestrial Environment; Kamide, Y., Chian, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 355–374. [Google Scholar]
- Koskinen, H.E.J. Magnetospheric Storms and Substorms. In Physics of Space Storms: From the Solar Surface to the Earth; Koskinen, H.E.J., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 56, pp. 323–370. [Google Scholar]
- Zhang, X. Source, Evolution, and Properties of Non-Parker-spiral IMF and Its Role on Geomagnetic Activity. Ph.D. Dissertation, The University of Michigan, Ann Arbor, MI, USA, 2015. [Google Scholar]
- Dungey, J.W. Interplanetary Magnetic Field and the Auroral Zones. Phys. Rev. Lett. 1961, 6, 47–48. [Google Scholar] [CrossRef]
- Antonova, E.E.; Pulinets, M.S.; Riazantseva, M.O.; Znatkova, S.S.; Kirpichev, I.P.; Stepanova, M.V. Turbulence in the magnetosheath and the problem of plasma penetration inside the magnetosphere. In Exploring the Solar Wind; Lazar, M., Ed.; IntechOpen: London, UK, 2012. [Google Scholar] [CrossRef]
- Safránková, J.; Hayosh, M.; Gutynska, O.; Němeek, Z.; Pech, L. Reliability of prediction of the magnetosheath BZ component from interplanetary magnetic field observations. J. Geophys. Res. 2009, 114, A12213. [Google Scholar] [CrossRef]
- Turc, L.; Fontaine, D.; Savoini, P.; Kilpua, E.K.J. Magnetic clouds’ structure in the magnetosheath as observed by Cluster and Geotail: Four case studies. Ann. Geophys. 2014, 32, 1247–1261. [Google Scholar] [CrossRef]
- Akasofu, S.-I. Energy coupling between the solar wind and the magnetosphere. Space Sci. Rev. 1981, 28, 121–190. [Google Scholar] [CrossRef]
- Akasofu, S.-I. A Review of the Current Understanding in the Study of Geomagnetic Storms. Int. J. Earth Sci. Geophys. 2018, 4, 18. [Google Scholar] [CrossRef]
- Axford, W.I.; Hines, C.O. A unifying theory of high latitude geophysical phenomena and geomagnetic storms. Can. J. Phys. 1961, 39, 936–967. [Google Scholar] [CrossRef]
- Chapman, S.; Ferraro, V.C.A. A new theory of magnetic storms. J. Geophys. Res. 1931, 36, 171–186. [Google Scholar] [CrossRef]
- Guo, J.; Feng, X.; Emery, B.A.; Zhang, J.; Xiang, C.; Shen, F.; Song, W. Energy transfer during intense geomagnetic storms driven by interplanetary coronal mass ejections and their sheath regions. J. Geophys. Res. Space Phys. 2011, 116, A05106. [Google Scholar] [CrossRef]
- Turner, N.E.; Cramer, W.D.; Earles, S.K.; Emery, B.A. Geoefficiency and energy partitioning in CIR-driven and CME-driven storms. J. Atmos. Sol.-Terr. Phys. 2009, 71, 1023–1031. [Google Scholar] [CrossRef]
- Zong, Q.G.; Yue, C.; Fu, S.Y. Shock Induced Strong Substorms and Super Substorms: Preconditions and Associated Oxygen Ion Dynamics. Space Sci. Rev. 2021, 217, 33. [Google Scholar] [CrossRef]
- Richardson, I.G.; Cane, H.V. Regions of abnormally low proton temperature in the solar wind (1965–1991) and their association with ejecta. J. Geophys. Res. 1995, 100, 23397–23412. [Google Scholar] [CrossRef]
- Wu, C.-C.; Lepping, R.P. Statistical Comparison of Magnetic Clouds with Interplanetary Coronal Mass Ejections for Solar Cycle 23. Sol. Phys. 2011, 269, 141–153. [Google Scholar] [CrossRef]
- Burlaga, L.F. Magnetic clouds and force-free fields with constant alpha. J. Geophys. Res. 1988, 93, 7217–7224. [Google Scholar] [CrossRef]
- Lopez, R.E. Solar cycle invariance in solar wind proton temperature relationships. J. Geophys. Res. 1987, 92, 11189–11194. [Google Scholar] [CrossRef]
- Richardson, I.G.; Cane, H.V. Identification of interplanetary coronal mass ejections at 1 AU using multiple solar wind plasma composition anomalies. J. Geophys. Res. 2004, 109, A09104. [Google Scholar] [CrossRef]
- Jian, L.K.; Russell, C.T.; Luhmann, J.G. Comparing Solar Minimum 23/24 with Historical Solar Wind Records at 1 AU. Sol. Phys. 2011, 274, 321–344. [Google Scholar] [CrossRef]
- Richardson, I.G.; Cane, H.V. Near-Earth Interplanetary Coronal Mass Ejections During Solar Cycle 23 (1996 – 2009): Catalog and Summary of Properties. Sol. Phys. 2010, 264, 189–237. [Google Scholar] [CrossRef]
- Shen, C.; Chi, Y.; Wang, Y.; Xu, M.; Wang, S. Statistical comparison of the ICME’s geoeffectiveness of different types and different solar phases from 1995 to 2014. J. Geophys. Res. Space Phys. 2017, 122, 5931–5948. [Google Scholar] [CrossRef]
- Alves, M.V.; Echer, E.; Gonzalez, W.D. Geoeffectiveness of corotating interaction regions as measured by Dst index. J. Geophys. Res. 2006, 111, A07S05. [Google Scholar] [CrossRef]
- Despirak, I.V.; Lyubchich, A.A.; Kleimenova, N.G. Solar Wind Streams of Different Types and High-Latitude Substorms. Geomagn. Aeron. 2019, 59, 1–6. [Google Scholar] [CrossRef]
- Tsurutani, B.T.; Gonzalez, W.D.; Gonzalez, A.L.C.; Guarnieri, F.L.; Gopalswamy, N.; Grande, M.; Kamide, Y.; Kasahara, Y.; Lu, G.; Mann, I.; et al. Corotating solar wind streams and recurrent geomagnetic activity: A review. J. Geophys. Res. 2006, 111, A07S01. [Google Scholar] [CrossRef]
- Tsurutani, B.T.; Lakhina, G.S.; Verkhoglyadova, O.P.; Gonzalez, W.D.; Echer, E.; Guarnieri, F.L. A review of interplanetary discontinuities and their geomagnetic effects. J. Atmos. Sol. -Terr. Phys. 2011, 73, 5–19. [Google Scholar] [CrossRef]
- Zhang, J.; Richardson, I.G.; Webb, D.F.; Gopalswamy, N.; Huttunen, E.; Kasper, J.; Nitta, N.V.; Poomvises, W.; Thompson, B.J.; Wu, C.C.; et al. Correction to “Solar and interplanetary sources of major geomagnetic storms (Dst ≤ −100 nT) during 1996–2005”. J. Geophys. Res. Space Phys. 2007, 112, A12103. [Google Scholar] [CrossRef]
- Gosling, J.; Mccomas, D.J.; Phillips, J.L.; Bame, S.J. Geomagnetic activity associated with earth passage of interplanetary shock disturbances and coronal mass ejections. J. Geophys. Res. 1991, 96, 7831–7839. [Google Scholar] [CrossRef]
- Wu, C.-C.; Lepping, R.P. Relationships Among Geomagnetic Storms, Interplanetary Shocks, Magnetic Clouds, and Sunspot Number During 1995–2012. Sol. Phys. 2016, 291, 265–284. [Google Scholar] [CrossRef]
- Chi, Y.; Shen, C.; Wang, Y.; Xu, M.; Ye, P.; Wang, S. Statistical Study of the Interplanetary Coronal Mass Ejections from 1995 to 2015. Sol. Phys. 2016, 291, 2419–2439. [Google Scholar] [CrossRef]
- Echer, E.; Gonzalez, W.D. Geoeffectiveness of interplanetary shocks, magnetic clouds, sector boundary crossings and their combined occurrence. Geophys. Res. Lett. 2004, 31, L09808. [Google Scholar] [CrossRef]
- Echer, E.; Tsurutani, B.T.; Gonzalez, W.D. Interplanetary origins of moderate (−100 nT < Dst ≤ −50 nT) geomagnetic storms during solar cycle 23 (1996–2008). J. Geophys. Res. Space Phys. 2013, 118, 385–392. [Google Scholar] [CrossRef]
- Tsurutani, B.T.; Gonzalez, W.D.; Tang, F.M.; Akasofu, S.-I.; Smith, E.J. Origin of interplanetary southward magnetic fields responsible for major magnetic storms near solar maximum (1978–1979). J. Geophys. Res. 1988, 93, 8519–8531. [Google Scholar] [CrossRef]
- Yermolaev, Y.I.; Nikolaeva, N.S.; Lodkina, I.G.; Yermolaev, M.Y. Catalog of large-scale solar wind phenomena during 1976–2000. Cosm. Res. 2009, 47, 81–94. [Google Scholar] [CrossRef]
- Borovsky, J.E.; Denton, M.H. Differences between CME-driven storms and CIR-driven storms. J. Geophys. Res. 2006, 111, A07S08. [Google Scholar] [CrossRef]
- Cramer, W.D.; Turner, N.E.; Fok, M.C.; Buzulukova, N.Y. Effects of different geomagnetic storm drivers on the ring current: CRCM results. J. Geophys. Res. Space Phys. 2013, 118, 1062–1073. [Google Scholar] [CrossRef]
- Yermolaev, Y.I.; Nikolaeva, N.S.; Lodkina, I.G.; Yermolaev, M.Y. Geoeffectiveness and efficiency of CIR, sheath, and ICME in generation of magnetic storms. J. Geophys. Res. Space Phys. 2012, 117, A00L07. [Google Scholar] [CrossRef]
- Huttunen, K.E.J. Variability of magnetospheric storms driven by different solar wind perturbations. J. Geophys. Res. 2002, 107, SMP-20. [Google Scholar] [CrossRef]
- Echer, E.; Gonzalez, W.D.; Tsurutani, B.T. Interplanetary conditions leading to superintense geomagnetic storms (Dst ≤ −250 nT) during solar cycle 23. Geophys. Res. Lett. 2008, 35, L06S03. [Google Scholar] [CrossRef]
- Echer, E.; Gonzalez, W.D.; Tsurutani, B.T.; Gonzalez, A.L.C. Interplanetary conditions causing intense geomagnetic storms (Dst ≤ −100 nT) during solar cycle 23 (1996–2006). J. Geophys. Res. Space Phys. 2008, 113, A05221. [Google Scholar] [CrossRef]
- Echer, E.; Gonzalez, W.D.; Tsurutani, B.T. Statistical studies of geomagnetic storms with peak Dst ≤ −50 nT from 1957 to 2008. J. Atmos. Sol.-Terr. Phys. 2011, 73, 1454–1459. [Google Scholar] [CrossRef]
- Burton, R.K.; McPherron, R.L.; Russell, C.T. An empirical relationship between interplanetary conditions and Dst. J. Geophys. Res. 1975, 80, 4204–4214. [Google Scholar] [CrossRef]
- Russell, C.T.; McPherron, R.L.; Burton, R.K. On the cause of geomagnetic storms. J. Geophys. Res. 1974, 79, 1105–1109. [Google Scholar] [CrossRef]
- Wu, C.-C. Effect of solar wind velocity on magnetic cloud-associated magnetic storm intensity. J. Geophys. Res. 2002, 107, SSH 3-1–SSH 3-4. [Google Scholar] [CrossRef]
- Wu, C.-C. Effects of magnetic clouds on the occurrence of geomagnetic storms: The first 4 years of Wind. J. Geophys. Res. 2002, 107, SMP 19-1–SMP 19-8. [Google Scholar] [CrossRef]
- Wang, Y.; Shen, C.L.; Wang, S.; Ye, P.Z. An empirical formula relating the geomagnetic storm’s intensity to the interplanetary parameters: −VBz and Δt. Geophys. Res. Lett. 2003, 30, SSC2.1–SSC2.4. [Google Scholar] [CrossRef]
- Le, G.-M.; Liu, G.-A.; Zhao, M.-X. Dependence of Major Geomagnetic Storm Intensity (Dst≤−100nT) on Associated Solar Wind Parameters. Sol. Phys. 2020, 295, 108. [Google Scholar] [CrossRef]
- Ontiveros, V.; Gonzalez-Esparza, J.A. Geomagnetic storms caused by shocks and ICMEs. J. Geophys. Res. Space Phys. 2010, 115, A10244. [Google Scholar] [CrossRef]
- Lockwood, M.; Mcwilliams, K.A. On optimum solar wind–magnetosphere coupling functions for transpolar voltage and planetary geomagnetic activity. J. Geophys. Res. Space Phys. 2021, 126, e2021JA029946. [Google Scholar] [CrossRef]
- Newell, P.T.; Sotirelis, T.; Liou, K.; Meng, C.-I.; Rich, F.J. A nearly universal solar wind-magnetosphere coupling function inferred from 10 magnetospheric state variables. J. Geophys. Res. 2007, 112, A01206. [Google Scholar] [CrossRef]
- Gonzalez, W.D.; Echer, E. A study on the peak Dst and peak negative Bz relationship during intense geomagnetic storms. Geophys. Res. Lett. 2005, 32, L18103. [Google Scholar] [CrossRef]
- Perreault, P.D.; Akasofu, S.-I. A study of geomagnetic storms. Geophys. J. Int. 1978, 54, 547–573. [Google Scholar] [CrossRef]
- Pearson, K. Mathematical Contributions to the Theory of Evolution. III. Regression, Heredity, and Panmixia. Philos. Mag. Ser. 5 1896, 42, 343–414. [Google Scholar]
- Cremades, H.; Cyr, O.C.S. Coronal mass ejections: Solar cycle aspects. Adv. Space Res. 2007, 40, 1042–1048. [Google Scholar] [CrossRef]





| 23rd Solar Cycle (210 Events) | 24th Solar Cycle (116 Events) | September 1996–August 2000 (71 Events) | January 2009–December 2012 (38 Events) | January 2020–December 2023 (58 Events) | ||
|---|---|---|---|---|---|---|
| ICME | Moderate | 32 (15.24%) | 30 (25.86%) | 15 (21.13%) | 10 (26.32%) | 14 (24.14%) |
| Intense | 25 (11.90%) | 8 (6.90%) | 10 (14.08%) | 2 (5.26%) | 1 (1.72%) | |
| Big | 2 (0.95%) | 0 (0.00%) | 2 (2.82%) | 0 (0.00%) | 0 (0.00%) | |
| Sheath-ICME | Moderate | 13 (6.19%) | 7 (6.03%) | 6 (8.45%) | 2 (5.26%) | 2 (3.45%) |
| Intense | 16 (7.62%) | 7 (6.03%) | 5 (7.04%) | 5 (13.16%) | 1 (1.2%) | |
| Big | 7 (3.32%) | 1 (0.86%) | 2 (2.82%) | 0 (0.00%) | 1 (1.72%) | |
| Sheath | Moderate | 5 (2.38%) | 9 (7.76%) | 1 (1.41%) | 5 (13.16%) | 2 (3.45%) |
| Intense | 15 (7.14%) | 2 (1.72%) | 3 (4.23%) | 2 (5.26%) | 1 (1.72%) | |
| Big | 3 (1.43%) | 0 (0.00%) | 1 (1.41%) | 0 (0.00%) | 0 (0.00%) | |
| Shock | Moderate | 7 (3.33%) | 1 (0.86%) | 4 (5.63%) | 1 (2.63%) | 0 (0.00%) |
| Intense | 0 (0.00%) | 2 (1.72%) | 0 (0.00%) | 0 (0.00%) | 0 (0.00%) | |
| Big | 0 (0.00%) | 0 (0.00%) | 0 (0.00%) | 0 (0.00%) | 0 (0.00%) | |
| Others | Moderate | 76 (36.19%) | 48 (41.38%) | 19 (26.76%) | 11 (28.95%) | 35 (60.34%) |
| Intense | 9 (4.29%) | 1 (0.86%) | 3 (4.23%) | 0 (0.00%) | 1 (1.72%) | |
| Big | 0 (0.00%) | 0 (0.00%) | 0 (0.00%) | 0 (0.00%) | 0 (0.0%) |
| −50 nT | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| September 1996–December 2023 (384 events) | 0.773 | −0.770 | −0.327 | −0.542 | −0.266 | −0.751 | 0.512 | −0.677 | −0.120 * | −0.377 | −0.162 | −0.827 |
| 23rd solar cycle (210 events) | 0.801 | −0.788 | −0.373 | −0.525 | −0.244 | −0.756 | 0.553 | −0.700 | − | −0.334 | − | −0.835 |
| 24th solar cycle (116 events) | 0.636 | −0.614 | − | −0.499 | −0.312 | −0.612 | 0.397 | −0.539 | − | −0.389 | −0.269 * | −0.735 |
| September 1996–August 2000 (71 events) | 0.799 | −0.807 | −0.403 | −0.589 | − | −0.771 | 0.523 | −0.677 | − | −0.335 * | − | −0.790 |
| January 2009–December 2012 (38 events) | 0.705 | −0.698 | − | − | − | −0.630 | − | − | − | − | − | −0.626 |
| January 2020–December 2023 (58 events) | 0.701 | −0.716 | − | −0.591 | − | −0.823 | 0.662 | −0.707 | − | −0.616 | −0.484 | −0.867 |
| 384 storms | −50 nT | 0.773 | −0.770 | −0.327 | −0.542 | −0.266 | −0.751 | 0.512 | −0.677 | −0.120 * | −0.377 | −0.162 | −0.827 |
| Moderate (281) | 0.312 | −0.333 | - | −0.205 | - | −0.313 | 0.254 | −0.287 | - | −0.179 * | - | −0.402 | |
| Strong (103) | 0.710 | −0.691 | −0.420 | −0.394 | - | −0.691 | 0.357 | −0.576 | - | - | −0.051 | −0.808 | |
| ICME-related (204) | 0.788 | −0.776 | −0.485 | −0.512 | −0.274 | −0.749 | 0.470 | −0.669 | - | −0.378 | - | −0.827 | |
| Others (180) | 0.537 | −0.498 | - | −0.433 | −0.275 | −0.535 | 0.272 | −0.286 | - | −0.307 | −0.302 | −0.532 | |
| Moderate-ICME (113) | 0.276 * | −0.386 | - | - | - | −0.384 | - | −0.288 * | - | - | - | −0.417 | |
| Moderate-Others (168) | 0.355 | −0.334 | - | −0.259 | - | −0.285 | - | - | - | - | - | −0.315 | |
| Strong-ICME (91) | 0.706 | −0.686 | −0.431 | −0.374 | - | −0.682 | 0.347 | −0.571 | - | - | - | −0.804 | |
| Strong-Others (12) | - | - | - | −0.798 * | - | −0.775 * | - | - | - | −0.749 * | - | - | |
| January 2020–December 2023 (58 storms) | −50 nT | 0.701 | −0.716 | - | −0.591 | - | −0.823 | 0.662 | −0.707 | - | −0.616 | −0.484 | −0.867 |
| Moderate (53) | 0.482 | −0.435 | - | - | - | −0.539 | - | - | - | - | - | −0.465 | |
| Strong (5) | - | - | - | - | - | - | - | - | - | - | - | - | |
| ICME-related (22) | 0.668 | −0.731 | - | - | - | −0.811 | 0.764 | −0.829 | - | −0.624 * | - | −0.899 | |
| Others (36) | 0.674 | −0.613 | - | −0.624 | - | −0.852 | 0.474 * | - | - | −0.663 | −0.661 | −0.784 | |
| Moderate-ICME (18) | - | - | - | - | - | - | - | - | - | - | - | - | |
| Moderate-Others (35) | 0.507 * | - | - | - | - | −0.577 | - | - | - | - | - | - | |
| September 1996–August 2000 (71 storms) | −50 nT | 0.799 | −0.807 | −0.403 | −0.589 | - | −0.771 | 0.523 | −0.677 | - | −0.335 * | - | −0.790 |
| ICME-related (45) | 0.792 | −0.807 | −0.565 | −0.537 | - | −0.764 | 0.461 | −0.649 | - | - | - | −0.776 | |
| Others (26) | 0.780 | −0.802 | - | −0.766 | - | −0.746 | - | - | - | - | - | −0.602 |
| 174 storms | −50 nT | 0.836 | −0.822 | −0.533 | −0.665 | −0.294 | −0.788 | 0.438 | −0.617 | −0.224 * | −0.445 | - | −0.804 | 0.639 |
| Moderate (108) | 0.395 | −0.393 | - | −0.298 * | −0.196 * | −0.402 | 0.331 | −0.419 | −0.244 * | −0.308 | - | −0.511 | 0.618 | |
| Strong (66) | 0.798 | −0.778 | −0.532 | −0.639 | −0.250 * | −0.770 | 0.203 * | −0.439 | - | −0.244 * | - | −0.753 | 0.678 | |
| ICME-related (123) | 0.837 | −0.821 | −0.545 | −0.659 | −0.284 | −0.787 | 0.370 | −0.577 | - | −0.367 | - | −0.795 | 0.652 | |
| Others (51) | 0.687 | −0.605 | - | −0.408 * | - | −0.605 | 0.314 * | −0.398 * | - | −0.389 * | - | −0.661 | 0.447 | |
| Moderate-ICME (65) | 0.35 * | −0.421 | - | - | - | −0.402 | - | - | - | - | - | −0.439 | 0.642 | |
| Moderate-Others (43) | 0.477 | - | - | - | - | - | 0.524 | −0.550 | - | - | - | −0.652 | 0.455 | |
| Strong-ICME (58) | 0.801 | −0.776 | −0.515 | −0.635 | - | −0.764 | - | −0.411 | - | - | - | −0.745 | 0.668 | |
| Strong-Others (8) | - | - | - | - | - | - | - | - | - | - | - | - | - | |
| 68 storms | −50 nT | 0.914 | −0.922 | −0.605 | −0.696 | - | −0.914 | 0.578 | −0.743 | - | −0.407 | - | −0.875 | 0.362 * |
| Moderate (36) | −0.488 * | −0.503 * | −0.478 * | −0.598 | 0.395 * | |||||||||
| Strong (32) | 0.921 | −0.929 | −0.618 | −0.655 | - | −0.940 | - | −0.616 | - | - | - | −0.845 | - | |
| ICME-related (63) | 0.917 | −0.923 | −0.600 | −0.697 | - | −0.915 | 0.565 | −0.734 | - | −0.389 * | - | −0.872 | 0.342 | |
| Others (5) | - | - | - | - | - | - | - | - | - | - | - | - | - | |
| Moderate-ICME (31) | 0.493 * | −0.545 * | - | - | - | −0.548 | - | - | - | - | - | −0.603 | 0.371 * | |
| Moderate-Others (5) | - | - | - | - | - | - | - | - | - | - | - | - | - | |
| Strong-ICME (32) | 0.921 | −0.929 | −0.618 | −0.655 | - | −0.940 | - | −0.616 | - | - | - | −0.845 | - | |
| Strong-Others (0) | - | - | - | - | - | - | - | - | - | - | - | - | - |
| 384 storms | −50 nT | −0.751 | −0.657 | −0.646 | −0.726 |
| Moderate (281) | −0.313 | −0.282 | −0.303 | −0.330 | |
| Strong (103) | −0.691 | −0.563 | −0.529 | −0.632 | |
| ICME-related (204) | −0.749 | −0.656 | −0.637 | −0.727 | |
| Others (180) | −0.535 | −0.418 | −0.471 | −0.506 | |
| Moderate-ICME (113) | −0.384 | −0.360 | −0.346 | −0.388 | |
| Moderate-Others (168) | −0.285 | −0.273 | −0.315 | −0.329 | |
| Strong-ICME (91) | −0.682 | −0.553 | −0.516 | −0.624 | |
| Strong-Others (12) | −0.775 * | - | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, X.; Zhima, Z.; Duan, S.; Hu, Y.; Lu, C.; Ran, Z. Statistical Analysis of the Correlation between Geomagnetic Storm Intensity and Solar Wind Parameters from 1996 to 2023. Remote Sens. 2024, 16, 2952. https://doi.org/10.3390/rs16162952
Sun X, Zhima Z, Duan S, Hu Y, Lu C, Ran Z. Statistical Analysis of the Correlation between Geomagnetic Storm Intensity and Solar Wind Parameters from 1996 to 2023. Remote Sensing. 2024; 16(16):2952. https://doi.org/10.3390/rs16162952
Chicago/Turabian StyleSun, Xiaoying, Zeren Zhima, Suping Duan, Yunpeng Hu, Chao Lu, and Zilin Ran. 2024. "Statistical Analysis of the Correlation between Geomagnetic Storm Intensity and Solar Wind Parameters from 1996 to 2023" Remote Sensing 16, no. 16: 2952. https://doi.org/10.3390/rs16162952
APA StyleSun, X., Zhima, Z., Duan, S., Hu, Y., Lu, C., & Ran, Z. (2024). Statistical Analysis of the Correlation between Geomagnetic Storm Intensity and Solar Wind Parameters from 1996 to 2023. Remote Sensing, 16(16), 2952. https://doi.org/10.3390/rs16162952







