Inversion Uncertainty of OH Airglow Rotational Temperature Based on Fine Spectral Measurement
Abstract
1. Introduction
2. Methods
2.1. Detection Principle
2.2. Instrument
2.3. Data Processing and Inversion Algorithms
2.3.1. Original Image Processing
2.3.2. Spectral Intensity Extraction
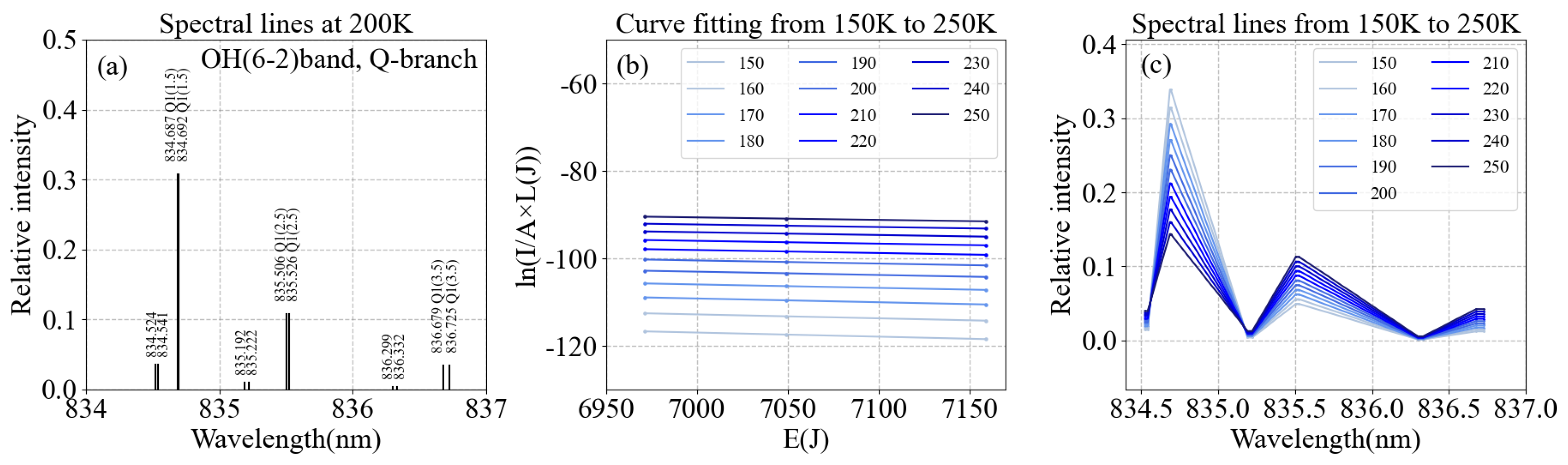
2.3.3. Rotational Temperature Retrieval
3. Results and Analysis
3.1. Observations and Data
3.2. Temperature Inversion Results
3.2.1. Sampling Methods for Fitting Residual Background Noise
3.2.2. Temperature Inversion Results Based on Peak Values
3.2.3. Comparison of Results from Different Spectral Line Extraction Methods
3.2.4. Comparison of Multi-Day Detection Data
3.3. Discussion of the Factors Influencing Differences in Inversion Results
3.3.1. Influencing Factors
3.3.2. Data Comparison
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lu, D.; Chen, Z.; Guo, X.; Tian, W. Recent progress in near space atmospheric environment study. Adv. Mech. 2009, 39, 674–682. [Google Scholar]
- Qian, L.; Laštovička, J.; Roble, R.; Solomon, S. Progress in observations and simulations of global change in the upper atmosphere. J. Geophys. Res. 2011, 116, A00H03. [Google Scholar] [CrossRef]
- Wan, W.; Xu, J. Recent investigation on the coupling between the ionosphere and upper atmosphere. Sci. China Earth Sci. 2014, 57, 1995–2012. [Google Scholar] [CrossRef]
- Yue, J.; Russell, J., III; Jian, Y.; Rezac, L.; Garcia, R.; López-Puertas, M.; Mlynczak, M.G. Increasing carbon dioxide concentration in the upper atmosphere observed by SABER. Geophys. Res. Lett. 2015, 42, 7194–7199. [Google Scholar] [CrossRef]
- Chen, Z.; Xu, J.; Hu, X.; Chen, H.; Chen, W.; Wei, K.; Dou, X. Advances in the Researches of the Middle and Upper Atmosphere in China in 2014−−2016. Chin. J. Space Sci. 2016, 36, 738–752. [Google Scholar] [CrossRef]
- Sargoytchev, S.I.; Brown, S.; Solheim, B.H.; Cho, Y.M.; Shepherd, G.G.; López-González, M.J. Spectral airglow temperature imager (SATI): A ground-based instrument for the monitoring of mesosphere temperature. Appl. Opt. 2004, 43, 5712–5721. [Google Scholar] [CrossRef] [PubMed]
- Wiens, R.H.; Zhang, S.P.; Peterson, R.N.; Shepherd, G.G. MORTI: A mesopause oxygen rotational temperature imager. Planet. Space Sci. 1991, 39, 1363–1375. [Google Scholar] [CrossRef]
- Marshall, R.A.; Smith, S.; Baumgardner, J.; Chakrabarti, S. Continuous ground-based multiwavelength airglow measurements. J. Geophys. Res.-Space Phys. 2011, 116, A11304. [Google Scholar] [CrossRef]
- Liu, W.; Xu, J.; Smith, A.K.; Yuan, W. Comparison of rotational temperature derived from ground-based OH airglow observations with TIMED/SABER to evaluate the Einstein coefficients. J. Geophys. Res.-Space Phys. 2015, 120, 10069–10082. [Google Scholar] [CrossRef]
- Hagan, M.; Portnyagin, Y.; Shepherd, G. PSMOS 2000 workshop-Planetary scale mesopause observing system. J. Atmos. Sol.-Terr. Phys. 2002, 64, 873–874. [Google Scholar] [CrossRef]
- Reisin, E.R.; Scheer, J.; Dyrland, M.E.; Sigernes, F.; Deehr, C.S.; Schmidt, C.; von Savigny, C. Traveling planetary wave activity from mesopause region airglow temperatures determined by the Network for the Detection of Mesospheric Change (NDMC). J. Atmos. Sol.-Terr. Phys. 2014, 119, 71–82. [Google Scholar] [CrossRef]
- Wang, C.; Xu, J.; Liu, L.; Xue, X.; Zhang, Q.; Hao, Y.; Wang, J. Contribution of the Chinese Meridian Project to space environment research: Highlights and perspectives. Sci. China Earth Sci. 2023, 66, 1423–1438. [Google Scholar] [CrossRef]
- Yan, Z.; Hu, X.; Guo, W.; Guo, S.; Cheng, Y.; Gong, J.; Yue, J. Development of a mobile Doppler lidar system for wind and temperature measurements at 30–70 km. J. Quant. Spectrosc. Radiat. Transf. 2017, 188, 52–59. [Google Scholar] [CrossRef]
- Ba, J.; Yan, Z.; Hu, X.; Guo, S.; Guo, W.; Cheng, Y. Characteristics of vertical wind perturbations in the mesopause region based on lidar measurements and dynamic simulations ormalsize (in Chinese). Chin. J. Space Sci. 2017, 37, 554–563. [Google Scholar] [CrossRef]
- Guo, S.; Hu, X.; Yan, Z.; Cheng, Y.; Tu, C. Studies for mesopause temperature distribution characteristics based on the sodium lidar data (in Chinese). Chin. J. Space Sci. 2022, 42, 913–918. [Google Scholar] [CrossRef]
- Wiens, R.H.; Moise, A.; Brown, S.; Sargoytchev, S.; Peterson, R.N.; Shepherd, G.G. SATI: A spectral airglow temperature imager. Adv. Space Res. 1997, 19, 677–680. [Google Scholar] [CrossRef]
- Dalin, P.; Perminov, V.; Pertsev, N.; Romejko, V. Updated long-term trends in mesopause temperature, airglow emissions, and noctilucent clouds. J. Geophys. Res.-Atmos. 2020, 125, e2019JD030814. [Google Scholar] [CrossRef]
- Oberheide, J.; Offermann, D.; Russell, J.M., III; Mlynczak, M.G. Intercomparison of kinetic temperature from 15 μm CO2 limb emissions and OH*(3, 1) rotational temperature in nearly coincident air masses: SABER, GRIPS. Geophys. Res. Lett. 2006, 33, L14811. [Google Scholar] [CrossRef]
- Smith, S.M.; Baumgardner, J.; Mertens, C.J.; Russell, J.M.; Mlynczak, M.G.; Mendillo, M. Mesospheric OH temperatures: Simultaneous ground-based and SABER OH measurements over Millstone Hill. Adv. Space Res. 2010, 45, 239–246. [Google Scholar] [CrossRef]
- Zhao, Y.; Taylor, M.J.; Chu, X. Comparison of simultaneous Na lidar and mesospheric nightglow temperature measurements and the effects of tides on the emission layer heights. J. Geophys. Res.-Atmos. 2005, 110, D09S07. [Google Scholar] [CrossRef]
- Shiokawa, K.; Otsuka, Y.; Suzuki, S.; Katoh, T.; Katoh, Y.; Satoh, M.; Shimomai, T. Development of airglow temperature photometers with cooled-CCD detectors. Earth Planets Space 2007, 59, 585–599. [Google Scholar] [CrossRef]
- Liu, W. The Detection and Study on Airglow Spectra in Middle and Upper Atmosphere. Ph.D. Dissertation, University of Chinese Academy of Sciences, Beijing, China, 2016. [Google Scholar]
- Wang, W. Simulation and Inversion of Spatial Heterodyne Interferometric Hyperspectral Temperature Detection from O2 4-band Night Glow in Mesosphere and Lower Thermosphere. Ph.D. Dissertation, University of Science and Technology of China, Hefei, China, 2023. [Google Scholar]
- Niu, S.; Gao, H.; Yan, Z.; Ren, K.; Kou, L.; Jiang, B.; Bu, L. High-precision temperature retrieval algorithm and verification for mesospheric airglow spectrum photometer. Sci. China Earth Sci. 2024, 67, 1639–1651. [Google Scholar] [CrossRef]
- Shiokawa, K.; Otsuka, Y.; Ogawa, T.; Takahashi, H.; Nakamura, T.; Shimomai, T. Comparison of OH rotational temperatures measured by the spectral airglow temperature imager (SATI) and by a tilting-filter photometer. J. Atmos. Sol.-Terr. Phys. 2004, 66, 891–897. [Google Scholar] [CrossRef]
- Lopez-Gonzalez, M.J.; Rodriguez, E.; Wiens, R.H.; Shepherd, G.G.; Sargoytchev, S.; Brown, S.; Cho, Y.M. Seasonal variations of O2 atmospheric and OH (6−2) airglow and temperature at mid-latitudes from SATI observations. Ann. Geophys. 2004, 22, 819–828. [Google Scholar] [CrossRef]
- Mies, F.H. Calculated vibrational transition probabilities of OH (X2Π). J. Mol. Spectrosc. 1974, 53, 150–188. [Google Scholar] [CrossRef]
- Langhoff, S.R.; Werner, H.J.; Rosmus, P. Theoretical transition probabilities for the OH Meinel system. J. Mol. Spectrosc. 1986, 118, 507–529. [Google Scholar] [CrossRef]
- Takahashi, H.; Nakamura, T.; Tsuda, T.; Buriti, R.A.; Gobbi, D. First measurement of atmospheric density and pressure by meteor diffusion coefficient and airglow OH temperature in the mesopause region. Geophys. Res. Lett. 2002, 29, 6-1–6-4. [Google Scholar] [CrossRef]












| Parameter | Unit | Value |
|---|---|---|
| Cylindrical Mirror | Size (mm) | 53 × 50.8 |
| Focal Length (mm) | 50.8 | |
| Optical Slit | Size (mm) | 40 × 10 |
| Collimating Mirror I | Size (mm) | φ50.8 |
| Focal Length (mm) | 400 | |
| Echelle Grating | Size (mm) | 100 × 50 × 9.5 |
| Blaze (°) | 64 | |
| LD (L/mm) | 31 | |
| Folding Mirror I | Size (mm) | 50 × 50 |
| Folding Mirror II | Size (mm) | 50 × 50 |
| Collimating Mirror II | Size (mm) | φ50.8 |
| Focal Length (mm) | 180 | |
| Filter | Size (mm) | φ50 |
| Center Wavelength (nm) | 835 | |
| Passband (nm) | 5.1 | |
| CCD Camera Lens | Focal Length (mm) | 50 |
| Aperture | F1.4 | |
| Scientific Grade CCD Camera | Resolution | 1024 × 1024 |
| Pixel Size (μm) | 13 × 13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, B.; Gao, H.; Niu, S.; Ren, K.; Sun, S. Inversion Uncertainty of OH Airglow Rotational Temperature Based on Fine Spectral Measurement. Remote Sens. 2024, 16, 2940. https://doi.org/10.3390/rs16162940
Jiang B, Gao H, Niu S, Ren K, Sun S. Inversion Uncertainty of OH Airglow Rotational Temperature Based on Fine Spectral Measurement. Remote Sensing. 2024; 16(16):2940. https://doi.org/10.3390/rs16162940
Chicago/Turabian StyleJiang, Baichuan, Haiyang Gao, Shuqi Niu, Ke Ren, and Shaoyang Sun. 2024. "Inversion Uncertainty of OH Airglow Rotational Temperature Based on Fine Spectral Measurement" Remote Sensing 16, no. 16: 2940. https://doi.org/10.3390/rs16162940
APA StyleJiang, B., Gao, H., Niu, S., Ren, K., & Sun, S. (2024). Inversion Uncertainty of OH Airglow Rotational Temperature Based on Fine Spectral Measurement. Remote Sensing, 16(16), 2940. https://doi.org/10.3390/rs16162940






