Clutter Rank Estimation Method for Bistatic Radar Systems Based on Prolate Spheroidal Wave Functions
Abstract
1. Introduction
- (1)
- Addressing the gap in existing research through proposing a bistatic clutter rank estimation method based on PSWF, providing crucial design indicators for reduced dimension and rank STAP in bistatic radar.
- (2)
- The proposed method enables the estimation of clutter rank for either the entire range bin or limited observation areas, whether in side-looking or non-side-looking mode, rapidly evaluating clutter rank for diverse relationships between the relative velocity and antenna of two platforms within different observation areas, thus supporting bistatic configuration design and observation area optimization.
- (3)
- Establishing the corresponding relationship between clutter rank, clutter Doppler bandwidth, and azimuth resolution, and elucidating the variation rule of clutter rank. This finding serves as a valuable theoretical foundation for optimizing the configuration of bistatic radar.
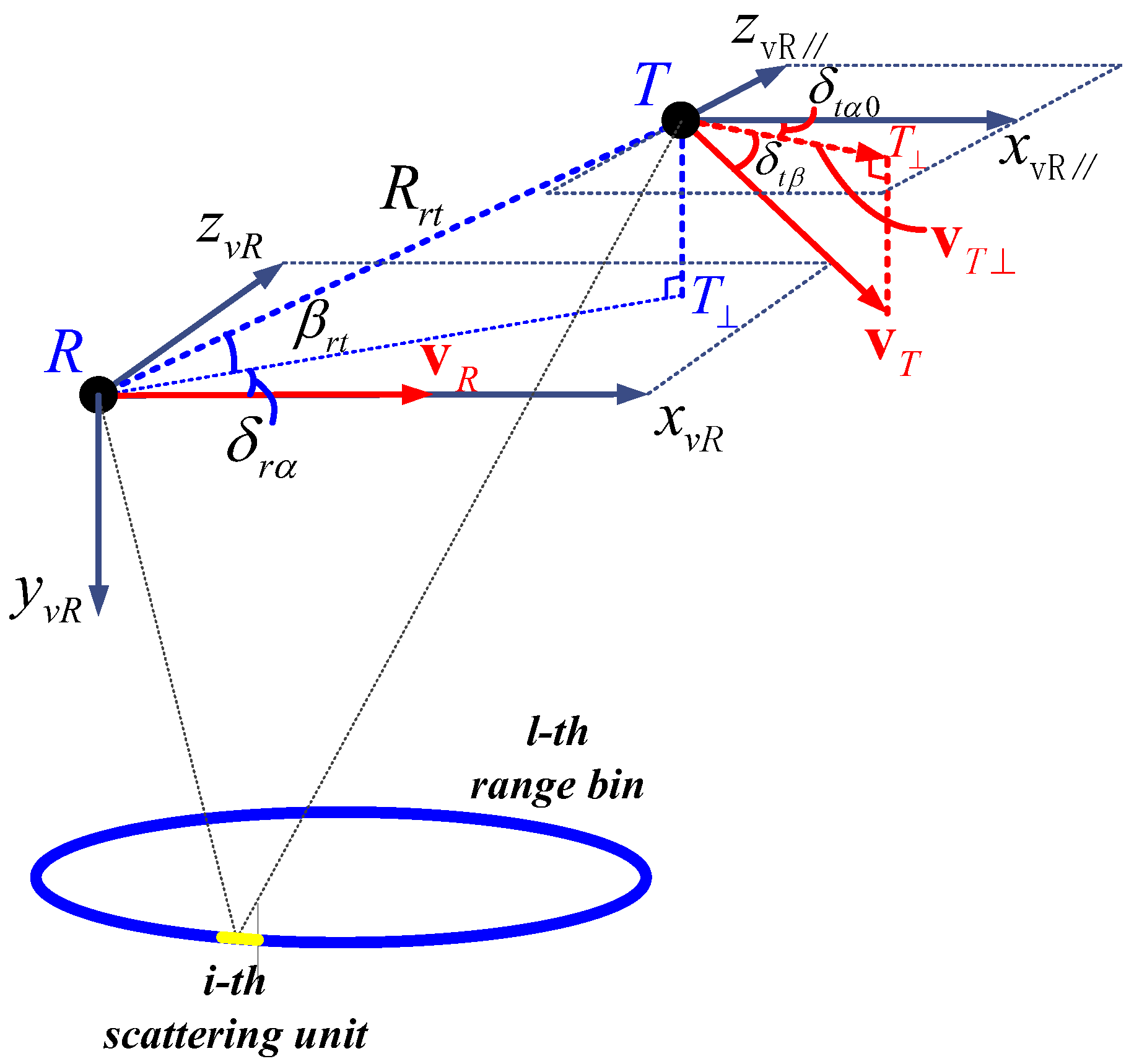
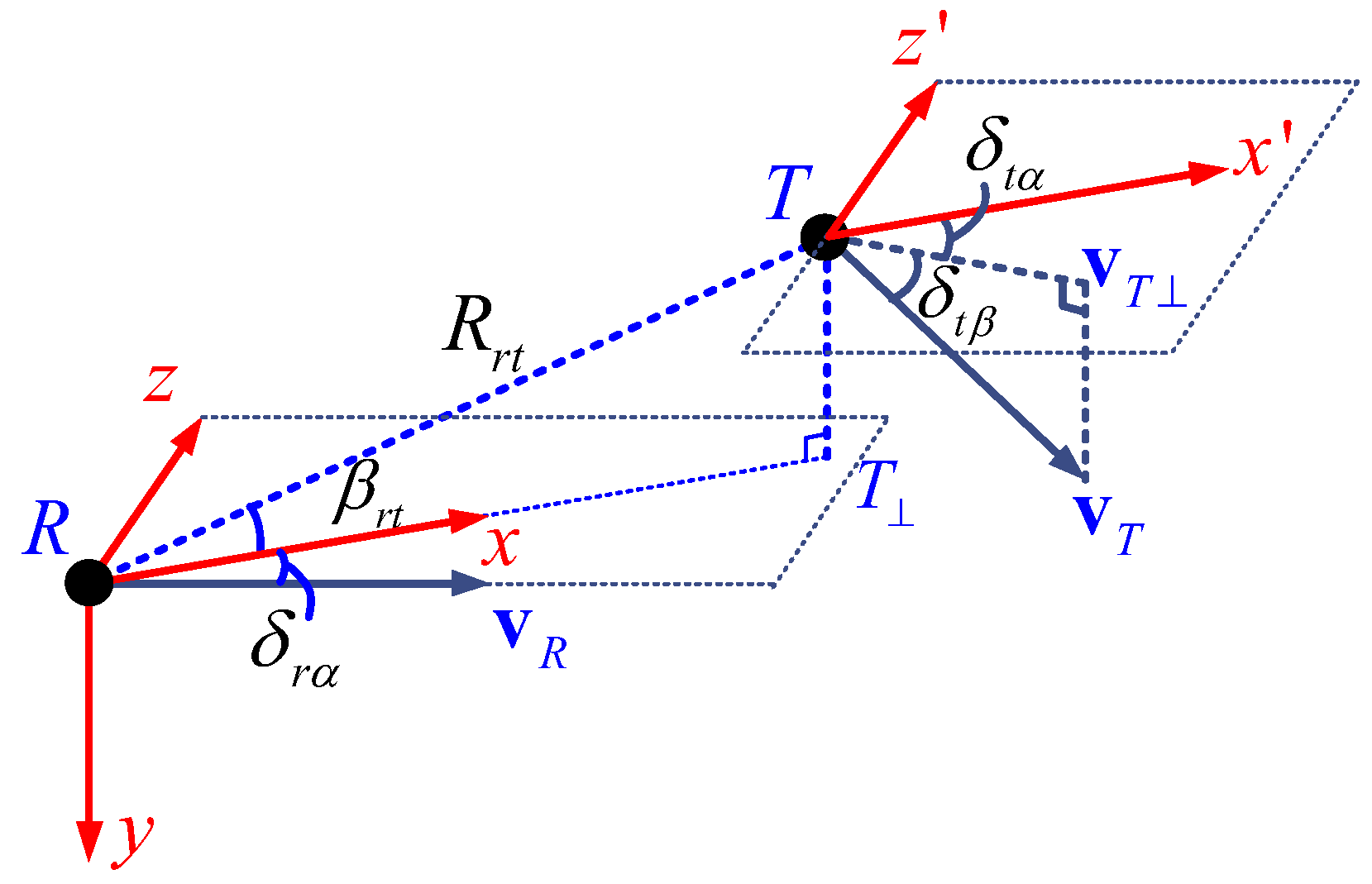
2. Signal Model
3. Proposed Method
3.1. Challenge of Clutter Rank Estimation in Bistatic Radar
3.2. Calculation of Weq
3.2.1. Calculation Method A
3.2.2. Calculation Method B
| Algorithm 1. Proposed clutter rank estimation method |
| Input: , , , , PRF, , , , |
| Procedure: (1) Obtain (2) For = 1 to do Obtain end for (3) Obtain after procedure (2) (4) Obtain (5) Obtain by Equation (47) (6) Obtain by Equation (42) |
| Output: The estimation rank by Equation (48) |
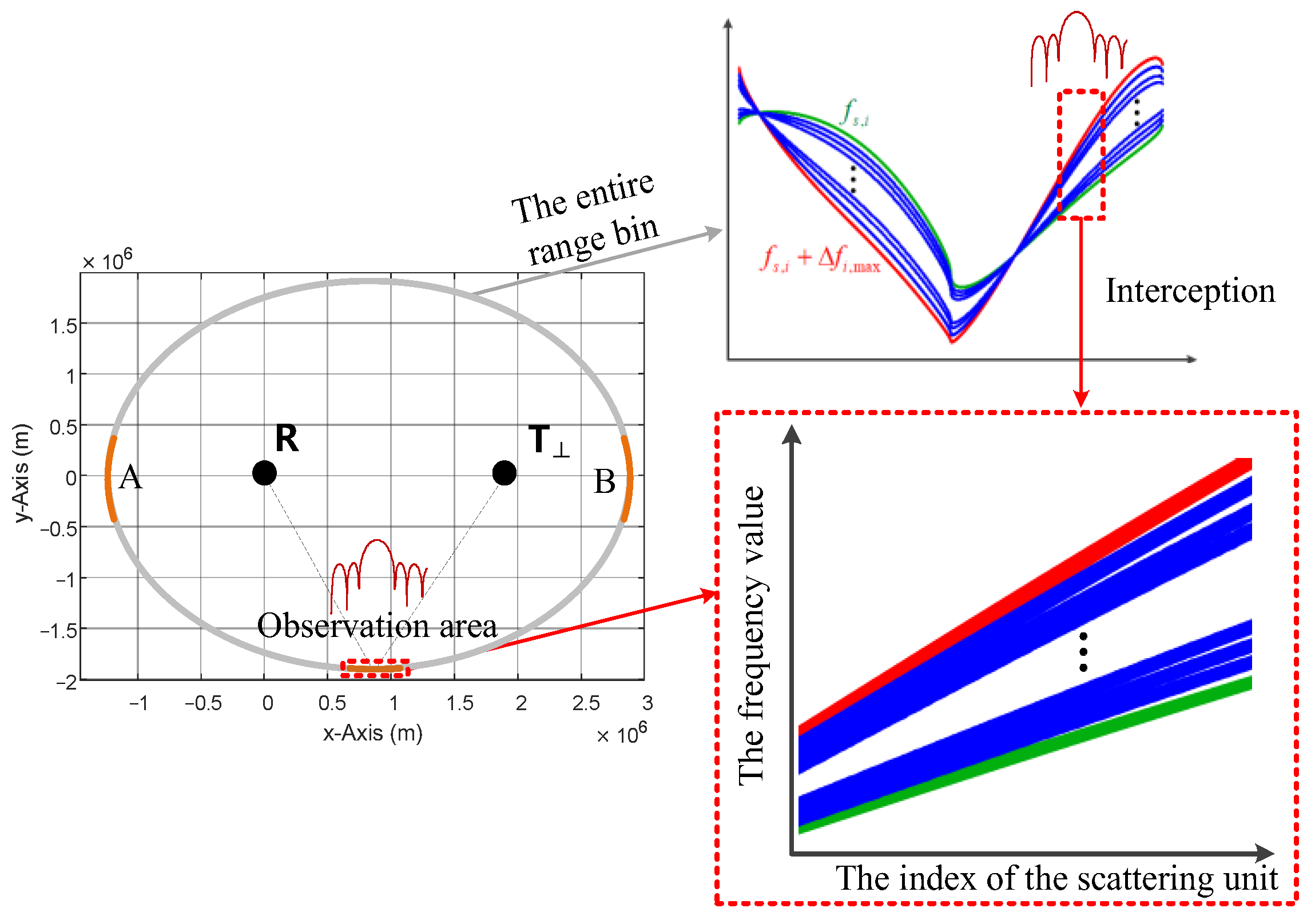
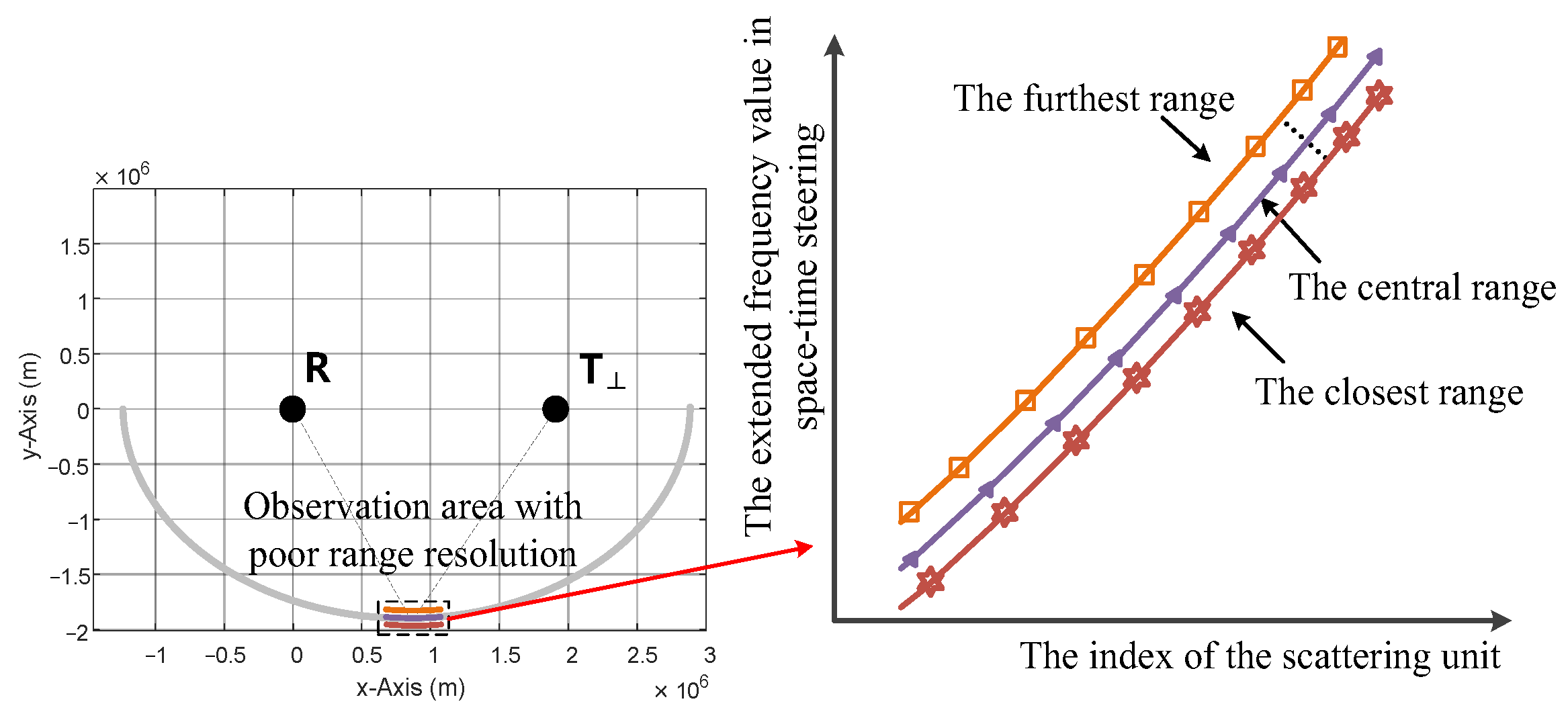
3.3. Extended Applicability Analysis of the Method
- A.
- Non-side-looking mode of receiving platform
- B.
- Limited observation area
4. Numerical Examples
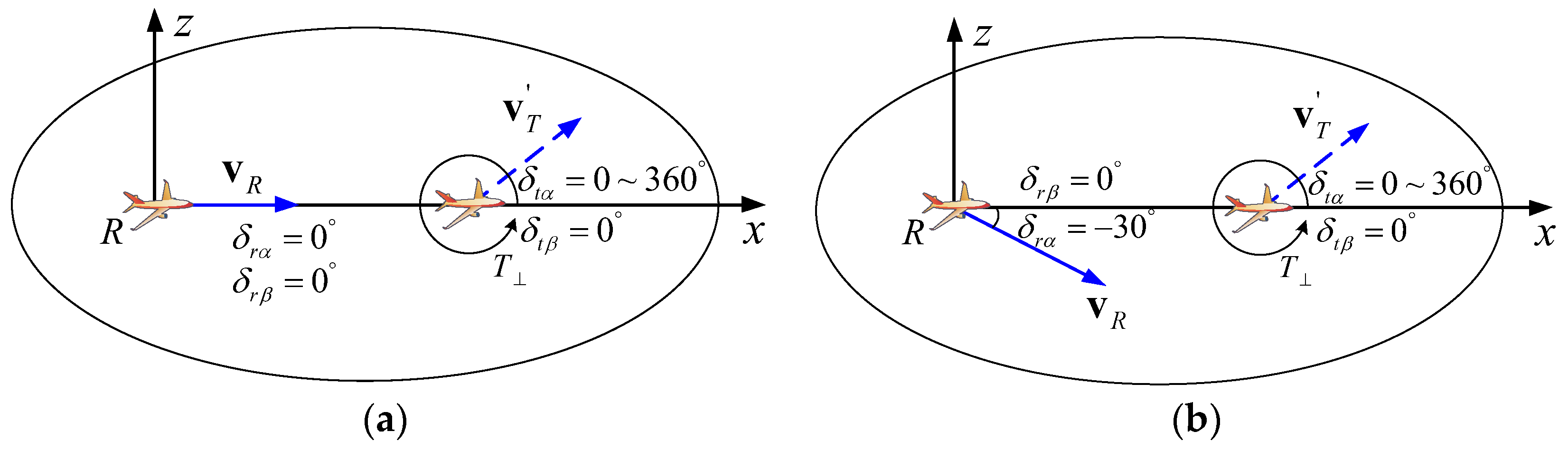
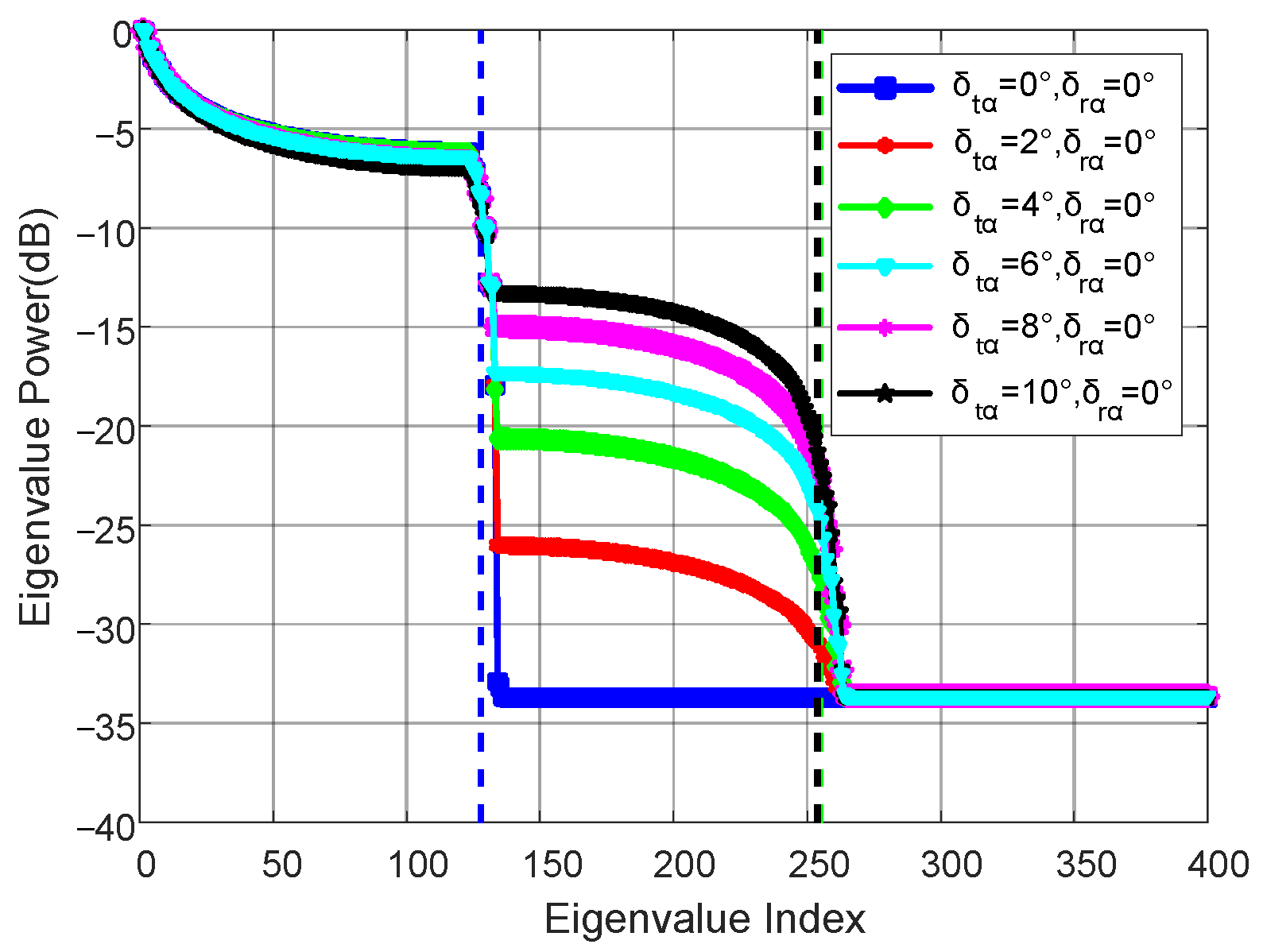
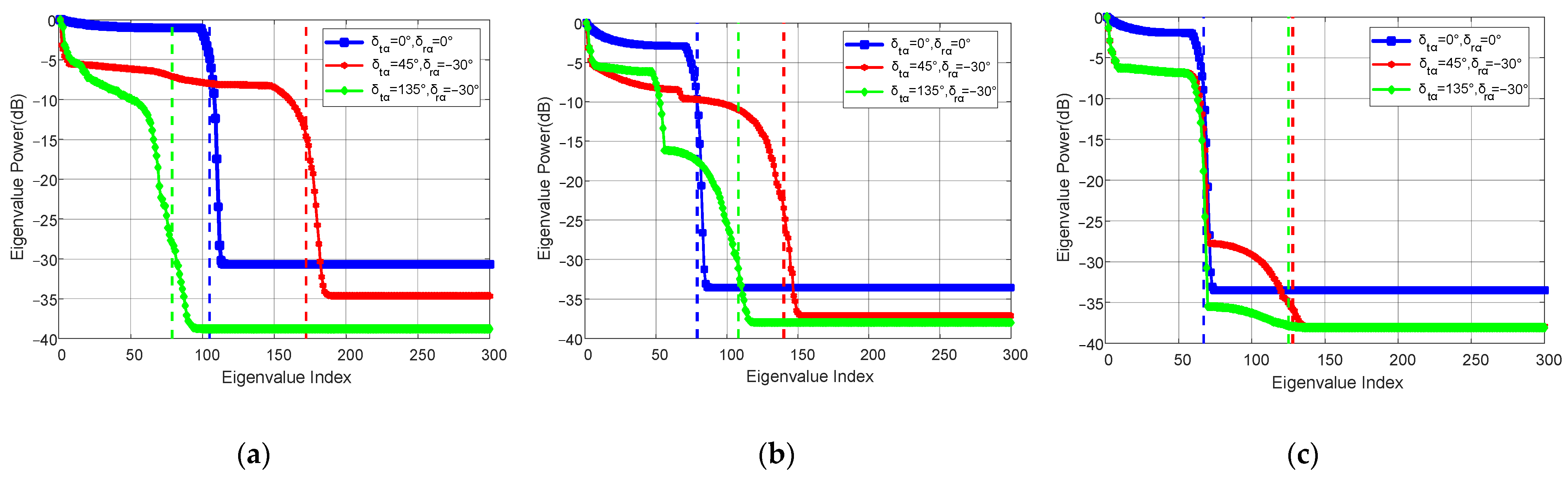
4.1. Experiment 1: Clutter Rank Estimation for Airborne Bistatic Radar
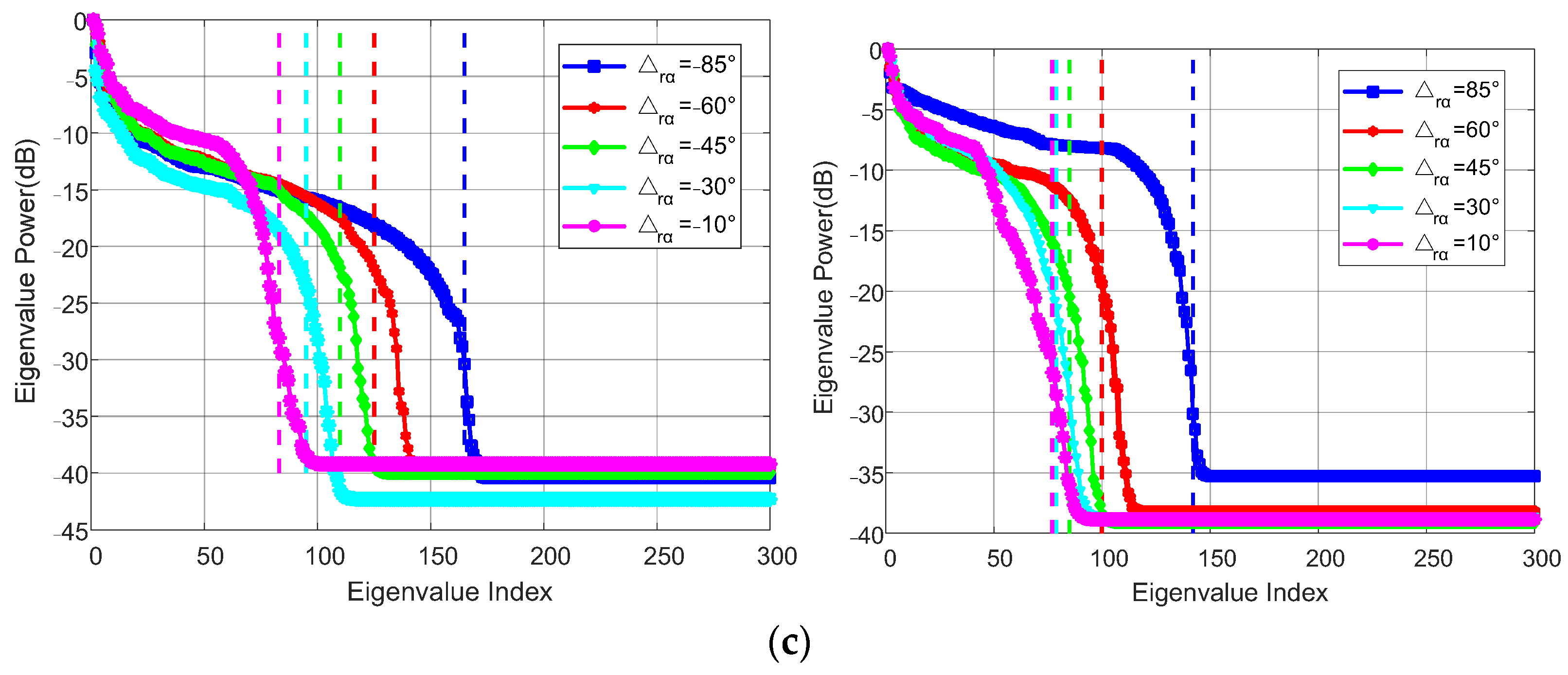
4.2. Experiment 2: Clutter Rank Estimation for Spaceborne Bistatic Radar
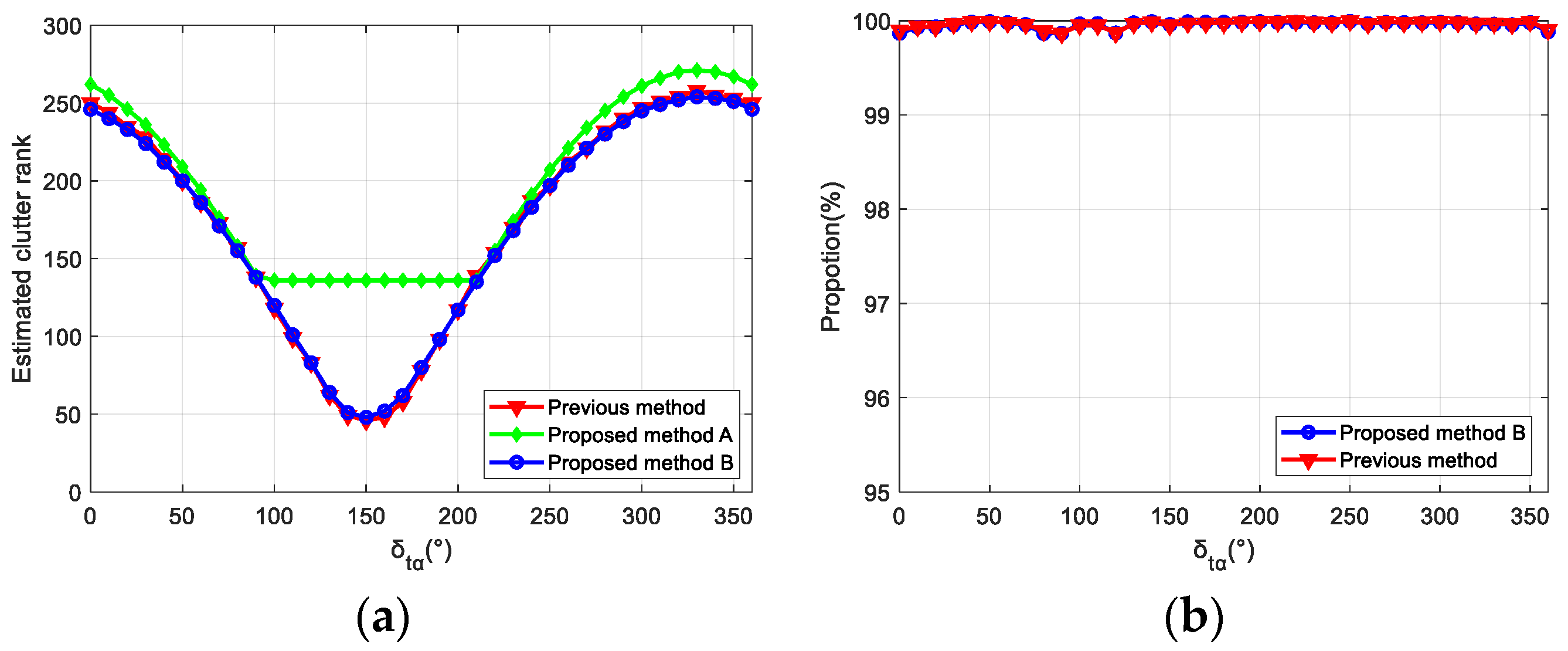
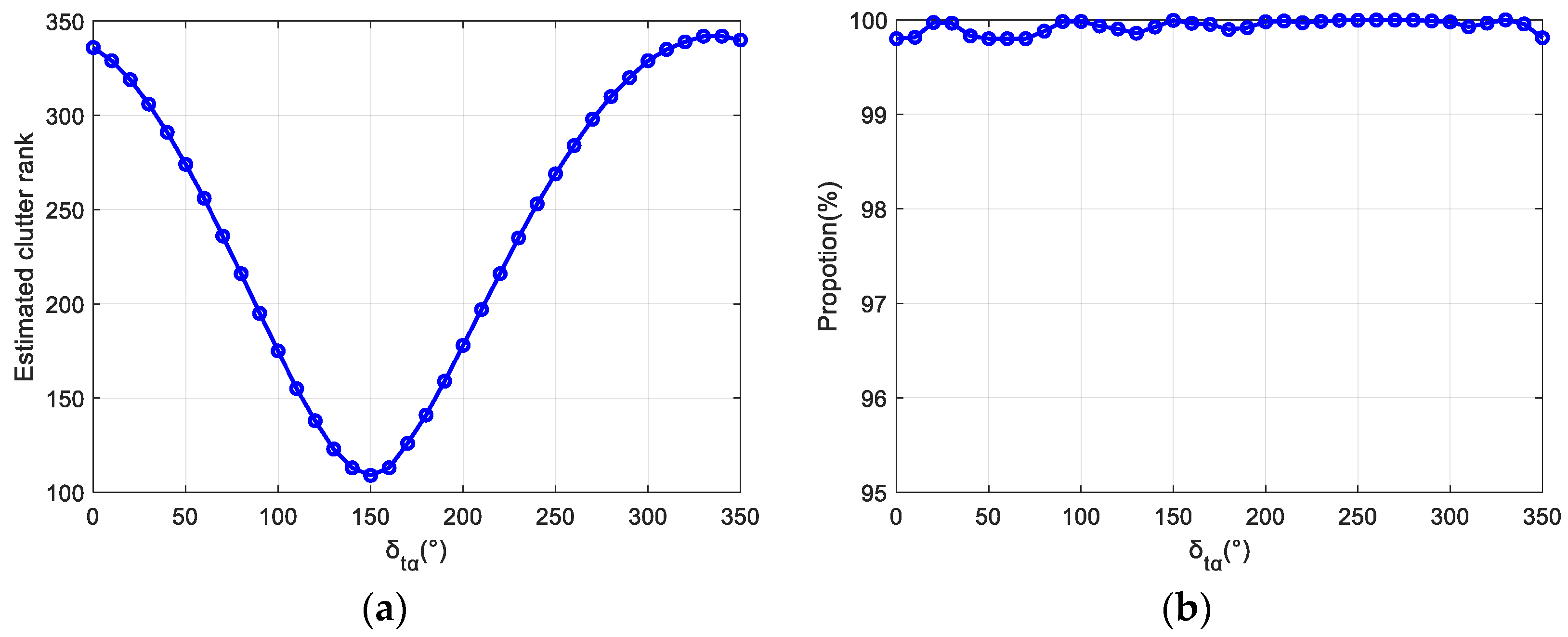
4.3. Experiment 3: Clutter Rank Estimation of Non-Side-Looking Mode
4.4. Experiment 4: Clutter Rank Estimation in a Limited Area
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
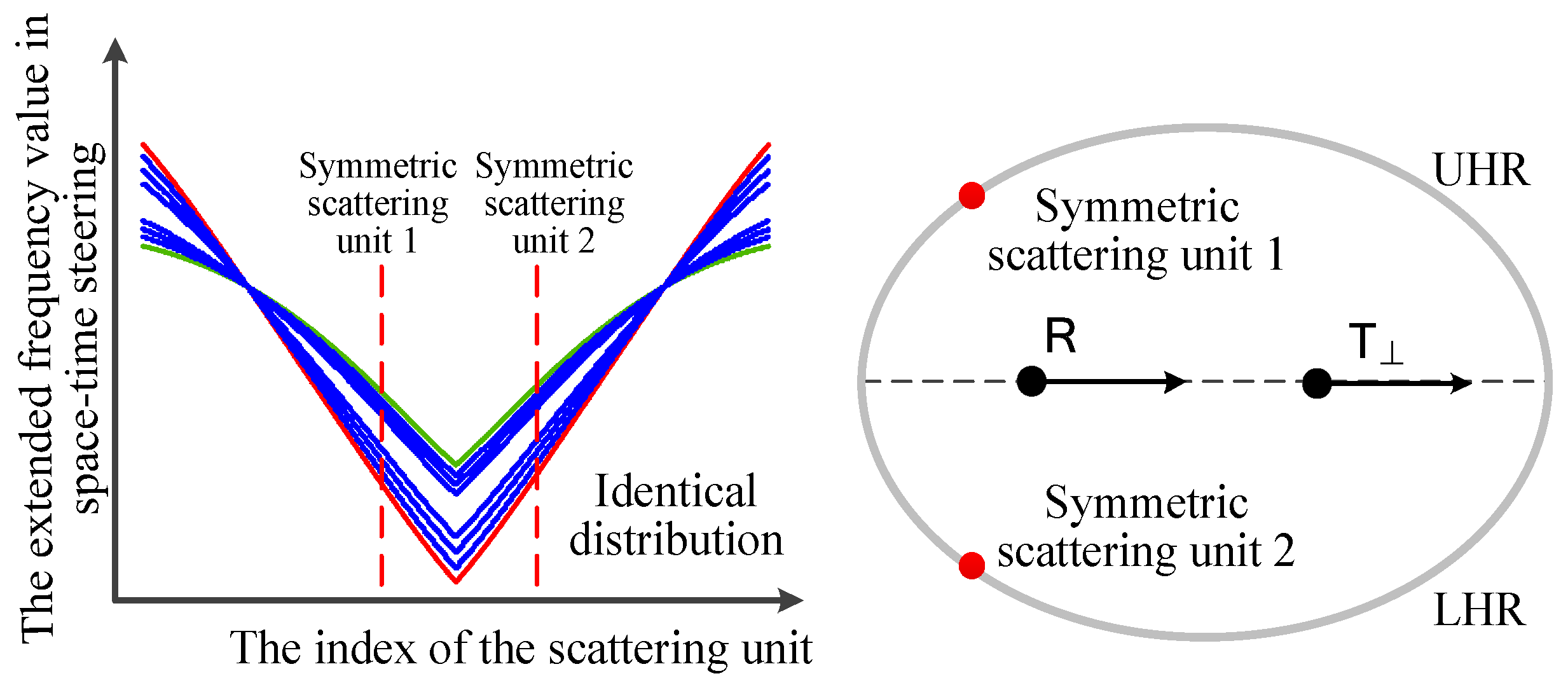
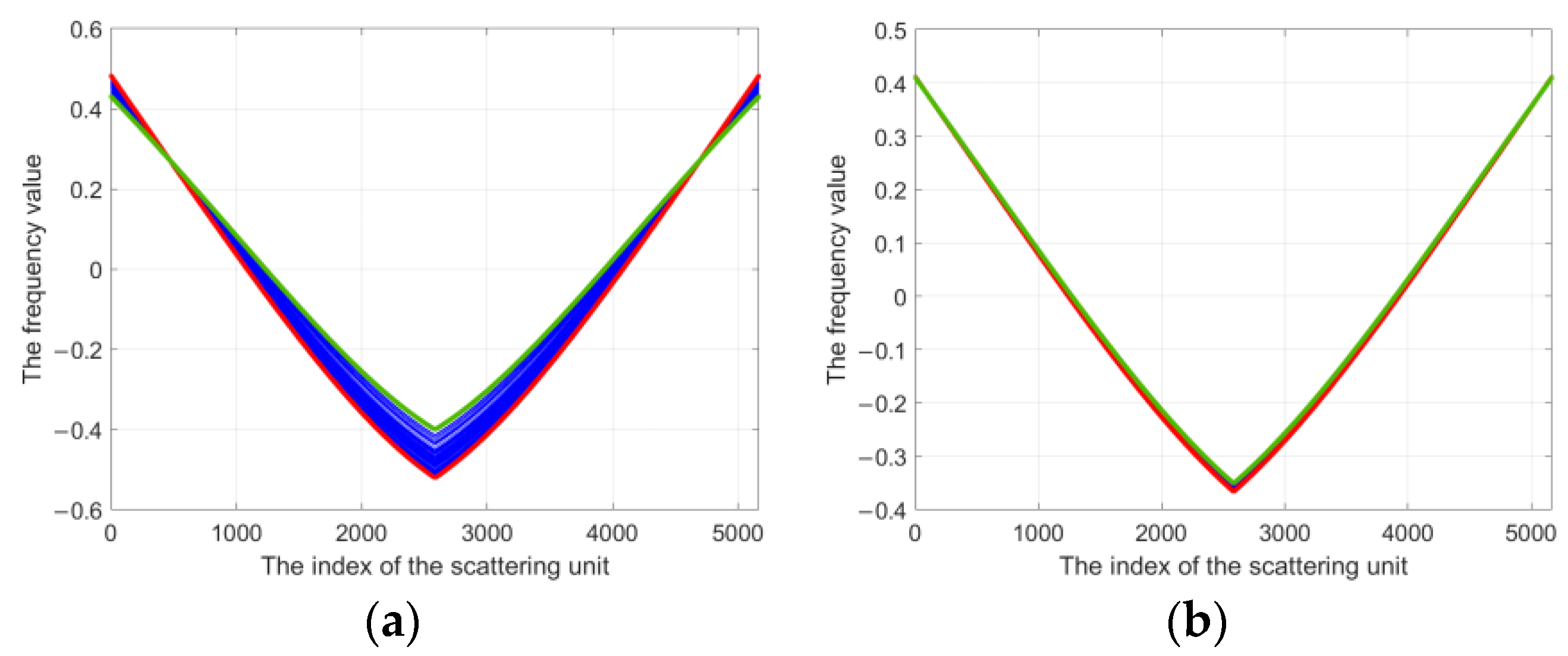
Appendix A.1. Case A: Extended Frequency Values of Different Scattering Units Are Not Identical
Appendix A.2. Case B: Extended Frequency Values of Different Scattering Units Are Identical
References
- Ward, J. Space-Time Adaptive Processing for Airborne Radar. In Proceedings of the IEE Colloquium on Space-Time Adaptive Processing, Lexington, MA, USA, 26–29 June 1994; pp. 20–51. [Google Scholar]
- Croci, R.; Delfino, A.; Marchetti, F. Space based radar technology evolution. In Proceedings of the European Radar Conference, Rome, Italy, 30 September–2 October 2009; pp. 601–604. [Google Scholar]
- Hartnett, M.P. Ground and airborne target detection with bistatic adaptive space based radar. In Proceedings of the IEEE Radar Conference, Waltham, MA, USA, 22 April 1999. [Google Scholar]
- Hartnett, M.P.; Davis, M.E. Bistatic surveillance concept of operations. In Proceedings of the IEEE Radar Conference, Huntsville, AL, USA, 5–8 May 2003; pp. 75–80. [Google Scholar]
- Cristallini, D.; Walterscheid, I. Joint monostatic and bistatic STAP for improved SAR-GMTI capabilities. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1834–1848. [Google Scholar] [CrossRef]
- Graziano, M.D. Novel constellation design method for spaceborne/airborne bistatic SAR systems. Trans. Aerosp. Electron. Syst. 2016, 54, 1834–1848. [Google Scholar] [CrossRef]
- Kang, X.; Wan, J.; Li, D.; Liu, Q.; Liu, H.; Hu, R.; Chen, Z. Spaceborne distributed aperture radar maneuvering target detection approach with space-time 2D hybrid integration technique. Signal Process. 2024, 217, 109348. [Google Scholar] [CrossRef]
- Zou, Z.H.; Ma, J.T.; Huang, P.H.; Xia, X.G.; Chen, J.L.; Xi, P.L.; Liu, X.Z. Multichannel Sea Clutter Modeling and Clutter Suppression Performance Analysis for Spaceborne Bistatic Surveillance Radar Systems. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–24. [Google Scholar] [CrossRef]
- Melvin, W.L.; Davis, M.E. Adaptive Cancellation Method for Geometry-Induced Nonstationary Bistatic Clutter Environments. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 651–672. [Google Scholar] [CrossRef]
- Huang, P.; Zou, Z.; Xia, X.G.; Liu, X.; Liao, G.; Xin, Z. Multichannel sea clutter modeling for spaceborne early warning radar and clutter suppression performance analysis. IEEE Trans. Geosci. Remote Sens. 2021, 59, 8349–8366. [Google Scholar] [CrossRef]
- Brennan, L.E.; Reed, L.S. Theory of adaptive radar. IEEE Trans. Aerosp. Electron. Syst. 1973, 2, 237–252. [Google Scholar] [CrossRef]
- Liu, W.; Liu, J.; Hao, C.; Gao, Y.; Wang, Y. Multichannel adaptive signal detection: Basic theory and literature review. Sci. China: Inf. Sci. 2022, 65, 5–44. [Google Scholar] [CrossRef]
- Li, J.; Yang, Q.; Zhang, X.; Ji, X.; Xiao, D. Space-Time Adaptive Processing Clutter-Suppression Algorithm Based on Beam Reshaping for High-Frequency Surface Wave Radar. Romote Sens. 2022, 14, 2935. [Google Scholar] [CrossRef]
- Xiong, Y.; Xie, W.; Wang, Y. Space time adaptive processing for airborne MIMO radar based on space time sampling matrix. Signal Process. 2023, 211, 109119. [Google Scholar] [CrossRef]
- Wen, C.; Ma, C.; Peng, J.; Wu, J. Bistatic FDA-MIMO radar space-time adaptive processing. Signal Process. 2019, 163, 201–212. [Google Scholar] [CrossRef]
- Klemm, R. Comparison between Monostatic and Bistatic Antenna Configurations for STAP. IEEE Trans. Aerosp. Electron. Syst. 2000, 36, 596–608. [Google Scholar] [CrossRef]
- Klemm, R. Ambiguities in Bistatic STAP Radar. In Proceedings of the IEEE Radar Conference, Alexandria, Egypt, 7–12 May 2000; pp. 1009–1011. [Google Scholar]
- Zhang, Y.H.; Himed, B. Effects of Geometry on Clutter Characteristics of Bistatic Radars. In Proceedings of the IEEE Radar Conference, Huntsville, AL, USA, 5–8 May 2003; pp. 417–424. [Google Scholar]
- Himed, B. Effects of bistatic clutter dispersion on STAP systems. IEEE Proc. Radar Sonar Navigat. 2003, 150, 28–32. [Google Scholar] [CrossRef]
- Li, H.; Tang, J.; Peng, Y. Clutter Modeling and Characteristics Analysis for Bistatic SBR. In Proceedings of the IEEE Radar Conference, Waltham, MA, USA, 17–20 April 2007; pp. 513–517. [Google Scholar]
- Liu, J.H.; Liao, G.S. Spaceborne-airborne bistatic radar clutter modeling and analysis. In Proceedings of the IEEE CIE International Conference on Radar, Chengdu, China, 24–27 October 2011. [Google Scholar]
- Klemm, R. Principles of Space-Time Adaptive Processing; The Institution of Electrical Engineers: London, UK, 2002. [Google Scholar]
- Guerci, J.R.; Goldstein, J.S.; Reed, I.S. Optimal and Adaptive Reduced-rank STAP. IEEE Trans. Aerosp. Electron. Syst. 2000, 36, 647–661. [Google Scholar] [CrossRef]
- Fa, R.; De Lamare, R.C. Reduced-Rank STAP Algorithms using Joint Iterative Optimization of Filters. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 1668–1684. [Google Scholar] [CrossRef]
- Degurse, J.F.; Savy, L.; Marcos, S. Reduced-rank STAP for target detection in heterogeneous environments. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 1153–1162. [Google Scholar] [CrossRef]
- Wong, M.; Aboutanios, E.; Rosenberg, L. A STAP Detection Scheme for Low Sample Support Maritime Environments. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 5671–5683. [Google Scholar] [CrossRef]
- Sun, K.; Meng, H.; Wang, Y.; Wang, X. Direct data domain STAP using sparse representation of clutter spectrum. Signal Process. 2011, 91, 2222–2236. [Google Scholar] [CrossRef]
- Duan, K.; Liu, W.; Wang, Y. Off-grid effects mitigation exploiting knowledge of the clutter ridge for sparse recovery STAP. IET Radar Sonar Navig. 2018, 12, 557–564. [Google Scholar] [CrossRef]
- Li, Z.; Ye, H.; Liu, Z.; Sun, Z. Bistatic SAR clutter-ridge matched STAP method for nonstationary clutter suppression. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Tan, X.; Yang, Z.; Li, X.; Mao, Y.; Jiang, D. Gridless sparse recovery STAP algorithm with array amplitude-phase errors for non-uniform linear array. Digit. Signal Process. 2024, 144, 104296. [Google Scholar] [CrossRef]
- Yang, Z.; Li, X. Sparsity-aware Space-time Adaptive Processing; Science Press: Beijing, China, 2018; pp. 39–42. [Google Scholar]
- Varadarajan, V.; Krolik, J.L. Joint Space-Time Interpolation for Distorted Linear and Bistatic Array Geometries. IEEE Trans. Signal Process. 2006, 54, 848–869. [Google Scholar] [CrossRef]
- Goodman, N.A.; Stiles, J.M. On Clutter Rank Observed by Arbitrary Arrays. IEEE Trans. Signal Process. 2007, 55, 178–186. [Google Scholar] [CrossRef]
- Zhang, Q.; Mikhael, W.B. Estimation of the Clutter Rank in the Case of Subarraying for Space-Time Adaptive Processing. Electron. Lett. 1997, 33, 419–420. [Google Scholar] [CrossRef]
- Brennan, L.E.; Staudaher, F.M. Subclutter Visibility Demonstration; Technical Report RL-TR-92-21; Adaptive Sensors, Inc.: Santa Monica, CA, USA, 1992. [Google Scholar]
- Chen, C.-Y.; Vaidyanathan, P.P. MIMO Radar Space-Time Adaptive Processing Using Prolate Spheroidal Wave Functions. IEEE Trans. Signal Process. 2008, 56, 623–635. [Google Scholar] [CrossRef]
- Du, W.; Liao, G.; Yang, Z. Robust space-time processing based on bi-iterative scheme of secondary data selection and PSWF method. Digit. Signal Process. 2015, 52, 64–71. [Google Scholar] [CrossRef]
- Tang, W.; Jiang, H.; Zhang, Q.; Jiang, H. PSWF-based decoupled atomic norm minimization for DOD and DOA estimation in MIMO radar with arbitrary linear arrays. Signal Process. 2023, 212, 109136. [Google Scholar] [CrossRef]
- Zulch, P.; Davis, M.; Adzima, I. The Earth Rotation Effect on a LEO L-Band GMTI SBR and Mitigation Strategies. In Proceedings of the IEEE Radar Conference, Philadelphia, PA, USA, 26–29 April 2004; pp. 27–32. [Google Scholar]
- Jia, F.; He, Z.S. Clutter Rank Estimation for Diving Platform Radar. IEICE Trans. Fundam. 2018, 101, 600–603. [Google Scholar] [CrossRef]
- Xu, J.; Li, Y. Statistics Essentials; China Machine Press: Beijing, China, 2016; pp. 53–89. [Google Scholar]








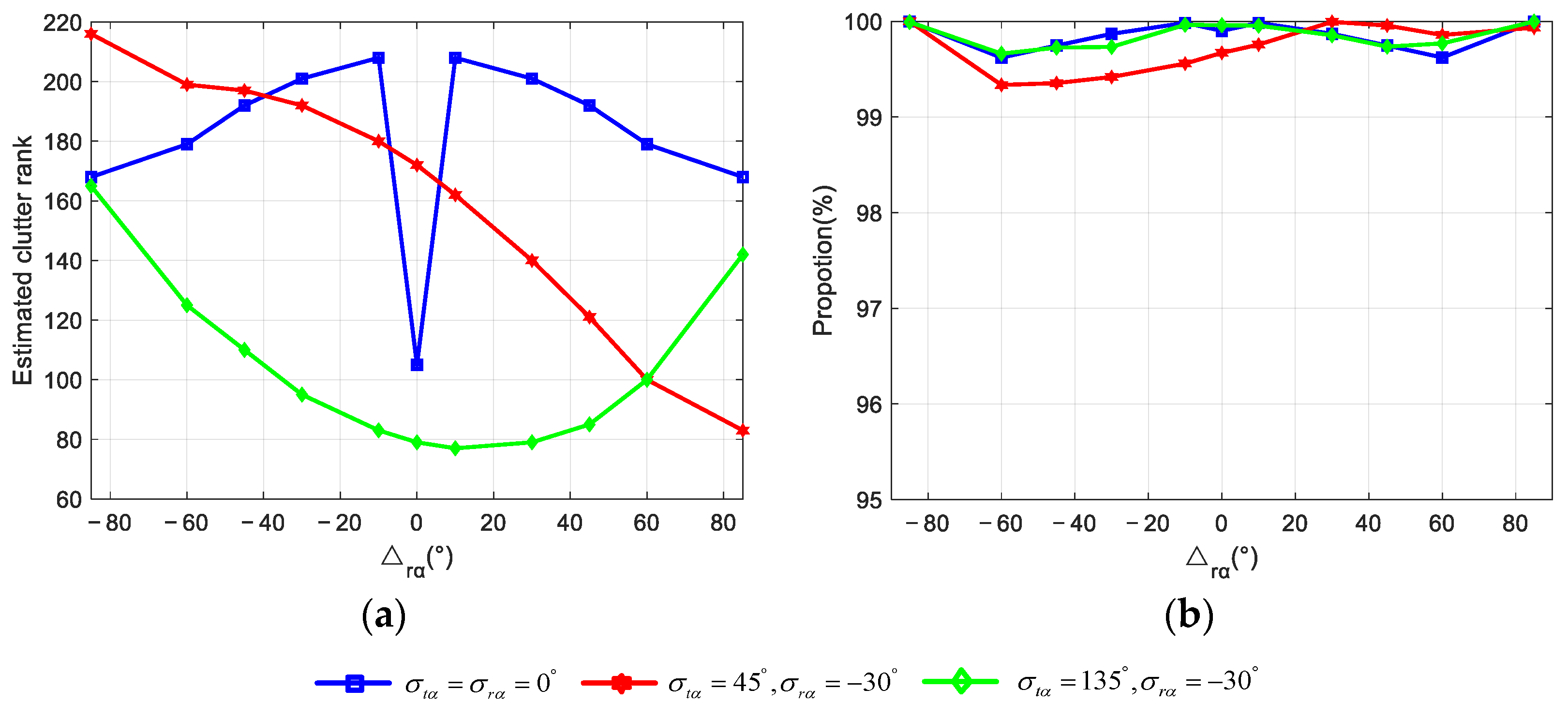

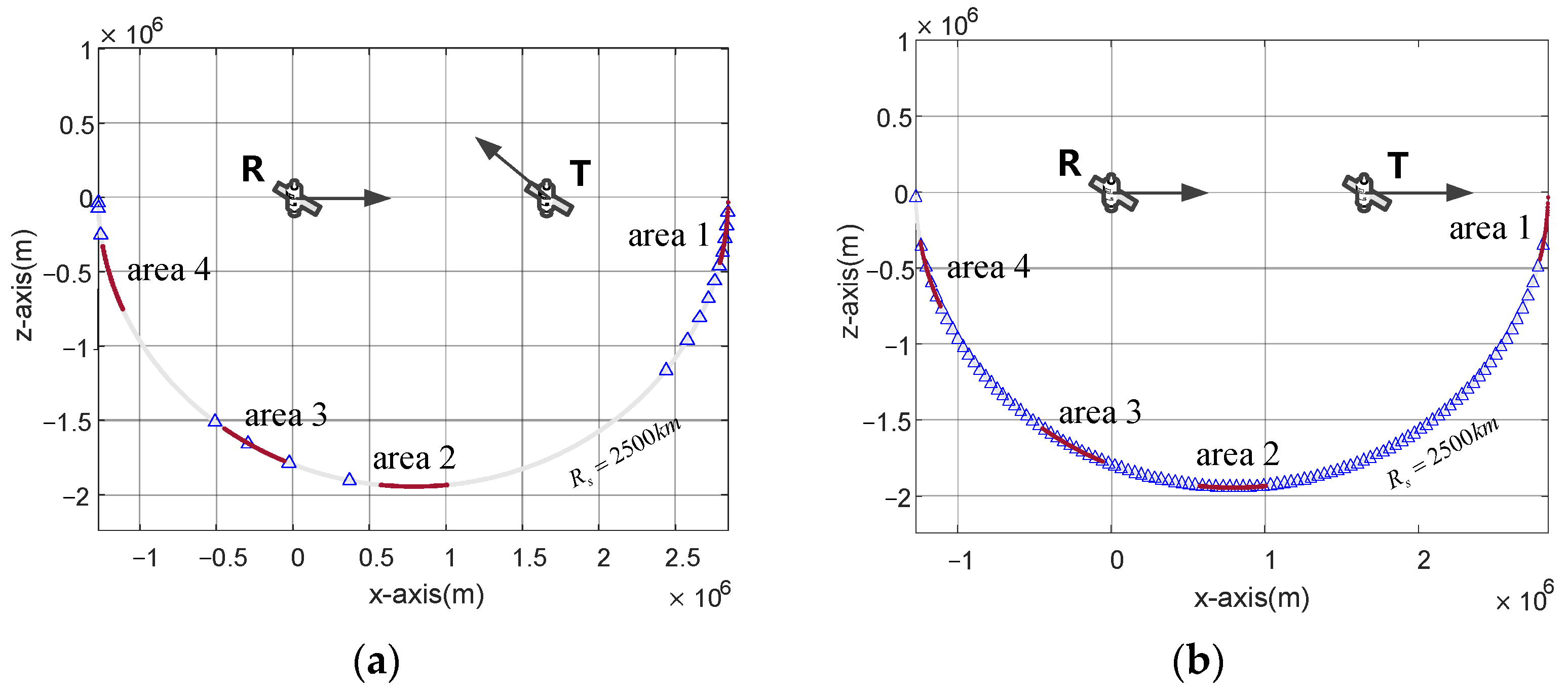

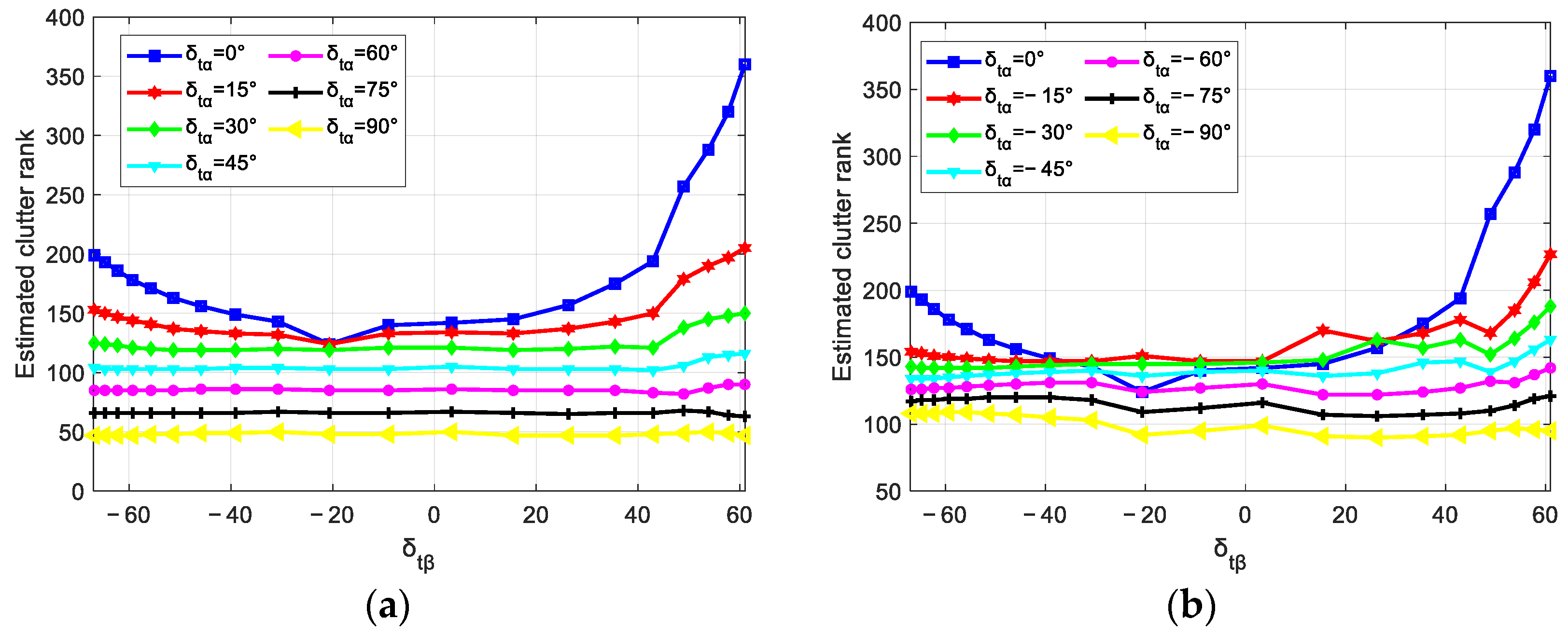
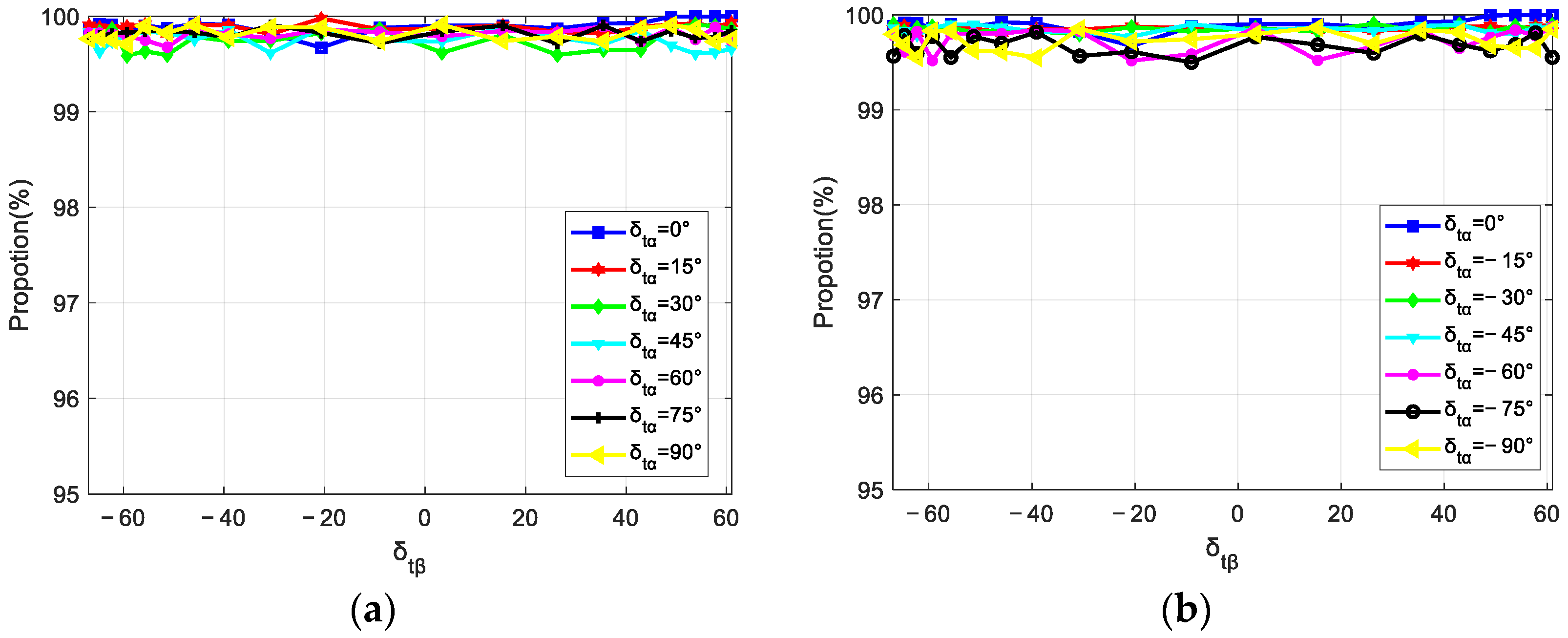
| (a) Configuration Parameters | ||
| Parameter | Value | Unit |
| Bistatic range sum | 60 | km |
| PRF | 4000 | Hz |
| Altitude of transmitting aircraft | 10 | km |
| Altitude of receiving aircraft | 10 | km |
| Velocity of transmitting aircraft | 200 | m/s |
| Velocity of receiving aircraft | 200 | m/s |
| The distance between the sub-aircraft points of two aircrafts | 15 | km |
| (b) System Parameters | ||
| Parameter | Value | Unit |
| Signal wavelength | 0.2 | m |
| Channel spacing | 0.1 | m |
| Number of channels | 6 | - |
| Number of pulses | 128 | - |
| CNR | 50 | dB |
| Parameter | Value | Unit | ||
|---|---|---|---|---|
| Bistatic range sum | LEO-LEO | 2500 | km | |
| MEO-LEO | 6200 | km | ||
| GEO-LEO | 19,000 | km | ||
| PRF | LEO-LEO | 147,074 | Hz | |
| MEO-LEO | 126,200 | Hz | ||
| GEO-LEO | 115,950 | Hz | ||
| Transmitter | Receiver | |||
| Orbit altitude | 1000/8000/ 35,786 | 1000 | km | |
| Orbit inclination | 0/45/135 | 0/−30/−30 | ° | |
| Right ascension of ascending node | 15 | 0 | ° | |
| Argument of perigee angle | 0 | 0 | ° | |
| Eccentricity | 0 | 0 | ° | |
| True near location angle | 0 | 0 | ° | |
| LEO-LEO | MEO-LEO | GEO-LEO | ||||
|---|---|---|---|---|---|---|
| Nr | η | Nr | η | Nr | η | |
| 105 | 99.58% | 79 | 99.86% | 67 | 99.76% | |
| 172 | 99.64% | 140 | 99.95% | 128 | 99.99% | |
| 79 | 99.96% | 108 | 99.99% | 125 | 99.99% | |
| δtα | 0° | 45° | 90° | 135° | 180° | −45° | −90° | −135° |
|---|---|---|---|---|---|---|---|---|
| 99.83% | 99.50% | 99.89% | 99.93% | 99.59% | 99.76% | 99.77% | 99.82% | |
| 99.78% | 99.75% | 99.80% | 99.54% | 99.93% | 99.86% | 99.62% | 99.69% | |
| 99.33% | 99.76% | 99.78% | 99.33% | 99.60% | 99.65% | 99.63% | 99.40% | |
| 99.84% | 99.82% | 99.76% | 99.28% | 99.52% | 99.71% | 99.92% | 99.46% |
| Observation Area | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 44 | 6 | 26 | 11 | ||
| 99.99 | 99.93 | 99.93 | 99.68 | ||
| 25 | 143 | 140 | 59 | ||
| 99.20 | 99.83 | 99.79 | 99.80 | ||
| The Mean Value | RMSE | |
|---|---|---|
| Experiment 1 | 99.94% | 0.07% |
| Experiment 2 | 99.85% | 0.20% |
| Experiment 3 | 99.83% | 0.24% |
| Experiment 4 | 99.82% | 0.23% |
| Total Experiments | 99.84% | 0.20% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, X.; Yang, Z.; Li, X.; Liu, L.; Li, X. Clutter Rank Estimation Method for Bistatic Radar Systems Based on Prolate Spheroidal Wave Functions. Remote Sens. 2024, 16, 2928. https://doi.org/10.3390/rs16162928
Tan X, Yang Z, Li X, Liu L, Li X. Clutter Rank Estimation Method for Bistatic Radar Systems Based on Prolate Spheroidal Wave Functions. Remote Sensing. 2024; 16(16):2928. https://doi.org/10.3390/rs16162928
Chicago/Turabian StyleTan, Xiao, Zhiwei Yang, Xianghai Li, Lei Liu, and Xiaorui Li. 2024. "Clutter Rank Estimation Method for Bistatic Radar Systems Based on Prolate Spheroidal Wave Functions" Remote Sensing 16, no. 16: 2928. https://doi.org/10.3390/rs16162928
APA StyleTan, X., Yang, Z., Li, X., Liu, L., & Li, X. (2024). Clutter Rank Estimation Method for Bistatic Radar Systems Based on Prolate Spheroidal Wave Functions. Remote Sensing, 16(16), 2928. https://doi.org/10.3390/rs16162928





