A Method for Extracting Acoustic Water Surface Waves Based on Phase Compensation
Abstract
:1. Introduction
2. Models
2.1. The Model of an Acoustic Water Surface Wave
2.2. Phase Discontinuity Model
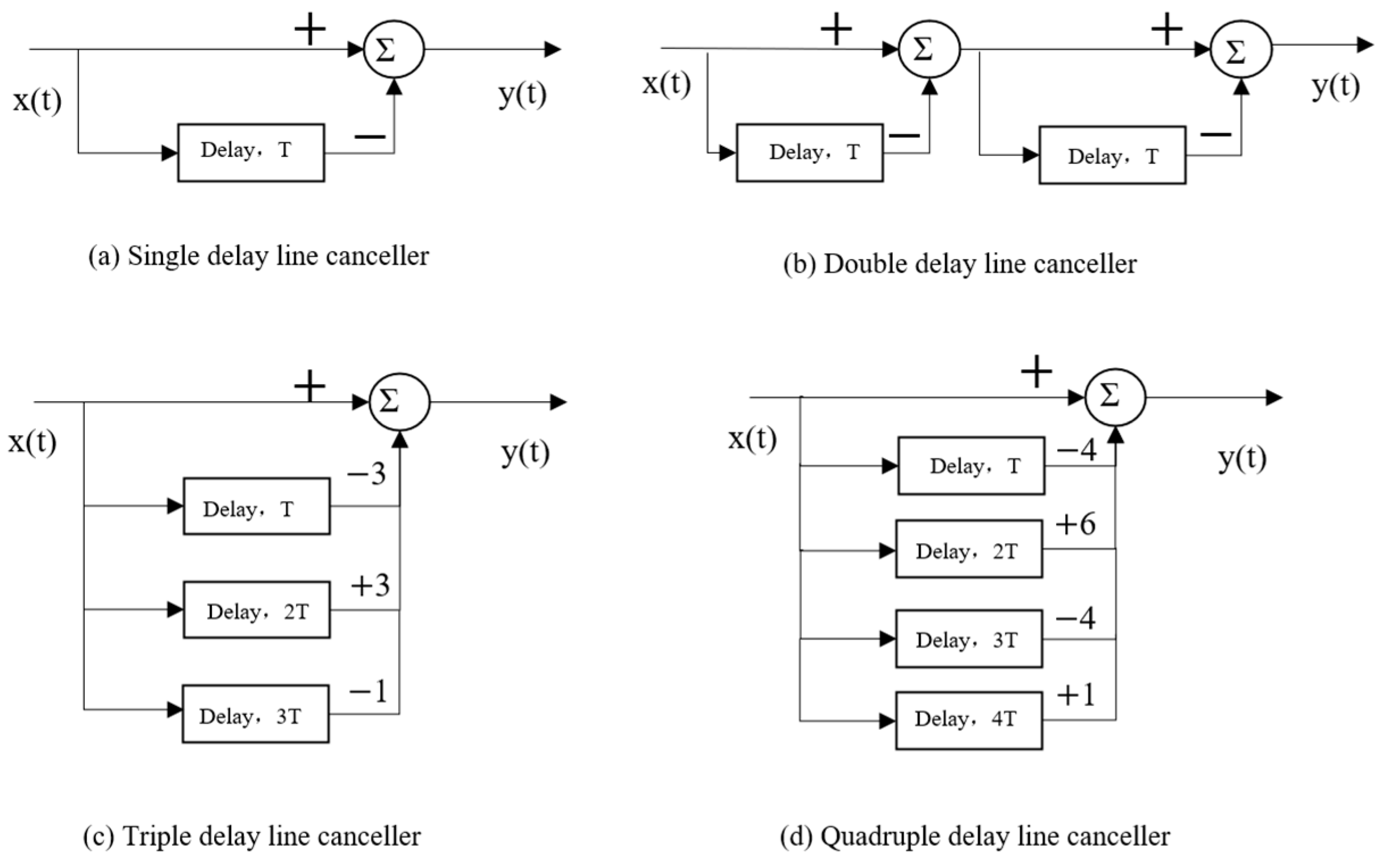
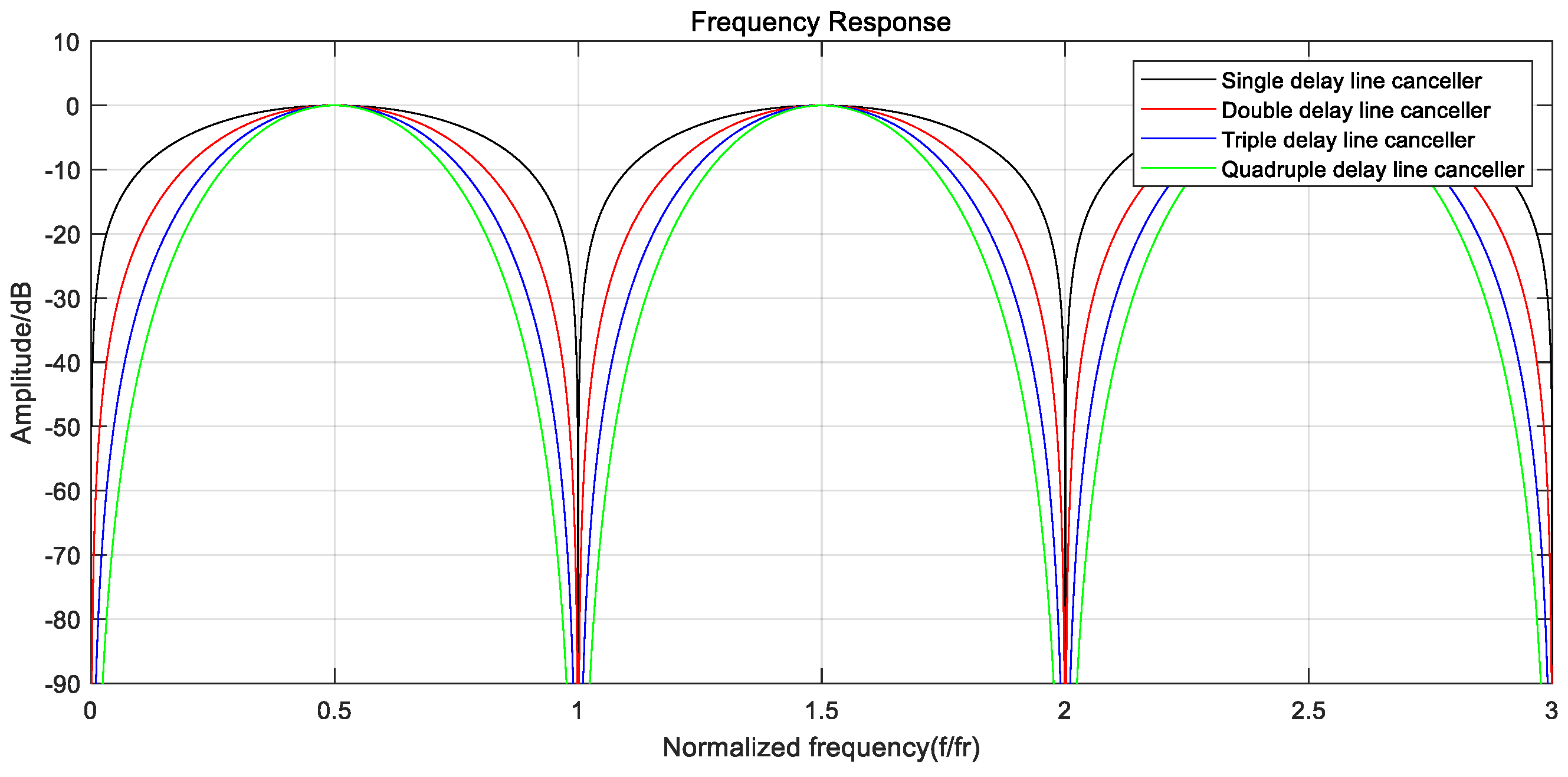
3. Method
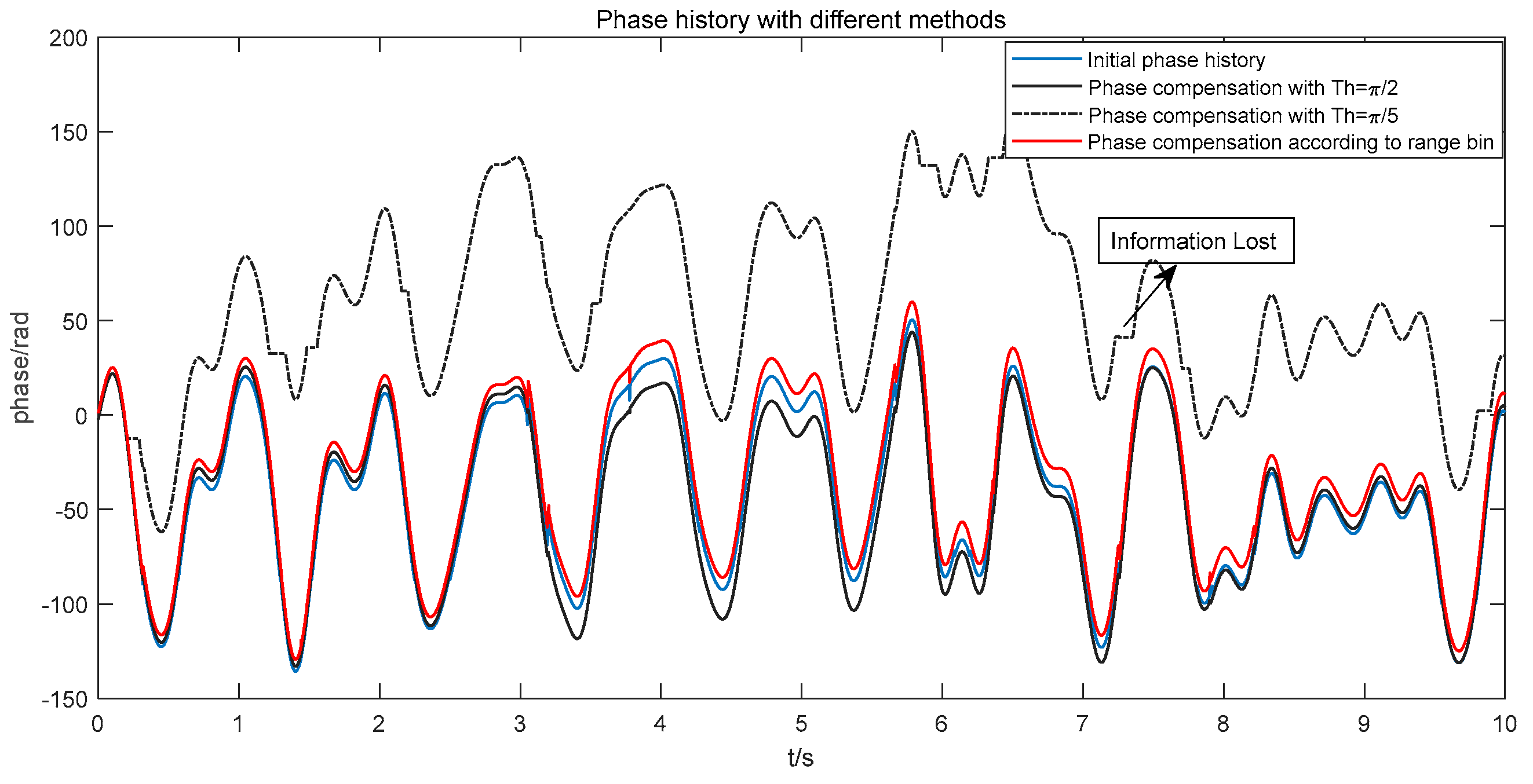
3.1. Phase Compensation
3.2. Second-Order Differential Joint Outlier Removal
4. Simulation and Experiment
4.1. Simulation
4.2. Experiment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Menon, K.A.U.; Shibina, J.S.; Menon, V.N. Intelligent system for remote health monitoring of divers using underwater acoustic communication. In Proceedings of the Fifth International Conference on Computing, Communications and Networking Technologies (ICCCNT), Hefei, China, 11–13 July 2014; pp. 1–7. [Google Scholar] [CrossRef]
- Prabha, K.R.; Nataraj, B.; Pandithurai, S.; Raj, A.R.C.; Prassath, A. Deep-Sea Survival Assistance and Health Monitoring System. In Proceedings of the 2023 Third International Conference on Smart Technologies, Communication and Robotics (STCR), Sathyamangalam, India, 9–10 December 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Manik, H.M. Underwater acoustic signal processing for detection and quantification of fish. In Proceedings of the 2011 International Conference on Electrical Engineering and Informatics, Bandung, Indonesia, 17–19 July 2011; pp. 1–3. [Google Scholar] [CrossRef]
- Thomas, G.L.; Hahn, T.; Thorne, R.E. Combining passive and active underwater acoustics with video and laser optics to assess fish stocks. In Proceedings of the OCEANS 2006, Boston, MA, USA, 18–21 September 2006; pp. 1–4. [Google Scholar] [CrossRef]
- Parton, S.; Dalgleish, F.; Beaujean, P.P.; Ouyang, B.; Caimi, F. Acquisition and registration of bathymetric acoustic data and MOFSLI (multiple overlapping field of view serial laser imager). In Proceedings of the 2013 MTS/IEEE OCEANS, Bergen, Norway, 10–14 June 2013; pp. 1–8. [Google Scholar] [CrossRef]
- Tonolini, F.; Adlib, F. Networking across Boundaries Enabling Wireless Communication through the Water-Air Interface. In Proceedings of the SIGCOMM 18th, Budapest, Hungary, 20–25 August 2018. [Google Scholar] [CrossRef]
- Qian, J.; Qu, F.; Su, J.; Wei, Y.; Cheng, M.; Guo, H.; Zhu, J.; Wang, J. Theoretical Model and Experiments of Focused Phased Array for Cross-Medium Communication in Misaligned Transmitter/Receiver Scenarios. IEEE J. Ocean. Eng. 2023, 48, 1348–1361. [Google Scholar] [CrossRef]
- Qian, J.; Lu, X.; Zhang, M.; Qu, F.; Wei, Y. Cross-Medium Communication Combining Acoustic Wave and Millimeter Wave: Anechoic Pool, Lake, Swimming Pool Experiments. In Proceedings of the OCEANS 2023, Limerick, Ireland, 5–8 June 2023; pp. 1–7. [Google Scholar] [CrossRef]
- Qu, F.; Qian, J.; Wang, J.; Lu, X.; Zhang, M.; Bai, X.; Ran, Z.; Tu, X.; Liu, Z.; Wei, Y. Cross-Medium Communication Combining Acoustic Wave and Millimeter Wave: Theoretical Channel Model and Experiments. IEEE J. Ocean. Eng. 2022, 47, 483–492. [Google Scholar] [CrossRef]
- Gai, Y.; Tan, Q.; Zhang, Y.; Zhao, Z.; Yang, Y.; Liu, Y.; Zhang, R. A corss-medium uplink communication model merging acoustic and millimeter waves. J. Mar. Sci. Eng. 2023, 11, 2102. [Google Scholar] [CrossRef]
- Zeng, Y.; Shen, S.; Xu, Z. Water Surface Acoustic Wave Detection by a Millimeter Wave Radar. Remote Sens. 2023, 15, 4022. [Google Scholar] [CrossRef]
- Deng, B.; Li, T.; Tang, B.; Yi, J.; Wang, H.; Yang, Q. Detection of acoustic sea surface micro-amplitude waves based on terahertz radar. J. Radar 2023, 12, 817–831. [Google Scholar] [CrossRef]
- Luo, J.; Liang, X.; Guo, Q.; Zhang, L.; Bu, X. Combined Improved CEEMDAN and Wavelet Transform Sea Wave Interference Suppression. Remote Sens. 2023, 15, 2007. [Google Scholar] [CrossRef]
- Fu, X.; Xia, W.; Dong, S. Radar water surface acoustic wave extraction for cross water and air medium communication. Acoust. Technol. 2023, 42, 452–461. [Google Scholar] [CrossRef]
- Zhang, X.; Mao, H.; Li, K.; Tang, W. Amplitude detection of low frequency water surface acoustic wave based on phase demodulation. Infrared Laser Eng. 2019, 48, 0506001. [Google Scholar] [CrossRef]
- Dai, Z.; Sun, J.; Sui, P. Theoretical study on one-dimensional model of transverse microwave on water surface. J. Yantai Univ. 2003, 16, 23–28. [Google Scholar] [CrossRef]
- Ducrozet, G.; Bonnefoy, F.; Le Touzé, D.; Ferrant, P. A modified High-Order Spectral method for wavemaker modeling in a numerical wave tank. Eur. J. Mech. —B/Fluids 2012, 34, 19–34. [Google Scholar] [CrossRef]
- Bonnefoy, F.; Ducrozet, G.; Le Touzé, D.; Ferrant, P. Time domain simulation of nonlinear water waves using spectral methods. In Advances in Numerical Simulation of Nonlinear Water Waves; World Scientific: Singapore, 2010; pp. 129–164. [Google Scholar] [CrossRef]
- Singh, A.; Rehman, S.U.; Yongchareon, S.; Chong, P.H.J. Multi-Resident Non-Contact Vital Sign Monitoring Using Radar: A Review. IEEE Sens. J. 2021, 21, 4061–4084. [Google Scholar] [CrossRef]
- Hasselmann, K.; Barnett, T.; Bouws, E.; Carlson, H.; Cartwright, D.; Enke, K.; Ewing, J.; Gienapp, H.; Hasselmann, D.; Kruseman, P.; et al. Measurements of wind-wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP). Deut. Hydrogr. Z. 1973, 8, 1–95. [Google Scholar]














| Parameters | Quantity | Value |
|---|---|---|
| Sound pressure level | 170 dB | |
| Frequency of the underwater source | 100 Hz | |
| c | Sound speed in the water | 1450 m/s |
| Water density | 1000 | |
| Gravitational acceleration | 9.8 | |
| Surface tension coefficient | 0.07275 |
| Parameters | Value |
|---|---|
| Start Frequency | 77 GHz |
| Bandwidth | 4 GHz |
| Samples | 256 |
| PRF | 1000 Hz |
| Sound pressure level | 170 dB |
| Significant wave height | 0.03 m |
| Spectral peak period | 1 s |
| Height of the radar | 1 m |
| Depth of the underwater transmitter | 0.3 m |
| Frequency of the underwater transmitter | 100 Hz, 200 Hz |
| Methods | Wavelet–Kalman Filtering | Compensation with a Threshold | The Proposed Method |
|---|---|---|---|
| Variance/m2 | 8.18 × 10−14 | 2.24 × 10−14 | 1.55 × 10−16 |
| Parameters | Value |
|---|---|
| Start frequency | 77 GHz |
| Bandwidth | 4 GHz |
| Samples | 256 |
| PRF | 1000 Hz |
| Sound pressure level | 170 dB |
| Significant wave height | 0.03 m |
| Spectral peak period | 1 m |
| Height of the radar | 0.5 m |
| Depth of the underwater transmitter | 0.3 m |
| Frequency of the underwater transmitter | 100 Hz, 200 Hz |
| Methods | Wavelet–Kalman Filtering | Compensation with a Threshold | The Proposed Method |
|---|---|---|---|
| Variance/m2 | 1.0310 × 10−11 | 1.9238 × 10−12 | 1.3156 × 10−12 |
| Method | Number of Erroneous Bits | Bit Error Rate |
|---|---|---|
| Wavelet–Kalman Filtering | 37 | 6.5% |
| Phase compensation based on a threshold and High-pass Filtering | 30 | 5.2% |
| The Proposed Method | 10 | 1.7% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Liang, X.; Zhang, Y.; Xin, J.; Jiang, N.; Guo, Q.; Wang, M.; Wei, J.; Bu, X. A Method for Extracting Acoustic Water Surface Waves Based on Phase Compensation. Remote Sens. 2024, 16, 2911. https://doi.org/10.3390/rs16162911
Li M, Liang X, Zhang Y, Xin J, Jiang N, Guo Q, Wang M, Wei J, Bu X. A Method for Extracting Acoustic Water Surface Waves Based on Phase Compensation. Remote Sensing. 2024; 16(16):2911. https://doi.org/10.3390/rs16162911
Chicago/Turabian StyleLi, Miaomiao, Xingdong Liang, Yuan Zhang, Jihao Xin, Nanyi Jiang, Qichang Guo, Mingming Wang, Jiashuo Wei, and Xiangxi Bu. 2024. "A Method for Extracting Acoustic Water Surface Waves Based on Phase Compensation" Remote Sensing 16, no. 16: 2911. https://doi.org/10.3390/rs16162911
APA StyleLi, M., Liang, X., Zhang, Y., Xin, J., Jiang, N., Guo, Q., Wang, M., Wei, J., & Bu, X. (2024). A Method for Extracting Acoustic Water Surface Waves Based on Phase Compensation. Remote Sensing, 16(16), 2911. https://doi.org/10.3390/rs16162911