Rational-Function-Model-Based Rigorous Bundle Adjustment for Improving the Relative Geometric Positioning Accuracy of Multiple Korea Multi-Purpose Satellite-3A Images
Abstract
:1. Introduction
2. Materials and Methods
2.1. Tie Point Extraction with SIFT Algorithm
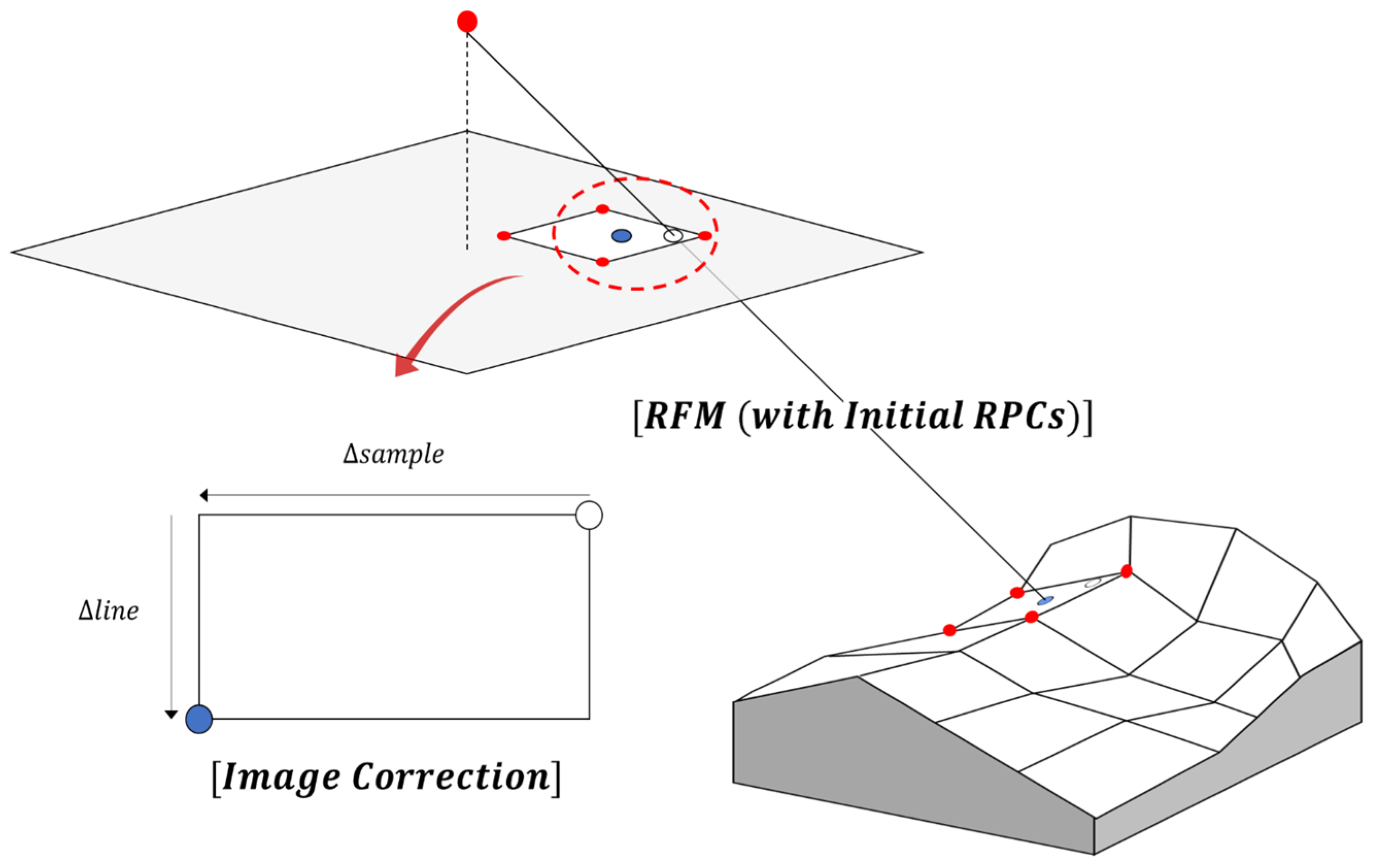
2.2. RFM-Based Observation Equation
2.3. Rigorous Bundle Adjustment
2.4. Result Image Generation Based on Virtual DEM
3. Test Results
3.1. Result of Rigorous Bundle Adjustment
3.2. Relative Positional Accuracies of the Check Points
3.3. Corrected Result Images
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Park, J.; Lee, D.; Lee, J.; Cheon, E.; Jeong, H. Study on Disaster Response Strategies Using Multi-Sensors Satellite Imagery. Korean J. Remote Sens. 2023, 39, 755–770. [Google Scholar]
- Liu, Y.; Shen, C.; Chen, X.; Hong, Y.; Fan, Q.; Chan, P.; Lan, J. Satellite-Based Estimation of Roughness Length over Vegetated Surfaces and Its Utilization in WRF Simulations. Remote Sens. 2023, 15, 2686. [Google Scholar] [CrossRef]
- Afaq, Y.; Manocha, A. Analysis on Change Detection Techniques for Remote Sensing Applications: A Review. Ecol. Inform. 2021, 63, 101310. [Google Scholar] [CrossRef]
- Jiang, Y.H.; Zhang, G.; Chen, P.; Li, D.R.; Tang, X.M.; Huang, W.C. Systematic Error Compensation Based on a Rational Function Model for Ziyuan1-02C. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3985–3995. [Google Scholar] [CrossRef]
- Yoon, W.; Park, H.; Kim, T. Feasibility Analysis of Precise Sensor Modelling for KOMPSAT-3A Imagery Using Unified Control Points. Korean J. Remote Sens. 2018, 34, 1089–1100. [Google Scholar]
- Saleh, T.M.; Zahran, M.I.; Al-Shehaby, A.R.; Gomaa, M.S. Performance Enhancement of Rational Function Model (RFM) for Improved Geo-Position Accuracy of IKONOS Stereo Satellite Imagery. J. Geomat. 2018, 12, 1–12. [Google Scholar]
- Tong, X.; Liu, S.; Weng, Q. Bias-Corrected Rational Polynomial Coefficients for High Accuracy Geo-Positioning of QuickBird Stereo Imagery. ISPRS J. Photogramm. Remote Sens. 2010, 65, 218–226. [Google Scholar] [CrossRef]
- Son, J.H.; Yoon, W.; Kim, T.; Rhee, S. Iterative Precision Geometric Correction for High-Resolution Satellite Images. Korean J. Remote Sens. 2021, 37, 431–447. [Google Scholar]
- Deng, M.; Zhang, G.; Cai, C.; Xu, K.; Zhao, R.; Guo, F.; Suo, J. Improvement and Assessment of the Absolute Positioning Accuracy of Chinese High-Resolution SAR Satellites. Remote Sens. 2019, 11, 1465. [Google Scholar] [CrossRef]
- Cabo, C.; Sanz-Ablanedo, E.; Roca-Pardiñas, J.; Ordóñez, C. Influence of the Number and Spatial Distribution of Ground Control Points in the Accuracy of UAV-SfM DEMs: An Approach Based on Generalized Additive Models. IEEE Trans. Geosci. Remote Sens. 2021, 59, 10618–10627. [Google Scholar] [CrossRef]
- Ma, Z.; Wu, X.; Yan, L.; Xu, Z. Geometric Positioning for Satellite Imagery without Ground Control Points by Exploiting Repeated Observation. Sensors 2017, 17, 240. [Google Scholar] [CrossRef] [PubMed]
- Sánchez, M.; Cuartero, A.; Barrena, M.; Plaza, A. A New Method for Positional Accuracy Analysis in Georeferenced Satellite Images without Independent Ground Control Points. Remote Sens. 2020, 12, 4132. [Google Scholar] [CrossRef]
- Yang, B.; Pi, Y.; Li, X.; Wang, M. Relative Geometric Refinement of Patch Images without Use of Ground Control Points for the Geostationary Optical Satellite GaoFen4. IEEE Trans. Geosci. Remote Sens. 2017, 56, 474–484. [Google Scholar] [CrossRef]
- Sommervold, O.; Gazzea, M.; Arghandeh, R. A Survey on SAR and Optical Satellite Image Registration. Remote Sens. 2023, 15, 850. [Google Scholar] [CrossRef]
- Hou, X.; Gao, Q.; Wang, R.; Luo, X. Satellite-Borne Optical Remote Sensing Image Registration Based on Point Features. Sensors 2021, 21, 2695. [Google Scholar] [CrossRef]
- Velesaca, H.O.; Bastidas, G.; Rouhani, M.; Sappa, A.D. Multimodal Image Registration Techniques: A Comprehensive Survey. Multimed. Tools Appl. 2024, 83, 63919–63947. [Google Scholar] [CrossRef]
- Yang, B.; Wang, M.; Xu, W.; Li, D.; Gong, J.; Pi, Y. Large-Scale Block Adjustment without Use of Ground Control Points Based on the Compensation of Geometric Calibration for ZY-3 Images. ISPRS J. Photogramm. Remote Sens. 2017, 134, 1–14. [Google Scholar] [CrossRef]
- Fu, Q.; Liu, S.; Tong, X.; Wang, H. Block Adjustment of Large-Scale High-Resolution Optical Satellite Imagery without GCPs Based on the GPU. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 42, 91–94. [Google Scholar] [CrossRef]
- Fu, Q.; Tong, X.; Liu, S.; Ye, Z.; Jin, Y.; Wang, H.; Hong, Z. GPU-Accelerated PCG Method for the Block Adjustment of Large-Scale High-Resolution Optical Satellite Imagery without GCPs. Photogramm. Eng. Remote Sens. 2023, 89, 211–220. [Google Scholar] [CrossRef]
- Zitova, B.; Flusser, J. Image Registration Methods: A Survey. Image Vis. Comput. 2003, 21, 977–1000. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, J. A Two-Stage Deep Learning Registration Method for Remote Sensing Images Based on Sub-Image Matching. Remote Sens. 2021, 13, 3443. [Google Scholar] [CrossRef]
- Marí, R.; de Franchis, C.; Meinhardt-Llopis, E.; Anger, J.; Facciolo, G. A generic bundle adjustment methodology for indirect RPC model refinement of satellite imagery. Image Process. Line 2021, 11, 344–373. [Google Scholar] [CrossRef]
- Agarwal, S.; Snavely, N.; Seitz, S.M.; Szeliski, R. Bundle Adjustment in the Large. In Proceedings of the 11th European Conference on Computer Vision, Heraklion, Greece, 5–11 September 2010. [Google Scholar]
- Zareei, S.; Kelbe, D.; Sirguey, P.; Mills, S.; Eyers, D.M. Virtual Ground Control for Survey-Grade Terrain Modelling from Satellite Imagery. In Proceedings of the 36th International Conference on Image and Vision Computing New Zealand (IVCNZ), Wellington, New Zealand, 1–6 December 2021. [Google Scholar]
- Yang, B.; Wang, M.; Pi, Y. Block-Adjustment without GCPs for Large-Scale Regions Only Based on the Virtual Control Points. Acta Geod. Cartogr. Sin. 2017, 46, 874. [Google Scholar]
- Pi, Y.; Yang, B.; Li, X.; Wang, M. Robust correction of relative geometric errors among GaoFen-7 regional stereo images based on posteriori compensation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 3224–3234. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Grodecki, J.; Dial, G. Block Adjustment of High-Resolution Satellite Images Described by Rational Polynomials. Photogramm. Eng. Remote Sens. 2003, 69, 59–68. [Google Scholar] [CrossRef]
- McGlone, J.C.; Mikhail, E.; Bethel, J. Manual of Photogrammetry; American Society for Photogrammetry and Remote Sensing: Bethesda, MD, USA, 2004. [Google Scholar]
- Bartier, P.M.; Keller, C.P. Multivariate Interpolation to Incorporate Thematic Surface Data Using Inverse Distance Weighting (IDW). Comput. Geosci. 1996, 22, 795–799. [Google Scholar] [CrossRef]















| Dataset | Image | Date of Acquisition | Image Center Latitude | Image Center Longitude | Column GSD | Row GSD | Average Bisector Elevation Angle | Average Convergence Angle |
|---|---|---|---|---|---|---|---|---|
| A | 1 | 25 September 2017 | 37.66915019° | 126.69710367° | 0.636 m | 0.738 m | 58.63° | 3.48° |
| 2 | 30 October 2017 | 37.67087524° | 126.70190406° | 0.648 m | 0.722 m | |||
| B | 1 | 19 January 2018 | 37.44616080° | 126.67440106° | 0.622 m | 0.692 m | 62.21° | 22.05° |
| 2 | 27 January 2018 | 37.47981407° | 126.66328898° | 0.662 m | 0.703 m | |||
| C | 1 | 15 April 2016 | 34.52600627° | 127.22193512° | 0.542 m | 0.539 m | 80.29° | 16.37° |
| 2 | 19 August 2016 | 34.49270726° | 127.27720400° | 0.557 m | 0.568 m | |||
| 3 | 31 December 2016 | 34.53265698° | 127.23364734° | 0.613 m | 0.582 m | |||
| D | 1 | 8 January 2016 | 37.48699304° | 126.98696326° | 0.678 m | 0.779 m | 62.62° | 19.98° |
| 2 | 15 February 2017 | 37.51165646° | 126.94987635° | 0.702 m | 0.672 m | |||
| 3 | 23 February 2017 | 37.51529077° | 126.94700648° | 0.578 m | 0.620 m | |||
| 4 | 24 February 2017 | 37.46389359° | 126.96478021° | 0.652 m | 0.609 m |
| Dataset | Number of Images | Number of Pairs | Total Number of Feature Points | Total Number of Tie Points (After RANSAC) | Average Model Error (Initial) | Average Check Error (Initial) |
|---|---|---|---|---|---|---|
| A | 2 | 1 | 13,773 | 9669 | 21.29 pixels | 20.57 pixels |
| B | 2 | 1 | 13,878 | 4183 | 4.43 pixels | 4.08 pixels |
| C | 3 | 3 | 32,728 | 2956 | 30.71 pixels | 30.01 pixels |
| D | 4 | 6 | 83,760 | 18,796 | 37.66 pixels | 38.05 pixels |
| Iteration Count | Average Absolute Increments (Dataset A) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 11.13112 | 5.82 × 10−5 | 0.00331 | 7.16572 | 4.03 × 10−5 | 0.00085 | 7.54 × 10−5 | 4.80 × 10−6 | 14.26810 |
| 2 | 0.06689 | 4.20 × 10−7 | 2.93 × 10−5 | 0.00955 | 1.28 × 10−6 | 6.01 × 10−6 | 7.61 × 10−5 | 5.08 × 10−7 | 1.37377 |
| 3 | 0.00038 | - | - | 1.73 × 10−5 | - | - | 1.47 × 10−7 | 9.03 × 10−9 | 0.02504 |
| 4 | - | - | - | - | - | - | 1.06 × 10−7 | 7.88 × 10−9 | 3.94 × 10−5 |
| 5 | - | - | - | - | - | - | 5.25 × 10−8 | 4.13 × 10−9 | 1.03 × 10−7 |
| 6 | - | - | - | - | - | - | - | - | - |
| Iteration Count | Average Absolute Increments (Dataset B) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2.41720 | 3.57 × 10−5 | 0.00035 | 4.88137 | 0.00053 | 0.00058 | 4.80 × 10−5 | 3.80 × 10−6 | 10.41926 |
| 2 | 0.03722 | 3.32 × 10−6 | 1.25 × 10−5 | 0.01179 | 9.95 × 10−7 | 3.54 × 10−6 | 5.74 × 10−6 | 5.49 × 10−7 | 1.02884 |
| 3 | 0.00015 | - | 1.15 × 10−7 | 2.94 × 10−5 | - | - | 2.38 × 10−7 | 2.58 × 10−8 | 0.02372 |
| 4 | - | - | - | - | - | - | 1.82 × 10−7 | 2.46 × 10−8 | 0.00017 |
| 5 | - | - | - | - | - | - | 6.85 × 10−8 | 1.07 × 10−8 | 2.06 × 10−6 |
| 6 | - | - | - | - | - | - | - | - | - |
| Iteration Count | Average Absolute Increments (Dataset C) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 14.71461 | 0.00072 | 0.00044 | 12.29137 | 0.00117 | 0.00047 | 2.02 × 10−4 | 1.71 × 10−4 | 30.48027 |
| 2 | 0.23150 | 0.00014 | 9.31 × 10−5 | 0.19389 | 0.00010 | 7.45 × 10−5 | 2.94 × 10−6 | 2.01 × 10−6 | 1.49510 |
| 3 | 0.00076 | 4.70 × 10−7 | 2.43 × 10−7 | 0.00069 | 3.30 × 10−7 | 2.50 × 10−7 | 6.13 × 10−9 | 3.31 × 10−9 | 0.00389 |
| 4 | - | - | 1.00 × 10−7 | - | - | - | 8.12 × 10−9 | - | - |
| 5 | - | - | - | - | - | - | - | - | - |
| Iteration Count | Average Absolute Increments (Dataset D) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 9.40009 | 0.00082 | 0.00105 | 14.61643 | 0.00105 | 0.00421 | 2.06 × 10−4 | 2.27 × 10−4 | 27.31976 |
| 2 | 0.70476 | 1.88 × 10−5 | 0.00030 | 0.24589 | 7.9 × 10−5 | 5.01 × 10−5 | 5.53 × 10−6 | 5.08 × 10−6 | 0.92514 |
| 3 | 0.00104 | 2.75 × 10−8 | 4.35 × 10−7 | 0.00033 | 1.15 × 10−7 | - | 8.34 × 10−9 | 7.10 × 10−9 | 0.00111 |
| 4 | - | - | 1.45 × 10−7 | - | - | - | 5.32 × 10−9 | 4.12 × 10−9 | - |
| 5 | - | - | - | - | - | - | - | - | - |
| Dataset | Image | Image RPC Correction Parameter | |||||
|---|---|---|---|---|---|---|---|
| A | 1 | 9.0938 | 7.85 × 10−5 | −0.0024 | −6.7058 | 6.10 × 10−5 | −0.0011 |
| 2 | −13.1718 | −3.74 × 10−5 | 0.0042 | 7.6217 | −1.99 × 10−5 | 0.0006 | |
| B | 1 | 1.7469 | −5.20 × 10−7 | −0.0002 | 6.3413 | −0.0006 | −0.0006 |
| 2 | −3.0970 | 6.87 × 10−5 | 0.0005 | −3.3978 | 0.0005 | 0.0005 | |
| C | 1 | −17.3310 | 0.0009 | 0.0002 | −17.9893 | 0.0016 | −0.0009 |
| 2 | −4.4031 | 0.0008 | 8.50 × 10−5 | 7.3781 | 0.0013 | −0.0005 | |
| 3 | 23.1065 | −0.0008 | 0.0011 | 11.7404 | 0.0005 | −0.0001 | |
| D | 1 | 10.8340 | −0.0005 | 0.0012 | −30.8398 | 0.0011 | 0.0039 |
| 2 | 2.7666 | −0.0010 | 0.0021 | −8.5713 | 0.0014 | 0.0086 | |
| 3 | −8.4264 | −0.0008 | 0.0001 | 4.1117 | 0.0007 | −0.0029 | |
| 4 | −15.2881 | −0.0010 | 0.0016 | −15.8881 | 0.0012 | 0.0017 | |
| Dataset | Image Pair | Before Adjustment | After Adjustment | ||
|---|---|---|---|---|---|
| Model Error | Check Error | Model Error | Check Error | ||
| A | 1 and 2 | 21.29 pixels | 20.57 pixels | 1.02 pixels | 2.14 pixels |
| B | 1 and 2 | 4.43 pixels | 4.08 pixels | 0.67 pixels | 1.75 pixels |
| C | 1 and 2 | 25.81 pixels | 26.26 pixels | 1.75 pixels | 2.10 pixels |
| 1 and 3 | 41.3 pixels | 40.10 pixels | 1.27 pixels | 2.05 pixels | |
| 2 and 3 | 26.01 pixels | 25.73 pixels | 1.71 pixels | 2.57 pixels | |
| D | 1 and 2 | 50.58 pixels | 49.25 pixels | 1.40 pixels | 2.43 pixels |
| 1 and 3 | 34.12 pixels | 33.68 pixels | 1.27 pixels | 2.00 pixels | |
| 1 and 4 | 44.86 pixels | 45.32 pixels | 1.36 pixels | 2.93 pixels | |
| 2 and 3 | 28.70 pixels | 24.40 pixels | 1.08 pixels | 2.19 pixels | |
| 2 and 4 | 44.12 pixels | 44.02 pixels | 0.80 pixels | 2.31 pixels | |
| 3 and 4 | 16.87 pixels | 16.80 pixels | 0.99 pixels | 1.89 pixels | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ban, S.; Kim, T. Rational-Function-Model-Based Rigorous Bundle Adjustment for Improving the Relative Geometric Positioning Accuracy of Multiple Korea Multi-Purpose Satellite-3A Images. Remote Sens. 2024, 16, 2890. https://doi.org/10.3390/rs16162890
Ban S, Kim T. Rational-Function-Model-Based Rigorous Bundle Adjustment for Improving the Relative Geometric Positioning Accuracy of Multiple Korea Multi-Purpose Satellite-3A Images. Remote Sensing. 2024; 16(16):2890. https://doi.org/10.3390/rs16162890
Chicago/Turabian StyleBan, Seunghwan, and Taejung Kim. 2024. "Rational-Function-Model-Based Rigorous Bundle Adjustment for Improving the Relative Geometric Positioning Accuracy of Multiple Korea Multi-Purpose Satellite-3A Images" Remote Sensing 16, no. 16: 2890. https://doi.org/10.3390/rs16162890
APA StyleBan, S., & Kim, T. (2024). Rational-Function-Model-Based Rigorous Bundle Adjustment for Improving the Relative Geometric Positioning Accuracy of Multiple Korea Multi-Purpose Satellite-3A Images. Remote Sensing, 16(16), 2890. https://doi.org/10.3390/rs16162890







