Advanced GNSS Spoofing Detection: Aggregated Correlation Residue Likelihood Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. Spoofing Attack Pattern and Signal Model
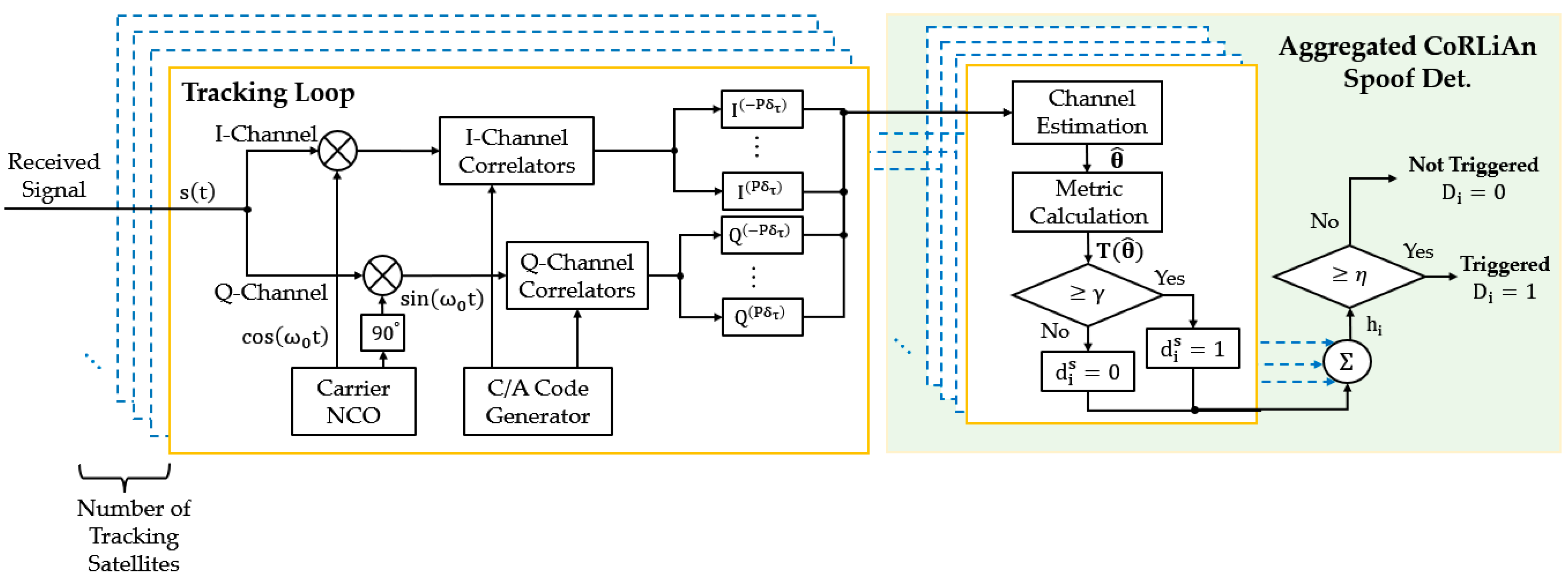
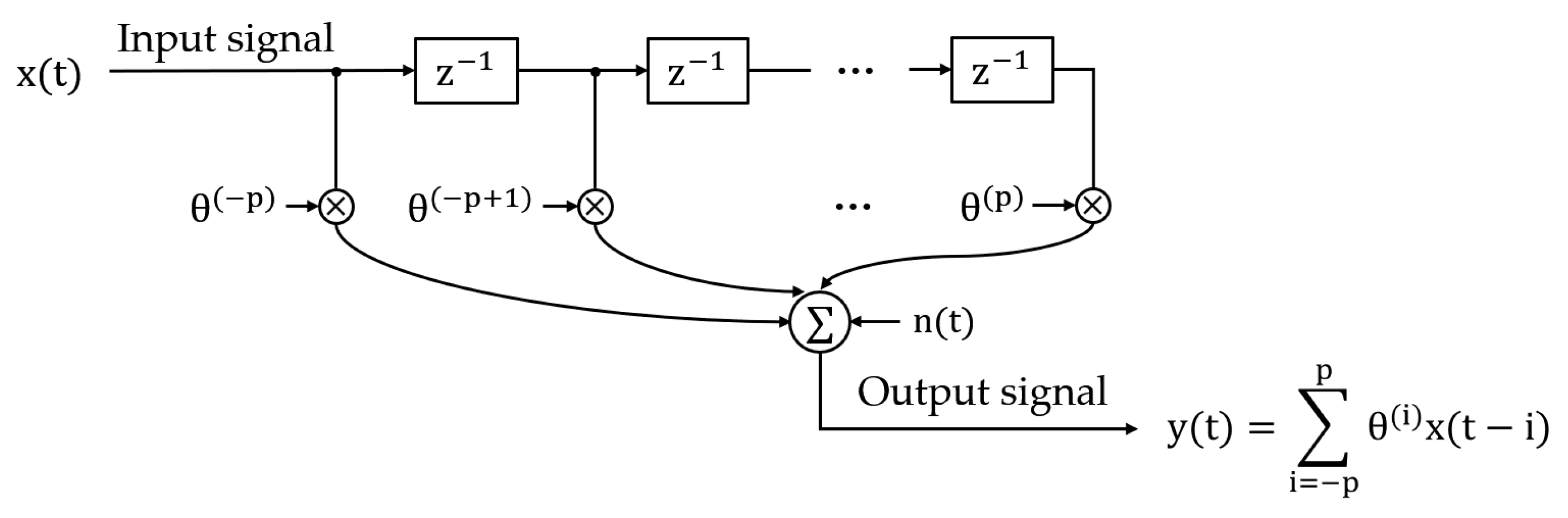
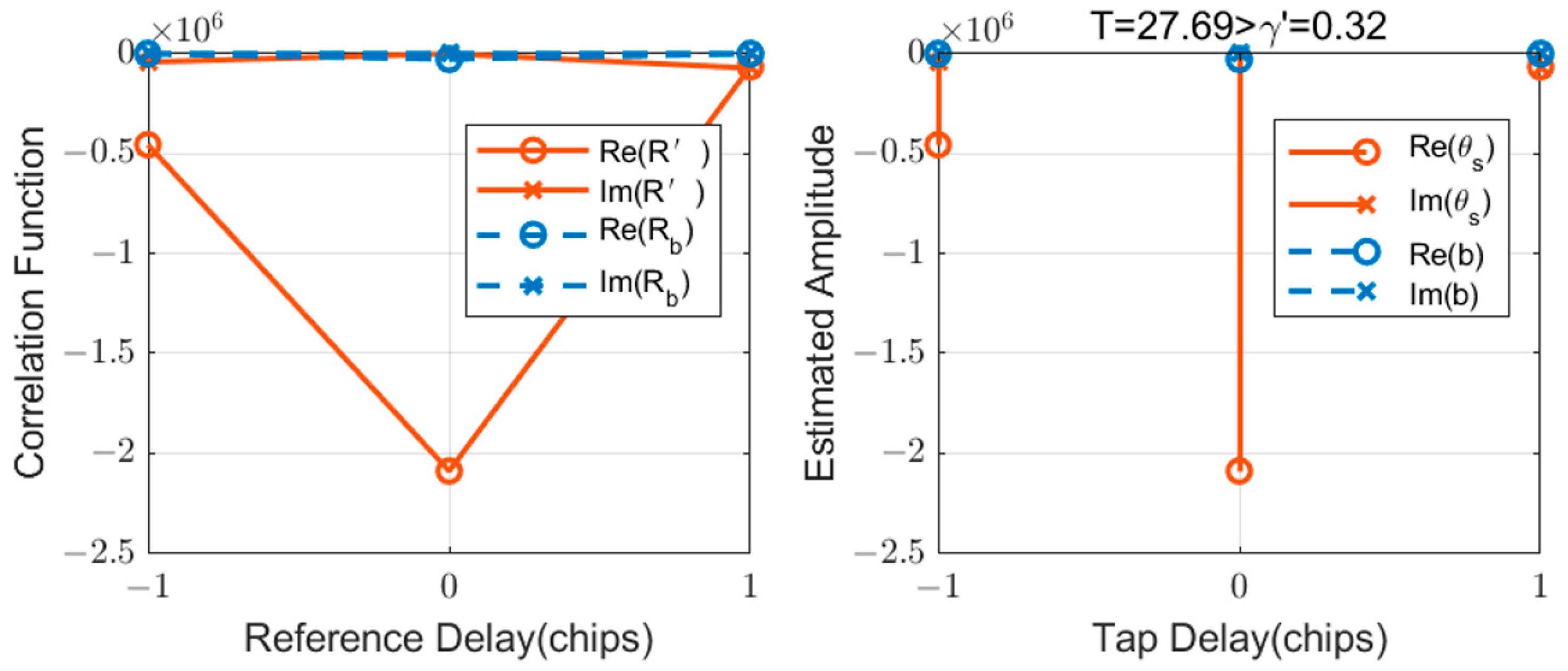
2.2. A-CoRLiAn Method
- Step 1.
- Channel estimation;
- Step 2.
- Metric computation;
- Step 3.
- Single-satellite decision-making;
- Step 4.
- Multi-satellite decision aggregation.
2.3. Theoretical Performance Analysis
2.3.1. Performance Analysis of Estimation
- A.
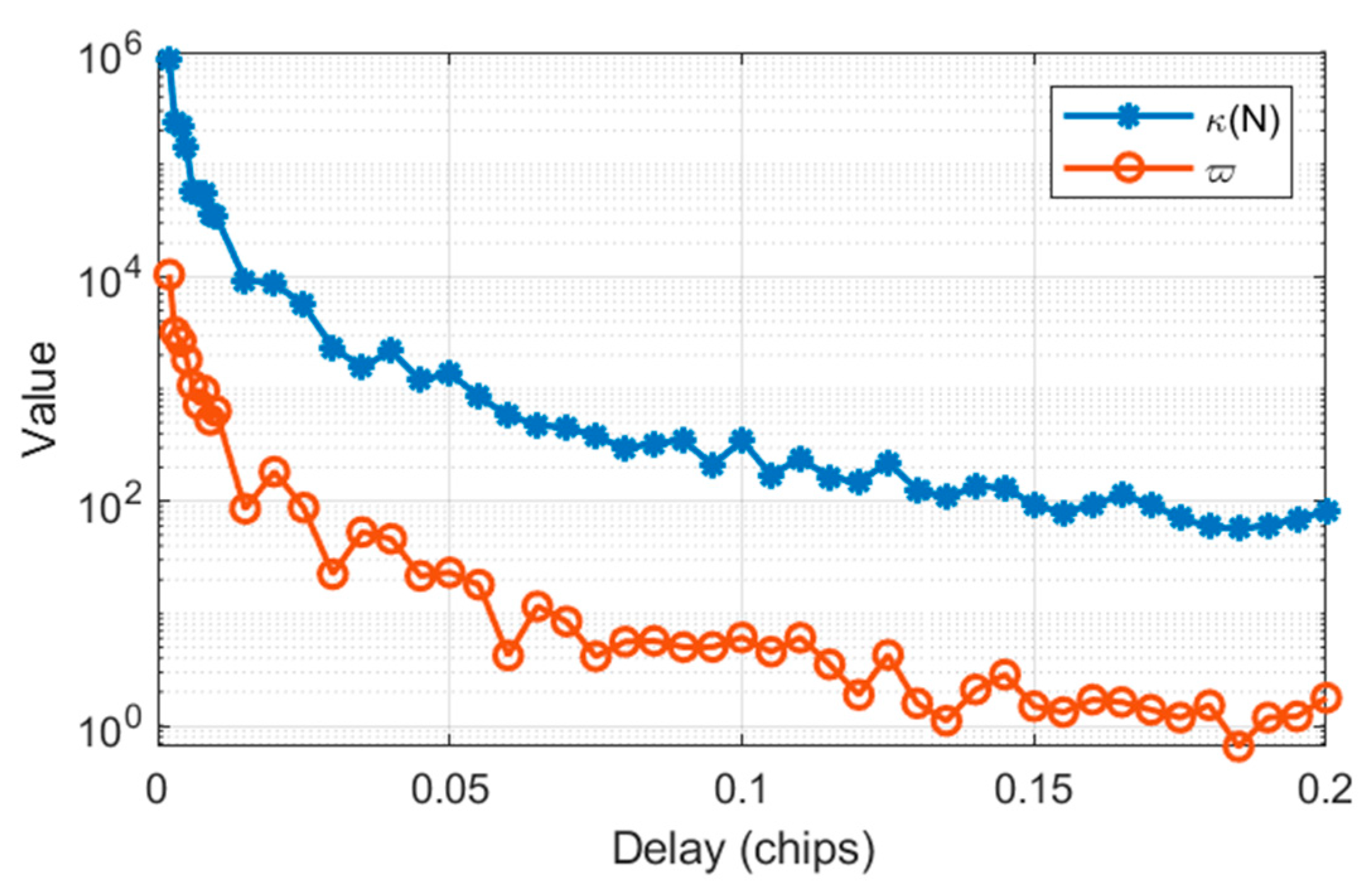
- Influence of Correlator Spacing
- B.
- Necessity of Additional Correlators
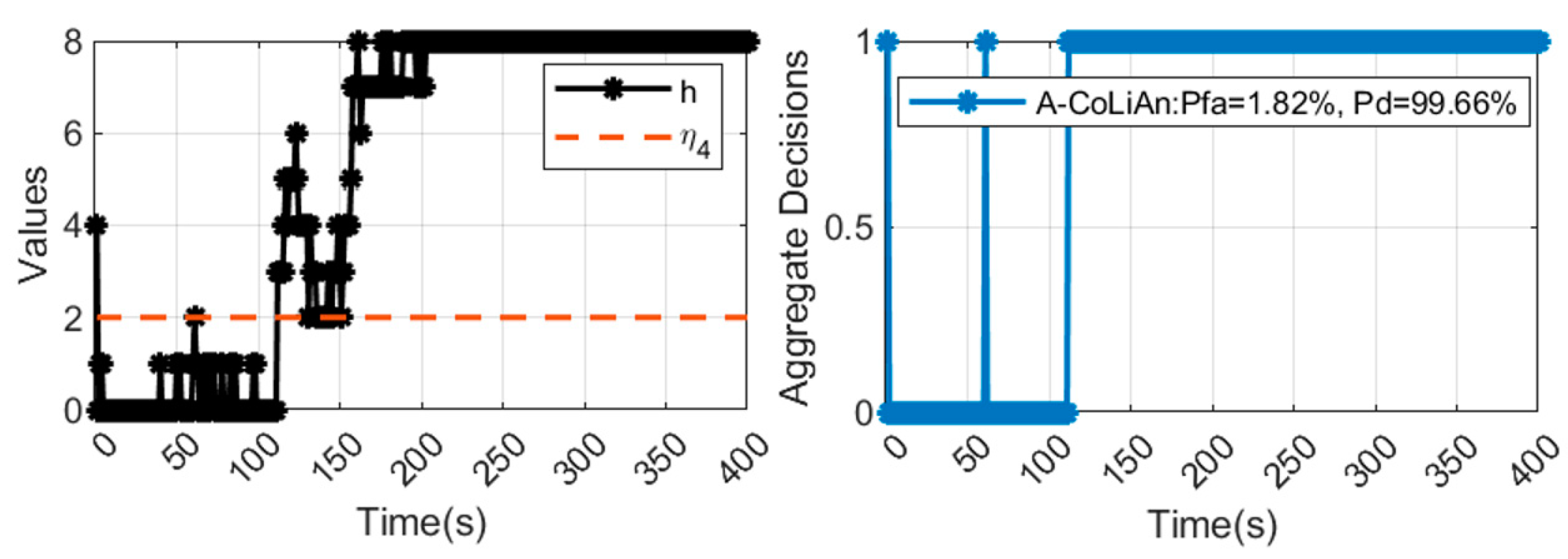
2.3.2. Performance Analysis of Aggregated Decision
2.4. Preparation for Performance Evaluation: Dataset and Analytical Methods
3. Detection Results of A-CoRLiAn Method
3.1. Performance of A-CoRLiAn Method
- A.
- Decisions of CoRLiAn
- B.
- Decisions of Aggregated CoRLiAn
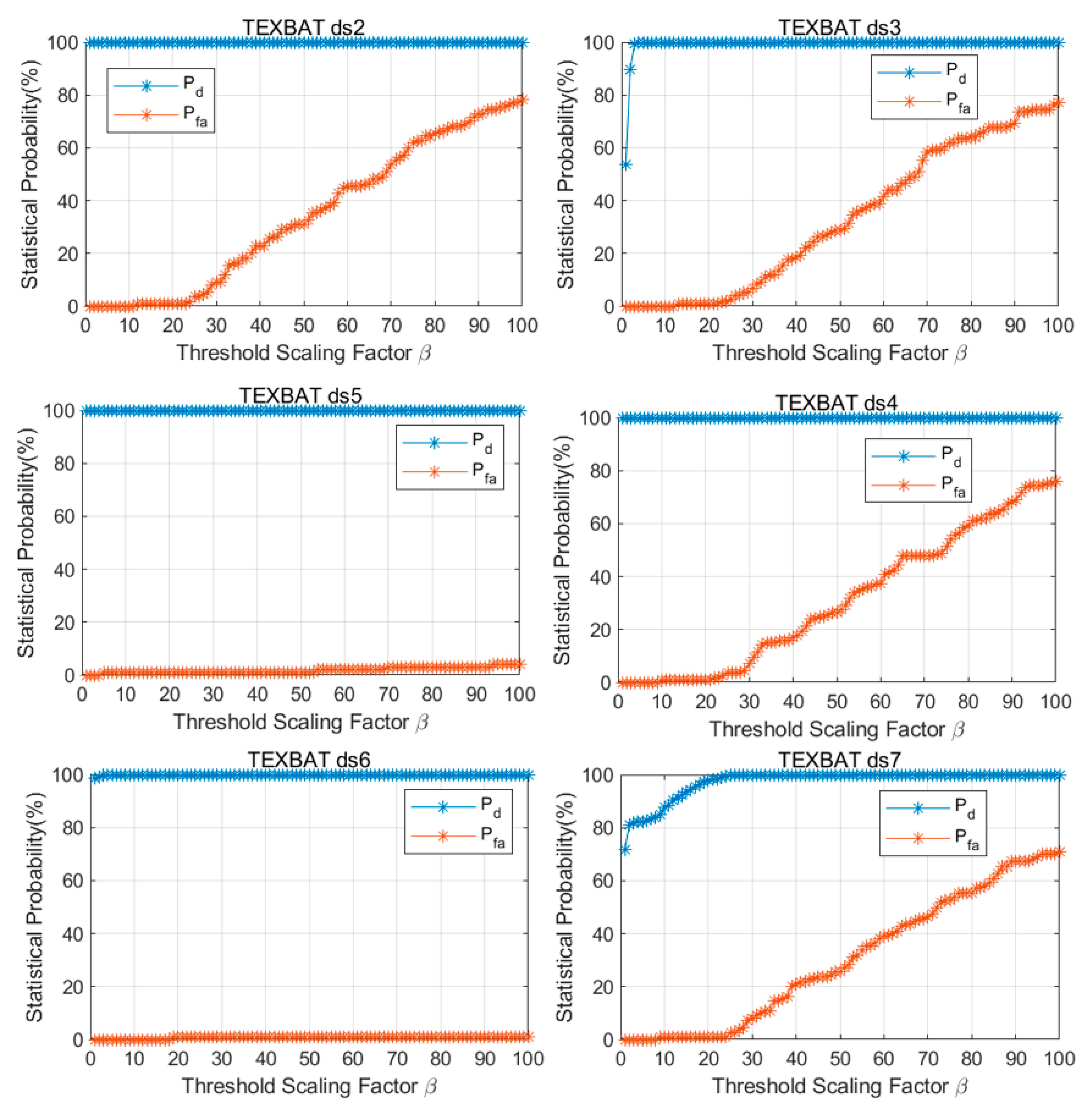
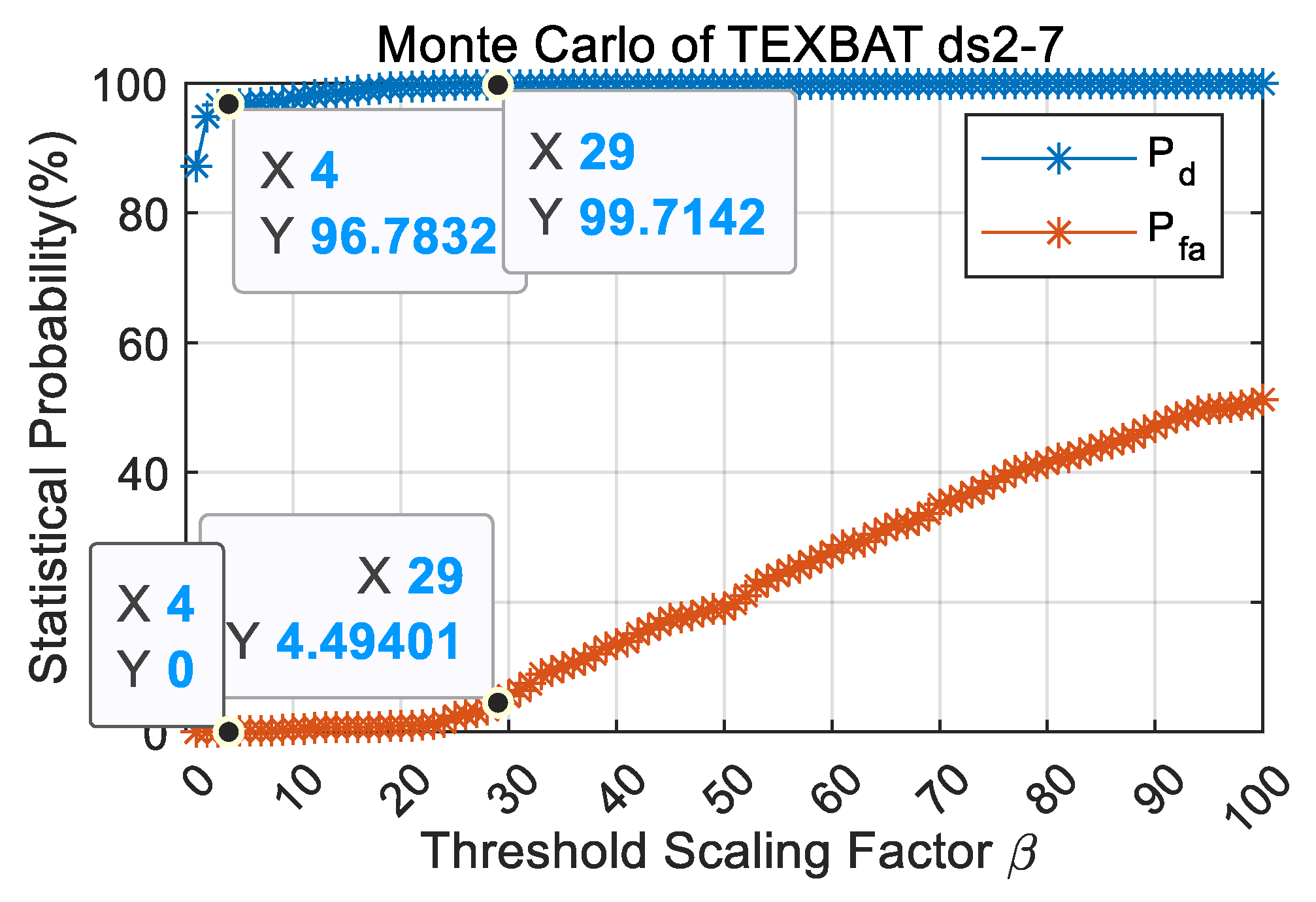
3.2. Influence of Threshold Scaling Factor
4. Discussion
4.1. Performance Analysis
4.2. Limitations and Prospects
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qi, Y. Research on GNSS Multi Spoofing Strategy Based on Software Defined Receiver. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2019. [Google Scholar]
- Jahromi, A.J.; Broumandan, A.; Nielsen, J.; Lachapelle, G. GPS spoofer countermeasure effectiveness based on signal strength, noise power, and C/N0 measurements. Int. J. Satell. Commun. Netw. 2012, 30, 181–191. [Google Scholar] [CrossRef]
- T. R. Laboratory, Texbat Data Sets 7 and 8. Available online: http://radionavlab.ae.utexas.edu/datastore/texbat/texbat_ds7_and_ds8.pdf (accessed on 6 October 2023).
- Ji, N.; Rao, Y.; Wang, X.; Zou, D.; Chen, X.; Guo, Y. Spoofing Traction Strategy Based on the Generation of Traction Code. Remote Sens. 2023, 15, 500. [Google Scholar] [CrossRef]
- Psiaki, M.L.; Humphreys, T.E. GNSS Spoofing and Detection. Proc. IEEE 2016, 104, 1258–1270. [Google Scholar] [CrossRef]
- Fernandez-Hernandez, I.; Winkel, J.; O’Driscoll, C.; Cancela, S.; Terris-Gallego, R.; López-Salcedo, J.A.; Seco-Granados, G.; Chiara, A.D.; Sarto, C.; Blonski, D.; et al. Semiassisted Signal Authentication for Galileo: Proof of Concept and Results. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 4393–4404. [Google Scholar] [CrossRef]
- Seco-Granados, G.; Gómez-Casco, D.; López-Salcedo, J.A.; Fernández-Hernández, I. Detection of replay attacks to GNSS based on partial correlations and authentication data unpredictability. GPS Solut. 2021, 25, 33. [Google Scholar] [CrossRef]
- Mao, P.R.; Yuan, H.; Chen, X.; Gong, Y.K.; Li, S.H.; Li, R.; Luo, R.D.; Zhao, G.Y.; Fu, C.A.; Xu, J.J. A GNSS Spoofing Detection and Direction-Finding Method Based on Low-Cost Commercial Board Components. Remote Sens. 2023, 15, 2781. [Google Scholar] [CrossRef]
- Xiao, L.; Li, X.; Liao, Z. GNSS Spoofing Detection with Using Linear Array. In Proceedings of the 2020 IEEE 8th International Conference on Computer Science and Network Technology (ICCSNT), Dalian, China, 20–22 November 2020; pp. 181–185. [Google Scholar]
- Neish, A.; Lo, S.; Chen, Y.H.; Enge, P.; Inst, N. Uncoupled Accelerometer Based GNSS Spoof Detection for Automobiles using Statistic and Wavelet Based Tests. In Proceedings of the 2018 31st International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2018), Miami, FL, USA, 24–28 September 2018; pp. 2938–2962. [Google Scholar]
- Kwon, K.C.; Shim, D.S. Performance Analysis of Direct GPS Spoofing Detection Method with AHRS/Accelerometer. Sensors 2020, 20, 954. [Google Scholar] [CrossRef] [PubMed]
- Varshosaz, M.; Afary, A.; Mojaradi, B.; Saadatseresht, M.; Parmehr, E.G. Spoofing Detection of Civilian UAVs Using Visual Odometry. ISPRS Int. J. Geo-Inf. 2020, 9, 6. [Google Scholar] [CrossRef]
- Qiao, Y.R.; Zhang, Y.X.; Du, X. A Vision-Based GPS-Spoofing Detection Method for Small UAVs. In Proceedings of the 2017 13th International Conference ON Computational Intelligence and Security (CIS), Hong Kong, China, 15–18 December 2017; pp. 312–316. [Google Scholar]
- Broumandan, A.; Lachapelle, G. Spoofing Detection Using GNSS/INS/Odometer Coupling for Vehicular Navigation. Sensors 2018, 18, 1305. [Google Scholar] [CrossRef]
- Vagle, N.; Broumandan, A.; Lachapelle, G. Multiantenna GNSS and Inertial Sensors/Odometer Coupling for Robust Vehicular Navigation. IEEE Internet Things J. 2018, 5, 4816–4828. [Google Scholar] [CrossRef]
- Wei, Y.; Li, H.; Lu, M. Spoofing profile estimation-based GNSS spoofing identification method for tightly coupled MEMS INS/GNSS integrated navigation system. IET Radar Sonar Navig. 2020, 14, 216–225. [Google Scholar] [CrossRef]
- Wang, S.Z.; Zhan, X.Q.; Zhai, Y.W.; Liu, B.Y. Fault Detection and Exclusion for Tightly Coupled GNSS/INS System Considering Fault in State Prediction. Sensors 2020, 20, 590. [Google Scholar] [CrossRef] [PubMed]
- Mosavi, M.R.; Nasrpooya, Z.; Moazedi, M. Advanced Anti-Spoofing Methods in Tracking Loop. J. Navig. 2016, 69, 883–904. [Google Scholar] [CrossRef]
- Cavaleri, A.; Motella, B.; Pini, M.; Fantino, M. Detection of Spoofed GPS Signals at Code and Carrier Tracking Level. In Proceedings of the 5th ESA Workshop on Satellite Navigation Technologies/European Workshop on GNSS Signals and Signal Processing (NAVITEC), European Space Res & Technol Ctr, Noordwijk, The Netherlands, 8–10 December 2010. [Google Scholar]
- Yang, Y.C.; Li, H.; Lu, M.Q. Performance Assessment of Signal Quality Monitoring Based GNSS Spoofing Detection Techniques. In Proceedings of the 6th China Satellite Navigation Conference (CSNC), Xi’an, China, 13–15 May 2015; pp. 783–793. [Google Scholar]
- Dehghanian, V.; Nielsen, J.; Lachapelle, G. GNSS Spoofing Detection Based on Signal Power Measurements: Statistical Analysis. Int. J. Navig. Obs. 2012, 2012, 313527. [Google Scholar] [CrossRef]
- Gao, Y.; Li, H.; Lu, M.Q.; Feng, Z. Intermediate Spoofing Strategies and Countermeasures. Tsinghua Sci. Technol. 2013, 18, 599–605. [Google Scholar]
- Phelts, R.E. Multicorrelator Techniques for Robust Mitigation of Threats to GPS Signal Quality. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2001. [Google Scholar]
- Mubarak, O.M.; Dempster, A.G. Analysis of early late phase in single-and dual-frequency GPS receivers for multipath detection. GPS Solut. 2010, 14, 381–388. [Google Scholar] [CrossRef]
- Sun, C.; Cheong, J.W.; Dempster, A.G.; Demicheli, L.; Cetin, E.; Zhao, H.; Feng, W. Moving variance-based signal quality monitoring method for spoofing detection. GPS Solut. 2018, 22, 83. [Google Scholar] [CrossRef]
- Gamba, M.T.; Truong, M.D.; Motella, B.; Falletti, E.; Ta, T.H. Hypothesis testing methods to detect spoofing attacks: A test against the TEXBAT datasets. GPS Solut. 2017, 21, 577–589. [Google Scholar] [CrossRef]
- Miralles, D.; Levigne, N.; Bornot, A.; Rouquette, P.; Akos, D.M.; Chen, Y.H.; La, S.; Walter, T. An Assessment of GPS Spoofing Detection Via Radio Power and Signal Quality Monitoring for Aviation Safety Operations. IEEE Intell. Transp. Syst. Mag. 2020, 12, 136–146. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, L.J.; Wu, R.B. GNSS Spoofing Detection Based on Power Monitoring Combined with SQM. J. Signal Process. 2023, 39, 505–515. [Google Scholar]
- Wesson, K.D.; Gross, J.N.; Humphreys, T.E.; Evans, B.L. GNSS Signal Authentication Via Power and Distortion Monitoring. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 739–754. [Google Scholar] [CrossRef]
- Gross, J.N.; Kilic, C.; Humphreys, T.E. Maximum-Likelihood Power-Distortion Monitoring for GNSS-Signal Authentication. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 469–475. [Google Scholar] [CrossRef]
- Zhou, S.; Ou, G.; Tang, X.M. Clustering sparse fitting scheme for GNSS multipath channel simulation. J. Natl. Univ. Def. Technol. 2023, 45, 87–94. [Google Scholar]
- Kay, S. Fundamentals of Statistical Signal Processing: Estimation Theory; Prentice-Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Kay, S. Fundamentals of Statistical Signal Processing: Detection Theory; Prentice-Hall: Englewood Cliffs, NJ, USA, 1998. [Google Scholar]
- Blanco-Delgado, N.; Nunes, F.D. Multipath Estimation in Multicorrelator GNSS Receivers using the Maximum Likelihood Principle. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 3222–3233. [Google Scholar] [CrossRef]
- Humphreys, T.E.; Bhatti, J.A.; Shepard, D.; Wesson, K. The Texas Spoofing Test Battery: Toward a Standard for Evaluating GPS Signal Authentication Techniques. In Proceedings of the 25th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS 2012), Nashville, TN, USA, 17–21 September 2012. [Google Scholar]
- T. R. Laboratory, Texas Spoofing Test Battery (TEXBAT). Available online: http://radionavlab.ae.utexas.edu/texbat (accessed on 6 October 2023).
- Sun, C.; Cheong, J.W.; Dempster, A.G.; Zhao, H.; Feng, W. GNSS Spoofing Detection by Means of Signal Quality Monitoring (SQM) Metric Combinations. IEEE Access 2018, 6, 66428–66441. [Google Scholar] [CrossRef]
- Sun, C.; Cheong, J.W.; Dempster, A.G.; Zhao, H.; Bai, L.; Feng, W. Robust Spoofing Detection for GNSS Instrumentation Using Q-Channel Signal Quality Monitoring Metric. IEEE Trans. Instrum. Meas. 2021, 70, 1–15. [Google Scholar] [CrossRef]
- Wang, W.; Gong, J. GNSS spoofing detection algorithm based on composite SQM variance#br#. J. Civil Aviat. Univ. China 2020, 38, 7–12. [Google Scholar]
- Turner, M.; Wimbush, S.; Enneking, C.; Konovaltsev, A. Spoofing Detection by Distortion of the Correlation Function. In Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, OR, USA, 20–23 April 2020; pp. 566–574. [Google Scholar]
- Wang, W.Y.; Gong, J.; Wang, J.M. GNSS spoofing interference detection based on variance of SCB. Syst. Eng. Electron. 2021, 43, 2254–2262. [Google Scholar]
- Wang, W.Y.; Li, N.; Wu, R.; Closas, P. Detection of Induced GNSS Spoofing Using S-Curve-Bias. Sensors 2019, 19, 922. [Google Scholar] [CrossRef]
- Zhu, R.C.; Wang, W.Y. SCS-based multi-star joint induced spoofing detection algorithm. Mod. Electron. Tech. 2023, 46, 1–8. [Google Scholar]
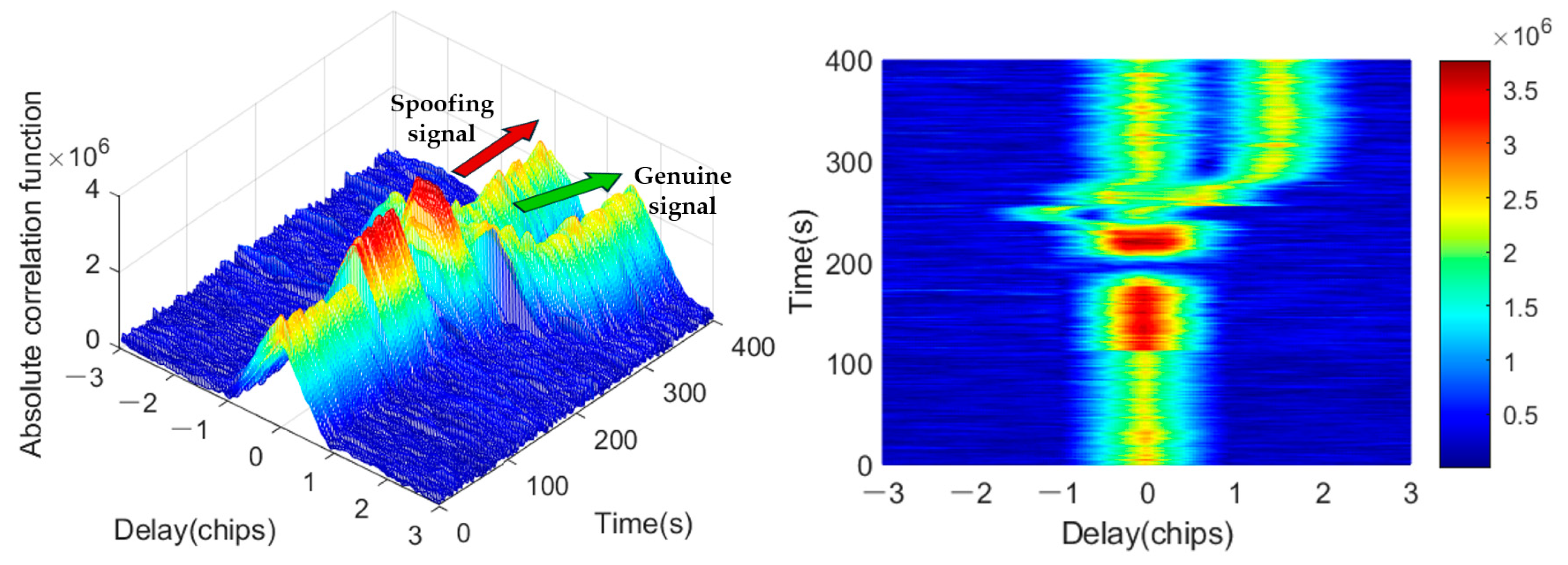




| No. | Spoofing Type | Platform Mobility | Power Adv. | Frequency Lock | Entry Time (s) |
|---|---|---|---|---|---|
| ds2 | Time | Static | Overpowered | Unlocked | 110.1 |
| ds3 | Time | Matched | Locked | 118.9 | |
| ds4 | Position | Matched | Locked | 113.8 | |
| ds5 | Time | Dynamic | Overpowered | Unlocked | 100 |
| ds6 | Position | Matched | Locked | 100 | |
| ds7 | Time | Static | Matched | Locked | 110 |
| Mode | Prob. | ds2 | ds3 | ds4 | ds5 | ds6 | ds7 | Monte Carlo (ds2–ds7) |
|---|---|---|---|---|---|---|---|---|
| Low Sensitivity | 0% | 0% | 0% | 0% | 0% | 0% | 0% | |
| 100.0% | 99.65% | 99.65% | 99.67% | 99.67% | 82.07% | 96.78% | ||
| High Sensitivity | 1.82% | 1.69% | 2.65% | 1% | 1% | 1.82% | 1.66% | |
| 100.0% | 99.65% | 99.65% | 99.67% | 99.67% | 99.66% | 99.71% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, N.; Rao, Y.; Wang, X.; Zou, D. Advanced GNSS Spoofing Detection: Aggregated Correlation Residue Likelihood Analysis. Remote Sens. 2024, 16, 2868. https://doi.org/10.3390/rs16152868
Ji N, Rao Y, Wang X, Zou D. Advanced GNSS Spoofing Detection: Aggregated Correlation Residue Likelihood Analysis. Remote Sensing. 2024; 16(15):2868. https://doi.org/10.3390/rs16152868
Chicago/Turabian StyleJi, Ning, Yongnan Rao, Xue Wang, and Decai Zou. 2024. "Advanced GNSS Spoofing Detection: Aggregated Correlation Residue Likelihood Analysis" Remote Sensing 16, no. 15: 2868. https://doi.org/10.3390/rs16152868
APA StyleJi, N., Rao, Y., Wang, X., & Zou, D. (2024). Advanced GNSS Spoofing Detection: Aggregated Correlation Residue Likelihood Analysis. Remote Sensing, 16(15), 2868. https://doi.org/10.3390/rs16152868





