Ionograms Trace Extraction Method Based on Multiscale Transformer Network
Abstract
1. Introduction
2. Related Work
2.1. Echo Trace Extraction of Ionograms
2.2. Transformer Neural Network
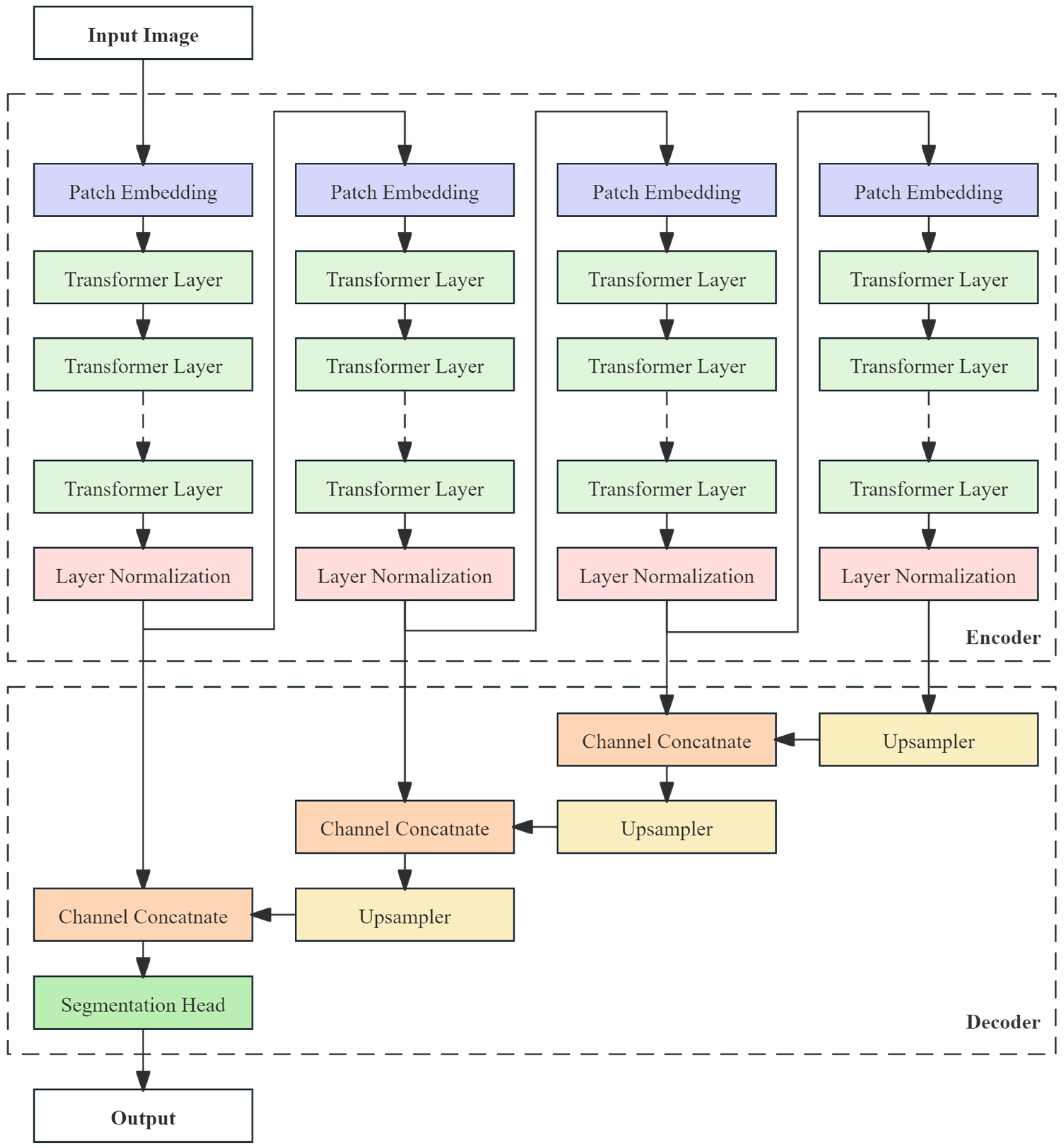
3. Methodology
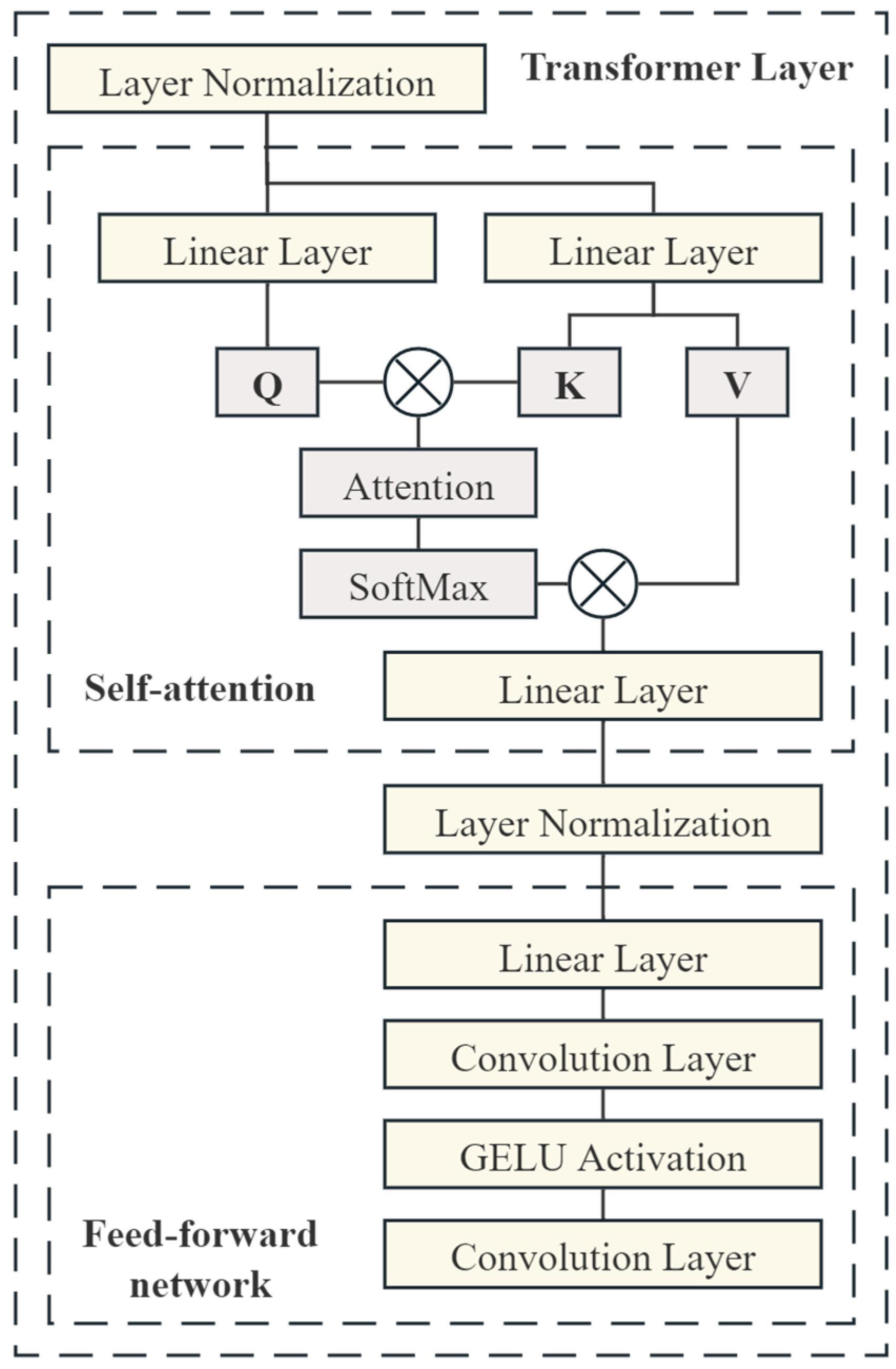
3.1. Multiscale Transformer Encoder
- (1)
- Patch Embedding Layer
- (2)
- Transformer Layer
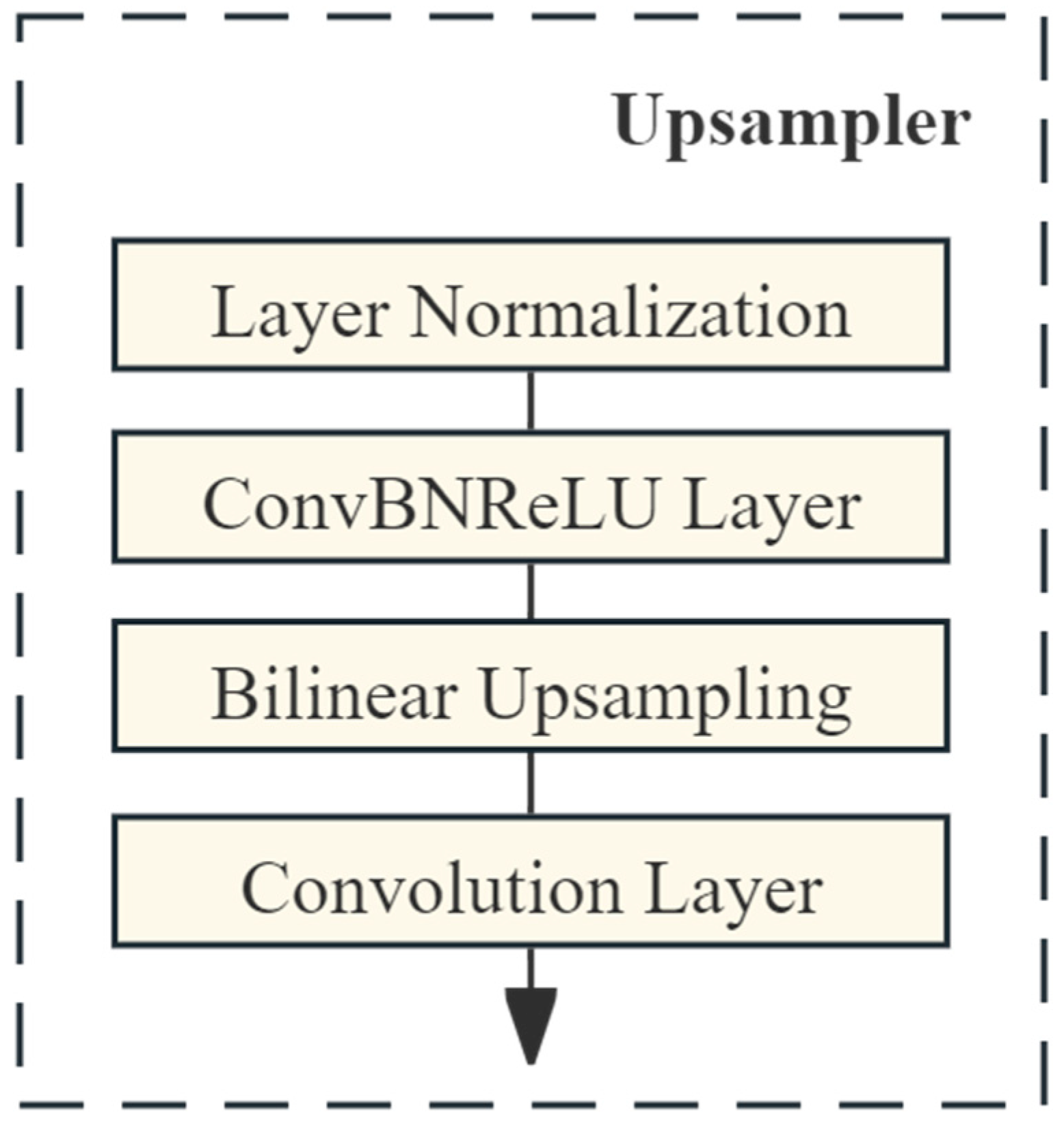
3.2. Multiscale Decoder
- (1)
- Up-sampler
- (2)
- Semantic segmentation head
3.3. Loss Function
- (1)
- Cross-Entropy Loss Function
- (2)
- OhemCrossEntropy loss function
4. Experiments and Analysis
4.1. System Description
4.2. Dataset
4.3. Experiment Setup
4.3.1. State-of-the-Art Methods
- (1)
- FCN (Fully Convolutional Network): FCN is a pioneering work in the field of semantic segmentation that replaces the fully connected layer with a convolutional layer, enabling the network to accept input images of arbitrary size and output segmentation maps of corresponding size [7].
- (2)
- U-Net: U-Net is a popular network for medical image segmentation with a symmetric U-shaped structure that combines deep features with shallow features through jump connections to preserve edge information [9].
- (3)
- CCNet (Criss-Cross Network): CCNet captures long-distance dependencies between features by means of the Recurrent Criss-Cross Attention Module (RCCA), which helps to provide denser contextual information and thus aids in image understanding [10].
- (4)
- DeepLabV3+: DeepLabV3+ uses Atrous Convolution and Spatial Pyramid Pooling (ASPP) modules in its encoder to introduce multiscale information. In addition, it introduces a decoder module to improve the accuracy of the segmentation boundaries by fusing the underlying and higher-level features [30].
- (5)
- EncNet (Context Encoding Network): EncNet introduces the Context Encoding Module (CEM) on top of the pre-trained ResNet to strengthen the network by utilizing the null convolution to better utilize the global context information [31].
- (6)
- OCRNet (Occlusion Reasoning Network): OCRNet deals with the occlusion problem in the scene by introducing an occlusion inference mechanism, which improves the accuracy of segmentation by learning the relationship between the occluded and non-occluded regions [32].
- (7)
- PSPNet (Pyramid Scene Parsing Network): PSPNet uses Pyramid Scene Parsing Pooling (PSPNet) to capture contextual information at different scales, which helps the model to understand the scene at different scales [33].
- (8)
- SETR (Segmentation Transformer): SETR applies the Transformer architecture to semantic segmentation, capturing global dependencies through a self-attention mechanism while using an encoder–decoder structure to process image sequences [34].
4.3.2. Implementation Details
4.3.3. Evaluation Indicators
- (1)
- mIoU (mean intersection union): mIoU calculates the IoU (intersection and concurrency ratio) of each category and then takes the average of these IoUs as a comprehensive index, which can reflect the segmentation effect of the model on different categories. The result ranges from 0 to 1, and the closer it is to 1, the higher the accuracy rate. Its specific calculation formula is as follows:where TP denotes True Positive, TN denotes True Negative, FP denotes False Positive, and FN denotes False Negative, denoting different categories.
- (2)
- Kappa coefficient (Cohen’s Kappa): The principle of Kappa coefficient is to measure the degree of consistency between two evaluators (or evaluation methods) in categorizing the same dataset, not only considering the actual consistency (i.e., the proportion of the two evaluators who give the same classification), but also considering the random consistency (i.e., the proportion of consistency that would be expected in a random situation), taking the range of values from −1 (complete inconsistency) to 1 (complete consistency), with 0 indicating random consistency. The process of calculating the Kappa coefficient can be expressed as follows:where and denote the observed consistency proportion and the desired consistency proportion, respectively.
- (3)
- Dice coefficient: The Dice coefficient serves as a valuable statistical metric for quantifying the degree of similarity between two sets, particularly in the context of evaluating the alignment between a model’s segmentation predictions and the actual annotations. It is calculated by taking the ratio of the 2-fold sum of the intersection (overlap) between the binary images—representing the model’s segmentation (foreground and background)—and the true binary labeled images. This coefficient provides a measure that encapsulates both the accuracy and the completeness of the segmentation, with the computational formula given by the following:
- (4)
- AUC-ROC (area under the receiver operating characteristic curve): AUC-ROC is defined as the area under the ROC curve, which provides a single metric to assess the overall performance of the classifier. The value of AUC ranges from 0 to 1, where 1 indicates a perfect classifier (i.e., that correctly distinguishes between positive and negative samples in all cases), 0.5 indicates a random guess, and less than 0.5 indicates a classifier that does not perform as well as a random guess. The AUC-ROC formulation does not directly involve the semantic segmentation of images, but rather calculates the area under the ROC curve by the following steps: (i) calculating the TPR and the FPR for different thresholds; (ii) in the ROC space (FPR vs. TPR); (iii) plotting a point for each threshold (FPR, TPR); and (iv) calculating the area under the curve formed by these points, which is the AUC value.
4.4. Experimental Results
4.4.1. Comparison of Trace Extraction Performance
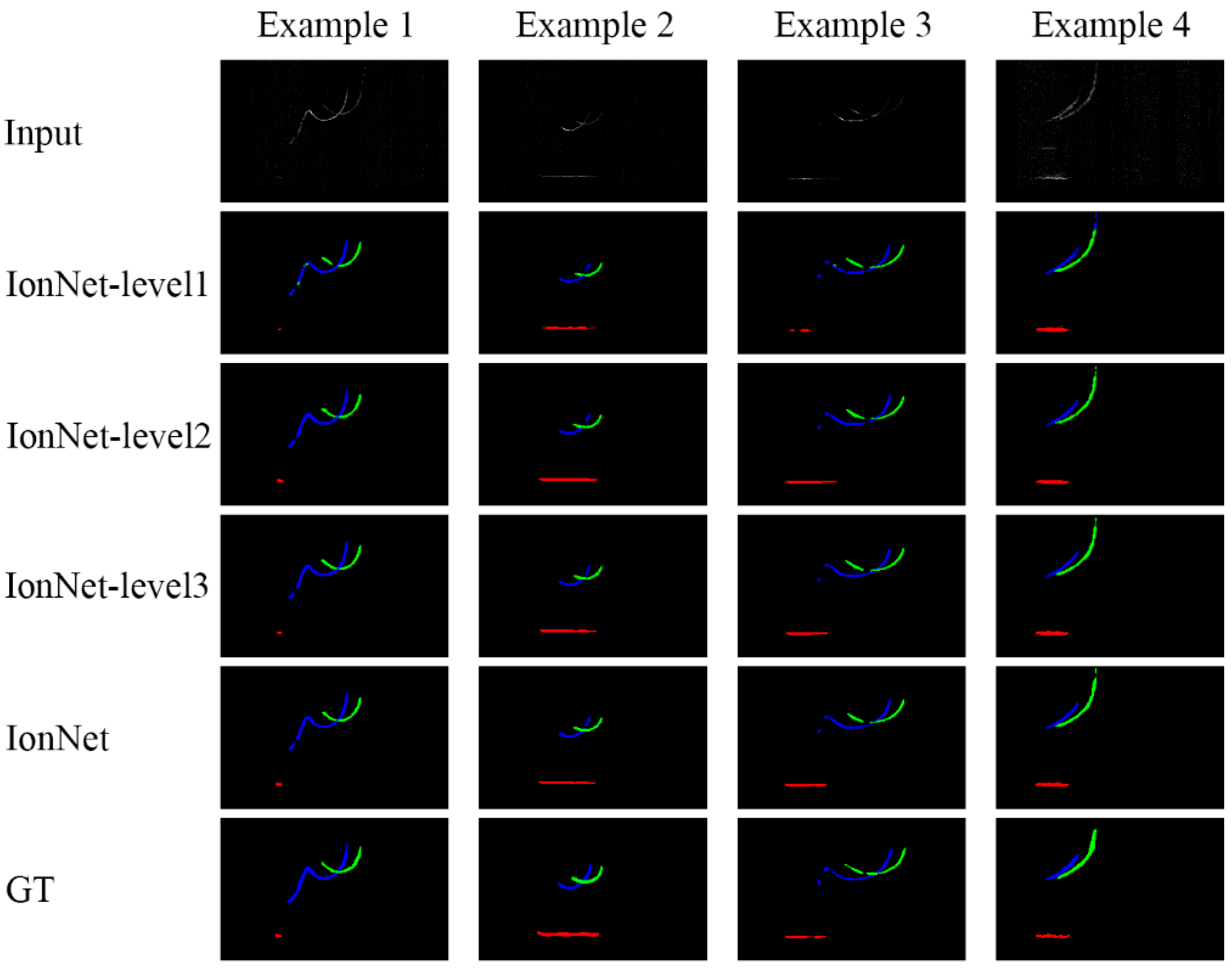
4.4.2. Ablation Analysis
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- John, M. Goodman the Ionosphere. In Space Weather & Telecommunications; Kluwer Academic Publishers: Boston, MA, USA, 2005; pp. 81–173. [Google Scholar]
- Davies, K. Ionospheric Radio; P. Peregrinus on behalf of the Institution of Electrical Engineers: London, UK, 1989; ISBN 086341186X. [Google Scholar]
- Reinisch, B.W.; Xueqin, H. Automatic Calculation of Electron Density Profiles from Digital Ionograms: 1. Automatic O and X Trace Identification for Topside Ionograms. Radio Sci. 1982, 17, 421–434. [Google Scholar] [CrossRef]
- Reinisch, B.W.; Xueqin, H. Automatic Calculation of Electron Density Profiles from Digital Ionograms: 3. Processing of Bottomside Ionograms. Radio Sci. 1983, 18, 477–492. [Google Scholar] [CrossRef]
- Xueqin, H.; Reinisch, B.W. Automatic Calculation of Electron Density Profiles from Digital Ionograms: 2. True Height Inversion of Topside Ionograms with the Profile-fitting Method. Radio Sci. 1982, 17, 837–844. [Google Scholar] [CrossRef]
- Bilitza, D.; Pezzopane, M.; Truhlik, V.; Altadill, D.; Reinisch, B.W.; Pignalberi, A. The International Reference Ionosphere Model: A Review and Description of an Ionospheric Benchmark. Rev. Geophys. 2022, 60, e2022RG000792. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Yuille DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 834–848. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Huang, Z.; Wang, X.; Wei, Y.; Huang, L.; Shi, H.; Liu, W.; Huang, T.S. CCNet: Criss-Cross Attention for Semantic Segmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Lu, H. Study on Automatic Scaling of E, Es in Ionogram Based on Image Processing; Ocean University of China: Qingdao, China, 2013. [Google Scholar]
- Xu, G. Study on Parameters Extraction in Ionogram Based on Image Processing; Ocara University of China: Qingdao, China, 2014. [Google Scholar]
- Guo, W.; Sun, X.; Ji, Y.; Jia, X. Ionospheric TEC Prediction Based on QPSO-LSTM Model. Chin. J. Space Sci. 2024. [Google Scholar]
- Ding, Z. Studies on Autoscaling and Analysis of Ionograms; Wuhan Institute of Physics and Mathematics & Institute of Geology and Geophysics, Chinese Academy of Sciences: Wuhan, China, 2006. [Google Scholar]
- Jiang, C.; Yang, G.; Zhao, Z.; Zhang, Y.; Zhu, P.; Sun, H.; Zhou, C. A Method for the Automatic Calculation of Electron Density Profiles from Vertical Incidence Ionograms. J. Atmos. Sol.-Terr. Phys. 2014, 107, 20–29. [Google Scholar] [CrossRef]
- Jiang, C.; Liu, Z.; Zhao, C.; Liu, T.; Yang, G.; Shen, H.; Huang, W. A Regional Model of Topside Ionospheric Effective Scale Heights Derived from Ionosonde and GNSS TEC. Space Weather 2023, 21, e2023SW003515. [Google Scholar] [CrossRef]
- Wu, R. Automatic Scaling of F Layer for Ionogram Based on BP Neural Network; South-Central University for Nationalities: Wuhan, China, 2015. [Google Scholar]
- Mochalov, V.; Mochalova, A. Application of Deep Learning to Recognize Ionograms. In Proceedings of the 2019 Russian Open Conference on Radio Wave Propagation (RWP), Kazan, Russia, 1–6 July 2019; pp. 477–479. [Google Scholar]
- Xiao, Z.; Wang, J.; Li, J.; Zhao, B.; Hu, L.; Liu, L. Deep-Learning for Ionogram Automatic Scaling. Adv. Space Res. 2020, 66, 942–950. [Google Scholar] [CrossRef]
- Luwanga, C.; Fang, T.; Chandran, A.; Lee, Y. Automatic Spread-F Detection Using Deep Learning. Radio Sci. 2022, 57, 1–16. [Google Scholar] [CrossRef]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer Using Shifted Windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image Is Worth 16x16 Words: Transformers for Image Recognition at Scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- He, K.; Chen, X.; Xie, S.; Li, Y.; Dollár, P.; Girshick, R. Masked Autoencoders Are Scalable Vision Learners. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022. [Google Scholar]
- Jaegle, A.; Gimeno, F.; Brock, A.; Zisserman, A.; Vinyals, O.; Carreira, J. Perceiver: General Perception with Iterative Attention. In Proceedings of the International Conference on Machine Learning, Online, 18–24 July 2021. [Google Scholar]
- Fan, H.; Xiong, B.; Mangalam, K.; Li, Y.; Yan, Z.; Malik, J.; Feichtenhofer, C. Multiscale Vision Transformers. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021. [Google Scholar]
- Chen, C.-F.; Fan, Q.; Panda, R. CrossViT: Cross-Attention Multi-Scale Vision Transformer for Image Classification. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021. [Google Scholar]
- Shao, K.; Wang, M.; Wang, G. Transformer-Based Multiscale Remote Sensing Semantic Segmentation Network. CAAI Trans. Intell. Syst. 2024. [Google Scholar]
- Han, S.; Guo, W.; Liu, P.; Wang, T.; Wang, C.; Fang, Q.; Yang, J.; Li, L.; Liu, D.; Huang, J. Chaotic Coding for Interference Suppression of Digital Ionosonde. Remote Sens. 2023, 15, 3747. [Google Scholar] [CrossRef]
- Jin, M.; Guo, W.; Liu, P.; Wang, C. Design of Digital Control System for High-Performance Ionosonde Based on FPGA. Chin. J. Space Sci. 2021, 41, 580–588. [Google Scholar] [CrossRef]
- Chen, L.-C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-Decoder with Atrous Separable Convolution for Semantic Image Segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Zhang, H.; Dana, K.; Shi, J.; Zhang, Z.; Wang, X.; Tyagi, A.; Agrawal, A. Context Encoding for Semantic Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Yuan, Y.; Chen, X.; Chen, X.; Wang, J. Segmentation Transformer: Object-Contextual Representations for Semantic Segmentation. arXiv 2019, arXiv:1909.11065. [Google Scholar]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid Scene Parsing Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Zheng, S.; Lu, J.; Zhao, H.; Zhu, X.; Luo, Z.; Wang, Y.; Fu, Y.; Feng, J.; Xiang, T.; Torr, P.H.S.; et al. Rethinking Semantic Segmentation from a Sequence-to-Sequence Perspective with Transformers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021. [Google Scholar]






| Item | Specification |
|---|---|
| Antenna | A pair of orthogonal Δ |
| Transmitted peak power | 500 W |
| Coding sequence | 40-bit Bernoulli or Barker-like |
| Coding chip width | 10 μs |
| Operating frequency | 1–30 MHz |
| Frequency step | 25 kHz, 50 kHz, 100 kHz |
| Receiver bandwidth | 100 kHz |
| IF | 70 MHz |
| ADC sampling | 40 MHz |
| Coherent accumulation times | 100 |
| Detecting range | 67.5–560.1 km |
| Range resolution | 1.5 km |
| Models | mIoU↑ | Kappa↑ | Dice↑ | AUC-ROC↑ | Para. Cnt↓ | Flops↓ |
|---|---|---|---|---|---|---|
| FCN | 0.5586 | 0.7324 | 0.6320 | 0.8496 | 65.93 M | 14.61 G |
| U-Net | 0.7167 | 0.7738 | 0.8253 | 0.9988 | 13.40 M | 19.42 G |
| CCNet | 0.5689 | 0.5770 | 0.6960 | 0.9948 | 66.55 M | 43.48 G |
| DeepLabV3+ | 0.7133 | 0.7656 | 0.8227 | 0.9757 | 45.83 M | 29.99 G |
| EncNet | 0.5163 | 0.4933 | 0.6401 | 0.9964 | 60.48 M | 39.21 G |
| OCRNet | 0.7246 | 0.7779 | 0.8314 | 0.9927 | 70.45 M | 10.12 G |
| PSPNet | 0.4955 | 0.4601 | 0.6165 | 0.9969 | 86.94 M | 53.69 G |
| SETR | 0.6092 | 0.6395 | 0.7346 | 0.9977 | 306.7 M | 56.99 G |
| IonNet (ours) | 0.7380 | 0.7945 | 0.8414 | 0.9990 | 42.19 M | 5.68 G |
| Models | Background mIoU↑ | E Layer mIoU↑ | F Layer O Trace mIoU↑ | F Layer X Trace mIoU↑ |
|---|---|---|---|---|
| FCN | 0.9955 | 0 | 0.6169 | 0.6221 |
| U-Net | 0.9963 | 0.6598 | 0.6037 | 0.6069 |
| CCNet | 0.9934 | 0.5234 | 0.3773 | 0.3816 |
| DeepLabV3+ | 0.9958 | 0.6627 | 0.5937 | 0.6011 |
| EncNet | 0.9927 | 0.4754 | 0.3001 | 0.2971 |
| OCRNet | 0.9962 | 0.6654 | 0.6209 | 0.6160 |
| PSPNet | 0.9924 | 0.4524 | 0.2691 | 0.2681 |
| SETR | 0.9943 | 0.5684 | 0.4312 | 0.4430 |
| IonNet (ours) | 0.9965 | 0.6745 | 0.6388 | 0.6425 |
| Models | mIoU↑ | Kappa↑ | Dice↑ | AUC-ROC↑ |
|---|---|---|---|---|
| IonNet-level1 | 0.6548 | 0.7436 | 0.7755 | 0.9972 |
| IonNet-level2 | 0.7251 | 0.7853 | 0.8319 | 0.9988 |
| IonNet-level3 | 0.7378 | 0.7941 | 0.8412 | 0.9990 |
| IonNet | 0.7380 | 0.7945 | 0.8414 | 0.9990 |
| Models | mIoU↑ | Kappa↑ | Dice↑ | AUC-ROC↑ |
|---|---|---|---|---|
| IonNet (w/o SA, FFN) | 0.7227 | 0.7838 | 0.8301 | 0.9986 |
| IonNet (w/o FFN) | 0.7283 | 0.7870 | 0.8342 | 0.9987 |
| IonNet (w/o SA) | 0.7343 | 0.7924 | 0.8387 | 0.9986 |
| IonNet | 0.7380 | 0.7945 | 0.8414 | 0.9990 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, S.; Guo, W.; Wang, C. Ionograms Trace Extraction Method Based on Multiscale Transformer Network. Remote Sens. 2024, 16, 2697. https://doi.org/10.3390/rs16152697
Han S, Guo W, Wang C. Ionograms Trace Extraction Method Based on Multiscale Transformer Network. Remote Sensing. 2024; 16(15):2697. https://doi.org/10.3390/rs16152697
Chicago/Turabian StyleHan, Sijia, Wei Guo, and Caiyun Wang. 2024. "Ionograms Trace Extraction Method Based on Multiscale Transformer Network" Remote Sensing 16, no. 15: 2697. https://doi.org/10.3390/rs16152697
APA StyleHan, S., Guo, W., & Wang, C. (2024). Ionograms Trace Extraction Method Based on Multiscale Transformer Network. Remote Sensing, 16(15), 2697. https://doi.org/10.3390/rs16152697




