Effect of Target Properties on Regolith Production
Abstract
1. Introduction
2. Materials and Methods
2.1. Regolith Thickness Distribution at the Ejecta of Copernicus Crater
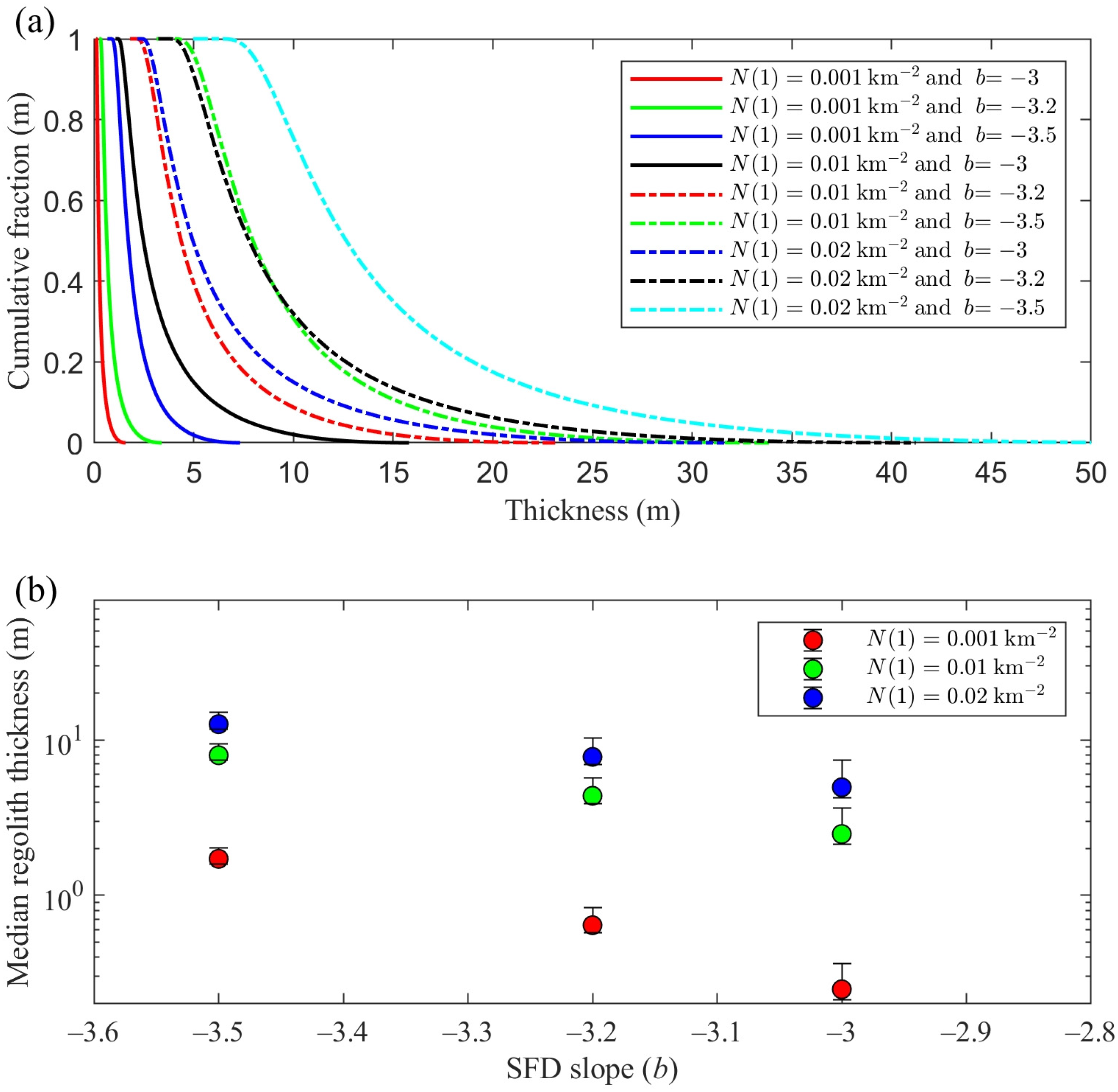
2.2. Regolith Thickness Distribution Model
- (i)
- Determine the largest craters in equilibrium by calculating the intersection point between the production and equilibrium populations.
- (ii)
- Calculate the distribution of regolith based on craters in equilibrium.
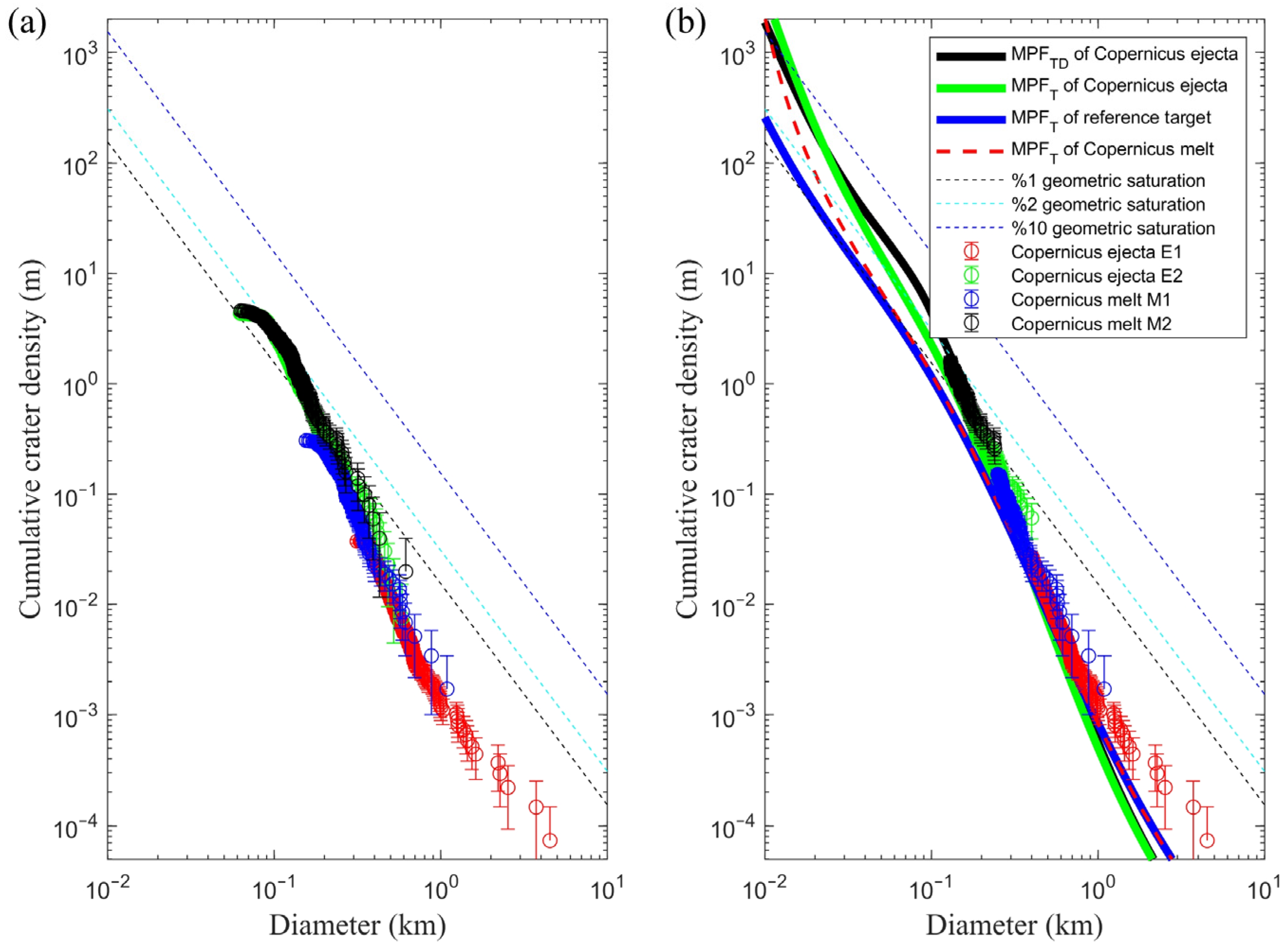
2.3. Crater Size–Frequency Distributions
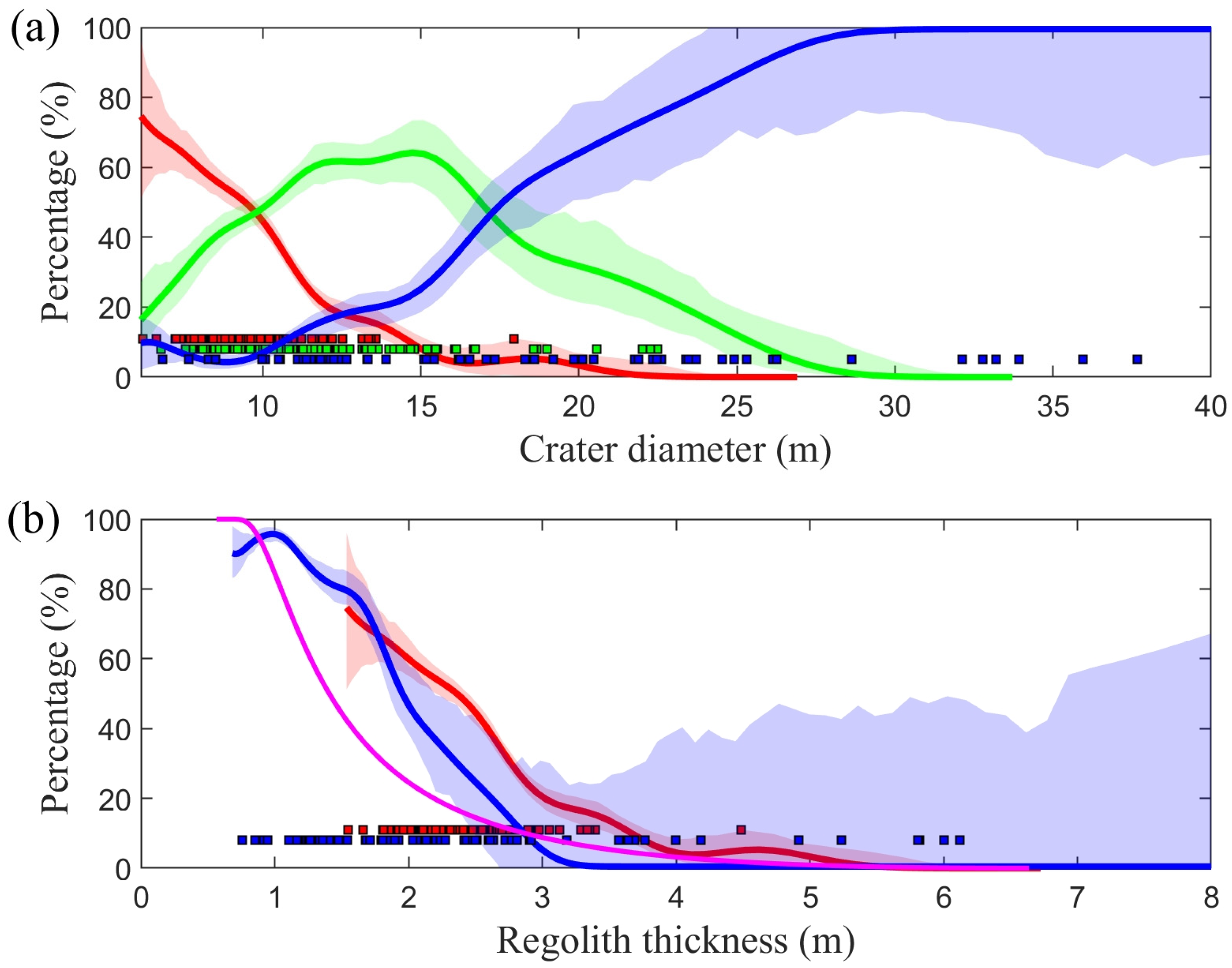
3. Results
4. Discussion
4.1. The Contribution of Regolith Growth from Secondary Cratering
4.2. The Effect of Target Properties on Regolith Production
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Melosh, H.J. Impact Cratering: A Geologic Process; Oxford University Press: New York, NY, USA, 1989; p. 253. [Google Scholar]
- McKay, D.S.; Heiken, G.; Basu, A.; Blanford, G.; Simon, S.; Reedy, R.; French, B.M.; Papike, J. The lunar regolith. In Lunar Sourcebook; Cambridge University Press: Cambridge, UK, 1991; pp. 285–356. [Google Scholar]
- Head, J.W.; Wilson, L. Rethinking Lunar Mare Basalt Regolith Formation: New Concepts of Lava Flow Protolith and Evolution of Regolith Thickness and Internal Structure. Geophys. Res. Lett. 2020, 47, e2020GL088334. [Google Scholar] [CrossRef]
- Molaro, J.; Byrne, S. Rates of temperature change of airless landscapes and implications for thermal stress weathering. J. Geophys. Res. 2012, 117, E10011. [Google Scholar] [CrossRef]
- Fruchter, J.; Rancitelli, L.; Laul, J.; Perkins, R. Lunar regolith dynamics based on analysis of the cosmogenic radionuclides Na-22, Al-26, and Mn-53. In Proceedings of the 8th Lunar Science Conference, Houston, TX, USA, 14–18 March 1977; pp. 3595–3605. [Google Scholar]
- Fa, W.; Jin, Y. Global inventory of Helium-3 in lunar regoliths estimated by a multi-channel microwave radiometer on the Chang-E 1 lunar satellite. Chinese. Sci. Bull. 2010, 55, 4005–4009. [Google Scholar] [CrossRef]
- Xie, M.; Xiao, Z.; Xu, L.; Fa, W.; Xu, A. Change in the Earth–Moon impactor population at about 3.5 billion years ago. Nat. Astron. 2021, 5, 128–133. [Google Scholar] [CrossRef]
- Isachenkov, M.; Chugunov, S.; Akhatov, I.; Shishkovsky, I. Regolith-based additive manufacturing for sustainable development of lunar infrastructure—An overview. Acta Astronaut. 2021, 180, 650–678. [Google Scholar] [CrossRef]
- Nakamura, Y.; Dorman, J.; Duennebier, F.; Lammlein, D.; Latham, G. Shallow lunar structure determined from the passive seismic experiment. Moon 1975, 13, 57–66. [Google Scholar] [CrossRef]
- Cooper, M.R.; Kovach, R.L.; Watkins, J.S. Lunar near-surface structure. Rev. Geophys. 1974, 12, 291–308. [Google Scholar] [CrossRef]
- Quaide, W.L.; Oberbeck, V.R. Thickness determinations of the lunar surface layer from lunar impact craters. J. Geophys. Res. 1968, 73, 5247–5270. [Google Scholar] [CrossRef]
- Fa, W.; Liu, T.; Zhu, M.H.; Haruyama, J. Regolith thickness over Sinus Iridum: Results from morphology and size-frequency distribution of small impact craters. J. Geophys. Res. 2014, 119, 1914–1935. [Google Scholar] [CrossRef]
- Bart, G.D. The quantitative relationship between small impact crater morphology and regolith depth. Icarus 2014, 235, 130–135. [Google Scholar] [CrossRef]
- Di, K.; Sun, S.; Yue, Z.; Liu, B. Lunar regolith thickness determination from 3D morphology of small fresh craters. Icarus 2016, 267, 12–23. [Google Scholar] [CrossRef]
- Shoemaker, E.; Batson, R.; Holt, H.; Morris, E.; Rennilson, J.; Whitaker, E. Observations of the lunar regolith and the Earth from the television camera on Surveyor 7. J. Geophys. Res. 1969, 74, 6081–6119. [Google Scholar] [CrossRef]
- Shoemaker, E.M.; Morris, E.C. Physical Characteristics of the Lunar Regolith Determined From Surveyor Television Observations. Radio Sci. 1970, 5, 129–155. [Google Scholar] [CrossRef]
- Wilcox, B.; Robinson, M.; Thomas, P.; Hawke, B. Constraints on the depth and variability of the lunar regolith. Meteorit. Planet. Sci. 2005, 40, 695–710. [Google Scholar] [CrossRef]
- Fa, W.; Wieczorek, M.A. Regolith thickness over the lunar nearside: Results from Earth-based 70-cm Arecibo radar observations. Icarus 2012, 218, 771–787. [Google Scholar] [CrossRef]
- Shkuratov, Y.G.; Bondarenko, N.V. Regolith layer thickness mapping of the Moon by radar and optical data. Icarus 2001, 149, 329–338. [Google Scholar] [CrossRef]
- Ding, C.; Li, Q.; Xu, J.; Lei, Z.; Li, J.; Su, Y.; Huang, S. Moon-Based Ground Penetrating Radar Derivation of the Helium-3 Reservoir in the Regolith at the Chang’E-3 Landing Site. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 2764–2776. [Google Scholar] [CrossRef]
- Hirabayashi, M.; Howl, B.A.; Fassett, C.I.; Soderblom, J.M.; Minton, D.A.; Melosh, H.J. The Role of Breccia Lenses in Regolith Generation From the Formation of Small, Simple Craters: Application to the Apollo 15 Landing Site. J. Geophys. Res. 2018, 123, 527–543. [Google Scholar] [CrossRef]
- Bart, G.D.; Nickerson, R.D.; Lawder, M.T.; Melosh, H.J. Global survey of lunar regolith depths from LROC images. Icarus 2011, 215, 485–490. [Google Scholar] [CrossRef]
- Xie, M.; Xiao, Z.; Xu, A. Time-Dependent Production Functions of Lunar Simple Craters on Layered Targets With Consideration of Topographic Degradation. Geophys. Res. Lett. 2019, 46, 10987–10996. [Google Scholar] [CrossRef]
- Kneissl, T.; van Gasselt, S.; Neukum, G. Map-projection-independent crater size-frequency determination in GIS environments—New software tool for ArcGIS. Planet. Space Sci. 2011, 59, 1243–1254. [Google Scholar] [CrossRef]
- Oberbeck, V.R.; Quaide, W.L. Estimated thickness of a fragmental surface layer of Oceanus Procellarum. J. Geophys. Res. 1967, 72, 4697–4704. [Google Scholar] [CrossRef]
- Robinson, M.; Brylow, S.; Tschimmel, M.; Humm, D.; Lawrence, S.; Thomas, P.; Denevi, B.; Bowman-Cisneros, E.; Zerr, J.; Ravine, M. Lunar reconnaissance orbiter camera (LROC) instrument overview. Space Sci. Rev. 2010, 150, 81–124. [Google Scholar] [CrossRef]
- Robbins, S.J.; Riggs, J.D.; Weaver, B.P.; Bierhaus, E.B.; Chapman, C.R.; Kirchoff, M.R.; Singer, K.N.; Gaddis, L.R. Revised recommended methods for analyzing crater size-frequency distributions. Meteorit. Planet. Sci. 2018, 53, 891–931. [Google Scholar] [CrossRef]
- Bevington, P.R.; Robinson, D.K. Data Reduction and Error Analysis for Physical Sciences; McGraw-Hill: New York, NY, USA, 2003. [Google Scholar]
- Oberbeck, V.; Quaide, W.; Mahan, M.; Paulson, J. Monte Carlo calculations of lunar regolith thickness distributions. Icarus 1973, 19, 87–107. [Google Scholar] [CrossRef]
- Zhang, M.; Fa, W.; Barnard, E.M.; Eke, V.R. Modeling the Evolution of Lunar Regolith: 2. Growth Rate and Spatial Distribution. J. Geophys. Res. 2023, 128, e2023JE008035. [Google Scholar] [CrossRef]
- Gault, D.E. Saturation and equilibrium conditions for impact cratering on the lunar surface: Criteria and implications. Radio Sci. 1970, 5, 273–291. [Google Scholar] [CrossRef]
- Haruyama, J.; Ohtake, M.; Matsunaga, T.; Morota, T.; Yokota, Y.; Honda, C.; Hirata, N.; Demura, H.; Iwasaki, A.; Nakamura, R. Planned radiometrically calibrated and geometrically corrected products of lunar high-resolution Terrain Camera on SELENE. Adv. Space Res. 2008, 42, 310–316. [Google Scholar] [CrossRef]
- Kirchoff, M.R.; Marchi, S. New insights into lunar terrain properties and their effect on derivation of absolute model ages using Apollo landing sites. Icarus 2023, 391, 115336. [Google Scholar] [CrossRef]
- Williams, J.P.; Pathare, A.V.; Costello, E.S.; Gallinger, C.L.; Hayne, P.O.; Ghent, R.R.; Paige, D.A.; Siegler, M.A.; Russell, P.S.; Elder, C.M. The Effects of Terrain Properties Upon the Small Crater Population Distribution at Giordano Bruno: Implications for Lunar Chronology. J. Geophys. Res. 2022, 127, e2021JE007131. [Google Scholar] [CrossRef]
- Stöffler, D.; Ryder, G. Stratigraphy and isotope ages of lunar geologic units: Chronological standard for the inner solar system. Space Sci. Rev. 2001, 96, 9–54. [Google Scholar] [CrossRef]
- Xiao, Z.; Werner, S.C. Size-frequency distribution of crater populations in equilibrium on the Moon. J. Geophys. Res. 2015, 120, 2277–2292. [Google Scholar] [CrossRef]
- Namiki, N.; Honda, C. Testing hypotheses for the origin of steep slope of lunar size-frequency distribution for small craters. Earth Planets Space 2003, 55, 39–51. [Google Scholar] [CrossRef]
- Hiesinger, H.; Bogert, C.; Pasckert, J.; Funcke, L.; Giacomini, L.; Ostrach, L.; Robinson, M. How old are young lunar craters? J. Geophys. Res. 2012, 117, E00H10. [Google Scholar] [CrossRef]
- Ostrach, L.; Robinson, M.; Denevi, B.; Thomas, P. Effects of incidence angle on crater counting observations. Proc. Lunar Planet. Sci. Conf. 2011, 42, 1202. [Google Scholar]
- Xie, M.; Xiao, Z. A new chronology from debiased crater densities: Implications for the origin and evolution of lunar impactors. Earth. Planet. Sci. Lett. 2023, 602, 117963. [Google Scholar] [CrossRef]
- Shoemaker, E.M. Preliminary analysis of the fine structure of the lunar surface in Mare Cognitum. In The Nature of the Lunar Surface; Hess, W., Menzel, D., O’Keeffe, J., Eds.; Johns Hopkins Press: Baltimore, MA, USA, 1965; pp. 23–77. [Google Scholar]
- McEwen, A.S.; Bierhaus, E.B. The importance of secondary cratering to age constraints on planetary surfaces. Annu. Rev. Earth Planet. Sci. 2006, 34, 535–567. [Google Scholar] [CrossRef]
- Xiao, Z. On the importance of self-secondaries. Geosci. Lett. 2018, 5, 17. [Google Scholar] [CrossRef]
- Marchi, S.; Mottola, S.; Cremonese, G.; Massironi, M.; Martellato, E. A new chronology for the Moon and Mercury. Astron. J. 2009, 137, 4936. [Google Scholar] [CrossRef]
- Williams, J.-P.; Pathare, A.V.; Aharonson, O. The production of small primary craters on Mars and the Moon. Icarus 2014, 235, 23–36. [Google Scholar] [CrossRef]
- Xie, M.; Zhu, M.-H.; Xiao, Z.; Wu, Y.; Xu, A. Effect of Topography Degradation on Crater Size-Frequency Distributions: Implications for Populations of Small Craters and Age Dating. Geophys. Res. Lett. 2017, 44, 10,171–10,179. [Google Scholar] [CrossRef]
- Senft, L.E.; Stewart, S.T. Modeling impact cratering in layered surfaces. J. Geophys. Res. 2007, 112, E11002. [Google Scholar] [CrossRef]
- Ahrens, T.J.; Xia, K.; Coker, D. Depth of cracking beneath impact craters: New constraint for impact velocity. In AIP Conference Proceedings, Proceedings of the Shock Compression of Condensed Matter—2001: 12th APS Topical Conference, Atlanta, GA, USA, 24–29 June 2001; AIP Publishing: Melville, NY, USA, 2002; pp. 1393–1396. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, M.; Li, Y. Effect of Target Properties on Regolith Production. Remote Sens. 2024, 16, 2650. https://doi.org/10.3390/rs16142650
Xie M, Li Y. Effect of Target Properties on Regolith Production. Remote Sensing. 2024; 16(14):2650. https://doi.org/10.3390/rs16142650
Chicago/Turabian StyleXie, Minggang, and Yan Li. 2024. "Effect of Target Properties on Regolith Production" Remote Sensing 16, no. 14: 2650. https://doi.org/10.3390/rs16142650
APA StyleXie, M., & Li, Y. (2024). Effect of Target Properties on Regolith Production. Remote Sensing, 16(14), 2650. https://doi.org/10.3390/rs16142650




