1. Introduction
Due to the outstanding stability of radar systems in dark or adverse weather conditions, radar technology has become indispensable across the military, civilian, and industrial sectors. Concurrently, the advent of deep learning has facilitated the development of an increasing number of sophisticated radar target detection and recognition algorithms [
1,
2]. However, the ‘black box’ nature of deep learning models significantly impedes their broader application. Specifically, in areas with high safety requirements, such as global maritime surveillance [
3] and autonomous driving [
4,
5,
6,
7,
8], providing model explainability becomes particularly crucial. Therefore, in-depth research into the explanatory mechanisms of deep learning models has become an important task in current research.
In deep learning, explainability methods aim to elucidate the principles behind model decisions [
9]. Depending on the focus of the research, explainability approaches can be categorized into two main types: intrinsic explainability [
10] and post hoc explainability. Intrinsic explainability methods ensure that models are designed with clear explainability from the very beginning. In contrast, post hoc explainability methods apply explanatory techniques to clarify the working principles of existing models. Due to the inherent lack of built-in explanatory mechanisms in most deep learning models, post hoc explanatory analysis has become a key method for elucidating these models’ decision-making processes. Currently, post hoc explainability encompasses a wide array of methods that target decision attribution, primarily including feature attribution and concept attribution. Within feature attribution methods, a series of Class Activation Mapping (CAM) [
11,
12,
13,
14,
15] techniques provide visual explanations by generating activation maps. While activation maps can display the areas focused on by the model, CAM and its derivatives primarily reveal pixel-level, low-level features, which can diverge from human understanding of higher-level concepts to some extent. Moreover, these methods often provide only localized explanations [
16] and are unreliable in attributions under input transformations [
17] and adversarial perturbations [
18]. However, methods based on concept attribution can overcome these limitations and offer explainability in understandable terms (i.e., concepts) to humans [
19]. Among these, the Testing with Concept Activation Vectors (TCAV) method [
20] allows users to define concepts of interest and the datasets representing these concepts to detect the sensitivity of target categories to these concepts and provide a global explanation of the model by calculating TCAV scores. This robust explanatory capability has led to the application of TCAV across numerous deep learning domains, including image classification [
16,
21,
22], among others [
23,
24].
In the field of image classification, models typically deal with concrete optical images—such as animals, plants, and everyday objects—where the concepts are relatively intuitive to humans. For example, in analyzing the GoogleNet [
25] model for the category ‘zebra’, the developers of TCAV were able to easily identify prominent features such as ‘striped’, ‘zigzagged’, and ‘dotted’ as key concepts. In contrast, the inherent abstraction and analytical complexity of millimeter-wave (MMW) radar data make the concepts less apparent. Therefore, we have designed the following method to explore and discover concepts, aiming to reveal the hidden complexities within MMW radar data.
Initially, we employ visualization techniques to convert the MMW radar’s Range-Angle (RA) spectrogram data into visual images. Based on expert experience in the radar field, we provided a series of basic concepts through visual analysis that reflect the characteristics of radar target recognition. These concepts not only have practical application value but also align with human cognitive attributes.
However, due to the subjectivity of manual concept annotation and the high complexity of MMW radar spectrograms, relying solely on manual concept annotation methods may overlook key concepts in radar data that are difficult to detect. These concepts may be crucial for the model’s prediction accuracy during the actual recognition process. Additionally, since basic concept definitions typically focus on a single aspect, they may neglect other key concepts, potentially leading to a vague correspondence between concepts and recognition categories. Furthermore, as the definitions of basic concepts vary among individuals, it becomes challenging to generalize these concepts to specific tasks. To more comprehensively explain the model and improve concept quality, we propose a Basic Concept-Guided Deep Embedding Clustering (BCG-DEC) method aimed at uncovering task-specific composite concepts guided by domain expertise.
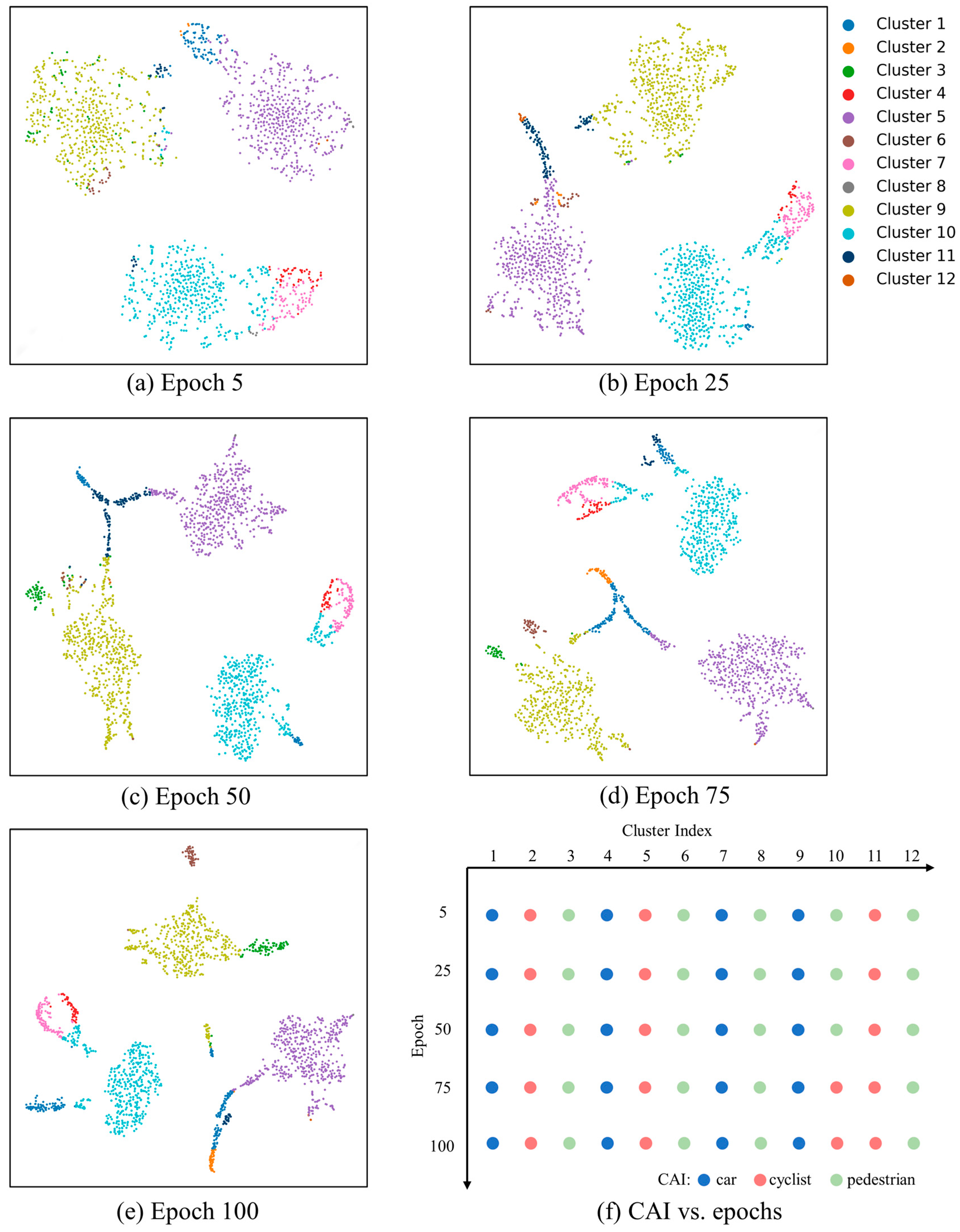
BCG-DEC trains an autoencoder on a large set of RA spectrograms to learn general feature representations of MMW radar data and employs the encoder segment to extract embeddings from the concept dataset. Initial clustering centroids are determined through k-means [
26] clustering of these embeddings. During the deep clustering process, this method utilizes existing basic concepts to adjust the initial centroids in feature space, effectively ensuring that task-specific composite concepts focus on multiple meaningful key attributes of MMW radar targets. After that, we evaluate the quality of clustering by clustering entropy. For the clustering results that do not meet the standard, we choose to re-cluster so as to find the concept that has a clear correspondence with the category. The concepts discovered by BCG-DEC are highly abstract and complex. To make the task-specific composite concepts more comprehensible to humans, we introduced a ‘Category Association Index’ (CAI) to describe the categories represented by the concepts. Ultimately, we employed TCAV scores to quantify the importance of basic and task-specific composite concepts for different recognition categories, thus providing a quantitative explanation of which concepts are critical for the model to accurately predict certain types of targets.
Our research contributions are summarized as follows:
This study is the first, to our knowledge, to deeply explore and validate the basic concepts learned during the process of MMW radar target recognition using the TCAV method. This novel approach allows for a clearer understanding of how these basic concepts contribute to target recognition.
We innovatively propose the BCG-DEC method, which effectively resolves the ambiguity in the correspondence between basic concepts and categories, as well as the subjectivity and variability inherent in manually annotated concept methods. The BCG-DEC method’s capability to discover concepts in MMW radar data is an innovative development in the field.
Our research not only pioneers the process of concept discovery within MMW radar target recognition models but also provides a valuable framework for future research in this area that utilizes both basic concepts and task-specific composite concepts for explanation. This framework offers a useful reference for further improving the explainability of radar target recognition models.
Experimental results demonstrate the importance of the discovered concepts for MMW radar target recognition. These outcomes not only confirm the effectiveness of our newly developed methodologies but also highlight their substantial practical relevance and potential for broad applicability in real-world radar systems.
3. Explanation Based on Basic Concepts
Concepts are units that are easier for humans to understand than individual features, pixels, characters, etc. It can be used to explain the rationality of deep learning models. The definition of a precise concept usually needs to satisfy three properties: meaningfulness, coherency, and importance. Meaningfulness indicates that a concept belongs semantically to a certain class of objects. Coherency indicates that the data constituting the same concept are perceptually similar. Importance means that the concept is necessary for the prediction of that class [
27]. Building on a thorough consideration of the aforementioned three properties, we will discuss methods for discovering basic concepts in MMW radar data and how these discovered concepts can be used to explain the model.
In the process of radar target recognition, certain discriminative features can help differentiate between objects [
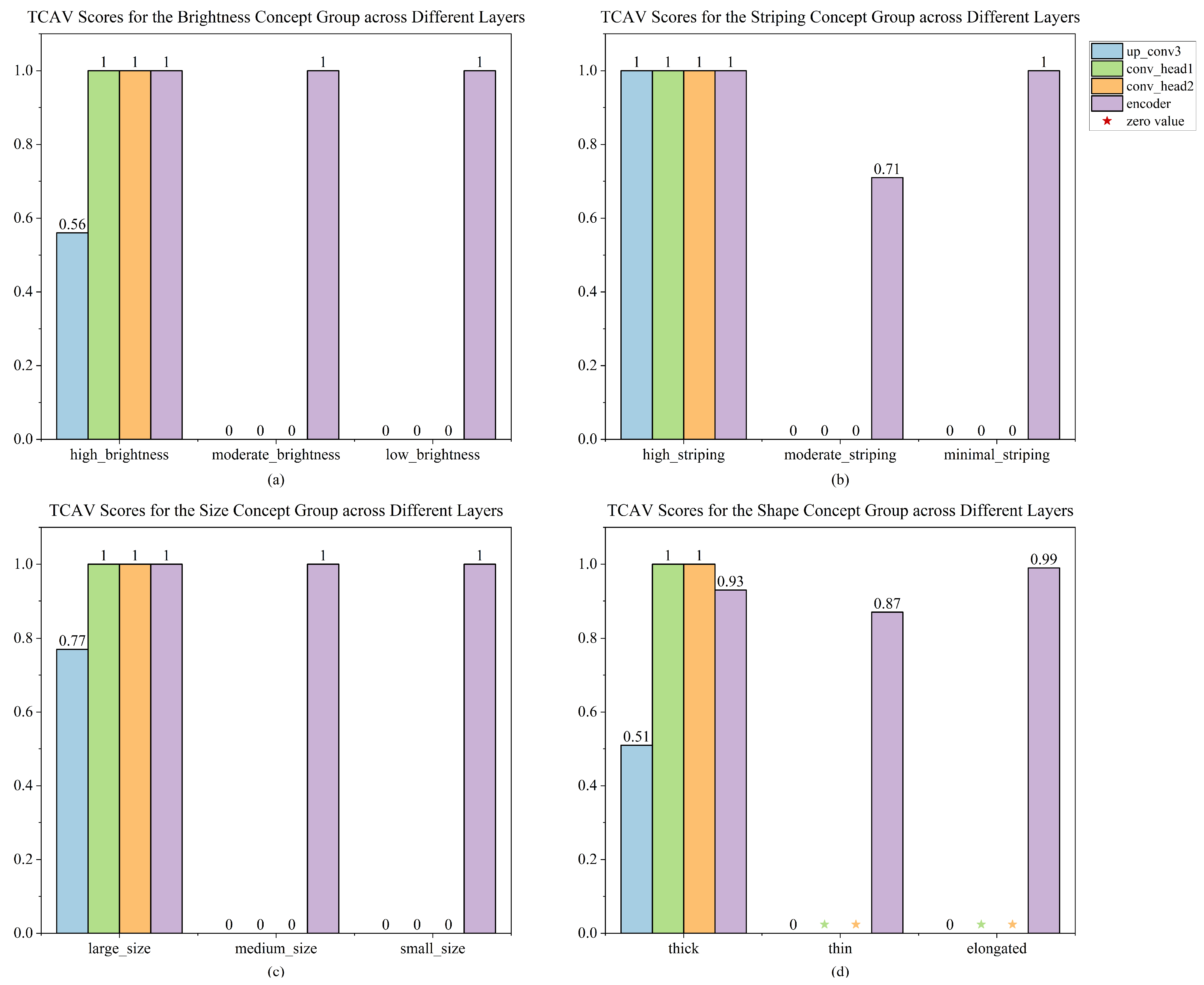
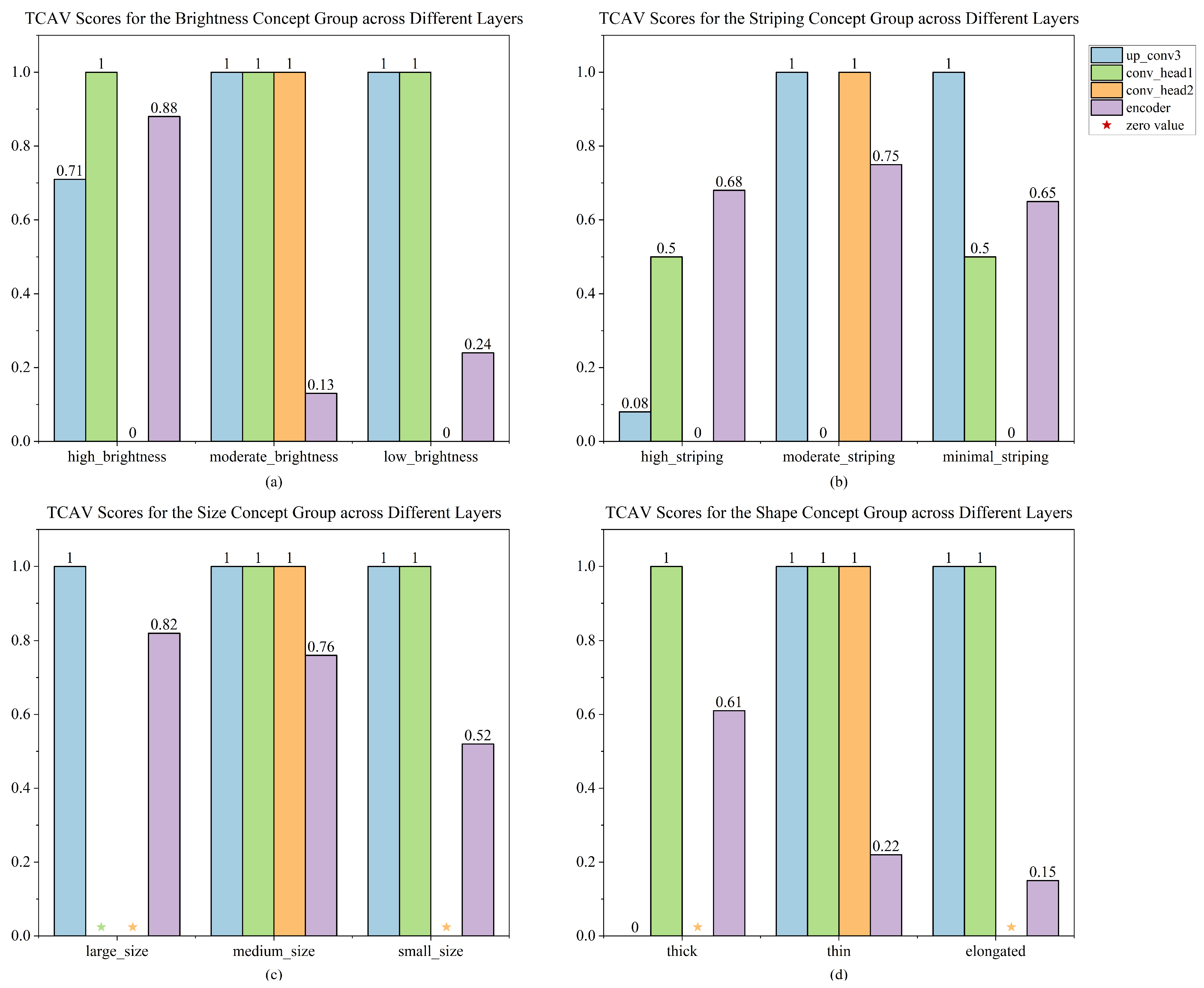
28], including polarization characteristics, size, and shape, among others. Polarization refers to the orientation of the electric field in electromagnetic waves. Given that polarization properties are a crucial aspect for understanding and interpreting MMW radar images, we analyzed radar images based on how the surface characteristics of an object affect the polarization state of reflected waves. We observed that smooth metallic surfaces might reflect waves of specific polarization more strongly, producing brighter signals on the radar spectrogram. Typically, if a target has a larger radar cross-section (RCS), its reflected signal will be stronger, resulting in greater brightness on the spectrogram. Based on this observation, we define brightness as a concept for radar target recognition.
In radar spectrograms, the characteristic of striping is also vital for classifying targets. Variations in the number of stripes generally reflect the complexity of the target. Complex targets with multiple independent structures or parts may each reflect radar waves separately. From a structural perspective, objects with cavities or frameworks, such as certain vehicles, may produce additional striping in the spectrogram due to reflections from external structures. Based on these observations, we selected striping as one of our basic concepts.
Beyond brightness and striping, the size and shape of bright spots in the spectrogram are crucial for understanding the physical characteristics of a target. Size refers to how large the target appears on the spectrogram, which is useful for estimating the target’s actual size. Shape in the spectrogram typically refers to the geometric outline of the target, which can reflect its structural characteristics. For example, large and complex shapes may represent large vehicles or structures, while small dots might indicate individual pedestrians or small objects.
Based on the above analysis, we have discovered four groups of concepts: brightness, striping, size, and shape. Our experience indicates that these concepts are meaningful for inferring the types of targets. Throughout the experimental process, we ensure that radar spectrograms within the same concept dataset exhibit similarity, thereby maintaining the coherency of concepts. Next, we use the TCAV [
20] method to demonstrate the importance of these basic concepts.
For the four groups of basic concepts that have been discovered, we assign sub-concepts of basic concepts to each group based on the target categories of the dataset. These sub-concepts of basic concepts reflect finer-grained attributes in the context of each basic concept, corresponding to the recognition characteristics of different categories of radar targets. Throughout this paper, for simplicity, we will use ‘sub-concepts’ to refer to these ‘sub-concepts of basic concepts’. Drawing from our experience with TCAV, we selected 100 radar data samples for each sub-concept.
To better understand the discovered concepts, we use TCAV scores to characterize the importance of concepts for the model to recognize a particular category. Before the computation of the TCAV score, it is imperative to determine several critical parameters integral to the TCAV methodology. Initially, a concept
C, such as the aforementioned sub-concept, must be selected. Subsequently, the target class
k, which the model is intended to recognize (e.g., a car), should be determined. Lastly, the hidden layer
l that will be used to extract activations from the input data must be determined in the model. After these parameters are determined, we need to prepare a dataset corresponding to concept
C, a random concept dataset without concept
C, and a dataset
corresponding to target class
k. Using these datasets, we can calculate the concept activation vector (CAV), the directional derivative
,
, and the TCAV score, in turn, using the theory introduced in
Section 2.1. The final TCAV score reflects the proportion of the radar target recognition model that is positively influenced by concept
C when predicting
as the class
k.
To prevent getting meaningless CAVs, the developers of TCAV perform statistical significance tests to ensure that concepts are important. We use the same method to perform a two-sided t-test on TCAV scores on the basis of multiple training CAVs, and the results shown are all CAVs that pass the test. In our experiments, TCAV is implemented in PyTorch instead of Tensorflow by the original authors.
4. Explanation Based on Task-Specific Composite Concepts
In the context of utilizing concept-based explanations for deep learning models in radar target recognition, relying solely on basic concepts and manual annotation methods presents numerous challenges.
First, the inherent subjectivity of manual annotations and the complex nature of MMW radar spectrograms make it difficult to comprehensively discover and utilize key concepts, which are crucial for accurate model predictions. Additionally, basic concepts are often overly simplistic and defined with a focus on a single attribute, leading to a lack of clarity in their correspondence with actual recognition categories. This issue is compounded by the variability of these definitions across different individuals, which hinders the generalization of the concepts to specific tasks. For instance, a concept deemed ‘high brightness’ in ship recognition tasks might not be applicable in the context of autonomous driving, underscoring the ambiguity of basic concepts across tasks. Each task may require a redefinition of concepts, adding to the complexity and inefficiency of the process. We prefer to find concepts that can describe a certain class of targets, which is of great significance to verify whether the model can correctly recognize a certain class of targets. To address these issues, this study employs clustering methods to explore more task-specific composite concepts within MMW radar to characterize the features of different target categories.
However, common deep clustering approaches, such as those that extract features using models pre-trained on other datasets followed by traditional clustering methods, often fail to adequately capture the characteristics of the current dataset. Furthermore, the constant fixation of pre-trained model parameters can lead to a lack of adaptability to the specific clustering tasks currently underway. Deep Embedding Clustering (DEC) [
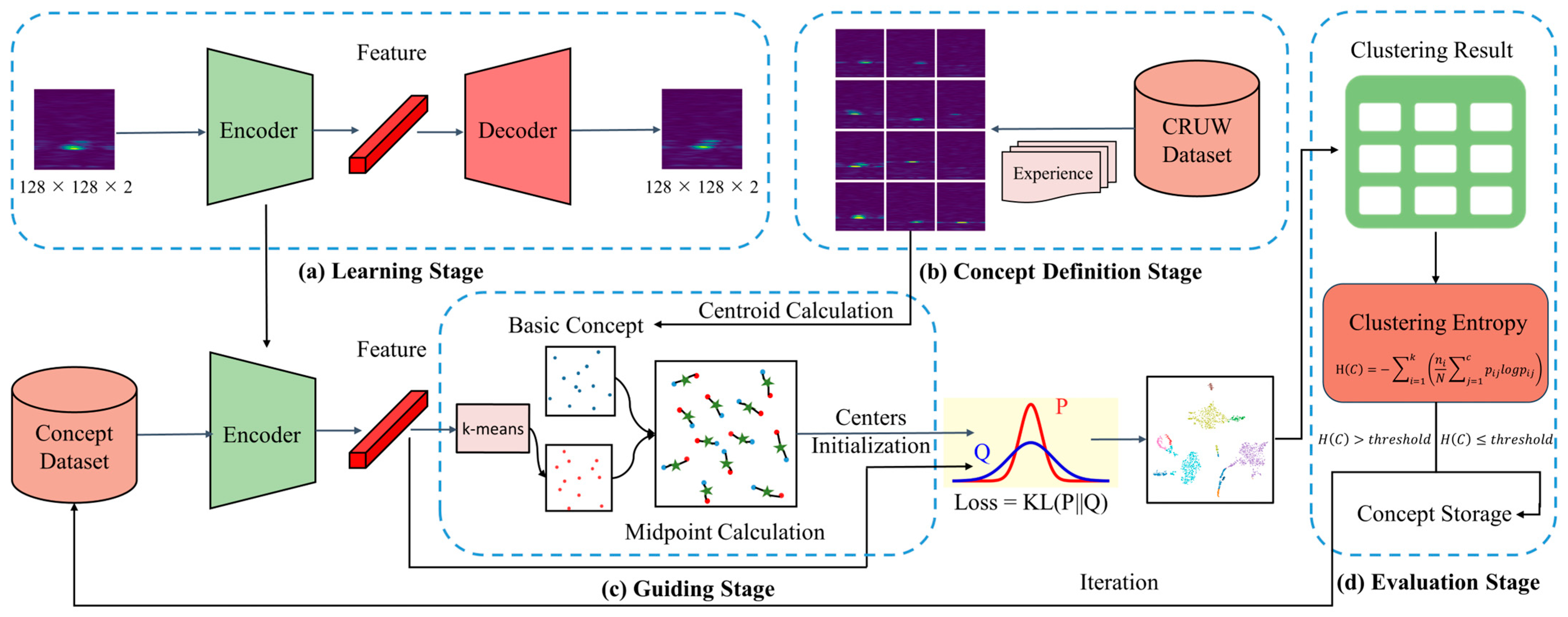
29], proposed by J. Xie et al., can better deal with the above problems because it optimizes the representation of data points in the feature space during the training process and overcomes the limitations of traditional clustering methods that heavily rely on predefined feature space and distance metrics. Inspired by the DEC method, we propose a Basic Concept-Guided Deep Embedding Clustering (BCG-DEC) method to solve the problems of manually labeling concept methods. BCG-DEC is capable of exploring task-specific composite concepts that more accurately reflect the multifaceted attributes of targets and more effectively adapt to specific task requirements. It comprises four stages: In the first stage, the autoencoder is trained on a large amount of MMW radar data to learn the representations of Range-Angle (RA) spectrograms. In the second stage, we define each basic concept dataset based on existing concepts and our experience with visual analysis of MMW radar. In the third stage, the training of the clustering model is guided by computing the centroids of each basic concept dataset. In the fourth stage, clustering entropy is used to evaluate the quality of clustering results from the perspective of task-specific composite concept discovery, and if it is greater than our empirical threshold, deep clustering will be iterated. Through these four stages, BCG-DEC achieves joint tuning of pre-trained model parameters and the clustering process, thereby facilitating the perception of meaningful concepts within the MMW radar data domain during the clustering. The implementation process of the proposed method is shown in
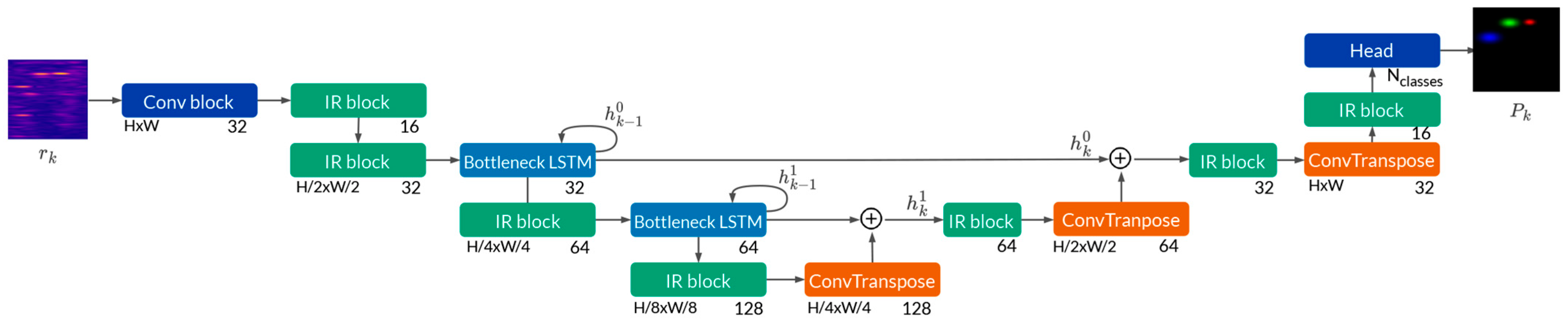
Figure 2.
We now provide a detailed description of the implementation process for the BCG-DEC method. Initially, to thoroughly mine the deep semantic features contained within radar data, we designed a CNN-based autoencoder for the data space X during the first stage to learn the subtle features of a large volume of spectrograms. The training loss function employed is the Mean Squared Error (MSE). Upon completion of training, we obtain the initial nonlinear mapping : X→Z, where θ represents the learnable parameters within the encoder, and Z denotes the latent features learned by the autoencoder. We then extract the encoder part of the autoencoder and incorporate it into the basic concept-guided clustering model to perceive the task-specific composite concepts from the concept dataset.
Subsequently, in the second stage—the concept definition stage—we select the RA spectrogram of the corresponding concept from a large number of MMW radar data based on the discovered basic concepts, and our visual analytical experience ensures the importance of the concept. In addition, we will check the selected RA spectrograms to ensure that the spectrograms of the same concept are similar to ensure the coherency of the concept.
Next, we enter the third stage—the guiding stage. At the start of this stage, we employ the k-means algorithm to cluster the embeddings generated by the encoder, thus obtaining the initial cluster centers, μ. To utilize meaningful information from basic concepts in concept discovery and prevent clustering around centers of irrelevant features, we introduce basic concepts to correct the initial μ positions in the feature space. Each basic concept corresponds to multiple RA spectrograms selected in the second stage, yet we only need one representative center for guidance. Therefore, we will calculate the centroid of the basic concept set as follows:
Given a concept dataset
H ⊂ X, each radar data
∈
H is encoded into a latent vector
=
. To fully consider the density and structure of the latent data distribution, the centroid of set
H,
, is determined through an adaptive weighting scheme in the feature space, as shown in Equation (3).
The adaptive weighting scheme employs a distance-based weighted average, where the weight of each data point is a decreasing function of its distance to other points in the cluster. Weights are implemented using a Gaussian kernel function , where represents the Euclidean distance between point and other points in H, and σ is the bandwidth parameter of the Gaussian kernel, controlling the influence range of neighboring points on the centroid.
We assign the center
of each basic concept set
H, computed by Equation (3), to a set
. For each initial cluster center
determined by the k-means algorithm, BCG-DEC searches for the
with the closest Euclidean distance to
, and takes the midpoint between
and
as the new cluster center
, as shown in Equation (4).
Equation (4) reflects the process in which latent features are guided by basic concepts. We can then use the new cluster center
to calculate the Q distribution (i.e., soft assignment), which is designed to calculate the probability of each embedding assignment to each cluster center. As shown in the following equation:
is the latent representation of the input sample obtained by the encoder . reflects the probability that the sample is assigned to the new cluster center .
To improve the cluster purity and assign the radar samples to clusters with high confidence, we compute the auxiliary distribution P [
29] based on the distribution Q, following the method in DEC, as follows:
where
denotes the soft assignment frequency of all sample points in cluster
j,
represents the index variable used in the summation process, iterating over all possible cluster centers.
We calculate the KL divergence of the Q distribution and P distribution as the loss function of the basic concept-guided clustering model training and jointly tune the cluster centers and encoder parameters by Stochastic Gradient Descent (SGD).
Finally, in the fourth stage—the evaluation stage—we hope to obtain task-specific composite concepts to overcome the subjectivity of manual concept annotation and the oversimplification of basic concept definitions. A task-specific composite concept usually characterizes the main features of a certain class of objects, that is, clusters that mainly contain one class of data points. To judge whether the clustering results meet the above requirements, we evaluate the quality of the clustering results using clustering entropy, which can measure the uncertainty of the distribution of the classes within each cluster. A cluster that describes a certain class well has a lower entropy, while a cluster with a uniform class distribution has a higher entropy. We calculate the entropy of each cluster and weighted average the entropy of all clusters to obtain H, the entropy of the whole cluster. The calculation formula is shown in Equation (7):
where
is the relative frequency of category
j in cluster
i,
c is the category number of the data itself,
is the total number of data points in cluster
i,
N is the total number of data points in the dataset, and
k is the number of clusters.
If the clustering entropy is greater than the empirical threshold, it represents that the current clustering result has weak correspondence with the category, which is not suitable as a task-specific composite concept, and deep clustering needs to be performed again. If the clustering entropy is less than the empirical threshold, the current clustering results can be saved as concepts.
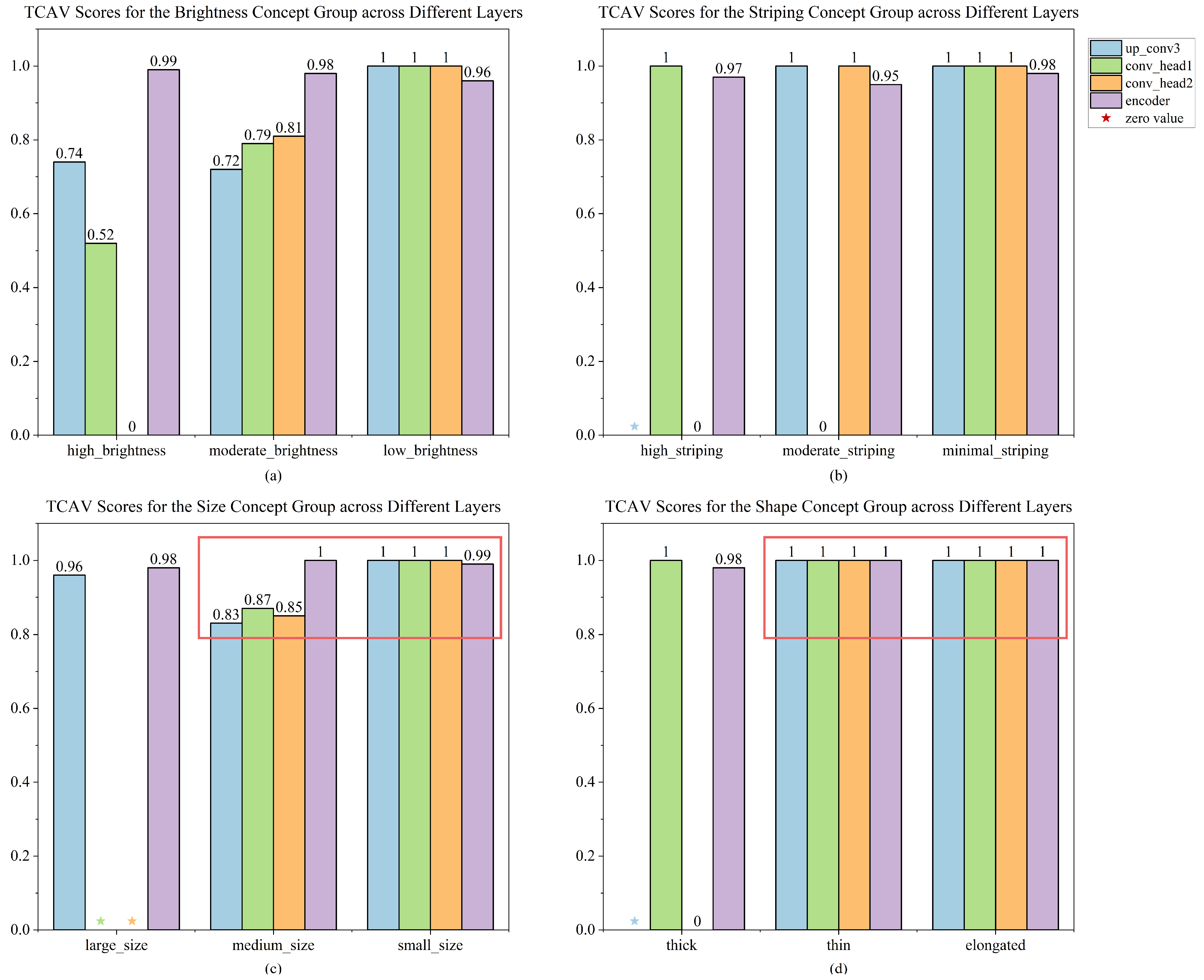
Considering that BCG-DEC cannot give a human-understandable description of the mined task-specific composite concepts, we give an indicator to characterize the task-specific composite concepts, which is the Category Association Index (CAI), as shown in the following equation:
CAI is used to describe the category represented by the concept set C. is the set of all data belonging to class k. is the number of data points belonging to category k in the concept set C. By calculating CAI, we can determine which kinds of targets have the greatest degree of relevance to the task-specific composite concepts discovered, so that these concepts are easier for users to understand.
With this, we have completed the exploration and description of task-specific composite concepts. By using basic concepts to guide the discovery of task-specific composite concepts and employing clustering entropy to filter the clustering results, we have enhanced their meaningfulness. During the experimental process, we will also filter out the concepts obtained by the BCG-DEC method that have less MMW radar data in the clustering results to further ensure their meaningfulness. Among the retained task-specific composite concepts, we will manually inspect the RA spectrograms within each concept to verify their coherency.
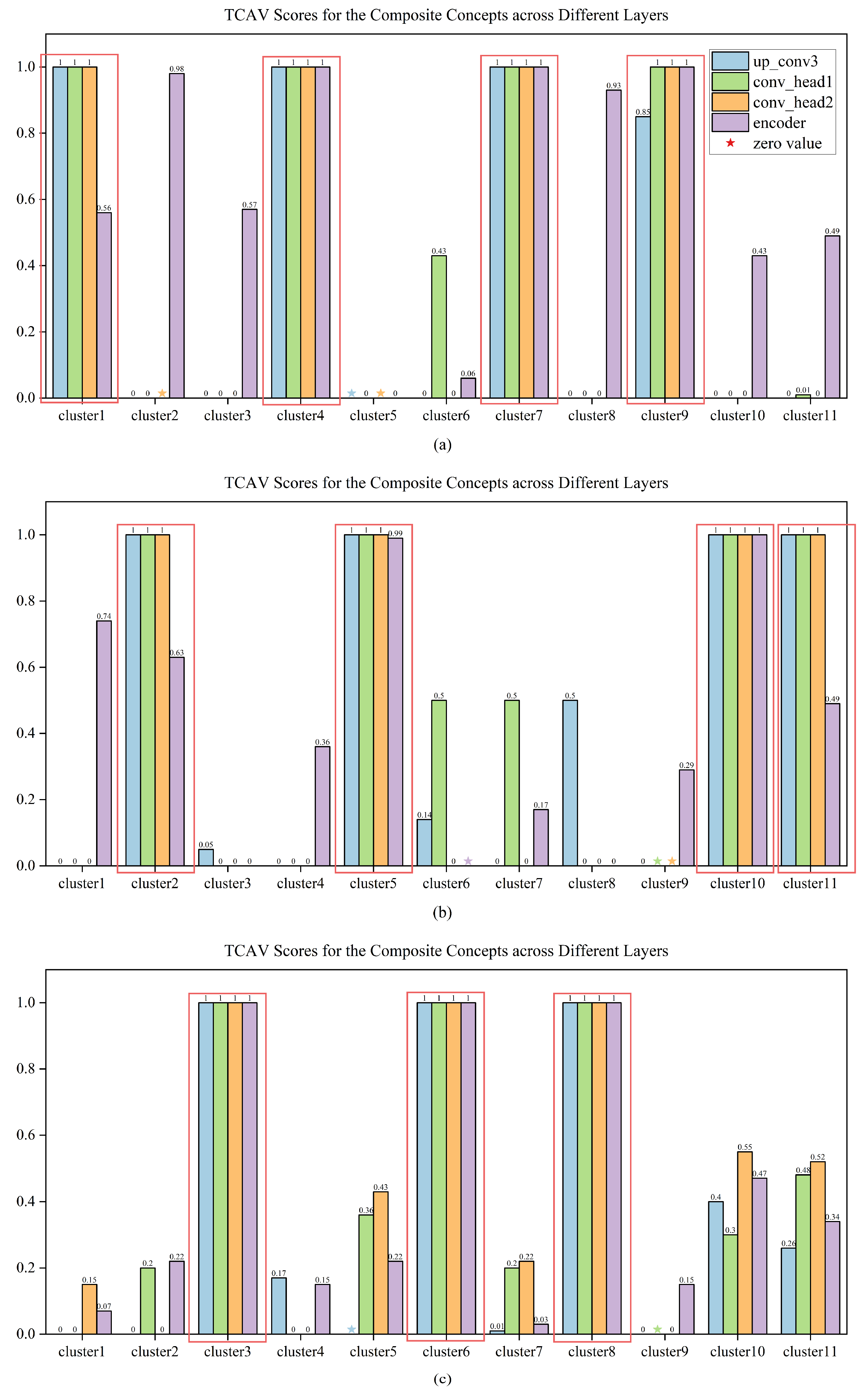
For the task-specific composite concepts that have been discovered, similarly, we adopt the TCAV approach described in
Section 3 to emphasize the importance of the concept. It is important to note that since the task-specific composite concepts are the outcomes of clustering, each concept’s associated radar data may exceed 100 samples, and the clusters may contain multiple categories. So, we employ stratified sampling based on the proportion of categories within each cluster and select 100 radar data samples for each task-specific composite concept.