Monitoring the Vertical Variations in Chlorophyll-a Concentration in Lake Chaohu Using the Geostationary Ocean Color Imager
Abstract
1. Introduction
2. Data and Processing
2.1. Study Area
2.2. Field-Measured Data
2.3. Satellite Image Acquisition and Processing
2.4. Meteorological and Hydrological Data
2.5. Accuracy Assessment
3. Methods
3.1. Fitting the Chla Vertical Profiles Using Field-Measured Data
3.2. Correlation of Surface Chla with Rrs_G
3.3. Decision Tree for Classifying Vertical Profiles
3.4. Chla(z) Inversion Model Development
4. Results
4.1. Fitting of the Field Chla(z) Profiles
4.2. Calibration and Validation of Chla(z)
4.2.1. Decision Tree of Chla(z)
4.2.2. Chla Inversion Model for Vertically Uniform
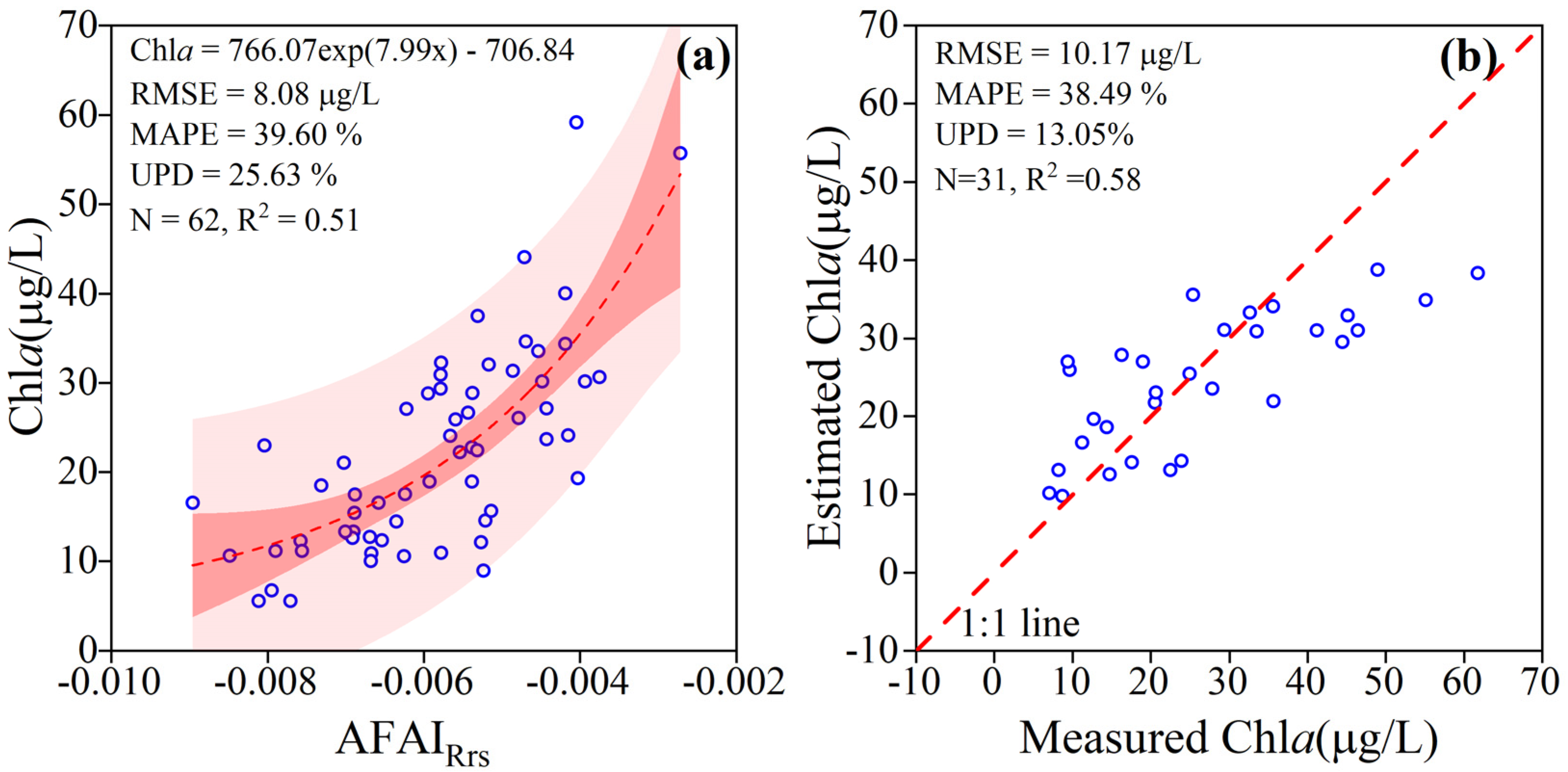
4.2.3. Estimation of Chla(z) Inversion Model in the Non-Uniform Vertical Distribution
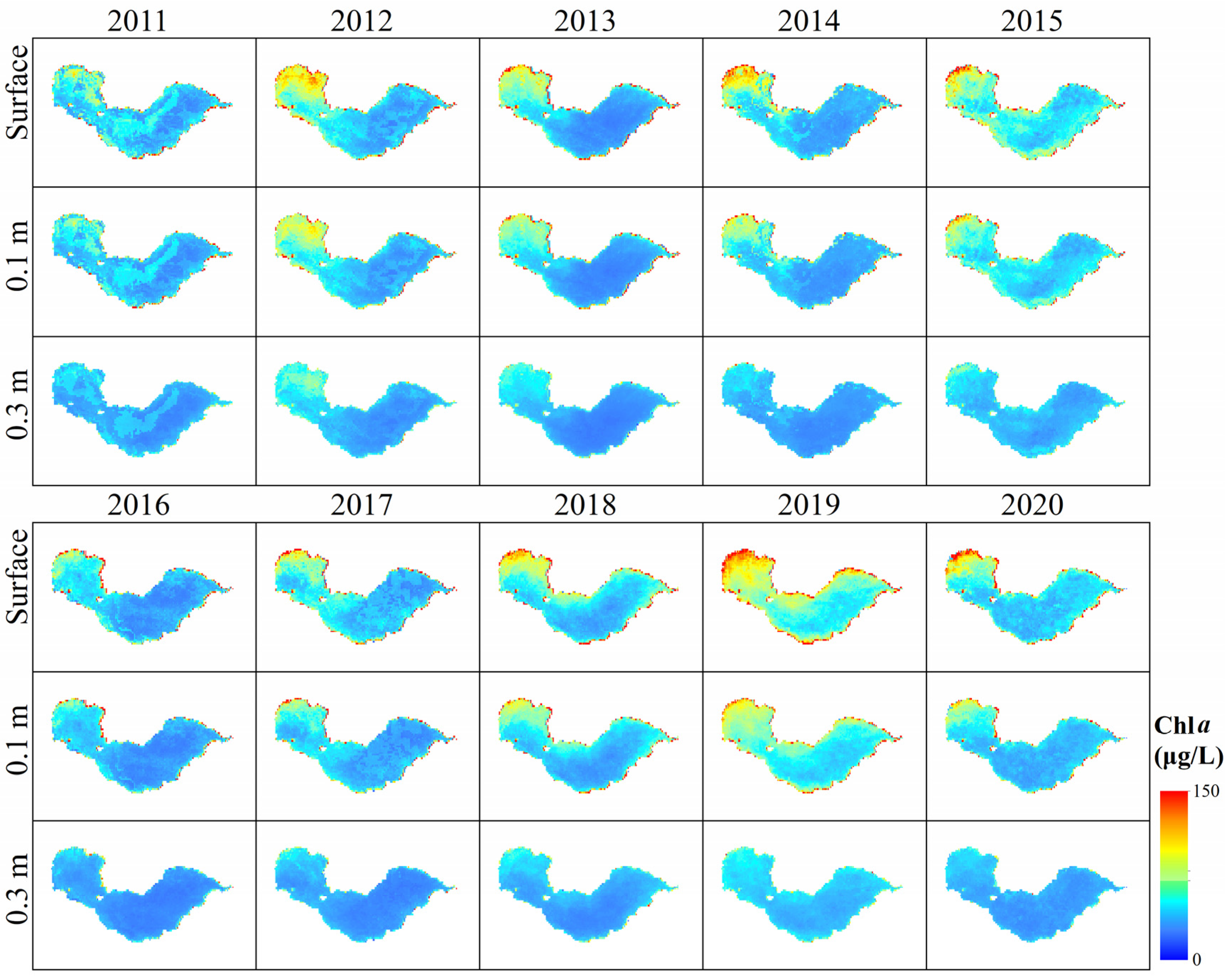
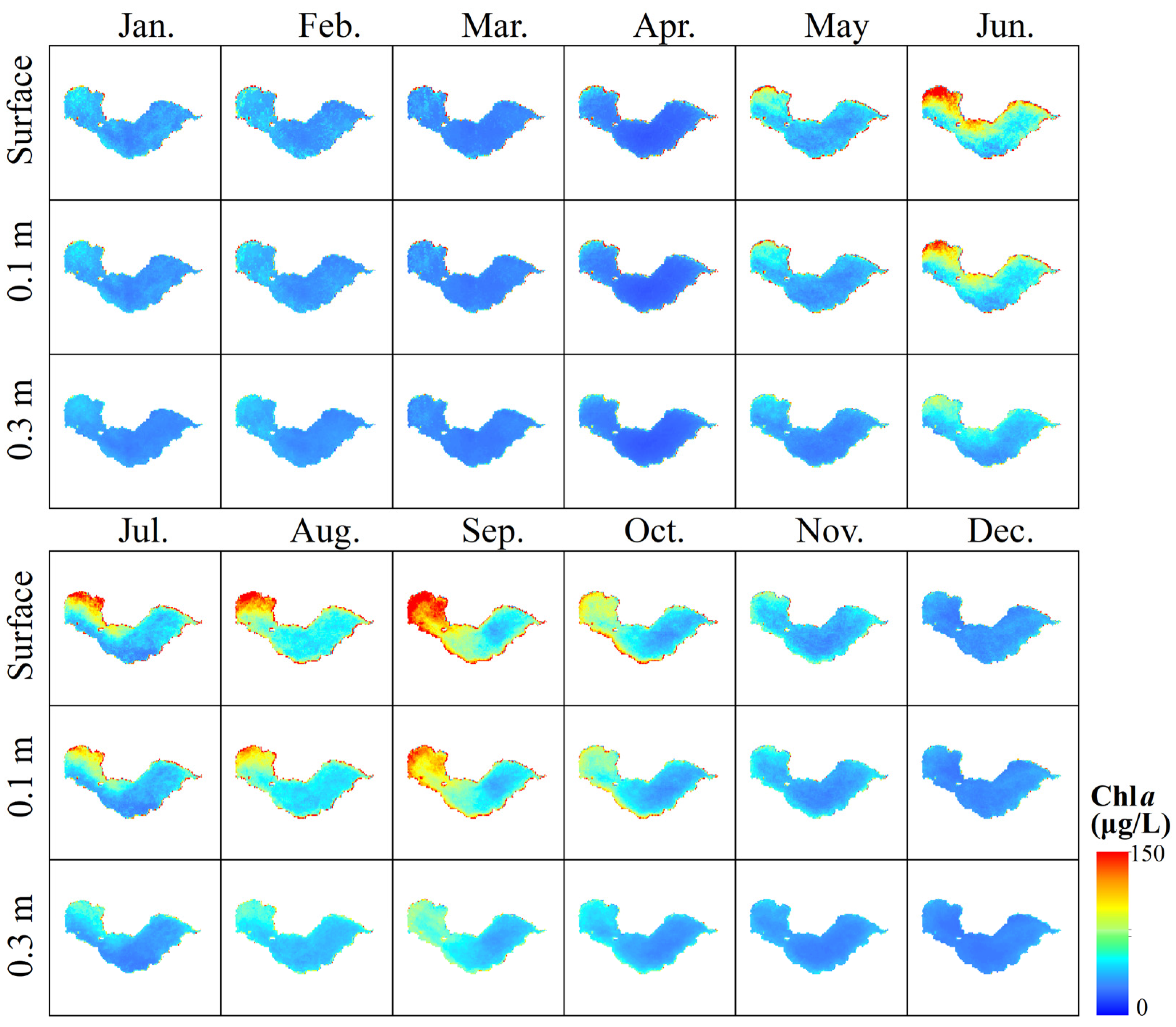
4.3. Temporal and Spatial Variations in Chla(z)
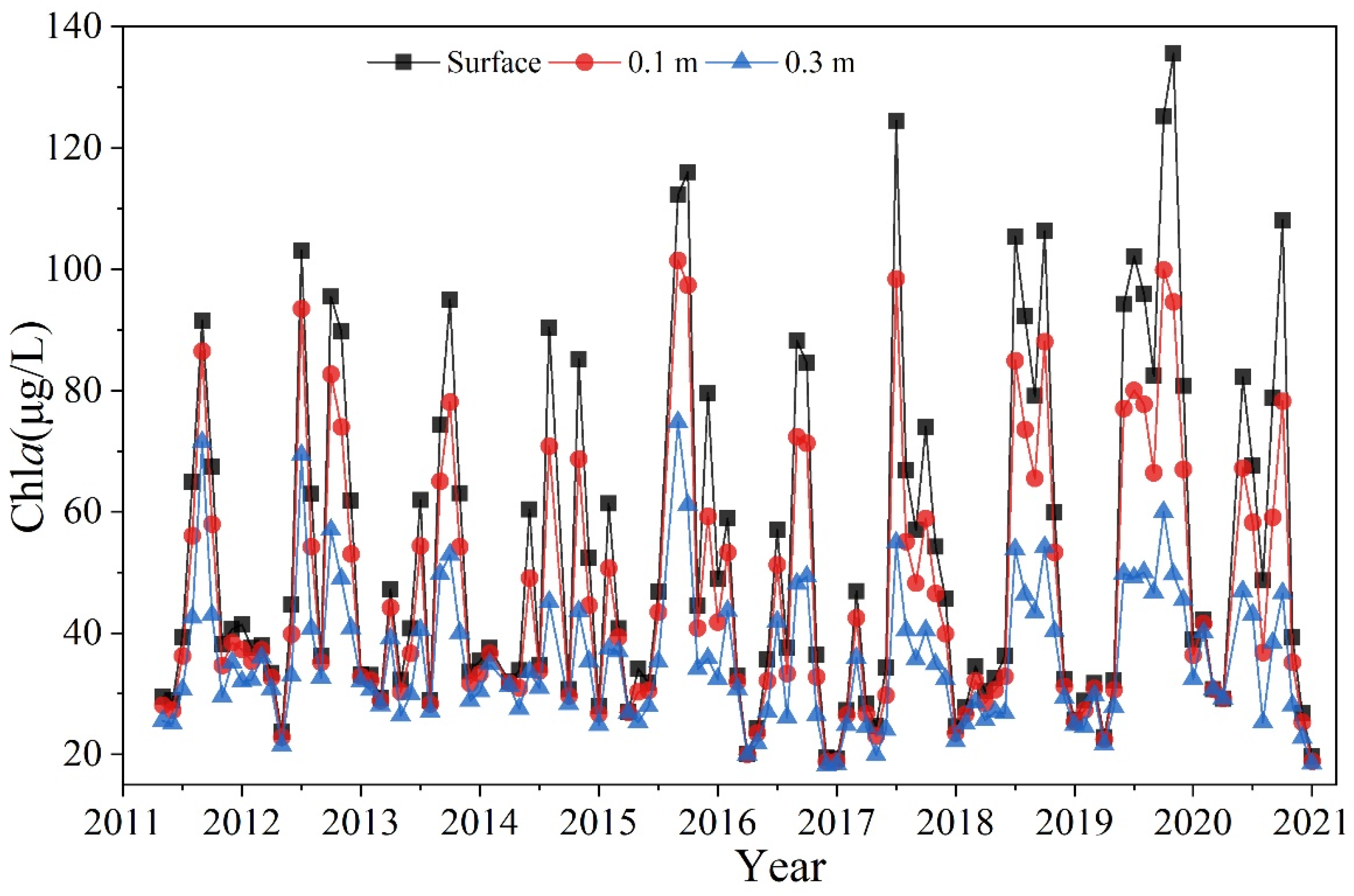
4.3.1. Interannual Variation in Chla(z)
4.3.2. Monthly Variation in Chla(z)
4.3.3. Diurnal Variations in Chla(z)
4.4. Dynamics of the Vertical Structural Parameters
5. Discussion
5.1. Advantages of the Proposed Chla(z) Inversion Model
5.2. Drivers of Diurnal Variation in Chla(z)
5.3. Uncertainties and Limitations
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jiang, Y.; He, W.; Liu, W.; Qin, N.; Ouyang, H.; Wang, Q.; Kong, X.; He, Q.; Yang, C.; Yang, B.; et al. The seasonal and spatial variations of phytoplankton community and their correlation with environmental factors in a large eutrophic Chinese lake (Lake Chaohu). Ecol. Indic. 2014, 40, 58–67. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, Y.; Zhao, Y.; Wang, L.; Chen, Y.; Yang, L. Spatiotemporal heterogeneities and driving factors of water quality and trophic state of a typical urban shallow lake (Taihu, China). Environ. Sci. Pollut. Res. 2022, 29, 53831–53843. [Google Scholar] [CrossRef] [PubMed]
- Le, C.; Hu, C.; English, D.; Cannizzaro, J.; Kovach, C. Climate-driven chlorophyll-a changes in a turbid estuary: Observations from satellites and implications for management. Remote Sens. Environ. 2013, 130, 11–24. [Google Scholar] [CrossRef]
- Ritchie, J.C.; Zimba, P.V.; Everitt, J.H. Remote Sensing Techniques to Assess Water Quality. Photogramm. Eng. Remote Sens. 2003, 69, 695–704. [Google Scholar] [CrossRef]
- Liu, D.; Yu, S.; Cao, Z.; Qi, T.; Duan, H. Process-oriented estimation of column-integrated algal biomass in eutrophic lakes by MODIS/Aqua. Int. J. Appl. Earth Obs. Geoinf. 2021, 99, 102321. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Shi, K.; Zhou, Y.; Zhang, Y.; Liu, X.; Guo, Y. Spatiotemporal dynamics of chlorophyll-a in a large reservoir as derived from Landsat 8 OLI data: Understanding its driving and restrictive factors. Environ. Sci. Pollut. Res. Int. 2018, 25, 1359–1374. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.; Ma, R.; Hu, M.; Xue, K.; Cao, Z.; Xiong, J. An improved algorithm for the column-integrated algal biomass retrieval in Lake Chaohu, a large eutrophic lake. Int. J. Appl. Earth Obs. Geoinf. 2024, 127, 103670. [Google Scholar] [CrossRef]
- Shen, M.; Luo, J.; Cao, Z.; Xue, K.; Qi, T.; Ma, J.; Liu, D.; Song, K.; Feng, L.; Duan, H. Random forest: An optimal chlorophyll-a algorithm for optically complex inland water suffering atmospheric correction uncertainties. J. Hydrol. 2022, 615, 128685. [Google Scholar] [CrossRef]
- Duan, H.; Ma, R.; Xu, J.; Zhang, Y.; Zhang, B. Comparison of different semi-empirical algorithms to estimate chlorophyll-a concentration in inland lake water. Environ. Monit. Assess. 2010, 170, 231–244. [Google Scholar] [CrossRef]
- Huang, X.; Zhu, J.; Han, B.; Jamet, C.; Tian, Z.; Zhao, Y.; Li, J.; Li, T. Evaluation of Four Atmospheric Correction Algorithms for GOCI Images over the Yellow Sea. Remote Sens. 2019, 11, 1631. [Google Scholar] [CrossRef]
- Wang, M.; Shi, W.; Jiang, L. Characterization of ocean color retrievals and ocean diurnal variations using the Geostationary Ocean Color Imager (GOCI). Int. J. Appl. Earth Obs. Geoinf. 2023, 122, 103404. [Google Scholar] [CrossRef]
- Cao, Z.; Ma, R.; Pahlevan, N.; Liu, M.; Melack, J.M.; Duan, H.; Xue, K.; Shen, M. Evaluating and Optimizing VIIRS Retrievals of Chlorophyll-a and Suspended Particulate Matter in Turbid Lakes Using a Machine Learning Approach. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–17. [Google Scholar] [CrossRef]
- Li, J.; Ma, R.; Xue, K.; Zhang, Y.; Loiselle, S. A Remote Sensing Algorithm of Column-Integrated Algal Biomass Covering Algal Bloom Conditions in a Shallow Eutrophic Lake. ISPRS Int. J. Geo Inf. 2018, 7, 466. [Google Scholar] [CrossRef]
- Qi, L.; Hu, C.; Duan, H.; Barnes, B.; Ma, R. An EOF-Based Algorithm to Estimate Chlorophyll a Concentrations in Taihu Lake from MODIS Land-Band Measurements: Implications for Near Real-Time Applications and Forecasting Models. Remote Sens. 2014, 6, 10694–10715. [Google Scholar] [CrossRef]
- O’Reilly, J.E.; Werdell, P.J. Chlorophyll algorithms for ocean color sensors—OC4, OC5 & OC6. Remote Sens. Environ. 2019, 229, 32–47. [Google Scholar] [PubMed]
- Hu, C.; Lee, Z.; Franz, B. Chlorophylla algorithms for oligotrophic oceans: A novel approach based on three-band reflectance difference. J. Geophys. Res. Ocean. 2012, 117, C01011. [Google Scholar] [CrossRef]
- Wang, M.; Son, S. VIIRS-derived chlorophyll-a using the ocean color index method. Remote Sens. Environ. 2016, 182, 141–149. [Google Scholar] [CrossRef]
- Niu, C.; Tan, K.; Wang, X.; Du, P.; Pan, C. A semi-analytical approach for estimating inland water inherent optical properties and chlorophyll a using airborne hyperspectral imagery. Int. J. Appl. Earth Obs. Geoinf. 2024, 128, 103774. [Google Scholar] [CrossRef]
- Le, C.; Li, Y.; Zha, Y.; Sun, D.; Huang, C.; Lu, H. A four-band semi-analytical model for estimating chlorophyll a in highly turbid lakes: The case of Taihu Lake, China. Remote Sens. Environ. 2009, 113, 1175–1182. [Google Scholar] [CrossRef]
- Pan, Y.; Guo, Q.; Sun, J.; Ma, R. Advances in remote sensing inversion method of chlorophyll a concentration. Sci. Surv. Mapp. 2017, 42, 43–48. [Google Scholar]
- Carder, K.L.; Chen, F.R.; Cannizzaro, J.P.; Campbell, J.W.; Mitchell, B.G. Performance of the MODIS semi-analytical ocean color algorithm for chlorophyll-a. Adv. Space Res. 2004, 33, 1152–1159. [Google Scholar] [CrossRef]
- Lee, Z.; Shang, S.; Qi, L.; Yan, J.; Lin, G. A semi-analytical scheme to estimate Secchi-disk depth from Landsat-8 measurements. Remote Sens. Environ. 2016, 177, 101–106. [Google Scholar] [CrossRef]
- Kratzer, S.; Brockmann, C.; Moore, G. Using MERIS full resolution data to monitor coastal waters—A case study from Himmerfjärden, a fjord-like bay in the northwestern Baltic Sea. Remote Sens. Environ. 2008, 112, 2284–2300. [Google Scholar] [CrossRef]
- Huang, C.; Yang, H.; Zhu, A.; Zhang, M.; Lü, H.; Huang, T.; Zou, J.; Li, Y. Evaluation of the Geostationary Ocean Color Imager (GOCI) to monitor the dynamic characteristics of suspension sediment in Taihu Lake. Int. J. Remote Sens. 2015, 36, 3859–3874. [Google Scholar] [CrossRef]
- Kutser, T.; Metsamaa, L.; Dekker, A.G. Influence of the vertical distribution of cyanobacteria in the water column on the remote sensing signal. Estuar. Coast. Shelf Sci. 2008, 78, 649–654. [Google Scholar] [CrossRef]
- Uitz, J.; Claustre, H.; Morel, A.; Hooker, S.B. Vertical distribution of phytoplankton communities in open ocean: An assessment based on surface chlorophyll. J. Geophys. Res. Ocean. 2006, 111, C08005. [Google Scholar] [CrossRef]
- Morel, A.; Berthon, J. Surface Pigments, Algal Biomass Profiles, and Potential Production of the Euphotic Layer: Relationships Reinvestigated in View of Remote-Sensing Applications. Limnol. Oceanogr. 1989, 34, 1545–1562. [Google Scholar] [CrossRef]
- Lewis, M.R.; Cullen, J.J.; Platt, T. Phytoplankton and thermal structure in the upper ocean: Consequences of nonuniformity in chlorophyll profile. J. Geophys. Res. Ocean. 1983, 88, 2565–2570. [Google Scholar] [CrossRef]
- Kimura, N.; Yoshihiro, O. Estimation of vertical profile of chlorophyll concentration around the Antarctic Peninsula derived from satellite image. J. Sch. Mar. Sci. Technol. Tokai Univ. 1997, 10, 75–93. [Google Scholar]
- Platt, T.; Shubha, S.; Carla-M, C.; Al, E. Ocean primary production and available light: Further algorithms for remote sensing. Deep. Sea Res. Part A Oceanogr. Res. Pap. 1988, 35, 855–879. [Google Scholar] [CrossRef]
- Siswanto, E.; Ishizaka, J.; Yokouchi, K. Estimating Chlorophyll-a Vertical Profiles from Satellite Data and the Implication for Primary Production in the Kuroshio Front of the East China Sea. J. Oceanogr. 2005, 61, 575–589. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, R.; Duan, H.; Loiselle, S.; Xu, J. A Spectral Decomposition Algorithm for Estimating Chlorophyll-a Concentrations in Lake Taihu, China. Remote Sens. 2014, 6, 5090–5106. [Google Scholar] [CrossRef]
- Cui, T.W.; Liang, X.J.; Gong, J.L.; Tong, C.; Xiao, Y.F.; Liu, R.J.; Zhang, X.; Zhang, J. Assessing and refining the satellite-derived massive green macro-algal coverage in the Yellow Sea with high resolution images. ISPRS J. Photogramm. Remote Sens. 2018, 144, 315–324. [Google Scholar] [CrossRef]
- Millán Núñez, R.; Alvarez Borrego, S.; Trees, C.C. Modeling the vertical distribution of chlorophyll in the California Current System. J. Geophys. Res. 1997, 102, 8587–8595. [Google Scholar] [CrossRef]
- Hu, Y.; Chen, J. Vertical distribution of chlorophyll a fluorescence and its response to temperature and salinity near Taiwan Bank in summer. J. Trop. Oceanogr. 2008, 27, 18–24. [Google Scholar]
- Xue, K.; Zhang, Y.; Duan, H.; Ma, R.; Loiselle, S.; Zhang, M. A Remote Sensing Approach to Estimate Vertical Profile Classes of Phytoplankton in a Eutrophic Lake. Remote Sens. 2015, 7, 14403–14427. [Google Scholar] [CrossRef]
- Lai, L.; Zhang, Y.; Cao, Z.; Liu, Z.; Yang, Q. Algal biomass mapping of eutrophic lakes using a machine learning approach with MODIS images. Sci. Total Environ. 2023, 880, 163357. [Google Scholar] [CrossRef]
- Serodio, J.; Cartaxana, P.; Coelho, H.; Vieira, S. Effects of chlorophyll fluorescence on the estimation of microphytobenthos biomass using spectral reflectance indices. Remote Sens. Environ. 2009, 113, 1760–1768. [Google Scholar] [CrossRef]
- Jeffrey, S.W.; Humphrey, G.F. New spectrophotometric equations for determining chlorophylls a, b, c1 and c2 in higher plants, algae and natural phytoplankton. Biochemie. Physiologie. Pflanzen. 1975, 167, 191–194. [Google Scholar] [CrossRef]
- Lorenzen, C.J. Determination of chlorophyll and pheo-pigments: Spectrophotometric equations. Limnol. Oceanogr. 1967, 12, 343–346. [Google Scholar] [CrossRef]
- Tang, J.; Tian, G.; Wang, X.; Wang, X.; Song, Q. The Methods of Water Spectra Measurement and Analysis Ⅰ: Above-Water Method. J. Remote Sens. 2004, 8, 37–44. [Google Scholar]
- Mobley, C.D. Estimation of the remote-sensing reflectance from above-surface measurements. Appl. Optics. 1999, 38, 7442–7455. [Google Scholar] [CrossRef] [PubMed]
- Jiang, L.; Wang, M. Improved near-infrared ocean reflectance correction algorithm for satellite ocean color data processing. Opt. Express 2014, 22, 21657–21678. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Ahn, J.; Jiang, L.; Shi, W.; Son, S.; Park, Y.; Ryu, J. Ocean color products from the Korean Geostationary Ocean Color Imager (GOCI). Opt. Express 2013, 21, 3835–3849. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Wei, X.; Huang, Z.; Li, H.; Ma, R.; Cao, Z.; Shen, M.; Xue, K. Retrievals of Chlorophyll-a from GOCI and GOCI-II Data in Optically Complex Lakes. Remote Sens. 2023, 15, 4886. [Google Scholar] [CrossRef]
- Xue, K.; Ma, R.; Shen, M.; Wu, J.; Hu, M.; Guo, Y.; Cao, Z.; Xiong, J. Horizontal and vertical migration of cyanobacterial blooms in two eutrophic lakes observed from the GOCI satellite. Water Res. 2023, 240, 120099. [Google Scholar] [CrossRef] [PubMed]
- Hunter, P.D.; Tyler, A.N.; Willby, N.J.; Gilvear, D.J. The spatial dynamics of vertical migration by Microcystis aeruginosa in a eutrophic shallow lake: A case study using high spatial resolution time-series airborne remote sensing. Limnol. Oceanogr. 2008, 53, 2391–2406. [Google Scholar] [CrossRef]
- Molina, M.O.; Gutiérrez, C.; Sánchez, E. Comparison ofERA5 surface wind speed climatologies over Europe with observations from theHadISD dataset. Int. J. Climatol. 2021, 41, 4864–4878. [Google Scholar] [CrossRef]
- Qi, L.; Hu, C.; Visser, P.M.; Ma, R. Diurnal changes of cyanobacteria blooms in Taihu Lake as derived from GOCI observations. Limnol. Oceanogr. 2018, 63, 1711–1726. [Google Scholar] [CrossRef]
- Cai, X.; Cui, T.; Zheng, R.; Qin, P.; Mu, B. Comparison of algorithms for green macro-algae bloom detection based on geostationary ocean color imager. J. Remote Sens. 2014, 29, 44–50. [Google Scholar]
- Zhang, X.; Zheng, X. Comparison of inversion of Chlorophyll concentration in the Bohai Bay based on GOCI Data. Mar. Sci. Bull. 2017, 19, 62–74. [Google Scholar]
- Shi, K.; Zhang, Y.; Zhou, Y.; Liu, X.; Zhu, G.; Qin, B.; Gao, G. Long-term MODIS observations of cyanobacterial dynamics in Lake Taihu: Responses to nutrient enrichment and meteorological factors. Sci. Rep. 2017, 7, 40326. [Google Scholar] [CrossRef] [PubMed]
- Feng, T.; Pang, Z.; Jiang, W. Remote sensing retrieval of chlorophyll-a concentration in Lake Chaohu based on zhuhai-1 hyperspectral satellite. Spectrosc. Spectr. Anal. 2022, 42, 2642–2648. [Google Scholar]
- Bengio, Y.; Grandvalet, Y. No Unbiased Estimator of the Variance of K-Fold Cross-Validation. J. Mach. Learn. Res. 2004, 5, 1089–1105. [Google Scholar]
- Qin, B. Shallow lake limnology and control of eutrophication in Lake Taihu. J. Lake Sci. 2020, 32, 1229–1243. [Google Scholar]
- Li, J.; Zhang, Y.; Ma, R.; Duan, H.; Loiselle, S.; Xue, K.; Liang, Q. Satellite-Based Estimation of Column-Integrated Algal Biomass in Nonalgae Bloom Conditions: A Case Study of Lake Chaohu, China. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2017, 10, 450–462. [Google Scholar] [CrossRef]
- Hu, M.; Zhang, Y.; Ma, R.; Xue, K.; Cao, Z.; Chu, Q.; Jing, Y. Optimized remote sensing estimation of the lake algal biomass by considering the vertically heterogeneous chlorophyll distribution: Study case in Lake Chaohu of China. Sci. Total Environ. 2021, 771, 144811. [Google Scholar] [CrossRef] [PubMed]
- Duan, H.; Tao, M.; Loiselle, S.A.; Zhao, W.; Cao, Z.; Ma, R.; Tang, X. MODIS observations of cyanobacterial risks in a eutrophic lake: Implications for long-term safety evaluation in drinking-water source. Water Res. 2017, 122, 455–470. [Google Scholar] [CrossRef] [PubMed]
- Leach, T.H.; Beisner, B.E.; Carey, C.C.; Pernica, P.; Rose, K.C.; Huot, Y.; Brentrup, J.A.; Domaizon, I.; Grossart, H.P.; Ibelings, B.W.; et al. Patterns and drivers of deep chlorophyll maxima structure in 100 lakes: The relative importance of light and thermal stratification. Limnol. Oceanogr. 2018, 63, 628–646. [Google Scholar] [CrossRef]
- Li, Y.; Shi, K.; Zhang, Y.; Zhu, G.; Qin, B.; Zhang, Y.; Liu, M.; Zhu, M.; Dong, B.; Guo, Y. Remote sensing of column-integrated chlorophyll a in a large deep-water reservoir. J. Hydrol. 2022, 610, 127918. [Google Scholar] [CrossRef]
- Page, B.P.; Kumar, A.; Mishra, D.R. A novel cross-satellite based assessment of the spatio-temporal development of a cyanobacterial harmful algal bloom. Int. J. Appl. Earth Obs. Geoinf. 2018, 66, 69–81. [Google Scholar] [CrossRef]
- Hu, C.; Lee, Z.; Ma, R.; Yu, K.; Li, D.; Shang, S. Moderate Resolution Imaging Spectroradiometer (MODIS) observations of cyanobacteria blooms in Taihu Lake, China. J. Geophys. Res. Ocean. 2010, 115, C04002. [Google Scholar] [CrossRef]
- Xu, N.; Lu, H.; Li, W.; Gong, P. Natural lakes dominate global water storage variability. Sci. Bull. 2024, 69, 1016–1019. [Google Scholar] [CrossRef] [PubMed]



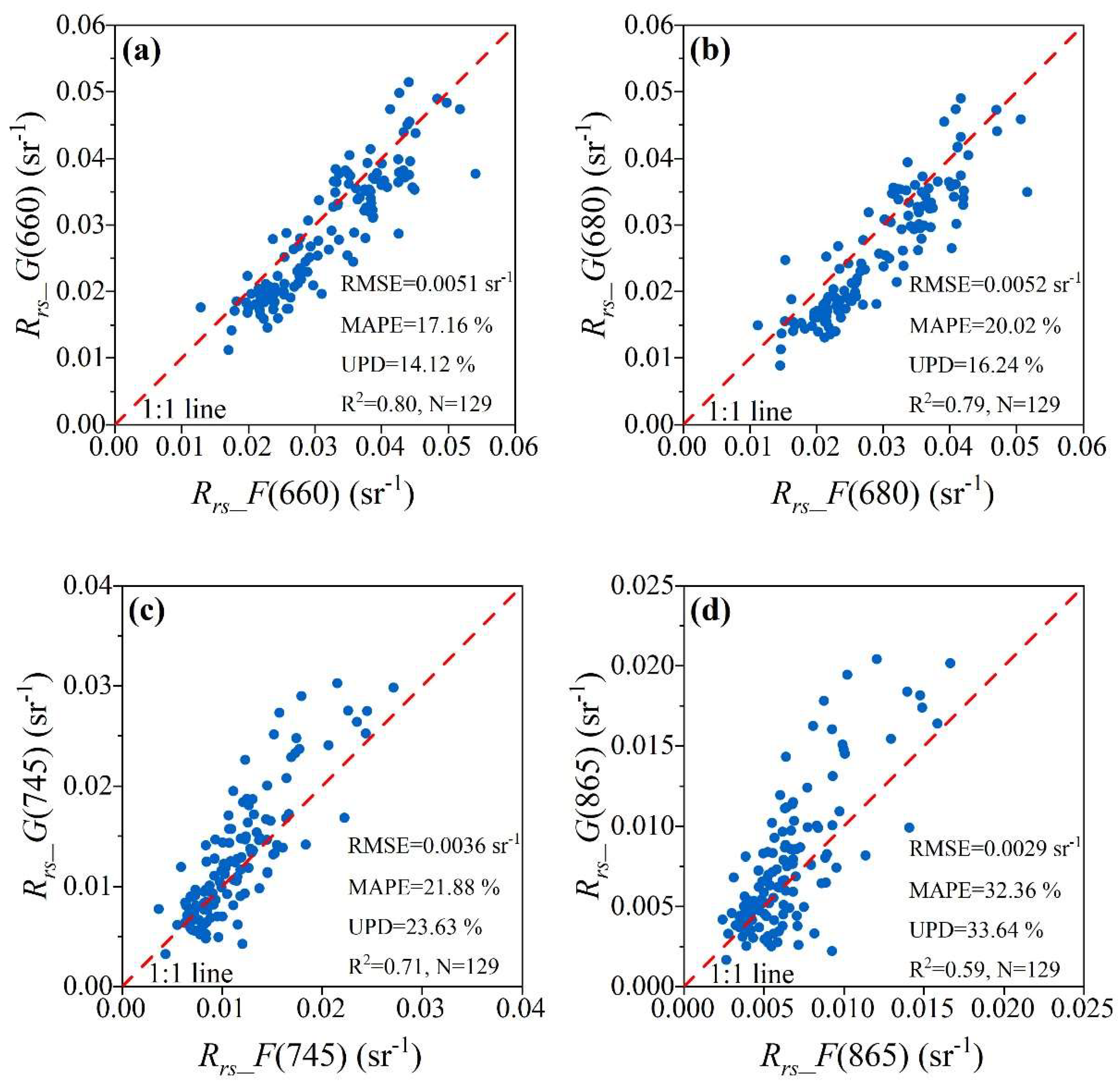
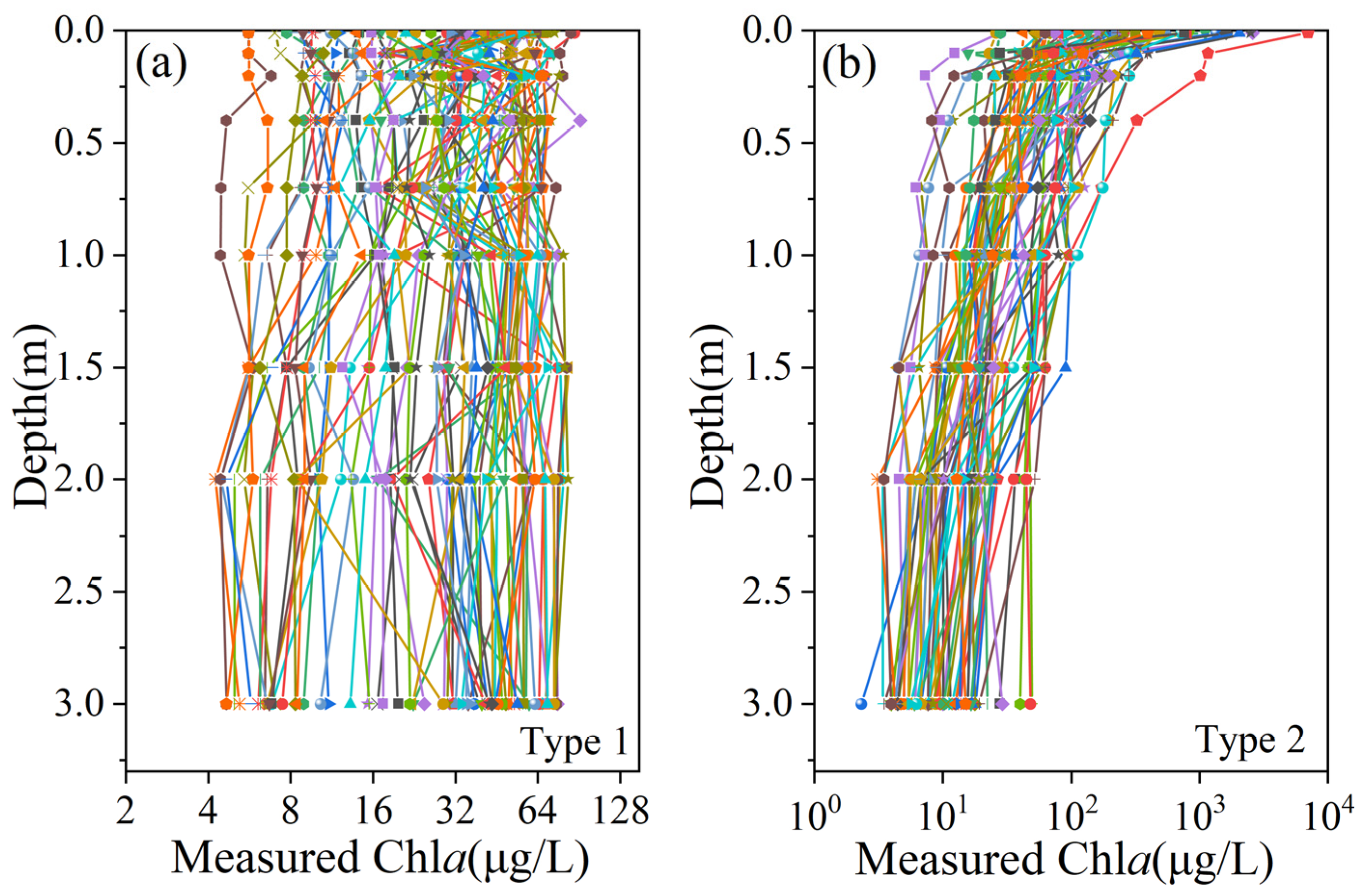
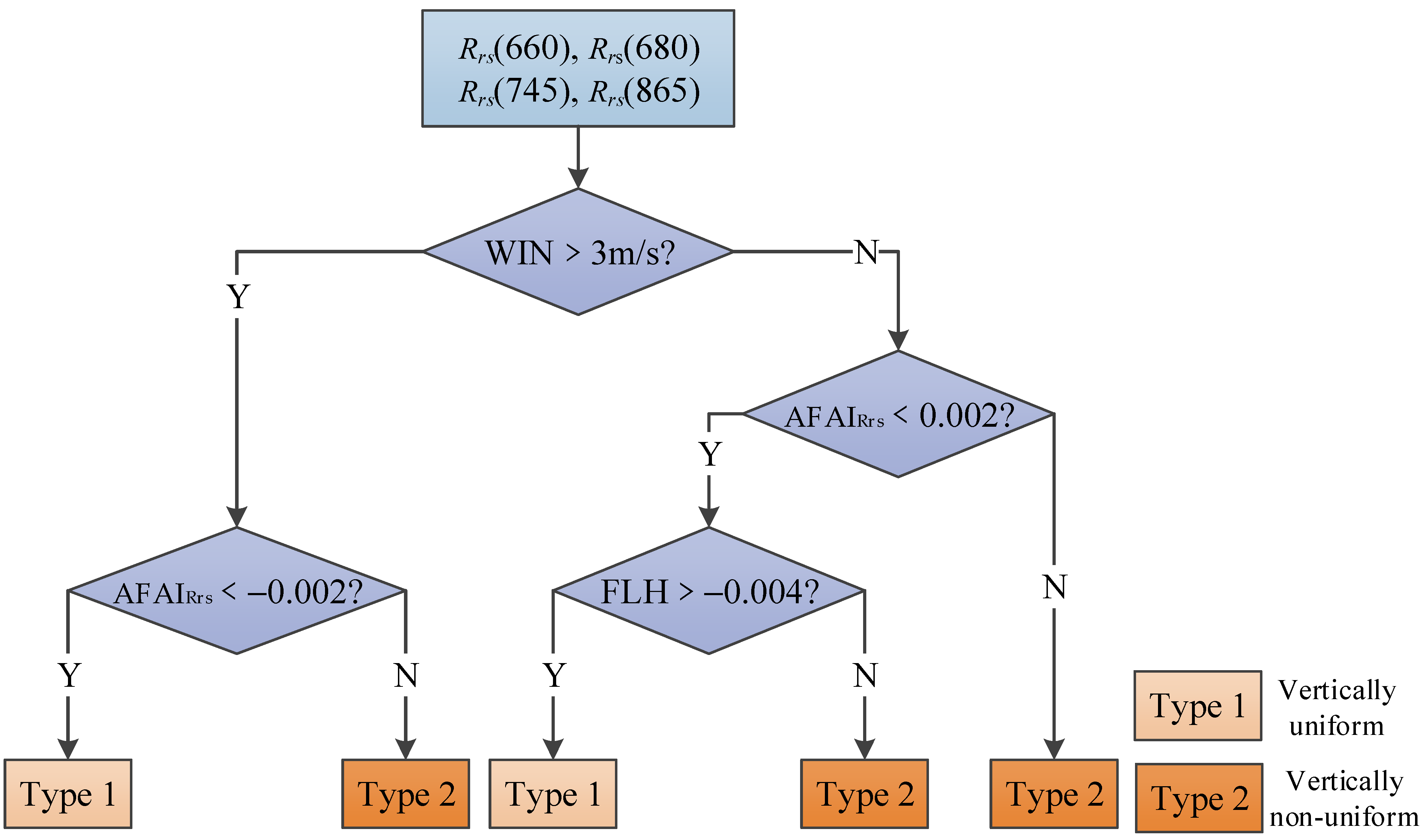
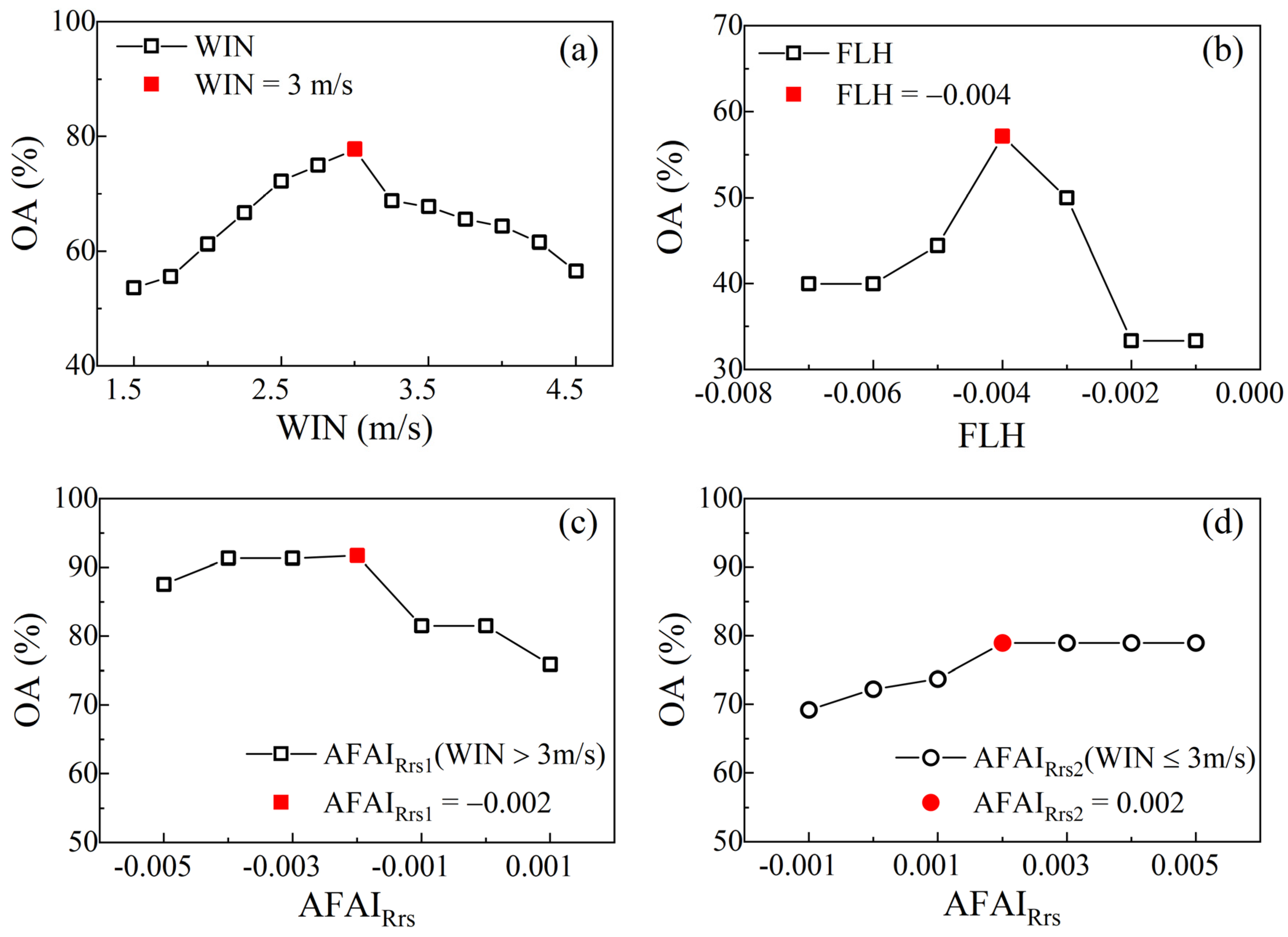



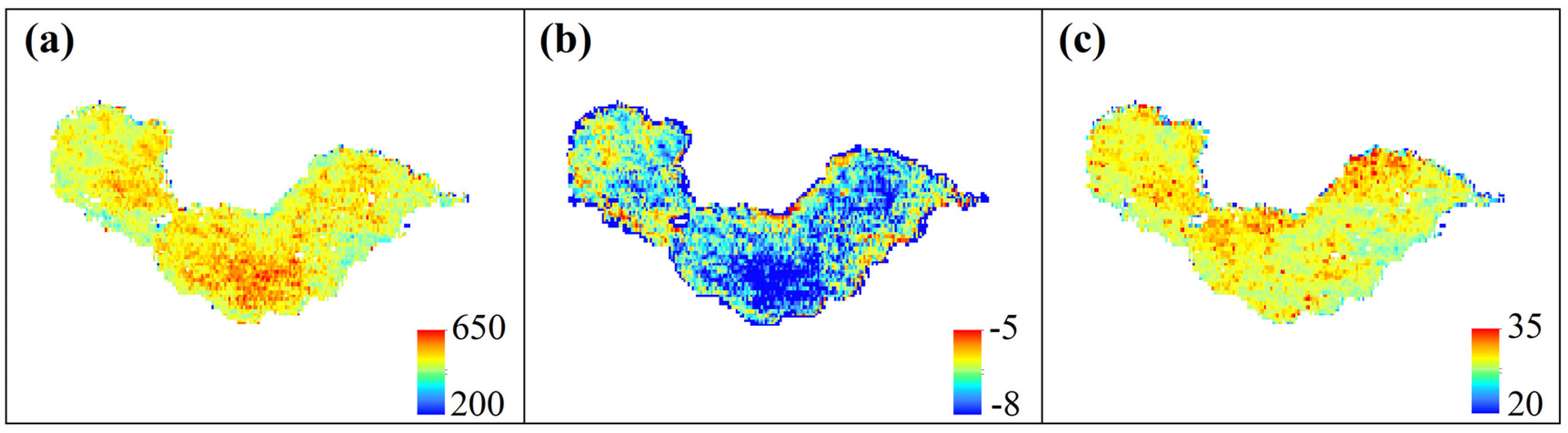
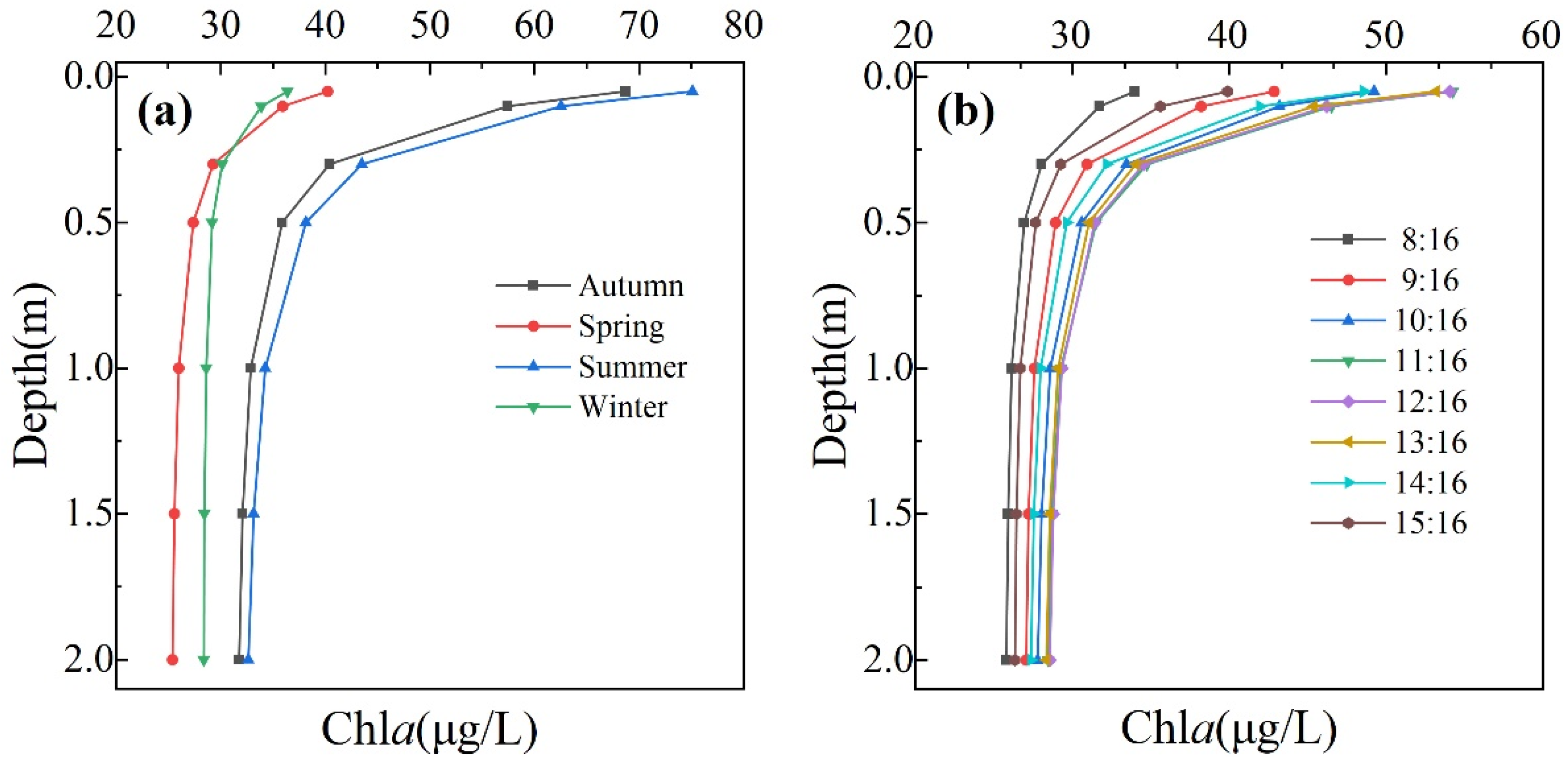
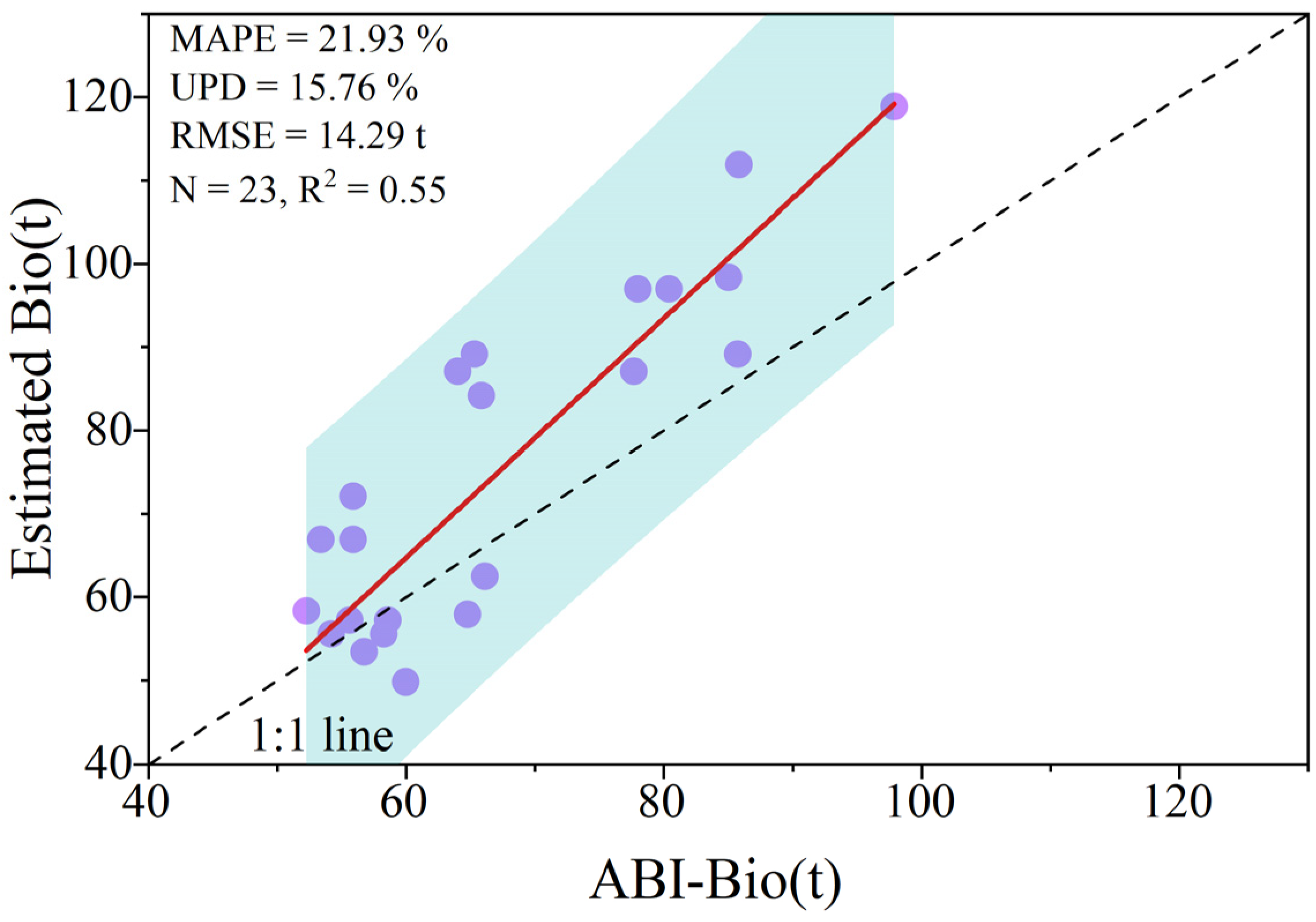

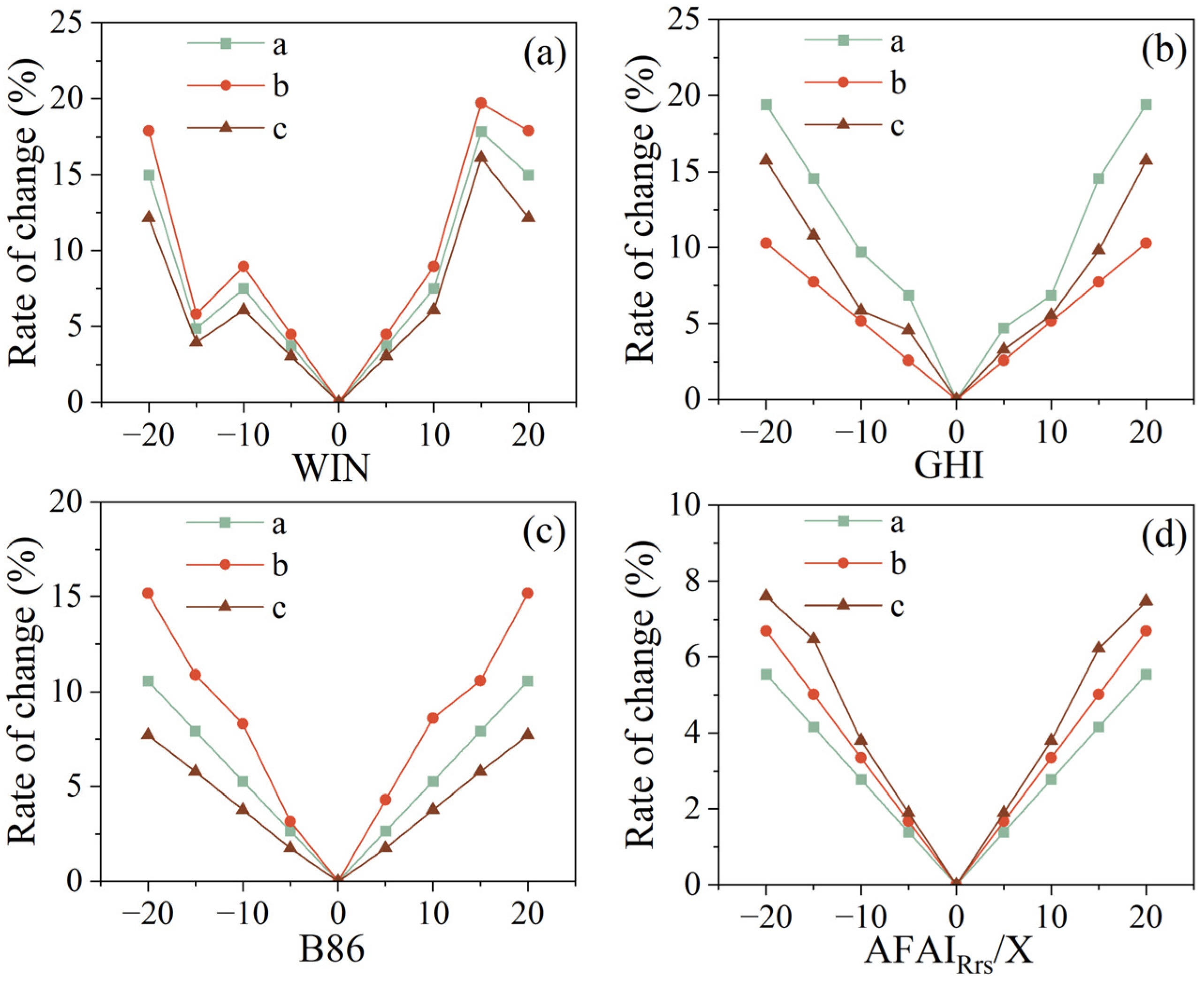
| Single-Band Factor | r | Index Factor | r | Index Factor | r |
|---|---|---|---|---|---|
| B5 (660 nm) | −0.34 | AFAIRrs (B7, B5, B8) | 0.67 | NDVI (B7, B5) | 0.66 |
| B6 (680 nm) | −0.44 | FLH (B6, B5, B7) | −0.51 | B8/B7 (B8, B7) | 0.17 |
| B7 (745 nm) | 0.27 | SI (B5, B8) | −0.55 | WIN | −0.45 |
| B8 (865 nm) | 0.26 | X (B5, B6, B7) | −0.41 |
| Name | Function | R² | RMSE (μg/L) | UPD (%) | MAPE (%) |
|---|---|---|---|---|---|
| Model 1 | Chla(z) = a × exp(b × z) + c | 0.98 | 38.15 | 23.03 | 17.15 |
| Model 2 | Chla(z) = a2 × exp(b2 × z + c2) | 0.97 | 45.15 | 29.28 | 20.05 |
| Model 3 | Chla(z) = a3 × exp(b3 × z) | 0.97 | 45.43 | 27.60 | 21.00 |
| Model 4 | Chla(z) = a4 × zb4 + c4 | 0.92 | 96.28 | 51.35 | 37.41 |
| Model 5 | Chla(z) = a5 × zb5 | 0.97 | 38.08 | 26.44 | 21.14 |
| Measured Class | User’s Accuracy | ||||
|---|---|---|---|---|---|
| Type 1 | Type 2 | Total | |||
| Predicted class | Type 1 | 28 | 5 | 33 | 85% |
| Type 2 | 2 | 33 | 35 | 94% | |
| Total | 30 | 38 | 68 | ||
| Producer’s Accuracy | 93% | 87% | |||
| Overall Accuracy | 89% | Kappa | 0.79 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Wei, X.; Huang, Z.; Liu, H.; Ma, R.; Wang, M.; Hu, M.; Jiang, L.; Xue, K. Monitoring the Vertical Variations in Chlorophyll-a Concentration in Lake Chaohu Using the Geostationary Ocean Color Imager. Remote Sens. 2024, 16, 2611. https://doi.org/10.3390/rs16142611
Li H, Wei X, Huang Z, Liu H, Ma R, Wang M, Hu M, Jiang L, Xue K. Monitoring the Vertical Variations in Chlorophyll-a Concentration in Lake Chaohu Using the Geostationary Ocean Color Imager. Remote Sensing. 2024; 16(14):2611. https://doi.org/10.3390/rs16142611
Chicago/Turabian StyleLi, Hanhan, Xiaoqi Wei, Zehui Huang, Haoze Liu, Ronghua Ma, Menghua Wang, Minqi Hu, Lide Jiang, and Kun Xue. 2024. "Monitoring the Vertical Variations in Chlorophyll-a Concentration in Lake Chaohu Using the Geostationary Ocean Color Imager" Remote Sensing 16, no. 14: 2611. https://doi.org/10.3390/rs16142611
APA StyleLi, H., Wei, X., Huang, Z., Liu, H., Ma, R., Wang, M., Hu, M., Jiang, L., & Xue, K. (2024). Monitoring the Vertical Variations in Chlorophyll-a Concentration in Lake Chaohu Using the Geostationary Ocean Color Imager. Remote Sensing, 16(14), 2611. https://doi.org/10.3390/rs16142611







