Abstract
The consistent speckle noise in SAR images easily interferes with the semantic information of the target. Additionally, the limited quantity of supervisory information available in one-shot learning leads to poor performance. To address the aforementioned issues, we creatively propose an SAR target recognition model based on one-shot learning. This model incorporates a background noise removal technique to eliminate the interference caused by consistent speckle noise in the image. Then, a global and local complementary strategy is employed to utilize the data’s inherent a priori information as a supplement to the supervisory information. The experimental results show that our approach achieves a recognition performance of 70.867% under the three-way one-shot condition, which attains a minimum improvement of 7.467% compared to five state-of-the-art one-shot learning methods. The ablation studies demonstrate the efficacy of each design introduced in our model.
1. Introduction
Thanks to its exceptional resolution and dynamic imaging capability [1,2,3], synthetic aperture radar (SAR) has been widely utilized in various domains, particularly in military target surveillance and early warning, urban planning, land resource identification, marine ecological protection, and natural disaster mitigation. The process of SAR target identification involves the efficient detection of spatial targets using electromagnetic waves, which yields a great deal of significant information about the target. Nevertheless, due to the intricacy of SAR imaging, the grayscale images frequently exhibit a significant level of background noise [4]. Consequently, relying solely on conventional manual target recognition methods becomes challenging when attempting to extract useful information efficiently. Hence, researchers have been increasingly interested in SAR target recognition, which possesses the capability to capture target properties automatically [5]. This technique offers a streamlined approach to processing and analyzing intricate data in SAR images, resulting in a notable enhancement in the precision and efficiency of information extraction.
With the rapid advancement of deep learning technology in recent years, various approaches have been developed for autonomous target recognition in SAR [6,7,8,9] and hyperspectral detection [10,11,12,13,14]. However, the majority of these approaches require substantial labeled samples to achieve exceptional recognition performance. However, in crucial areas such as intelligence gathering and military target selection, the quantity of accessible samples is limited [15], occasionally consisting of only one or a few samples. In this case, the model is extremely prone to overfitting [16]. While there have been studies examining SAR target recognition under few-shot conditions, one-shot learning is more common and challenging in real-world applications [17]. This indicates that it is necessary to solve the SAR target recognition problem in the context of one-shot learning.
Furthermore, the high level of coherence in the radar scattering process results in the presence of coherent speckle noise in SAR grayscale images, which presents a significant obstacle to achieving high image quality [18]. The noise not only alters the genuine semantic content of the objects but also causes the deficiency of object details. Moreover, the production of superior SAR images is intrinsically a laborious and intricate process which requires advanced signal processing and image reconstruction techniques. The application of these methods not only demands substantial time but also necessitates considerable processing resources. Therefore, these technical difficulties present a significant barrier to the extensive utilization of SAR imaging in the domain of automated identification and real-time surveillance.
In this paper, we propose a one-shot learning model to address the issue of SAR recognition. To tackle the aforementioned problems, this study introduces an SAR target recognition model based on one-shot learning. We propose a background adaptive denoising technique with KSW entropy to address the interference from coherent speckle noise in SAR grayscale images. The objective of this method is to eliminate coherent speckle noise and mitigate the impact of background noise on image recognition. Given the scarcity of information from a single sample, it is more probable for the model to overfit. Our approach involves integrating both global and local perspectives to optimize the exploitation of the information obtained from individual samples.
To assess the effectiveness of our model, we employ the MSTAR dataset and generate a dataset called MiniSAR for one-shot learning. Subsequently, the dataset is employed for all the one-shot methods to evaluate their performances. The following are the contributions of this paper:
- To the best of our knowledge, this work is the first study that addresses the issue of SAR’s problem using one-shot learning.
- A novel denoising technique is introduced which utilizes KSW entropy to adaptively remove background noise from SAR grayscale images. This method effectively mitigates recognition interference caused by noise.
- We propose a mutual learning approach that combines global and local viewpoints to effectively extract prior information from individual samples.
- We propose an adaptive, stochastic-cropping data augmentation technique that redirects the model’s attention away from irrelevant areas and focuses it solely on learning the target regions.
- To address the challenge of acquiring SAR images, we present a metric-based one-shot learning method. Experimental findings demonstrate that our model has achieved the best recognition performance compared with other one-shot learning methods.
The subsequent sections of this work are structured in the following manner: Section 2 presents a thorough and extensive examination of the relevant literature. In Section 3, we provide a comprehensive explanation of our suggested approach. Section 4 provides an overview of the experimental data and displays the corresponding results. Finally, we summarize our efforts and derive conclusions.
2. Related Work
2.1. Metric-Based One Shot Learning
For the efficient categorization of images with limited data, it is essential to comprehend the distance or similarity function in an embedding space in one-shot recognition methods that rely on metric learning. Koch et al. [19] created Siamese neural networks that evaluate the similarity of inputs by utilizing distinctive properties to provide predictions for fresh data and categories. Vinyals et al. [20] created matching networks, which utilize a framework that combines deep neural characteristics with external memories to quickly adapt to new class types. Snell et al. [21] introduced prototypical networks, which streamline one-shot learning by computing distances to class prototypes in a metric space that is learned. In their study, Sung et al. [22] devised the relation network, which utilizes deep distance metrics to compare tiny sets of images. This approach seems to be effective in extending to one-shot learning situations. Hu et al. [23] addressed the task of identifying text in historical manuscripts using a one-shot method that matches spatial characteristics across images. Gao et al. [24] proposed a graph neural network approach for detecting faults in rolling bearings. They utilized one-shot learning to provide reliable performance even in changing situations. Abdi et al. [25] improved the accuracy of one-shot object identification by utilizing their sequential encoders network (SENet), which effectively enhances performance even while dealing with changes in domains. In their study, Wang et al. [26] specifically investigated myoelectric pattern recognition and employed one-shot learning to efficiently adjust interfaces in various contexts. In their study, Ma et al. [27] utilized one-shot learning techniques to analyze temporal knowledge graphs. Their objective was to extend reasoning to dynamic relationships with limited data. Together, these improvements demonstrate several uses of metric-based one-shot learning, each expanding the limits of what can be accomplished with a small number of training samples.
2.2. SAR Target Classification
SAR has gained significant attention because of its ability to capture high-resolution images regardless of weather and lighting conditions. As technology progresses, SAR target categorization can be categorized into two primary methods: those that rely on machine learning and those that rely on deep learning.
Machine learning methods depend on the use of manually crafted features for identification. Anagnostopoulos [28] investigated the discriminatory ability of target outline description features when combined with support vector machine (SVM)-based classification committees SAR target detection. Nilubol et al. [29] proposed the use of hidden Markov models (HMMs) to achieve translational and rotational invariant automated target identification (TRIATR) in SAR imagery. Yang et al. [30] performed empirical experiments on several methods of extracting features and classifiers for SAR image data, providing valuable insights into the field of autonomous target recognition. Zhang et al. [31] introduced an SAR target classification technique that utilizes Bayesian compressive sensing (BCS) with scattering center characteristics. The efficiency of this method was demonstrated through experiments conducted on SAR databases. Wang et al. [32] proposed a target detection technique for high-resolution SAR images using Bayesian-morphological saliency. This method combines Bayesian and morphological studies to achieve accurate target detection in complicated scenarios.
Deep learning techniques employ convolutional neural networks (CNNs) to automatically extract information of identification. Ding et al. [33] examined the effectiveness of CNNs in conjunction with data augmentation methods for recognizing SAR targets. They showed that this approach achieved exceptional results even under difficult settings. Chen et al. [34] proposed the use of all-convolutional networks (A-ConvNets) for SAR target categorization. These networks are able to achieve high accuracy by autonomously learning hierarchical features from sufficient training data. Wagner [35] proposed a hybrid method that combines CNNs and SVM for automatic target detection in SAR images. This approach improves the accuracy of classification by reducing the impact of imaging errors and variations in the target. Guo et al. [36] introduced SAR capsule networks, which utilize an extension of Hinton’s capsule network in a convolutional neural network to perform precise and resilient categorization of SAR images. Zheng et al. [37] introduced a location-aware graph neural network that enhances the model’s capacity to identify a limited number of samples by utilizing self-attention to capture the spatial correlation of position in the feature map.
3. Proposed Method
3.1. Overview
Our approach is inspired by [38], which adopts an image-to-class metric for the construction of the metric space. We present an SAR recognition model that utilizes one-shot learning which we will refer to as SOS for the sake of clarity in our explanation. The SOS consists of two phases, namely a background noise cancellation phase and a meta-training phase. The overall framework of the SOS model is shown in Figure 1 and Figure 2.

Figure 1.
Schematic of the background noise cancellation phase in the proposed model.
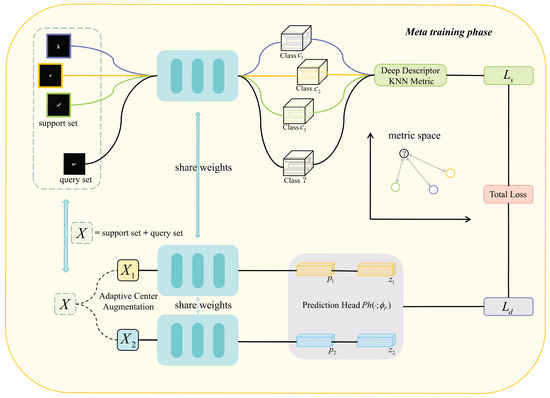
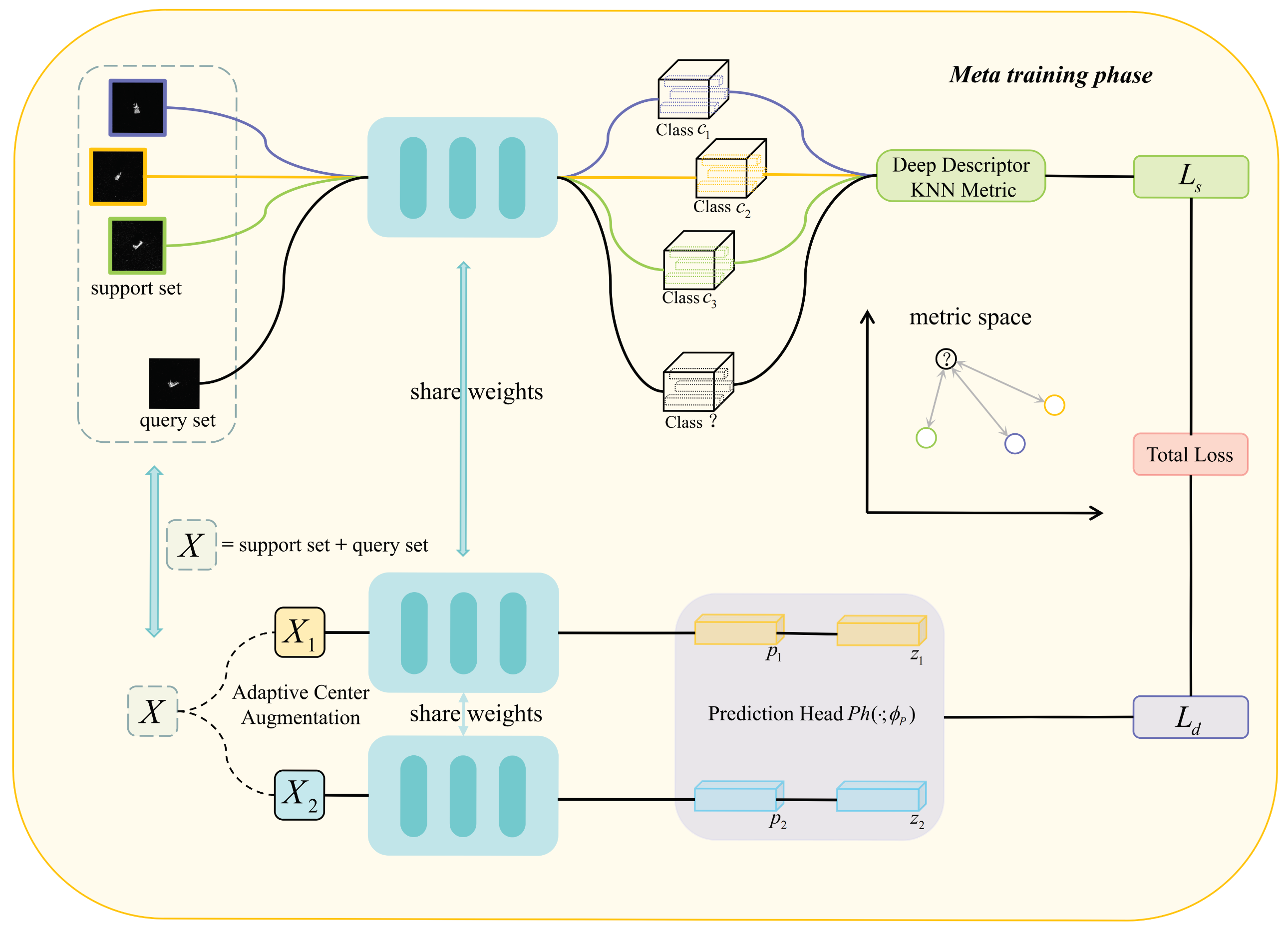
Figure 2.
Schematic representation of the meta-training phase in the proposed model.
Our model uses only two parameter modules: the embedding network and the predictor head module . are the parameters of the two modules, respectively. In the background noise cancellation phase, the input image I sampled using an -way -shot method is first subjected to grayscaling and pixel adjustment with median filtering to get a gray-smoothed image . The entropy of the image is computed after the normalization operation, the optimal threshold is computed using , threshold segmentation of the image is performed to get the finalized mask image, and the original image is weighted with the mask image to get the background noise cancellation image.
In the meta-training phase, the background noise cancellation image X obtained in the previous phase is first input into the embedding network to obtain the intermediate features , where and represent the support set and the query set, respectively. The K nearest neighbor algorithm L with cosine similarity metric is used to obtain the depth similarity score r, and is obtained from score r. Next, X is subjected to adaptive center augmentation in order to obtain two different viewpoints, and , and is inputted into the embedding network to obtain the intermediate features and for the different viewpoints. These are mapped by the prediction head to obtain and , and finally, is calculated from and . The overall objective function at this stage is:
where is the weighting factor, denotes local metric loss, and denotes global metric loss.
3.2. Background Inference Cancellation Strategy
The main objective of the metric-based one-shot approach is to establish a precise metric space, and the construction of this metric space relies on the selection of the metric method, as mentioned in literature [39]. There are typically two common metrics: image-to-image metrics (such as Proto and Relation) and image-to-class metrics (such as DN4 and ATL). However, regardless of the specific metrics used, the presence of coherent speckle noise in SAR images causes the target semantic information to be affected by irrelevant features. This, in turn, affects the model’s understanding of the target semantics. As a result, the model’s performance deteriorates. Therefore, we suggest implementing a background elimination strategy that utilizes the Kolmogorov Sinai Weiss (KSW) entropy mask. The procedural stages of the technique are as follows:
First, the input image I is grayed out and adjusted to uniform pixels, the image pixel value is adjusted to 256 × 256, and the image is filtered using a median filter of 3 × 3 size to eliminate some noise:
where M is the median filter, which effectively removes the pretzel noise from the image while retaining the edge information. For the filtered grayscale smoothed image , the histogram H can be calculated by the following equation:
where W and H are the width and height of the image, respectively, and 1 is the indicator function. Then, we normalize the histogram to obtain .
The entropy of the image is calculated from the normalized histogram:
where is a very small positive number used to avoid the error of dividing by zero when calculating logarithms.
The KSW entropy method was then used to determine the optimal threshold. For each potential threshold t, the cumulative histogram and cumulative entropy are computed. After determining the optimal threshold T, the image is thresholded and segmented in order to obtain the binarized mask image . Finally, the original image is superimposed with the mask image with given weights ( and ) to obtain the background noise cancellation image X:
3.3. Self-Supervised Global Complementary Learning Metric Space-Assisted Construction
Existing one-shot learning approaches frequently have limitations in their feature extraction and generalization capabilities when dealing with complicated and changeable SAR image classification applications. To address these difficulties, this study suggests a construction strategy that utilizes a self-supervised global complementary learning metric space. This strategy is based on self-supervision, which aims to fully exploit the latent prior knowledge in known single samples. It achieves this by learning the latent data space topology in unlabeled data [40] in order to complement the imperfect local metric rules.
The implementation of this strategy includes two main components: a Conv64F [38] encoder for extracting features from the original image and a self-supervised predictor to augment the feature representation learning process. The self-supervised predictor is composed of a projection head and a prediction head, as described in the literature [41]. This approach enables the model to not only capture the local features of the image but also learn the global relationships and patterns among these features. The Conv64F encoder, which utilizes a commonly used four-layer convolutional neural network as an embedding network, includes four convolutional blocks. Each block comprises a convolutional layer, a batch normalization layer, and a Leaky ReLU layer. Additionally, a maximum pooling layer follows each of the first two convolutional blocks. The embedding network is named Conv64F because each convolutional layer contains 64 filters of size .
The main task of self-supervised learning is to learn consistent and discriminative features by comparing and aligning image representations from different viewpoints. This process involves constructing pairs of images, each pair augmented by our proposed adaptive center augmentation method to simulate different viewing perspectives.
3.3.1. Adaptive Center Augmentation Method
In this work, we propose a novel cropping method based on the target center of images and which we call adaptive center augmentation, or ACA for short. Initially, the input image X is converted to grayscale and resized to uniform pixels of :
The OTSU thresholding method is used to calculate the optimal threshold, and the number of pixels at each gray level is tallied. Let represent the total number of pixels with gray level i in the image; then, the probability of a pixel being of gray level i is given by:
Segmenting the image with the threshold t yields average gray values for the background and target regions, denoted by and , respectively. These are calculated as follows:
where represents the probability of a pixel being at gray level i.
The total mean level of the image can be expressed as:
The intraclass variance is given by:
To find the optimal threshold, we let t traverse the range . The value of t that maximizes the inter-class variance is deemed the optimal threshold . Following this, for the binary image segmented using the OTSU algorithm, we iterate through the coordinates of all the white pixels to calculate the feature center coordinates, which are given by
where S represents the set of white pixel coordinates, and specifies the coordinates of a pixel that has a gray value of 255. Here, denotes the gray value at those coordinates. is the total count of points in set S, and and are, respectively, the horizontal and vertical coordinates of the i-th white pixel within the binary image.
After deriving the center coordinates , we perform random cropping based on the center coordinates and set up four random cropping ranges for the top, bottom, left, and right in order to ensure the integrity of the features:
where Left, Right, Upper, and Lower correspond to the left, right, top, and bottom boundary values, respectively, and the value of is taken as 25.
The image is centered on the coordinates and cropped to get the image based on the above four cropping ranges:
Finally, the image was obtained by randomized 45 degree rotation augmentation:
3.3.2. Implementation of Self-Supervised Contrastive Learning
The self-supervised loss calculation is performed based on the feature representations and , which are obtained by inputting the two augmented images and , generated from the original image X, into the encoder network :
These features are then processed by the predictor head to obtain the feature and and and :
The similarity loss is computed using the cosine similarity as follows:
where:
Here, denotes the -norm. A gradient-stopping strategy is used in this loss optimization process.
3.4. Localized Metric Rule Construction Based on Visual Exchangeability
Constructing effective metric rules is crucial in one-shot learning, as there is only one example available for reference. As referenced in [38], the image-to-class metric utilizes the visually exchangeable property to improve model recognition compared to the image-to-image metric. In this paper, we primarily use the local metric as the main metric for our model. This means that the testing is also based solely on the local metric rule. The self-supervised global complementary learning module mentioned in the previous subsection serves as a complement to the local metric rule. The objective of establishing effective metric norms is accomplished through the utilization of both local and global complementary learning. The local metric includes two main components: an embedding network and a parameterless KNN metric module . It should be noted that the parameterless KNN metric module can effectively alleviate the overfitting of the model. The embedding network is used to extract detailed local feature descriptors from the images, while the metric module computes the scores for image-to-class metrics.
The primary purpose of the embedding network is to acquire the ability to obtain the feature representations of image samples from both the image and support set. This module can be constructed using any appropriate CNNs. In contrast to alternative methods, the exclusively incorporates convolutional layers and does not incorporate fully connected layers. This distinction arises from the system’s reliance on deep local descriptors as features for the computation of the image-to-class metric. Localized feature descriptors that are numerous in nature possess a greater amount of information and are more suited for relational metrics compared to feature vectors derived from fully connected layers. In summary, when provided with an image X, the function produces a tensor of size . This tensor can be conceptualized as a collection of d-dimensional local descriptors:
where is the i-th descriptor that is localized at the depth. Through our studies, we were able to determine that and when given an image with a resolution of . This implies that there exists a collective sum of 100 descriptors that are localized in terms of depth for every image.
The KNN metric module utilizes metric learning methods to extract distance measures between images. Within metric space, the cosine similarity between each image and the class is calculated using the k-nearest neighbor search algorithm, obtaining the similarity between them. Specifically, after processing through the embedding network , the sparse feature representation of image q is given by . For each descriptor , the k most similar points , where k is 3, are found within the local descriptor set obtained from the support set from class c, the cosine similarity is calculated, and the sum of all similarities is accumulated to define the image-to-class similarity between image q and class c:
where:
The optimization is performed using cross-entropy loss:
Here, N denotes the number of samples; C is the total number of classes; indicates that sample i belongs to class k with a value of 1, otherwise 0; is the model’s similarity score for sample i belonging to class k; and is the model’s similarity score for sample i belonging to class j.
3.5. Training
Our model is trained for both and . At this stage, our total loss is calculated as Formula (1). where is the weighting factor, and its algorithmic pseudo-code is shown in Algorithm 1.
| Algorithm 1 Training Procedure. |
|
4. Experiment and Analysis
The U.S. Department of Defense Advanced Research Projects Agency (DARPA) and the Air Force Research Laboratory (AFRL) work together to develop and evaluate advanced automatic target recognition (ATR) systems as part of the Moving and Stationary Target Acquisition and Recognition (MSTAR) program. Sandia National Laboratories (SNL) used the STARLOS sensor to collect target imagery near Huntsville, Alabama. The available data consists of SAR images of ten specific targets, including tanks, armored vehicles, weapons systems, and military engineering vehicles. The targets encompass several armored vehicles, including BMP-2, BRDM-2, BTR-60, and BTR-70, as well as tanks such as T-62 and T-72. Additionally, armament systems like 2S1, air defense units like ZSU-234, trucks like ZIL-131, and bulldozers like D7 are also included. The Sandia X-band radar was employed to collect these data.
This research converts transforms the MSTAR dataset into the MiniSAR dataset using the partitioning technique outlined in Table 1.

Table 1.
MiniSAR dataset composition.
4.1. Experimental Details
The SAR images were standardized to a resolution of 84 × 84. The studies were conducted using NVIDIA GeForce GTX 3090 GPUs and Intel Core i7-12700f CPUs. The Adam optimizer was employed with B1 = 0.5 and B2 = 0.999, with a constant learning rate (lr) of 0.001, and an epoch value of 100. Due to the randomness of the process, a single test can result in significant accuracy errors. Therefore, we conducted five independent tests and took the average test accuracy as the final target recognition accuracy. The episode was configured to 100, the alpha value was set to 0.1, and all trials were conducted using the PyTorch framework.
4.2. Comparison With the State-of-the-Art Methods
The objective of this study is to evaluate the proposed technique by comparing it with five other one-shot learning methods, specifically DN4 [38], Proto [21], Relation [22], Versa [42], and Convm [43], inside a three-way one-shot learning scenario.
4.3. Quantitative Comparison
The performance comparison of our proposed model with other comparison methods is shown in Table 2, and it is evident that our model outperforms the other methods in various experiments. Notably, the accuracy of our model is improved by a minimum of 7.467% under the three-way one-shot conditions.

Table 2.
Classification accuracy results for different methods (%).
Table 2 reveals that numerous prevalent one-shot learning models currently exhibit subpar performance. The recognition accuracy of the metric-based one-shot learning model depends on the construction of a high-quality metric space. However, one-shot learning only relies on a single sample for recognition, which can result in an imperfect construction of the metric rules if prior knowledge is not fully utilized. This can lead to a decline in performance. Based on the tabular data, it can be shown that metric-based one-shot learning models (such as Relation, DN4, Proto, and Convm) have a greater average accuracy compared to optimization-based one-shot learning models (Versa). The reason for this is that the optimization-based models under the one-shot data-only scenario are prone to biased parameter learning and negative migration, resulting in generally inferior performance of the optimization-based methods. The superior performance of the Relation model among comparative methods based on metric learning can be attributed to several factors. First, in one-shot learning, there is only one sample, which simplifies the relationship between the categories in the support set. Second, the relationship module facilitates the establishment of a mapping between the categories, making it easier to establish effective metric rules.
Furthermore, the DN4 exhibits superior recognition accuracy compared to other comparison methods. This can be attributed to the utilization of local metrics, which effectively mitigates the influence of irrelevant features and thus enhances accuracy. The Proto approach constructs category prototypes using individual samples. However, this method is susceptible to distributional bias, which leads to a decline in the model’s effectiveness. Furthermore, the covariance matrix utilized by the Convm to represent the learned categories of individual samples is susceptible to bias, resulting in poor model performance.
In comparison to other methods, SOS is capable of fully exploiting a single sample’s prior knowledge, employing a strategy of complementing local and global perspectives, and constructing effective metric rules. These capabilities contribute to a superior performance relative to other methods.
4.4. Qualitative Comparison
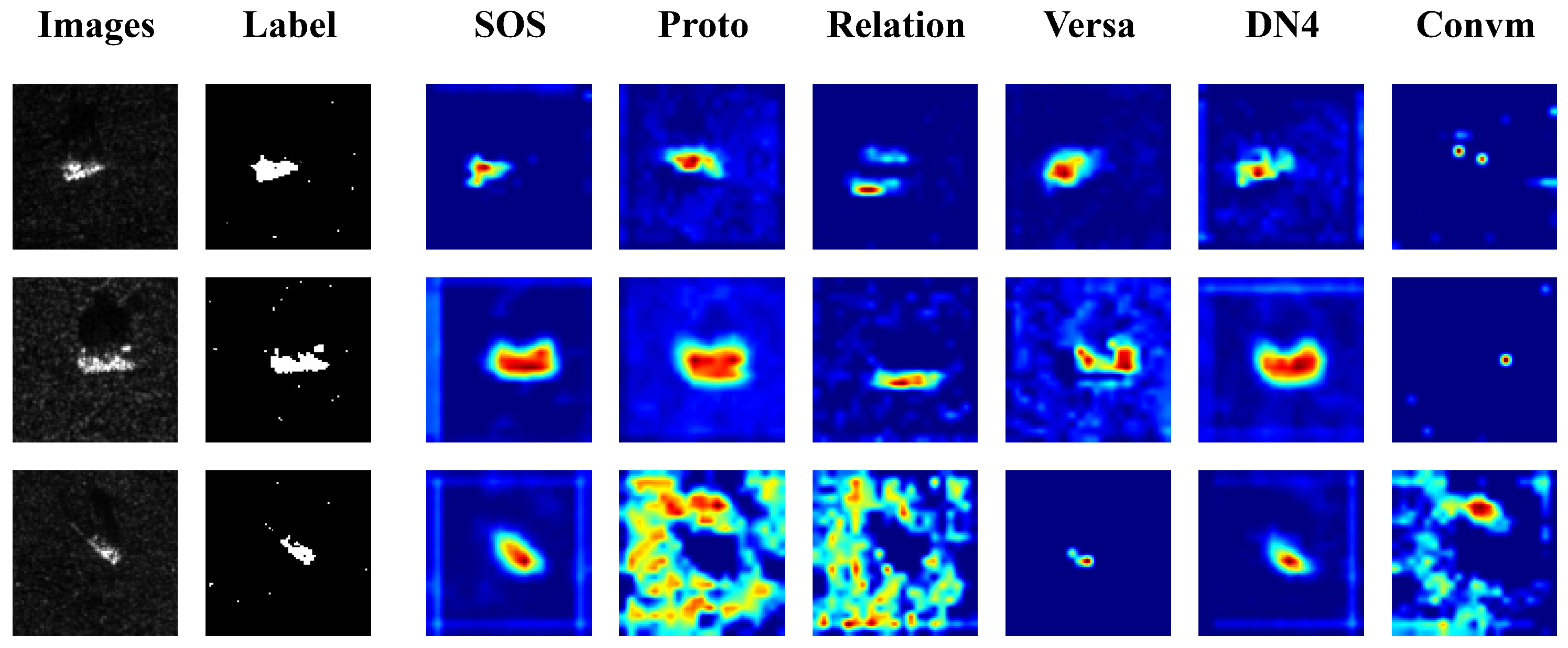
To assess the efficacy of the model presented in this research, we employed Grad-CAMs to visualize the regions of interest of the different methods on SAR images. Figure 3 displays the experimental findings. The visualization maps reveal two phenomena. First, Proto and Relation excessively focus on non-target regions of the image. These irrelevant regions contain noisy features that negatively affect the models’ performance. Second, Convm lack attention towards the target region of the image. This indicates a deficiency in global attention, leading to a decline in recognition performance. Unlike other models, our model focuses exclusively on the target region in the image and disregards any irrelevant information in the non-target region. This approach demonstrates that the proposed model effectively combines global and local perspectives, allowing it to leverage prior knowledge from single sample to accurately identify the target.
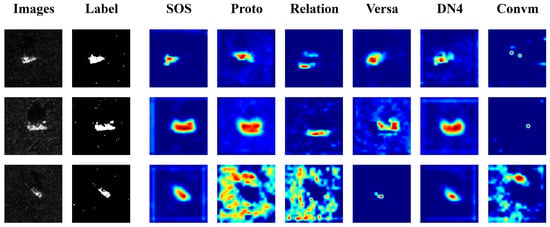
Figure 3.
Gradcam diagrams for comparison methods.
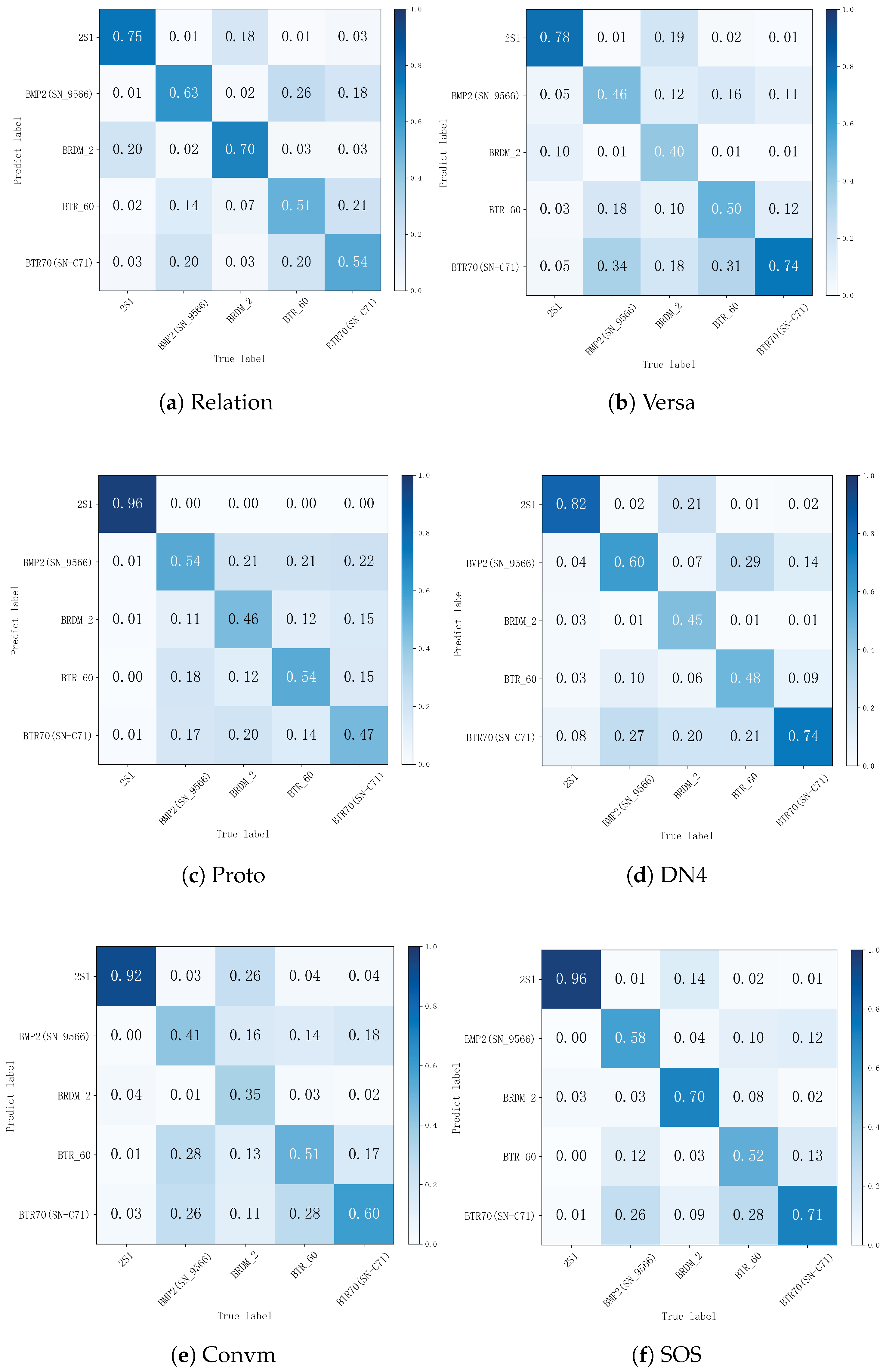
The confusion matrixes of the models are depicted in Figure 4. The analysis shows the difficulty in accurately categorizing BRDM-2 armored reconnaissance vehicles. We believe that the substantial overlap of BRDM-2’s characteristics in SAR images with other types of vehicles, particularly when there are changes in the viewing angle and when the vehicle is partially hidden. The distinctive configuration of the BRDM-2 makes it challenging to identify in SAR imagery when compared to other types of targets. This difficulty may be attributed to its flatter top and side design, which influence its radar reflection characteristics. Furthermore, the latter category, characterized by its bigger size and distinctive architectural profile, generates more consistent and sharper reflections in SAR imaging compared to higher-performing groups like APCs. In contrast, the BRDM-2 has fewer geometric design details and less distinctive features in the SAR images, posing additional challenges to the classification method.
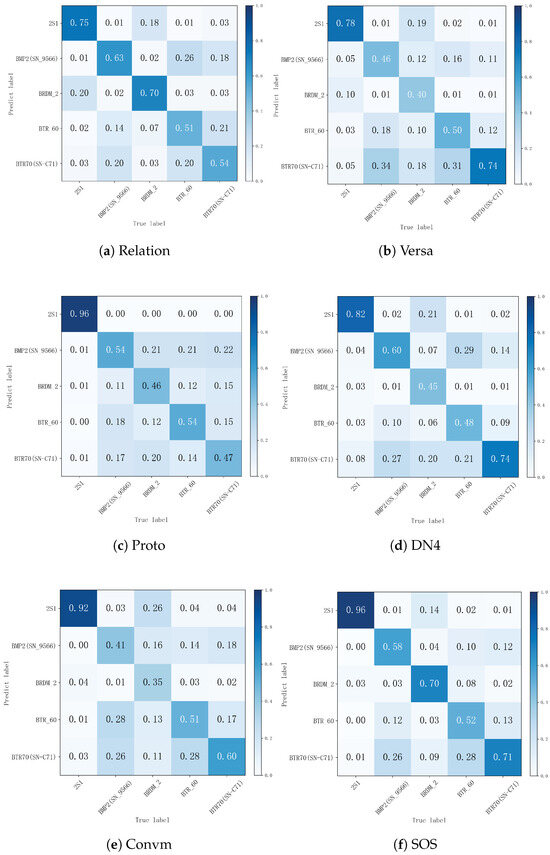
Figure 4.
Confusion matrix for different methods.
4.5. Ablation Analysis
In this study, the impact of the background interference cancellation strategy (hereinafter referred to as BNC) and the global self-supervised perspective module (hereinafter referred to as GSSL) is evaluated through ablation experiments, to evaluate their effectiveness, BNC and GSSL are executed independently, the same experimental parameter configurations as those in the main experiments are adopted, and the ablation experiments are carried out on the same dataset, and the results of the experiments are shown in Table 3.

Table 3.
Classification accuracy results of ablation experiments (%).
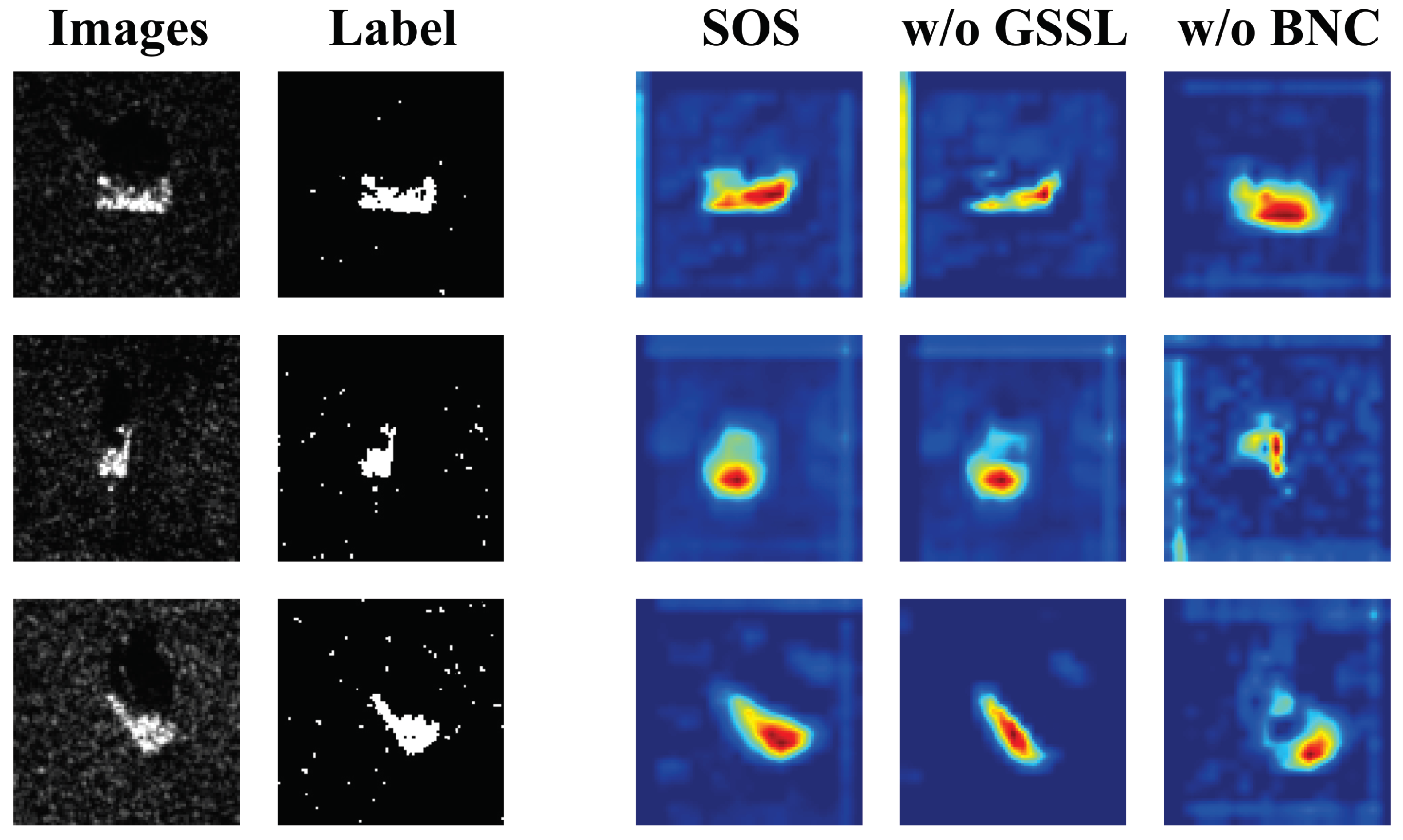
This research utilizes Grad-CAM plots to quantitatively examine the impact of each inventive component on the model’s performance. The analysis is conducted under the three-way one-shot experimental design, as depicted in Figure 5.
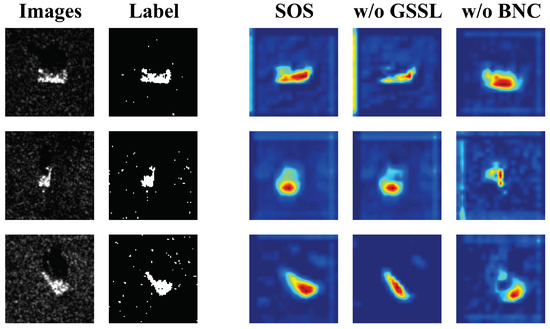
Figure 5.
Gradcam diagrams for ablation experiments.
- The elimination strategy for background interference was implemented by removing the BNC. As a result, the accuracy of the model in the three-way one-shot setup decreased from 70.867% to 68.733%. Additionally, in the Grad-CAM plots, the model exhibited an increased focus on irrelevant regions after the elimination strategy was applied. This suggests that removing the noise improved the model’s ability to recognize the target, thus confirming the effectiveness of the proposed strategy.
- Removing the GSSL module resulted in a decrease in model accuracy from 70.867% to 67.467% in the three-way one-shot setting. Additionally, the model lost the ability to perceive the global target in the Grad-CAM plot. This suggests that the global–local complementary learning, which allows the model to understand the target as a whole, is dependent on the presence of the GSSL module. Removing the GSSL module also hindered the model’s ability to effectively utilize prior knowledge from single samples, verifying the effectiveness of the GSSL module design.
The ablation experiments show that the designed BNC strategy with the GSSL module can significantly increase the classification accuracy of the model.
5. Discussion
5.1. Global and Local Mutual Learning Balance
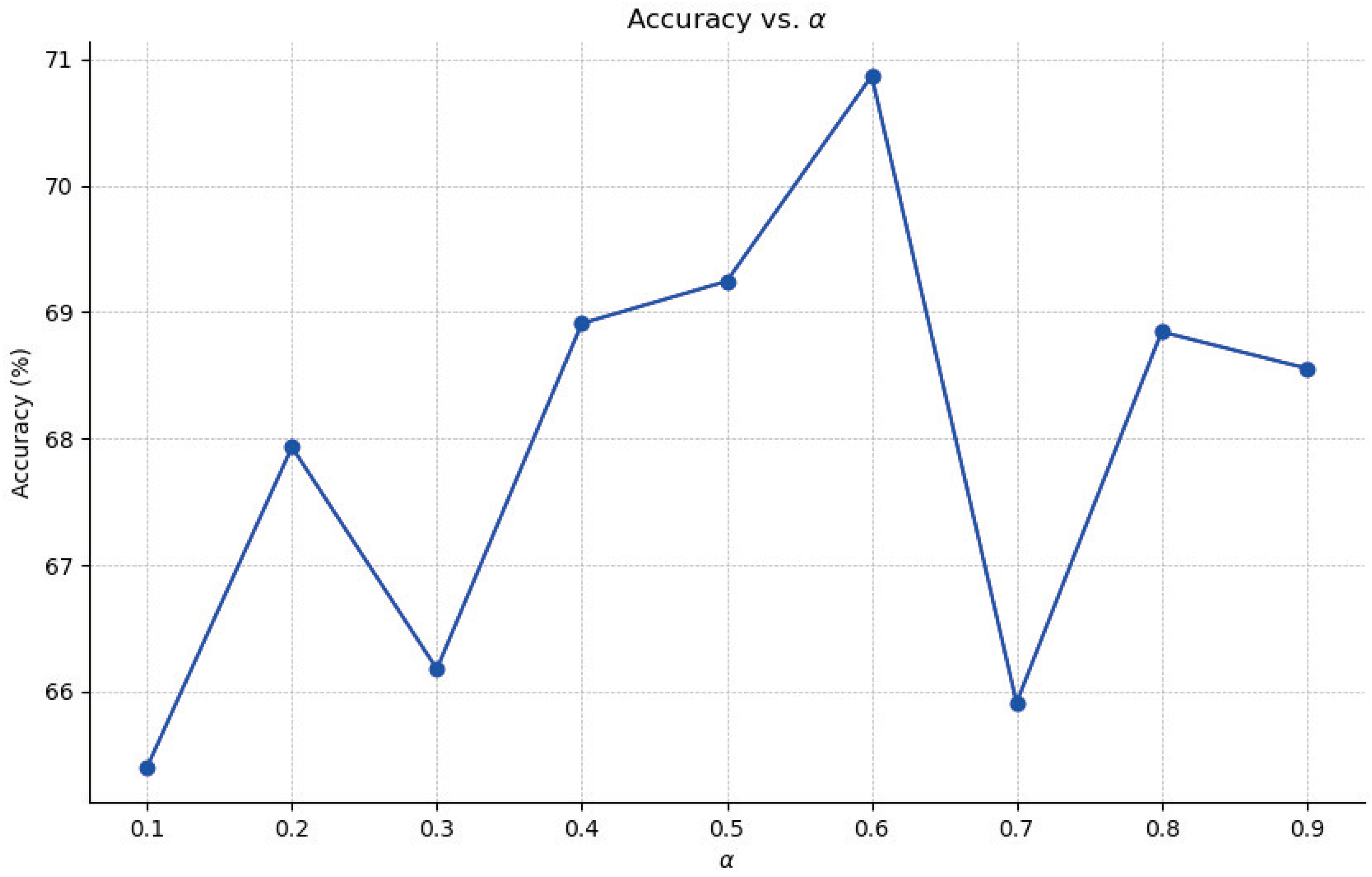
The weight factor is used in this paper to achieve a balance between global learning and local learning. To assess the influence of the weight factor on the model’s performance, the weight factor is modified within the range of 0.1 to 0.9. The experimental outcomes are depicted in Figure 6. By gradually adjusting the weight factor from 0.1 to 0.9, the model’s performance follows a pattern of initially increasing and then decreasing. When the weight factor is set to 0.6, the model achieves its optimal performance with an accuracy rate of 70.867%. This suggests that global and local learning are mutually beneficial and that relying solely on either one may lead to insufficient recognition information. Therefore, it is crucial to strike a balance between global and local learning in order to maximize the model’s performance. Achieving optimal performance in the model requires a careful balance between global learning and local learning. In addition, it also reflects the reasonableness of the values taken in this paper.
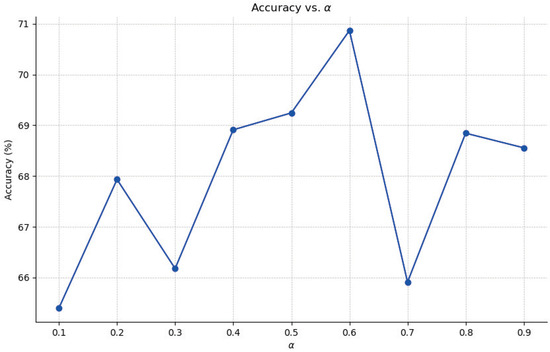
Figure 6.
Classification accuracy results of varying parameter .
5.2. Effectiveness Analysis of Adaptive Center Augmentation
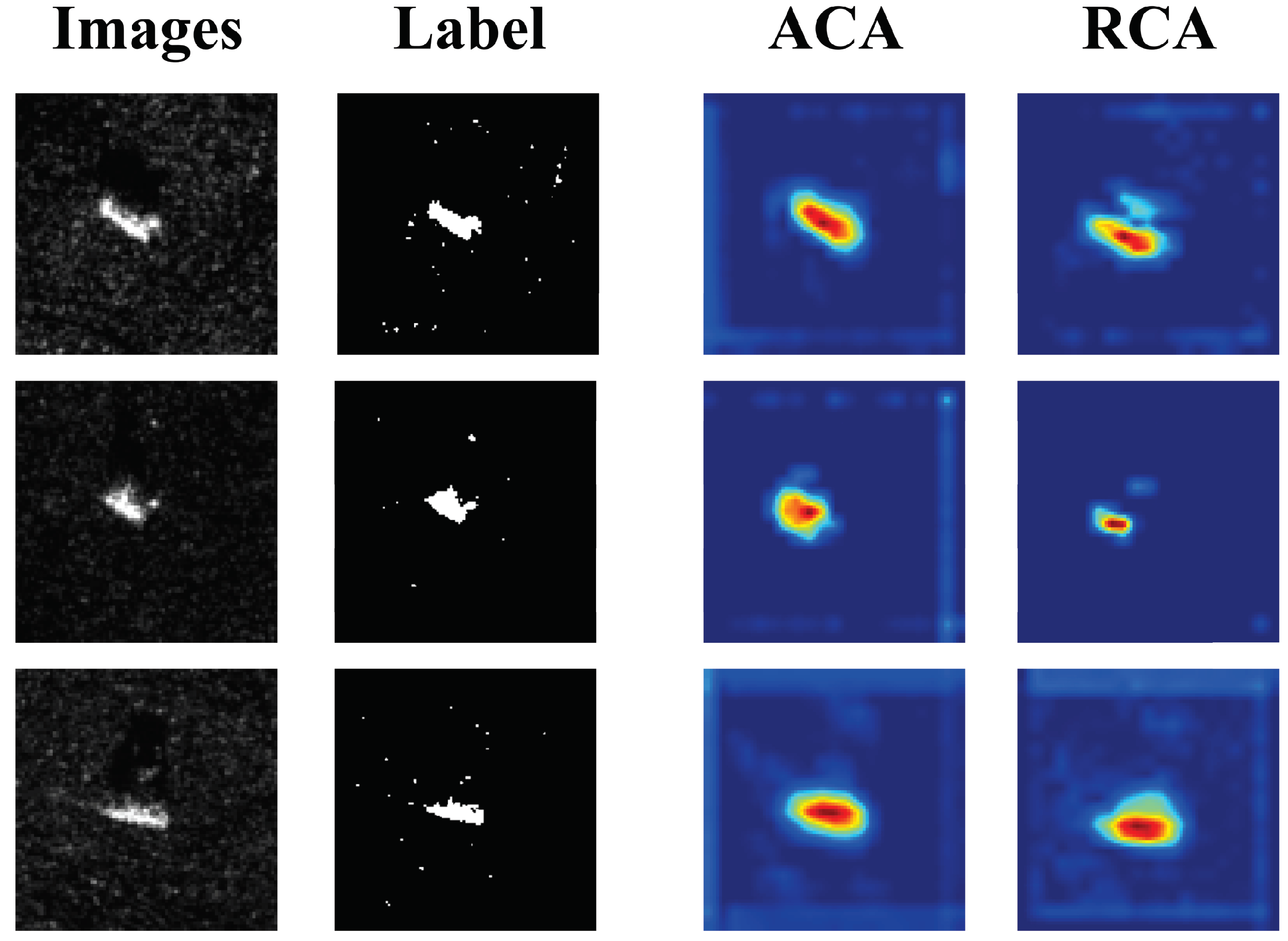
In order to investigate the effectiveness of the adaptive ACA proposed in the model of this paper, the ACA is replaced with random cropping augmentation (RCA), and experiments are conducted under different settings, the specific results are shown in Table 4 and Figure 7. From the table, it can be observed that the use of ACA can significantly increase the accuracy of the model, which is due to the fact that RCA has a certain probability of cropping to the non-target region, which causes the model’s understanding of the semantics to be biased and triggers the performance degradation.

Table 4.
Classification accuracy results of different augmentation (%).
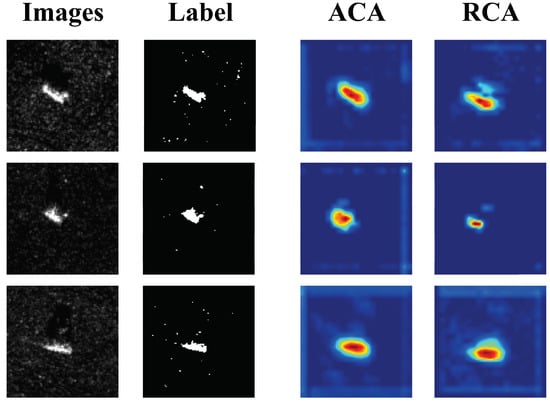
Figure 7.
Gradcam diagram for different augmentation.
To further discuss the model deployment potential of the proposed model, the parameter amounts of different comparison models are calculated in the table. As shown in Table 5, the parameter amount of the proposed model is only 0.1 GMac, which verifies that the proposed model has strong deployment potential.

Table 5.
Parameter Comparison of All Methods.
6. Conclusions
In this paper, we have proposed an SAR target recognition model called SOS based on metric learning. The model addresses the automatic recognition task of SAR images using a one-shot learning approach. Our model has effectively removed the background interference and irrelevant features, ensuring that only relevant semantic information can be utilized. In addition, our model has created a high-quality metric space by incorporating both global and local learning, enabling us to effectively leverage one-shot prior knowledge. As a result, our model achieves an accuracy of 70.867% under the three-way one-shot condition, outperforming all other one-shot methods. The ablation and discussion experiments confirm the effectiveness of each component.
Author Contributions
Conceptualization, B.C.; methodology, B.C.; software, B.C.; validation, B.C.; formal analysis, B.C.; investigation, B.C.; resources, B.C.; data curation, B.C.; writing—original draft preparation, B.C. and Z.Z.; writing—review and editing, B.C., Z.Z. and C.L.; visualization, B.C. and J.Z; supervision, B.C.; project administration, J.Z.; funding acquisition, J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of China under Grant 62172321.
Data Availability Statement
The MSTAR dataset used in the paper can be obtained at: https://www.sdms.afrl.af.mil/index.php?collection=mstar (accessed on 27 May 2024).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SAR | Synthetic Aperture Radar |
| SVM | Support Vector Machine |
| HMMs | Hidden Markov Models |
| TRIATR | Translational and Rotational Invariant Automated Target Identification |
| BCS | Bayesian Compressive Sensing |
| CNNs | Convolutional Neural Networks |
| KSW | Kolmogorov Sinai Weiss |
| SENet | Sequential Encoders Network |
| SOS | SAR Recognition Model Based on One-Shot Learning |
| ACA | Adaptive Center Augmentation |
| RCA | Random Cropping Augmentation |
References
- Magnuson, S. Mercury Systems Debuts Synthetic Aperture Radar Test Bed. Natl. Def. 2024, 108, 8–9. [Google Scholar]
- Trinder, J.C. Editorial for Special Issue “Applications of Synthetic Aperture Radar (SAR) for Land Cover Analysis”. Remote Sens. 2020, 12, 2428. [Google Scholar] [CrossRef]
- Di Traglia, F.; Ciampalini, A.; Pezzo, G.; Battaglia, M. Synthetic aperture radar and natural hazards: Applications and outlooks. Front. Earth Sci. 2019, 7, 191. [Google Scholar] [CrossRef]
- Sun, Y.; Jiang, W.; Yang, J.; Li, W. SAR target recognition using cGAN-based SAR-to-optical image translation. Remote Sens. 2022, 14, 1793. [Google Scholar] [CrossRef]
- Oghim, S.; Kim, Y.; Bang, H.; Lim, D.; Ko, J. SAR Image Generation Method Using DH-GAN for Automatic Target Recognition. Sensors 2024, 24, 670. [Google Scholar] [CrossRef] [PubMed]
- Pei, J.; Wang, Z.; Sun, X.; Huo, W.; Zhang, Y.; Huang, Y.; Wu, J.; Yang, J. FEF-Net: A deep learning approach to multiview SAR image target recognition. Remote Sens. 2021, 13, 3493. [Google Scholar] [CrossRef]
- Sun, Z.; Leng, X.; Zhang, X.; Xiong, B.; Ji, K.; Kuang, G. Ship Recognition for Complex SAR Images via Dual-Branch Transformer Fusion Network. IEEE Geosci. Remote Sens. Lett. 2024, 21, 4009905. [Google Scholar] [CrossRef]
- Sun, Z.; Dai, M.; Leng, X.; Lei, Y.; Xiong, B.; Ji, K.; Kuang, G. An Anchor-Free Detection Method for Ship Targets in High-Resolution SAR Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 7799–7816. [Google Scholar] [CrossRef]
- Sun, Z.; Leng, X.; Lei, Y.; Xiong, B.; Ji, K.; Kuang, G. BiFA-YOLO: A Novel YOLO-Based Method for Arbitrary-Oriented Ship Detection in High-Resolution SAR Images. Remote Sens. 2021, 13, 4209. [Google Scholar] [CrossRef]
- Cheng, X.; Huo, Y.; Lin, S.; Dong, Y.; Zhao, S.; Zhang, M.; Wang, H. Deep feature aggregation network for hyperspectral anomaly detection. IEEE Trans. Instrum. Meas. 2024. early access. [Google Scholar] [CrossRef]
- Cheng, X.; Zhang, M.; Lin, S.; Li, Y.; Wang, H. Deep self-representation learning framework for hyperspectral anomaly detection. IEEE Trans. Instrum. Meas. 2023, 73, 5002016. [Google Scholar] [CrossRef]
- Cheng, X.; Zhang, M.; Lin, S.; Zhou, K.; Zhao, S.; Wang, H. Two-stream isolation forest based on deep features for hyperspectral anomaly detection. IEEE Geosci. Remote Sens. Lett. 2023, 20, 5504205. [Google Scholar] [CrossRef]
- Lin, S.; Cheng, X.; Zeng, Y.; Huo, Y.; Zhang, M.; Wang, H. Low-Rank and Sparse Representation Inspired Interpretable Network for Hyperspectral Anomaly Detection. IEEE Trans. Instrum. Meas. 2024. early access. [Google Scholar] [CrossRef]
- Huo, Y.; Cheng, X.; Lin, S.; Zhang, M.; Wang, H. Memory-augmented Autoencoder with Adaptive Reconstruction and Sample Attribution Mining for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote. Sens. 2024, 62, 5518118. [Google Scholar] [CrossRef]
- Ying, Z.; Xuan, C.; Zhai, Y.; Sun, B.; Li, J.; Deng, W.; Mai, C.; Wang, F.; Labati, R.D.; Piuri, V. TAI-SARNET: Deep transferred atrous-inception CNN for small samples SAR ATR. Sensors 2020, 20, 1724. [Google Scholar] [CrossRef]
- Wang, Y.; Yao, Q.; Kwok, J.T.; Ni, L.M. Generalizing from a few examples: A survey on few-shot learning. ACM Comput. Surv. (Csur) 2020, 53, 1–34. [Google Scholar] [CrossRef]
- Li, J.; Wang, D.; Liu, X.; Shi, Z.; Wang, M. Two-branch attention network via efficient semantic coupling for one-shot learning. IEEE Trans. Image Process. 2021, 31, 341–351. [Google Scholar] [CrossRef] [PubMed]
- Kumar, B.; Ranjan, R.K.; Husain, A. A Survey on Techniques Used for De-speckling of SAR Images. Int. J. Soc. Ecol. Sustain. Dev. (IJSESD) 2022, 13, 1–14. [Google Scholar] [CrossRef]
- Koch, G.; Zemel, R.; Salakhutdinov, R. Siamese neural networks for one-shot image recognition. In Proceedings of the ICML Deep Learning Workshop, Lille, France, 2–4 July 2015; Volume 2. [Google Scholar]
- Vinyals, O.; Blundell, C.; Lillicrap, T.; Wierstra, D. Matching networks for one shot learning. Adv. Neural Inf. Process. Syst. 2016, 29, 3637–3645. [Google Scholar]
- Snell, J.; Swersky, K.; Zemel, R. Prototypical networks for few-shot learning. Adv. Neural Inf. Process. Syst. 2017, 30, 4080–4090. [Google Scholar]
- Sung, F.; Yang, Y.; Zhang, L.; Xiang, T.; Torr, P.H.S.; Hospedales, T.M. Learning to compare: Relation network for few-shot learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1199–1208. [Google Scholar]
- Hu, W.; Zhan, H.; Liu, C.; Yin, B.; Lu, Y. OTS: A One-shot Learning Approach for Text Spotting in Historical Manuscripts. arXiv 2023, arXiv:2304.00746. [Google Scholar]
- Gao, Y.; Wu, H.; Liao, H.; Chen, X.; Yang, S.; Song, H. A fault diagnosis method for rolling bearings based on graph neural network with one-shot learning. EURASIP J. Adv. Signal Process. 2023, 2023, 101. [Google Scholar] [CrossRef]
- Abdi, N.; Parvaresh, F.; Sabahi, M.F. SENet: Sequential Encoders for One-Shot Learning. Authorea Preprints. Authorea Prepr. 2023. [Google Scholar]
- Wang, X.; Zhang, X.; Chen, X.; Chen, X.; Lv, Z.; Liang, Z. Similarity function for one-shot learning to enhance the flexibility of myoelectric interfaces. IEEE Trans. Neural Syst. Rehabil. Eng. 2023, 31, 1697–1706. [Google Scholar] [CrossRef] [PubMed]
- Ma, R.; Mei, B.; Ma, Y.; Zhang, H.; Liu, M.; Zhao, L. One-shot relational learning for extrapolation reasoning on temporal knowledge graphs. Data Min. Knowl. Discov. 2023, 37, 1591–1608. [Google Scholar] [CrossRef]
- Anagnostopoulos, G.C. SVM-based target recognition from synthetic aperture radar images using target region outline descriptors. Nonlinear Anal. Theory Methods Appl. 2009, 71, e2934–e2939. [Google Scholar] [CrossRef]
- Nilubol, C.; Pham, Q.H.; Mersereau, R.M.; Smith, M.J.T.; Clements, M.A. Hidden Markov modelling for SAR automatic target recognition. In Proceedings of the 1998 IEEE International Conference on Acoustics, Speech and Signal Processing, ICASSP’98 (Cat. No. 98CH36181), Seattle, WA, USA, 12–15 May 1998; Volume 2, pp. 1061–1064. [Google Scholar]
- Yang, Y.; Qiu, Y.; Lu, C. Automatic target classification-experiments on the MSTAR SAR images. In Proceedings of the Sixth International Conference on Software Engineering, Artificial Intelligence, Networking and Parallel/Distributed Computing and First ACIS International Workshop on Self-Assembling Wireless Network, New York, NY, USA, 16–18 May 2005; pp. 2–7. [Google Scholar]
- Zhang, X.; Qin, J.; Li, G. SAR target classification using Bayesian compressive sensing with scattering centers features. Prog. Electromagn. Res. 2013, 136, 385–407. [Google Scholar] [CrossRef]
- Wang, Z.; Du, L.; Su, H. Target detection via Bayesian-morphological saliency in high-resolution SAR images. IEEE TRansactions Geosci. Remote Sens. 2017, 55, 5455–5466. [Google Scholar] [CrossRef]
- Ding, J.; Chen, B.; Liu, H.; Huang, M. Convolutional neural network with data augmentation for SAR target recognition. IEEE Geosci. Remote Sens. Lett. 2016, 13, 364–368. [Google Scholar] [CrossRef]
- Chen, S.; Wang, H.; Xu, F.; Jin, Y.-Q. Target classification using the deep convolutional networks for SAR images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4806–4817. [Google Scholar] [CrossRef]
- Wagner, S.A. SAR ATR by a combination of convolutional neural network and support vector machines. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 2861–2872. [Google Scholar] [CrossRef]
- Guo, Y.; Pan, Z.; Wang, M.; Wang, J.; Yang, W. Learning capsules for SAR target recognition. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4663–4673. [Google Scholar] [CrossRef]
- Zheng, J.; Li, M.; Zhang, P.; Wu, Y.; Chen, H. Position-Aware Graph Neural Network for Few-Shot SAR Target Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 8028–8042. [Google Scholar] [CrossRef]
- Li, W.; Wang, L.; Xu, J.; Huo, J.; Gao, Y.; Luo, J. Revisiting local descriptor based image-to-class measure for few-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 7260–7268. [Google Scholar]
- Li, X.; Yang, X.; Ma, Z.; Xue, J.-H. Deep metric learning for few-shot image classification: A review of recent developments. Pattern Recognit. 2023, 138, 109381. [Google Scholar] [CrossRef]
- Guo, H.; Liu, W. S3L: Spectrum Transformer for Self-Supervised Learning in Hyperspectral Image Classification. Remote Sens. 2024, 16, 970. [Google Scholar] [CrossRef]
- Chen, X.; He, K. Exploring simple siamese representation learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 15750–15758. [Google Scholar]
- Gordon, Jonathan; Bronskill, John and Bauer, Matthias et al. Meta-learning probabilistic inference for prediction. arXiv 2018, arXiv:1805.09921.
- Li, W.; Xu, J.; Huo, J.; Wang, L.; Gao, Y.; Luo, J. Distribution consistency based covariance metric networks for few-shot learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; ACM: New York, NY, USA, 2021; Volume 33, pp. 8642–8649. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).