1. Introduction
Synthetic-aperture radar (SAR), as a sensor utilizing microwaves for imaging, possesses the capability to conduct all-weather day-and-night imaging without being influenced by factors such as lighting and weather conditions. Through imaging processing algorithms, high-resolution images can be obtained, enabling the accurate extraction of feature information for target recognition [
1]. Therefore, SAR holds significant application value in both military and civilian domains [
2]. In recent years, with the rapid development of deep learning, deep neural networks (DNNs) have made significant breakthroughs in SAR automatic target recognition (ATR). With the end-to-end training method and powerful feature extraction capability, it has dramatically surpassed the traditional recognition methods in terms of recognition efficiency and accuracy [
3,
4,
5,
6,
7,
8,
9].
However, the internal working process and decision-making mechanisms of DNN models are not transparent, and their reliability and robustness still need improvement. Recent research has shown that DNN models are vulnerable to adversarial examples, which are crafted by adding subtle yet carefully designed perturbations to the input images [
10,
11]. While appearing virtually indistinguishable from the original images to the human eyes, they can cause the DNN models to produce incorrect results. The existence of adversarial examples reveals the vulnerability inherent in DNN models, which poses significant security risks for their deployment and application in radar intelligent recognition systems [
12]. Consequently, this issue has garnered widespread attention and has become a hot topic in the SAR-ATR field.
Current research on SAR adversarial attacks primarily focuses on white-box scenarios, where the attacker has full access to the internal information of the target model, including its structures, parameters, and gradients [
13,
14,
15,
16]. However, in the real world, the opponent’s SAR systems and deep recognition models are typically unknown, making it impractical to employ white-box attacks directly. Consequently, it is imperative to conduct attacks in black-box settings, which do not necessitate any information about the target model and align with the SAR non-cooperative scenarios. One of the significant properties in black-box scenarios is the transferability of adversarial examples, whereby the adversarial examples generated on the surrogate model can also attack other models. Nevertheless, black-box attacks are unable to achieve comparable performance to white-box attacks, as the generated adversarial examples tend to overfit the surrogate model and have limited transferability on the target model. For instance, as contrasted in
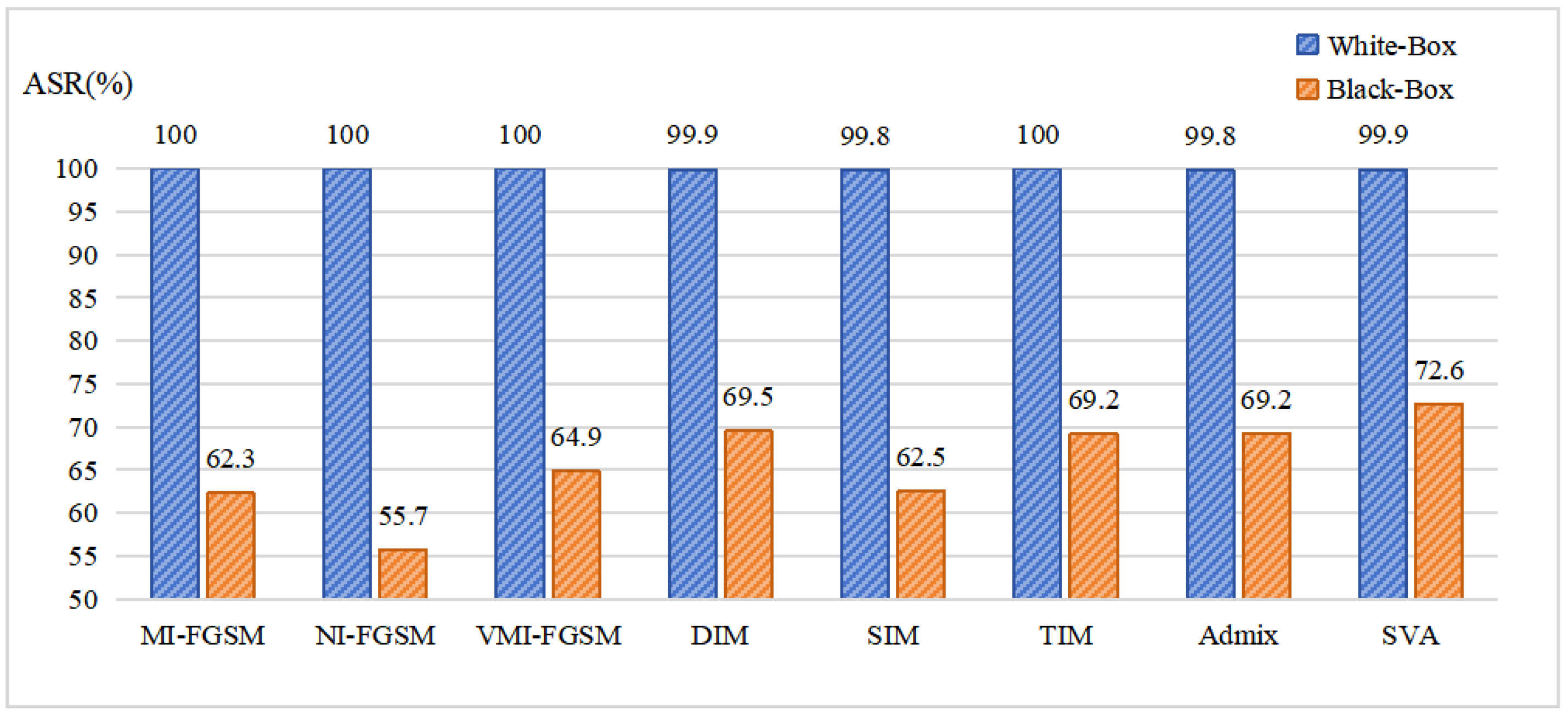
Figure 1, all attack algorithms achieve nearly 100% attack success rates in white-box settings. However, in black-box scenarios, the majority of attack algorithms exhibit transfer attack success rates between 60% and 70%, a significant decrease compared to their white-box performance. Consequently, enhancing the transferability of SAR adversarial examples is a significant and challenging problem.
Various methods have been proposed to enhance transferability, among which input transformations stand out as a prevailing strategy. The input transformation-based attacks aim to apply a series of transformations to enhance the input diversity and alleviate overfitting to the surrogate model. These transformations include resizing and padding [
17], scaling [
18], translation [
19], and so on. We proceed in this direction and discover that existing transformations typically neglect the unique characteristics of SAR images, such as the multiplicative speckle noise generated by the coherent principle, which results in limited diversity and insufficient transformations for SAR images. Moreover, Admix [
20] introduces images from other categories to achieve transformation. However, due to the high contrast and sharp edges between different regions in SAR images, its linear fusion strategy results in insufficient feature fusion and the disruption of original information.
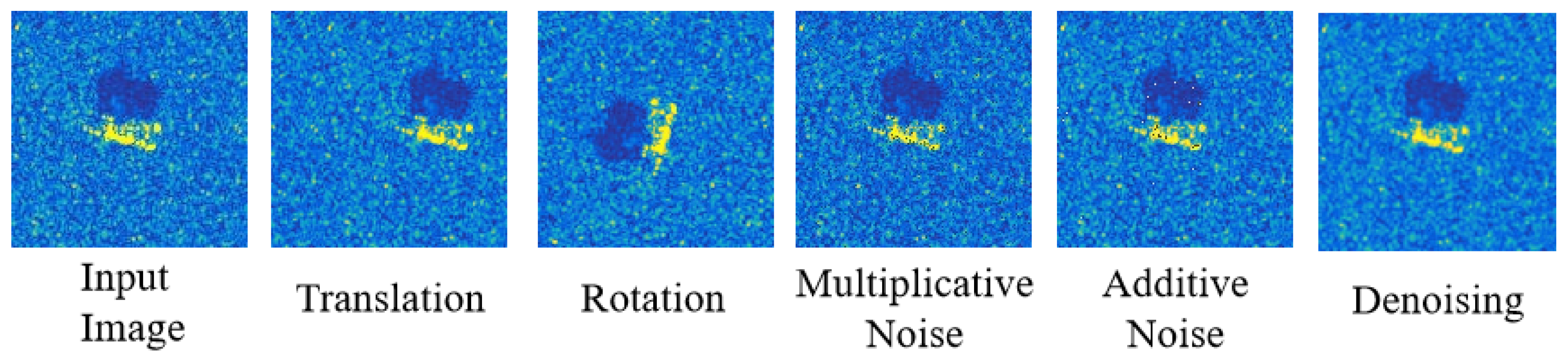
To tackle these problems, we have explored two special strategies via creating diverse input patterns. First, from the perspective of intra-class transformation, we argue that enhancing the input diversity and considering some transformations that align with the characteristics of SAR images can achieve a superior transformation effect and enrich the gradient information, thereby stabilizing the update direction to avoid falling into local optima and alleviating the overfitting to the surrogate model. Second, from the perspective of inter-class transformation, we believe that nonlinear fusion is more suitable for SAR images than a linear mixing strategy, thereby reducing damage to the original features and achieving a better fusion effect.
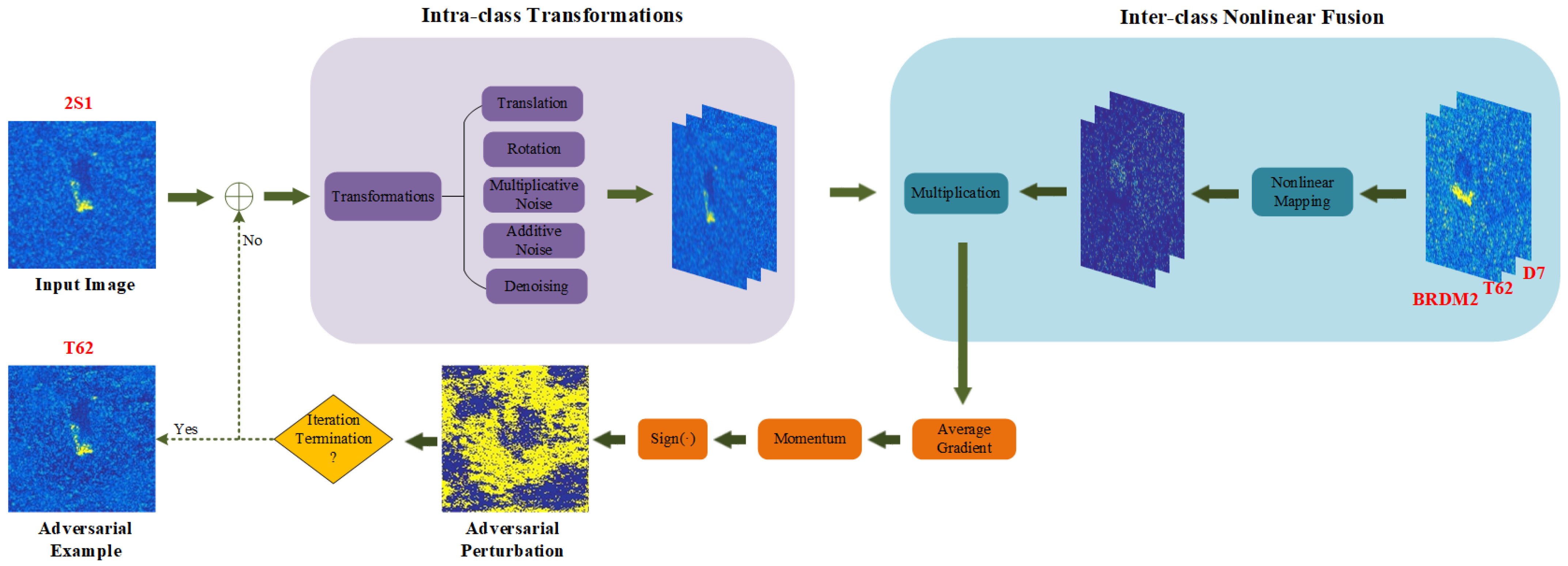
In this article, we propose a novel method called intra-class transformations and inter-class nonlinear fusion attack (ITINFA) to enhance transferability. At first, we employ a series of transformations on a single image to increase the input diversity. Subsequently, we nonlinearly integrate the information from other categories into the transformed images to guide the adversarial examples to cross the decision boundary. Finally, we utilize the various transformed and mixed images to calculate the average gradient and combine the momentum iterative process to generate more transferable SAR adversarial examples. Extensive experiments on the MSTAR and SEN1-2 datasets demonstrate that ITINFA outperforms the state-of-the-art transfer-based attacks, dramatically enhancing the transferability in black-box scenarios while preserving comparable attack performance in white-box scenarios. The main contributions are summarized as follows:
We propose a novel method called ITINFA for generating more transferable adversarial examples to fool the DNN-based SAR image classifiers in black-box scenarios.
To improve the limited diversity and insufficient transformations of existing methods commonly utilized for optical images, we fully consider the unique characteristics of SAR imagery and apply diverse intra-class transformations to obtain a more stable update direction, which helps to avoid falling into local optima and alleviates overfitting to the surrogate model.
To overcome the insufficient fusion and damage of existing linear mixing, we devise a nonlinear fusion strategy according to the high-contrast characteristic inherent in SAR images, which is beneficial to reduce the background clutter information and avoid excessive disruption of the original SAR image, thereby incorporating information from other categories more effectively.
Extensive evaluations based on the MSTAR and SEN1-2 datasets show that the proposed ITINFA significantly improves the transferability of SAR adversarial examples on various cutting-edge DNN models.
The remainder of this article is organized as follows.
Section 2 briefly reviews the related works.
Section 3 introduces the details of our proposed ITINFA.
Section 4 shows experimental results on the MSTAR and SEN1-2 datasets. Finally, we present the discussion and conclusions in
Section 5 and
Section 6.
4. Experiments
4.1. Datasets
4.1.1. MSTAR Dataset
The MSTAR dataset [
42] is a benchmark dataset for SAR-ATR, which contains a series of X-band SAR images with ten different classes of ground targets at different azimuth and elevation angles. The optical images and their corresponding SAR images are depicted in
Figure 4. In the experiments, we select the standard operation condition (SOC) that contains 2747 images collected at a 17° depression angle as the training dataset and 2426 images collected at a 15° depression angle as the test dataset. The detailed information of each category is shown in
Table 1.
4.1.2. SEN1-2 Dataset
The SEN1-2 dataset [
43] is an SAR–optical image pair dataset. It comprises four subsets, each corresponding to a different season—spring, summer, autumn, and winter—and contains 282,384 pairs of corresponding image patches. In this article, following the selection strategy adopted in [
25], we select the summer subset, which consists of two parts: s1 and s2. The s1 part contains SAR images, while the s2 part contains corresponding optical images. There are 49 folders within s1, each containing SAR images from the same area and representing the same category. After careful consideration, we selected ten distinct categories for our experiments, striving to ensure maximum difference among different categories while maintaining similarity within each category, thus supporting the tasks of target recognition and adversarial attack. Within each category, we selected 500 images for training and 300 images for testing, as summarized in
Table 1.
Figure 5 illustrates the examples of the SAR images alongside their corresponding optical images.
4.2. Experimental Setup
4.2.1. Models
We conduct the experiments on eight classical DNN models. Among them, AlexNet [
44], VGG11 [
45], ResNet50 [
46], ResNeXt50 [
47], and DenseNet121 [
48] are widely utilized as feature extraction networks and have achieved excellent target recognition performance. In addition, SqueezeNet [
49], ShuffleNetV2 [
50], and MobileNetV2 [
51] are lightweight DNN architectures that reduce the model parameters and sizes while achieving comparable performance in various target recognition tasks. All of these models are well trained on the MSTAR and SEN1-2 datasets to evaluate the transferability of adversarial examples, and the specific information and recognition accuracies are shown in
Table 2.
During the training process, we adopt the preprocessing strategy proposed in [
3]. At first, the single-channel gray-scale SAR images are normalized to [0, 1] to accelerate the convergence of the loss function. Subsequently, we randomly crop 88 × 88 patches of training images for data augmentation and centrally crop 88 × 88 patches of test images to evaluate the recognition performance. After that, we resize these images to 224 × 224 and input them into the DNN models. Furthermore, the cross-entropy loss function and the Adam optimizer [
52] are employed to train the models, with a learning rate of 0.0001, batch size of 20, and 500 training epochs.
4.2.2. Baselines
In the experiments, we compare our proposed ITINFA with several classic transfer-based attack algorithms, namely, MI-FGSM [
21], NI-FGSM [
18], and VMI-FGSM [
22]. Additionally, we also compare with several input transformation-based methods, namely, DIM [
17], SIM [
18], TIM [
19], Admix [
20], and SVA [
29]. The maximum perturbation budget
for all these algorithms is set to 16/255, with the number of iterations
T set to 10, step size
set to 16/2550, and decay factor
set to 1. We set the number of sampled examples in the neighborhood to 5 and the upper bound to 1.5 for VMI-FGSM. We adopt transformation probability
for DIM and the number of scaled copies
for SIM. For TIM, we adopt a Gaussian kernel with a size of 5 × 5. For Admix, we randomly sample
images from other categories with the strength of 0.2 and scale 30 images for each admixed image. For SVA, we adopt a median filter with a kernel size of 5 × 5 and tail
of the truncated exponential distribution. We set
,
, and
for our proposed ITINFA. For fair comparisons, all of these methods are integrated into momentum iteration.
4.2.3. Metrics
The transferability is evaluated by the attack success rate, which is defined as the ratio of the number of examples misclassified after the attack to the total number of correctly classified examples. The formula is expressed as follows:
where
is the indication function and
N is the total number of correctly classified examples.
In addition, the misclassification confidence [
33] is utilized to further evaluate the attack performance and transferability of various attack algorithms. This is obtained from the softmax output of the target model and denotes the confidence probability that the adversarial example is misclassified into the wrong category in a successful attack.
Adversarial attacks require not only deceiving the DNNs but also ensuring that the generated adversarial perturbations are sufficiently subtle and imperceptible to the human eye. In the experiments, the
norm and structural similarity (SSIM) are employed to evaluate the imperceptibility of adversarial examples. The
norm [
53] is a widely employed metric that measures the Euclidean distance between the adversarial example and the original image, while the SSIM [
54] is utilized to measure the similarity of these two images.
Finally, we calculate the average time consumption for generating a single adversarial example, serving as a metric to assess the computational efficiency of the attack algorithms.
4.2.4. Environment
In this article, the Python programming language (v3.11.8) and the Pytorch deep learning framework (v2.2.2) [
55] are used to implement all the experiments and evaluate the performance of various adversarial attack algorithms. All the experiments are supported by four NVIDIA RTX 6000 Ada Generation GPUs and powered by an Intel Xeon Silver 4310 CPU.
4.3. Single-Model Experiments
We first conduct experiments on a single model to evaluate the transferability of various attack algorithms. The adversarial examples are crafted on a single surrogate model and subsequently employed to attack the target models. If the surrogate model is identical to the target model, it denotes a white-box attack scenario; otherwise, it is classified as a black-box attack.
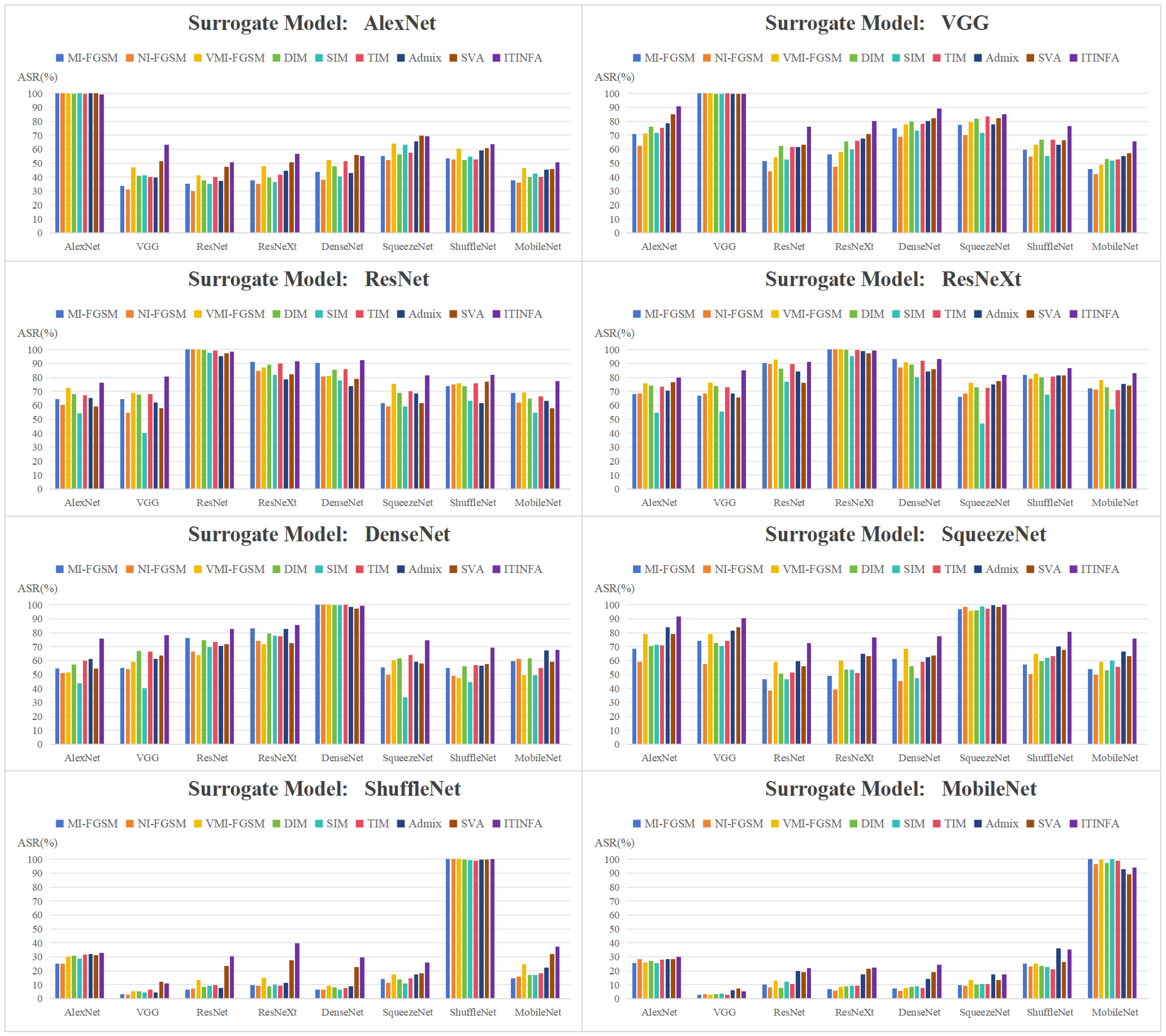
Figure 6 summarizes the attack success rates of adversarial examples generated by each algorithm when the surrogate models are AlexNet, VGG, ResNet, ResNeXt, DenseNet, SqueezeNet, ShuffleNet, and MobileNet, respectively.
It is evident that the attack success rates of white-box attacks for all the surrogate models notably surpass those of black-box attacks. Furthermore, for the AlexNet, VGG, and ShuffleNet models, the white-box attack success rates for all the employed algorithms nearly reach 100%. As for the black-box attack performance, it is discernible that diverse surrogate models exhibit significant discrepancies in the transferability of the generated adversarial examples. For instance, when ResNet and ResNeXt are employed as surrogate models, they achieve notable transferability among different target models, with the attack success rates consistently surpassing 50%. However, when ShuffleNet and MobileNet are utilized as surrogate models, the transferability is notably limited, with attack success rates scarcely exceeding 20%. Different attack algorithms also exhibit discrepancies in transferability across different target models. In comparison, NI-FGSM generally demonstrates inferior transferability on most models compared to MI-FGSM, which may suggest that Nesterov’s accelerated gradient is less effective than momentum on SAR images. Additionally, it can be observed that among several input transformation-based methods, SIM shows the poorest transferability on most target models. This indicates that the scaling transformation may not be suitable for SAR images with sparse characteristics. At the same time, both DIM and TIM exhibit similar transferability on most models, suggesting that the contributions of resizing and translation in improving transferability are comparable for SAR images. Compared to these baselines, our proposed ITINFA consistently achieves the best transferability across eight surrogate models. This consistent and superior attack performance indicates that ITINFA can effectively enhance transferability across various target models. At the same time, it is worth noting that although ITINFA exhibits a slightly lower white-box attack success rate on specific models (e.g., AlexNet, ResNet, MobileNet) compared to some baseline methods, it still ensures a satisfactory level of white-box attack effectiveness, and the slight reduction in white-box attack performance as a trade-off for enhanced transferability is a normal phenomenon.
To better present the experimental results of transferability,
Table 3 and
Table 4, respectively, demonstrate the average transfer attack success rates on the MSTAR and SEN1-2 datasets when each model serves as the surrogate model and generates adversarial examples to attack the other seven target models. The experimental results indicate that regardless of which model acts as the surrogate model, our proposed ITINFA consistently achieves the best transferability. Specifically, ITINFA outperforms the best baseline method with a clear margin of 9.0% on the MSTAR dataset and 8.1% on the SEN1-2 dataset, further underscoring that ITINFA can significantly enhance the transferability across different architectures.
In addition, we also calculate the average misclassification confidence,
norm, SSIM, and time consumption on the MSTAR dataset to further conduct a comprehensive evaluation of the proposed algorithm. VGG is utilized as the surrogate model to attack the other seven target models, and the experimental results are reported in
Table 5. It can be observed that ITINFA not only achieves the highest attack success rate but also attains the highest misclassification confidence, indicating that ITINFA is more effective than other baselines. At the same time, ITINFA demonstrates comparable
norm and SSIM values to other algorithms. This indicates that ITINFA maintains a similar level of imperceptibility as baseline methods, rendering the adversarial perturbations imperceptible to the human eye, especially when dealing with a limited perturbation budget. Moreover, both ITINFA and Admix require a longer execution time compared to other methods, indicating that the incorporation of additional image categories to guide the optimization of adversarial examples is more time-consuming than other transformation approaches. Although ITINFA takes a relatively longer time compared to other algorithms, it remains within an acceptable range, ensuring an average time consumption of less than 1 s for generating a single adversarial example. It is also worth mentioning that the computational efficiency of ITINFA is variable and positively correlates with the number of transformations and introduced samples. Reducing the number of transformations or introduced samples can significantly enhance computational efficiency at the cost of a slight decrease in attack success rate.
4.4. Ensemble-Model Experiments
To further validate the effectiveness of our proposed ITINFA, we conduct the ensemble-model experiments proposed in [
21], which fuse the logit outputs of various models to generate the adversarial examples. Based on the MSTAR dataset, we construct an ensemble model by integrating four surrogate models, including AlexNet, VGG, ResNet, and ResNeXt, and all the ensemble models are assigned equal weights. Subsequently, we evaluate the transferability by conducting attacks on DenseNet, SqueezeNet, ShuffleNet, and MobileNet. The results are shown in
Table 6.
From
Table 6, it is observed that adversarial examples generated on the ensemble model exhibit more stable transferability across various target models with different architectures, with the attack success rate consistently remaining within a specific range. Compared with all the baseline methods, ITINFA achieves the average attack success rate of 87.30% and outperforms the best baseline method with a clear margin of 4.40%. Meanwhile, it exhibits the highest misclassification confidence of 90.7%, demonstrating its superior performance in generating transferable adversarial examples on the ensemble model.
4.5. Ablation Studies
In this subsection, to further explore the superior transferability achieved by ITINFA, we conduct ablation studies on the MSTAR dataset to validate that both intra-class transformations and inter-class nonlinear fusion are beneficial to enhance transferability. We set up the following four configurations for ablation studies: (1) the original ITINFA; (2) removing intra-class transformations; (3) removing inter-class nonlinear fusion; (4) removing both intra-class transformations and inter-class nonlinear fusion. We employ AlexNet as the surrogate model to generate adversarial examples and attack the other seven models to evaluate the transferability.
The experimental results are shown in
Table 7. It is observed that configuration 1 exhibits the best transferability. However, removing either intra-class transformations module or inter-class nonlinear fusion module decreases transferability, and configuration 4 exhibits the poorest transferability when both modules are removed simultaneously. Therefore, it is evident that both intra-class transformations and inter-class nonlinear fusion are effective in enhancing transferability and can act synergistically to further enhance transferability.
4.6. Parameter Studies
In this subsection, we explore the impact of three hyper-parameters on the transferability: the number of transformations , the number of randomly sampled images from other categories , and the strength of nonlinear mapping r. All the adversarial examples are generated on VGG and utilized to attack the target models to evaluate transferability.
ITINFA applies
transformations to the input image to obtain the diverse gradient information. To explore the impact of
on the transferability, we conduct experiments with
varying from 5 to 50,
fixed to 3, and
r fixed to 0.8. The attack success rates are recorded in
Figure 7. It is evident that the white-box attack success rates consistently remain at a level close to 100%, and the transfer attack success rate is lowest when
. As
increases, the richness of the gradient information gradually enhances, leading to a gradual improvement in the transferability of adversarial examples. However, once
exceeds 30, the improvement in transferability becomes negligible, while the computational cost increases substantially. Therefore, we select
in the experiments to maintain a favorable balance between transferability and computational cost.
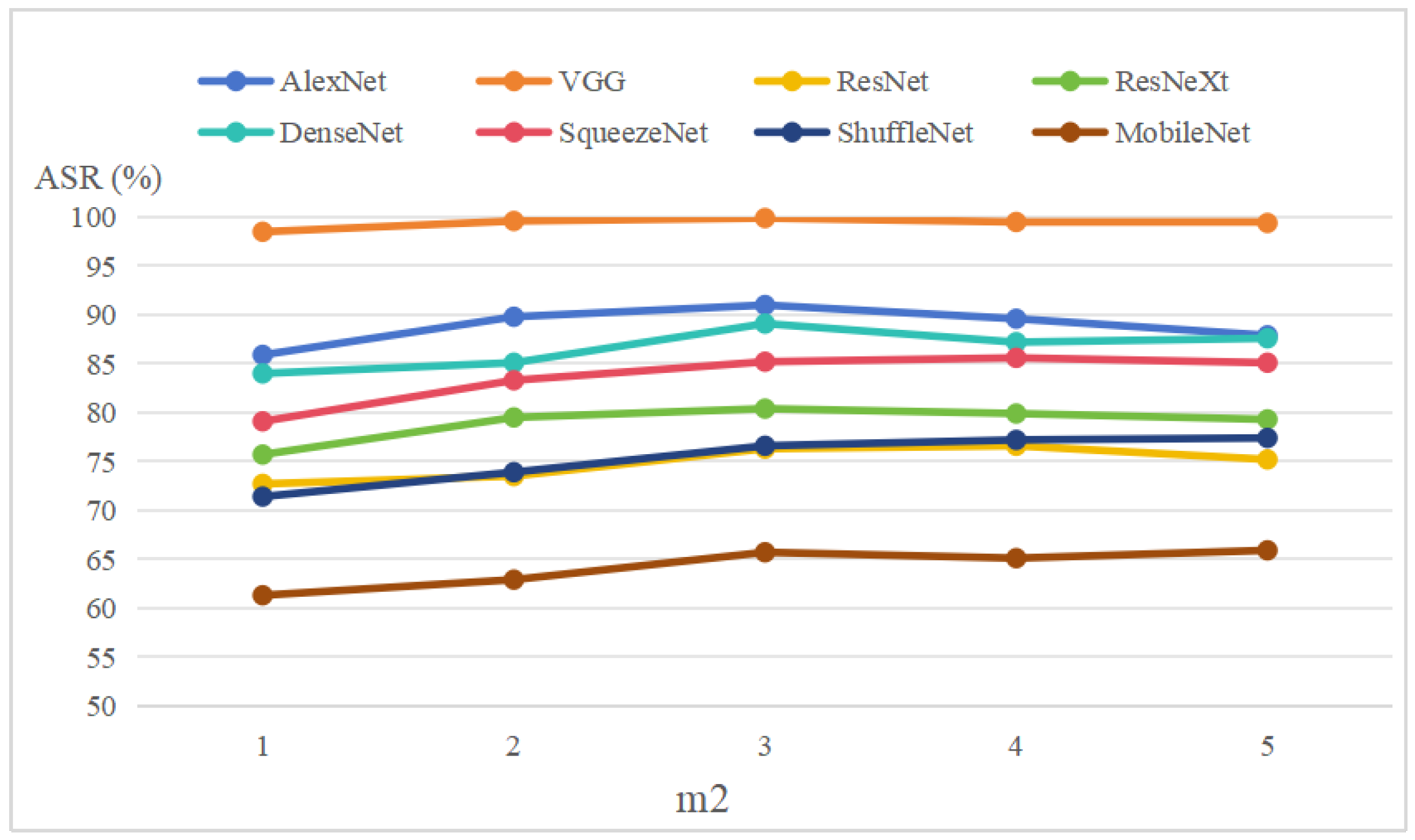
In
Figure 8, we further report the attack success rates of ITINFA with various values of
. We select
from 1 to 5, fix
to 30, and set
r to 0.8. When
, the transferability of adversarial examples on all the target models improves as the value of
increases. This suggests that incorporating the information from other categories more effectively guides the misclassification of adversarial examples. However, when
, the improvement in transferability becomes less pronounced and even shows a downward trend. This phenomenon might result from introducing excessive information from other categories, which impairs the transferability of adversarial examples. Additionally, increasing the value of
also brings excessive computational costs. Consequently,
is chosen for our experiments.
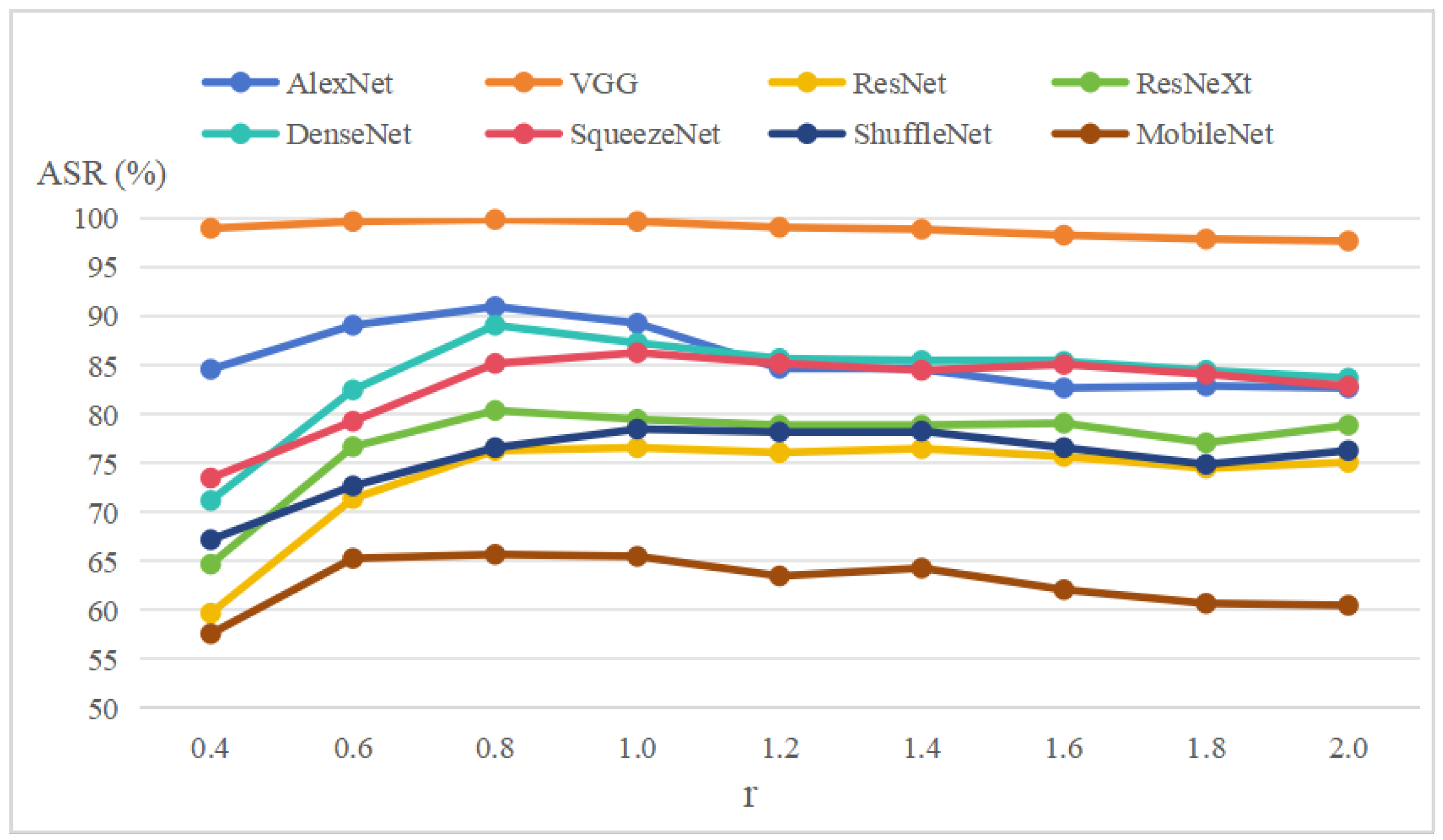
In addition, we also explored the impact of nonlinear mapping at different strengths on transferability, and the results are illustrated in
Figure 9. In the experiment,
r varies from 0.4 to 2.0,
is fixed to 30, and
is fixed to 3. It can be observed that when
r is lower than 0.8, the attack success rate increases significantly with the growth in
r. However, after
r surpasses 1, the attack success rates gradually converge to a stable range and begin to decline slowly. In most of the target models, an optimal attack performance is observed at
. Consequently, this value is selected as the designated setting for
r in our experiments.
4.7. Visualizations
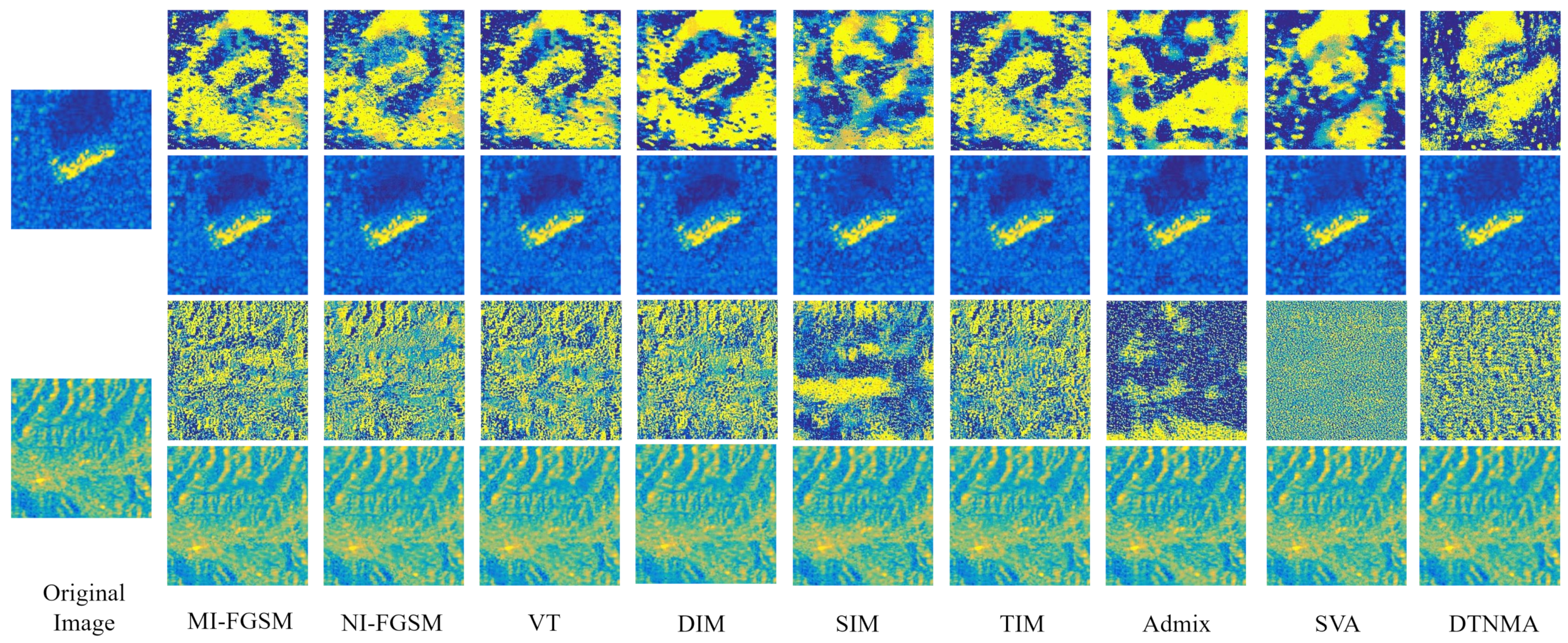
Some results of the adversarial perturbations and adversarial examples generated by the various algorithms are visualized in
Figure 10. The first two rows represent the examples from the MSTAR dataset, while the last two rows illustrate the examples from the SEN1-2 dataset. To enhance the visual effect, we utilize the Parula color map to visualize the gray-scale SAR images. It is evident that our proposed ITINFA is capable of achieving satisfactory visual imperceptibility. That is, the adversarial example generated by ITINFA can fool the target model while maintaining high similarity with the original image.
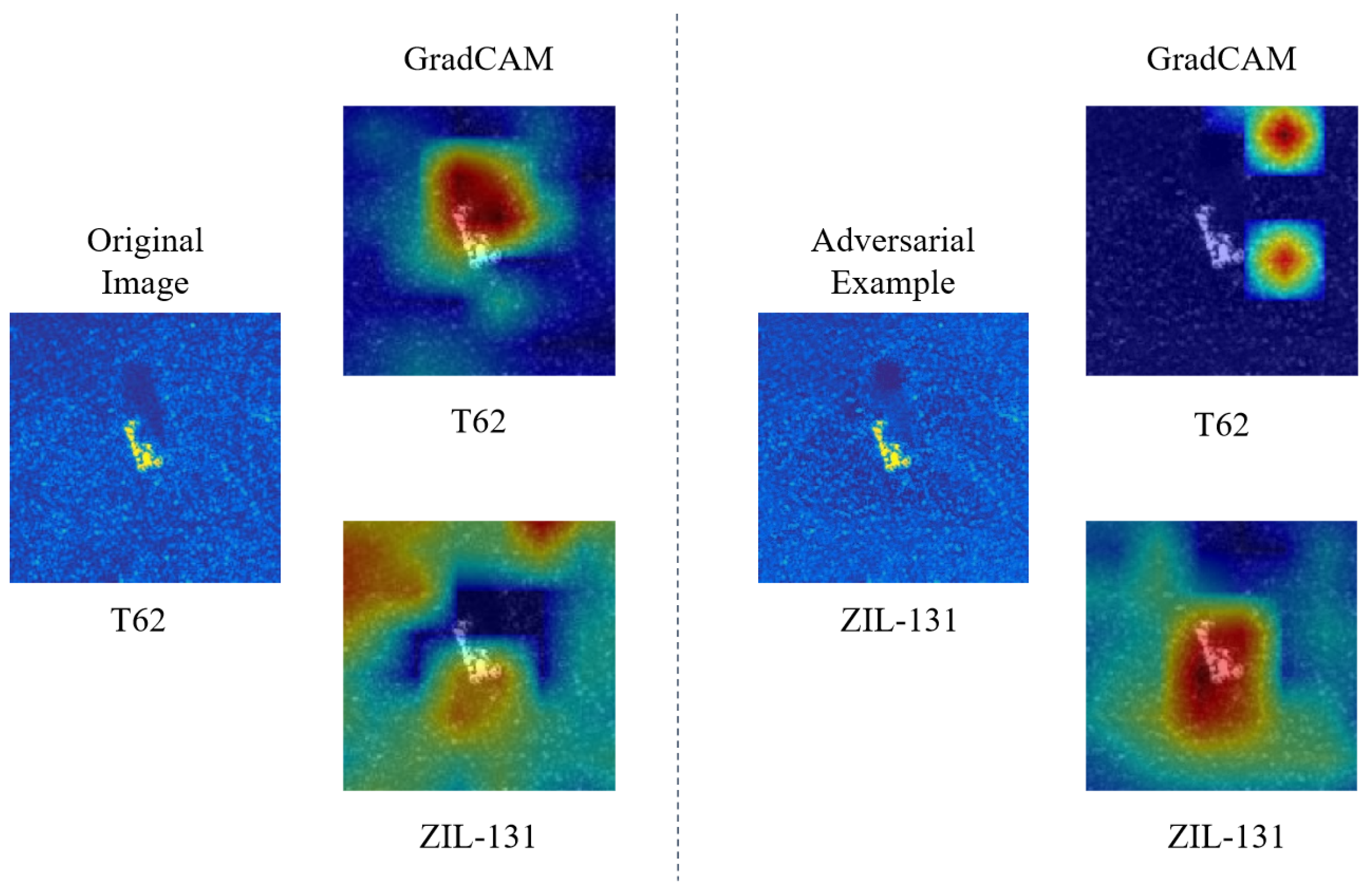
Figure 11 further illustrates an adversarial threat scenario in which a military target tank (T62) is erroneously recognized as a truck (ZIL-131) after the adversarial perturbation generated by ITINFA is added to the original image. We utilize the feature visualization technique GradCAM [
56] to visualize the output feature map weights of the last convolutional layer of VGG. It is evident that adding adversarial perturbation results in a significant alteration in the attention regions. When the target category is set to T62, the attention of the model is mainly focused on the target area of the original image, whereas for the adversarial example, it shifts to the background clutter area and relocates back to the target area when the target category is set to ZIL-131. This presentation further enhances the visual understanding of the attack process and indicates the potential of ITINFA for application in real-world scenarios.
5. Discussion
In the field of adversarial attacks on SAR-ATR, due to the highly non-cooperative nature and the secretive characteristics of adversary’s SAR systems it is typically challenging to acquire information about target models. Therefore, enhancing the transferability of adversarial examples to unknown target models becomes exceptionally crucial. Input transformation-based attacks represent a prevalent method for boosting transferability today. The essence of these approaches lies in employing data augmentation to process the input image, thereby generating richer gradient information. This facilitates a more generalized optimization direction for updates, avoiding local optima in the optimization process and alleviating the overfitting of adversarial examples on the surrogate model. Therefore, in this article, we continue to explore towards this direction.
The proposed ITINFA comprises two main modules: firstly, from the perspective of the image itself, diverse intra-class transformations are applied to the input SAR image. The transformations include typical techniques used in optical images and methods developed explicitly for the unique properties of SAR imagery. Secondly, from the perspective of the other category images, incorporating information from other categories to better guide adversarial examples to be misclassified, regardless of the target models. Notably, we employ a nonlinear multiplication for integration rather than linear addition. Experimental results indicate that this modulation approach can achieve better effects. Future research might also consider the effects of other nonlinear mapping methods, such as using a logarithmic function instead of an exponential one. However, due to space limitations, this article will not delve into those. Both the intra-class transformations and inter-class fusion modules have been proven in ablation studies to enhance the transferability of adversarial examples significantly, and they can also be organically integrated with other types of methods to further improve transferability, such as ensemble attacks [
57,
58] or specialized objective functions [
59,
60].
Future research in this field will focus on the following aspects. First, enhancing the transferability to unknown black-box models. Given the non-cooperative nature of SAR systems, how to generate highly transferable adversarial examples using a known surrogate model without accessing target models will remain an essential research direction. Second, improving the robustness of adversarial perturbations. Since there may be some degree of position deviation, perspective changes, and other uncontrollable errors when physically implanting adversarial perturbations, ensuring that the generated adversarial examples can still maintain attack capabilities in the face of uncertainties will be a significant challenge. Third, enhancing the physical realizability of adversarial perturbations. Current research primarily focuses on pixel-level perturbations in the digital domain. Although some studies [
53,
61,
62] have linked adversarial perturbations with electromagnetic scattering characteristics of the target by using the attribute scattering center model (ASCM), there is still a long way to go to realize adversarial perturbations physically. Future studies should consider passive interference methods like electromagnetic materials and metasurfaces [
63] to alter the target’s electromagnetic scattering properties, or using jammers and other active interference methods to add adversarial perturbations to the target’s echo signals, thereby physically realizing adversarial attacks in the real world and bridging the gap between theoretical advancements and practical applicability.