A Data and Model-Driven Clutter Suppression Method for Airborne Bistatic Radar Based on Deep Unfolding
Abstract
1. Introduction
- (1)
- We developed a detailed clutter signal model for airborne bistatic radar.
- (2)
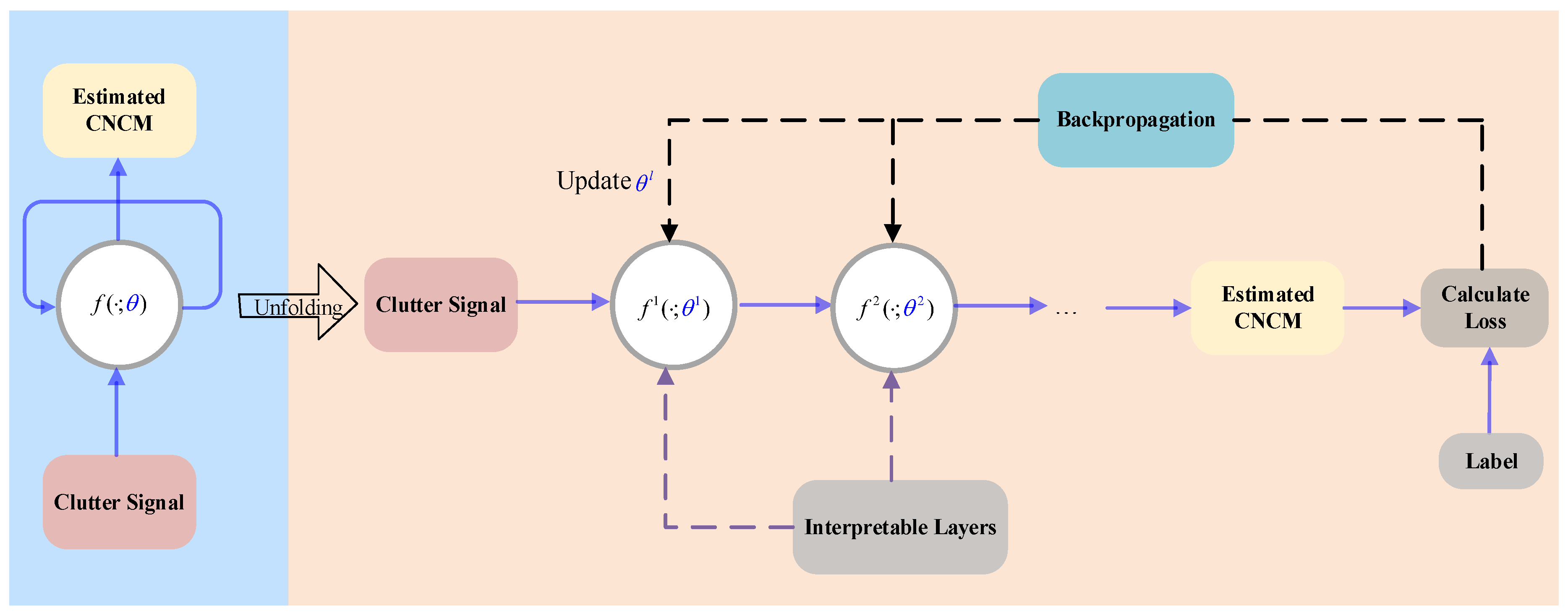
- To address the parameter setting difficulties of the ANM algorithm, we unfolded it into a deep neural network, which was called deep unfolding-based gridless sparse recovery bistatic STAP net (DUGLSR-BSTAP-Net). By selecting appropriate training data and labels to calculate the loss function and using the Adam optimizer for backpropagation to update parameters, the network can be trained to set different, more suitable parameters for each layer. This approach contrasts with traditional iterative algorithms, which maintain fixed preset parameters throughout the process.
- (3)
- We conducted extensive simulation experiments, comparing the proposed algorithm (DUGLSR-BSTAP-Net) with several classic SR-STAP methods across multiple aspects. These aspects included the clutter Capon spectrum, the eigenspectra of the estimated CNCM, improvement factor, and the variation of target detection probability with respect to the signal-to-noise ratio (SNR). The results validated that the proposed algorithm offers superior clutter suppression and target detection performance.
2. Signal Model and Overview of ANM-STAP
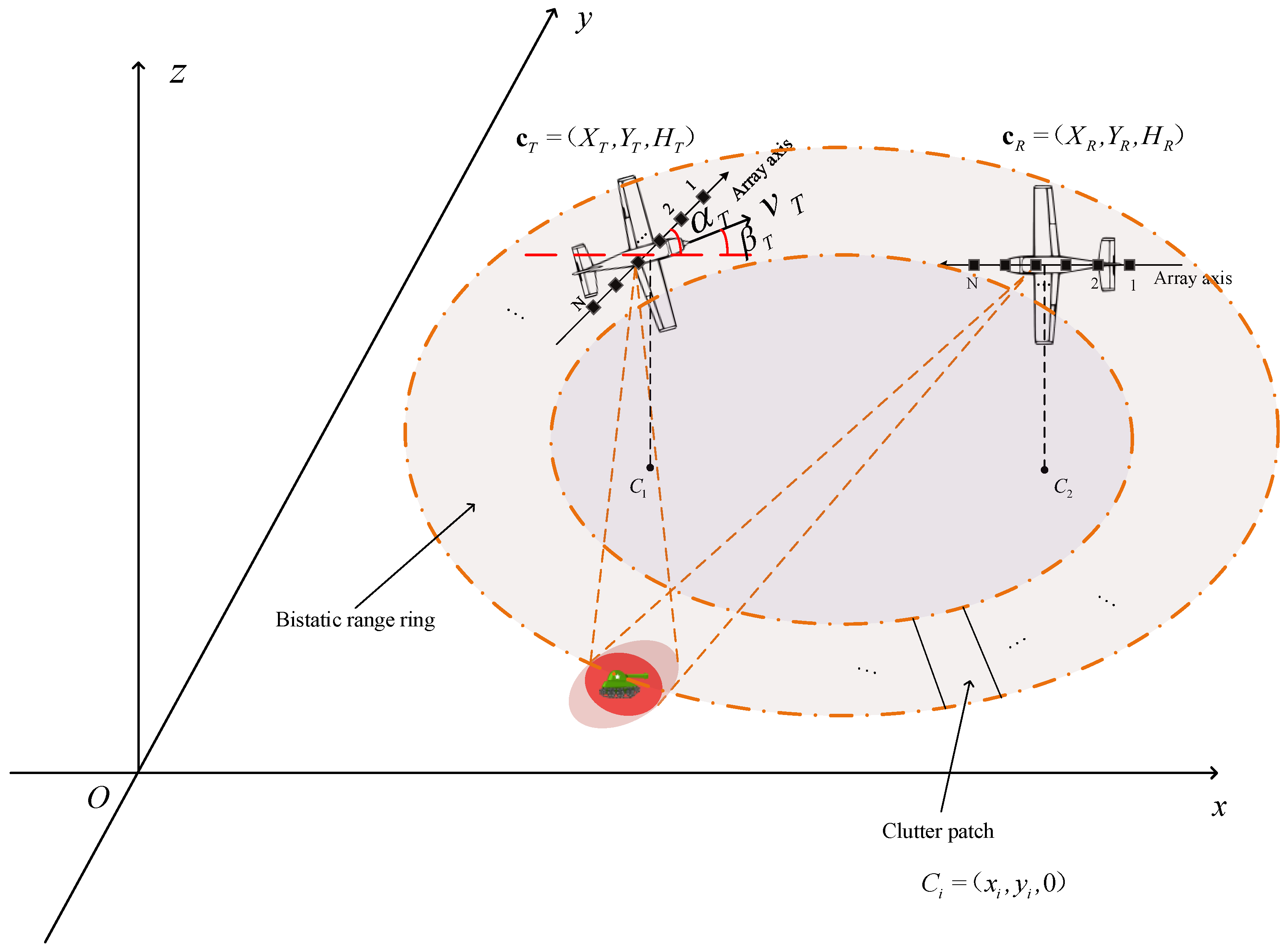
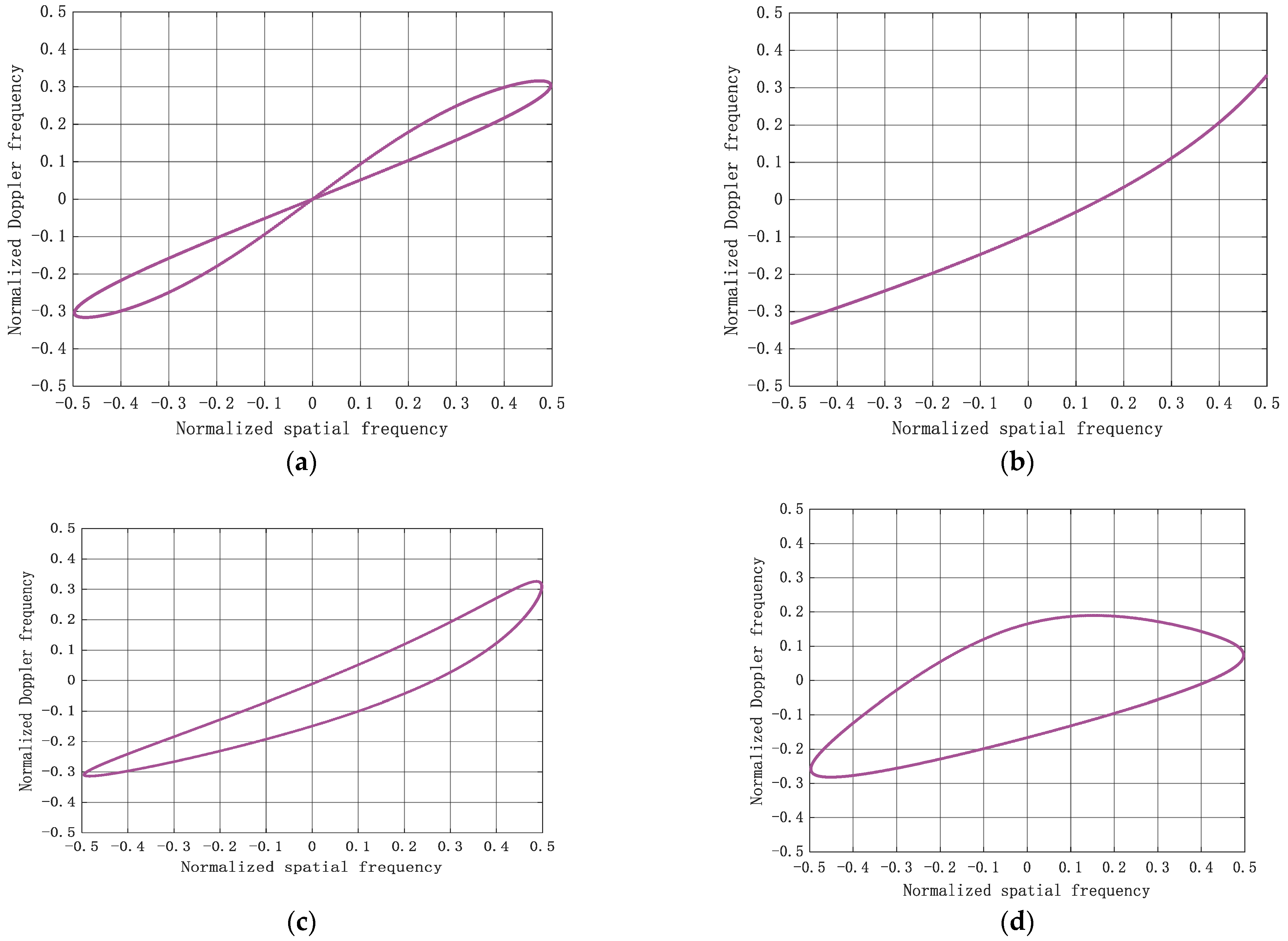
2.1. Airborne Bistatic Signal Model
2.2. ANM-STAP
3. Unfolding Gridless Sparse Recovery Bistatic STAP Algorithms into Deep Networks
3.1. Gridless Sparse Recovery Bistatic STAP(GLSR-BSTAP)
- (1)
- Update :
- (2)
- Update :
- (3)
- Update :
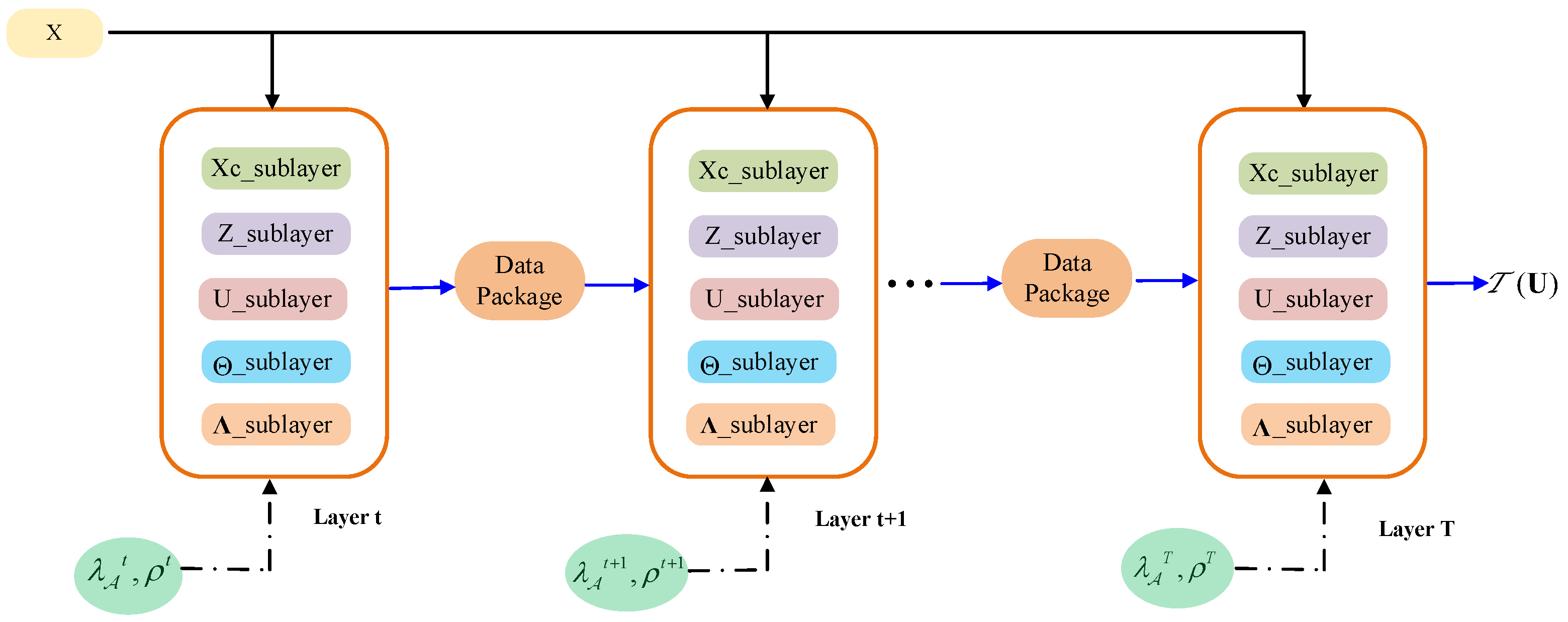
3.2. DUGLSR-BSTAP-Net
3.3. Network Structure Analysis
3.4. Generating the Training Dataset
3.5. Network Initialization and Training Method
4. Numerical Simulations
4.1. NMSE during Training
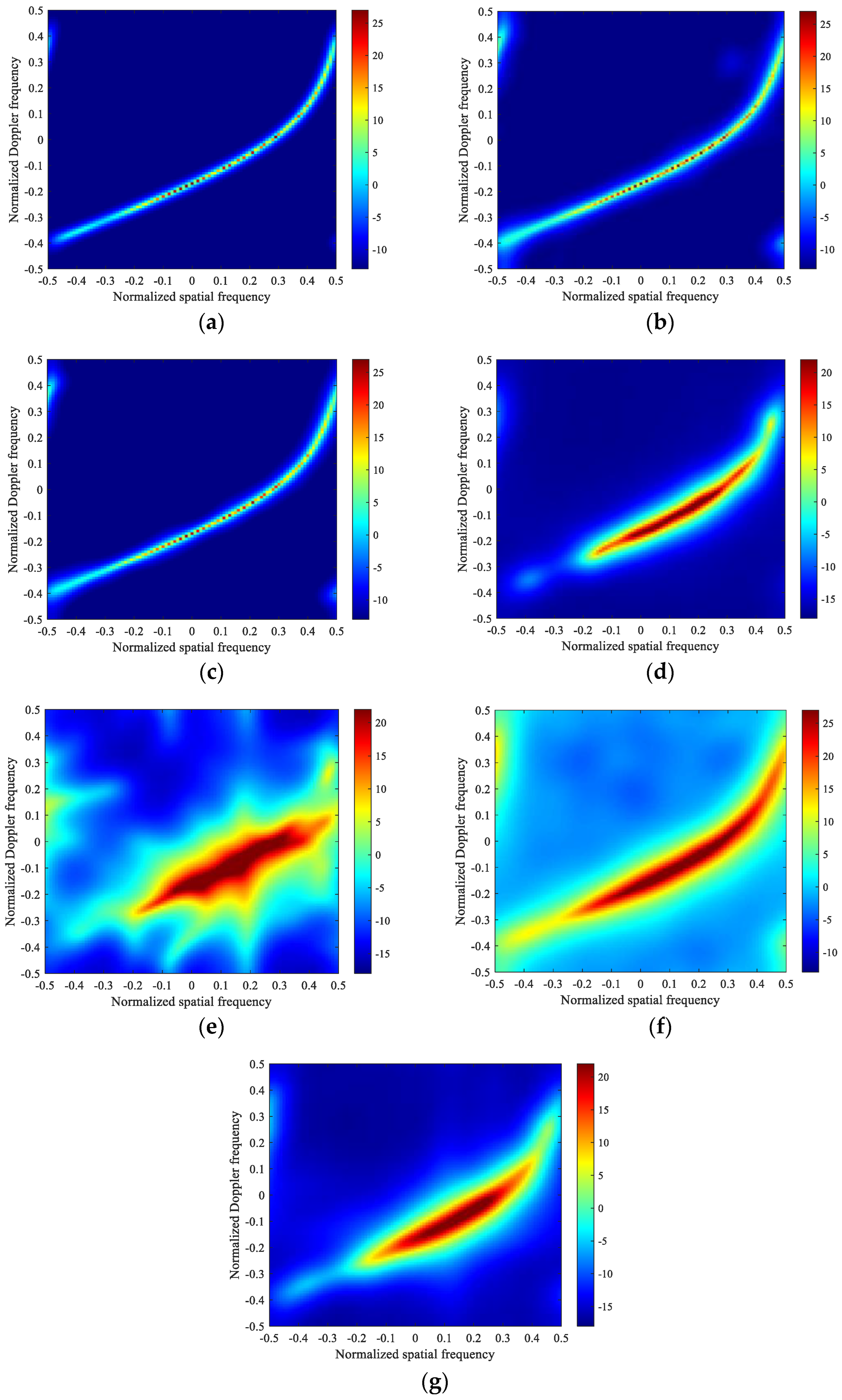
4.2. Recovered Capon Spectrum
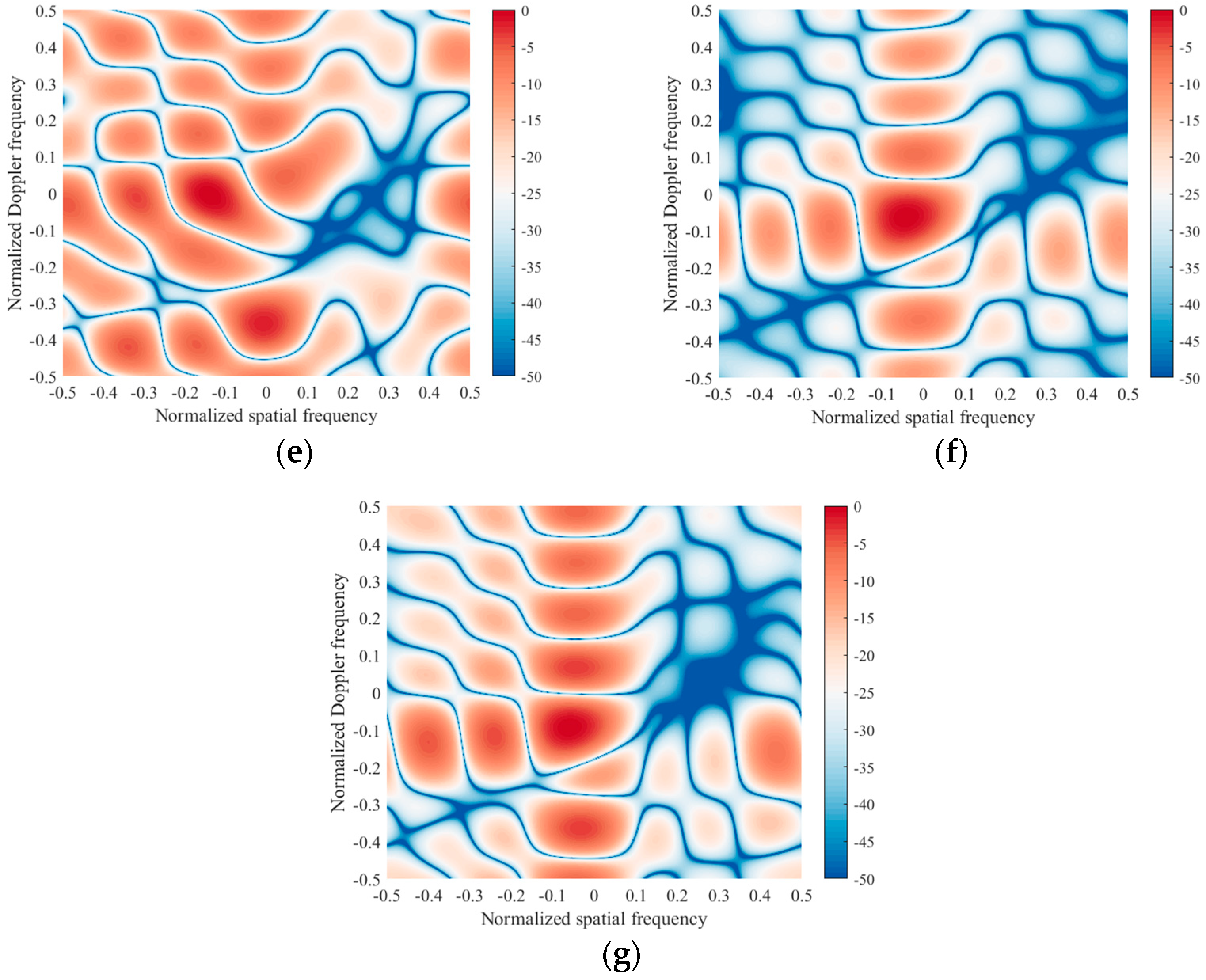
4.3. Adaptive Pattern
4.4. Comparison of Eigenspectra
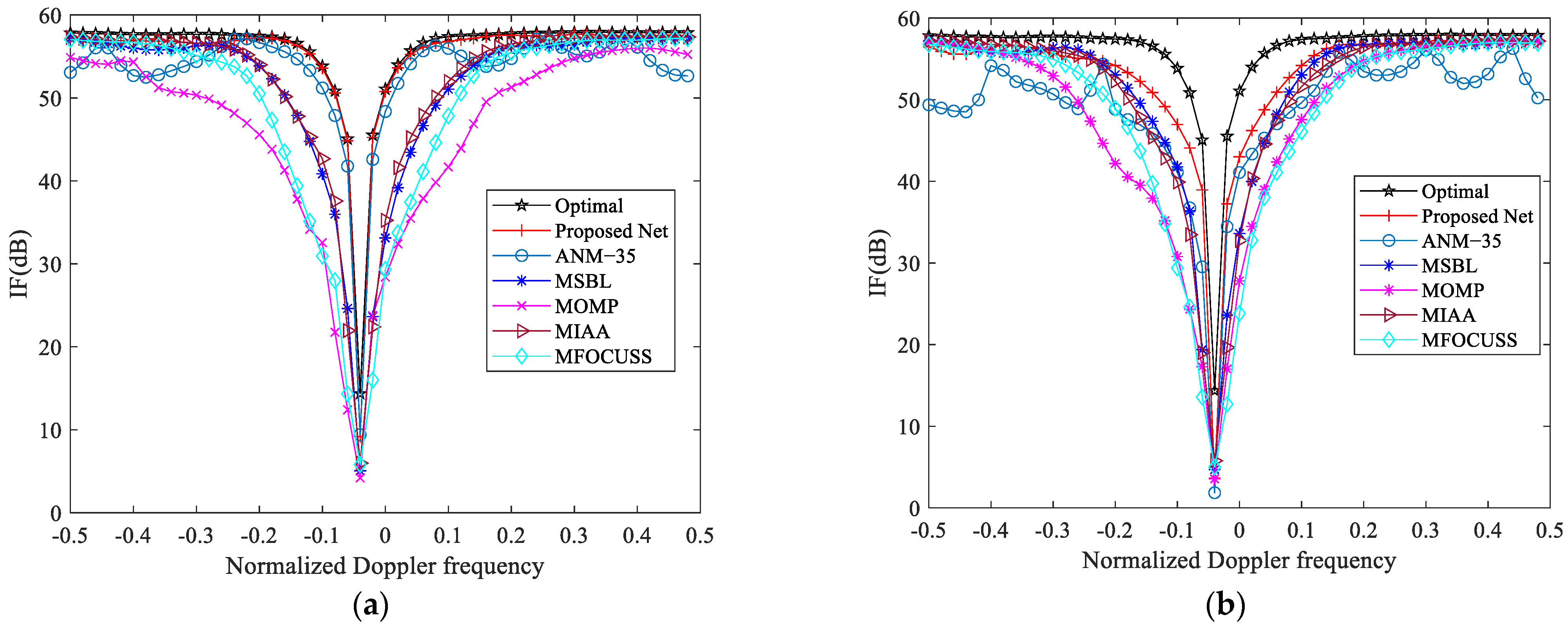
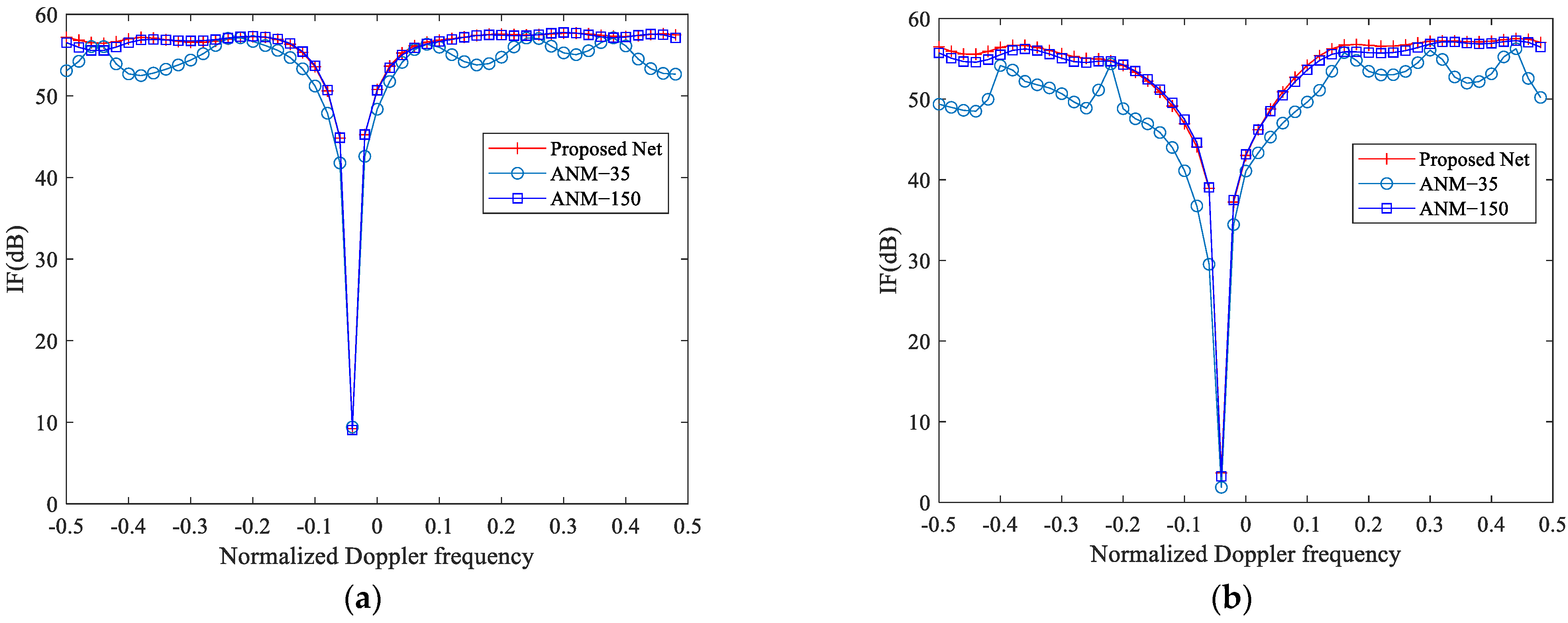
4.5. IF of Different Algorithms
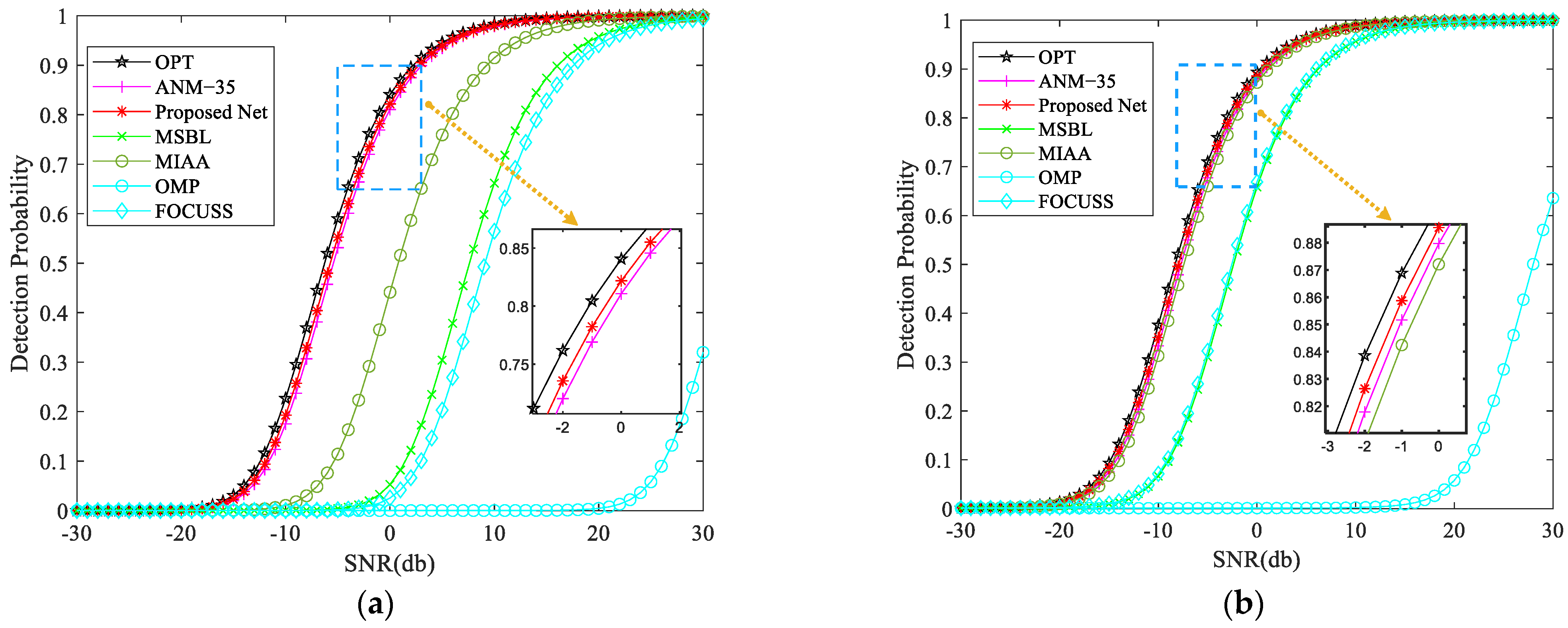
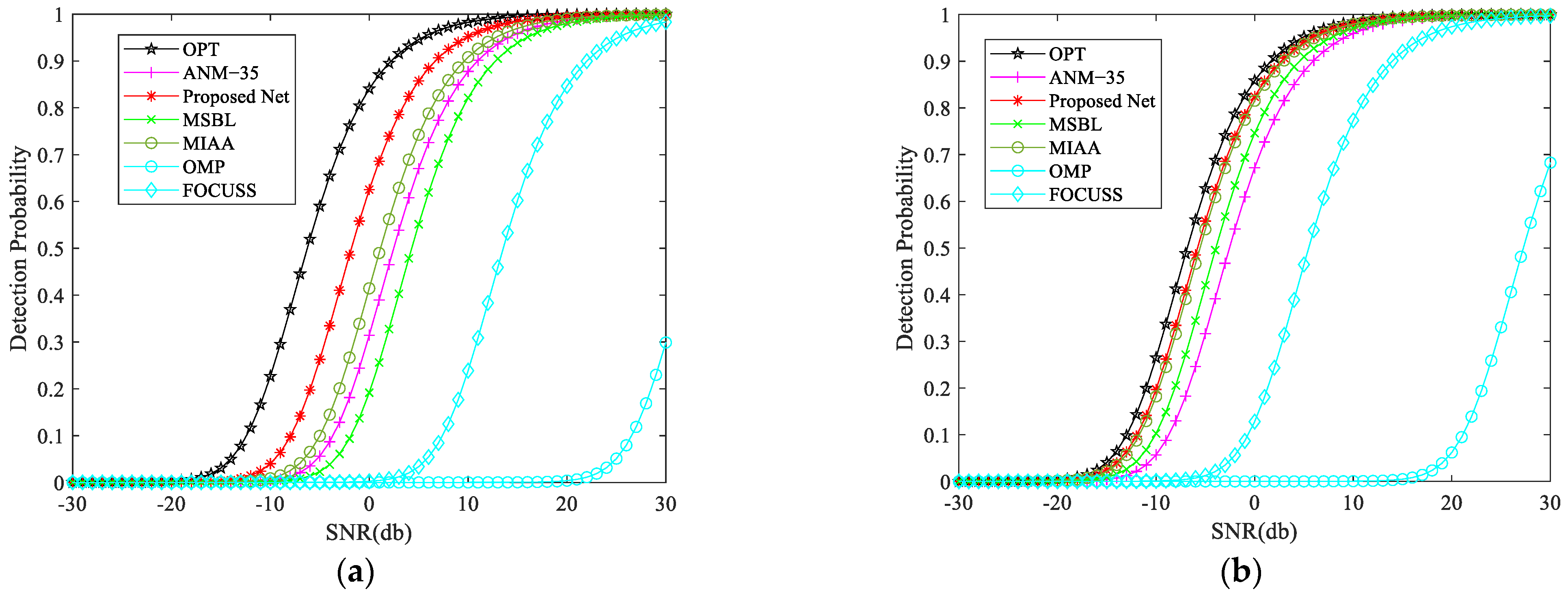
4.6. Target Detection Probability under Different SNR
4.7. Computational Efficiency
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Brennan, L.E.; Reed, L.S. Theory of Adaptive Radar. IEEE Trans. Aerosp. Electron. Syst. 1973, AES-9, 237–252. [Google Scholar] [CrossRef]
- Klemm, R. Principles of Space-Time Adaptive Processing. In Radar, Sonar and Navigation; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
- Melvin, W.L. Chapter 12—Space-Time Adaptive Processing for Radar. In Academic Press Library in Signal Processing; Sidiropoulos, N.D., Gini, F., Chellappa, R., Theodoridis, S., Eds.; Elsevier: Amsterdam, The Netherlands, 2014; Volume 2, pp. 595–665. ISBN 9780123965004. ISSN 2351-9819. [Google Scholar] [CrossRef]
- Ward, J. Space-time adaptive processing for airborne radar. In Proceedings of the 1995 International Conference on Acoustics, Speech, and Signal Processing, Detroit, MI, USA, 9–12 May 1995. [Google Scholar]
- Reed, I.S.; Mallett, J.D.; Brennan, L.E. Rapid Convergence Rate in Adaptive Arrays. IEEE Trans. Aerosp. Electron. Syst. 1974, AES-10, 853–863. [Google Scholar] [CrossRef]
- Maria, S.; Fuchs, J.-J. Application of the Global Matched Filter to Stap Data an Efficient Algorithmic Approach. In Proceedings of the 2006 IEEE International Conference on Acoustics Speech and Signal Processing Proceedings, Toulouse, France, 14–19 May 2006; p. 4. [Google Scholar] [CrossRef]
- Sun, K.; Zhang, H.; Li, G.; Meng, H.; Wang, X. A novel STAP algorithm using sparse recovery technique. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009; pp. V-336–V-339. [Google Scholar] [CrossRef]
- Sun, K.; Meng, H.; Wang, Y.; Wang, X. Direct data domain STAP using sparse representation of clutter spectrum. Signal Process. 2011, 91, 2222–2236. [Google Scholar] [CrossRef]
- Yang, Z.; Li, X.; Wang, H.; Jiang, W. Adaptive clutter suppression based on iterative adaptive approach for airborne radar. Signal Process. 2013, 93, 3567–3577. [Google Scholar] [CrossRef]
- Yang, Z.; Li, X.; Wang, H.; Jiang, W. On Clutter Sparsity Analysis in Space–Time Adaptive Processing Airborne Radar. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1214–1218. [Google Scholar] [CrossRef]
- Duan, K.; Wang, Z.; Xie, W.; Chen, H.; Wang, Y. Sparsity-based stap algorithm with multiple measurement vectors via sparse bayesian learning strategy for airborne radar. IET Signal Process. 2017, 11, 544–553. [Google Scholar] [CrossRef]
- Liu, C.; Wang, T.; Zhang, S.; Ren, B. Clutter suppression based on iterative reweighted methods with multiple measurement vectors for airborne radar. IET Radar Sonar Navig. 2022, 16, 1446–1459. [Google Scholar] [CrossRef]
- Cui, W.; Wang, T.; Wang, D.; Liu, C. An Improved Iterative Reweighted STAP Algorithm for Airborne Radar. Remote Sens. 2023, 15, 130. [Google Scholar] [CrossRef]
- Candès, E.J.; Fernandez-Granda, C. Towards a mathematical theory of super-resolution. Commun. Pure Appl. Math. 2014, 67, 906–956. [Google Scholar] [CrossRef]
- Tang, G.; Bhaskar, B.N.; Shah, P.; Recht, B. Compressed Sensing Off the Grid. IEEE Trans. Inf. Theory 2013, 59, 7465–7490. [Google Scholar] [CrossRef]
- Feng, W.; Guo, Y.; Zhang, Y.; Gong, J. Airborne radar space time adaptive processing based on atomic norm minimization. Signal Process. 2018, 148, 31–40. [Google Scholar] [CrossRef]
- Zhang, T.; Hu, Y.; Lai, R. Gridless super-resolution sparse recovery for non-sidelooking STAP using reweighted atomic norm minimization. Multidimens. Syst. Signal Process. 2021, 32, 1259–1276. [Google Scholar] [CrossRef]
- Li, Z.; Wang, T.; Su, Y. A fast and gridless stap algorithm based on mixed-norm minimisation and the alternating direction method of multipliers. IET Radar Sonar Navig. 2021, 15, 1340–1352. [Google Scholar] [CrossRef]
- Cui, W.; Wang, T.; Wang, D.; Zhang, X. A novel sparse recovery-based space-time adaptive processing algorithm based on gridless sparse Bayesian learning for non-sidelooking airborne radar. IET Radar Sonar Navig. 2023, 17, 1380–1390. [Google Scholar] [CrossRef]
- Duan, K.; Chen, H.; Xie, W.; Wang, Y. Deep learning for high-resolution estimation of clutter angle-Doppler spectrum in STAP. IET Radar Sonar Navig. 2022, 16, 193–207. [Google Scholar] [CrossRef]
- Zou, B.; Wang, X.; Feng, W.; Lu, F.; Zhu, H. Memory-Augmented Autoencoder-Based Nonhomogeneous Detector for Airborne Radar Space-Time Adaptive Processing. IEEE Geosci. Remote Sens. Lett. 2024, 21, 3502405. [Google Scholar] [CrossRef]
- Zhu, H.; Feng, W.; Feng, C.; Zou, B.; Lu, F. Deep unfolding based space-time adaptive processing method for airborne radar. J. Radars 2022, 11, 676–691. [Google Scholar] [CrossRef]
- Li, Y.; Chi, Y. Off-the-Grid Line Spectrum Denoising and Estimation with Multiple Measurement Vectors. IEEE Trans. Signal Process. 2016, 64, 1257–1269. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers; Foundations and Trends® in Machine Learning: Hanover, MA, USA, 2011. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Pati, Y.C.; Rezaiifar, R.; Krishnaprasad, P.S. Orthogonal matching pursuit: Recursive function approximation with applications to wavelet decomposition. In Proceedings of the 27th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 1–3 November 1993; IEEE: Piscataway, NJ, USA, 1993; pp. 40–44. [Google Scholar]
- Gorodnitsky, I.F.; Rao, B.D. Sparse signal reconstruction from limited data using FOCUSS: A re-weighted minimum norm algorithm. IEEE Trans. Signal Process. 1997, 45, 600–616. [Google Scholar] [CrossRef]
- Li, Z.; Wang, T. ADMM-Based Low-Complexity Off-Grid Space-Time Adaptive Processing Methods. IEEE Access 2020, 8, 206646–206658. [Google Scholar] [CrossRef]
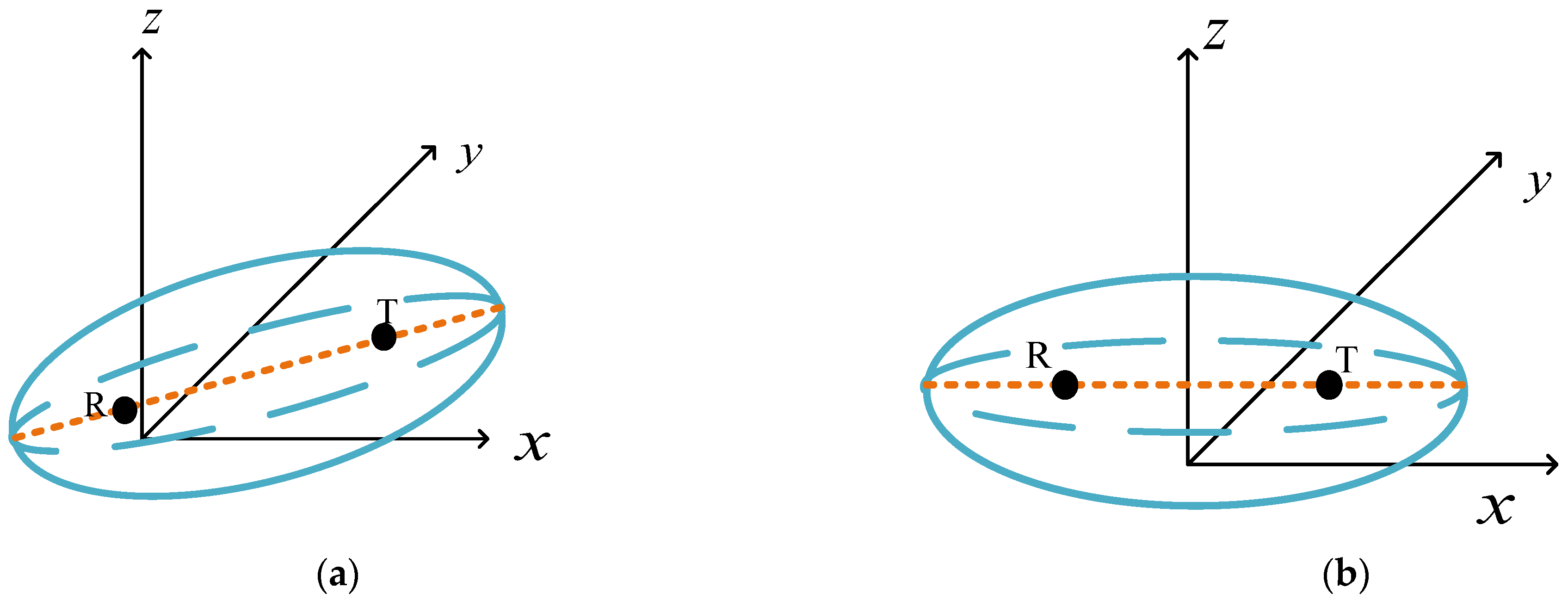




| Parameter | Value | Unit |
|---|---|---|
| Number of transmitter and receiver array element N | 8 | - |
| Number of pulses K | 8 | - |
| Pulse repetition frequency | 2000 | Hz |
| 0.3 | m | |
| Bandwidth | 2.5 | MHz |
| Velocity of transmitter and receiver | 120 | m/s |
| CNR | 40 | dB |
| Algorithm | Time | Unit |
|---|---|---|
| ANM-35 | 0.283 | s |
| ANM-150 | 0.847 | s |
| MSBL | 14.425 | s |
| MIAA | 2.100 | s |
| MOMP | 0.025 | s |
| MFOCUSS | 3.687 | s |
| DUGLSR-BSTAP-Net | 0.304 | s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, W.; Wang, T.; Liu, K. A Data and Model-Driven Clutter Suppression Method for Airborne Bistatic Radar Based on Deep Unfolding. Remote Sens. 2024, 16, 2516. https://doi.org/10.3390/rs16142516
Huang W, Wang T, Liu K. A Data and Model-Driven Clutter Suppression Method for Airborne Bistatic Radar Based on Deep Unfolding. Remote Sensing. 2024; 16(14):2516. https://doi.org/10.3390/rs16142516
Chicago/Turabian StyleHuang, Weijun, Tong Wang, and Kun Liu. 2024. "A Data and Model-Driven Clutter Suppression Method for Airborne Bistatic Radar Based on Deep Unfolding" Remote Sensing 16, no. 14: 2516. https://doi.org/10.3390/rs16142516
APA StyleHuang, W., Wang, T., & Liu, K. (2024). A Data and Model-Driven Clutter Suppression Method for Airborne Bistatic Radar Based on Deep Unfolding. Remote Sensing, 16(14), 2516. https://doi.org/10.3390/rs16142516





