Elevation Changes of A’nyemaqen Snow Mountain Revealed with Satellite Remote Sensing

Abstract

A’nyemaqen Snow Mountain (ASM) is the largest glacier area in the Yellow River source area and has been experiencing significant ablation in recent years. To investigate spatial–temporal elevation changes in ASM, a 21–year Digital Elevation Model (DEM) time series was obtained using the MicMac ASTER (MMASTER) algorithm and ASTER L1A V003 data. It covers the period from January 2002 to January 2023. The mean elevation of ASM decreased by −7.88 ± 3.37 m during this period, with highly spatial variation. The elevation decrease occurred mainly in the lower elevations and opposite in the higher elevations. The corresponding elevation decrease was −12.99 ± 11.29 and −4.45 ± 11.36 m at the southern Yehelong Glacier and the northern Weigeledangxiong Glacier, respectively. Moreover, there exists a temporal variation in ASM. The maximum elevation was observed in February for both ASM and the southern Yehelong Glacier but March for Weigeledangxiong Glacier, with about 1 month lagged. With the elevation time series and climate data from ERA5 datasets, we applied the random forest technique and found that the temperature is the main factor to elevation change in ASM. Furthermore, the response of elevation changes to temperature appeared with a lag and varied with the location. Based on the elevation time series, the ARIMA model was further used to forecast the elevation changes in the next 5 years. All regions will experience the elevation decrease, with a mean decline −1.74 ± 0.39 m and a corresponding rate −0.35 ± 0.08 m/a in ASM. This is similar to that of −0.38 ± 0.16 m/a between 2002 and 2003, showing its stability in the near future.

1. Introduction

The High Mountain Asia (HMA) region is home to many glaciers, rivers and lakes and viewed as “Asia’s Water Tower” [1,2]. Dozens of rivers in Asia are highly dependent on its meltwater recharge, and it is related to the production and living water of more than 2 billion people [3,4]. In addition, changes in HMA glaciers are closely associated with the recently frequent disasters, such as debris flow landslides, ice avalanches, glacial lake outbursts and glacial debris flows [5,6,7]. The Tibetan Plateau, as the main body of the HMA, is one of the regions experiencing strong global warming, with the glaciers experiencing great mass loss and area shrinkage. The mass loss is especially pronounced in Southeast Tibet, followed by the southern edge of the Himalayas. However, little mass losses and even mass gains were observed in some glaciers, such as the Pamir, Karakoram and West Kunlun regions. Moreover, HMA alpine glaciers are projected to potentially lose between 29 $\pm$ 12% and 67 $\pm$ 10% relative to 2015 by the end of this century for RCP 2.6 and RCP 8.5, respectively [8].

The mass balance of a glacier can be estimated in situ and with model simulations and remote sensing. Currently, data were collected with field observations in about 30 out of over 80,000 glaciers in High Asia. The number is less with long–term monitoring [9]. In addition, the coverage of the collected data is limited and may be not considered as representative of the region [10,11,12,13]. The Open Global Glacier Model (OGGM) is a classical model used for simulating and predicting global glacier changes [14]. For instance, this model was utilized to simulate responses to climate change at nine typical glaciers in the HMA region [15]. Yet, model simulations require substantial data support and entail certain uncertainties in their results [16]. Satellite remote sensing technology, with its low cost, high efficiency and larger coverage, has gradually become the main tool for glacier monitoring, especially for area change monitoring [17,18]. Besides the area change, elevation change is derived with satellite altimetry and DEM analysis [19,20,21,22,23,24]. For the latter, long time series results can be obtained. For example, the mass balance of global glaciers over the past twenty years was calculated by constructing a DEM time series, showing an overall negative and accelerated mass loss of 48 ± 16 Gt/(10a) [25]. The mass balance of the Fox and Franz Josef glaciers located in New Zealand was derived with a DEM time series with a resolution of 15 m [26].

A’nyemaqen Snow Mountain (ASM) is a typical glacier in the Eastern Kunlun region, the largest glacier area in the Yellow River source region. It regulates the changes in the Yellow River’s tributaries and runoff, influencing the local ecological balance and economic development [27,28]. The area decrease and average elevation decrease rate from 2000 to 2018 in ASM was firstly revealed at about 29.4 km² from 1966 to 2018 and −0.42 $\pm$ 0.07 m/y using remote sensing data [28].The elevation decrease from 2000 to 2013 was further derived with TerraSAR–X/TanDEM–X interferometric measurements at −4.16 $\pm$ 3.70, −8.73 $\pm$ 3.70 and −13.0 $\pm$ 3.70 m for Weigeledangxiong, Halong and Yehelong Glaciers, respectively [29]. Moreover, it was found that precipitation and temperature impact the elevation changes and mass balance of the glaciers [30,31].

In this paper, ASTER L1A V003 (https://lpdaac.usgs.gov/products/ast_l1av003/, accessed on 10 June 2024; NASA/METI/AIST/Japan Spacesystems and U.S./Japan ASTER Science Team, 2001), TanDEM–X and Randolph Glacier Inventory data were utilized to produce a high–precision DEM time series of ASM and derive its surface elevation change from January 2002 to January 2023. Then, we discuss the relationship between elevation change and the precipitation, as well as temperature. Finally, an ARIMA model is used to predict the elevation change of ASM until 2028.

2. Study Area

As shown in Figure 1a, ASM is located in the northeastern part of the Tibetan Plateau between 34°20′–35°N and 99°10′–101°30′E, belonging to the eastern branch of the Kunlun Mountain. It is approximately 200 km long and 60 km wide, with a summit of 6282 m shown in Figure 1b. This region is impacted by the East Asian summer winds and westerly circulation [32]. Maqin Station, a national meteorological station located about 80 km away from ASM, collected massive observations from 1961 to 2013, showing that the average temperature and precipitation in the area are −0.2 °C and 514 mm. Moreover, the summer precipitation accounts for about 58% of the annual [33].

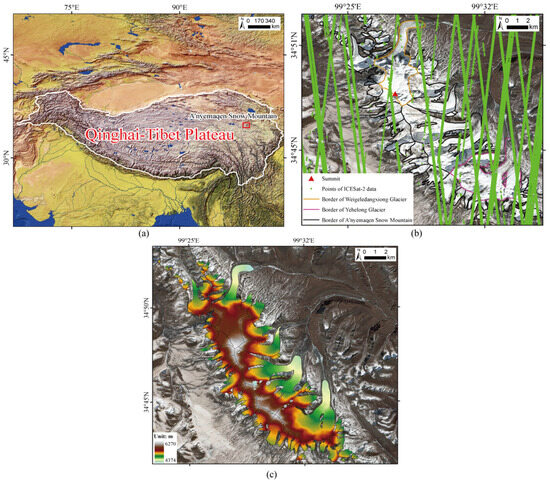
Figure 1. (a) Location of A’nyemaqen Snow Mountain. (b) Coverage and summit of ASM from a Sentinel–2 image on 30 January 2023, location of the Weigeledangxiong and Yehelong Glaciers and ICESat–2 tracks, and (c) the DEM in January 2023.

ASM is a glacier center in the Sanjiangyuan region, covering 124 km² with 46 current glaciers [34]. It is the water resource of the Yellow River Basin, and its mass balance has a substantial influence [35]. Here, we select two typical glaciers, Weigeledangxiong in the north and Yehelong Glacier in the south. The area of the two glaciers is 12.53 and 17.63 km², respectively.

3. Materials and Methods

3.1. Data

As shown in Table 1, Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) L1A V003, TanDEM–X, Randolph Glacier Inventory (RGI), ICESat–2 and ERA 5 data were used in this paper. ASTER L1A V003, TanDEM–X and RGI data were utilized to generate DEMs for further surface elevation change calculations. ICESat–2 data were used for DEM accuracy validation.

Table 1. Data used in this study.

Datasets	Time	Spatial Resolution	Source
ASTER L1A V003	12 May 2002–29 November 2022	15 m	https://www.earthdata.nasa.gov/ (accessed on 14 February 2023)
TanDEM–X	December 2010 to 2015	90 m	https://download.geoservice.dlr.de/TDM90/ (accessed on 3 April 2023)
ICESat–2	5 January 2019–28 December 2022	~17 m (along track)	https://www.earthdata.nasa.gov/ (accessed on 28 September 2023)
Randolph Glacier Inventory 6.0	28 July 2017	–	https://www.glims.org/RGI/ (accessed on 3 April 2023)
ERA 5	January 2002–December 2023	31 km	https://psl.noaa.gov/data/atmoswrit/timeseries (accessed on 26 February 2024)

3.1.1. ASTER L1A V003

The ASTER Earth Observation Satellite specializes in capturing stereoscopic imagery with minimal temporal discrepancies and reduced sensor modeling errors [36,37]. It features 14 spectral channels, spanning visible and near–infrared (VNIR), short–wave infrared (SWIR) and thermal infrared (TIR). Its viewing geometry is suitable for DEM generation, even without ground control points. ASTER remote sensing data cover wide areas with a revisit period of approximately 16 days, facilitating multiple captures of the same area to monitor land surface changes. Moreover, they are freely available. ASTER L1A stereo images with bands 3N and 3B between 12 May 2002 and 29 December 2022 were used, with a 15 m spatial resolution.

3.1.2. TanDEM–X

TanDEM–X data were acquired between 2010 and 2015. It is based on the WGS84 ellipsoid and has an absolute linear height error of less than 2m at a 90% confidence level [38,39]. The precision makes TanDEM–X an external elevation dataset for co–registration with ASTER DEMs, significantly mitigating residual errors.

3.1.3. Randolph Glacier Inventory

To mitigate motion–related errors and extract the glacier extent, unstable terrain such as water and large mountains was masked. This was indirectly achieved by the Randolph Glacier Inventory (RGI), a comprehensive global collection of digital glacier profiles [40,41]. The distribution of ASM is shown in Figure 1b with the RGI.

3.1.4. ICESat–2

Here, we used ICESat–2 data to verify the accuracy of DEM from ASTER data. The L3A Land and Vegetation Height V008 (ATL08) product of ICESat–2 was selected, covering the period from 5 January 2019 to 28 December 2022. The coverage is shown in Figure 1b, where there are 10 tracks with a 15 m resolution along the tracks [42]. ATL08 is widely used for DEM accuracy verification. Studies have shown that the accuracy of ATL08 terrain height data can reach 0.70 m [43]. Compared to ATL06, ATL08 offers a broader coverage with nearly consistent accuracy in non–vegetated areas for both the summer and winter [44].

3.1.5. ERA5

ERA5 is a state–of–the–art reanalysis product released by the European Center for Medium–Range Weather Forecasts (ECMWF) [45]. The dataset has been capable of providing global meteorological data since 1950. Compared with other datasets, it has a 31 km horizontal resolution [46]. Moreover, the dataset has been proven to reproduce temperature and precipitation trends well and has been widely used in meteorological studies in China [47,48,49]. We used this dataset to extract precipitation and temperature data from January 2002 to January 2023 for ASM.

3.2. Methods

3.2.1. DEM Time Series Determination

Composed of a tool to calculate Rational Polynomial Coefficient (RPC) models from the ASTER metadata, MicMac ASTER (MMASTER) is a helpful method to produce DEM. It improves the quality of the matching by identifying and correcting jitter–induced cross–track parallax errors. Compared to NASA’s standard AST14DMO product (https://lpdaac.usgs.gov/products/ast14dmov003/, accessed on 10 June 2024; NASA/METI/AIST/Japan Spacesystems and U.S./Japan ASTER Science Team, 2007), MMASTER produces DEMs with higher accuracy, fewer mismatch areas and less overall noise [50].

Pyddem is a commonly used python package for building DEM times. DEMs were firstly stacked to create a three–dimensional arrays, and then, gaussian process regression (GPR) used to model the elevation time series [25]. It is allowed to capture the nonlinear elevation change of the glaciers, making the interpolated results closer to reality. GPR takes a kernel ${{\sigma }_h(x,y,∆t)}^2$ as the input:

$$\begin{gathered} {{\sigma }_h(x,y,∆t)}^2=PL\left(x,y,∆t\right)+ESS\left({\varphi }_{per},{\sigma }_{per}^2,∆t\right)+RBF\left({∆t}_{loc},{\sigma }_{loc}^2,∆t\right) \\ +RQ\left({∆t}_{nl},{\sigma }_{nl},∆t\right)\ast PL\left(x,y,∆t\right)+{{\sigma }_h(t,x,y)}^2 \end{gathered}$$

(1)

where PL is a pairwise linear kernel, representing the long–term elevation trend of the pixel, ESS is a periodic exponential sine–squared kernel, representing the seasonality of the elevation changes, RBF is a local radial basis function kernel, showing the elevation closeness with varying time differences, RQ is a rational quadratic kernel multiplied by a linear kernel, to capture the long–time nonlinear trends, and ${{\sigma }_h(t,x,y)}^2$ is the white noise representing the average measurement errors at time $t$.

The workflow for producing the DEM time series is shown in Figure 2. RGI data were used to extract the glacier extent of ASM. The MMASTER algorithm was then applied to extract the DEMs from the ASTER L1A V003 images, and TanDEM–X, as well as RGI, were introduced to co–register the ASTER results. In this process, a higher–resolution TanDEM–X is obtained with 30 m resolution after upsampling and masking with RGI. To eliminate the data gap in the results, 53 DEMs with RMSE less than 10 m in the co–registration were stacked, and the python package pyddem was used to interpolate and calculate the final DEM time series from January 2002 to January 2023. Finally, the accuracy of the DEMs was evaluated with the ICESat–2 data.

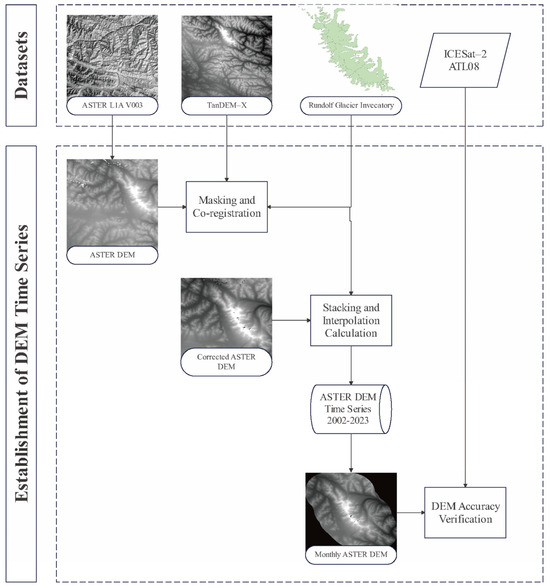
Figure 2. Workflow of the DEM time series from ASTER L1A V003 and TanDEM–X data.

3.2.2. DEM Verification

As the resolution of ICESat–2 and ASTER DEM is different, the ASTER DEM grid data were interpolated according to the time epoch of ICESat–2. Then, the elevation differences in stable glacier–free regions between ASTER DEM and ICESat–2 were calculated. Icepyx is a widely used python library for processing ICESat–2 data, with the functions querying, obtaining, analyzing and manipulating ICESat–2 datasets [51,52]. With Icepyx, we computed the elevation difference at the points between our ASTER DEMs and ICESat–2 datasets:

$$∆h=H_1-H_0$$

(2)

where $∆h$ is the elevation difference between two datasets and $H_0$ and $H_1$ the elevation of ICESat–2 and ASTER DEM, respectively.

3.2.3. Contribution and Correlation Analysis

To investigate the effects of temperature and precipitation on elevation changes, the random forest (RF) technique was used [53], so 80% of the datasets were randomly selected as training set and the remaining 20% as the test set. In RF, the mean squared error (MSE) is used as a metric to classify split nodes. Meanwhile, the decision tree selects the feature with the largest reduction in MSE for splitting. The contribution of each feature is further obtained by the weighted average of the percentage of MSE reduction of that feature in each decision tree. In addition, ${\mathrm{R}}^2$ was used to characterize the accuracy of the model.

$$R^2=1-\frac{\sum {{(y}_i-x_i)}^2}{\sum {{(y}_i-\overline{y})}^2}$$

(3)

where $x_i$ and $y_i$ are the observed and predicted values from the model and $\overline{y}$ the average value of $y_i$.

To analyze the correlation of the time series between two parameters, such as the elevation and the temperature or precipitation, Pearson’s correlation coefficient $r$ was used [54,55]:

$$r=\frac{\sum _{i=1}^n\left(x_i-\overline{x}\right)\left(y_i-\overline{y}\right)}{(n-1)·S_x·S_y}$$

(4)

where $n$ is the number of the time series and $(S_x,S_y)$ the standard deviation of two parameters.

3.2.4. Elevation Forecast

The Auto–regressive Integrated Moving Average (ARIMA) model is a typical tool for the time series forecast [56]. This method can be interpreted as a synthesis of the latest observations and long–term historical trends [57]. The predicted value $Y_t$ of the ARIMA model at time epoch t can be obtained:

$$Y_t=c+\sum _{i=1}^p{\phi }_i{Y}_{t-i}+\sum _{i=1}^q{\theta }_i{\epsilon }_{t-i}+{\epsilon }_t$$

(5)

where $c$ and ${\phi }_i$ are a constant term and the coefficient of the auto–regressive component, ${\mathsf{\theta }}_{\mathrm{i}}$ the coefficient of the moving average component and ${\epsilon }_t$ the residual at time epoch t. The three parameters p, d and q represent the orders of auto–regressive, differencing and moving average parts, respectively. To measure the accuracy of model fitting, Akaike Information Criterion (AIC) was used [58]:

$$AIC=2k-\mathit{ln}\left(L\right)$$

(6)

where $k$ is the parameter numbers and $L$ the likelihood function of the model. The smaller the AIC value, the better the accuracy. To mitigate trends and seasonal variations, difference and smoothing were applied. The parameters p, d and q vary with the ranges [0, 3], [0, 1] and [0, 1], respectively [59]. To obtain the optimal results, the calculation was iterative and the optimal obtained when the AIC value was minimized.

4. Results

4.1. Accuracy Evaluation of the DEM

Following the workflow shown in Figure 2 of Section 3.2, the final DEM time series of ASM was derived from ASTER data spanning from January 2002 to January 2023. Taking the DEM in January 2023 as an example, the elevation in the ASM is usually above 4300 m, as shown in Figure 1c. However, there exists a large spatial difference among glaciers. The elevation at ASM varies between 4374.22 and 6269.50 m, with the average 5088.94 m. A higher average elevation of 5357.76 m is observed at Weigeledangxiong Glacier, varying between 4382.19 and 6202.00 m. For Yehelong Glacier, the elevation varies between 4477.58 and 6193.01 m, with the smaller average of 4991.83 m.

ICESat–2 data were used to evaluate the DEM accuracy from ASTER data. There exists a systematic error of 2.93 m between ICESat–2 and ASTER DEM in stable non–ice regions, and the value was added to monthly ASTER DEMs [60]. Excluding the points with slopes greater than 60 degrees, the RMSE of the differences from 2019 to 2023 was 9.54 m. This is smaller than 11.47 m in the Qinghai–Tibet Plateau between ASTER GDEM V1 products and ICESat–2 ATL08 products, indicating the improvement of the MMASTER method.

4.2. Elevation Change

We further calculated the elevation change time series. To show the error of the results, we firstly calculated the elevation difference between January 2023 and January 2002, and the distribution is shown in Figure 3a. In addition, the elevation difference between January 2007, 2011, 2015, 2019 and January 2002, respectively were shown in Figure A1. The elevation change of ASM varies between −94.06 and 57.93 m, with the average at −7.88 m. Higher glaciers appear with a lower elevation decrease. For example, Weigeledangxiong Glacier has a smaller elevation decrease at −4.45 m, while Yehelong Glacier experiences a larger ice loss with a value of −12.99 m. Moreover, the ice tongue of Yehelong Glacier experienced the most mass loss in the figure. As time passed, the elevation decrease in the ice tongue portion became more severe. However, there is a significant elevation increase in the middle of the ice tongue of Weigeledangxiong Glacier, which may be due to the relative lower elevation of the ice tongue.

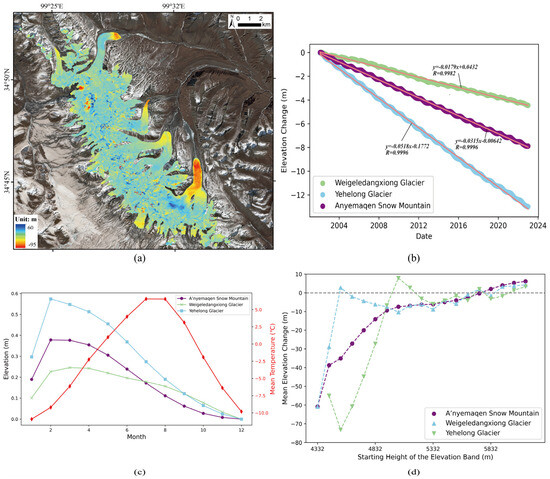
Figure 3. (a) The elevation difference between January 2023 and January 2002; (b) the average elevation time series and the fitting relative to January 2002 of A’nyemaqen Snow Mountain, Weigeledangxiong Glacier and Yehelong Glacier; (c) the corresponding seasonal elevation and temperature time series and (d) the mean elevation distribution with a 100 m interval. The red line in subfigure (c) is mean temperature.

Using the ASTER DEM time series and RGI data, the average elevation time series of ASM was derived and is shown in Figure 3b. The decreasing elevation trend is shown, with a value of about −7.88 $\pm$ 3.37 m over the study period. The time series was fitted with linear and seasonal terms, and the rate estimated was −0.38 $\pm$ 0.16 m/a. We derived the seasonal elevation time series of ASM by averaging, showing seasonal variations with the amplitude of 0.35 m in Figure 3c [61]. Moreover, the maximum elevation is observed in February and decreases until December.

Using the glacier extent shown in Figure 1b, the average elevation time series of Weigeledangxiong Glacier and Yehelong Glacier was derived. Compared to the results of ASM, the northern glacier experiences slower glacier mass loss, with an elevation decrease of about −4.45 $\pm$ 11.36 m from 2002 to 2023. Moreover, the southern glacier has a larger elevation decrease at about −12.99 $\pm$ 11.29 m. With the average elevation time series shown in Figure 3c, linear fitting was applied, and the elevation change rate was estimated as −0.21 $\pm$ 0.54 and −0.62 $\pm$ 0.54 m/a for Weigeledangxiong Glacier and Yehelong Glacier, respectively. The monthly elevation time series of Weigeledangxiong Glacier and Yehelong Glacier are derived in Figure 3d, showing seasonal variations again. A larger amplitude is observed in Yehelong Glacier than that of ASM, but Weigeledangxiong Glacier is smaller. A similar phase is observed in both Yehelong Glacier and ASM, with the maximum and minimum in February and December. However, Weigeledangxiong Glacier lagged one more month relative to the other two.

The elevation of ASM ranges from 4374.22m to 6269.50 m, with elevation changes varying at different elevations. The pace of the elevation was set as 100 m, and the average elevation changes were calculated for each band, as shown in Figure 3d. We found that ASM experiences significant elevation changes, with an Equilibrium Line Altitude (ELA) of about 5700 m, which is 100 m higher than Weigeledangxiong Glacier. Meanwhile, an abnormal increase in elevation change is observed at 4500 m up Weigeledangxiong Glacier, where we investigate in Figure 4. We treat it as abnormal. The elevation change pattern for Yehelong Glacier is more complex. It decreases first and then increases rapidly. The maximum elevation increase appears at about 5000 m and then fluctuates. The ELA of Yehelong Glacier is estimated as 5100 m.

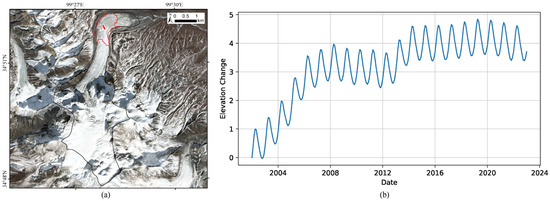
Figure 4. (a) Location of the selected central region A of the ice tongue of Weigeledangxiong Glacier, and (b) the average elevation time series of region A.

To investigate the elevation’s increase in the middle of the ice tongue of Weigeledangxiong Glacier, we extracted the average elevation time series of region A labeled in Figure 4a. The time series is shown in Figure 4b, with strong seasonal variations. From the figure, the elevation of this region increases from 2002 to 2008, keeps slightly decreasing until 2013, increases again between 2013 and 2015 and becomes stable until 2023. This needs further investigation.

5. Discussion

5.1. DEM and Elevation Changes

Since the DEM time series were obtained by interpolation, the accuracy of the DEM time series is highly dependent on the number and quantity of DEMs input during the stacking procedure. In addition, radar–based TanDEM–X can penetrate snow, leading to an elevation bias on the snow–covered terrain during co–registration.

We estimated that ASM experienced a decrease at a rate of −0.38 $\pm$ 0.16 m/a during 2002 to 2023. This is close to that of −0.42 $\pm$ 0.07 m/a between 2000 and 2018, indicating the stability of ASM after 2018 [28]. Compared to that of HMA, it is similar to that of −0.34 $\pm$ 0.07 m/a in HMA [62]. Moreover, a highly spatial variation was observed across HMA. A positive elevation rate of 0.14 $\pm$ 0.10 m/a was observed in Western Kunlun, followed by ASM and Tianshan at −0.38 $\pm$ 0.16 and −50 $\pm$ 0.10 m/a, respectively. Furthermore, the largest decrease rate at −1.07 $\pm$ 0.10m/a was shown in the Nyainqentanglha region [62].

5.2. Elevation Changes with Temperature and Precipitation

From the ERA5 datasets, the monthly temperature and precipitation time series between 2002 and 2023 was obtained and is shown in Figure 5a. The average temperature and precipitation of the 21–year period was −2.10 °C and 74.25 mm in ASM. Moreover, a positive trend is observed in both the temperature and precipitation time series, and the rate is estimated as 0.02 °C/a and 0.35 mm/a. Of which, precipitation is mainly concentrated in the summer.

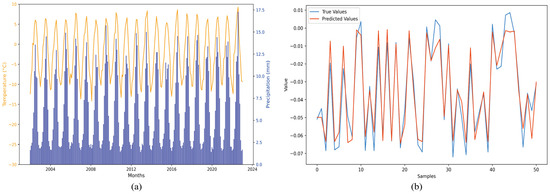
Figure 5. (a) Temperature and precipitation time series of A’nyemaqen Snow Mountain, and (b) the test set prediction results of the RF model. In subfigure (a), orange line is temperature and dark blue line is precipitation.

Simple linear regression was firstly used. The ${\mathrm{R}}^2$ between temperature and elevation was estimated as 0.94, which is slightly larger than that of 0.92 between precipitation and elevation. This indicates the two parameters lead to elevation change [63,64]. To make the contribution from the two parameters clearer, RF was applied. In RF, the number of estimators, max depth and random state are the key. These parameters control the number of decision trees, the longest path of decision trees and the randomness in self–sampling methods, respectively. After removing the trend term from the data, we obtained the optimal test results, as shown in Figure 5b, when setting 11, 8 and 25 as the corresponding parameters. The corresponding ${\mathrm{R}}^2$ is calculated as 0.93, indicating a strong correlation between the two parameters and glacier elevation changes. Moreover, the contribution of the temperature is 0.80, and the temperature is hence primary for the elevation change of ASM. This is similar to [30,31].

We further investigated the relationship between temperature and elevation. The monthly temperature of ASM was further derived, showing seasonal variations in Figure 3d. A correlation coefficient of −0.07 was first obtained, indicating there is a negative but not obvious relationship between elevation and temperature. As shown in Figure 3d, there exists a time lag $\tau$ between the two parameters [65]. Setting a range for the $\tau$ from 1 to 6, the optimal lag correlation coefficient of −0.96 was obtained when the lag time $\tau$ was 3. The optimal correlation coefficients of −0.92 and −0.95 were also estimated for Yehelong Glacier and Weigeledangxiong Glacier, with the corresponding lag times of 3 and 4. This indicates Weigeledangxiong Glacier was lagged for about another month compared to Yehelong Glacier and ASM.

It was found that the response in elevation change to the temperature is primarily controlled by the glacier slope rather than glacier size [66]. Moreover, steeper glaciers efficiently transfer mass and adapt rapidly [67]. The slope difference between Weigeledangxiong Glacier and Yehelong Glacier is 2.67° and may cause a longer response time to temperature in Weigeledangxiong Glacier. Furthermore, the resolution of the ERA5 dataset is only 31 km and may lead to errors as a result. This needs further research.

5.3. Elevation Change Prediction

An ARIMA model was then used to project the elevation change of ASM over the next five years. Using the elevation time series between 2002 and 2018, the elevation time series between 2019 and 2023 was predicted and compared to that of the observed one. The AICs were calculated from the three parameter p, d and q values, which were selected from [0, 3], [0, 1] and [0, 1]. It was found that the minimum AIC of −1851.80 was obtained when 2, 1 and 1 were selected as the p, d and q. With the selected parameters, the RMSE was estimated as 0.01, indicating that the model performs well. Applying the selected parameters to the elevation time series data between 2002 and 2023, the forecast elevation time series between 2024 and 2028 was derived and is shown in Figure 6b. It was found that the forecast of the average elevation of ASM will decrease −1.74 $\pm$ 0.39 m from January 2023 to January 2028. The corresponding rate was estimated as −0.35 $\pm$ 0.08 m/a, which is similar to that of −0.38 $\pm$ 0.16 m/a between 2002 and 2003, showing the stability of ASM in the near future.

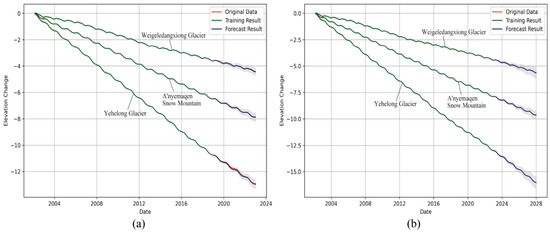
Figure 6. ARIMA test (a) and forecast (b) results for the time series.

Using the same procedure, the minimum AIC −1575.16 and −1603.49 for Weigeledangxiong Glacier and Yehelong Glacier was calculated, with the same parameters 2, 1 and 1 selected. The corresponding RMSE in the test set was calculated as 0.02 and 0.05, respectively. With the elevation time series 2002–2023 and the selected parameters, the elevation change time series of Weigeledangxiong Glacier and Yehelong Glacier between 2002 and 2028 was derived and is shown in Figure 6b. Weigeledangxiong Glacier and Yehelong Glacier are expected to experience an elevation decrease of −1.19 $\pm$ 0.52 and −3.04 $\pm$ 0.56 m during 2023–2028, with the corresponding rates 0.24 $\pm$ 0.10 and −0.61 $\pm$ 0.11 m/a. The results are similar to that of −0.21 $\pm$ 0.54 and −0.62 $\pm$ 0.54 m/a between 2002 to 2023, also indicating the stability of the two glaciers in the near future.

The ARIMA model predicts the future based solely on historical data, using only current and past information. It handles only univariate time series and cannot incorporate other factors. Therefore, there is some uncertainty in its long–term prediction results. Additionally, the time series must satisfy the assumption of smoothness, which leads to the forecasting results not having particularly large fluctuations.

6. Conclusions

In this study, we employed ASTER L1A V003 data and used the MMASTER algorithm to develop a high–precision DEM time series for A’nyemaqen Snow Mountain (ASM) from January 2002 to January 2023. The accuracy of the derived ASTER DEMs was evaluated using ICESat–2 data, which revealed a better average vertical error than ASTER GDEM products. This was particularly notable for its higher stability in non–glacier regions.

ASM has undergone significant ablation, with a significant spatial–temporal difference. In terms of vertical elevation change, the lower elevation area ablated more ice than the higher area. Meanwhile, the southern Yehelong Glacier experienced the more severe ablation than the northern Weigeledangxiong Glacier. Within the annual cycle, ASM and Yehelong Glacier reach their maximum elevation in February, a month before Wegeledangxiong Glacier, and then decrease until December.

Applying the random forest technique, we found that the increase in temperature is the primary factor influencing the elevation changes observed in ASM. Notably, the response of glacier elevation to temperature changes exhibited a lag, with different lag times observed between ASM and Yehelong Glacier compared to Wegeledangxiong Glacier. It was possibly influenced by the differential slopes between these two glaciers. However, the spatial resolution of the ERA5 datasets at 31 km may introduce errors into these results, highlighting an area for future research to enhance the precision of climate data integration in glacier studies.

Moreover, forecasts from an ARIMA model based on the 21–year elevation time series suggest that ASM will continue to experience a stable decline in elevation over the next five years. By refining these methodologies and extending the temporal and spatial scope of the data, future research can provide even deeper insights into the complex interplay between climatic factors and glacier behavior.