1. Introduction
One of the most powerful means to assess the fundamental properties of Earth is via remote sensing: satellite-borne observations of its atmosphere, land, and ocean surface. Since the launch of the Television InfraRed Observation Satellite (TIROS) in 1960, the first of the non-military “weather satellites”, remote-sensing satellites have offered daily coverage of the globe to monitor our atmosphere [
1]. It was not until the 1970s that our attention was specifically directed at measuring ocean surface properties. Notably, three spacecraft were launched in 1978 that carried sensor payloads for observing in the visible portion of the electromagnetic (EM) spectrum to measure ocean color for biological applications, in the infrared (IR) range to estimate sea surface temperature (SST) and in the microwave band to estimate wind speed, sea surface height and SST [
2,
3,
4,
5]. These programs were followed by a large number of internationally launched satellites carrying a broad range of sensors providing improved spatial, temporal and radiometric resolution for terrestrial, oceanographic, meteorological and cryospheric applications [
6,
7,
8].
All satellite-borne sensors observing Earth’s surface or atmosphere sample some portion of the EM spectrum, with the associated EM waves passing through some or all of the atmosphere. The degree to which the signal sampled is affected by the atmosphere is a strong function of the EM wavelength as well as the composition of the atmosphere, with wavelengths from the visible through the thermal infrared (400 nm–15
m) being the most affected. This is also the portion of the spectrum used to sample a wide range of surface parameters, such as land use, vegetation, ocean color, SST, snow cover, etc. Retrieval algorithms are designed to compensate for the atmosphere for many of these parameters, but these algorithms fail if the density of particulates, such as dust, liquid or crystalline water (e.g., clouds) is too large. The pixels for which this occurs are generally flagged and ignored. This results in a sparse field, with the masked regions ranging from single pixels to regions covering tens of thousands of pixels in size. On average, for example, only ∼15% of ocean pixels return an acceptable estimate of SST (e.g., [
9]).
These gaps represent hurdles in the analysis, especially those requiring complete fields. For example, process-oriented or dynamics-focused research, for which accurate knowledge of the ocean surface is key, suffer tremendously. Moreover, as handling missing data is a common step in most algorithms making use of these data, gap-filling or so-called inpainting techniques introduce errors in the data stream. Finally, even algorithms that properly handle sparse data necessarily bias their results because of the absence of values, e.g., in seasonally, cloud-dominated regions or where other processes hinder accurate measurements. These additional processes might include rain and human-induced radiation in the case of microwave measurements of winds and SST.
To address such data gaps, multiple datasets are often used together with objective analysis interpolation programs to produce what are referred to as Level-4 (L4) products: gap-free fields (e.g., [
10,
11]). Researchers have also introduced a diversity of algorithms to fill in clouds (see [
12] for a review) including methods using interpolation [
9], principal component analyses [
13,
14,
15,
16], and, most recently, convolutional neural networks [
17,
18]. For SST, these methods achieve average root mean square errors of ≈0.2–0.5 K and have input requirements ranging from individual images to an extensive time series.
In this manuscript, we introduce an approach, referred to as
Enki, similar and independently developed to that recently undertaken by Goh et al. [
19], both inspired by the vision transformer masked autoencoder (ViTMAE) model of [
20] to reconstruct masked pixels in satellite-derived fields. Guided by the intuition that (1) natural images (e.g., dogs, landscapes) can be described by a language and therefore analyzed with natural language processing (NLP) techniques and (2) one can frequently recover the sentiment of sentences that are missing words and then predict these words, [
20] demonstrated the remarkable effectiveness of ViTMAE to reconstruct masked images. This included images with 75% masked data, a remarkable inference. ViTMAE achieves this by splitting an image into patches and tokenizing them. The tokens are processed through a transformer block (encoder) to generate latent vectors. These latent vectors, which represent the model’s understanding of a token’s relationship to other tokens, are then passed through another transformer block (decoder) that reconstructs the image. Central to ViTMAE’s success was its training on a large corpus of unmasked, natural images, and, given the reduced complexity of most remote-sensing data compared to natural images, one may expect even better performance.
We show below that Enki reconstructs images of SST anomalies (SSTa) far more accurately than conventional inpainting algorithms. We demonstrate that the combination of high-fidelity model output and state-of-the-art artificial intelligence produces the unprecedented ability to predict critical missing data for both climate-critical and commercial applications. Furthermore, the methodology allows for the comprehensive estimation of uncertainty and an assessment of systematics. The combined power of NLP algorithms and realistic model outputs represent a significant advance for image reconstruction of remote sensing applications.
2. Methods
The architecture we use for
Enki, shown in
Figure 1, inputs and outputs a single-channel image, adopts a patch size of
, and uses 256-dimension latent vectors for the embedding and a 512-dimension embedding for the decoder.
Enki works as follows: (1) Images are broken down into 4 × 4 non-overlapping patches. Patches with missing data are masked or, in the case of training, a percentage of patches are randomly masked. The unmasked patches are tokenized, each with a 256-dimensional latent vector, and assigned a positional embedding. (2) The tokens are passed through a standard Transformer encoder, where self-attention is performed to compute a set of attention weights for each latent vector based on its similarity and association to other latent vectors in the image. These latent vectors represent reduced, numerical representations of data that ideally capture the essential characteristics or features of the data. (3) Masked patches are reintroduced, the latent vectors are run through a Transformer decoder, and the full image is reconstructed as 512-dimension latent vectors. (4) A linear projection layer is used to convert the image back to its original size. The final image is created by replacing the unmasked patches of the reconstructed image with the unmasked patches of the original image.
Enki was trained with SST fields from the global, fine-scale (
, 90-level) LLC4320 (Latitude/Longitude-Cap-4320) [
21] ocean simulation undertaken as part of the Estimating the Circulation and Climate of the Ocean (ECCO) project. The
MIT General Circulation Model (MITgcm) [
22,
23], on which the LLC4320 is based, is a primitive equation model that integrates the equations of motion on a 1/48° Latitude/Longitude/polar-Cap grid. It is initialized from lower resolution products of the ECCO project and is progressively spun up at higher resolutions. The highest resolution version, LLC4320, is forced at the ocean surface by European Centre for Medium-rangeWeather Forecasting (ECMWF) reanalysis winds, heat fluxes, and precipitation, and at the boundaries by barotropic tides. The approximate one-year simulation (13 September 2011 to 14 November 2012) provides hourly snapshots of model variables, e.g., temperature, salinity and vector currents, at a spatial resolution of ≈1–2 km.
As opposed to using this simulation for training, we could, of course, have used “cloud-free” portions of SST fields obtained from satellite-borne sensors. However, we often find undetected or improperly masked clouds in these fields, which would impact the training of
Enki. Furthermore, these fields are geographically biased [
9] and would yield a highly imbalanced training set.
The LLC4320 simulations have been widely used in studies investigating submesoscale phenomena [
24,
25,
26], baroclinic tides [
27,
28], and mission support for the Surface Water and Ocean Topography (SWOT) satellite sensor [
29]. As it has a horizontal grid resolution comparable to but slightly coarser than the spatial resolution of most IR satellite SST measurements, and as it is free from fine-scale atmospheric affects, it represents an oceanographic surface approximately equivalent to but reduced in noise relative to IR satellite SST. See [
30] for further details about the implementation of atmospheric effects in the LLC4320. Global model-observation comparisons at these fine horizontal scales can also be found in [
31,
32,
33].
Every two weeks beginning on 13 September 2011, we uniformly extracted 2,623,152 “cutouts” of from the global ocean at latitudes lower than 57° N, avoiding land. Each of these initial cutouts were re-sized to pixelcutouts with linear interpolation and mean subtracted. No additional pre-processing was performed.
We constructed a complementary, validation dataset of 655,788 cutouts in a similar fashion. These were drawn from the ocean model on the last day of every 2 months starting 30 September 2011. They were also offset by in longitude from the spatial locations of the training set.
A primary hyperparameter of the ViTMAE is the training percentage (
); i.e., the percentage of pixels masked during training (currently a fixed value). A value of
= 30, for example, indicates 30% of the pixels in each training cutout has been randomly masked. While ref. [
20] advocates
= 75 to insure generalization, we generated
Enki models with
= [10,20,35,50,75]. In part, this is because we anticipated applying
Enki to images with less than 50% masked data (
).
For the results presented here, we train using patches with randomly assigned location (and zero overlap). This approach does, however, lead to an inaccurate representation of actual clouds which exhibit spatial correlation on a wide range of scales. Future work will explore how more representative masking affects the results.
Enki was trained on eight NVIDIA-A10 Graphics Processing Unit (GPUs) on the Nautilus computing system. The most expensive = 10 model requires 200 h to complete 400 training epochs with a learning rate of .
In addition to the LLC4320 validation dataset, we apply
Enki to actual remote sensing data. These were extracted from the Level-2 (L2) product of the National Oceanic and Atmospheric Administration (NOAA) processed granules of the Visible-Infrared Imager-Radiometer Suite (VIIRS) sensor [
34]. We included data from 2012–2021 and only included
cutouts without any masked data. These data consist of 923,751 cutouts with geographic preference to coastal regions and the equatorial Pacific (see [
31]). We caution that while we selected “cloud-free”
regions, we have reason to believe that a portion of these data are, in fact, affected by clouds (e.g., [
35]).
3. Results
Figure 2 shows the reconstruction of a representative example from the validation dataset for the
Enki model. In this case, the model was trained on cutouts characterized by 20% of the pixels being masked (
= 20 model) but applied to a cutout having 30% of its pixels masked (
= 30). Aside from patches along the outer edge of the input image, it is difficult to visually differentiate the reconstructed pixels from the surrounding SSTa values. The greatest difference is 0.19 K and the highest root mean square error (RMSE) in a single
patch is
K with an average RMSE of
K. As described below, the performance does degrade with higher
and/or greater image complexity, but to levels generally less than standard sensor error.
In the following sub-sections, we present analyses of
Enki performance, first based on synthetic fields, for individual
masks (
Section 3.2), mask objects defined as contiguous, non-overlapping
masked regions (
Section 3.3), as a function of cutout complexity (
Section 3.4), compared with DINEOF (
Section 3.5), and compared with bi-harmonic inpainting (
Section 3.6) followed by an analysis with satellite-derived SST fields—real data (
Section 3.7).
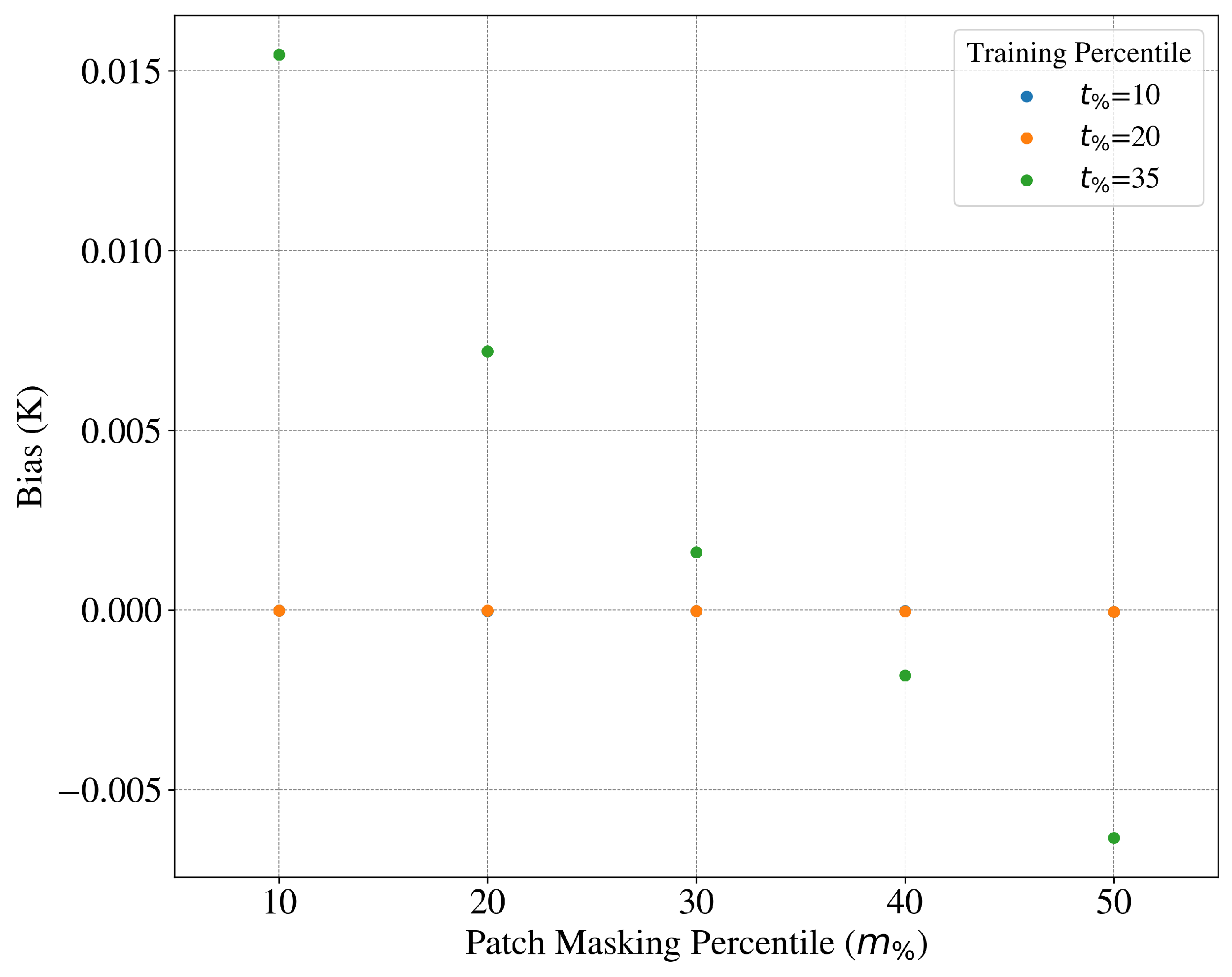
3.1. Bias in Enki
As described in [
36],
Enki exhibits a systematic bias for cases when
; i.e., mask fractions significantly lower than the training fraction.
Figure 3 describes the magnitude of this bias as a function of
and
as derived from the dataset. For the favored model (
= 20), the bias term is less than
K for all
tested, and can be considered negligible. Indeed, it is at least one order of magnitude smaller than the uncertainty in the average of a
patch in standard IR-based SST retrievals, where the pixel-to-pixel noise is approximately 0.1 K [
37]. For all of the results presented here, we have removed the bias calculated from the validation dataset before calculating any other statistic.
3.2. Enki Performance on Individual 4 × 4 pixel Masks—LLC4320 Cutouts
Quantitatively, we consider first the model performance for individual
patches.
Figure 4 presents the results of two analyses: (a) the RMSE of reconstruction as a function of the patch spatial location in the image; and (b) the quality of reconstruction as a function of patch complexity, defined by the standard deviation (
) of the patch in the original image. On the first point, it is evident from
Figure 4a that
Enki struggles to faithfully reproduce data in patches on the image boundary. This is a natural outcome driven by the absence of data on one or more sides of the patch (i.e., partial extrapolation vs. interpolation). Within this manuscript, we do not include boundary pixels or patches in any quantitative evaluation, and we emphasize that any systems built on a model like
Enki should ignore the boundary pixels in the reconstruction.
Figure 4b, meanwhile, demonstrates that
Enki reconstructs the data with an RMSE that is over one order of magnitude smaller than that anticipated from random chance. Instead, the results track the relation RMSE
. We speculate that the “floor” in RMSE at
K arises because of the loss of information in tokenizing the image patches. The nearly linear relation at larger
, however, indicates that the model performance is fractionally invariant with data complexity. We examine these results further in
Appendix A.
3.3. Enki Performance on Mask Objects—LLC4320 Cutouts
The above addresses the performance of Enki in the context of individual squares but two or more of these squares may adjoin one another resulting in larger patches, which we refer to as mask objects. Here, we examine Enki performance as a function of the 23+ million mask objects (for simplicity we will refer to these as masks) extracted from the cutouts of the validation dataset for = 20, . A mask was defined as the union of all regions, which were touching along a portion of one edge. Two regions with touching corners were not considered to be part of the same mask.
For each mask, its area and minor axis length (the length in pixels of the ellipse with the same normalized second central moment as the region) were determined along with the RMSE of the residual—the difference between SST values of the original field under the mask and the reconstructed field.
= 20 was selected for consistency with the other analyses presented and
to provide for a broad range of mask areas, the larger
, the more intersections of
masks resulting in larger masks. The median and the log-normalized mean RMSE of the residuals are shown in
Figure 5 as a function of (a) mask area and (b) minor axis length. The log-normalized mean is determined by taking the mean of the log of all values falling within a bin and then exponentiating the result. The fact that the log-normalized mean curves (red) and the median curves (black) are very close to the same is an indication that the distribution of the log of the RMSE is close to symmetric about the mean. The vertical gray bars—axis defined on the right hand side of each figure—is a probability histogram of the mask parameter. Because the imposed
mask elements are not permitted to overlap, the area histogram results in 16 pixel steps.
The RMSE of residuals increases linearly with the log10 of the area masked. It is not surprising that the RMSE increases with the area masked; the machine learning (ML) model needs to extrapolate over longer distances. What is surprising is that the rate of increase of the RMSE is so slow, with RMSE increasing from about 0.011 K for a 16 pixel mask to 0.019 K for a 100 pixel mask. The model is performing better than we had anticipated in this regard.
RMSE also increases with the log10 of the minor axis length although more rapidly at first and then more slowly than the dependence on area; i.e., unlike for area, the increase with minor axis length is not linear. The reason we probed the minor axis length is that this length is a measure of how far reconstructed pixels were from available pixels.
Again, in both cases, area and minor axis length, the rate of growth of the RMSE is slow.
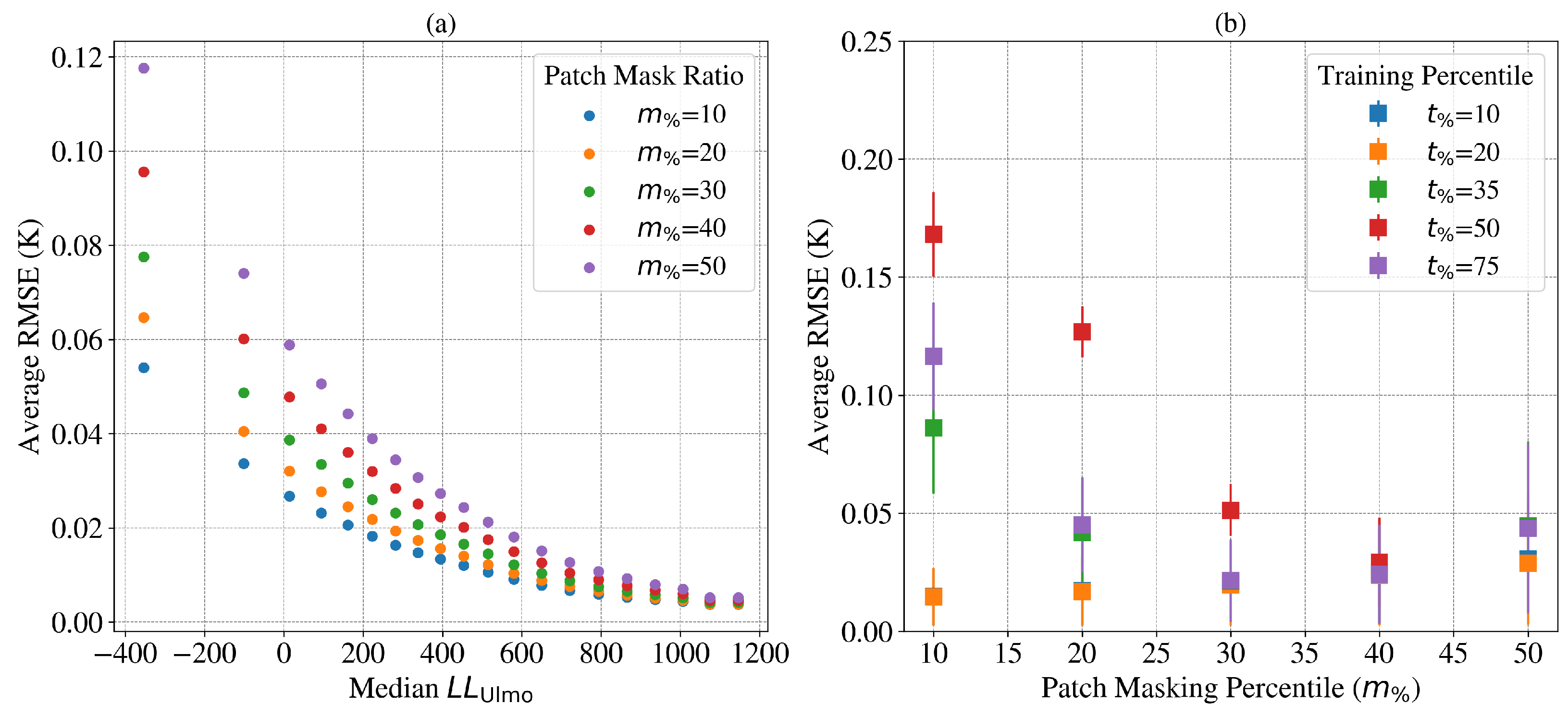
3.4. Enki Performance Based on the Complexity of LLC4320 Cutouts
Turning to performance at the full cutout level,
Figure 6a shows results as a function of cutout complexity. Here, we examine
image complexity versus
patch complexity discussed in the context of
Figure 4 (
Section 3.2) and
Figure 5 (
Section 3.3). To define cutout complexity, we adopt a deep-learning metric developed by [
9] to identify outliers in SSTa imagery. Their algorithm, named
Ulmo, calculates a log-likelihood value
designed to assess the probability of a given image occurring within a very large dataset of SST images. Refs. [
9,
35] demonstrate that data with the lowest
exhibit greater complexity, both in terms of peak-to-peak temperature anomalies and also in terms of the frequency and strength of fronts, etc.
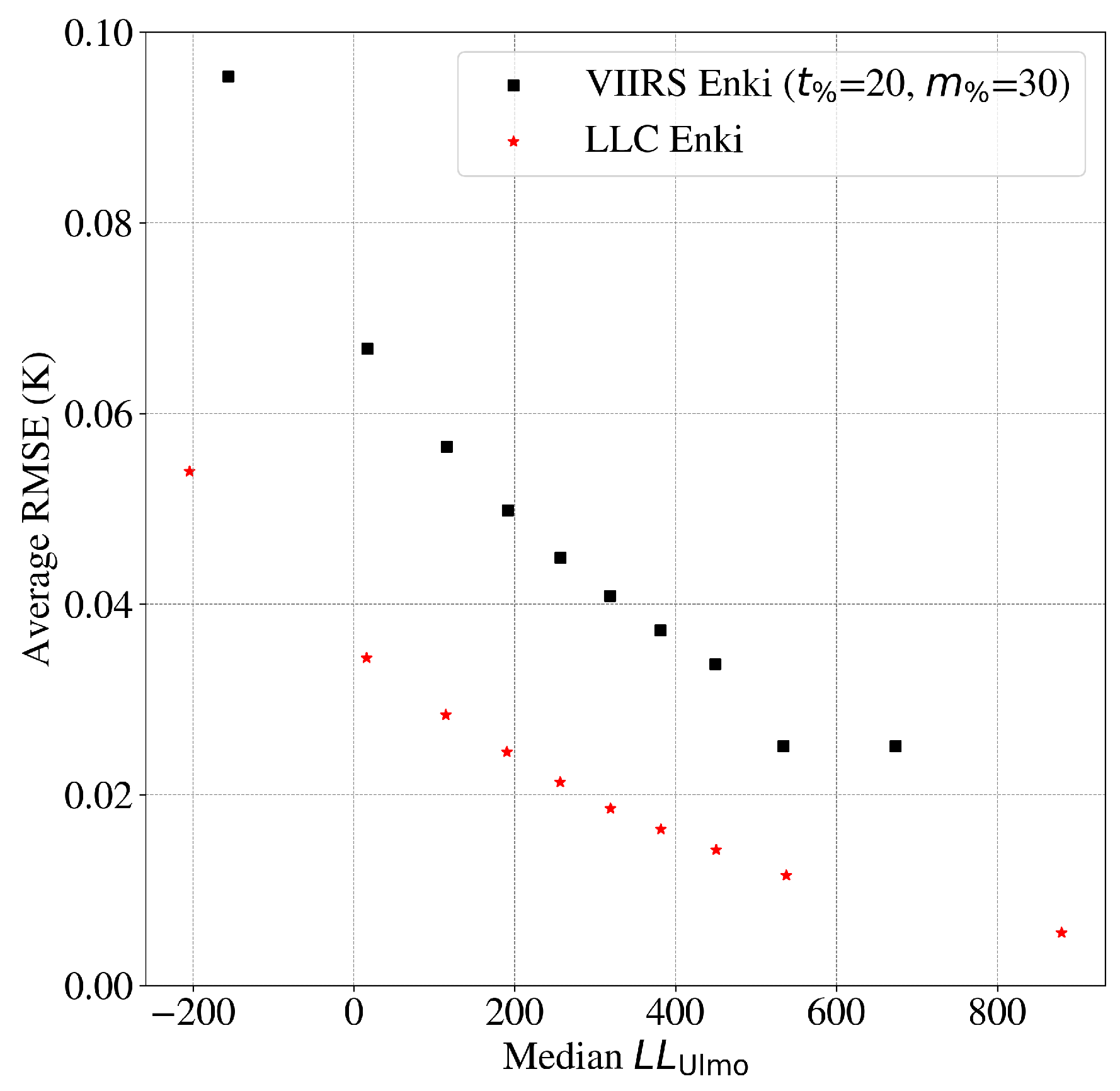
Figure 6a reveals that the reconstruction performance depends on
, with the most complex cutouts (
) showing
K. For less complex data (e.g.,
), the average
K which is effectively negligible for most applications. Even the largest RMSEs are smaller than the sensor errors found by [
37] for the pixel-to-pixel noise in SST fields retrieved from the Advanced Very-High-Resolution Radiometer (AVHRR;
K), and comparable or better than those for the Visible-Infrared Imager-Radiometer Suite (VIIRS;
K [
37]).
As described in
Section 2, we trained
Enki with a range of training mask percentiles expecting best performance with
= 75 as adopted by [
20].
Figure 6b shows that for effectively all masking percentiles
, the
= 20
Enki model provides best performance. We hypothesize that lower
models are optimal for data with lower complexity compared to natural images; i.e., one can sufficiently generalize with
. Furthermore, it is evident that models with
have not learned the small-scale structure apparent in SST imagery.
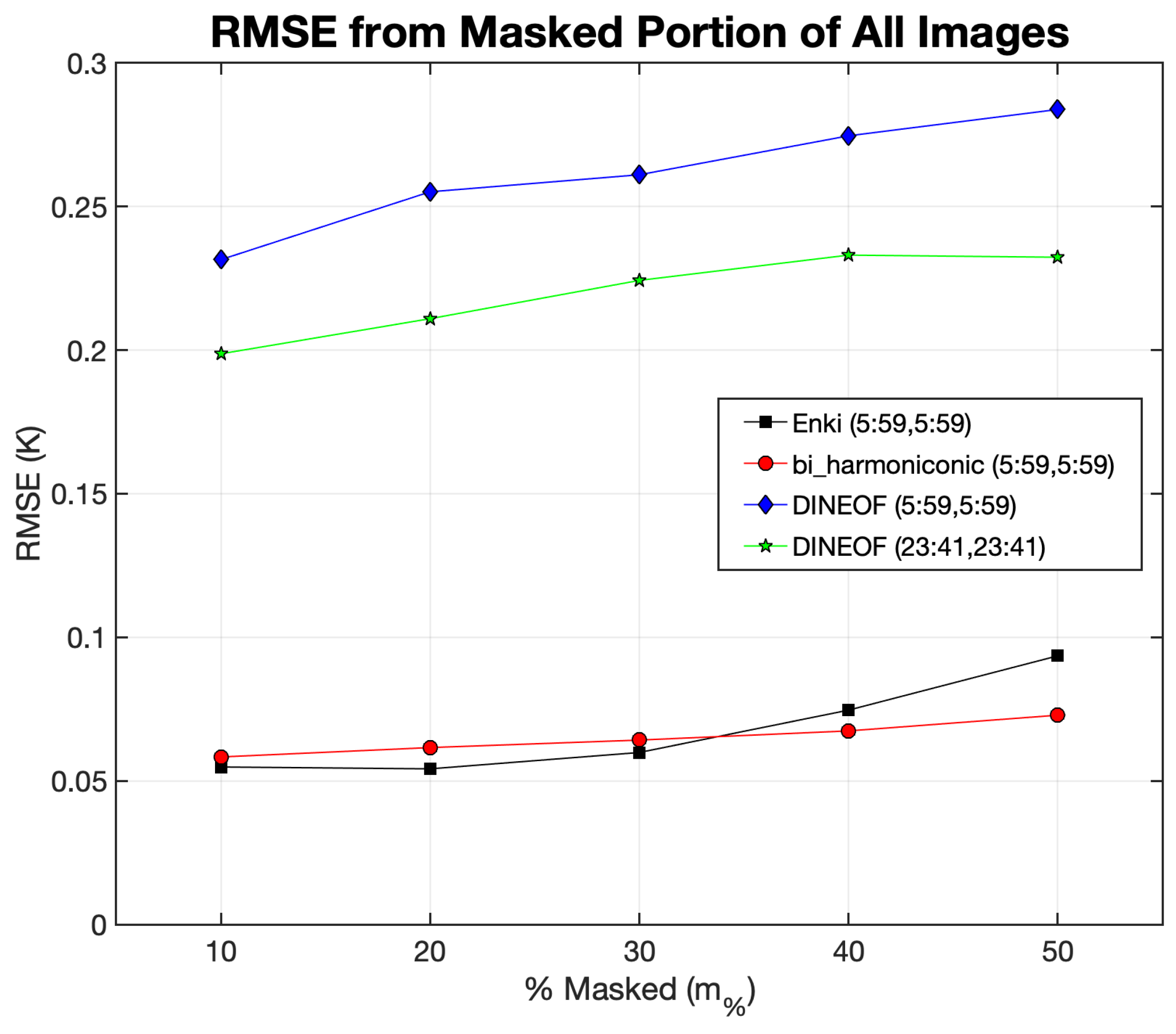
3.5. Enki Performance Compared with DINEOF—LLC4320 Cutouts
We begin our benchmark tests of
Enki by comparing the
Enki results to those from DINEOF (Data Interpolating Empirical Orthogonal Functions) [
14], termed the gold-standard by Ćatipović et al. [
12] based on the large fraction of manuscripts they reviewed in which it is used. Because DINEOF is based on an Empirical Orthogonal Function (EOF) analysis of the fields, we elected to use as our test dataset, a 180-day sequence of LLC4320 cutouts centered on (lat, lon) = (
N,
E) in the South China Sea. Each cutout in the time series was masked using random
patches obscuring a given fraction of the image
. This was repeated for
= [10%, 20% ...50%] and the
= 20 model was used for the
Enki reconstructions. The results are shown in
Figure 7. Because the
Enki reconstruction is based on surrounding pixels, a four-pixel-wide band at the edge of the cutout was excluded from the calculation of the RMSE for both reconstructions. A monotonic decrease in RMSE was found for the DINEOF reconstructions with increasing width of the excluded band. As an example of this, the RMSE of the DINEOF reconstruction excluding a 23-pixel band on the outer edge of the cutout is shown in
Figure 7. The same is not true for the
Enki and the biharmonic reconstructions (the latter discussed in the next section). Reconstruction errors are not shown for varying bands of
Enki or the biharmonic method in the figure; with the exception of bands smaller than four pixels, the curves are indistinguishable from those of the four-pixel wide band.
Similar to published results with DINEOF, we recover an average RMSE of
K, weakly dependent on
. In contrast, the
Enki reconstructions have an RMSE
; i.e.,
lower on average than the DINEOF algorithm. We also emphasize that first results using a convolutional neural network (DINCAE [
17]) yield RMSE values similar to DINEOF. Therefore, the ViTMAE approach of
Enki offers a qualitative advance over traditional deep-learning vision models.
As an alternative comparison, we have also calculated the Structural Similarity Index Measure (SSIM) on the reconstructed images, limiting the calculation to the reconstructed pixels. We find that the Enki yields values very close to 1 whereas DINEOF has SSIM . We conclude that Enki significantly outperforms DINEOF in this metric.
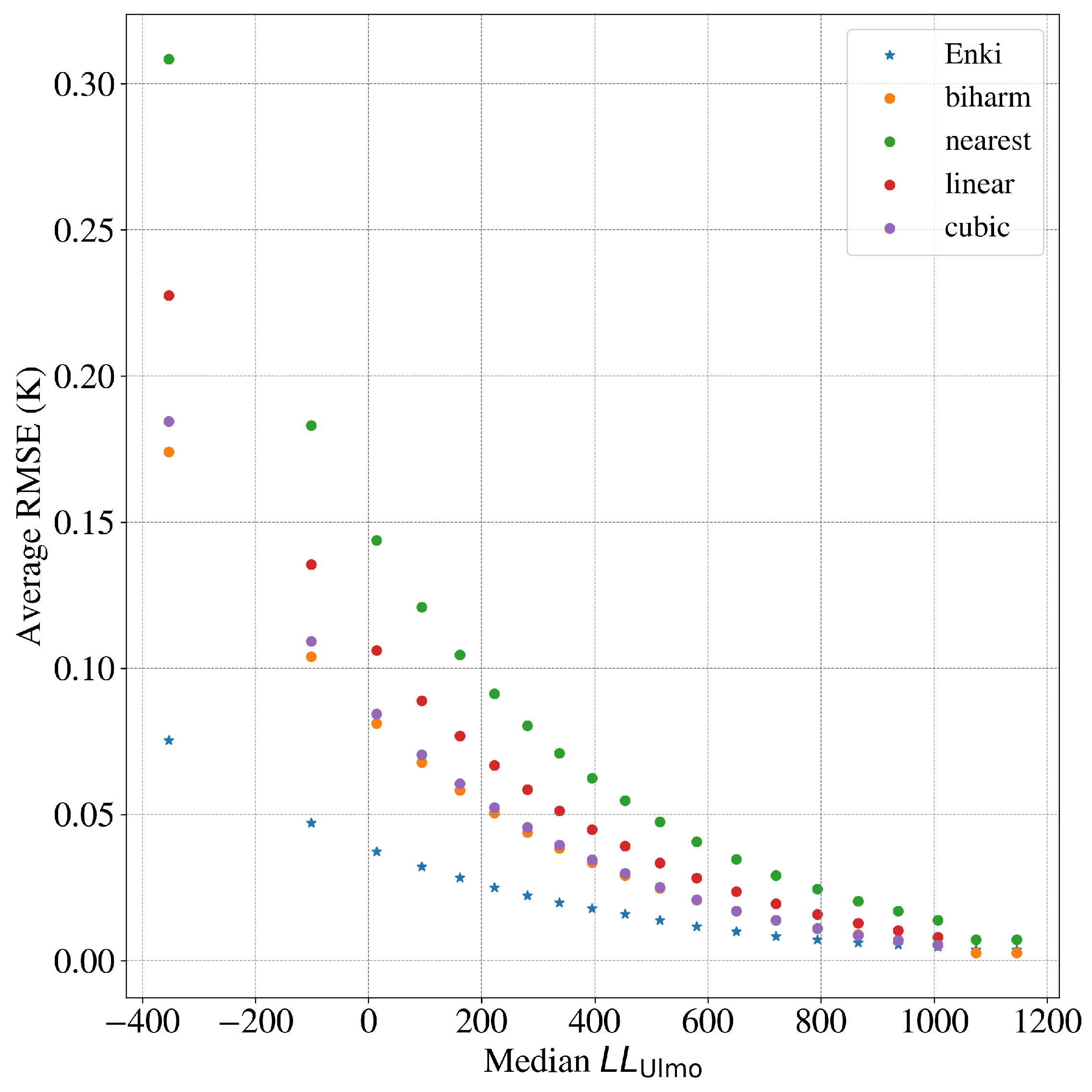
3.6. Enki Performance Compared with Other Inpainting Algorithms—LLC4320 Cutouts
In addition to DINEOF, Ćatipović et al. [
12] review a wide variety of other approaches, adopted by the community, to reconstruct remote sensing data. While a complete comparison to these is beyond the scope of this manuscript, we present additional tests here.
Figure 8 shows the results, applied to the full validation dataset consisting of
cutouts, of several of these interpolation schemes—more easily implemented than either DINEOF or
Enki—as a function of cutout complexity gauged by the
metric. Of these, the most effective is the biharmonic inpainting algorithm adopted in our previous work [
9]. The figure shows, however, that
Enki outperforms even this method by a factor of 2 to 3× in average RMSE aside from the featureless cutouts (
).
We also applied biharmonic inpainting to the 180-day sequence in the South China Sea discussed in the previous section, red circles in
Figure 7. For this subset of the data,
Enki performs slightly better than biharmonic inpainting for
while biharmonic inpainting appears to perform slightly better for larger values of
(As with
Enki the average RMSE was determined excluding a four-pixel-wide band around the edge of the cutout).
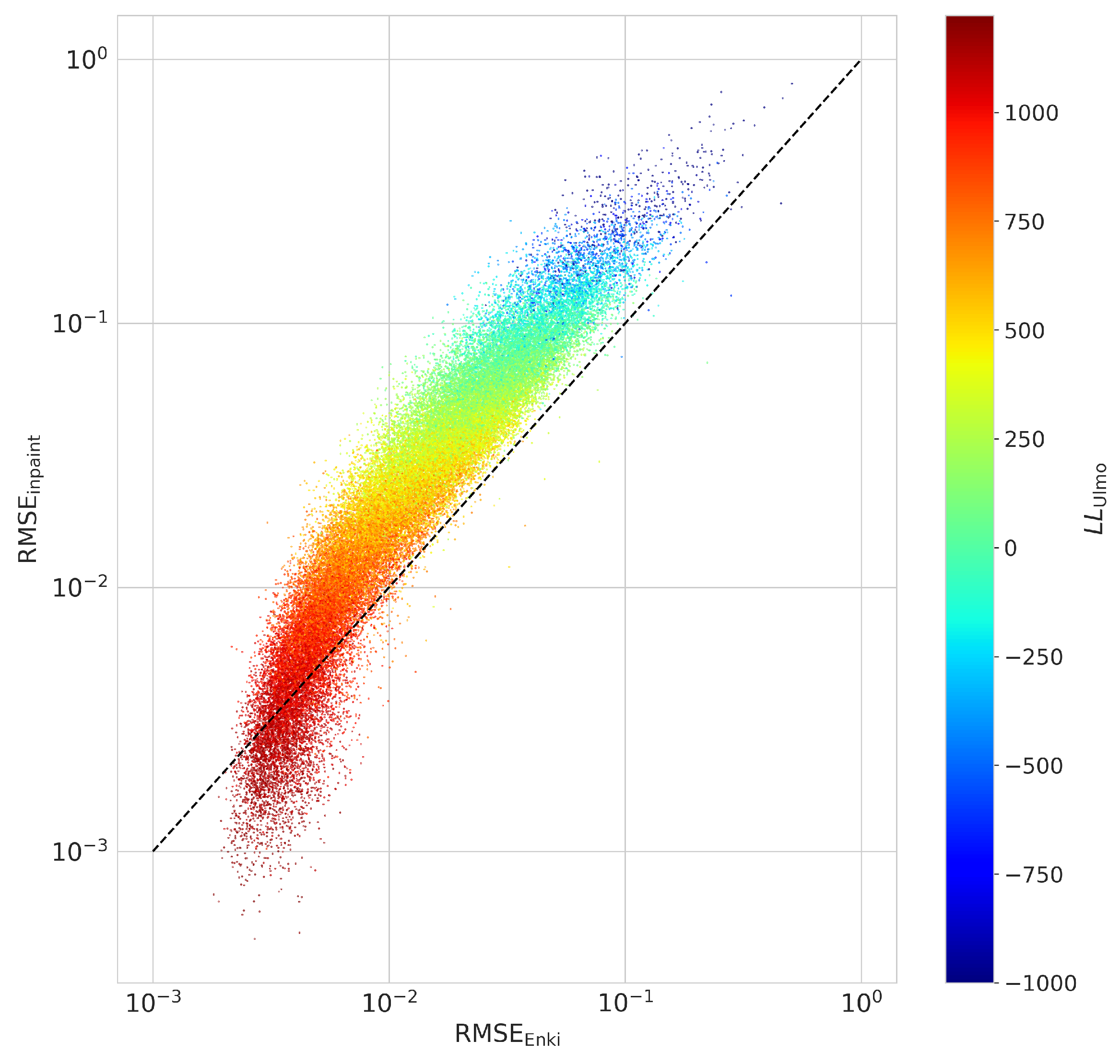
We explore the dependence on
in more detail in
Figure 9, a scatter plot of RMSE for biharmonic inpainting versus RMSE for
Enki, for all 650+ thousand LLC4320 cutouts examined. Colors in the figure denote
, a measure of image complexity, with lower values corresponding to more complexity. In >99.9% of the cases,
Enki outperforms biharmonic inpainting, and often by more than an order-of-magnitude. This relationship holds independent of the image complexity for
. At
, which corresponds to cutouts with very little structure, the biharmonic algorithm yields lower RMSE than
Enki. We hypothesize that there are small correlations in the model output that
Enki has not learned and are better fit by the interpolation scheme. In real data, however, the differences between the two approaches would be overwhelmed by sensor noise.
3.7. Enki Performance—VIIRS SST Fields
As a proof of concept for reconstructing real data, we applied
Enki to the VIIRS dataset described in
Section 2. For this exercise, we inserted randomly distributed clouds into cloud-free data, each with a size of
pixels.
Figure 10 shows that the average RMSE values for
Enki are less than sensor error (
) for cutouts with all complexity. The VIIRS reconstructions, however, do show higher average RMSE than those on the LLC4320 validation dataset. A portion of the difference is because the latter does not include sensor noise, which
Enki has (sensibly) not been trained to recreate. We attribute additional error to the fact that the unmasked data also suffers from sensor noise (see
Appendix A). And, we also anticipate a portion of the difference is because the VIIRS data have a higher spatial resolution than the LLC4320 model. Future experiments with higher-resolution models will test this hypothesis.
4. Conclusions
Satellite measurements are crucial for understanding the Earth’s climate system, requiring global and daily observations of the atmosphere, ocean, and land to comprehend their interactions. Currently, only space-based sensors can provide such comprehensive coverage, with our short-term predictive capabilities of these interactions relying heavily on current and historical satellite data. The Global Climate Observing System (GCOS), supported by international organizations, aims to ensure essential climate data, including 54 Essential Climate Variables (ECVs), are available, with satellites capable of measuring 26 of these ECVs. However, atmospheric conditions often limit satellite visibility to about 15% of the Earth’s surface at any time, posing significant challenges to climate science and prediction.
This study introduced Enki, a novel method to address data gaps in SST measurements using a NLP algorithm trained on ocean model outputs for image reconstruction. We have demonstrated that the Enki algorithm has reconstruction errors less than approximately K for images with up to 50% missing data. That is, the RMSE is comparable or less than typical sensor noise. Furthermore, Enki outperforms other widely adopted approaches by up to an order of magnitude in RMSE, especially for fields with significant SST structure. Systems built upon Enki (or perhaps future algorithms like it) may therefore represent an optimal approach to mitigating masked pixels in remote sensing data.
An immediate application of
Enki is the improvement of more than 40 years of SST measurements made by polar-orbiting and geosynchronous spacecraft [
36]. In addition to reduction in geographic and seasonal biases [
9,
31], improvement of these datasets would likely translate to enhanced time series analysis and teleconnections between Essential Climate Variables (ECVs) across the globe. One objective of the present work, for example, is the improvement of L2 (i.e., swath) SST from the MODerate-resolution Imaging Spectroradiometer (MODIS), a high-resolution (1 km pixels, twice daily) data record that extends from 2000 to the present. Additionally, we anticipate integrating portions of the
Enki encoder within comprehensive deep-learning models (e.g., [
38]) in order to predict dynamical processes and extrema at the ocean’s surface.
The optimal performance of
Enki may be achieved by iterative application of models with a range of
and/or trained on specific geographical locations. At the minimum, improvements in the present approach will require models that accommodate a wider range of spatial scales and resolution than has been considered here (e.g., [
39]). This is necessary, for example, to accommodate geostationary SST estimates, which have spatial resolutions closer to 5–10 km. We anticipate such improvements are straightforward to implement and are the focus of future work. Finally, we emphasize that the work presented here may be generalized to any remote sensing datasets in which a global corpus of realistic numerical output is available. In the oceanic context, this dataset might be ocean wind vectors, sea surface salinity, ocean color and—with improved biogeochemical modeling—even phytoplankton.
As noted in the introduction, Goh et al. [
19] introduce a similar algorithm, which they refer to as MAE for SST Reconstruction under Occlusion (MAESSTRO). Although the algorithms are similar, the approach to validation of the results is quite different, effectively complimenting one another. We encourage those interested in implementing this approach to consider both pieces of work.