Anomaly Detection of Sensor Arrays of Underwater Methane Remote Sensing by Explainable Sparse Spatio-Temporal Transformer
Abstract
1. Introduction
- (1)
- A classical self-attention mechanism was modified to lower the time complexity to O (n) by an explainable sparse block. The sparse block takes inspiration from graph sparsification methods and physical response features of sensor array data;
- (2)
- The traditional self-attention block was replaced by a spatio-temporal-enhanced attention block. This spatio-temporal attention block can automatically capture spatial characteristics of the gas sensor array signal with a query matrix and temporal features, including temperature information. This is accomplished with a key matrix, which is suitable for underwater methane remote sensing;
- (3)
- The anomaly detection threshold technology was set as a data-driven early warning system. This is an unsupervised method that removes the impact of the unknown anomaly signals of industrial sensor arrays to improve anomaly detection accuracy.
2. Theoretical Fundamentals
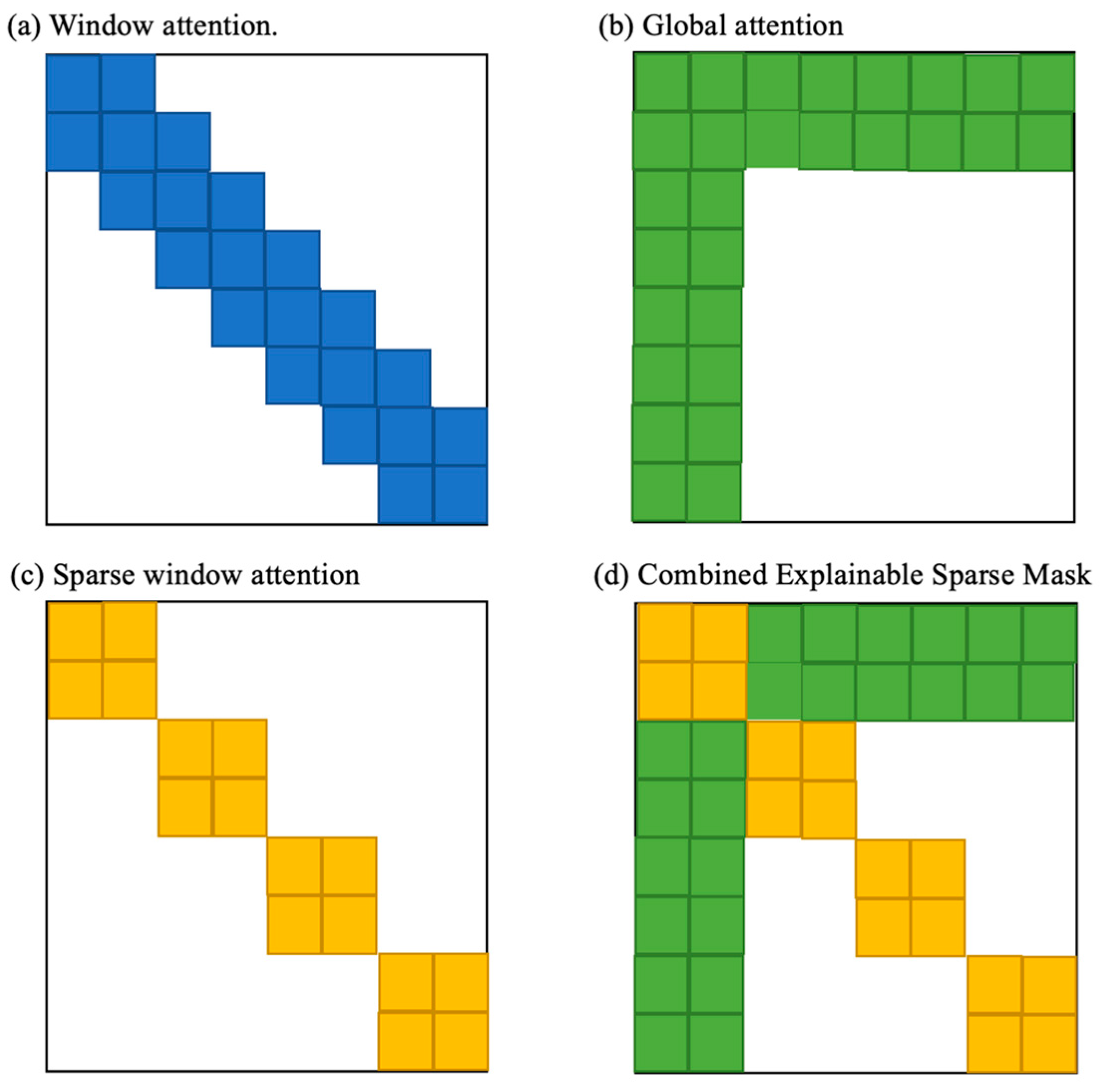
2.1. Explainable Sparse Mask
| Algorithm 1 Explainable Sparse Mask | |
| function | Explainable Sparse Mask (Xinput) |
| | | Qspatio ← Xinput |
| | | 8) |
| | | Qmask |
| | | return Qmask |
| End | |
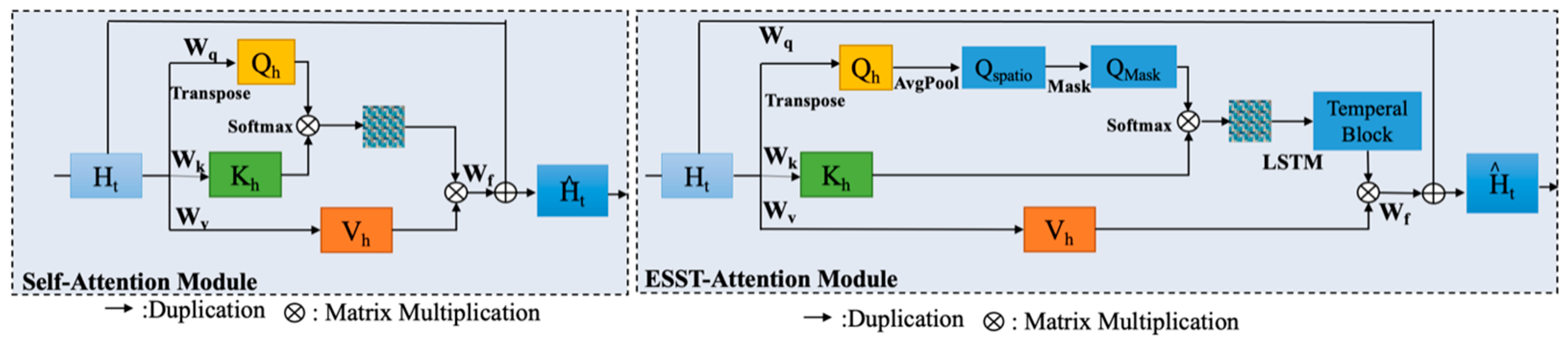
2.2. Explainable Sparse Spatio-Temporal Attention
| Algorithm 2 Explainable Sparse Spatio-Temporal Attention | ||
| function | ESST Attention (Xinput) | |
| | | Q, K, V ← XLinearized | |
| | | QSpatio ← AvgPool (Q) | (1,2) |
| | | Qmask ← M(QSpatio) | (3) |
| | | Scorespatio = Qmask ∗ KT | (4) |
| | | Temporal Block = LSTM [Softmax (ScoreSpatio)] | |
| | | V | (5) |
| | | return | |
| end | ||
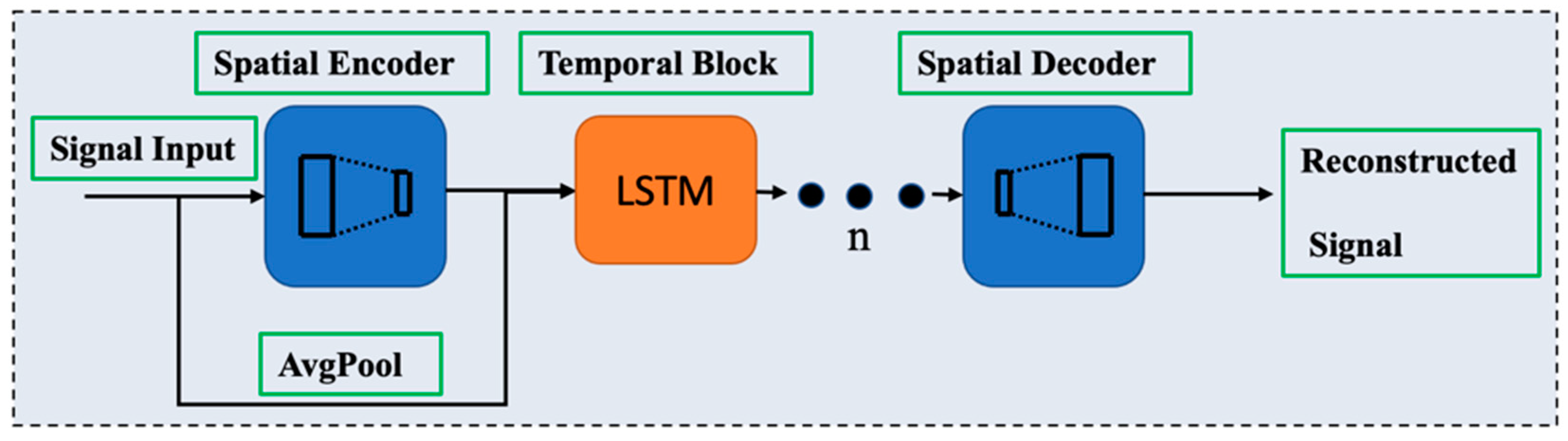
2.3. ESST Transformer Reconstruction Mechanism
2.3.1. ESST Transformer Model
2.3.2. Data Reconstruction by Generative ESST Trans.
2.4. Anomaly Signal Warning Systems
2.4.1. Traditional Anomaly Detection Methods
2.4.2. Adaptive Dynamic Threshold Design
| Algorithm 3 Anomaly Signal Warning Systems | ||
| function | Anomaly Detection (Xa, Xn) | |
| | | Ea, En ← Xa, Xn | |
| | | for i, Ea in range (Xa) do | |
| | | | for i, En in range (Xn) do | |
| | | | | (En) < Ea: | (8) |
| | | | | (En + Ea) | |
| | | | | elif Ea > En: | (8) |
| | | | | T ← Ea | |
| | | | end | |
| | | | if Ea > T: | (9) |
| | | | print (i, Ea) | |
| | | End | |
| Return i, Ea | ||
3. Experiment, Results, and Discussion
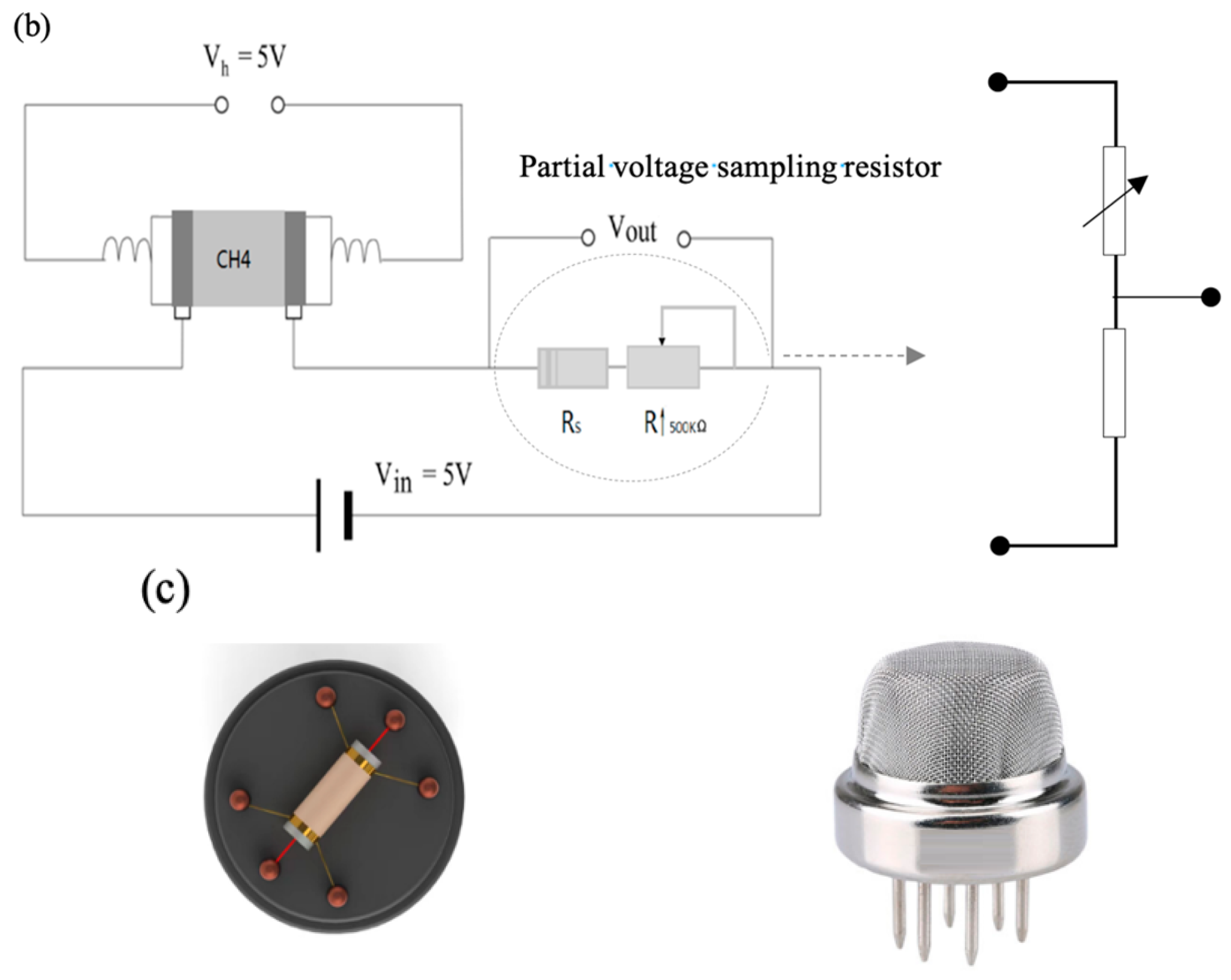
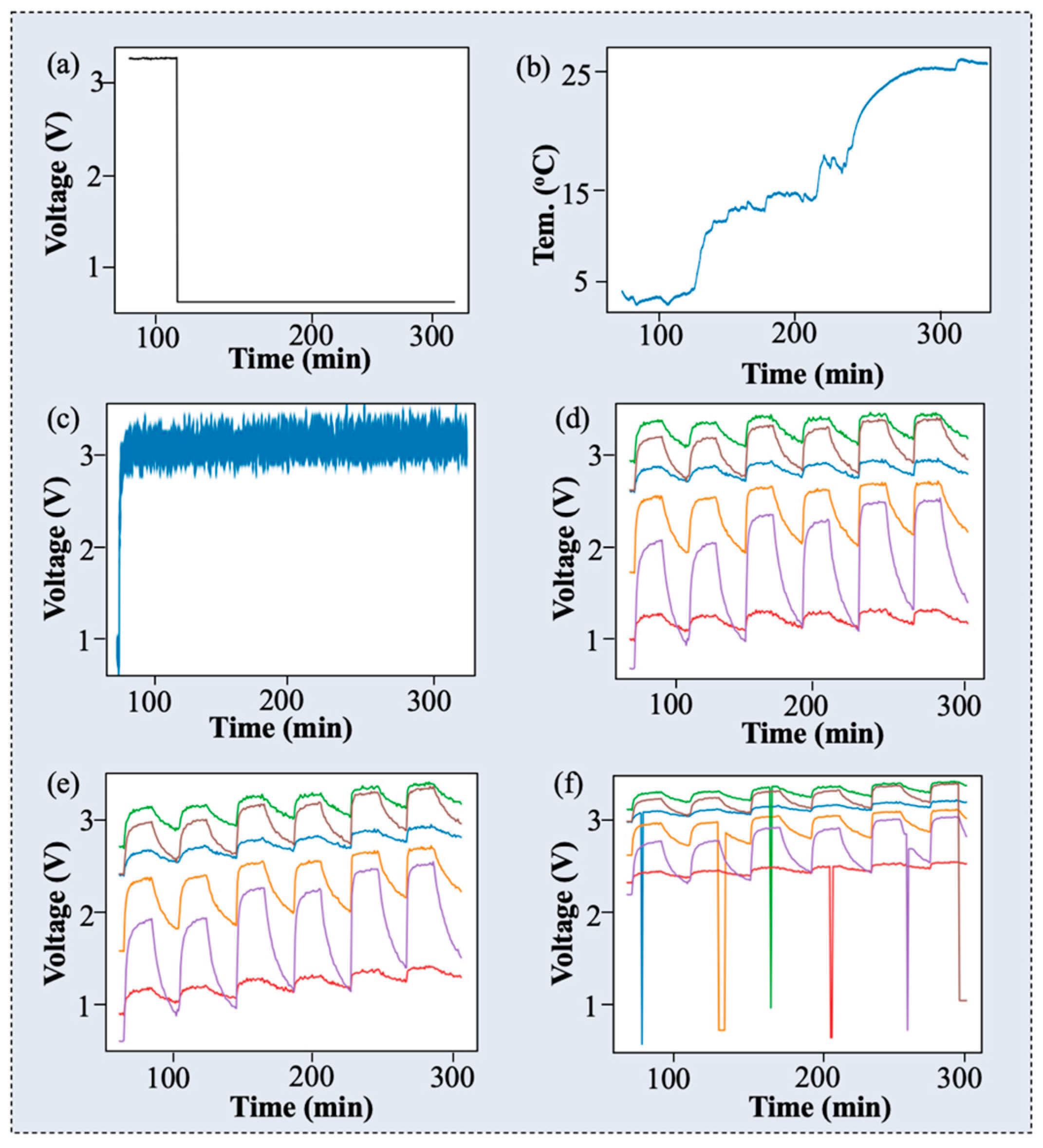
3.1. Experiment Setup
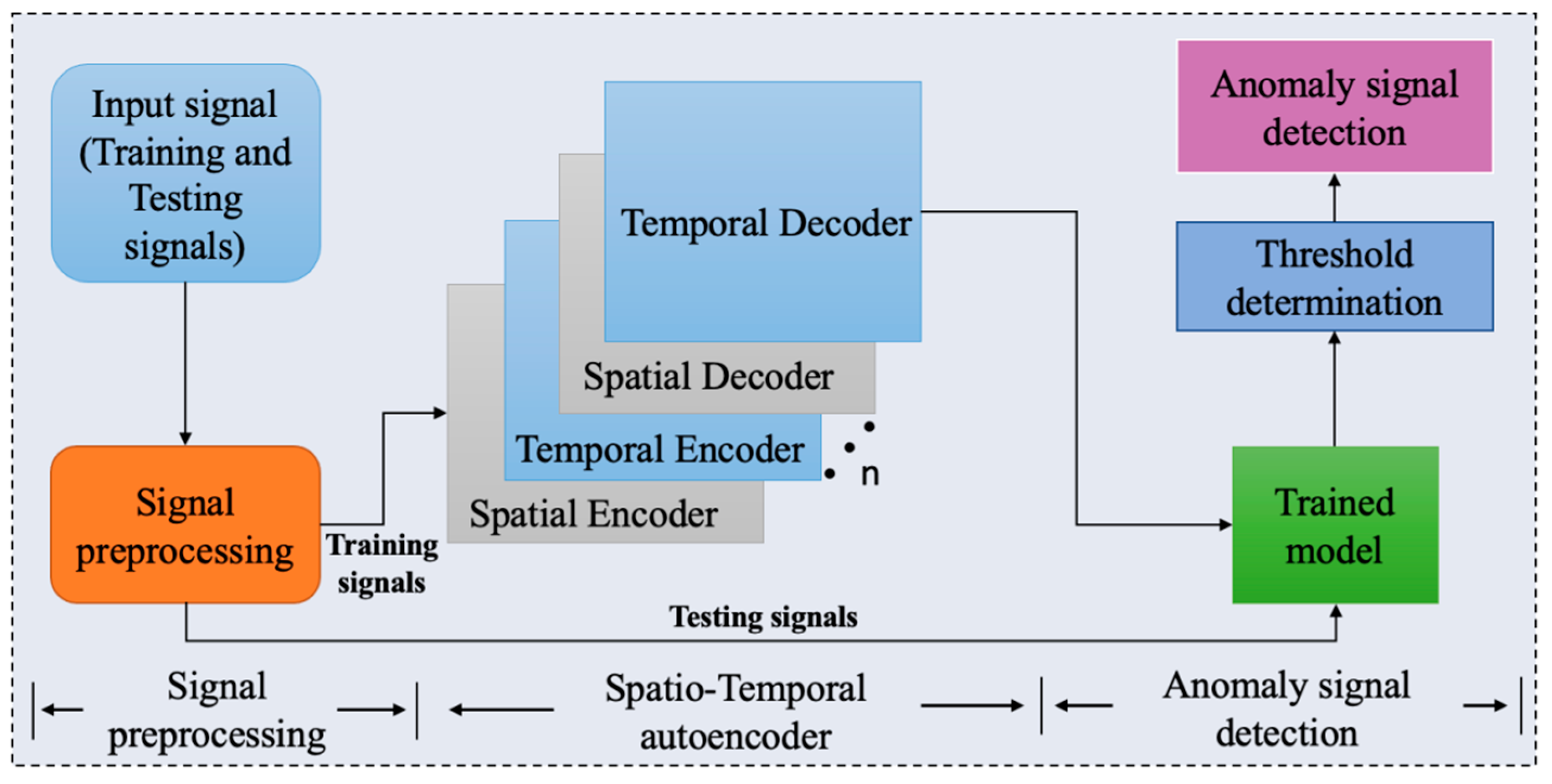
3.2. Experimental Flowchart of Anomaly Warning Detection Systems
3.3. Validation of Anomaly Detection Method and Inference
3.3.1. Anomaly Detection Evaluation Metrics
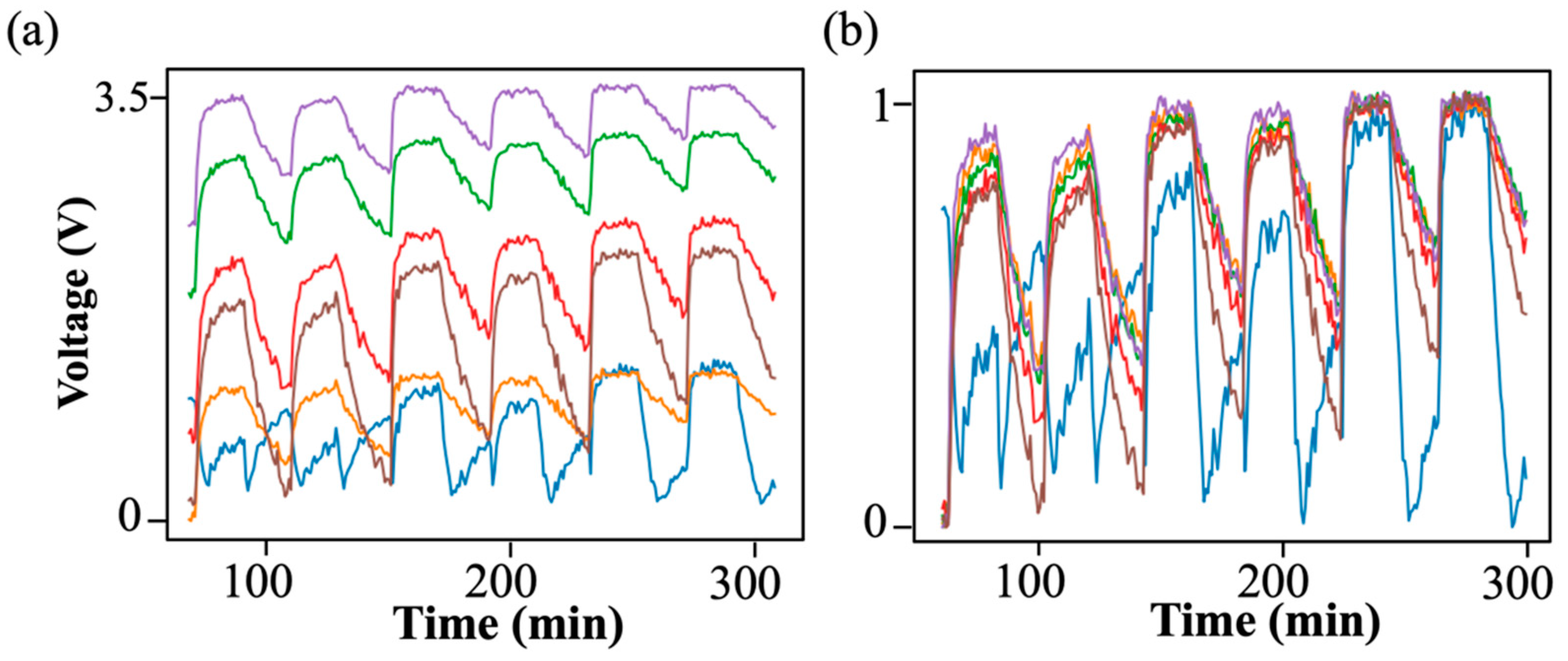
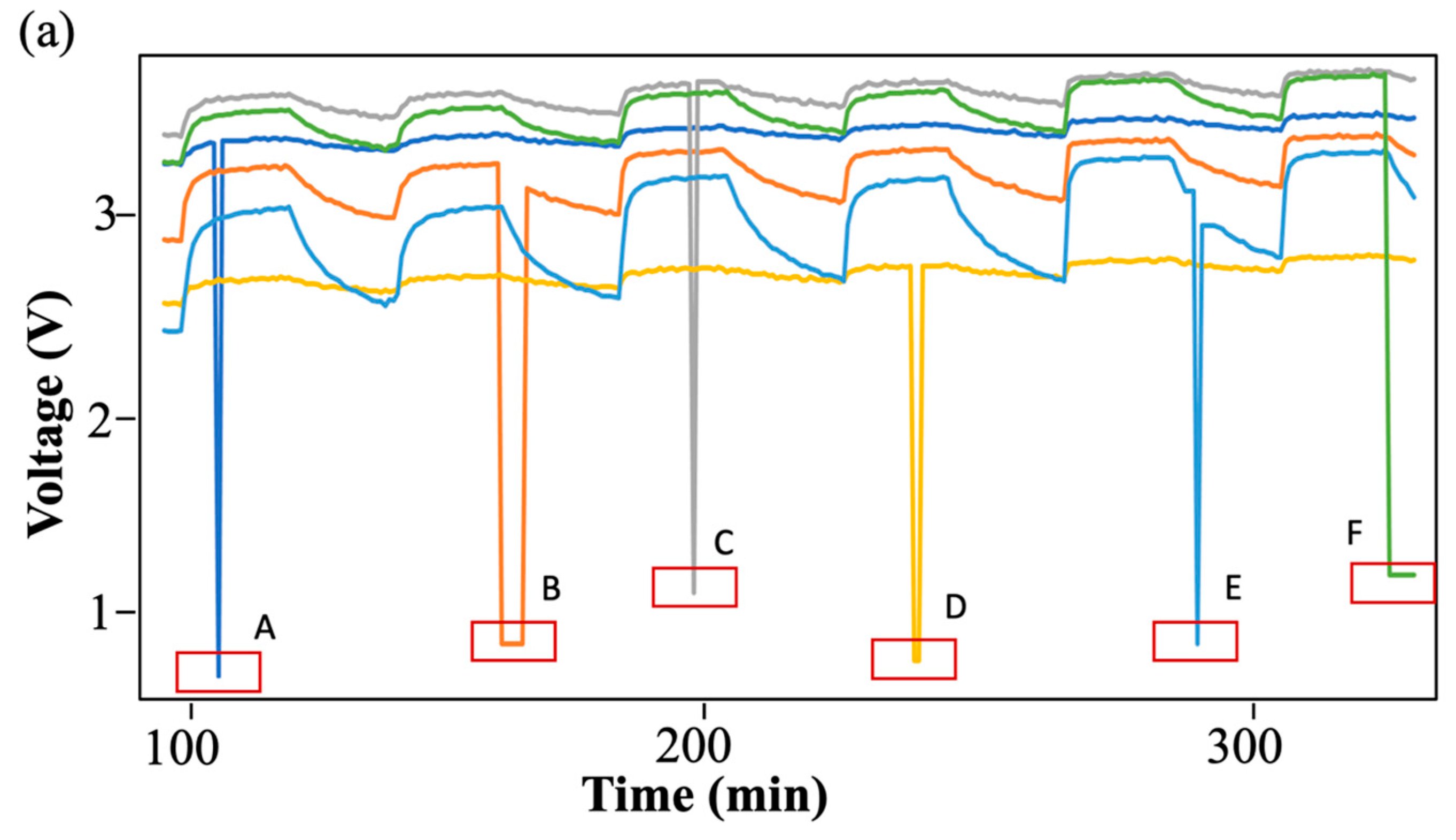
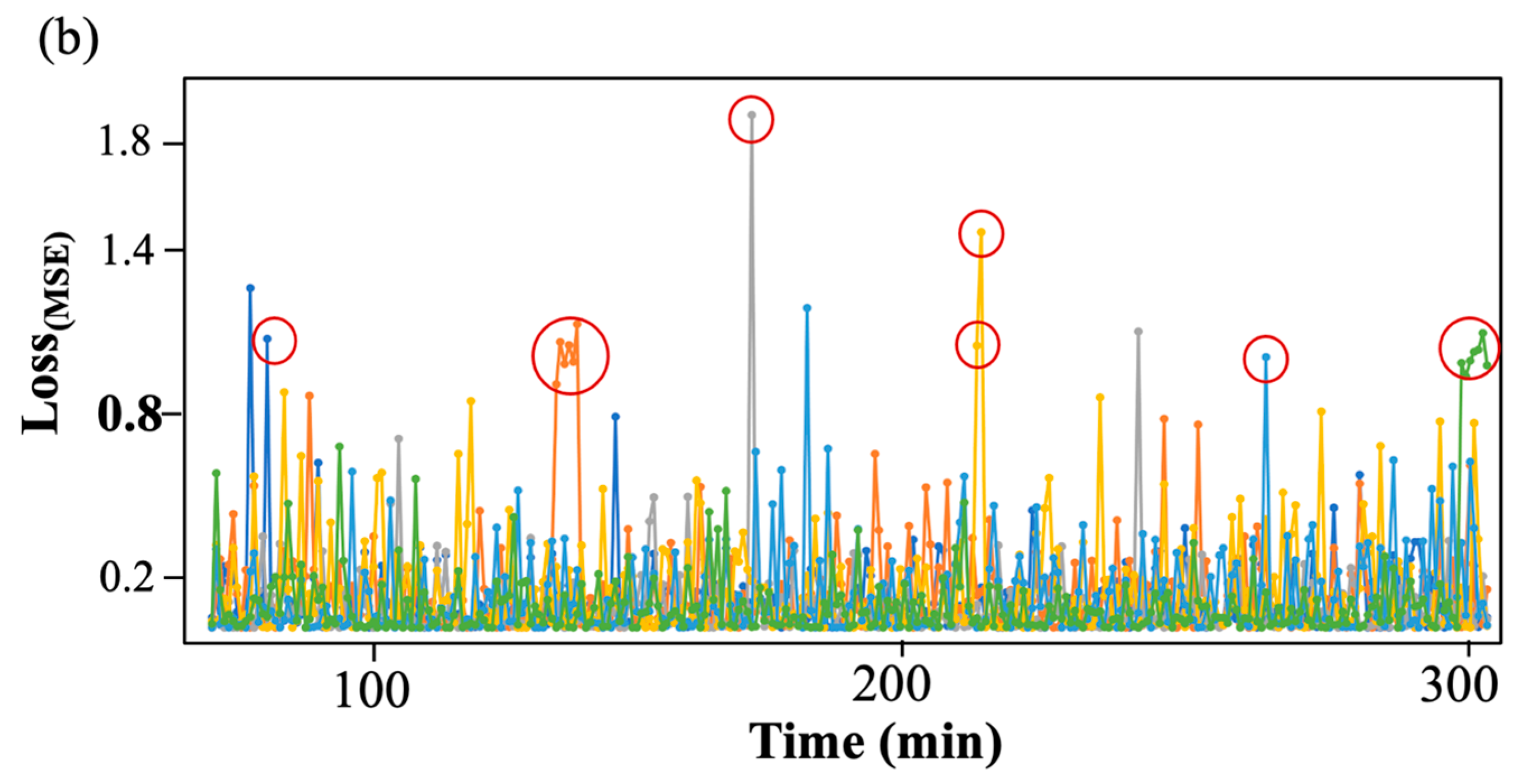
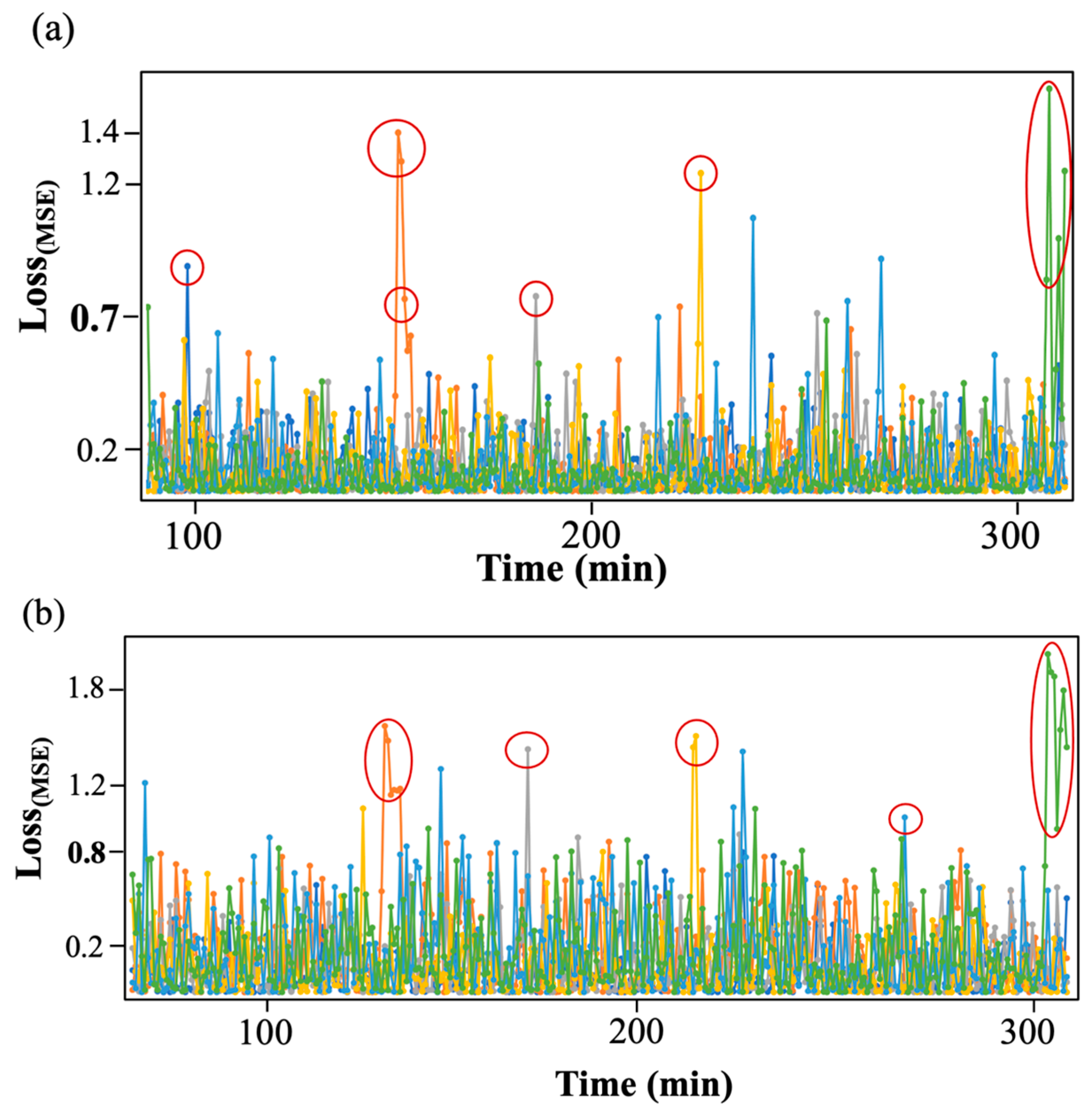
3.3.2. Results
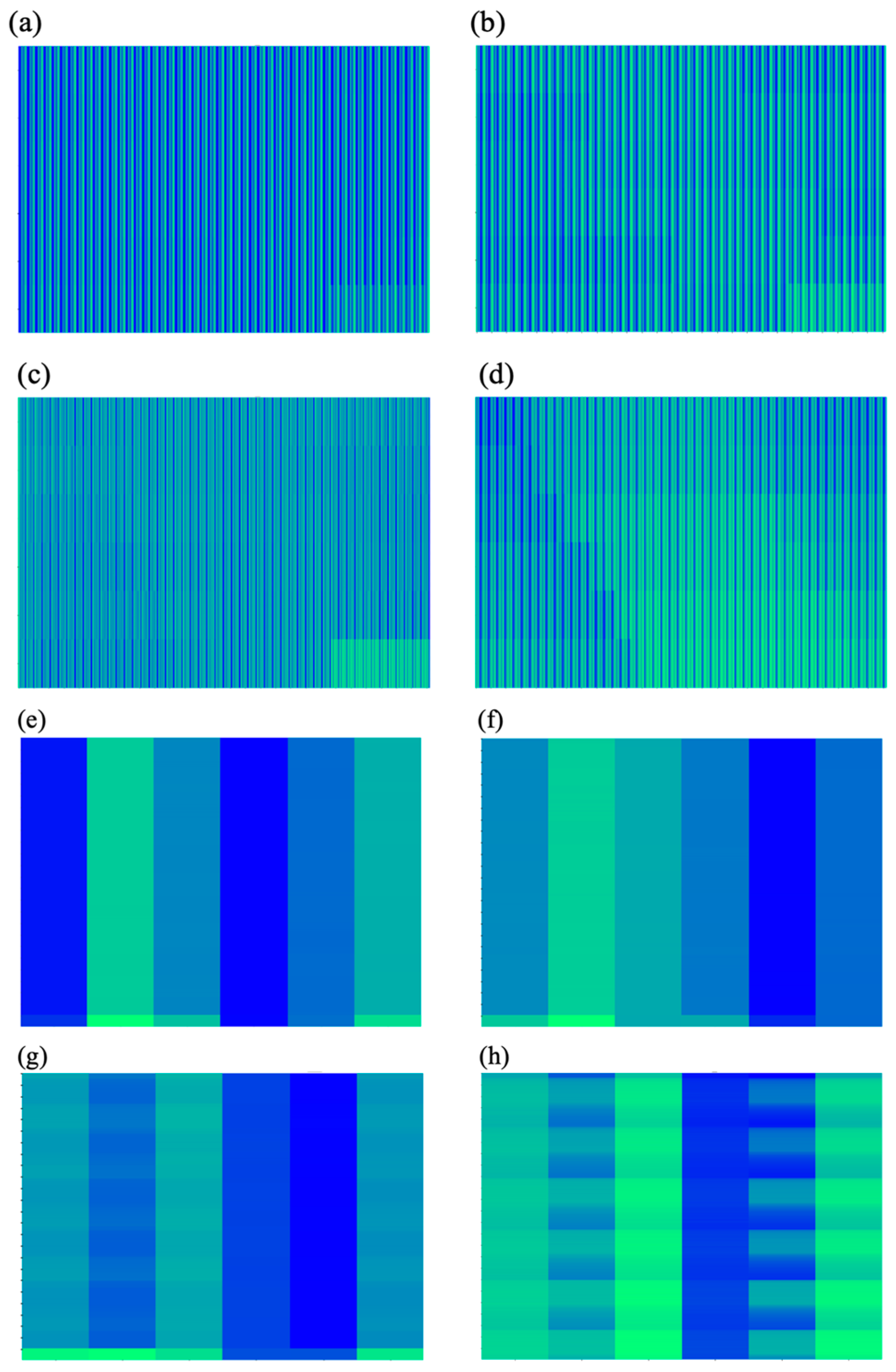
3.4. Attention Visualization for Anomaly Detection in Training Process
3.5. Contrast of Time Complexity with Different Models
3.6. Discussion
4. Conclusions
5. Future Work
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Irina, T.; Ilya, F.; Aleksandr, S. Mapping Onshore CH4 Seeps in Western Siberian Floodplains Using Convolutional Neural Network. Remote Sens. 2022, 14, 2611. [Google Scholar] [CrossRef]
- Ying, W.; Xu, G.; Hong, Z. Characteristics and emissions of isoprene and other non-methane hydrocarbons in the Northwest Pacific Ocean and responses to atmospheric aerosol deposition. Sci. Total Environ. 2023, 10, 162808. [Google Scholar]
- Liu, S.; Xue, M.; Cui, X.; Peng, W. A review on the methane emission detection during offshore natural gas hydrate production. Front. Energy Res. 2023, 11, 12607–12617. [Google Scholar] [CrossRef]
- Itziar, I.; Javier, G.; Daniel, Z. Satellites Detect a Methane Ultra-emission Event from an Offshore Platform in the Gulf of Mexico. Environ. Sci. Technol. Lett. 2022, 9, 520–525. [Google Scholar]
- Ian, B.; Vassilis, K.; Andrew, R. Simultaneous high-precision, high-frequency measurements of methane and nitrous oxide in surface seawater by cavity ring-down spectroscopy. Front. Mar. Sci. 2023, 10, 186–195. [Google Scholar]
- Zhang, X.; Zhang, M.; Bu, L.; Fan, Z.; Mubarak, A. Simulation and Error Analysis of Methane Detection Globally Using Spaceborne IPDA Lidar. Remote Sens. 2023, 15, 3239. [Google Scholar] [CrossRef]
- Wei, K.; Thor, S. A review of gas hydrate nucleation theories and growth models. J. Nat. Gas Sci. Eng. 2019, 61, 169–196. [Google Scholar]
- Gajanan, K.; Ranjith, P.G. Advances in research and developments on natural gas hydrate extraction with gas exchange. Renewable and Sustainable Energy Reviews. Renew. Sustain. Energy Rev. 2024, 190, 114045–114055. [Google Scholar] [CrossRef]
- Zhao, H.; Zhang, Y. Detection Method for Submarine Oil Pipeline Leakage under Complex Sea Conditions by Unmanned Underwater Vehicle. J. Coast. Res. 2020, 97, 122–130. [Google Scholar] [CrossRef]
- Liu, C.; Liao, Y.; Wang, S.; Li, Y. Quantifying leakage and dispersion behaviors for sub-sea natural gas pipelines. Ocean Eng. 2020, 216, 108–117. [Google Scholar] [CrossRef]
- Li, Z.; Ju, W.; Nicholas, N. Spatiotemporal Variability of Global Atmospheric Methane Observed from Two Decades of Satellite Hyperspectral Infrared Sounders. Remote Sens. 2023, 15, 2992. [Google Scholar] [CrossRef]
- Wang, P.; Wang, X.R.; Guo, Y.; Gerasimov, V.; Prokopenko, M.; Fillon, O.; Haustein, K.; Rowan, G. Anomaly detection in coal-mining sensor data, report 2: Feasibility study and demonstration. Tech. Rep. CSIRO 2007, 18, 21–30. [Google Scholar]
- Song, Z.; Liu, Z. Anomaly detection method of industrial control system based on behavior model. Comput. Secur. 2019, 84, 166–172. [Google Scholar]
- Jiang, W.; Liao, X. Anomaly event detection with semi-supervised sparse topic model. Neural Comput. Appl. 2018, 31, 3–10. [Google Scholar]
- Schmidl, S.; Wenig, P. Anomaly detection in time series: A comprehensive evaluation. Proc. VLDB Endow. 2022, 15, 1779–1797. [Google Scholar] [CrossRef]
- Bi, W.; Zao, M. Outlier detection based on Gaussian process with application to industrial processes. Appl. Soft Comput. 2019, 76, 505–510. [Google Scholar]
- Xi, Z.; Yi, H. Variational LSTM enhanced anomaly detection for industrial big data. IEEE Trans. Ind. Inf. 2020, 20, 87–94. [Google Scholar]
- Cheng, H.; Tan, P.N.; Potter, C.; Klooster, S. A robust graph-based algorithm for detection and characterization of anomalies in noisy multivariate time series. ICDM 2008, 4, 123–132. [Google Scholar]
- Bi, Z.; Qi, S. Deep autoencoding gaussian mixture model for unsupervised anomaly detection. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018; Volume 10, pp. 302–311. [Google Scholar]
- Lorenzo, B.; Rota, C. Natural gas consumption forecasting for anomaly detection. Expert Syst. Appl. 2016, 62, 190–201. [Google Scholar]
- Ma, S.; Nagpal, R. Macro programming through Bayesian networks: Distributed inference and anomaly detection. IEEE Int. Conf. Pervasive Comput. Commun. 2007, 5, 87–96. [Google Scholar]
- Markus, M.; Noah, D. LOF: Identifying density-based local outliers. In Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, Dallas, TX, USA, 16–18 May 2000; Volume 5, pp. 302–311. [Google Scholar]
- Mohammed, B.; Sindre, B. Unsupervised Anomaly Detection for IoT-Based Multivariate Time Series: Existing Solutions, Performance Analysis and Future Directions. Sensors 2023, 23, 2844. [Google Scholar] [CrossRef] [PubMed]
- Yan, S.; Shao, H.; Xiao, Y.; Liu, B.; Wan, J. Hybrid robust convolutional autoencoder for unsupervised anomaly detection of machine tools under noises. Robot. Comput.-Integr. Manuf. 2023, 79, 102441. [Google Scholar] [CrossRef]
- Malhotra, A.; Pankaj, D. Long short term memory networks for anomaly detection in time series. Comput. Intell. Mach. Learn. 2015, 10, 600–620. [Google Scholar]
- Yadav, M.; Malhotra, H. Ode-augmented training improves anomaly detection in sensor data from machines. NIPS Time Ser. Workshop. 2015, 20, 405–411. [Google Scholar]
- Chandola, V.; Banerjee, A. Anomaly detection: A survey. ACM Comput. Surv. 2009, 41, 15–22. [Google Scholar] [CrossRef]
- Bedeuro, K.; Mohsen, A. A Comparative Study of Time Series Anomaly Detection Models for Industrial Control Systems. Sensors 2023, 23, 1310. [Google Scholar] [CrossRef] [PubMed]
- Ting, K.; Bing, Y. Outlier detection for time series with recurrent autoencoder ensembles. IJCAI 2019, 20, 2725–2732. [Google Scholar]
- Buitinck, L.; Louppe, G. API design for machine learning software: Experiences from the scikit-learn project. ICLR 2013, 14, 14–20. [Google Scholar]
- Dark, P.; Yong, H. A multimodal anomaly detector for robot-assisted feeding using an LSTM-based variational autoencoder. IEEE Robot. Autom. Lett. 2018, 3, 1544–1551. [Google Scholar]
- An, J.; Cho, S. Variational autoencoder based anomaly detection using reconstruction probability. Spec. Lect. 2015, 30, 302–311. [Google Scholar]
- Pong, M.; Amakrishnan, K. LSTM-based encoder-decoder for multi-sensor anomaly detection. CVPR 2016, 10, 1267–1273. [Google Scholar]
- Chen, X.; Deng, L.; Huang, F.; Zhang, C.; Zhang, Z.; Zhao, Y.; Zheng, K. DAEMON: Unsupervised Anomaly Detection and Interpretation for Multivariate Time Series. In Proceedings of the 2021 IEEE 37th International Conference on Data Engineering (ICDE), Chania, Greece, 19–22 April 2021; Volume 20, pp. 3000–3020. [Google Scholar]
- Raghavendra, C.; Sanjay, C. Deep learning for anomaly detection: A survey. arXiv 2019, arXiv:1901.03407. [Google Scholar]
- Yasuhiro, I.; Kengo, T.; Yuusuke, N. Estimation of dimensions contributing to detected anomalies with variational autoencoders. AAAI 2019, 14, 104–111. [Google Scholar]
- Li, D.; Chen, D.; Jin, B.; Shi, L.; Goh, J.; Ng, S.K. Mad-Gan: Multivariate anomaly detection for time series data with generative adversarial networks. In Proceedings of the International Conference on Artificial Neural Networks, Gran Canaria, Spain, 12–14 June 2019; Springer: Berlin/Heidelberg, Germany, 2019; Volume 21, pp. 703–716. [Google Scholar]
- Zhang, C.; Song, D.; Chen, Y.; Feng, X.; Lumezanu, C.; Cheng, W.; Ni, J.; Zong, B.; Chen, H.; Chawla, N.V. A deep neural network for unsupervised anomaly detection and diagnosis in multivariate time series data. AAAI 2019, 33, 1409–1416. [Google Scholar] [CrossRef]
- Julien, A.; Pietro, M. USAD: Un-Supervised anomaly detection on multivariate time series. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual Event, 24 August 2020; Volume 20, pp. 3395–3404. [Google Scholar]
- Deng, A.; Hooi, B. Graph neural network-based anomaly detection in multivariate time series. AAAI 2021, 5, 403–411. [Google Scholar] [CrossRef]
- Li, L.; Yan, J.; Wang, H.; Jin, Y. Anomaly detection of time series with smoothness-inducing sequential variational auto-encoder. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 201–211. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Zhao, Y.; Han, J.; Su, Y.; Jiao, R.; Wen, X.; Pei, D. Multivariate time series anomaly detection and interpretation using hierarchical inter-metric and temporal embedding. KDD 2021, 3, 3220–3230. [Google Scholar]
- Dzmitry, B.; Kyunghyun, C. Neural machine translation by jointly learning to align and translate. arXiv 2015, arXiv:1409.0473. [Google Scholar]
- Ashish, V.; Noam, S. Attention is all you need. NIPS 2017, 3, 6000–6010. [Google Scholar]
- Luong, T.; Hieu, P. Effective approaches to attention-based neural machine translation. In Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, Lisbon, Portugal, 17–21 September 2015; Volume 15, pp. 1412–1421. [Google Scholar]
- Iz, B.; Matthew, P.; Arman, C. Longformer: The Long-Document Transformer. arXiv 2020, arXiv:2004.05150. [Google Scholar]
- Dai, Z.; Yang, Z.; Yang, Y.; Carbonell, J.; Le, Q.V.; Salakhutdinov, R. Transformer-XL: Attentive language models beyond a fixed-length context. arXiv 2019, arXiv:1901.02860. [Google Scholar]
- Rewon, C.; Scott, G. Generating long sequences with sparse transformers. arXiv 2019, arXiv:1904.10509. [Google Scholar]
- Nikita, K.; Lukasz, K. Reformer: The efficient transformer. In Proceedings of the International Conference on Learning Representations, Addis Ababa, Ethiopia, 30 April 2020; Volume 4, pp. 148–156. [Google Scholar]

| Layer Kind | Layer Type | Layer Description | Dropout | Mask Number |
|---|---|---|---|---|
| 1 | dff, dk, dv | 128, 32, 32 | no | - |
| 2 | dmodel | 16 | no | - |
| 3 | Multi-attention | Head = 2 | yes | 2 |
| 4 | Encoder | N = 4 | yes | 2 |
| 5 | Decoder | N = 4 | yes | 2 |
| Location | Estimated Classes | Actual | |
|---|---|---|---|
| Clean | Outlier | ||
| Sen.1 (14) | 0 | 1 | Outlier |
| Sen.2 (82–87) | 0 | 1 | Outlier |
| Sen.3 (128) | 0 | 1 | Outlier |
| Sen.4 (181–182) | 0 | 1 | Outlier |
| Sen.5 (249) | 0 | 1 | Outlier |
| Sen.6 (295–301) | 0 | 1 | Outlier |
| Location | Sensor Data (V) | ESST (MSE) | LSTM-AE (MSE) | CAE (MSE) | ||||
|---|---|---|---|---|---|---|---|---|
| Original | Anormal | Clean | Outliers | Clean | Outliers | Clean | Outliers | |
| Sen.1 (14) | 3.14 | 0.01 | 0.25 | 0.98 | 0.05 | 0.84 | ||
| Sen.2 (82–87) | 2.96 | 0.2 | 0.05 | 0.95 | 0.69 | |||
| Sen.3 (128) | 3.47 | 0.5 | 0.01 | 1.73 | ||||
| Sen.4 (181–182) | 2.41 | 0.1 | 0.15 | 1.12 | ||||
| Sen.5 (249) | 2.75 | 0.2 | 0.01 | 0.92 | ||||
| Sen.6 (295–301) | 3.47 | 0.6 | 0.1 | 0.93 | ||||
| Models | Training Time (s) | F1 Score (0~1) | Recall (%) | Precision (%) | Anomaly Acc. (%) |
|---|---|---|---|---|---|
| CAE | 600 | 0.81 | 94.44 | 70.83 | 94.44 |
| LSTM_AE | 520 | 0.66 | 55.56 | 76.92 | 55.56 |
| ESST Trans. | 560 | 0.92 | 100 | 85.71 | 100 |
| Model/Paper | Complexity | Decode | Class |
|---|---|---|---|
| Trans.-XL (Dai et al., 2019) [47] | O (n2) | RC | |
| Sparse Trans. (Child et al., 2019) [48] | ) | FP | |
| Reformer (Kitaev et al., 2020) [49] | O (n·log n) | LP | |
| ESST Trans. | O (n) | FP |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, K.; Ni, W.; Zhu, Y.; Wang, T.; Jiang, W.; Zeng, M.; Yang, Z. Anomaly Detection of Sensor Arrays of Underwater Methane Remote Sensing by Explainable Sparse Spatio-Temporal Transformer. Remote Sens. 2024, 16, 2415. https://doi.org/10.3390/rs16132415
Zhang K, Ni W, Zhu Y, Wang T, Jiang W, Zeng M, Yang Z. Anomaly Detection of Sensor Arrays of Underwater Methane Remote Sensing by Explainable Sparse Spatio-Temporal Transformer. Remote Sensing. 2024; 16(13):2415. https://doi.org/10.3390/rs16132415
Chicago/Turabian StyleZhang, Kai, Wangze Ni, Yudi Zhu, Tao Wang, Wenkai Jiang, Min Zeng, and Zhi Yang. 2024. "Anomaly Detection of Sensor Arrays of Underwater Methane Remote Sensing by Explainable Sparse Spatio-Temporal Transformer" Remote Sensing 16, no. 13: 2415. https://doi.org/10.3390/rs16132415
APA StyleZhang, K., Ni, W., Zhu, Y., Wang, T., Jiang, W., Zeng, M., & Yang, Z. (2024). Anomaly Detection of Sensor Arrays of Underwater Methane Remote Sensing by Explainable Sparse Spatio-Temporal Transformer. Remote Sensing, 16(13), 2415. https://doi.org/10.3390/rs16132415








