Abstract
A horizontal towed linear coherent hydrophone array is often employed to estimate the spatial intensity distribution of incident plane waves scattered from the geological and biological features in an ocean acoustic waveguide using conventional beamforming. However, due to the physical limitations of the array aperture, the spatial resolution after conventional beamforming is often limited by the fat main lobe and the high sidelobes. Here, we propose a method originated from computer vision deblurring based on deep learning to enhance the spatial resolution of beamformed images. The effect of image blurring after conventional beamforming can be considered a convolution of beam pattern, which acts as a point spread function (PSF), and the original spatial intensity distributions of incident plane waves. A modified U-Net-like network is trained on a simulated dataset. The instantaneous acoustic complex amplitude is assumed following circular complex Gaussian random (CCGR) statistics. Both synthetic data and experimental data collected from the South China Sea Experiment in 2021 are used to illustrate the effectiveness of this approach, showing a maximum 700% reduction in a 3 dB width over conventional beamforming. A lower normalized mean square error (NMSE) is provided compared with other deconvolution-based algorithms, such as the Richardson–Lucy algorithm and the approximate likelihood model-based deconvolution algorithm. The method is applicable in various acoustic imaging applications that employ linear coherent hydrophone arrays with one-dimensional conventional beamforming, such as ocean acoustic waveguide remote sensing (OAWRS).
1. Introduction
Conventional beamforming (CBF) is widely employed to visualize or measure the angular intensity distribution of incident plane waves originating from various acoustic sources and scatters, including marine organisms [1,2,3], ships [4,5], and geological features [6]. CBF delays and sums the received signals based on the sensor’s configuration relative to the steer angle. When the steer angle matches the direction of arrival (DOA) of targets, the target signals are coherently summed. Meanwhile, noise in each element input is uncorrelated and thus is incoherently summed. As a result, CBF improves the signal-to-noise ratio (SNR) and obtains array gain. However, CBF is subject to Rayleigh limits and imposes constraints on the angular resolution of the resulting images depending on the array aperture, the incident directions, and the operating frequency. Although the angular resolution can be enhanced by directly increasing the physical dimensions of the array aperture, it is not suitable for towed arrays used in shallow environments and is less cost-effective.
Various high-resolution methods have been proposed based on the operation of the signal covariance matrix to improve the angular resolution under certain constraints [7]. Well-known methods include adaptive beamforming (ABF), such as the minimum-variance distortionless response [8] (MVDR), the amplitude and phase estimation [9] (APES), the low complexity adaptive (LCA) beamformer [10], the coherence factor (CF) beamformer [11], spatial spectrum estimation techniques such as multiple signal classification [12] (MUSIC), and the estimating signal parameters via rotational invariance techniques [13] (ESPRIT). These algorithms provide narrow beamwidths that transcend the Rayleigh limit and effectively produce low sidelobe levels at the same time, making them better for interference rejection and intensity distribution estimation of targets with a small bearing separation. However, they are known to be sensitive to signal mismatches between the assumed and the actual signal wave front caused by the scattering or wrong receiver position [14]. These algorithms also require precise estimation of the signal covariance matrix from measurement samples and use diagonal loading in calculations, and hence, are computationally complex.
Sparse representation (SR) and compressed sensing techniques have emerged as novel motivators for DOA estimation because of their adaptability in diverse scenarios [15,16,17,18]. Following the idea of compressed sensing, numerous outstanding algorithms have been proposed, including orthogonal matching pursuit [19,20,21,22] (OMP) and atomic norm minimizing [23,24,25,26] (ANP). Both the OMP and ANP algorithms can greatly reduce the number of sensors to be used by utilizing the sparsity of the signal, and significantly decrease the number of samples required for signal restoration and bearing estimation. Although compressed sensing-based algorithms generally exhibit strong robustness compared to other covariance matrix-based algorithms, their performance is significantly constrained by the assumption of signal sparsity [27], which is commonly not applicable in ocean acoustical imaging of large fish aggregation, geological features, and other potential extended targets with unpredictable source quantity and intensity distribution.
Another approach to achieve high-resolution bearing estimation is deconvolution, which can be seen as a series of post-processing methods. The algorithms generally consider the conventional beamforming output as the convolution between the beam pattern, which is also known as the point spread function (PSF), and the ground truth spatial signal intensity distribution. The maximum likelihood (ML) deconvolution method, taking into account the circular complex Gaussian random (CCGR) statistics of acoustic fields, is firstly proposed to significantly enhance the angular resolution of images [28]. Modified likelihood model-based deconvolution (M-DCV) and approximate likelihood model-based deconvolution (AM-DCV) are then proposed to improve the deconvolution performance and computational efficiency [29]. To further overcome the computational complexity resulting from the global optimization algorithm required for maximum likelihood estimation, a series of Richardson–Lucy (R-L) algorithm [30]-based methods are purposed to iteratively deblur the spatial intensity distribution from the CBF output [14,31,32]. The R-L algorithm delivers good deconvolution results with a narrow beamwidth and low sidelobes. However, when dealing with features with steep edges, the R-L algorithm requires more iterations to converge, resulting in strong spurious oscillations [33]. Wide features could be fragmented into multiple narrow features, while the intensity of background noise near these features fluctuates significantly. This would diminish the imaging performance and pose challenges for further processing.
Recently, neural network (NN) has been shown to perform well in DOA estimation tasks in air [34,35] and under water [36,37]. NN has also been applied to underwater range estimation tasks [38,39]. Considering the similarity in blurring processes caused by optical and acoustical PSF and conventional beamforming, deep learning-based image deblurring methods show great potential in enhancing angular resolution and estimating ocean acoustic intensity distribution. Nah proposed a multi-scale structure that effectively preserves details at finer scales and handles long-range dependencies at coarser scales [40]. Notably, the blurred images in the datasets are generated by simulating the exposure process on sharp images. Tao utilized an encoder–decoder architecture and a multi-scale structure to extract features at various scales [41]. Meanwhile, Liu adopted deblurring and optic flow methods to recover consecutive frames [42]. Compared to typical optical image deblurring applications, deep learning-based ocean acoustic image enhancement poses significant challenges due to the difficulty in acquiring acoustic data and the limited amount of data available.
Here, we propose a deep learning deconvolution approach to enhance the angular resolution of CBF results. A modified U-Net structure, which originates from optical deblurring, is adopted to deconvolve the conventional beamforming outputs. The simulated dataset is generated following statistics of the instantaneous complex amplitude of an acoustic field in an ocean waveguide environment to address the issue of inadequate ocean acoustic data. The performance of the deconvolution is validated using both synthetic and experimental data.
2. Materials and Methods
2.1. Conventional Beamforming Using a Linear Receiver Array
The instantaneous pressure field after conventional beamforming can be represented as the convolution of the complex pressure amplitude of incident plane waves from different directions and the array beam pattern [28]. Considering M incident plane waves from different directions, the total beamformed pressure at scan angle and time t using a uniformly-spaced linear array can be expressed as follows:
where is the complex amplitude of the plane wave in the direction of the acoustic wavenumber vector , is the wave number, is the radial frequency of the plane wave, c is the sound speed, is the incident angle with respect to the array broadside, and i is an index for directions. For a uniformly-spaced linear array with N elements, the beam pattern B using a rectangle window can be expressed as:
where is the scan angle spanning corresponding to the array’s broadside, and d is the element spacing. After neglecting the time-harmonic term , the instantaneous beamformed plane wave intensity I at scan angle is:
The complex amplitude of the incident plane waves , subject to fluctuations from various mechanisms including waveguide multi-path propagation and scattering, follows circular complex Gaussian random (CCGR) statistics characterized by an expected value of [43,44,45,46]. The incident plane wave fields originating from different directions are assumed to be independent of each other for common ocean acoustical sensing applications, implying that where . The expected beamformed intensity at scan angle is then expressed as follows:
where .
We further use the wavenumber k and incident angle instead of the wavenumber vector to rewrite the expected incident plane wave intensity. The expected intensity derived from conventional beamforming (CBF) can now be considered as the discrete convolution of the expected ground truth intensity distribution and the square of the beam pattern as follows:
where . Considering as a vector comprising elements and letting represent the matrix, where each element is defined by , the expected beamformed intensity vector can be expressed as follows:
2.2. Deconvolution Using Neural Network
In this study, we employ a modified U-Net neural network structure, which was originally designed for tissue segmentation tasks in medical applications [47], to deconvolve the ground truth expected intensity distribution of incident plane waves from conventional beamforming outputs. The network structure is shown in Figure 1. This network benefits from its hierarchical structure, which utilizes pooling layers for downsampling (red arrows) and up-convolution layers for upsampling (green arrows), resulting in a relatively large receptive field. The skip connections (thin gray arrows) directly copy the output of the encoder, which is closer to the original input of the network and thus contains more spatial information, in each level to the input of the relevant decoder. This structure helps to supplement spatial information perceived by the decoder. However, it does not help to preserve spatial information when the encoder decreases the size and increases the dimensions of feature maps level by level. Much of the spatial information is forgotten while encoding across multiple levels of the network, and hence, the original U-Net lacks the capability of pixel perception [41]. As a result, the original U-Net is unsuitable for deconvolution tasks. At the same time, the network processes low-frequency features of images (such as extended geo-clutter echos and ambient noise) in higher dimensions, limiting its ability to recover the intensity of large size features. However, the original U-Net has insufficient convolutional layers in the encode part (left part) and thus is not able to precisely extract the sharp components of feature maps.
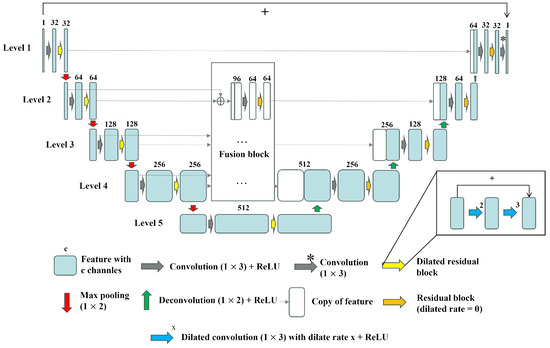
Figure 1.
Modified U-Net structure. The network comprises an encoder, fusion blocks, and a decoder, respectively responsible for extracting features, further extracting sharp features, and utilizing these features to generate the final output. Green boxes are feature maps, with the number of dimensions shown above each one. Gray arrows represent a convolutional layer (1 × 3) followed by a ReLU activation layer. Gray arrow with ‘*’ represents single convolutional layer. Yellow arrows represent dilated residual blocks, while orange arrows represent residual blocks without dilated convolution. Each dilated residual block consists of two dilated convolution layers with different dilation rates of 2 and 3, shown by blue arrows with numbers. Red arrows represent max pooling layers (1 × 2), while green arrows represent deconvolution layers. White boxes with arrows represent duplicates of corresponding features.
To address these issues, dilated residual blocks (yellow arrows) inspired by the residual block in the SRN-Net [41] are introduced to replace simple convolutions in the encoder, hence allowing more spatial information to be perceived. Each block contains two dilated kernels with different dilation rates to enlarge the receptive field and address the gridding effect issue [48]. We also add fusion blocks to fuse the features from adjacent levels, which perceive more spatial information necessary for deconvolution. Additionally, we modified the first level of the encoder by reducing the output channels from 64 to 32, as the expected intensity vector contains less information than an RGB image. The input of the neural network is the intensity distribution over propagation time and azimuthal angle. By assuming intensity to be time-independent, one-dimensional angular intensity distributions can be separately estimated and deconvolved in chronological order, and then recombined. As a result, we adjusted all the kernel sizes from 3 × 3 to 1 × 3. This modification reduces the number of parameters and eliminates the correlation in the time domain.
The one-dimensional angular intensity distribution input is initially processed by the encoder using a convolution layer and a dilated residual block at each level. The pooling output and the level output are concatenated and processed by fusion blocks, each containing a convolution layer and a residual block. Each decoder, except the last one at level 1, concatenates the fusion output from its corresponding level with outputs from the higher level. These features will be processed further by a convolution layer and a residual block. The output is then upsampled by the deconvolution layer of the U-Net. Finally, the output of the decoder is processed by one more convolutional layer without any activation function. The number of channels at each level in the feature maps is listed above the blue boxes in the figure, showing changes in feature map dimensions during encoding and decoding. Additionally, the size of the feature maps is halved after max pooling layers and doubled after deconvolution (transposed convolution) layers.
Simulated one-dimensional datasets with 2 million samples were utilized to train the model on a 1 NVIDIA 3060 GPU, with a batch size of 100. The learning rate was initially set to 0.001, with an exponential decay rate of 0.9. We used the Charbonnier Loss together with the Adam optimizer to handle outliers and improve performance. Each model is trained for 10 epochs, which takes approximately 6 h. The normalized mean square error changes in train data and validation data over epochs are shown in Figure 2. We use early stopping to obtain the final model with the lowest NMSE in validation data. This prevents the model from reaching any information from test data including synthetic and experimental data, which ensures that the test data correctly evaluates the robustness of the model.
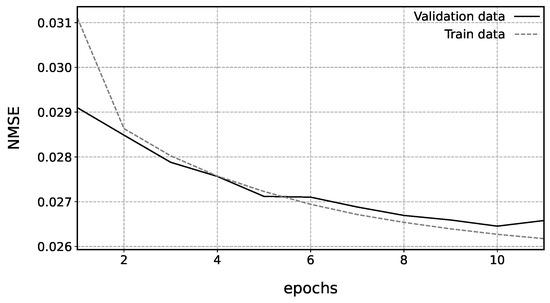
Figure 2.
Normalized mean square error changes over epochs.
The network is trained on simulated data instead of experimental data for several reasons. The ocean acoustic data are always collected using receiver arrays equipped on ships or other vehicles with weak mobility. Limited by perception range and movement speed, the receiver collects redundant data in a relatively fixed area. Meanwhile, the receiver cannot access ground truth data due to its limitation on aperture. Therefore, it is necessary to generate simulated data, which will be introduced in the next section.
2.3. Data Simulation Method
The data simulation method plays a significant role because the data need to contain all the information required for deconvolution. We take advantage of the relatively pervasive circular complex Gaussian random (CCGR) statistics of acoustic fields in the ocean that follow from the central limit theorem for many typical scenarios of propagation, radiation, or scattering [43,44,45,46,49,50,51,52]. The one-dimensional expected plane wave intensity vector comprising of M elements for is chosen as the ground truth for deconvolution, where each element represents the expected intensity of the incident plane wave from spanning from to . We specifically choose the domain because the point spread function (PSF) of beamforming is shift-invariant, enabling the neural network to learn angle-independent deconvolution parameters. Each one-dimensional expected plane wave intensity vector is assumed to contain an ambient expected plane wave intensity vector , where each element represents the intensity of incident plane waves from each discrete incident angle . This could be a good simulation of various extended features, such as ship noise, reverberation, and ambient noise in the ocean environment. In addition, one to four relatively narrow and strong designed features with intensity vector , where each element , are added to simulate obvious and regular features. The subscript q is an index for features. Then, the ground truth expected intensity is:
The ambient expected plane wave intensity vector in decibel units is first constructed using the Midpoint Displacement in OneDimension (MDOD) algorithm [53], which is described in Algorithm 1.
Here, are the lower and upper bounds of the features’ intensity in dB, respectively. The indices , corresponding to the angle , show the angular area of the feature in the current recursive iteration. The midpoint’s intensity inside the current area can vary within the range of in the next recursive iteration. The parameter is the decay rate of , which reduces the fluctuations of values during the recursive process. In practice, we set to dB, to 20 dB, and to 0.45. The ambient expected plane wave intensity vector is initialized by setting identical first and last elements . The value of the two elements is a random variable that is uniformly distributed in the range of dB. We also apply a 10-by-1 mean filter to the resulting intensity vector to simplify its details. Finally, the ambient expected plane wave intensity .
| Algorithm 1: Midpoint Displacement in OneDimension |
 |
The designed features are expected with a steeper edge and more regular distribution than . Here, we employ a Gaussian radial basis function (GRBF) with a flat peak to simulate the discrete intensity of the features at :
Here, we employ a uniformly distributed random variable in dB to control the q-th target size. are separately set to −0.7, 0.8 in the simulation. The center of the target is randomly assigned to ensure the targets across different directions. The parameter denotes half the angular width of the flat peak for the q-th target, which will be separately assigned in different cases. To diversify the sample, we randomly adjust the peak intensity of the targets by a uniformly distributed random variable dB.
In the simulation, four classes of designed features with different characteristics are included to ensure that their combination represents natural features well. Forty percent of the features are single narrow features with angular width degree. Twenty percent of the features are single wide features with angular width . We also force 20% of features consisting of three wide features with angular width , overlapping with each other. The rest of the features are a combination of two separated narrow features with angular width close to each other. The distribution of features under our strategy is far more similar to natural distribution than that of completely random features.
The total expected intensity vector can then be calculated following Equation (7). In the simulation, we consider the average plane wave intensity vector , which is calculated over ten snapshots generated from the expected intensity vector with CCGR distribution, as the target of deconvolution. The corresponding normalized expected beamformed intensity is used as input. This operation effectively prevents the network from filtering out potential features with small fluctuations. The normalized expected beamformed plane wave intensity vector is:
The scanning matrix is a normalized beam pattern defined as . This normalization effectively maintains the ambient intensity value after beamforming, and hence, stabilizes the learning process. Finally, we normalized and using the minimum , obtaining the and in dB domain:
The expected intensity distributions before and after beamforming are both normalized using minimum beamformed intensity as the calculation is only feasible for beamformed data. Additionally, we circularly pad as to enable the neural network to access enough information for processing intensity near end-fire. The neural network with parameters is then trained with the expected beamformed intensity vector to minimize the Charbonnier Loss between the network output and the averaged incident intensity vector :
where is set as 0.001 to smooth the loss function.
2.4. Experiment
We collected underwater acoustic data to validate our algorithm during an Ocean Acoustic Waveguide Remote Sensing (OAWRS) experiment in the South China Sea in June 2021. Reverberation from the continental shelf and continental rise of the South China Sea are both collected (Figure 3a). Two research vessels were deployed as a bi-static acoustic imaging system as shown in Figure 4. The source used in the experiment is a 10-element transducer vertical linear array with an array spacing of 0.417 m. The receiver is a horizontal towed linear array with 2 sub-apertures consisting of 128 hydrophones. In this research, the first sub-aperture consisting of 96 hydrophones with an array spacing of 0.417 m, corresponding to a half-wavelength of signal with a frequency of 1800 Hz, was utilized for conventional beamforming and deconvolution. During the experiment, the moored source was deployed with a center depth of approximately 50 m, while the receiver was towed along a predetermined path shown in Figure 3b,c at a depth of roughly 65 m. The source transmitted a series of Tukey-windowed linear frequency modulated (LFM) pulses centered at 1800 Hz with a 200 Hz bandwidth and 1 s duration every 40 s. The steer angles of the transducer array are separately set to 0 degrees on the continental shelf area and 14 degrees downward on the continental rise area. The image area for each steer angle along the west of the source is shown in Figure 5. The collected data also include the GPS location of two vessels and corresponding timestamps. Water-column sound speed profiles were measured using expendable conductivity–temperature–depth (XCTD) sensors at each experiment area. The average sound speed profile is shown in Figure 6.
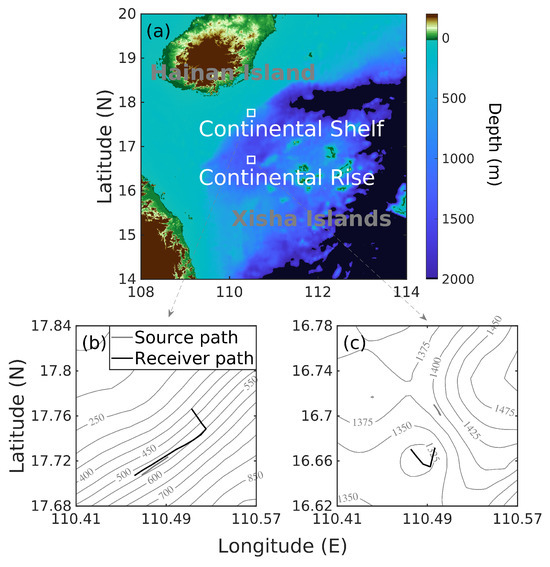
Figure 3.
(a) The location of the OAWRS experiment in the South China Sea during June 2021. The white box bounds the experimental areas on (b) the southern flank of the continental shelf in the south of Hainan Island, and (c) the continental rise region on the west of Xisha Islands, China. Gray and black lines illustrate the trajectories of the moored source and the towed receiver array, respectively.
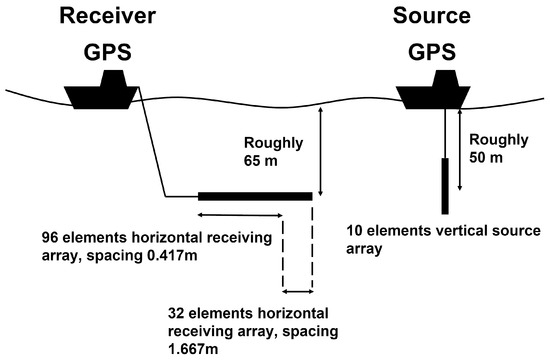
Figure 4.
Experimental setup diagram. The moored vertical source array, comprising 10 elements, is deployed by a research vessel at a center depth of 50 m and transmits signals with a source level of 210 dB. Each element of the source emits signal with power of 190 dB. The horizontal receiver array consists of 128 elements, with 96 of them spaced 0.417 m apart, and is towed by another research vessel at a depth of 65 m.
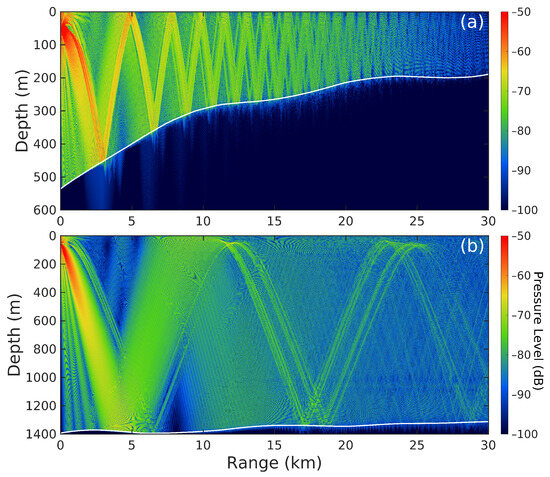
Figure 5.
Ray tracing in the west of the source located on (a) the southern flank of the continental shelf in the south of Hainan Island on 19 June 2021 at 20:34 UTC, and on (b) the continental rise region on the west of Xisha Islands, China, on 18 June 2021 at 08:28 UTC. The white line in both figures shows the real seabed.
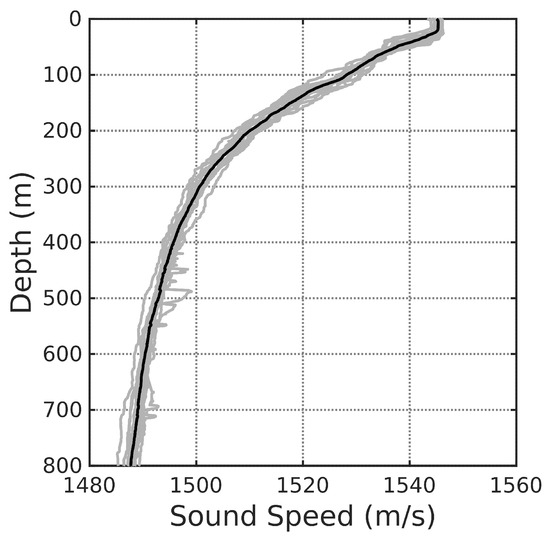
Figure 6.
Sound speed profile measured in the southern flank region of the continental shelf and continental rise region during the experiment. The gray lines are the experimental sound speed profiles and the black line is the average value of them.
OAWRS imaging comprises two main phases. Initially, the conventional beamforming (CBF) method with a Hanning spatial window is employed to approximate the arrival azimuth angle of incident signals. The beamforming output is then processed by a matched filter and charted into a Cartesian coordinate.
3. Results
3.1. Synthetic Data
In this section, we validate the performance of the deep learning (DL) deconvolution with synthetic data using various types of targets near the array broadside and end-fire direction, respectively (Figure 7, Figure 8 and Figure 9). We also provide results of CBF, AM-DCV, and the iterative R-L algorithm, which is another deconvolution method based on the PSF, for comparison to illustrate the performance improvement and robustness of the algorithm. This comparison is conducted with a 32-element array under a signal-to-noise ratio (SNR) of 20 dB. We also compare the imaging error and 3 dB beamwidth of deconvolved results near the broadside at different SNR levels and array sizes. The error in this case is quantified using the normalized mean square error (NMSE) between the deconvolved results and the ground truth distribution of incident intensity in decibel units , which is defined as:
where i indicates the element index of vector and . NMSE is employed to quantify the deconvolution performance because it can measure the similarity of the entire intensity distribution. Meanwhile, we utilize it to reduce the impact of different SNRs on the comparison of results. Notably, we define the SNR as the ratio of the highest intensity of features to the ambient intensity in each direction in the CBF results. We use this definition because our algorithm focuses on features that are challenging to discriminate or recognize but not unreadable.
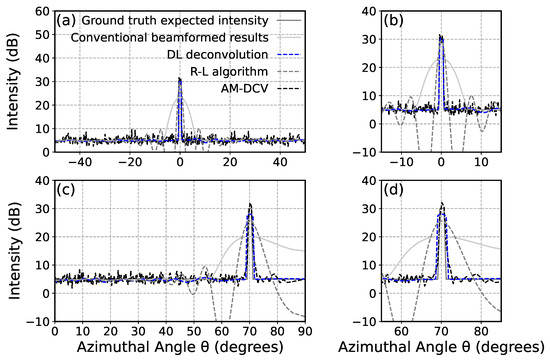
Figure 7.
A comparison between the intensity of a narrow feature (1°) near (a) the array broadside and (c) the end-fire direction by the DL deconvolution, the R-L algorithm, and CBF, respectively. (b,d) are zoom-in versions of (a,c) near the feature.
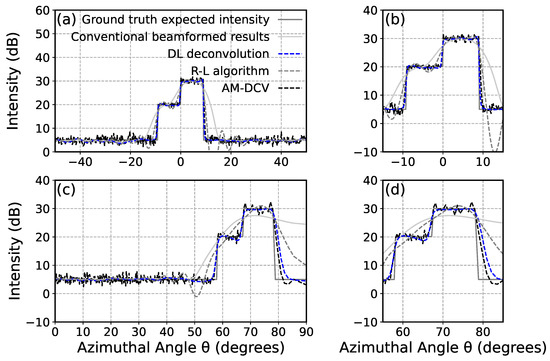
Figure 8.
A comparison between intensity of a wide feature consisting of two box-like features with 10° width and 10 dB difference in intensity near (a) the array broadside and (c) the end-fire direction by the DL deconvolution, the R-L algorithm, and CBF, respectively. (b,d) are zoom-in versions of (a,c) near the feature.
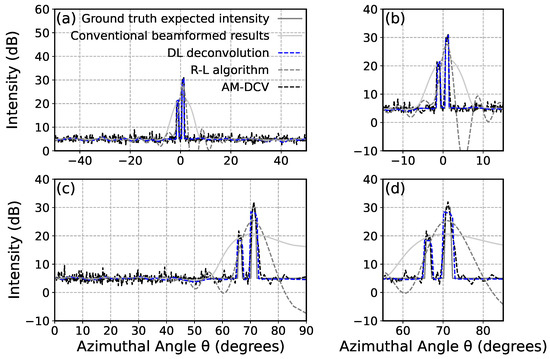
Figure 9.
A comparison between intensity of two narrow features (1°) with an angular separation of (a) 1° in array broadside and (c) 2.5° near array end-fire by the DL deconvolution, the R-L algorithm, and CBF, respectively. (b,d) are zoom-in versions of (a,c) near the feature.
In the case of narrow features (1°) as shown in Figure 7, all the deconvolution methods significantly reduce the 3 dB width of the main lobe and accurately estimate the angle of arrival near the broadside and end-fire compared with CBF. The results obtained through the DL deconvolution exhibit a narrow beamwidth and a steep edge, indicating its advantages in recovering the intensity distribution of the feature. Although the three deconvolution methods demonstrate similar performance in recovering the peak intensity, the results obtained by the R-L algorithm exhibit significant spurious oscillations in the estimation of the ambient noise level. In contrast, the results obtained by the DL deconvolution and AM-DCV appear stable and show good agreement with the ground truth ambient level. For features located near the array broadside (Figure 7a,b), the NMSE of the intensity obtained by the DL deconvolution is approximately 0.004, which is significantly lower than the NMSE of 0.516 obtained by CBF. Meanwhile, the NMSE of the deconvolved result using the R-L algorithm is approximately 1.117, which is twice as large as the NMSE obtained by CBF due to the spurious oscillations. The NMSE of AM-DCV is approximately 0.04. For the same narrow feature near the end-fire direction (Figure 7c,d), our method achieves an NMSE of about 0.060, while the R-L algorithm yields an NMSE of 0.753, higher than the 0.417 obtained by CBF. The NMSE of AM-DCV is approximately 0.05, indicating a better performance near array end-fire than DL deconvolution.
A wider feature with an intensity distribution as shown in Figure 8 is also set to evaluate the deconvolution ability of our method for extended targets. The target consists of two box-like features with 10° width and 10 dB difference in intensity. Though the three algorithms all obtain clearer intensity distribution than the CBF results in array broadside and end-fire, the results from DL deconvolution and AM-DCV show a steeper edge and a flatter peak than that from the R-L algorithm, especially in the case of array end-fire. Meanwhile, DL deconvolution and AM-DCV exhibit better performance in the recovery of intensity for the feature with a lower SNR, indicating their better ability to perceive intensity changes. For the ambient intensity, DL deconvolution and AM-DCV also show a better agreement with the ground truth value. For features located near the array broadside (Figure 8a,b), the NMSE obtained from the DL deconvolution is 0.006, which is lower than the NMSE of 0.076 obtained from the R-L algorithm and 0.02 obtained from AM-DCV, and significantly lower than the NMSE of 0.117 obtained from CBF. In the case of the same features near array end-fire (Figure 8c,d), the NMSE of our proposed method is 0.025, while the R-L algorithm yields an NMSE of 0.344, higher than the 0.232 from CBF. The NMSE of AM-DCV is 0.03.
To evaluate the ability to discriminate close features, two narrow features (1°) with an angular separation of 1° in array broadside and 2.5° near array end-fire are evaluated as shown in Figure 9. The intensity of two adjacent features in both cases is well recovered using DL deconvolution and AM-DCV with clear edges and an accurate peak intensity, which is not achievable using either the R-L algorithm or CBF. Notably, the R-L algorithm shows significant spurious oscillations in deconvolved ambient noise level and our method recovers it stably. For the two features near the array broadside (Figure 9a,b), our method achieves an NMSE of 0.0129, outperforming the R-L algorithm with an NMSE of 0.424, AM-DCV with an NMSE of 0.04, and the CBF results with an NMSE of 0.429. For features near array end-fire (Figure 9c,d), our method obtains an NMSE of 0.073, lower than the NMSE of 0.587 obtained by the R-L algorithm, and 0.433 obtained by CBF. AM-DCV has the lowest NMSE of 0.068.
To evaluate the performance of DL deconvolution, we assessed the deconvolved results of an ideal feature with negligible width near the array broadside and end-fire direction under different SNRs and array sizes as shown in Figure 10. Our method does not require training on different datasets to deconvolve samples with different SNRs. When the number of array elements varies, the model should be trained on appropriate datasets to account for variations in PSF. We first compare the root mean square error (RMSE) of estimated DOA, NMSE of intensity, and 3 dB beamwidth as a function of SNRs from DL deconvolution, the R-L algorithm, and CBF in array broadside and end-fire using a 32-element array (Figure 10a–c). For DOA estimation (Figure 10a), the R-L algorithm shows a good performance near array broadside, but it has a relatively big error near array end-fire when the SNR is low. In contrast, the DL deconvolution method exhibits a stable and better estimation accuracy for SNR ranging from 5 dB to 35 dB. AM-DCV shows the best DOA estimation accuracy near both array broadside and end-fire. Here, the RMSE of estimated DOA from CBF near end-fire is higher than 0.1 and not plotted inside the chart. The comparison of NMSE (Figure 10b) illustrates that our method has the best capacity for recovering the whole intensity distribution in all SNRs and positions. For comparison, the NMSEs of the R-L algorithm and CBF show a rapid increase as the SNR becomes higher. The comparison of 3 dB beamwidth (Figure 10c) illustrates that our method has the relatively narrow main lobe widths and outperforms the R-L algorithm when the SNR is low. Here, the results from CBF near end-fire are higher than 12 degrees and are not plotted. DL deconvolution shows a great stability and capability of recovering intensity distribution among the four methods, especially for low SNR cases.
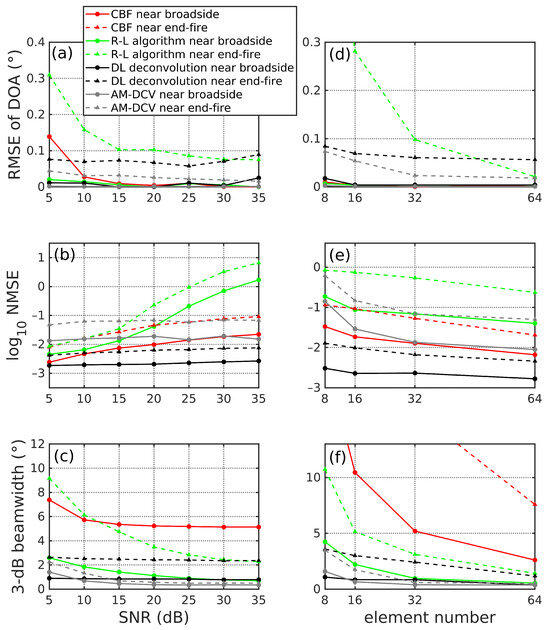
Figure 10.
Performance of DL deconvolution, the R-L algorithm, AM-DCV, and CBF as a function of (a–c) different SNRs and (d–f) element numbers near array broadside and end-fire direction. (a,d) show the RMSE of DOA in different SNRs and element number. The CBF results near the end-fire are much higher than 0.1, which are not plotted in both figures. (b,e) show the NMSE in log scale. (c,f) show the 3 dB beamwidth.
We then compare the performances of the four methods as a function of element numbers using the same quantification value mentioned above (Figure 10d–f). The SNR is set fixed to 20 dB in this case. For DOA estimation (Figure 10d), our method shows advantages over the R-L algorithm and CBF in both array broadside and end-fire, especially for the array with a small aperture. Here, the results from CBF are higher than 0.1 and are not plotted. Figure 10e illustrates DL deconvolution’s consistent advantage in recovering the whole intensity distribution for all aperture sizes. For 3 dB beamwidth (Figure 10f), our method outperforms the R-L algorithm both near array broadside and end-fire when the array aperture is small. When the array aperture becomes larger, the deconvolved 3 dB beamwidth from the R-L algorithm narrows the gap with the result from DL deconvolution. All the comparisons illustrate that DL deconvolution has good performance in different array apertures, especially in small aperture arrays.
We also compare the performances of these methods as a function of incident angles from 0 to 80 degrees as shown in Figure 11. The SNR is set to 20 dB and the element number is set to 32 in this case. For DOA estimation (Figure 11a), three deconvolution methods show similar performances near the array broadside. When the incident direction gets closer to the array end-fire, AM-DCV shows the best performance in DOA estimation accuracy and DL deconvolution performs the second best. Figure 11b illustrates that DL deconvolution obtains the best performance in recovering the whole intensity distribution for incident angles ranging from 5 degrees to 80 degrees. For 3 dB beamwidth (Figure 11c), DL deconvolution shows a better performance than the R-L algorithm in all mentioned incident angles. The comparisons illustrate that DL deconvolution works well in most incident directions.
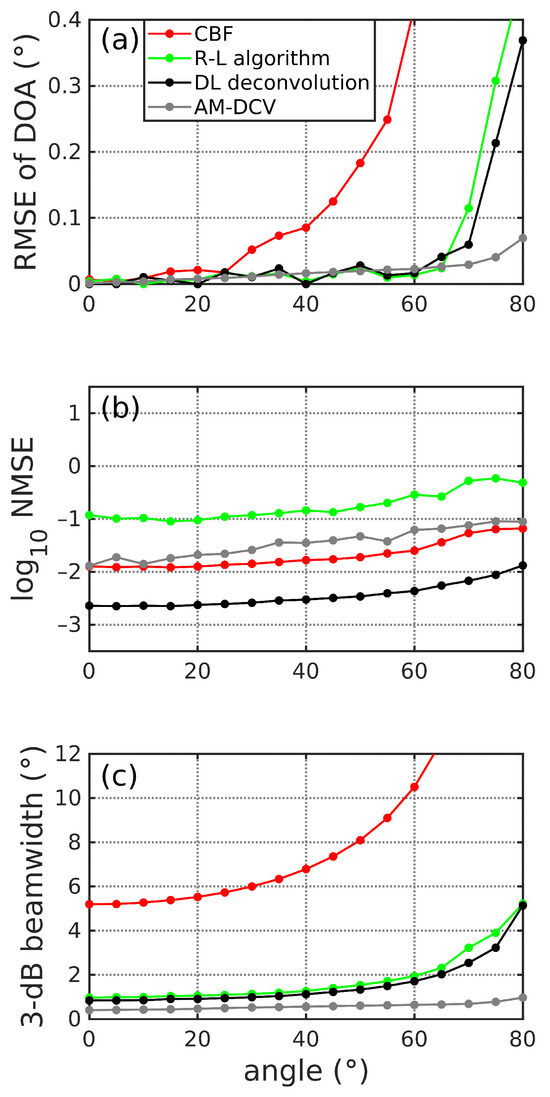
Figure 11.
Performance of DL deconvolution, the R-L algorithm, AM-DCV, and CBF as a function of different incident angles. (a) shows the RMSE of DOA in different SNRs and element numbers. (b) shows the NMSE in log scale. (c) shows the 3 dB beamwidth.
The one-dimensional synthetic data show that DL deconvolution has the best performance in recovering the whole intensity distribution measured by NMSE, and AM-DCV has the best performance in DOA estimation accuracy and 3 dB beamwidth. However, though AM-DCV significantly improves the computational efficiency of the maximum likelihood deconvolution method, it still takes at least 20 s to process one angular acoustic intensity vector. Furthermore, the processing time of AM-DCV increases when it deals with extended features. In comparison, DL deconvolution processes one-dimensional data within 0.1 s. For an acoustic image with an imaging range of 5 km and a range resolution of 6 m, our method takes seconds to obtain the whole deconvolved images. In contrast, AM-DCV takes several hours on the task.
We further show the performance of DL deconvolution in recovering the intensity of a 2-D acoustical image using a rectangular synthetic feature (Figure 12). The rectangular feature spans about 7 × 7 km2, with its center located roughly 31 km west and 28 km north from the center of the receiver array. Figure 12a shows the two-dimensional intensity distribution of the feature. Figure 12b,c are CBF and DL deconvolution results using a uniform linear array with 32 elements. The DL deconvolution results exhibit sharp edges over CBF while maintaining a stable ambient noise level. It also accurately recovers the detailed intensity distribution inside the feature. The CBF result using a 96-element array is plotted in Figure 12d for comparison. Here, the NMSE of the 32-element CBF results is 0.090, that of the 96-element CBF results is 0.027, and that of the DL deconvolution results is 0.004.
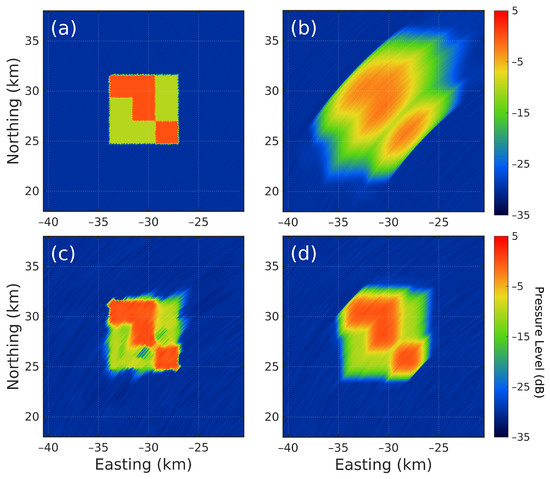
Figure 12.
A comparison between (a) expected intensity, (b) conventional beamformed intensity using an array with 32 elements, (c) the DL deconvolution results using an array with 32 elements, and (d) conventional beamformed intensity using 96 array elements of a rectangular synthetic feature located roughly 31 km west and 28 km north from the center of the receiver array.
3.2. Experimental Data
Here, we use the OAWRS images of underwater reverberation data collected during the experiment in the South China Sea during June 2021 to evaluate the performance of the DL deconvolution. The OAWRS image to be deconvolved is generated and then averaged over five different sub-apertures with an overlap of 50%, each of which consist of 32 hydrophone elements with an array spacing of 0.4167 m. We utilize the average of five sub-apertures to reduce imaging bias introduced by the selection of hydrophone elements. We also provide the conventional beamformed results obtained using sub-apertures consisting of 32 and 96 elements for comparison. The conventional beamformed results from 32 hydrophone elements are transformed into decibel units in bi-static polar coordinates. One-dimensional intensity distribution at different ranges is first normalized by subtracting its minimum value and then independently delivered to DL deconvolution. The deconvolved resulting one-dimensional intensity distribution is finally re-charted using the corresponding normalization factor and then transformed back into a Cartesian coordinate.
Figure 13 illustrates the CBF and DL deconvolved OAWRS images of reverberation from the southern flank of the continental shelf to the south of Hainan Island as shown in Figure 3b. As shown in Figure 13a, the CBF result using a 32-element array confuses many adjacent geological features and blurs their intensity distribution due to its wide main lobe. For comparison, the DL deconvolved result (Figure 13b) effectively enhances the angular resolution and properly recovers the detailed intensity distribution, making multiple adjacent features resolvable. Notice that the DL deconvolution results using 32 elements can roughly provide a similar performance as the CBF results using 96 hydrophones in Figure 13c.
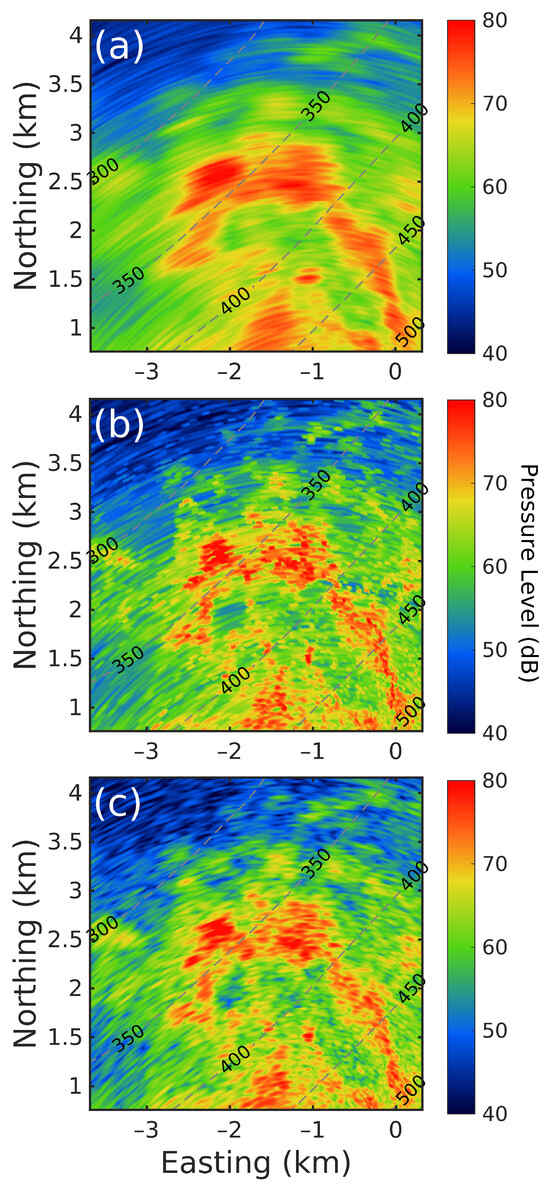
Figure 13.
A comparison between (a) 32-element conventional beamformed results, (b) its DL deconvolved results, and (c) 96-element conventional beamformed results measured on 19 June 2021 at 20:34 UTC. The gray dashed lines are the contour lines with depth shown by the black numbers.
Figure 14 shows three OAWRS images of reverberation from the continental rise region to the west of Xisha Islands as shown in Figure 3c. As shown in Figure 14a, the CBF result using a 32-element array blurs three intensity distributions of continental rises bounded in the red box. The angular distance among these features ranges from approximately 2° to 4°. Figure 14b illustrates that DL deconvolution clearly separates three continental rises and recovers their detailed intensity distribution. The DL deconvolution results using 32 elements provide a similar performance as the CBF results using 96 hydrophones in Figure 14c.
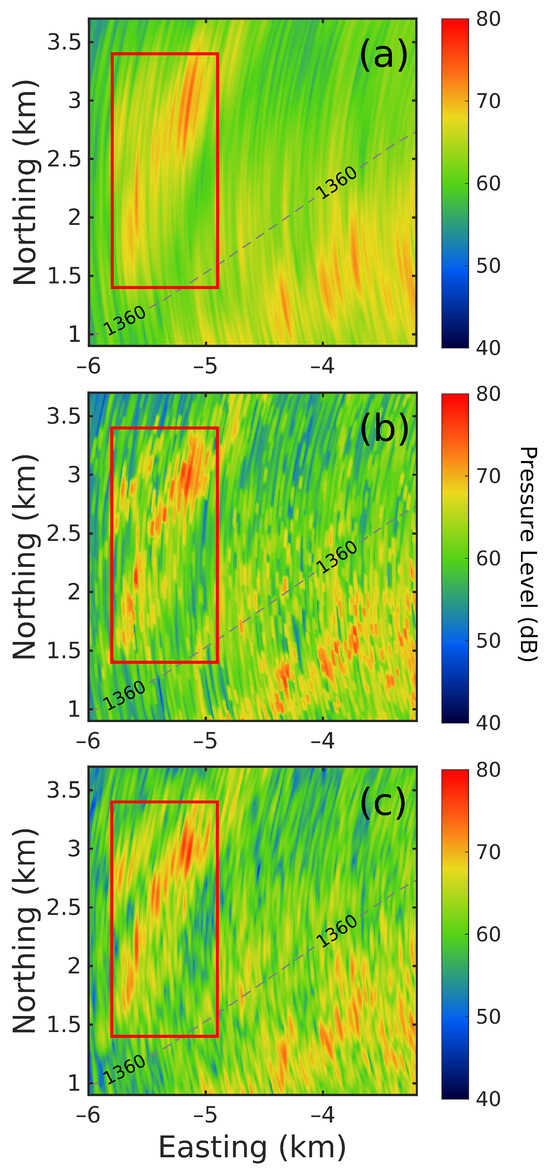
Figure 14.
A comparison between (a) 32-element conventional beamformed results, (b) its DL deconvolved results, and (c) 96-element conventional beamformed results measured on 18 June 2021 at 08:28 UTC. Three adjacent features are bounded by red boxes. The gray dashed lines are the contour lines with depth shown by the black numbers.
More experimental data are shown in Figure A1, Figure A2 and Figure A3 in Appendix A to illustrate the performance of DL deconvolution in experimental data.
4. Discussion
This study proposes a deep learning deconvolution method based on a modified U-Net structure which is trained using synthetic data following ocean acoustic statistics. We take advantage of the relatively pervasive circular complex Gaussian random (CCGR) statistics of acoustic fields in the ocean waveguide caused by random wave propagation and scattering according to the central limit theorem [43,44,45,46]. Acoustic fields that come from different directions are assumed to be independent with each other. This assumption is widely being used in various angular resolution enhancement approaches such as the maximum likelihood (ML) deconvolution method [28] since it effectively represents the physical characteristics of the acoustic wave in ocean waveguide environments. We used the synthetic data generated following such assumptions to train the network because experimental data are insufficient and lack ground truth.
Similar to those previously proposed deconvolution algorithms such as the R-L algorithm [14] and ML deconvolution [28], the proposed method in this paper acts as a deconvolution process that extracts the angular distribution of incident plane wave fields from conventional beamformed intensity images blurred by signal-dependent noise and the beam pattern. However, DL deconvolution avoids global optimization of likelihood or other similar discriminant functions which are extremely computationally expensive but take advantage of a data-driven approach. DL deconvolution provides better performance in intensity distribution estimation compared with CBF and the R-L algorithm. It shows a similar capacity with AM-DCV near array broadside, but slightly worse near array end-fire. Moreover, DL deconvolution gets rid of the cost-expensive global optimization process and costs less than 0.1 s on average for a one-dimensional angular intensity vector consisting of 640 elements, compared with that of more than 20 s for AM-DCV. As a result, DL deconvolution is more applicable in various imaging applications that require real-time processing.
There are also many neural network structures [40,41,42] designed for optical image deblurring tasks that can be adjusted to acoustic image deconvolution problems. However, the point spread functions (PSFs) in optical images always act on two dimensions and are inconsistent at different times. The corresponding networks thus utilize many parameters to adjust to different and relatively complex PSFs, which increase the parameter number and reduce the performance of deblurring. The blur effects on optical images also mostly occur in small areas so that the optical deblurring networks have relatively small receptive fields [54]. The DL deconvolution network uses a one-dimensional convolution kernel to deal with the angular effect of conventional beamforming, and adds fusion blocks to better deal with the intensity. We also enlarge the receptive fields of the neural network by adding dilated residual blocks.
Notably, DL deconvolution is significantly influenced by the data normalization method because it recovers the intensity of both features and ambient noise by perceiving relative changes over the angular domain. Scale normalization methods that change the relative intensity such as Z-scores and 0–1 normalization thus have worse performance compared with the method that directly minuses the minimum values. Moreover, the neural network is only required to be retrained as the beam pattern varies, and hence, can be applied for a static array aperture structure at a fixed operation frequency for various SNRs and snapshots.
5. Conclusions
This study introduces a novel deep learning-based computational efficient deconvolution method using a modified U-Net structure to estimate the angular intensity distribution of acoustic images from conventional beamforming results. The network is trained on simulated data generated following the CCGR statistics in ocean acoustic waveguide environments. Similar to optical image deblurring, the proposed method utilizes the PSF, which is the beam pattern of conventional beamforming, to deconvolve the blurred angular intensity distribution. DL deconvolution is shown to provide a significant improvement in angular resolution over conventional beamforming and the R-L algorithm using both synthetic and experimental data. It also has a much higher processing speed than methods requiring global optimization such as AM-DCV. Our method shows a maximum 1200% improvement in the NMSE of angular intensity distribution and a maximum 700% reduction in 3 dB width over CBF using a uniform linear array with 32 hydrophones. The maximum root mean square error of the estimated DOA is 0.09 degrees. Furthermore, the DL deconvolved results using a 32-element array show a similar performance as the CBF results using a 96-element array. The proposed method is applicable for OAWRS or other acoustic imaging applications that use small aperture arrays and conventional beamforming, and hence, can potentially reduce the array maintenance costs and deployment difficulties.
Author Contributions
Conceptualization, Z.Z. and D.W.; methodology, Z.Z., D.W. and S.W.; software, Z.Z., X.P. and D.W.; validation, Z.Z. and X.Y.; resources, X.Y. and D.W.; writing—original draft preparation, Z.Z.; writing—review and editing, Z.Z. and D.W.; visualization, Z.Z.; supervision, D.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China, grant number 62071419.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
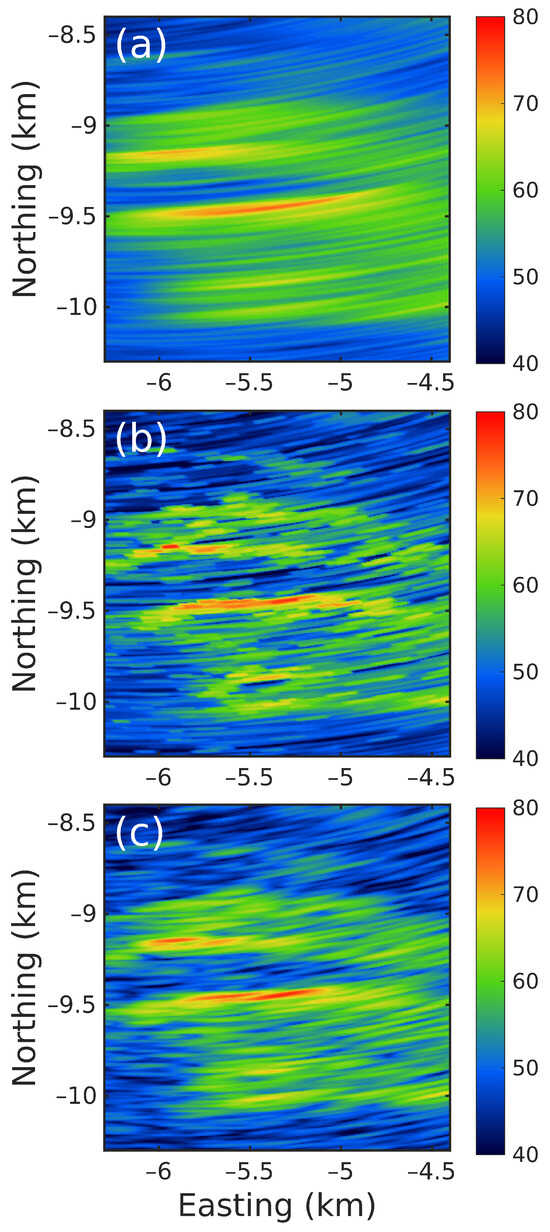
Figure A1.
A comparison between (a) 32-element conventional beamformed results, (b) its DL deconvolved results, and (c) 96-element conventional beamformed results measured on 14 June 2021 at 13:21 UTC.
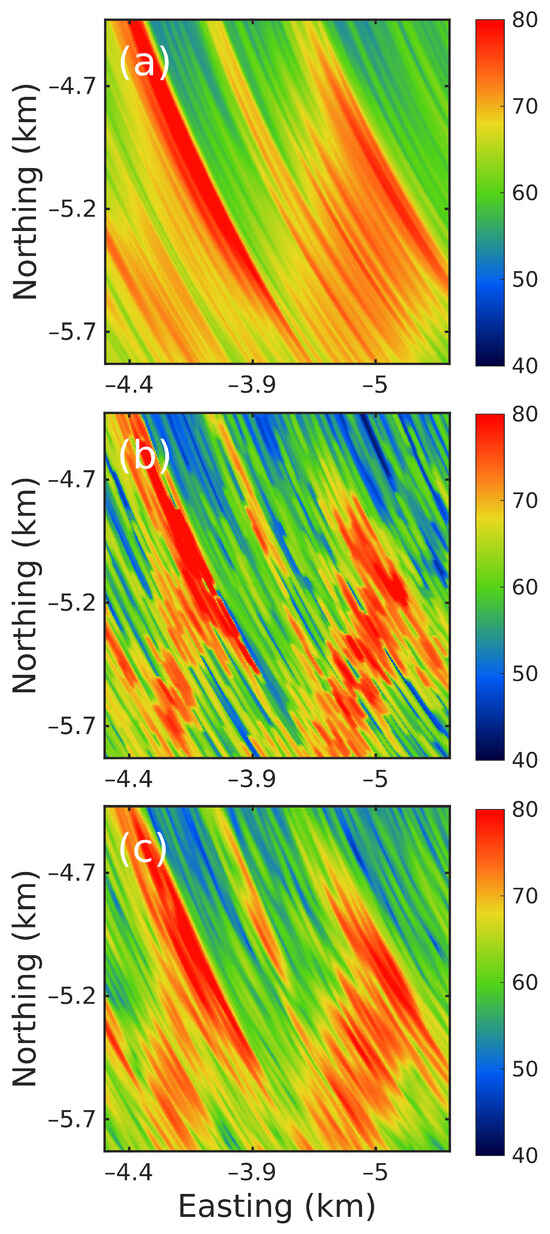
Figure A2.
A comparison between (a) 32-element conventional beamformed results, (b) its DL deconvolved results, and (c) 96-element conventional beamformed results measured on 15 June 2021 at 09:37 UTC.
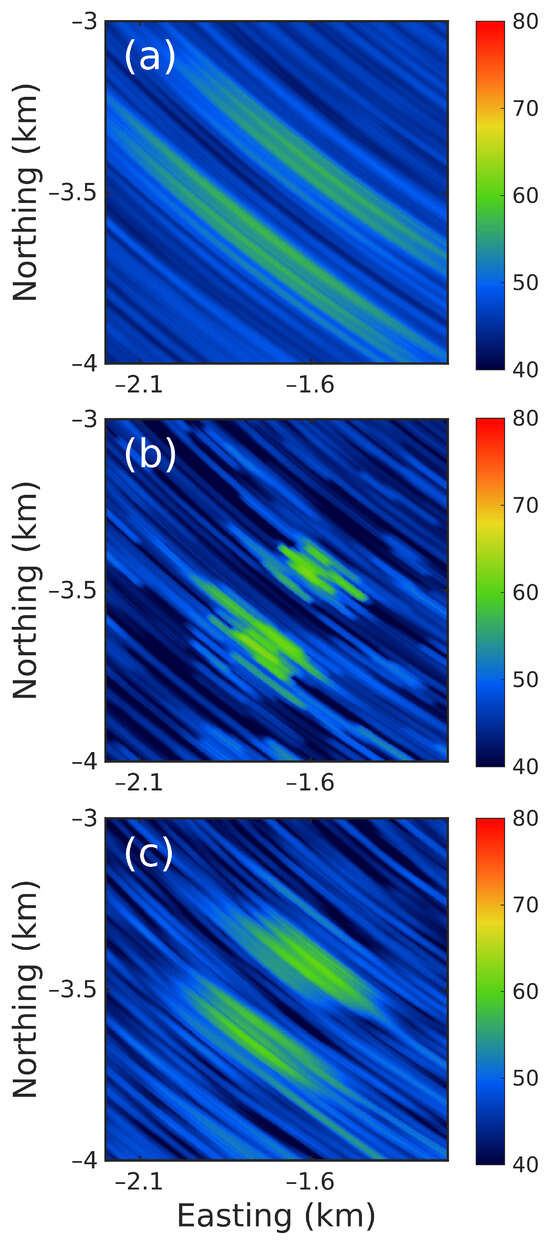
Figure A3.
A comparison between (a) 32-element conventional beamformed results, (b) its DL deconvolved results, and (c) 96-element conventional beamformed results measured on 17 June 2021 at 18:00 UTC.
References
- Makris, N.C.; Ratilal, P.; Symonds, D.T.; Jagannathan, S.; Lee, S.; Nero, R.W. Fish population and behavior revealed by instantaneous continental shelf-scale imaging. Science 2006, 311, 660–663. [Google Scholar] [CrossRef]
- Makris, N.C.; Ratilal, P.; Jagannathan, S.; Gong, Z.; Andrews, M.; Bertsatos, I.; Godø, O.R.; Nero, R.W.; Jech, J.M. Critical population density triggers rapid formation of vast oceanic fish shoals. Science 2009, 323, 1734–1737. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Garcia, H.; Huang, W.; Tran, D.D.; Jain, A.D.; Yi, D.H.; Gong, Z.; Jech, J.M.; Godø, O.R.; Makris, N.C.; et al. Vast assembly of vocal marine mammals from diverse species on fish spawning ground. Nature 2016, 531, 366–370. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Wang, D.; Garcia, H.; Godø, O.R.; Ratilal, P. Continental shelf-scale passive acoustic detection and characterization of diesel-electric ships using a coherent hydrophone array. Remote Sens. 2017, 9, 772. [Google Scholar] [CrossRef]
- Zhu, C.; Seri, S.G.; Mohebbi-Kalkhoran, H.; Ratilal, P. Long-range automatic detection, acoustic signature characterization and bearing-time estimation of multiple ships with coherent hydrophone array. Remote Sens. 2020, 12, 3731. [Google Scholar] [CrossRef]
- Makris, N.C.; Berkson, J.M. Long-range backscatter from the Mid-Atlantic Ridge. J. Acoust. Soc. Am. 1994, 95, 1865–1881. [Google Scholar] [CrossRef]
- Blomberg, A.E. Adaptive Beamforming for Active Sonar Imaging. Ph.D. Thesis, University of Oslo, Oslo, Norway, 2012. [Google Scholar]
- Capon, J. High-resolution frequency-wavenumber spectrum analysis. Proc. IEEE 1969, 57, 1408–1418. [Google Scholar] [CrossRef]
- Blomberg, A.E.; Holfort, I.K.; Austeng, A.; Synnevåg, J.F.; Holm, S.; Jensen, J.A. APES beamforming applied to medical ultrasound imaging. In Proceedings of the 2009 IEEE International Ultrasonics Symposium, Roma, Italy, 20–23 September 2009; pp. 2347–2350. [Google Scholar]
- Blomberg, A.; Hansen, R.; Synnes, S.; Austeng, A. Improved interferometric sonar performance in shallow water using adaptive beamforming. In Proceedings of the International Conference & Exhibition on Underwater Acoustic Measurements (UAM), Kos, Greece, 20–24 June 2011. [Google Scholar]
- Blomberg, A.E.A.; Nilsen, C.I.C.; Austeng, A.; Hansen, R.E. Adaptive sonar imaging using aperture coherence. IEEE J. Ocean. Eng. 2012, 38, 98–108. [Google Scholar] [CrossRef]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Van Trees, H.L. Optimum Array Processing: Part IV of Detection, Estimation, and Modulation Theory; John Wiley & Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- Yang, T. Deconvolved conventional beamforming for a horizontal line array. IEEE J. Ocean. Eng. 2017, 43, 160–172. [Google Scholar] [CrossRef]
- Yang, Z.; Li, J.; Stoica, P.; Xie, L. Sparse methods for direction-of-arrival estimation. In Academic Press Library in Signal Processing; Elsevier: Amsterdam, The Netherlands, 2018; Volume 7, pp. 509–581. [Google Scholar]
- Malioutov, D.; Cetin, M.; Willsky, A.S. A sparse signal reconstruction perspective for source localization with sensor arrays. IEEE Trans. Signal Process. 2005, 53, 3010–3022. [Google Scholar] [CrossRef]
- Yang, Z.; Xie, L.; Zhang, C. Off-grid direction of arrival estimation using sparse Bayesian inference. IEEE Trans. Signal Process. 2012, 61, 38–43. [Google Scholar] [CrossRef]
- Pal, P.; Vaidyanathan, P.P. A grid-less approach to underdetermined direction of arrival estimation via low rank matrix denoising. IEEE Signal Process. Lett. 2014, 21, 737–741. [Google Scholar] [CrossRef]
- Aich, A.; Palanisamy, P. On-grid DOA estimation method using orthogonal matching pursuit. In Proceedings of the 2017 International Conference on Signal Processing and Communication (ICSPC), Coimbatore, India, 28–29 July 2017; pp. 483–487. [Google Scholar]
- Li, Z.; Li, S.; Jia, J.; Ju, D. DOA estimation of underwater wideband signals based on improved OMP method. In Proceedings of the OCEANS 2019-Marseille, Marseille, France, 17–20 June 2019; pp. 1–6. [Google Scholar]
- Kim, J.; Wang, J.; Shim, B. Nearly optimal restricted isometry condition for rank aware order recursive matching pursuit. IEEE Trans. Signal Process. 2019, 67, 4449–4463. [Google Scholar] [CrossRef]
- Zhao, Y.; Xia, W.; He, G.; Yan, F.; Shen, L.; Zhang, Y.; Gao, Y. Direction of Arrival Estimation Based on Simplified Dictionary Matching Pursuit Algorithm with Rotational Invariance. In Proceedings of the 2022 14th International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, China, 1–3 November 2022; pp. 625–630. [Google Scholar]
- Chen, P.; Chen, Z.; Cao, Z.; Wang, X. A new atomic norm for DOA estimation with gain-phase errors. IEEE Trans. Signal Process. 2020, 68, 4293–4306. [Google Scholar] [CrossRef]
- Zhang, X.; Zheng, Z.; Wang, W.Q.; So, H.C. DOA estimation of coherent sources using coprime array via atomic norm minimization. IEEE Signal Process. Lett. 2022, 29, 1312–1316. [Google Scholar] [CrossRef]
- Tang, W.G.; Jiang, H.; Zhang, Q.; Jiang, H. PSWF-based decoupled atomic norm minimization for DOD and DOA estimation in MIMO radar with arbitrary linear arrays. Signal Process. 2023, 212, 109136. [Google Scholar] [CrossRef]
- Chen, T.; Li, M.; Liu, Z. The Joint Grid-Free DOA and Polarization Estimation Algorithm based on Atomic Norm Minimization. In Proceedings of the ICASSP 2024–2024 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Seoul, Republic of Korea, 14–19 April 2024; pp. 21–25. [Google Scholar]
- Wax, M.; Ziskind, I. On unique localization of multiple sources by passive sensor arrays. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 996–1000. [Google Scholar] [CrossRef]
- Jain, A.D.; Makris, N.C. Maximum likelihood deconvolution of beamformed images with signal-dependent speckle fluctuations from Gaussian random fields: With application to ocean acoustic waveguide remote sensing (OAWRS). Remote Sens. 2016, 8, 694. [Google Scholar] [CrossRef]
- Zheng, Y.; Ping, X.; Li, L.; Wang, D. Maximum Likelihood Deconvolution of Beamforming Images with Signal-Dependent Speckle Fluctuations. Remote Sens. 2024, 16, 1506. [Google Scholar] [CrossRef]
- White, R.L. Image restoration using the damped Richardson-Lucy method. In Proceedings of the Instrumentation in Astronomy VIII, Kona, HI, USA, 13–14 March 1994; Volume 2198, pp. 1342–1348. [Google Scholar]
- Sun, D.; Ma, C.; Yang, T.; Mei, J.; Shi, W. Improving the performance of a vector sensor line array by deconvolution. IEEE J. Ocean. Eng. 2019, 45, 1063–1077. [Google Scholar] [CrossRef]
- Liu, X.; Yang, Y.; Sun, C.; Zhuo, J.; Wang, Y.; Zhai, Q. High-angular-and range-resolution imaging using MIMO sonar with two-dimensional deconvolution. IET Radar Sonar Navig. 2023, 17, 991–1001. [Google Scholar] [CrossRef]
- Ehrenfried, K.; Koop, L. Comparison of iterative deconvolution algorithms for the mapping of acoustic sources. AIAA J. 2007, 45, 1584–1595. [Google Scholar] [CrossRef]
- Huang, H.; Yang, J.; Huang, H.; Song, Y.; Gui, G. Deep learning for super-resolution channel estimation and DOA estimation based massive MIMO system. IEEE Trans. Veh. Technol. 2018, 67, 8549–8560. [Google Scholar] [CrossRef]
- Kase, Y.; Nishimura, T.; Ohgane, T.; Ogawa, Y.; Kitayama, D.; Kishiyama, Y. DOA estimation of two targets with deep learning. In Proceedings of the 2018 15th Workshop on Positioning, Navigation and Communications (WPNC), Bremen, Germany, 25–26 October 2018; pp. 1–5. [Google Scholar]
- Liu, Y.; Chen, H.; Wang, B. DOA estimation based on CNN for underwater acoustic array. Appl. Acoust. 2021, 172, 107594. [Google Scholar] [CrossRef]
- Cao, H.; Wang, W.; Su, L.; Ni, H.; Gerstoft, P.; Ren, Q.; Ma, L. Deep transfer learning for underwater direction of arrival using one vector sensor. J. Acoust. Soc. Am. 2021, 149, 1699–1711. [Google Scholar] [CrossRef] [PubMed]
- Houégnigan, L.; Safari, P.; Nadeu, C.; André, M.; van der Schaar, M. Machine and deep learning approaches to localization and range estimation of underwater acoustic sources. In Proceedings of the 2017 IEEE/OES Acoustics in Underwater Geosciences Symposium (RIO Acoustics), Rio de Janeiro, Brazil, 25–27 July 2017; pp. 1–6. [Google Scholar]
- Huang, Z.; Xu, J.; Gong, Z.; Wang, H.; Yan, Y. Source localization using deep neural networks in a shallow water environment. J. Acoust. Soc. Am. 2018, 143, 2922–2932. [Google Scholar] [CrossRef] [PubMed]
- Nah, S.; Hyun Kim, T.; Mu Lee, K. Deep multi-scale convolutional neural network for dynamic scene deblurring. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3883–3891. [Google Scholar]
- Tao, X.; Gao, H.; Shen, X.; Wang, J.; Jia, J. Scale-recurrent network for deep image deblurring. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 8174–8182. [Google Scholar]
- Liu, P.; Janai, J.; Pollefeys, M.; Sattler, T.; Geiger, A. Self-supervised linear motion deblurring. IEEE Robot. Autom. Lett. 2020, 5, 2475–2482. [Google Scholar] [CrossRef]
- Makris, N.C. The effect of saturated transmission scintillation on ocean acoustic intensity measurements. J. Acoust. Soc. Am. 1996, 100, 769–783. [Google Scholar] [CrossRef]
- Makris, N.C. Parameter resolution bounds that depend on sample size. J. Acoust. Soc. Am. 1996, 99, 2851–2861. [Google Scholar] [CrossRef]
- Tran, D.; Andrews, M.; Ratilal, P. Probability distribution for energy of saturated broadband ocean acoustic transmission: Results from Gulf of Maine 2006 experiment. J. Acoust. Soc. Am. 2012, 132, 3659–3672. [Google Scholar] [CrossRef] [PubMed]
- Jagannathan, S.; Küsel, E.T.; Ratilal, P.; Makris, N.C. Scattering from extended targets in range-dependent fluctuating ocean-waveguides with clutter from theory and experiments. J. Acoust. Soc. Am. 2012, 132, 680–693. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Proceedings, Part III 18. Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Wang, P.; Chen, P.; Yuan, Y.; Liu, D.; Huang, Z.; Hou, X.; Cottrell, G. Understanding convolution for semantic segmentation. In Proceedings of the 2018 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, NV, USA, 12–15 March 2018; pp. 1451–1460. [Google Scholar]
- Makris, N.C.; Ratilal, P. A unified model for reverberation and submerged object scattering in a stratified ocean waveguide. J. Acoust. Soc. Am. 2001, 109, 909–941. [Google Scholar] [CrossRef] [PubMed]
- Ratilal, P.; Makris, N.C. Unified model for 3-D scattering and forward propagation in a stratified ocean waveguide with random seabed inhomogeneities. J. Acoust. Soc. Am. 2004, 116, 2527. [Google Scholar] [CrossRef]
- Galinde, A.; Donabed, N.; Andrews, M.; Lee, S.; Makris, N.C.; Ratilal, P. Range-dependent waveguide scattering model calibrated for bottom reverberation in a continental shelf environment. J. Acoust. Soc. Am. 2008, 123, 1270–1281. [Google Scholar] [CrossRef] [PubMed]
- Andrews, M.; Gong, Z.; Ratilal, P. High resolution population density imaging of random scatterers with the matched filtered scattered field variance. J. Acoust. Soc. Am. 2009, 126, 1057–1068. [Google Scholar] [CrossRef]
- Fournier, A.; Fussell, D.; Carpenter, L. Computer rendering of stochastic models. Commun. ACM 1982, 25, 371–384. [Google Scholar] [CrossRef]
- Cho, S.J.; Ji, S.W.; Hong, J.P.; Jung, S.W.; Ko, S.J. Rethinking coarse-to-fine approach in single image deblurring. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 4641–4650. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).