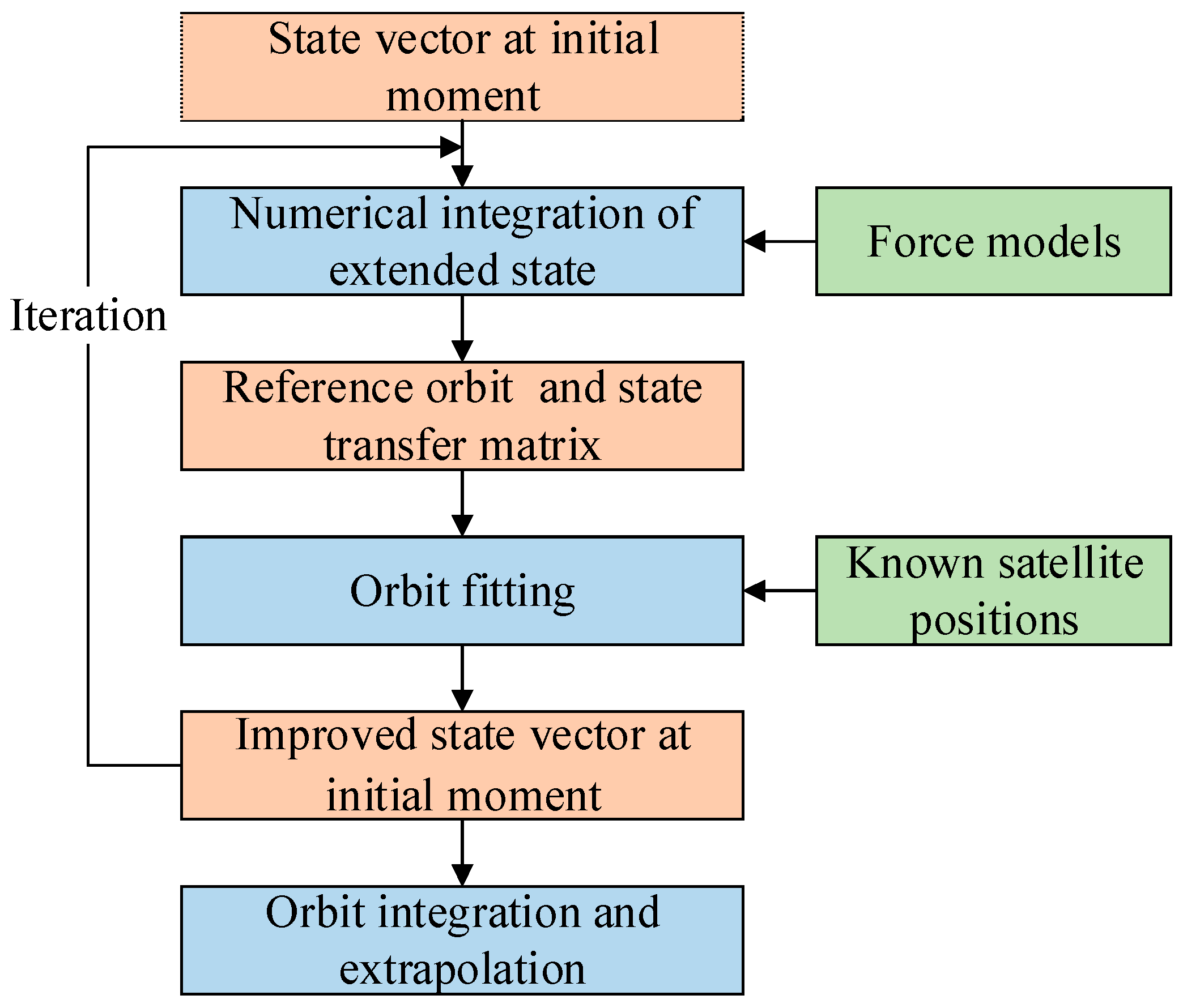
This section presents and analyzes the experimental results of orbit fitting and orbit extrapolation. By comparing the performances of different strategies, the effectiveness of calculating satellite velocity and acceleration by orbit fitting and orbit integration is verified.
5.1. Orbit Fitting Results
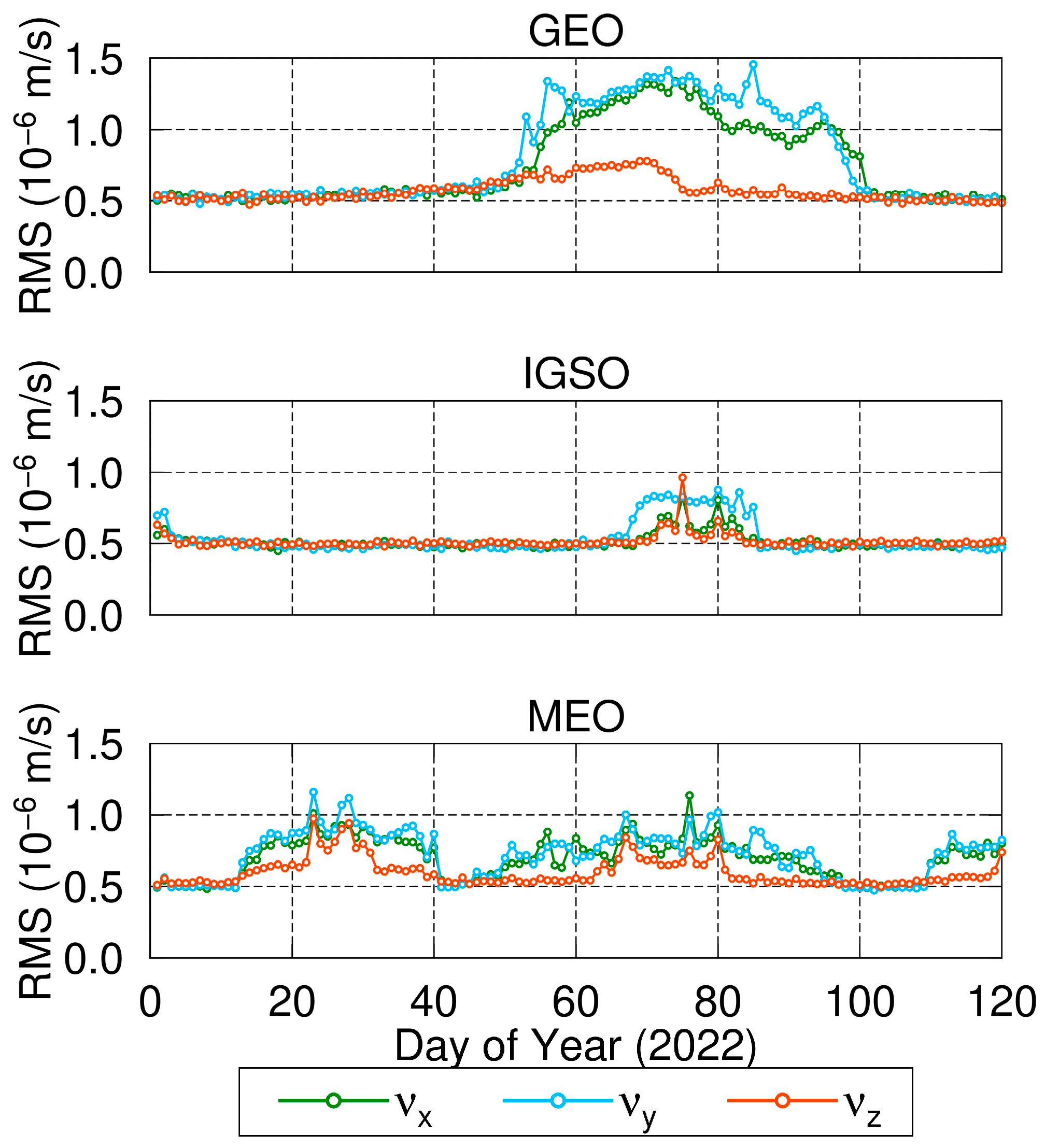
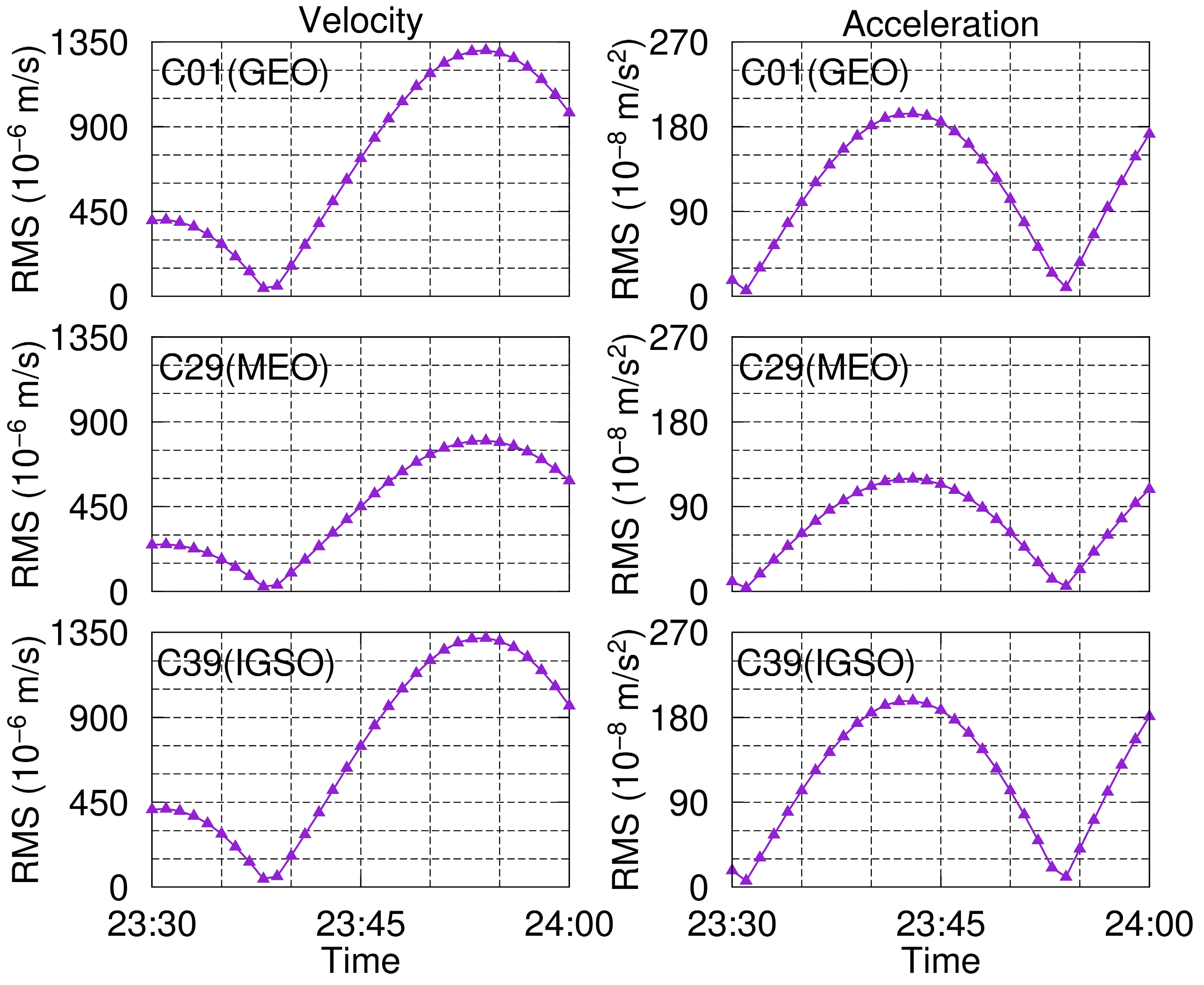
Figure 2 and
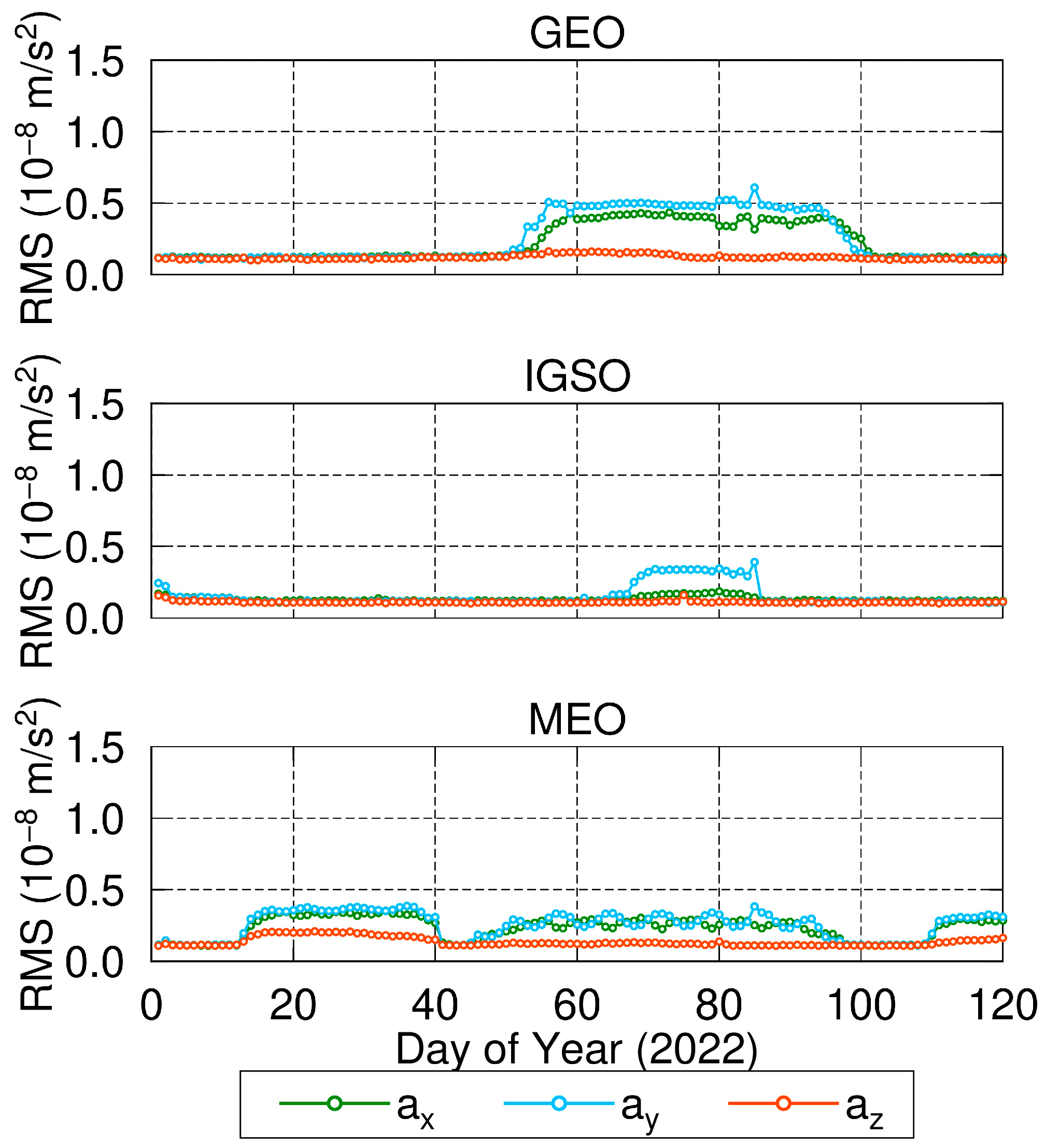
Figure 3 show the single-day root mean square (RMS) of satellite velocities and accelerations calculated by utilizing orbit fitting and orbit integration, respectively. The results were further classified according to GEO, IGSO, and MEO. As can be seen from
Figure 2, the satellite velocity discrepancy calculated by utilizing orbit integration and sliding window Lagrange interpolation is small, and each component of the three types of satellites is less than 1.5 × 10
−6 m/s. Furthermore, the calculation accuracy fluctuates between different days. This is mainly caused by the satellite orbit accuracy of that day, the corresponding orbit fitting accuracy and the transformation accuracy between ECI and ECEF.
From
Figure 3, it can be seen that the acceleration accuracy of each component for GEO satellites is less than 1.0 × 10
−8 m/s
2, and the corresponding accuracies for IGSO and MEO satellites are less than 0.5 × 10
−8 m/s
2. Therefore, the satellite velocity and acceleration calculated by the orbit fitting and orbit integration methods in this study have a high accuracy and can meet the requirements of high-precision applications.
To verify the correctness and accuracy of the transformation relationship between ECI and ECEF for satellite velocity and acceleration in this study, the multi-day average RMS for satellite velocity and acceleration calculated utilizing the approximate transformation model and the transformation model are as presented in
Table 2 and
Table 3, respectively. For comparison,
Table 4 shows the calculation accuracy when the first-order and second-order derivatives of
,
, and
are ignored in the new transformation model. In this case, the mathematical interpolation operation for the above three items is not required when calculating the transformation matrix.
As can be seen from
Table 2 and
Table 3, the satellite velocity accuracy calculated utilizing the ECI and ECEF transformation model in this study is greatly improved compared with that of the approximate transformation model. Except for the
and
components of the GEO satellites, which are improved by about 70%, and the other satellites, the enhancement of each component is by almost close to or more than one order of magnitude. The accuracy of satellite acceleration calculated utilizing different transformation models varies greatly, and for the
components, the model in this study improves the accuracy by one order of magnitude compared with the approximate model. For the
and
components, the computational error of the approximate model is large and reaches the 10
−2 m/s
2 level, while the computational error was reduced to the 10
−9 m/s
2 level when the transformation model in this study was adopted. This result is mainly caused by the neglect of the first- and second-order derivatives of the Earth rotation matrix, namely
and
. Furthermore, due to the Earth’s rotation around the Z-axis, neglecting the above two items mainly affects the x and y components. As a result, the acceleration of the x and y components in
Table 2 is much larger than that of the z component.
As can be seen from
Table 3 and
Table 4, when the first and second order derivatives of
,
, and
are neglected, the calculated satellite velocity and acceleration accuracy is lower than that of the rigorous transformation model in this study. Among them, the accuracies of the GEO satellite
and
components are reduced by about four times, and the accuracies of the
components and the velocities of the IGSO and MEO satellites are reduced by at least one order of magnitude. For the acceleration accuracies, except for the GEO
and
components, which are basically unchanged, the
component and IGSO and MEO accuracies are reduced by a factor of about three. However, since the mathematical interpolation operation is avoided by neglecting the three first- and second-order derivatives, the above simplified model can also be utilized when meeting the accuracy requirements of practical applications.
In addition, in order to improve the orbit fitting accuracy, the segmented velocity pulse was added in this study. To analyze whether the inclusion of the velocity pulse helps to improve the calculation accuracy of satellite velocity and acceleration, the multi-day average RMS values of the satellite velocity and acceleration for the non-eclipse seasons [
33] and the eclipse seasons were calculated utilizing the transformation model of this study, and the results are presented in
Table 5 and
Table 6, respectively.
As can be seen from
Table 5 and
Table 6, the multi-day average RMS in the non- eclipse season is lower than that in the eclipse season, and the satellite velocity accuracy measured by utilizing the segmented velocity pulse is greatly improved compared to that without the velocity pulse, especially for the GEO satellites and the IGSO satellites in the eclipse season. Therefore, the inclusion of the velocity pulse parameter should be considered in practical applications. However, the addition of the velocity pulse does not improve the acceleration accuracy significantly. This may be because small changes in satellite position and velocity have little effect on acceleration calculations.
5.2. Orbit Extrapolation Results
In order to avoid the edge effect of Lagrange interpolation, the precise ephemeris from 00:00 to 22:45 for each day is utilized for orbit fitting and then extrapolated for 15 min with orbit integration to calculate the satellite velocity and acceleration between 22:45 and 23:00. The initial moment of orbit integration is chosen to be 00:00. Since the extrapolation time period is far away from the edge of the interpolation arc at 21:15~23:45, the satellite velocity and acceleration can still be calculated reliably utilizing Lagrange interpolation, and the interpolation result can be utilized as a reference to evaluate the extrapolation accuracy of orbit integration. Meanwhile, the extrapolation results from the orbit integration are compared with the extrapolation results from the Lagrange fitting, which is different from using the Lagrange interpolation as a reference. The specific orbit extrapolation experiment scheme is shown in
Figure 4.
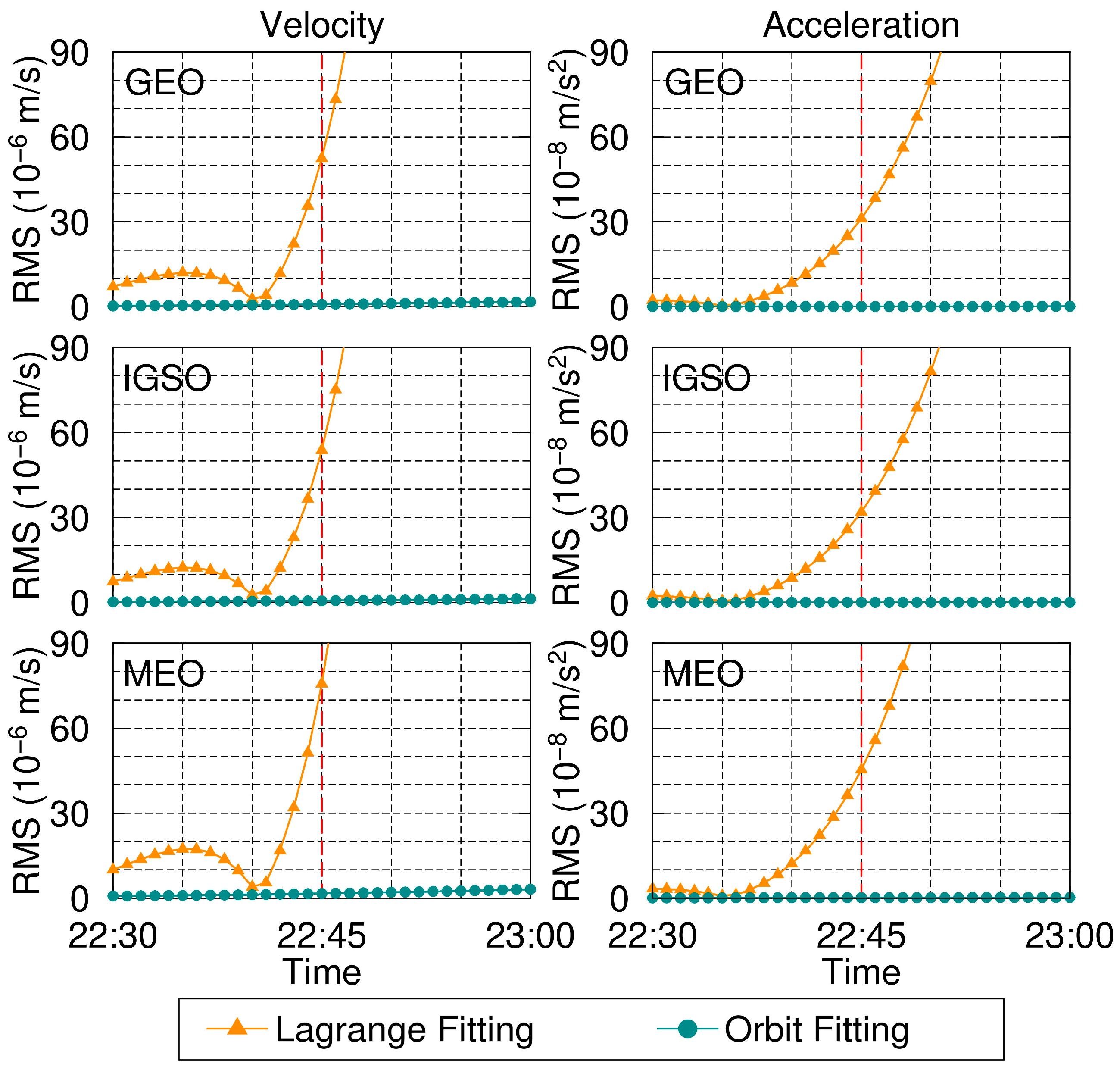
Figure 5 shows the 3D RMS of the satellite velocity and acceleration extrapolated utilizing orbit fitting and Lagrange fitting, respectively. It can be clearly seen that the satellite velocity and acceleration calculated by utilizing Lagrange fitting are affected by the edge effect, and the interpolation error increases earlier than in the interpolation of satellite positions [
16,
17]. Furthermore, the satellite velocity and acceleration error extrapolated utilizing Lagrange fitting is large compared to orbit fitting. As shown in
Table 7, the 15 min extrapolation error for velocity can reach 1~2 mm/s, and the acceleration error can reach 10
−6 m/s
2. By contrast, the extrapolation accuracy of orbit integration is high, and there is no significant increase in errors within 15 min for both satellite velocity and acceleration. Therefore, by utilizing orbit fitting, orbit integration, and orbit extrapolation, high-precision satellite velocities and accelerations can be obtained, albeit near the day boundary.
Considering the high extrapolation accuracy of orbit fitting and orbit integration methods, we take the result as a reference to further demonstrate the effect of day boundary discontinuity on the satellite velocity and acceleration interpolated utilizing the Lagrange interpolation method. The experimental scheme is shown in
Figure 6. As shown in the figure, the precise ephemeris of the adjacent day is combined for the Lagrange interpolation.
Figure 7 presents the experimental results. It is clearly shown that the day-boundary discontinuity affects the accuracy of interpolating velocity and acceleration for GEO, IGSO, and MEO satellites. These results further demonstrate that utilizing the Lagrange interpolation method by means of combining the adjacent ephemeris cannot obtain high-precision satellite velocity and acceleration near the day boundary.