A Two-Step Phase Compensation-Based Imaging Method for GNSS-Based Bistatic SAR: Extraction and Compensation of Ionospheric Phase Scintillation
Abstract
1. Introduction
- Two-Step Azimuth Phase Compensation Method: To address the issue of atmospheric disturbances in GNSS-BSAR systems during long-time observations, this paper proposes a two-step azimuth phase compensation method. This strategy decomposes the azimuth phase of the imaging channel into difference and reference phases. Through phase compensation, Doppler phase errors are eliminated, and the processing results of actual data demonstrate that the proposed method achieves precise focusing in GNSS-BSAR imaging.
- Novel Processing Mode: Unlike traditional autofocus-based error compensation algorithms, which have limitations requiring strong prominent points in the observation scene, multiple iterations for convergence, and limited capability for high-order phase error compensation, the proposed method utilizes the dual-channel receiving characteristic. It introduces a novel processing mode that directly uses the phase information extracted from the reference channel for error analysis and phase compensation, avoiding the practical challenges encountered by autofocus algorithms.
- Potential for Ionospheric-Related Studies: By extracting ionospheric phase scintillation at different times of the day, this work preliminarily illustrates the potential of this technology for ionospheric-related studies. Moreover, the proposed method can also be adapted to other passive SAR imaging systems based on dual-channel receiving modes, demonstrating a certain level of versatility.
2. System Model and Atmospheric Error Analysis
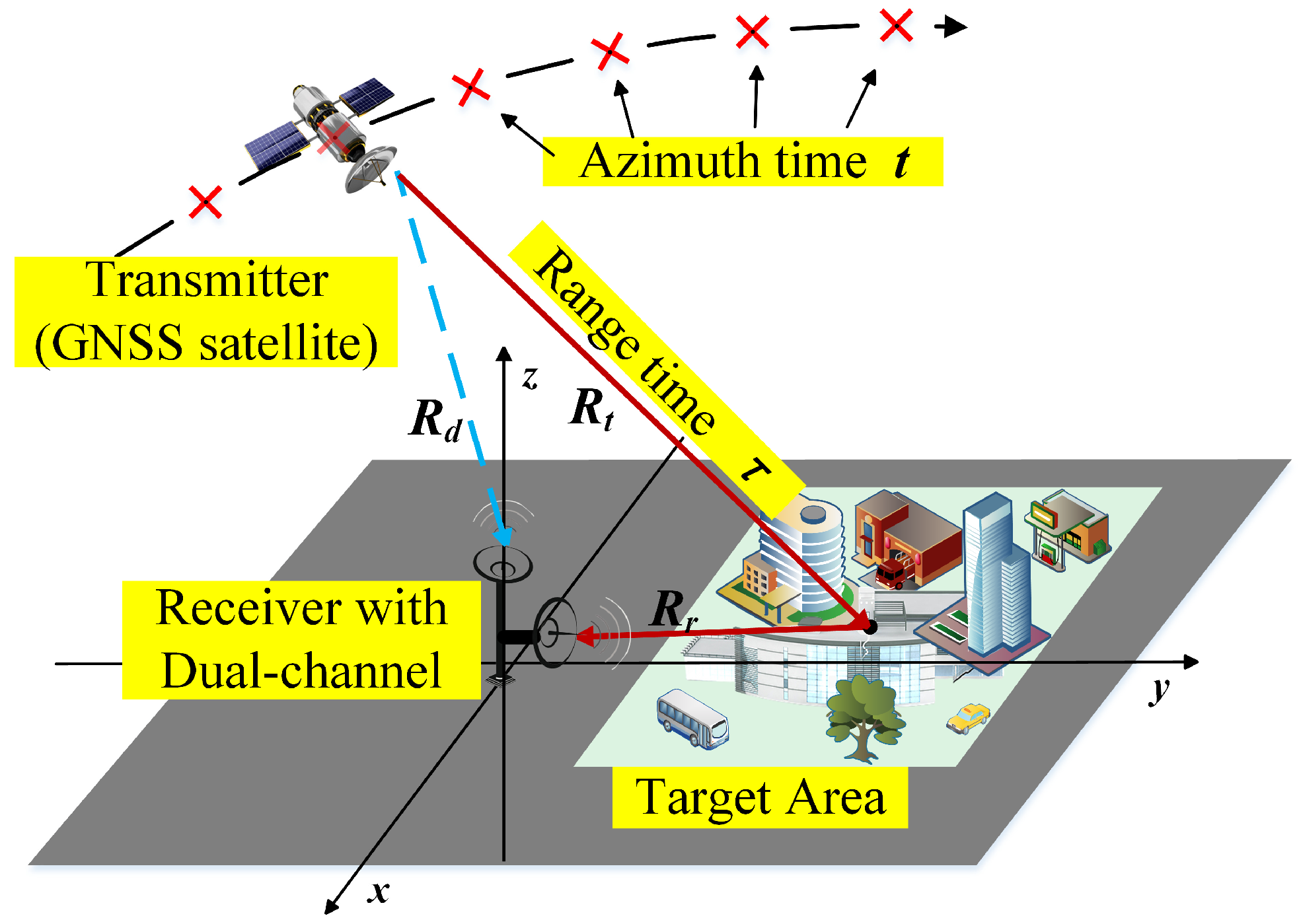
2.1. System Configuration
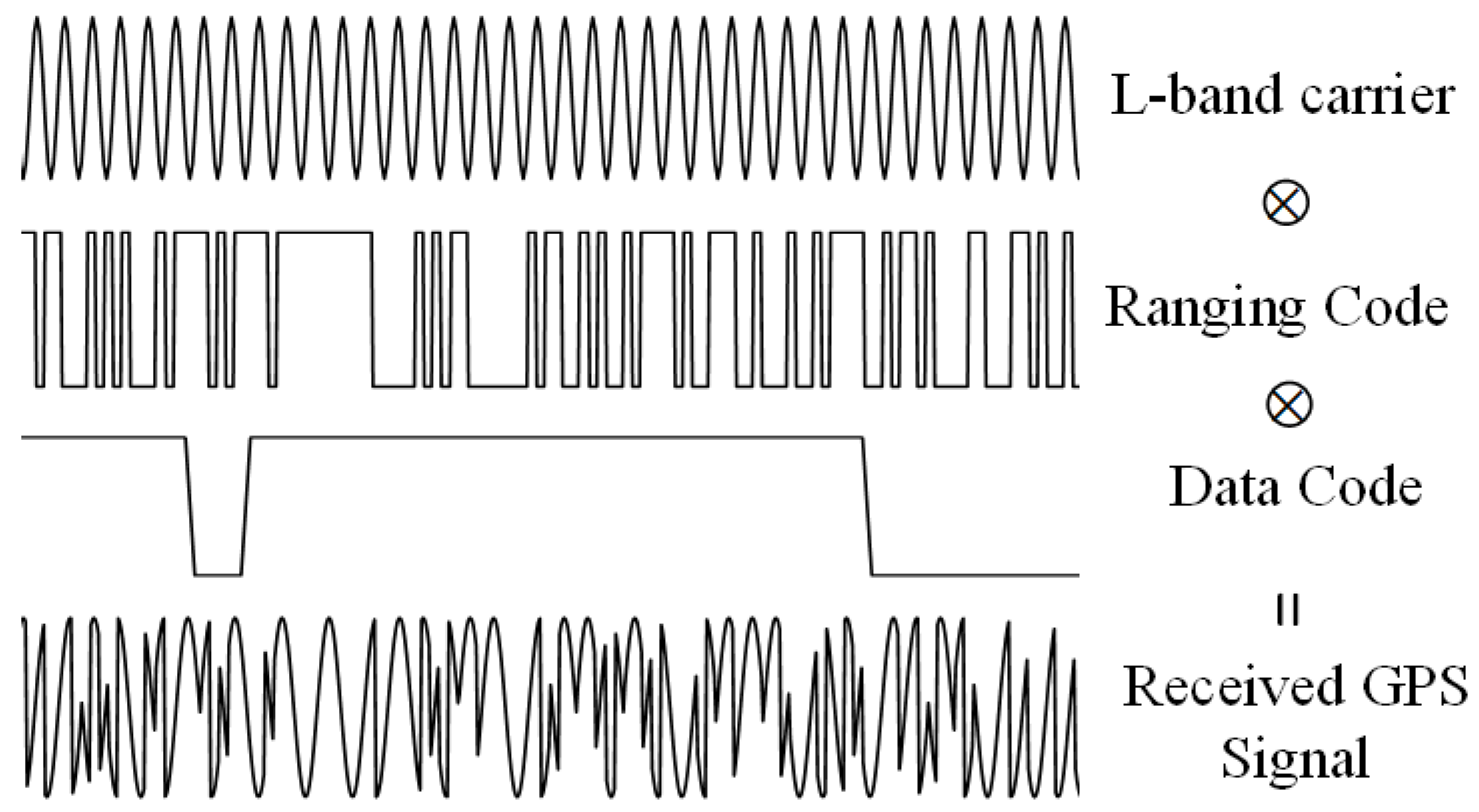
2.2. Signal Model of the GNSS-BSAR System
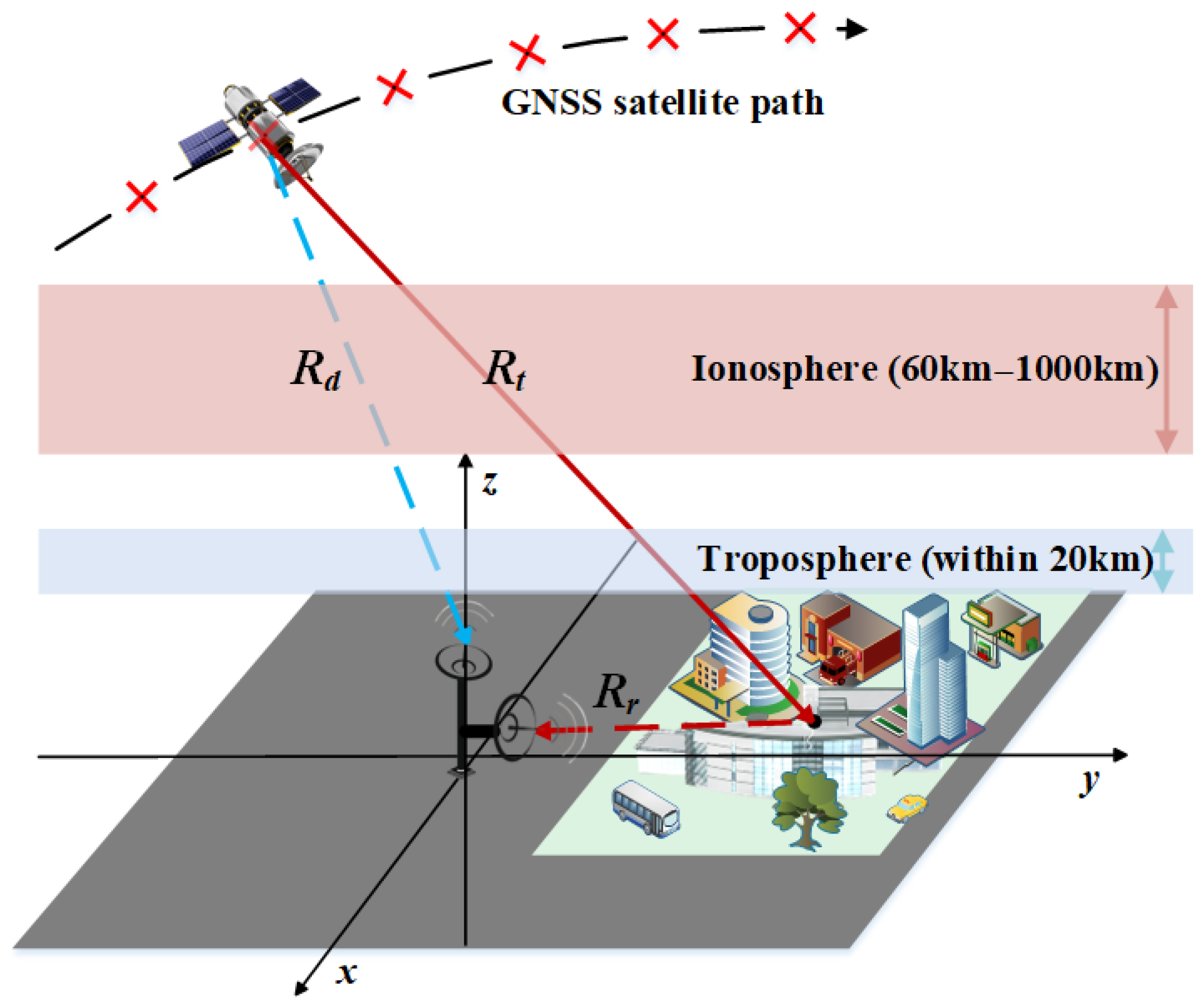
2.3. Analysis of Ionospheric Effects on GNSS-BSAR Imaging
- The atmosphere on the Earth’s surface is mainly divided into the troposphere and the ionosphere. In the studied GNSS-BSAR system, combining the signal and system characteristics, only the ionospheric effect is considered.
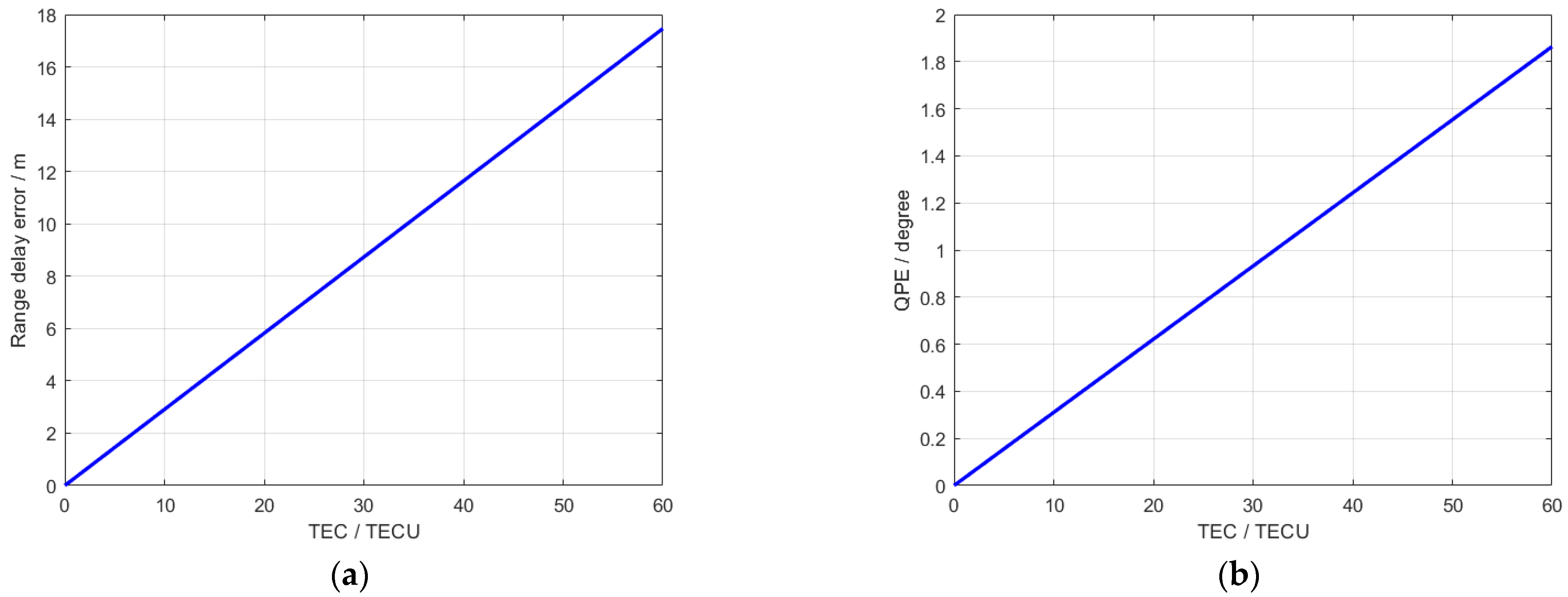
- The ionospheric dispersion effect is caused by the background ionosphere, which causes delays and pulse width changes in the range dimension of the echo, resulting in range delay error. Due to the limitation of GNSS signal resolution, the impact of this error can be negligible.
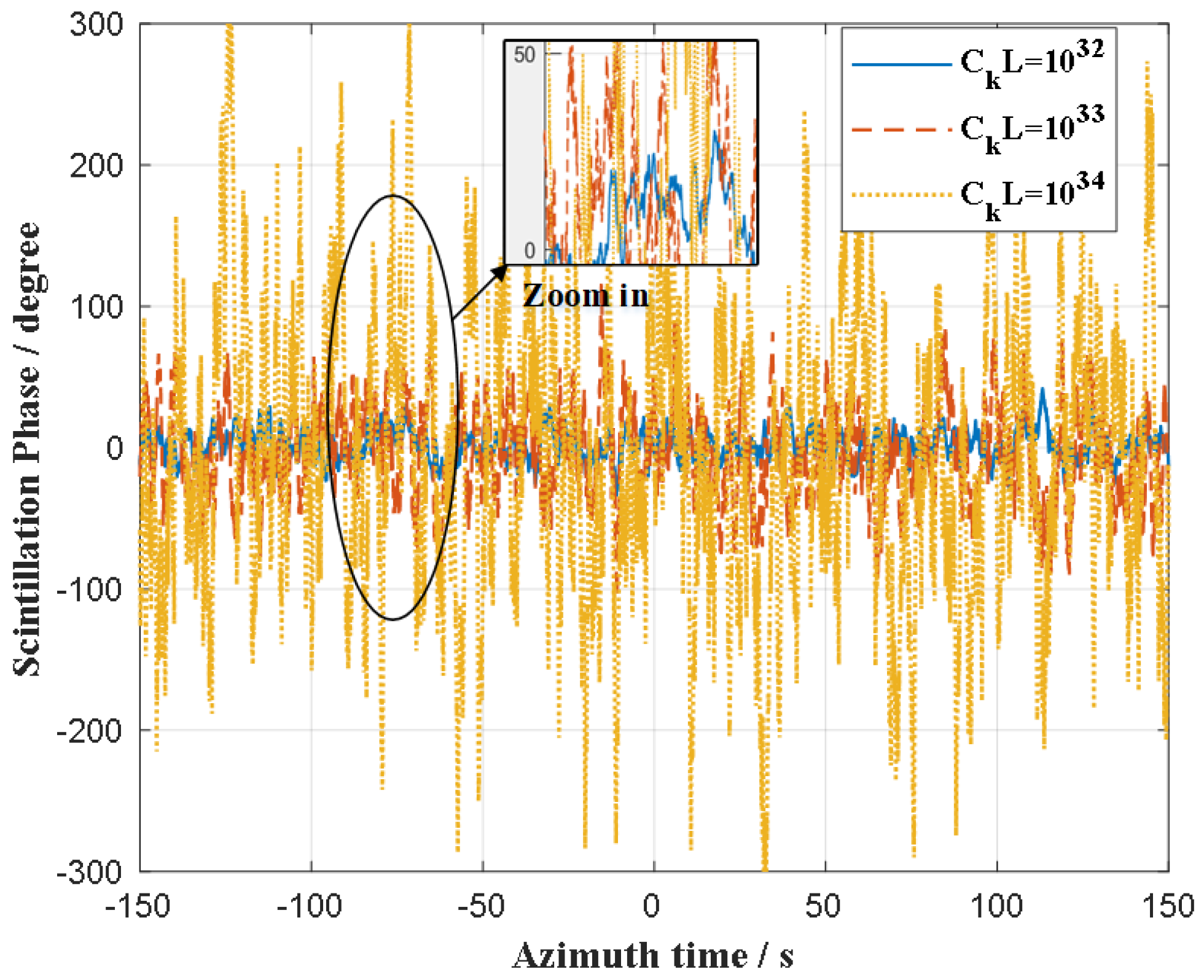
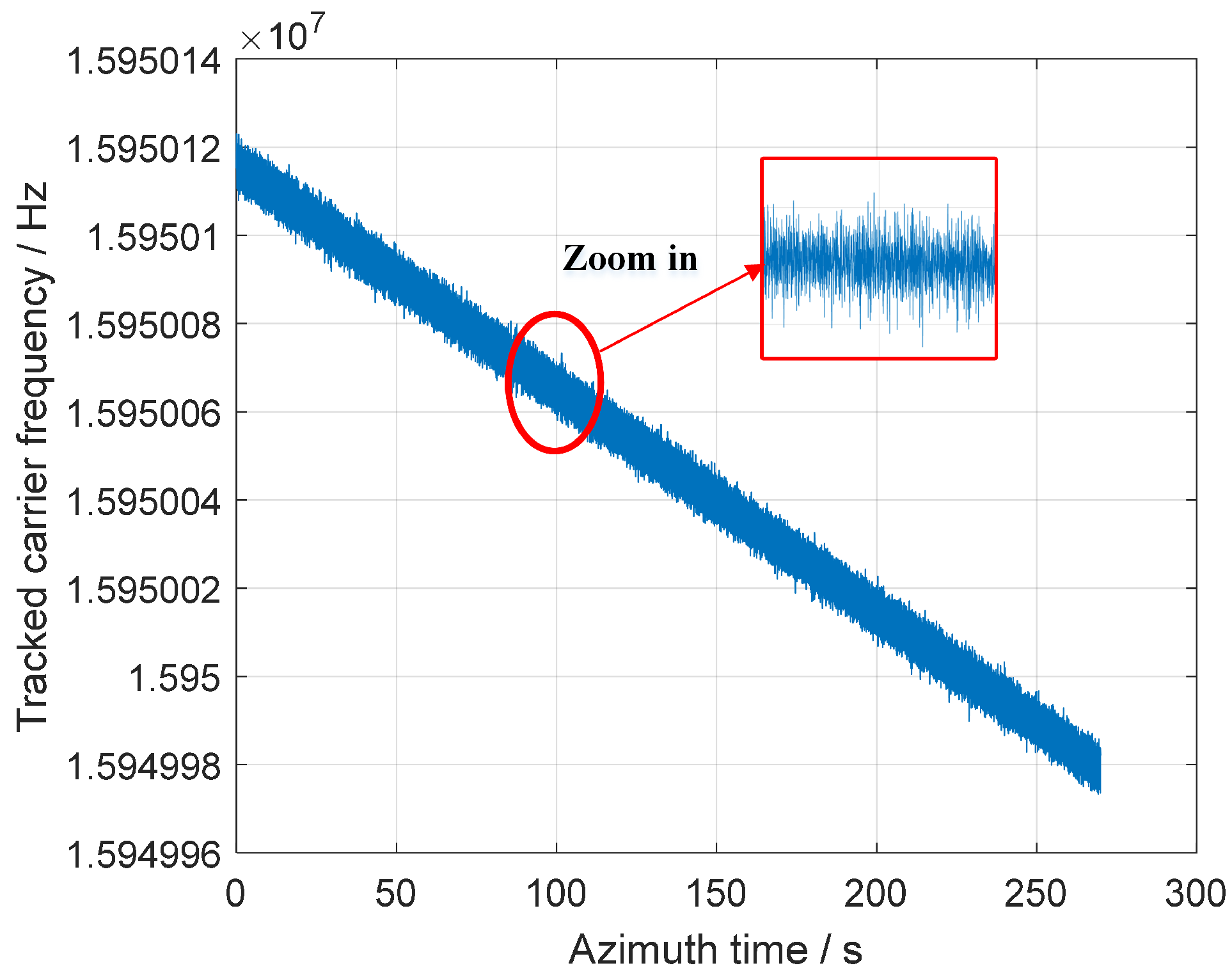
- The ionospheric scintillation effect will introduce random phase errors in the azimuth direction, thereby affecting the azimuth focusing and causing an overall increase in the side lobe level. The greater the intensity of the scintillation is, the worse the SAR image quality is. In next Section 3, the proposed ionospheric scintillation error extraction and compensation method based on the reference channel will be introduced in detail.
3. The Ionospheric Scintillation Compensation-Based Modified BP Imaging Method
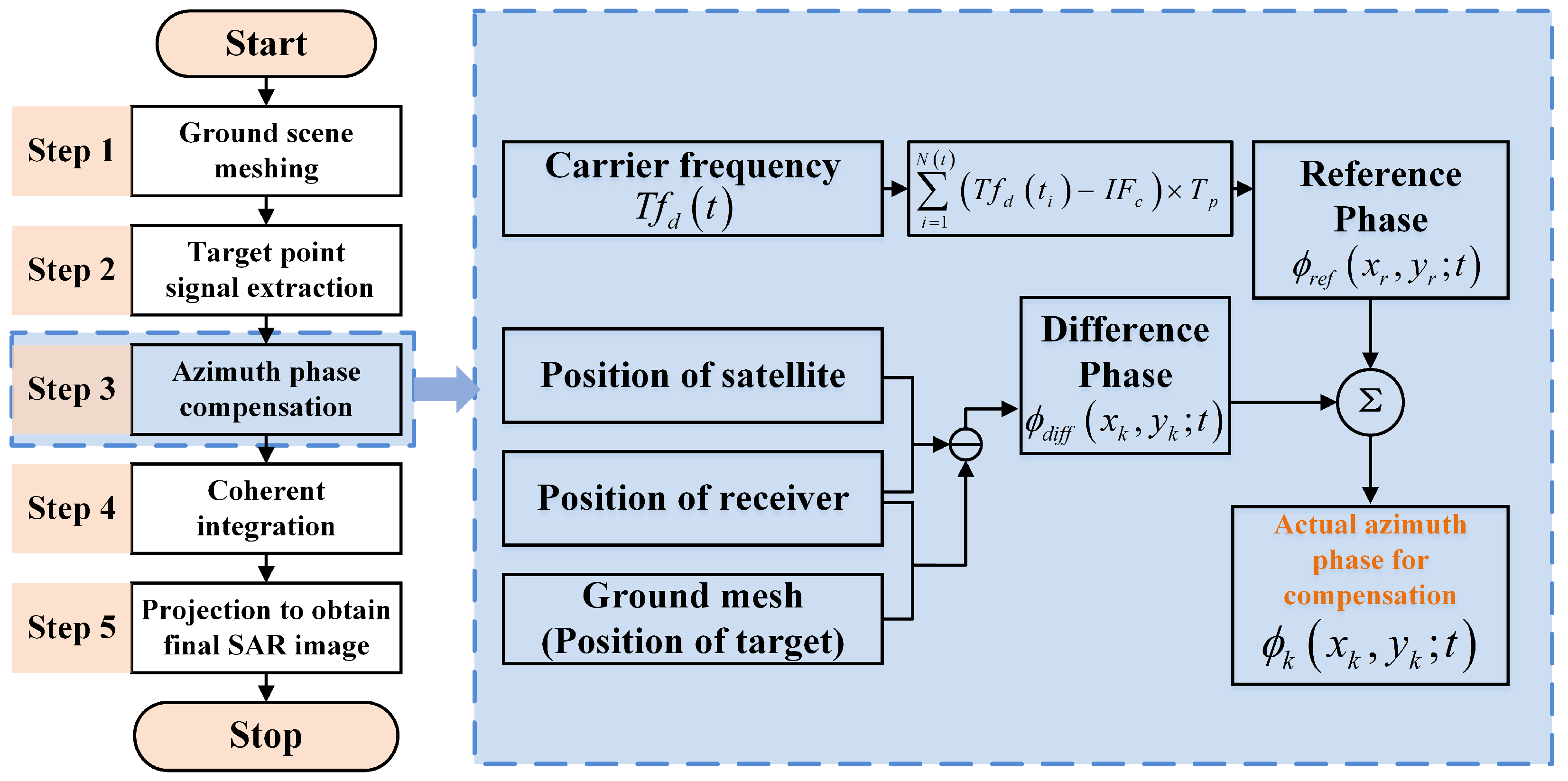
3.1. Basic Process and Analysis of BP Imaging Algorithm
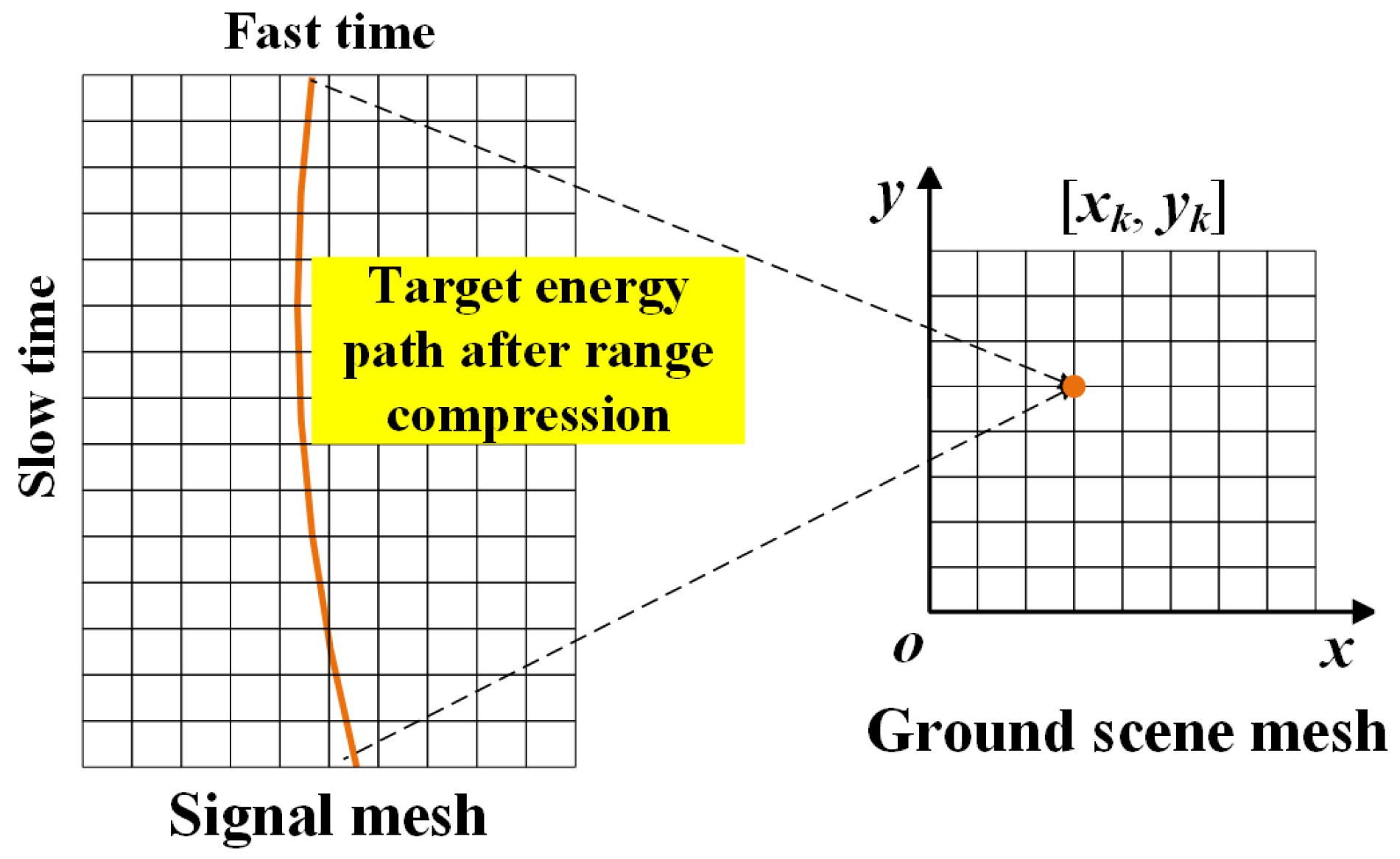
- The imaging area is divided into a two-dimensional ground mesh, where x and y are the two-dimensional coordinates corresponding to the grid points respectively. And the ground grid spacing and should be smaller than the imaging resolution in the corresponding directions.
- For a certain pixel point on the ground mesh, the range migration trajectory of the point is calculated according to its coordinate value and the positions of the GNSS transmitter and receiver. And then the energy of the target echo along the trajectory can be extracted. Finally, the azimuth-dimensional signal can be recombined.
- Based on the coordinate value and the positions of the transmitter and receiver, Doppler phase history of the grid point can also be calculated. The azimuth phase compensation is operated on the one-dimensional signal , that is, multiply it by the complex conjugate of the Doppler phase of the target echo at that point, eliminate its azimuth phase modulation.
- Accumulate the one-dimensional signal along the azimuth direction to obtain the coherent integrated energy of the target echo at that ground grid point and assign the integration result to .
- Traverse all points on the ground mesh and repeat the above steps 2–4 to obtain the final SAR image projected onto the ground.
3.2. The Proposed Modified BP Imaging Algorithm
3.2.1. Ionospheric Scintillation Error Extraction Based on Reference Channel Processing
3.2.2. The Two-Step Azimuth Phase Compensation-Based Modified BP Imaging Algorithm
4. Experimental Results
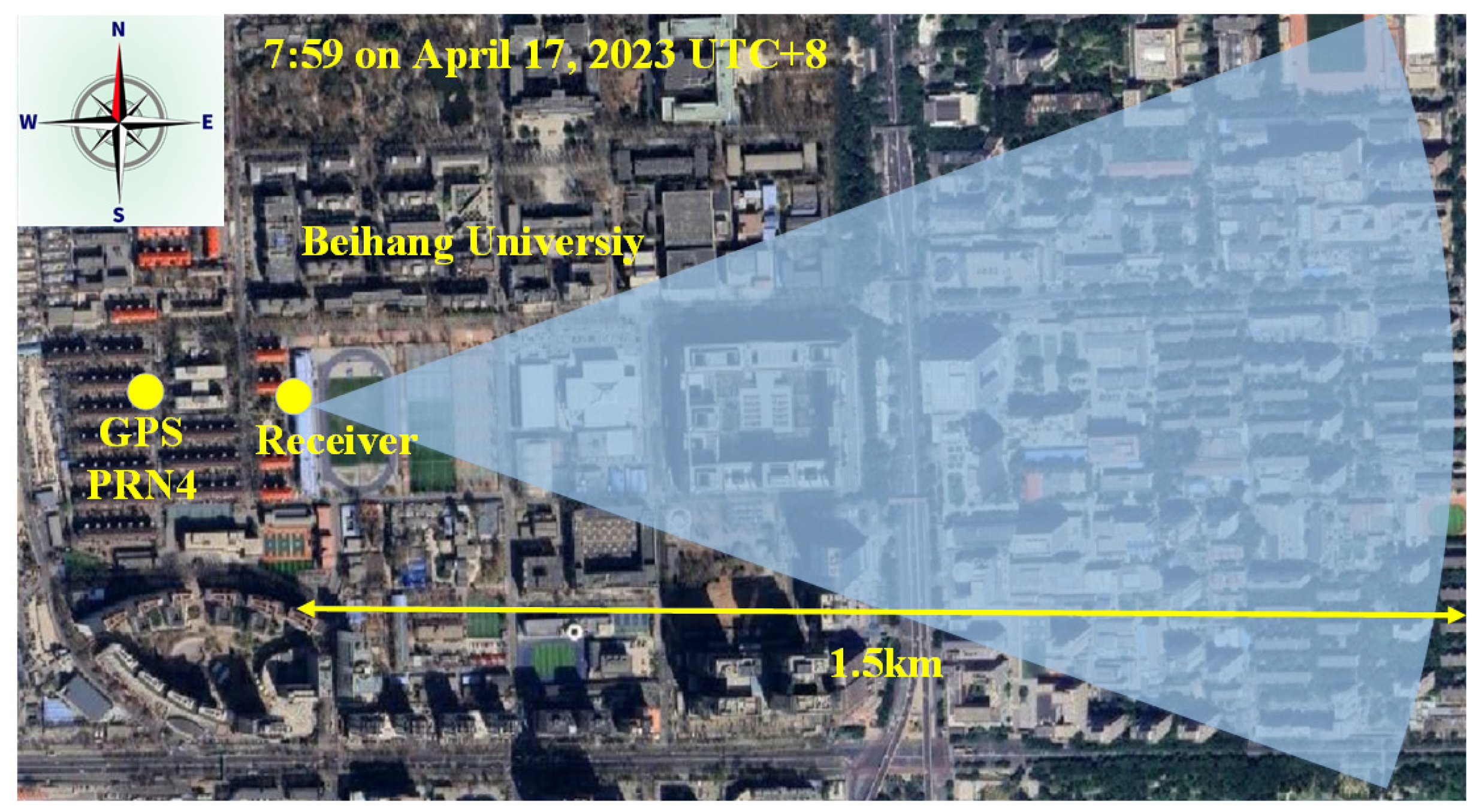
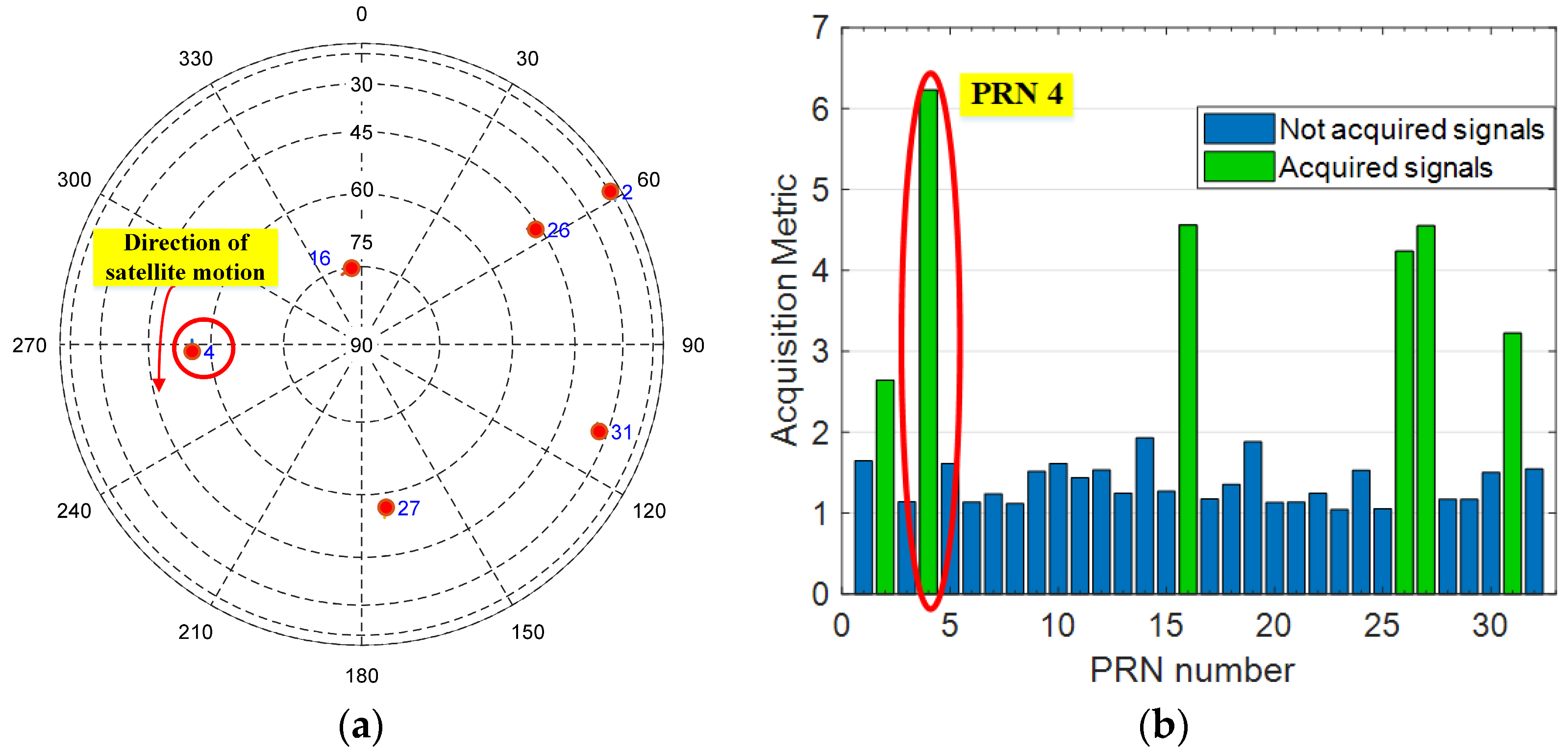
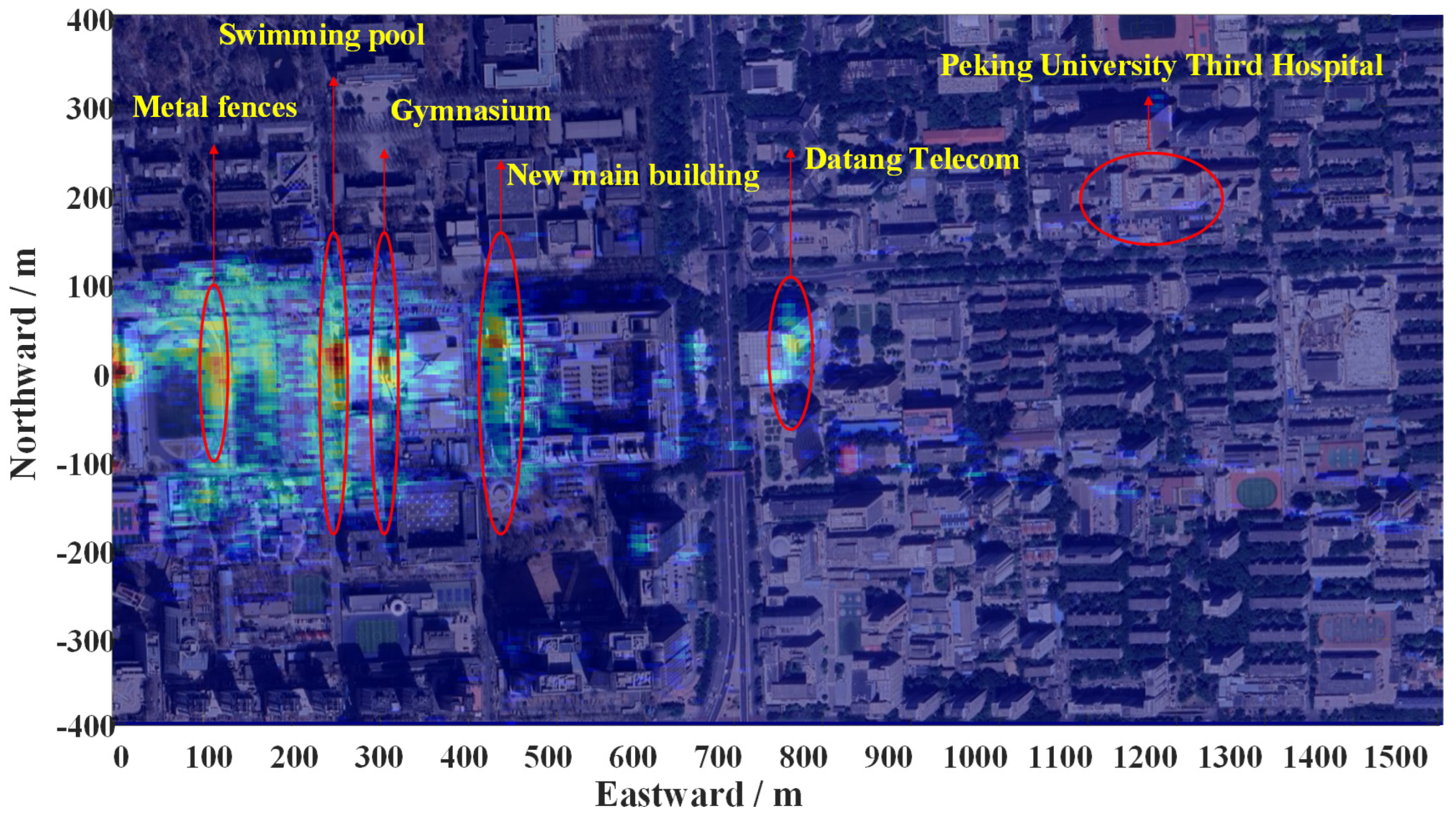
4.1. Experimental Setup
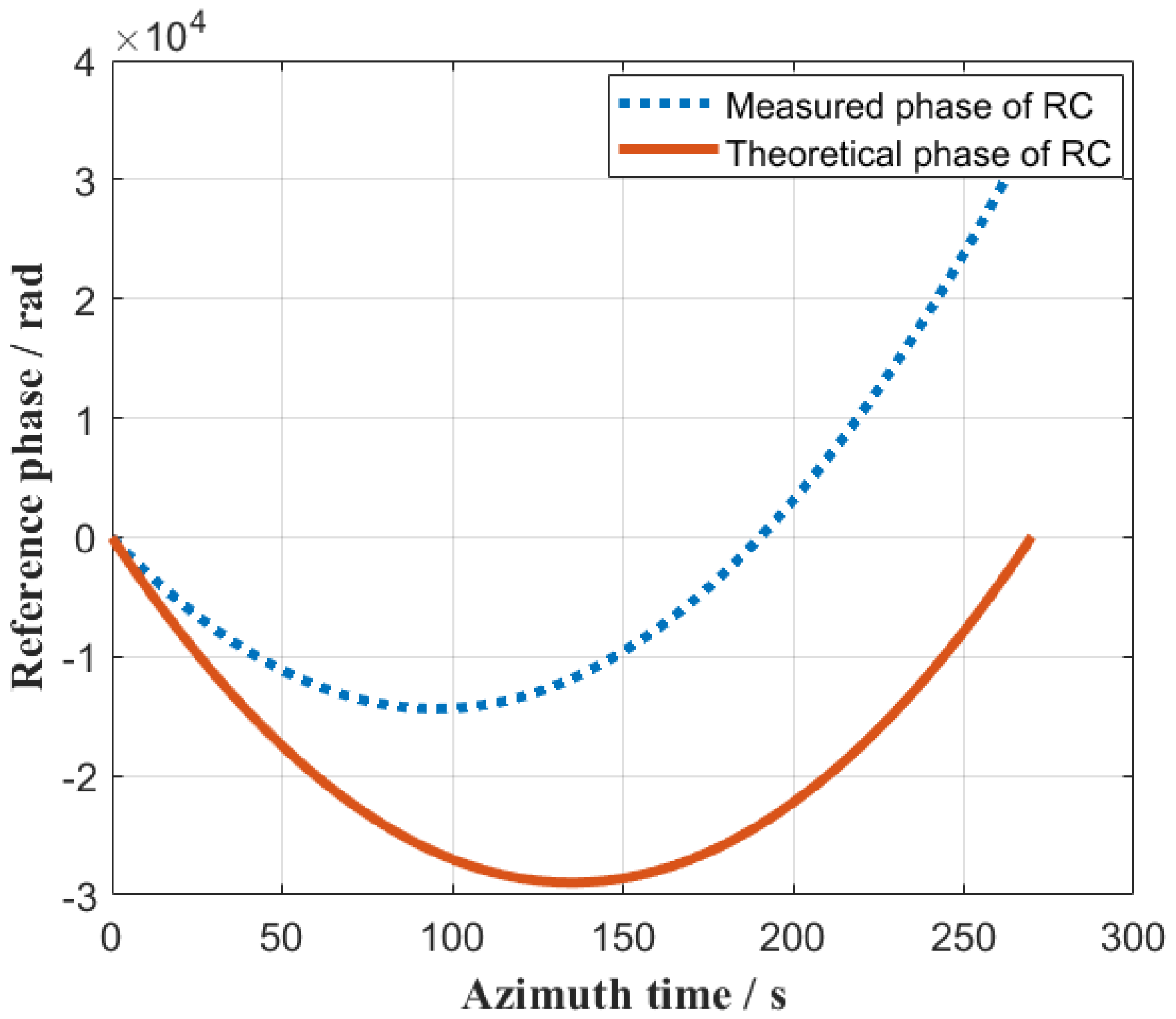
4.2. Reference Channel Processing Results
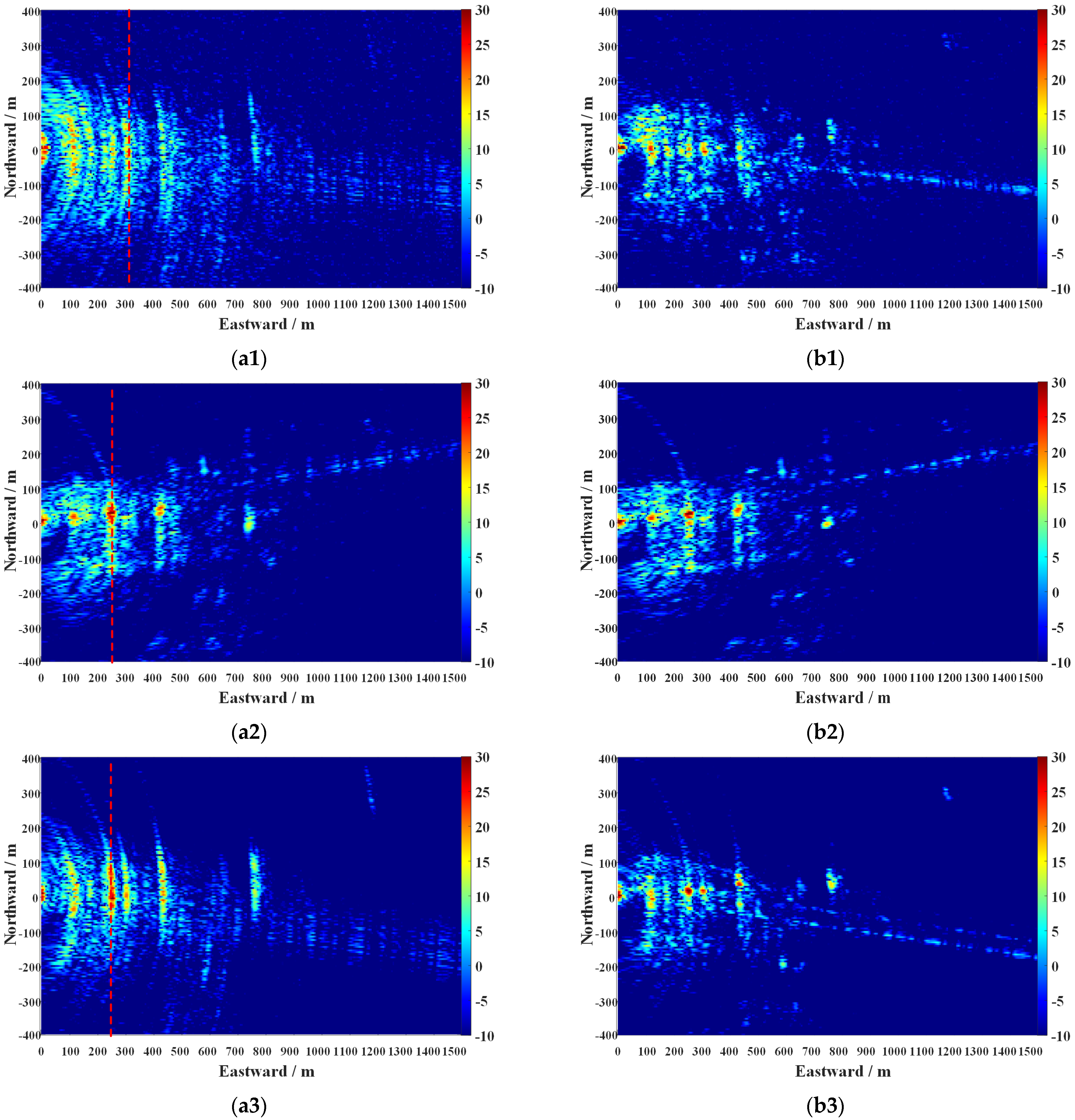
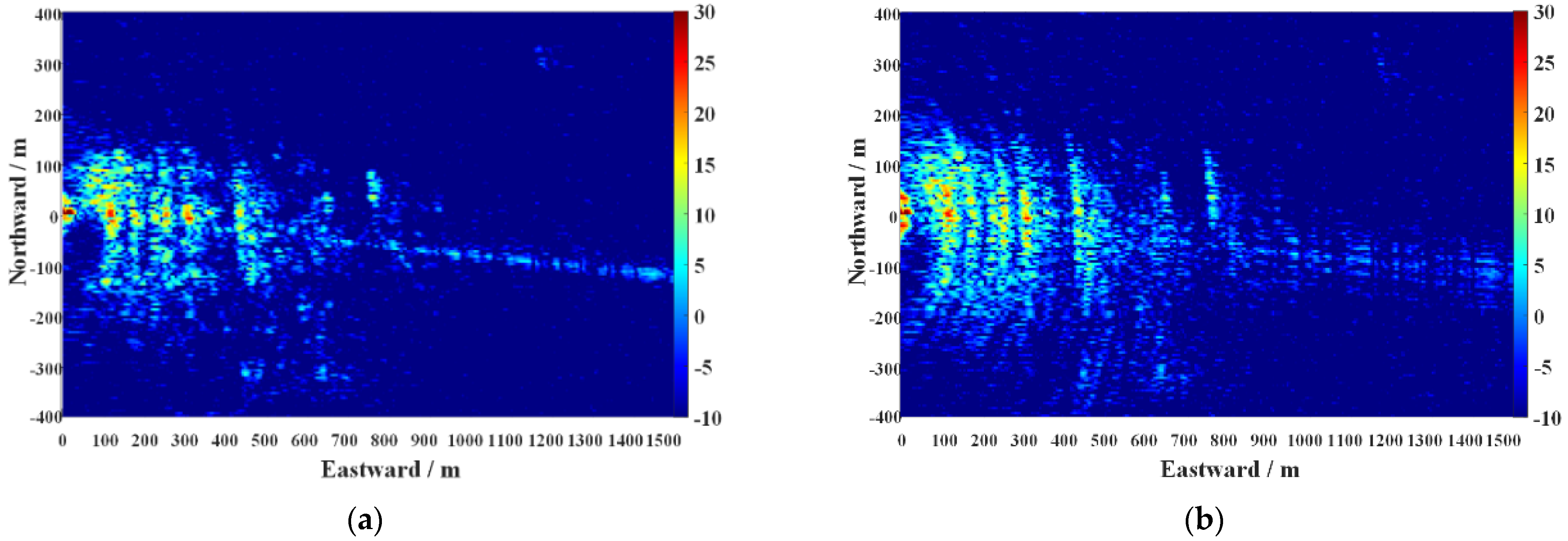
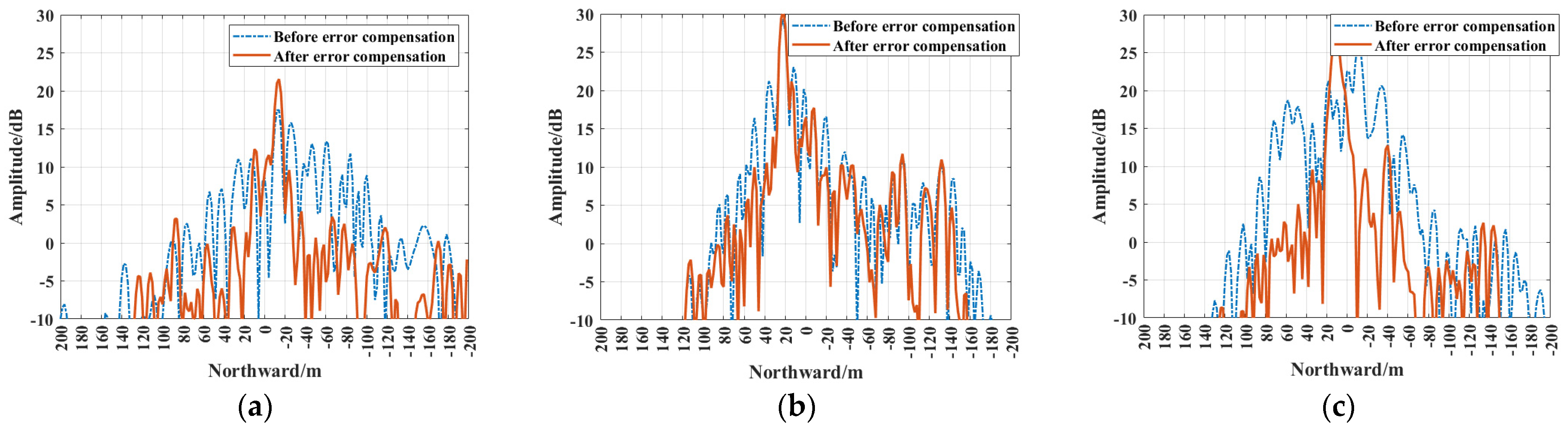
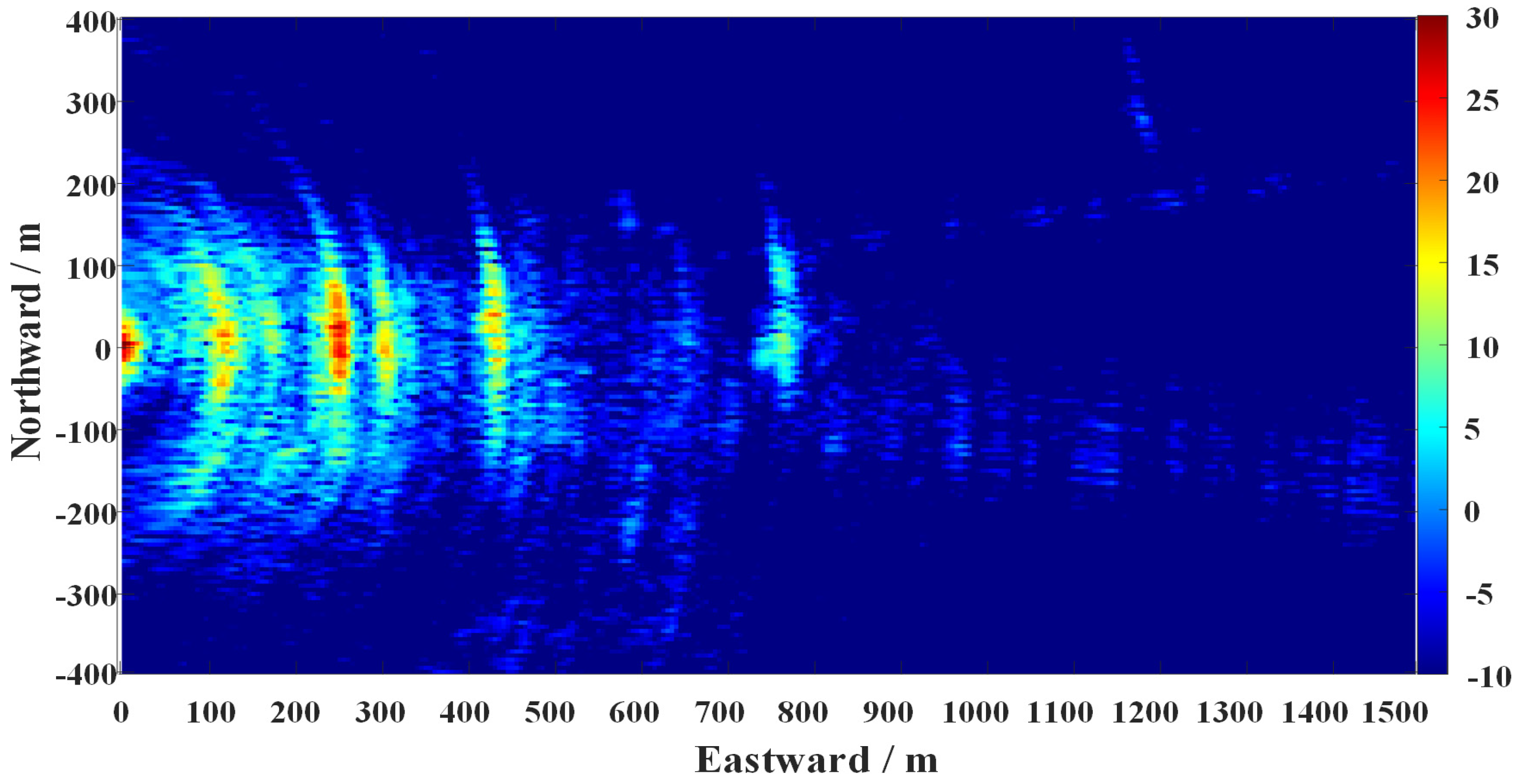
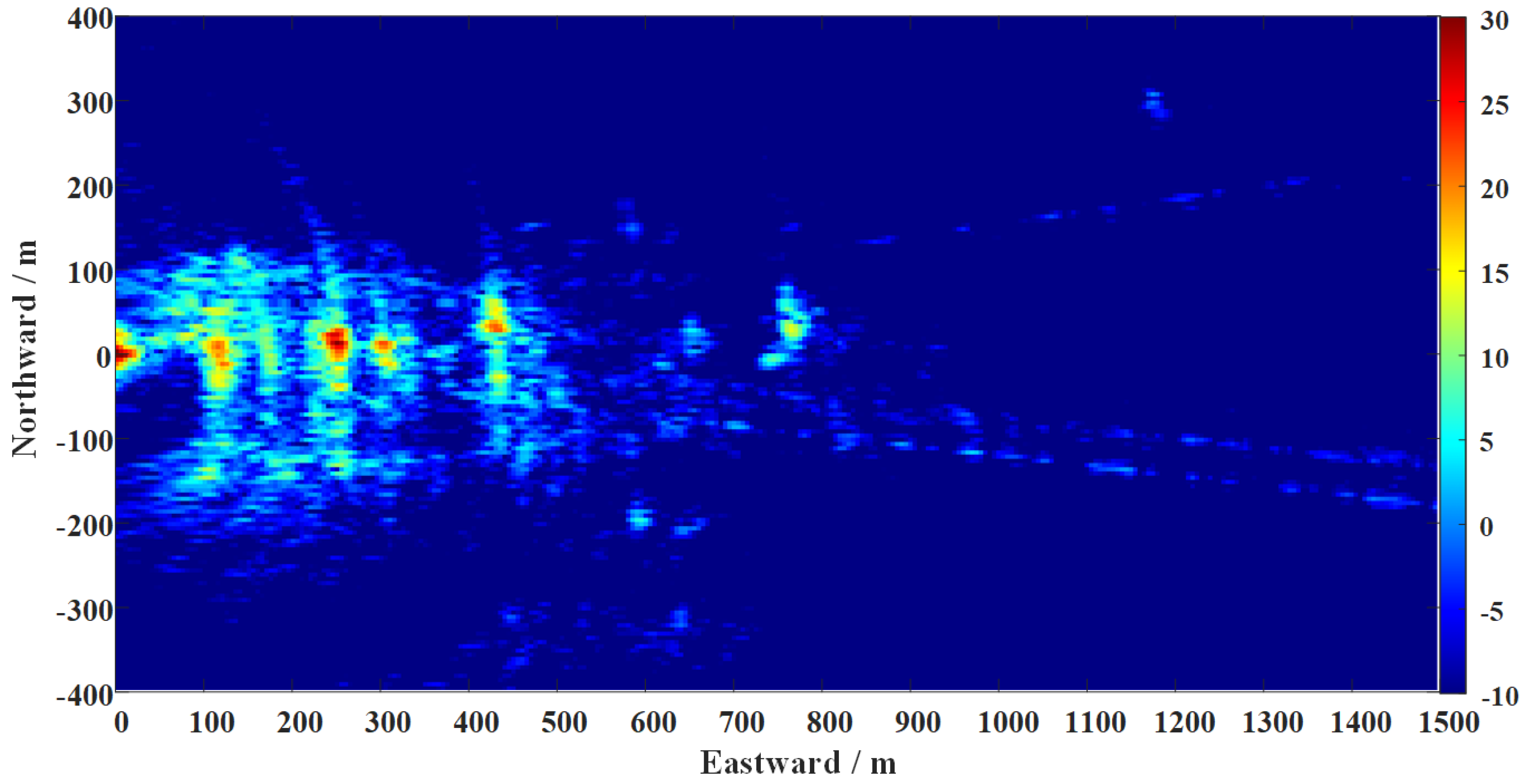
4.3. Imaging Channel Processing Results
5. Discussion
5.1. Performance Analysis of the Proposed Method
5.1.1. Comparative Analysis with Phase Gradient Autofocus (PGA)
5.1.2. Computational Complexity Analysis
5.2. Imaging Performance Evaluation
5.3. Limitaitons and Future Work
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Moreira, A.; Prats-Iraola, P.; Younis, M.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.P. A Tutorial on Synthetic Aperture Radar. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–43. [Google Scholar] [CrossRef]
- Wang, Y.; Min, R.; Li, L.; Ding, Z. High-Squint High-Frame-Rate Uniform-Resolution Video SAR: Parameter Design and Fast Imaging. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 9160–9176. [Google Scholar] [CrossRef]
- Koch, V.; Westphal, R. New Approach to a Multistatic Passive Radar Sensor for Air/Space Defense. IEEE Aerosp. Electron. Syst. Mag. 1995, 10, 24–32. [Google Scholar] [CrossRef]
- Glennon, E.; Dempster, A.; Rizos, C. Feasibility of Air Target Detection Using GPS as a Bistatic Radar. In 2005 International Symposium on GPS/GNSS; UNSW Library: Sydney, Australia, 2005. [Google Scholar]
- Ma, H.; Antoniou, M.; Cherniakov, M. Passive GNSS-Based SAR Resolution Improvement Using Joint Galileo E5 Signals. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1640–1644. [Google Scholar] [CrossRef]
- Santi, F.; Antoniou, M.; Pastina, D. Point Spread Function Analysis for GNSS-Based Multistatic SAR. IEEE Geosci. Remote Sens. Lett. 2015, 12, 304–308. [Google Scholar] [CrossRef]
- Zeng, T.; Liu, F.; Antoniou, M.; Cherniakov, M. GNSS-Based BiSAR Imaging Using Modified Range Migration Algorithm. Sci. China Inf. Sci. 2015, 58, 1–13. [Google Scholar] [CrossRef]
- Zhou, X.-K.; Chen, J.; Wang, P.-B.; Zeng, H.-C.; Fang, Y.; Men, Z.-R.; Liu, W. An Efficient Imaging Algorithm for GNSS-R Bi-Static SAR. Remote Sens. 2019, 11, 2945. [Google Scholar] [CrossRef]
- Wu, S.; Xu, Z.; Wang, F.; Yang, D.; Guo, G. An Improved Back-Projection Algorithm for GNSS-R BSAR Imaging Based on CPU and GPU Platform. Remote Sens. 2021, 13, 2107. [Google Scholar] [CrossRef]
- Antoniou, M.; Cherniakov, M. GNSS-Based Bistatic SAR: A Signal Processing View. EURASIP J. Adv. Signal Process. 2013, 2013, 98. [Google Scholar] [CrossRef]
- Antoniou, M.; Zeng, Z.; Feifeng, L.; Cherniakov, M. Experimental Demonstration of Passive BSAR Imaging Using Navigation Satellites and a Fixed Receiver. IEEE Geosci. Remote Sens. Lett. 2012, 9, 477–481. [Google Scholar] [CrossRef]
- Zhang, Q.; Antoniou, M.; Chang, W.; Cherniakov, M. Spatial Decorrelation in GNSS-Based SAR Coherent Change Detection. IEEE Trans. Geosci. Remote Sens. 2015, 53, 219–228. [Google Scholar] [CrossRef]
- Cherniakov, M.; Zeng, T. Passive Bistatic SAR with GNSS Transmitters. In Bistatic Radar: Emerging Technology; Wiley Online Library: Hoboken, NJ, USA, 2008; pp. 339–361. [Google Scholar]
- Liu, F.; Antoniou, M.; Zeng, Z.; Cherniakov, M. Coherent Change Detection Using Passive GNSS-Based BSAR: Experimental Proof of Concept. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4544–4555. [Google Scholar] [CrossRef]
- Ma, H.; Antoniou, M.; Cherniakov, M. Passive GNSS-Based SAR Imaging and Opportunities Using Galileo E5 Signals. Sci. China Inf. Sci. 2015, 58, 062305. [Google Scholar] [CrossRef]
- Zeng, H.-C.; Wang, P.-B.; Chen, J.; Liu, W.; Ge, L.; Yang, W. A Novel General Imaging Formation Algorithm for GNSS-Based Bistatic SAR. Sensors 2016, 16, 294. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.; Fan, X.; Zhang, T.; Liu, Q. GNSS-Based SAR Interferometry for 3-D Deformation Retrieval: Algorithms and Feasibility Study. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5736–5748. [Google Scholar] [CrossRef]
- Huang, C.; Li, Z.; An, H.; Sun, Z.; Wu, J.; Yang, J. Optimal GNSS-Based Passive SAR Large Field-of-View Imaging via Multistatic Configuration: Method and Experimental Validation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 9873–9884. [Google Scholar] [CrossRef]
- Meyer, F.; Bamler, R.; Jakowski, N.; Fritz, T. The Potential of Low-Frequency SAR Systems for Mapping Ionospheric TEC Distributions. IEEE Geosci. Remote Sens. Lett. 2006, 3, 560–564. [Google Scholar] [CrossRef]
- Belcher, D. Theoretical Limits on SAR Imposed by the Ionosphere. IET Radar Sonar Navig. 2008, 2, 435–448. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, M.; Xu, Z.-W.; Chen, C.; Guo, L.-X. Cubic Phase Distortion and Irregular Degradation on SAR Imaging Due to the Ionosphere. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3442–3451. [Google Scholar] [CrossRef]
- Hu, C.; Li, Y.; Dong, X.; Wang, R.; Ao, D. Performance Analysis of L-Band Geosynchronous SAR Imaging in the Presence of Ionospheric Scintillation. IEEE Trans. Geosci. Remote Sens. 2017, 55, 159–172. [Google Scholar] [CrossRef]
- Liu, F.; Fan, X.; Zhang, L.; Zhang, T.; Liu, Q. GNSS-Based SAR for Urban Area Imaging: Topology Optimization and Experimental Confirmation. Int. J. Remote Sens. 2019, 40, 4668–4682. [Google Scholar] [CrossRef]
- Santi, F.; Bucciarelli, M.; Pastina, D.; Antoniou, M.; Cherniakov, M. Spatial Resolution Improvement in GNSS-Based SAR Using Multistatic Acquisitions and Feature Extraction. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6217–6231. [Google Scholar] [CrossRef]
- Ji, Y.; Dong, Z.; Zhang, Y.; Zhang, Q. An Autofocus Approach With Applications to Ionospheric Scintillation Compensation for Spaceborne SAR Images. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 989–1004. [Google Scholar] [CrossRef]
- Lin, H.; Deng, Y.; Zhang, H.; Wang, J.; Liang, D.; Fang, T.; Wang, R. Estimating and Removing Ionospheric Effects for L-Band Spaceborne Bistatic SAR. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Dong, X.; Hu, J.; Hu, C.; Long, T.; Li, Y.; Tian, Y. Modeling and Quantitative Analysis of Tropospheric Impact on Inclined Geosynchronous SAR Imaging. Remote Sens. 2019, 11, 803. [Google Scholar] [CrossRef]
- Priyadarshi, S. A Review of Ionospheric Scintillation Models. Surv. Geophys. 2015, 36, 295–324. [Google Scholar] [CrossRef]
- Borre, K.; Akos, D.M.; Bertelsen, N.; Rinder, P.; Jensen, S.H. A Software-Defined GPS and Galileo Receiver: A Single-Frequency Approach; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]





| Quantity | Value | Quantity | Value |
|---|---|---|---|
| Satellite signal source | GPS L5 PRN 4 | Pulse width | 1 ms |
| Signal bandwidth | 20.46 MHz | Equivalent PRF | 1000 Hz |
| Receiver IF | 139.95 MHz | Reflect antenna gain | 12 dBi |
| Sampling Rate | 62 MHz | Integration time | 300 s |
| Na | Nin | Nx | Ny | dx | dy |
|---|---|---|---|---|---|
| 300,000 | 16 | 300 | 160 | 5 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, T.; Wang, P.; Chen, J.; Yao, H.; Ren, Z.; Zhao, P.; Zeng, H. A Two-Step Phase Compensation-Based Imaging Method for GNSS-Based Bistatic SAR: Extraction and Compensation of Ionospheric Phase Scintillation. Remote Sens. 2024, 16, 2345. https://doi.org/10.3390/rs16132345
Tang T, Wang P, Chen J, Yao H, Ren Z, Zhao P, Zeng H. A Two-Step Phase Compensation-Based Imaging Method for GNSS-Based Bistatic SAR: Extraction and Compensation of Ionospheric Phase Scintillation. Remote Sensing. 2024; 16(13):2345. https://doi.org/10.3390/rs16132345
Chicago/Turabian StyleTang, Tao, Pengbo Wang, Jie Chen, Huguang Yao, Ziheng Ren, Peng Zhao, and Hongcheng Zeng. 2024. "A Two-Step Phase Compensation-Based Imaging Method for GNSS-Based Bistatic SAR: Extraction and Compensation of Ionospheric Phase Scintillation" Remote Sensing 16, no. 13: 2345. https://doi.org/10.3390/rs16132345
APA StyleTang, T., Wang, P., Chen, J., Yao, H., Ren, Z., Zhao, P., & Zeng, H. (2024). A Two-Step Phase Compensation-Based Imaging Method for GNSS-Based Bistatic SAR: Extraction and Compensation of Ionospheric Phase Scintillation. Remote Sensing, 16(13), 2345. https://doi.org/10.3390/rs16132345







