1. Introduction
Digital elevation models (DEMs) fundamentally represent the Earth’s surface topography and offer essential insights for both academic and practical applications, such as landslide detection, navigation, climate research, hydrological modeling, and geospatial analysis [
1,
2,
3,
4]. Interferometric Synthetic Aperture Radar (InSAR) is an advancement in DEM technology that utilizes the phase differences between radar signals to generate precise 3D models of the Earth’s terrain [
5,
6,
7,
8]. Notably, the bistatic SAR system, which employs separate transmitters and receivers on different platforms, enhances the accuracy of DEMs [
9]. This configuration allows for single-pass data collection, accelerating the data-gathering process. Furthermore, the bistatic SAR system reduces temporal decorrelation impacts in a rapidly changing environment, ensuring more reliable data [
10,
11].
The launch of LuTan-1 (LT-1), China’s inaugural civilian bistatic SAR satellite, marks a significant leap in Earth observation technology [
12]. The LT-1 mission successfully launched two L-band SAR satellites, LT-1A and LT-1B, from the Jiuquan Satellite Launch Center on 26 January and 27 February 2022, respectively [
13]. LT-1 aims to achieve DEMs with the precision of 1:50,000 scale topographic maps, with the primary requirement being precise interferometric calibration [
14].
The accuracy of DEMs produced through InSAR is significantly influenced by various interferometric parameters, each affecting the height accuracy to different extents [
15,
16,
17]. These parameters include flight altitude error, slant range error, interferometric phase error, and baseline error, with their impact on InSAR-derived heights ranging from least to most substantial [
18]. Precision orbit determination is effectively employed to minimize flight altitude errors [
19], and geometric calibration methods proficiently address slant range inaccuracies [
20]. We primarily address the more challenging aspects of interferometric phase error and baseline error, which are more crucial than flight altitude error and slant range error for enhancing the accuracy and reliability of DEM.
Classical InSAR systems, such as the Shuttle Radar Topography Mission (SRTM) [
21] and TanDEM-X [
10], have set benchmarks in achieving precise interferometric calibration, which is pivotal for generating global DEMs. The SRTM used a collaborative calibration approach, employing sensitivity equations to fine-tune interferometric parameters simultaneously, thus facilitating accurate DEM production [
22]. However, this method introduced coupling errors due to the simultaneous calibration of parameters, impacting the precision in assessing systematic errors. Therefore, it is crucial to employ external reference data and establish a comprehensive calibration process to mitigate the error coupling among interferometric parameters
The TanDEM-X mission, the first spaceborne bistatic SAR mission, adopted an independent calibration strategy that capitalizes on the unique error characteristics of interferometric parameters [
16]. This approach achieved remarkable accuracies, with an interferometric phase precision of ±7.5 mm and baseline accuracy of 2 mm [
23,
24,
25]. TanDEM-X’s calibration success proved its efficacy and served as a blueprint for subsequent InSAR systems like Gaofen-3 and TH-2 satellites [
26], promoting advancements in interferometric calibration. Additionally, numerous studies have focused explicitly on independent baseline calibration methods [
27,
28,
29].
Despite TanDEM-X’s formidable calibration achievements, LT-1 faces distinct challenges in adopting similar methodologies due to differences in data formats and processing chains. The critical challenges for LT-1 calibration are as follows.
A primary concern is the -ambiguity in interferometric phases, a phenomenon unique to bistatic systems. This ambiguity arises from the synchronization link processing, where the sum of synchronization phases from two satellites results in a combined average, potentially deviating from the expected phase ambiguity to . Highlighted during the TanDEM-X mission, this issue underscores the complexity of understanding -ambiguity’s impact on phase calibration. However, the problem of -ambiguity remains unresolved, presenting an ongoing challenge in the field.
Moreover, the complexity of the LT-1 calibration process is compounded by its reliance on a differential global positioning system (DGPS) to compute spatial baseline vectors. The interferometric baseline vector, critical for accurately gauging the displacement between SAR antennas, cannot be directly derived from DGPS data due to the presence of temporal baselines [
29]. Unlike TanDEM-X, which does not address the temporal baseline within the calibration process, LT-1 incorporates initial baseline estimation into the interferometric processing, further complicating the error coupling issue. The greater baseline length of LT-1, compared to TanDEM-X, necessitates a refined baseline model to accommodate the rapid relative satellite motion.
A further complication arises from LT-1’s operation in the L-band, known for its significant penetration capability, which introduces meters of error due to uncertain penetration depths [
30,
31]. However, current methods for estimating penetration depth lack precision. To mitigate this, deploying corner reflectors with a strong Radar Cross Section (RCS) is essential for calibration, as the penetration depth of the L-band is minimal on such reflective targets [
32].
This study aims to develop a robust interferometric calibration model for LT-1 to address these challenges. It proposes a method for modeling interferometric phase calibration to resolve the -ambiguity. It explicitly examines and calibrates the baseline for LT-1. Data from corner reflectors are used to calibrate baseline and interferometric phase errors accurately.
The remaining sections of this paper are structured as follows.
Section 2 delves into the mechanics of interferometric calibration, detailing the flow of the process along with methodologies for absolute interferometric phase and baseline calibration.
Section 3 presents an overview of the calibration sites and the SAR data utilized in this study, including a statistical analysis of interferometric phase error, baseline error, and DEM results. In
Section 4, the discussion pivots to evaluating whether the precision of interferometric phase error and baseline error meets the accuracy requirements for DEM. This section also outlines future directions for this line of research.
Section 5 concludes the paper, summarizing this work’s key results and contributions.
2. Methodology
2.1. Interferometric Calibration Flow
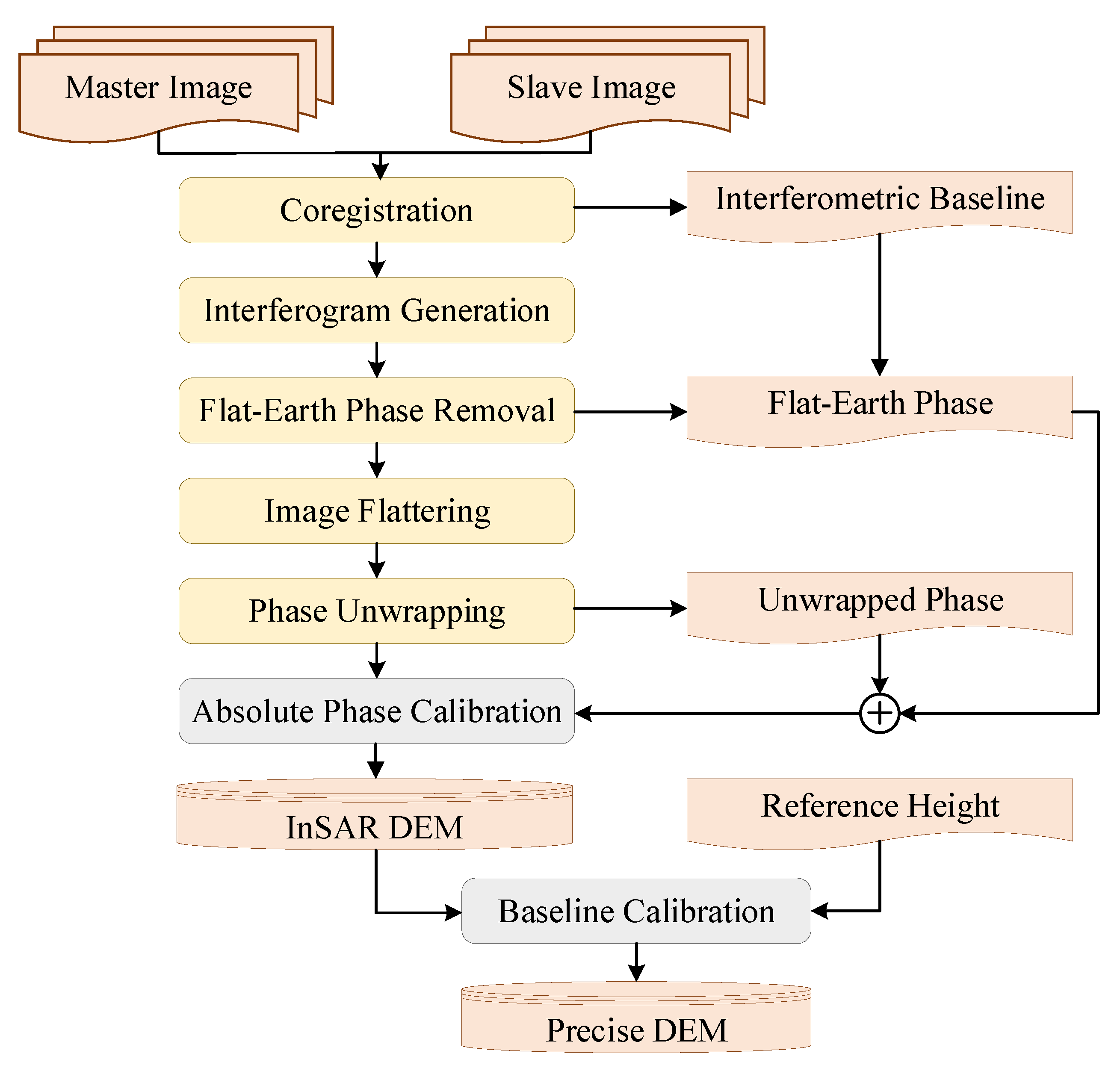
The process for calibrating the critical interferometric parameters is illustrated in
Figure 1, detailing the steps involved in the interferometric calibration workflow.
(1) Coregistration. The coregistration of master and slave SAR images is achieved through the correlation coefficient method [
33]. Initially, 1000 points boasting coherence coefficients above 0.9 are identified across the image. The registration offsets for these points are calculated, followed by the polynomial fitting of these offsets. Coregistration is deemed successful if the average residual of the polynomial fitted values to the actual values is under 0.06 pixels, ensuring high precision in image alignment. When traditional methods do not meet the accuracy requirements, advanced models can be used as references to obtain the registration offsets [
34,
35,
36].
(2) Interferometric baseline derivation. Utilizing registration offsets, the relative positions of the master and slave satellites are determined. This information is crucial for computing the temporal baseline, providing a foundation for accurate interferometric baseline measurements.
(3) Interferogram generation. SAR single-look complex (SLC) images, consisting of complex data (both real and imaginary components), undergo interferometric processing. This step involves the conjugate multiplication of two SAR complex images to compute phase differences at each corresponding point, resulting in a comprehensive interferometric phase map that includes amplitude and phase information.
(4) Flat-Earth phase removal. This step is designed to counteract the influence of Earth’s topography on interferometric phase measurements [
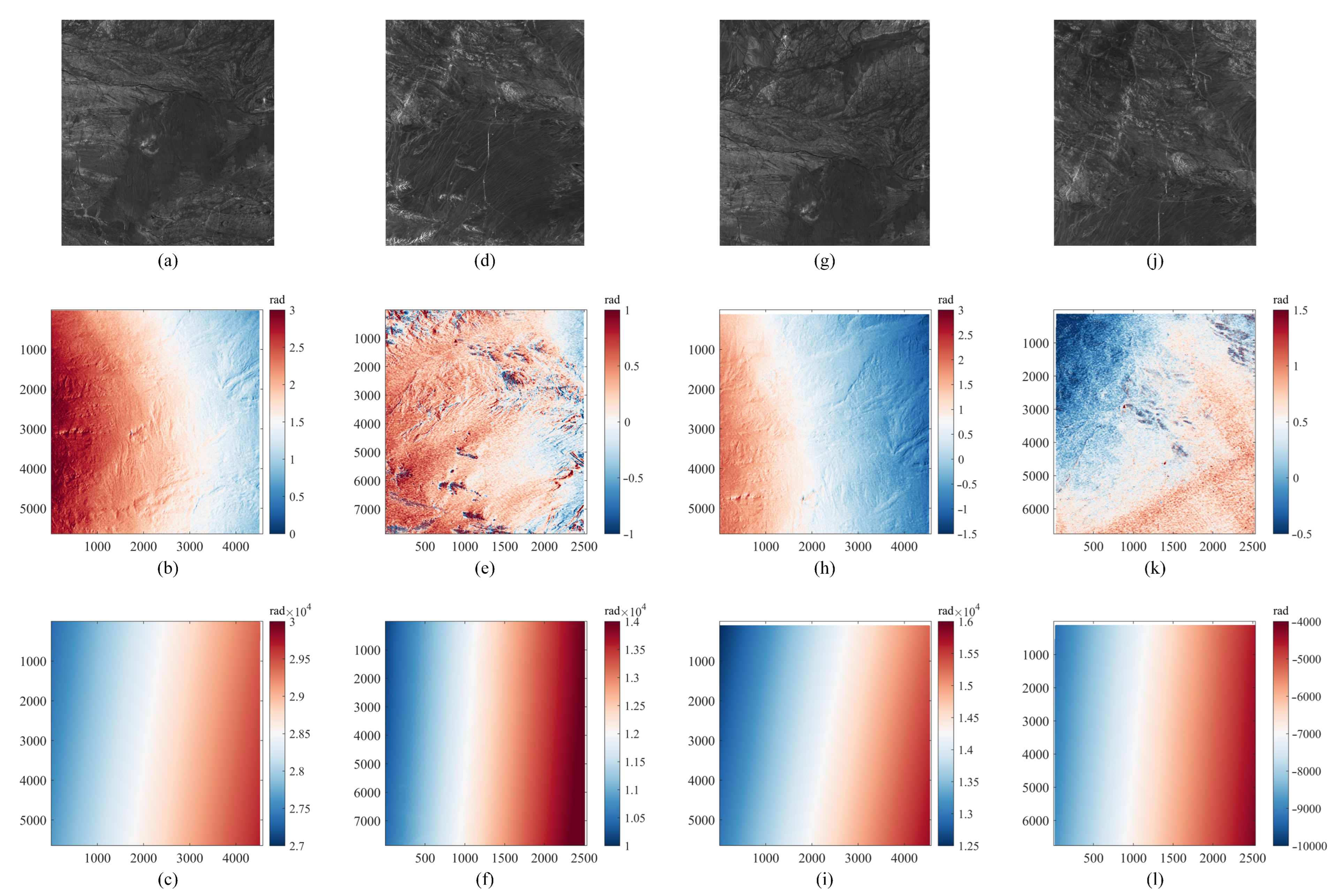
37]. In regions perceived as flat, terrain variations and the Earth’s inherent curvature generate overlaying interference fringes, complicating analyses such as phase unwrapping. By utilizing the interferometric baseline determined in a previous step and estimating the phase over a theoretically flat surface, this process subtracts the flat-Earth phase from the overall interferometric phase. This subtraction effectively isolates phase contributions due to terrain variations, simplifying the interpretation of interference fringes.
(5) Image flattering. During InSAR data analysis, unclear interference fringes, marked by “spikes” and discontinuities, can diminish the efficiency and accuracy of phase unwrapping. Addressing these anomalies is critical, as errors propagate through the phase unwrapping process. A mean filtering algorithm is applied at this juncture to refine the interferometric phase quality, paving the way for more precise analysis and interpretation.
(6) Phase unwrapping. The phase difference in an interferogram is represented by principal phase values within the range
. To accurately derive the actual phase difference, phase unwrapping is necessary. This critical step directly influences the height accuracy of the DEM, employing a default weighted branch cuts algorithm for phase unwrapping [
38]. Should the initial results prove inadequate, alternative methodologies, such as network flow-based or minimum spanning tree-based algorithms [
39], are considered.
(7) Absolute phase calibration. This crucial step addresses the residual phase offset following phase unwrapping. The radargrammetric method is employed to determine the absolute phase shift, ensuring alignment with real-world measurements and enhancing the fidelity of the DEM. This step will be elaborated further in the subsequent section.
(8) Baseline calibration. With the interferometric phase converted to the initial InSAR height, baseline calibration is performed using corner reflector heights. This final adjustment refines the baseline measurements, solidifying the accuracy of the DEM produced through the InSAR process.
(9) DEM generation. This step integrates the refined phase and baseline to obtain the DEM.
2.2. Absolute Phase Calibration Model
Discrepancies in the unwrapped phase compared to the accurate absolute interferometric phase are influenced by two primary components: the phase unwrapping algorithm’s starting point variances and the differential transmit/receive channels across the master and slave SAR systems [
15,
38]. Errors from the unwrapping process are categorized as algorithm-induced, distinguishing them from system-induced inaccuracies. Calibration of the interferometric phase is crucial, focusing on harmonizing the discrepancies caused by the diverse transmit/receive channels between the master and slave SARs.
Further complicating the accuracy of the absolute interferometric phase are errors introduced by phase synchronization issues between the master and slave SARs, errors arising during the imaging and interferometry processes, and phase perturbations caused by the radar’s inherent thermal noise and quantization noise [
17,
40]. These errors are generally random within the system. Using high signal-to-noise ratio corner reflectors can maintain these random errors within permissible bounds.
In bistatic mode, the phase of the master SAR echo and slave SAR echo at the ground point P can be expressed as follows [
41]:
where
is the phase of the master SAR echo;
is the phase of the slave SAR echo;
is the wavelength;
is the phase caused by the round-trip delay of electromagnetic waves between the satellite and the ground point;
is the transmitting channel delay;
is the receiving channel delay;
is the phase error caused by the processor;
is the phase error caused by noise;
is the phase error introduced by ground targets under specific polarization; and Subscripts 1 and 2 represent master SAR and slave SAR, respectively. Given that the bistatic SAR system’s antennas receive ground echo almost simultaneously in identical polarization modes, it is logical to conclude that ground targets remain constant and that the scattering matrix is the same for both SARs.
The interferometric phase is the phase difference of two radar echo signals, and it can be expressed as follows:
where
is the phase acquired by interferometric processing;
is the phase used for interferometric height measurement, simplified as
;
is the phase error caused by receiving the channel delay differences of two SARs; and
is the phase error caused by the processor differences of two SARs. Equation (
3) can be reinterpreted accordingly:
where
represents the interferometric phase of interest, and
.
denotes the phase shift caused by variations in the reception channels and processors.
is the combination of two Gaussian noises and can be considered as a single Gaussian noise.
The interferometric phase obtained through the interferometric processing is
, while the interferometric phase used to generate the DEM is
. Thus, absolute interferometric phase calibration involves extracting
from
and identifying the phase shift
in Equation (
4).
The formula for the reference interferometric phase, which is determined by the corner reflector’s coordinate, is given below:
where
is the reference interferometric phase;
and
are the positions of the master and slave SARs when observing the ground point, respectively; and
is the position of the corner reflector.
The absolute interferometric phase calibration model is established as follows:
where
is the interferometric phase error;
and
are the flat-Earth phase and unwrapped phase, respectively.
The flat-Earth phase refers to the phase component that results from the curvature of the Earth. When SAR signals are transmitted from a satellite and reflected back from the Earth’s surface, the Earth’s curvature introduces a predictable phase shift in the received signals. This phase shift needs to be removed to isolate the phase changes caused by topography and surface displacement.
The unwrapped phase is the result of phase unwrapping. SAR signals are inherently periodic and measured modulo , meaning the phase can only be observed within a range of to rad. Phase unwrapping aims to reconstruct the true phase values by resolving the ambiguities introduced by this wrapping, effectively “stitching together” the wrapped phase values to produce a continuous phase map. The unwrapped phase represents the actual phase differences, which can then be used to infer topographic height.
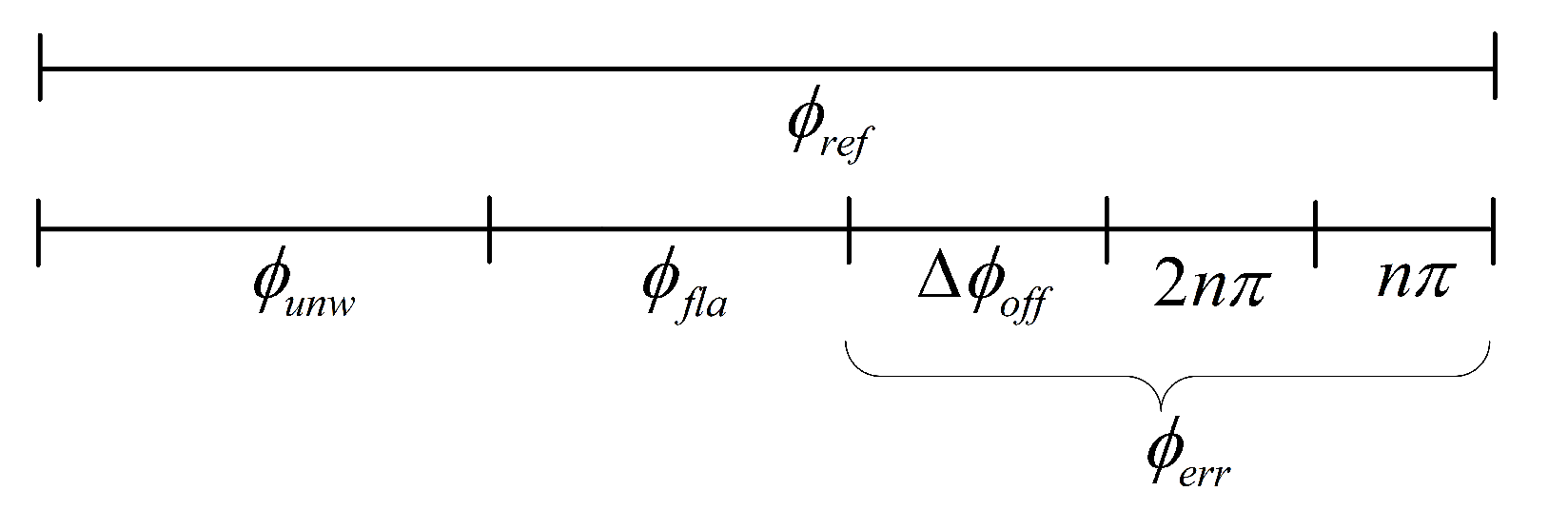
The composition of the interferometric phase is illustrated in
Figure 2. The data obtained from the interferometric processing include the unwrapped phase and the flat-Earth phase. The phase error
derived from Equation (
6) includes
and the integer multiples of
phase shift caused by interferometric processing and phase synchronization. Therefore, to obtain
and resolve the ambiguity in the interferometric phase resulting from phase unwrapping and the
-ambiguity caused by synchronization, it is essential to remove the integer multiples of
from
and retain only its fractional part as the absolute interferometric phase shift. This is achieved by performing a modulo operation of
with
:
where
stands for the modulo operation, and
refers to rounding the input number to the nearest integer.
After identifying the interferometric phase error, the initial interferometric phase can be refined through specific corrective measures as follows:
where the term
represents the sum of ambiguous phases introduced by the phase unwrapping and synchronization process. In regions lacking corner reflectors, the ambiguous phase can be acquired through the registration offset between the master and slave SAR images or through the utilization of external height [
42].
2.3. Baseline Calibration Model
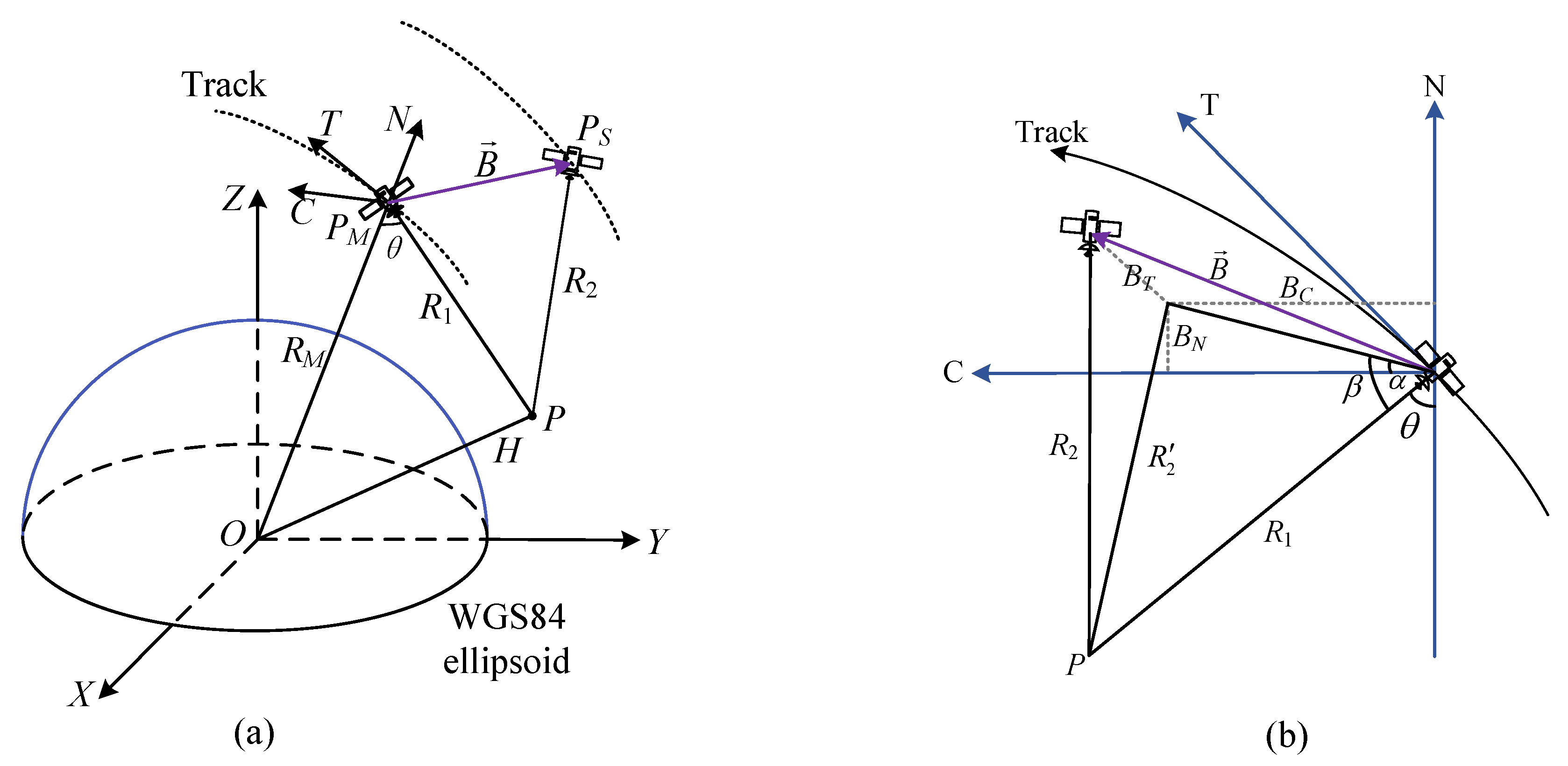
Figure 3a illustrates the geometric representation of ground point P observation within the bistatic system, showcasing two coordinate systems: the Earth-Centered, Earth-Fixed (ECEF) coordinate system and the Track Cross–Track Normal (TCN) coordinate system.
In the ECEF framework, the origin O is positioned at the Earth’s center. The Z-axis aligns parallel to the Earth’s rotational axis, directed towards the North Pole. The X-axis extends towards the equator’s intersection with the prime meridian, and the Y-axis, orthogonal to the XZ-plane, points eastward toward the equator’s crossing with the 90° east meridian.
The TCN coordinate system originates at the master SAR antenna, with the T-direction aligned along the satellite’s flight path, indicating the along-track direction. The N-direction extends from the Earth’s center towards the satellite, while the C-direction is orthogonal to the TN-plane, ensuring a right-handed coordinate system.
As depicted in
Figure 3a,
and
represent the positions of the master SAR and the slave SAR, respectively.
and
are the slant ranges from the master and slave SAR to the ground point
P, respectively.
is the distance from the master SAR to the Earth’s center.
H denotes the height of point
P from the Earth’s surface.
represents the interferometric baseline, which is defined as the vector difference between the positions of the two satellites when observing the same ground point. Typically, the two satellites do not observe the same point on the ground simultaneously. Therefore, the interferometric baseline can be defined as follows:
where
,
, and
are the baseline components along the X-axis, Y-axis, and Z-axis, respectively;
and
are the acquisition times of point P in the slave and master images, respectively. The relationship between
and
is as follows:
where
is the azimuth shift obtained by the coregistration step, and
is the azimuth sampling time.
The baseline vector is projected from the ECEF coordinate system onto the TCN coordinate system:
where
,
, and
represent the unit vectors of the
T-axis,
C-axis, and
N-axis, respectively.
,
, and
represent the baseline components along the
T-axis,
C-axis, and
N-axis, respectively.
Baseline calibration primarily focuses on identifying the baseline errors in the
C-axis and
N-axis, which correspond to the cross-track and radial baseline errors in the TanDEM-X system, respectively [
24]. Due to its minimal effect on height measurement, the baseline error in the
T-axis is typically not addressed by calibration, and it can be effectively corrected through coregistration. The vector representing baseline errors is formulated as follows:
where
and
represent the baseline errors in the
C-axis and
N-axis, respectively.
Therefore, the precise baseline is as follows:
Applying the phase-to-height conversion, we calculate the height of point
P:
where
is the radius of the Earth, and
is the incidence angle.
Based on the geometric relationship depicted in
Figure 3b, the incidence angle can be solved as follows:
where
is the elevation angle of the baseline;
is the baseline vector in the CN-plane, and
;
is the angle between the baseline
and the slant range
; and
is the length of the projection of
onto the CN-plane:
where
is the absolute interferometric phase.
By contrasting InSAR-derived height with the reference height
, we can ascertain the baseline error by formulating the following equation:
where
represents the InSAR height generated with the baseline
. The solution of Equation (
17) is as follows:
where
is a matrix composed of the height of several point targets.
4. Discussion
Compared to previous work, this study highlights several innovative aspects in the calibration of the LT-1 bistatic SAR system. Our work compensates for temporal baselines and provides a more detailed calibration process, offering valuable insights for bistatic SAR interferometric calibration. By addressing challenges such as -ambiguity and extended baseline lengths, our model improves upon previous missions like TanDEM-X. Integrating DGPS data for precise baseline estimation and employing corner reflectors to mitigate L-band penetration errors significantly enhance calibration accuracy, resulting in high-precision DEMs that meet the 5 m height accuracy requirement.
Additionally, an accuracy analysis of the interferometric phase and baseline is presented, ensuring the reliability of our results. Finally, this study outlines limitations and future recommendations to refine calibration techniques further.
4.1. Accuracy Analysis
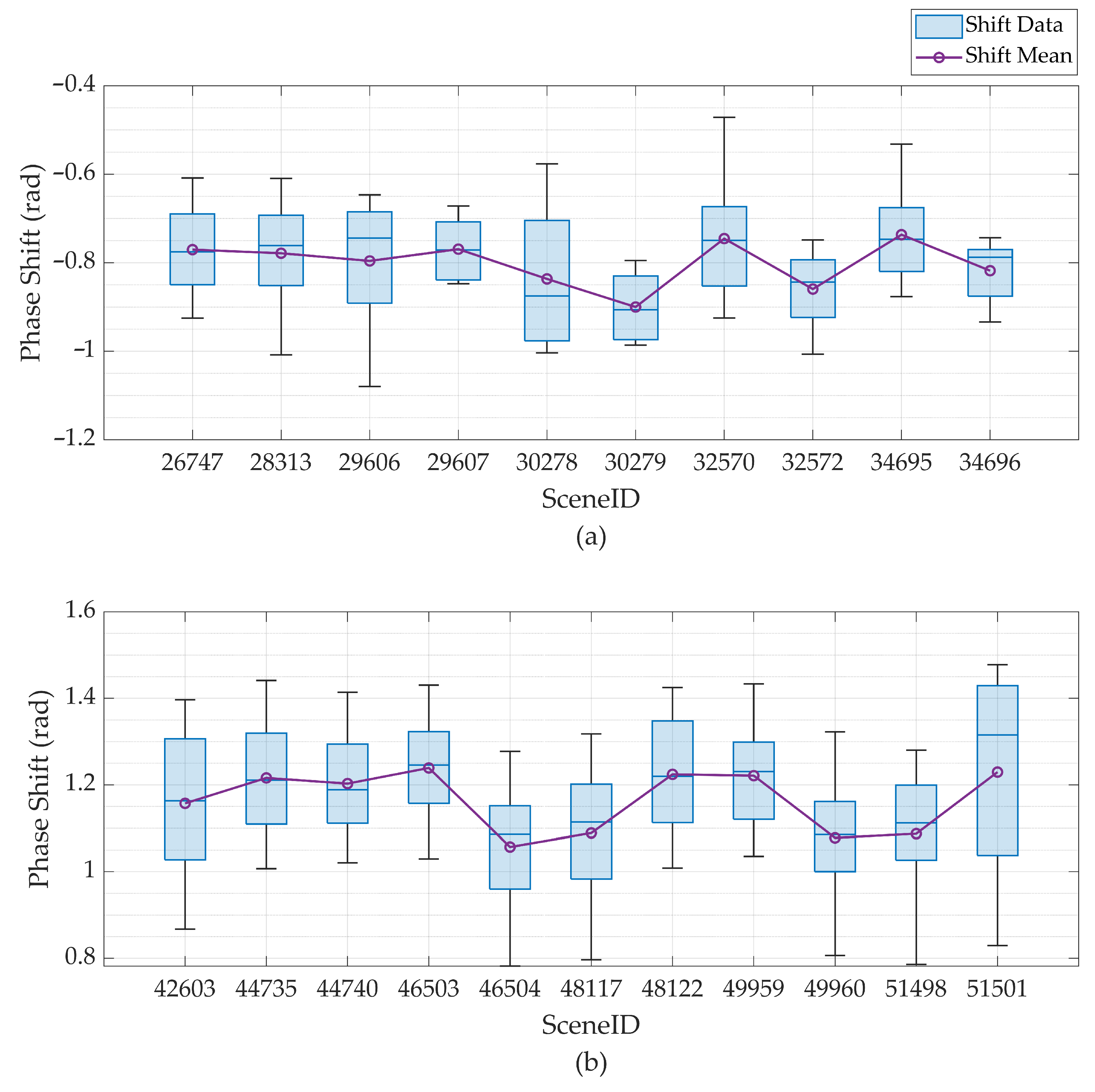
We found that the variation in interferometric errors is more closely linked to changes in the satellite system’s formation than to alterations in the beam swath. This variation can be attributed to adjustments in the attitudes of the master and slave SAR systems following formation changes, which influence a range of errors, including attitude measurement, beam pointing control, time synchronization, and phase synchronization errors. These errors, in turn, can affect various complex processes such as internal calibration, orbit control, imaging, and synchronization, leading to changes in interferometric errors. Hence, our experimental data suggest that interferometric errors are closely associated with the system’s formation.
While the DEMs generated in this study fulfill the accuracy requirements, the precision of the obtained interferometric errors has not been assessed. According to the phase-to-height conversion principle, the accuracy of height measurements depends on the accuracy of the baseline length and the interferometric phase. The question arises: how do variations in baseline length and interferometric phase impact height accuracy across different formations?
This section aims to explore this by deriving the relationship between height
H and variables
,
,
, and
through the combination of Equations (
14)–(
16):
where
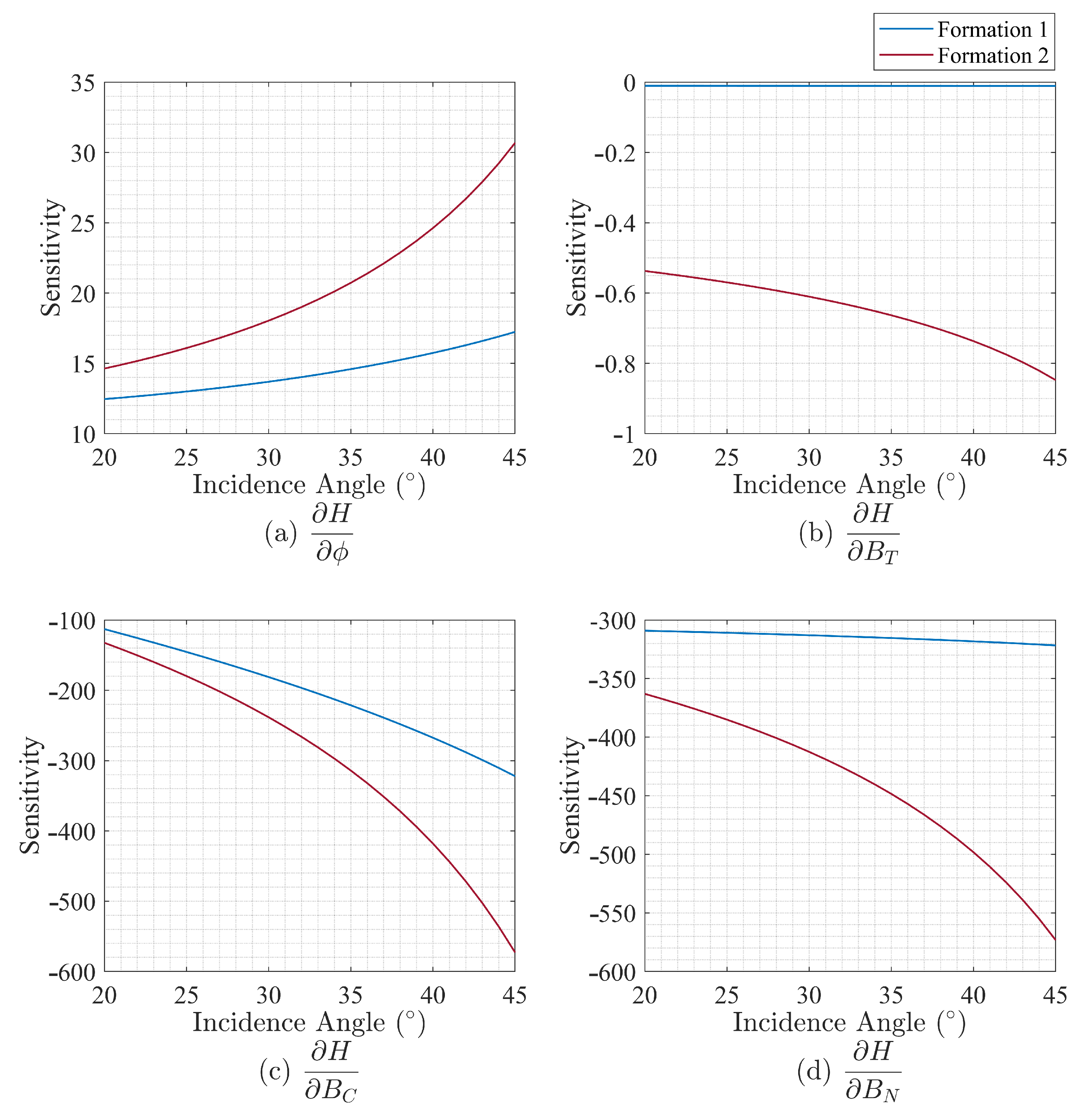
By inputting the parameters of LT-1 Formations 1 and 2 into the designated equations, we have determined the height error sensitivities, as showcased in
Figure 12. This figure illustrates the dependency of height sensitivity on the incidence angle, with distinct representations for each formation: Formation 1 is depicted with a blue curve, while a red curve represents Formation 2. Notably, Formation 2 demonstrates a strong impact of interferometric error on height, which intensifies with an increase in incidence angle. According to
Figure 12, the highest sensitivity is observed at the maximum incidence angle for Formation 2. Errors in the interferometric phase and baseline errors along the
C-axis and
N-axis result in significant height discrepancies.
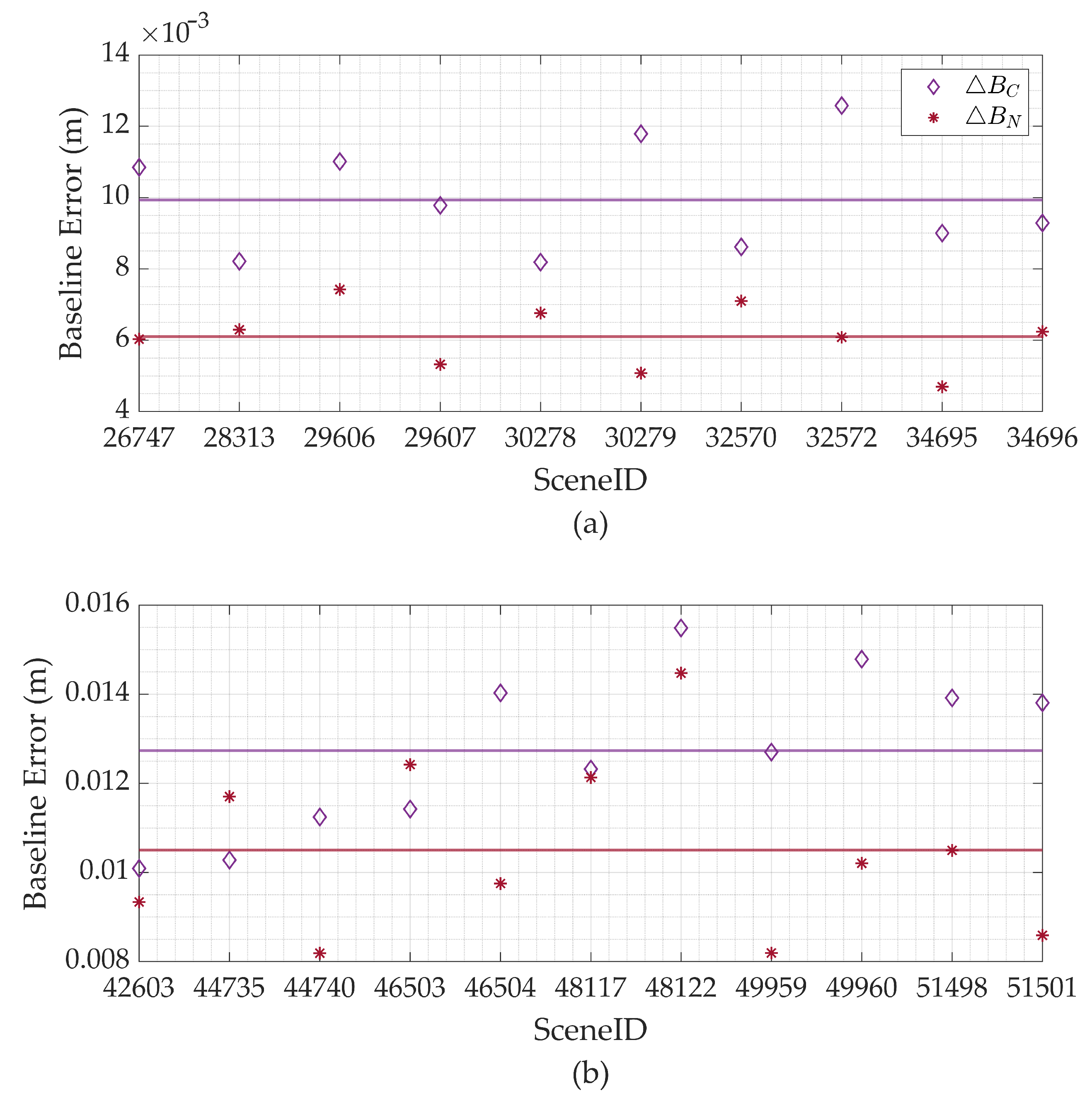
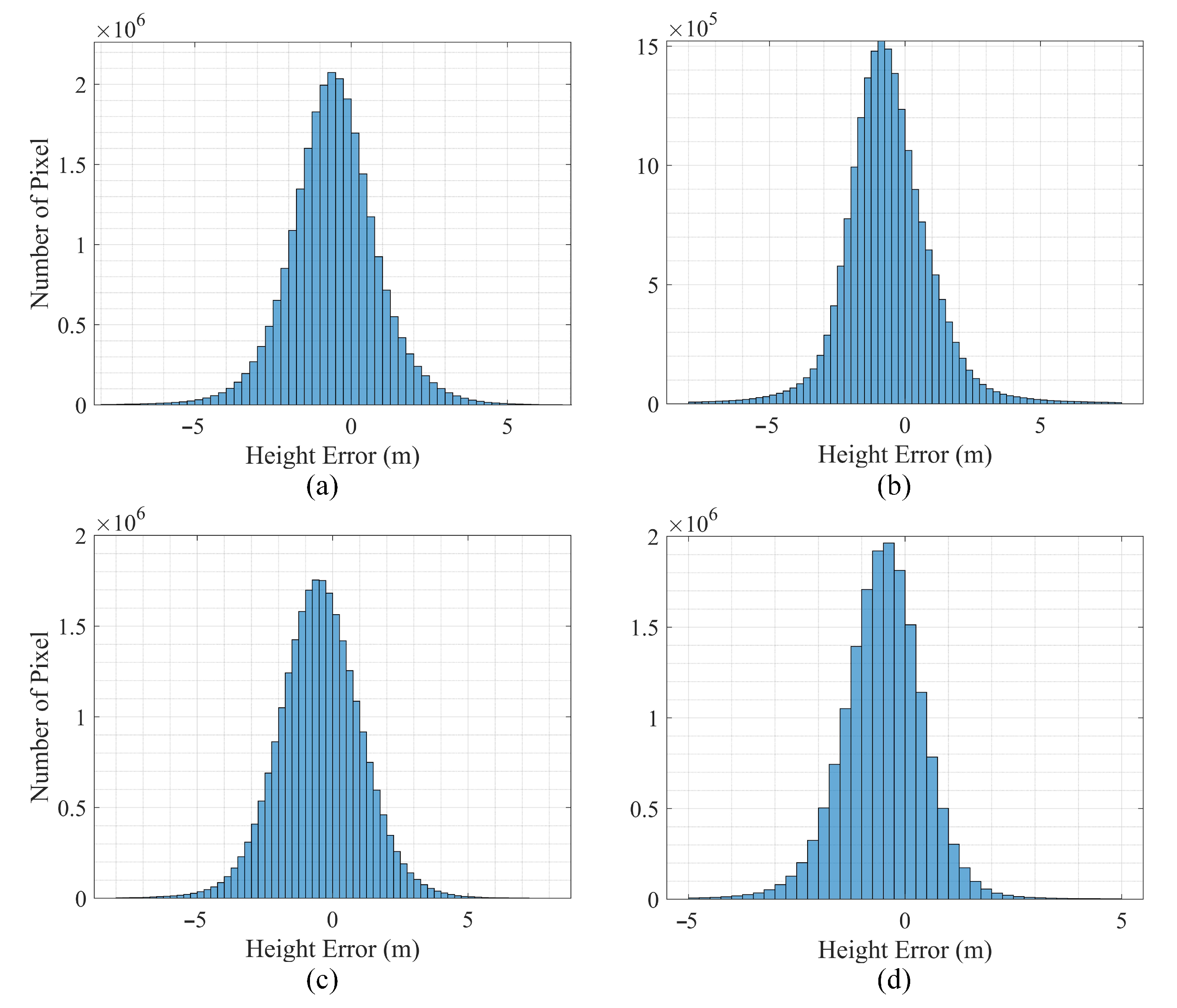
In the analysis of LT-1 data, the precision in interferometric phase error for Formation 1 is 0.049 rad, and the baseline errors are 1.54 mm for the C-axis and 0.87 mm for the N-axis. These result in height errors of 0.85 m, −0.49 m, and −0.28 m, respectively, at the maximum incidence angle. Meanwhile, Formation 2, with precisions of 0.068 rad for the interferometric phase, 1.82 mm for the C-axis, and 1.92 mm for N-axis baseline errors, incurs height errors of 2.08 m, −1.04 m, and −1.11 m. Through numerical analysis, it is demonstrated that the accuracy of the interferometric phase and baseline measurements in this study meets the height accuracy requirements.
4.2. Limitations and Future Recommendations
In finalizing the interferometric calibration for the LT-1 system, this study has achieved stable corrections for interferometric phase shift and baseline errors. Despite these advancements, several limitations require further exploration.
First, while the calibration method has shown promising results in the flat terrain of Xinjiang, China, its effectiveness in environments with challenging interferometric qualities, such as mountainous regions, forests, and urban areas, has yet to be assessed. These complex topography and variable surface characteristics may demand tailored or alternative calibration strategies.
Second, addressing the challenge of the penetration effect inherent in the low frequency system is critical. This study mitigated this effect through calibration with point targets, which exhibit strong scattering properties and significant RCS, thus minimizing penetration effects. Future research should explore the application of distributed targets, such as those derived from ICESat laser altimetry. Obtaining distributed target data is easier, more flexible, and less costly than acquiring point target data. However, it introduces complexities in accurately estimating reference heights and interferometric phases due to the L-band’s penetration depth. Overcoming these challenges is essential for extending the applicability of the proposed method and maintaining calibration accuracy across varied environments and satellite systems.
5. Conclusions
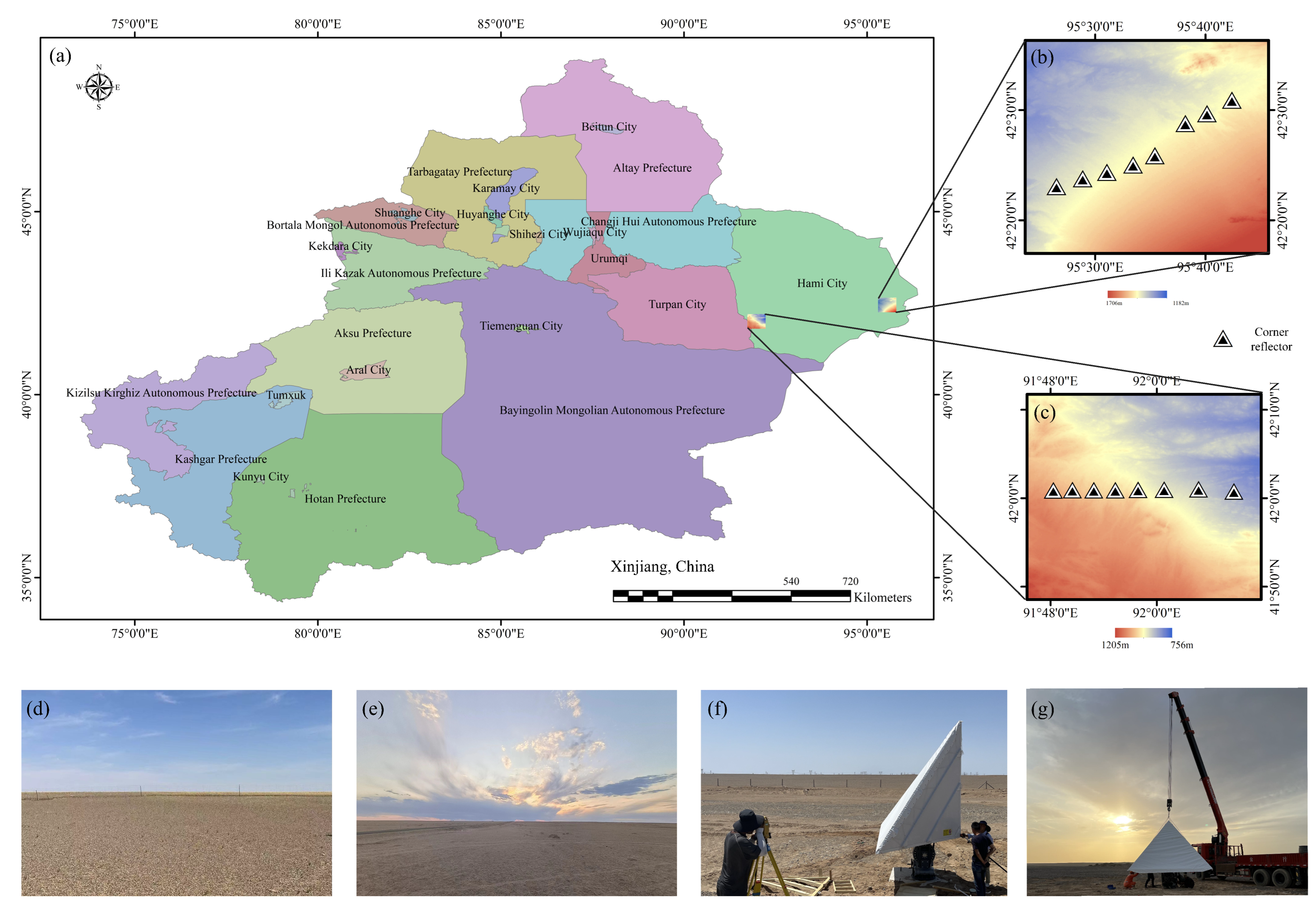
This paper aims to conduct an interferometric calibration of the bistatic SAR system LT-1 to produce high-precision DEMs. It details the calibration process for LT-1, focusing on preventing erroneous correlations between interferometric parameters, and introduces models for absolute phase and baseline calibration specific to the bistatic SAR system. This study successfully completed its calibration experiments by leveraging corner reflector data from Xinjiang, China, and analyzing SAR data from LT-1 collected between July and November 2022.
Our results demonstrate a clear correlation between the calibration outcomes and the operational formation of LT-1, which varied over the observation period. From July to mid-September, LT-1 operated in Formation 1, then transitioned to Formation 2. Notably, Formation 2 exhibited an extended baseline length relative to Formation 1. In terms of specific values, Formation 1 yielded an interferometric phase error of −0.80 rad (standard deviation: 0.049 rad), a C-axis baseline error of 9.93 mm (standard deviation: 1.54 mm), and an N-axis baseline error of 6.10 mm (standard deviation: 0.87 mm). Under Formation 2, the interferometric phase error increased to 1.16 rad (standard deviation: 0.068 rad). The C-axis baseline error was 12.73 mm (standard deviation: 1.82 mm), and the N-axis baseline error was 10.49 mm (standard deviation: 1.99 mm).
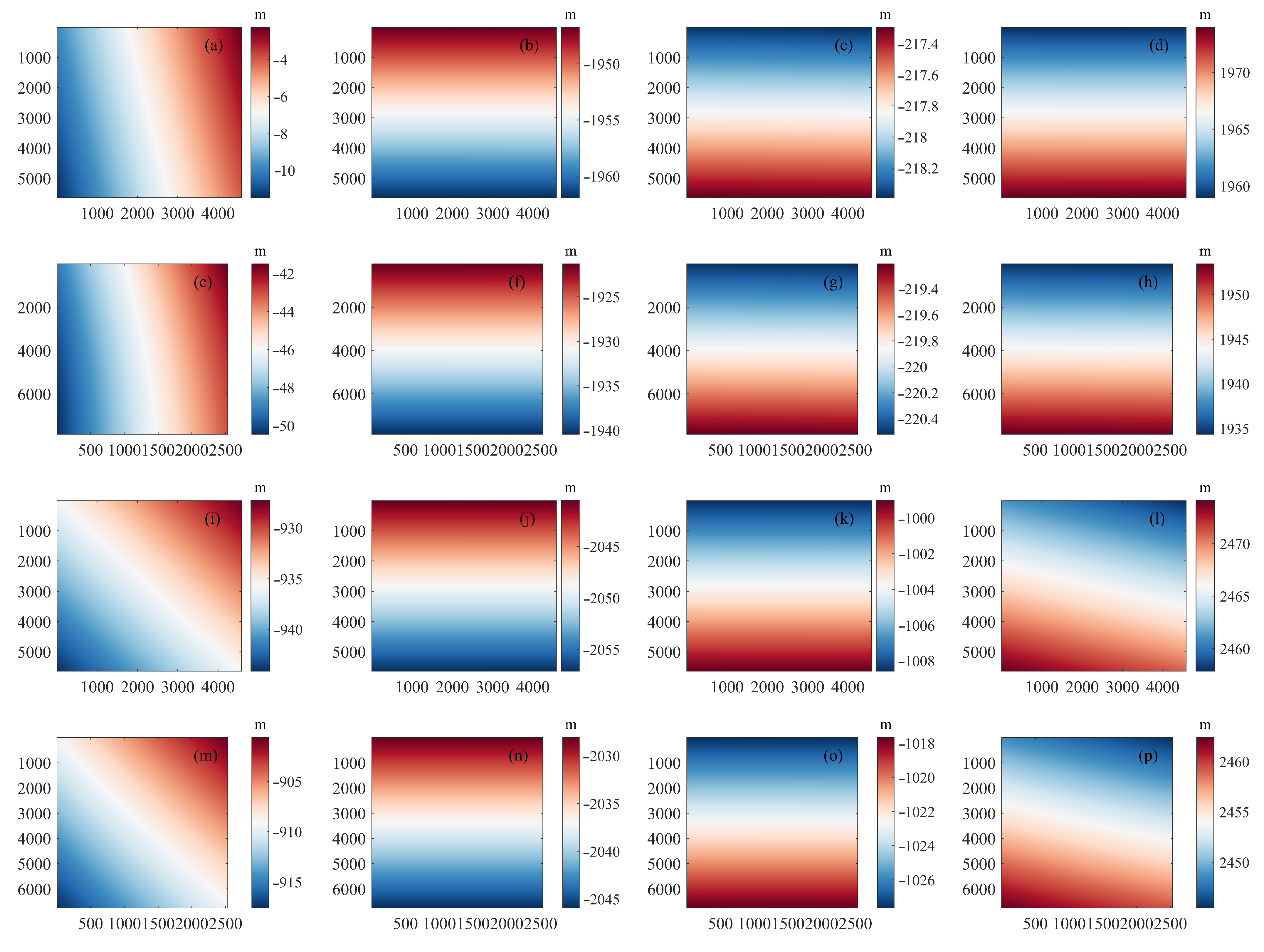
Following the application of compensated interferometric parameters, the generated DEMs satisfied the height accuracy requirement of 5 m. Further analysis confirmed that the calibration precision is adequate for producing DEMs with a 1:50,000 scale topographic map accuracy, validating the LT-1 calibration model.
This study plans to explore interferometric calibration with distributed targets and extend height accuracy validation beyond the Gobi desert, aiming to enhance the model’s applicability and precision across diverse geographical landscapes.