Inversion and Analysis of Global Ocean Chlorophyll-a Concentration Based on Temperature Zoning
Abstract
1. Introduction
2. Materials and Methods
2.1. Research Scope
2.2. Materials
2.2.1. Remote Sensing Data
- The VIIRS Level 3 monthly average remote sensing reflectance (Rrs) data produced by NASA’s Ocean Biology Processing Group (OBPG) includes a total of 36 global remote sensing reflectance images for the wavelengths of 443 nm, 486 nm, and 551 nm in January, April, July, and October of 2017, 2018, and 2019. Additionally, there were 93 daily global remote sensing reflectance images for the same wavelengths in October 2018. The data were downloaded from the OceanColor website (https://oceancolor.gsfc.nasa.gov/l3/, accessed on 2 June 2023).
- For the chlorophyll-a concentration data, the OC-CCI chlorophyll-a concentration data were selected. The global ocean chlorophyll-a products for January, April, July, and October of 2017, 2018, and 2019 were chosen. The chlorophyll-a concentration for the inversion sample points was chosen from the OC-CCI chlorophyll-a dataset, as it is considered the most accurate open-source product available [49]. This product selects algorithms that perform best in meeting the needs of climate users to process data from multiple satellite sensors [41]. The merged chlorophyll-a concentration is validated against in-situ observations [50,51,52]. The data were downloaded from the European Space Agency’s Climate Office website (https://climate.esa.int/en/projects/ocean-colour/, accessed on 8 June 2023).
- NOAA’s Optimally Interpolated Sea Surface Temperature (OISST) data were selected for analysis. This included a total of 12 global sea surface temperature maps for January, April, July, and October of 2017, 2018, and 2019, as well as 31 daily global SST maps for October 2018.NOAA’s OISST provides a comprehensive ocean temperature field by combining bias-adjusted observations from various platforms (satellites, ships, buoys) onto a regular global grid and filling in gaps through interpolation methods. Compared to other global ocean temperature products, OISST exhibits overall superior performance and significant advantages [53,54,55,56]. The data were downloaded from the NOAA Physical Sciences Laboratory (PSL) website (https://psl.noaa.gov/data/gridded/index.html, accessed on 18 June 2023).
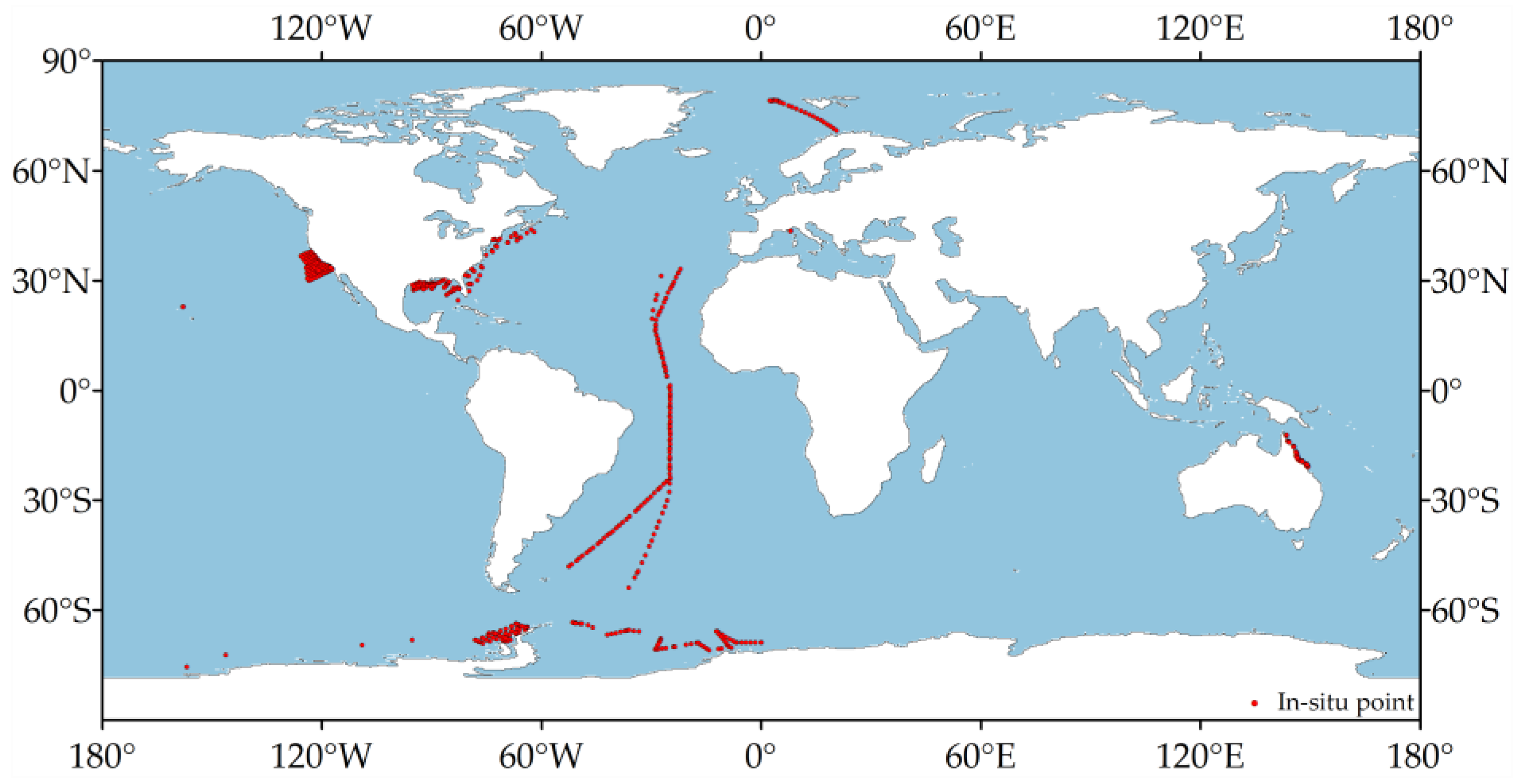
2.2.2. In-Situ Data
2.2.3. Data Preprocessing
2.3. Methods
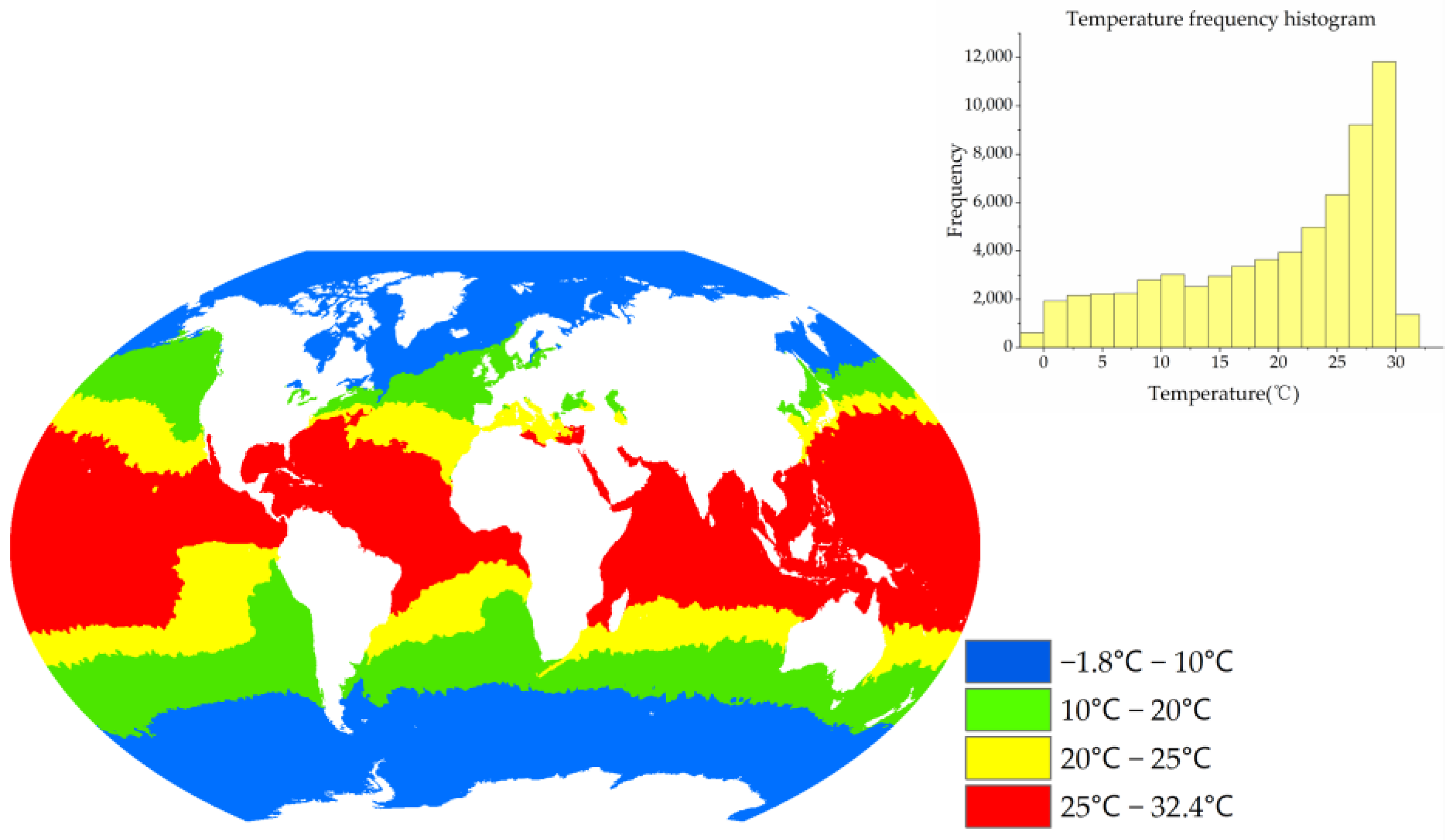
2.3.1. Temperature Zoning Idea
2.3.2. OC3V Inversion Algorithm Based on Temperature Zoning
2.3.3. Precision Evaluation Index
3. Results
3.1. Temperature Zoning Result
3.2. Determination of Inversion Independent Variables
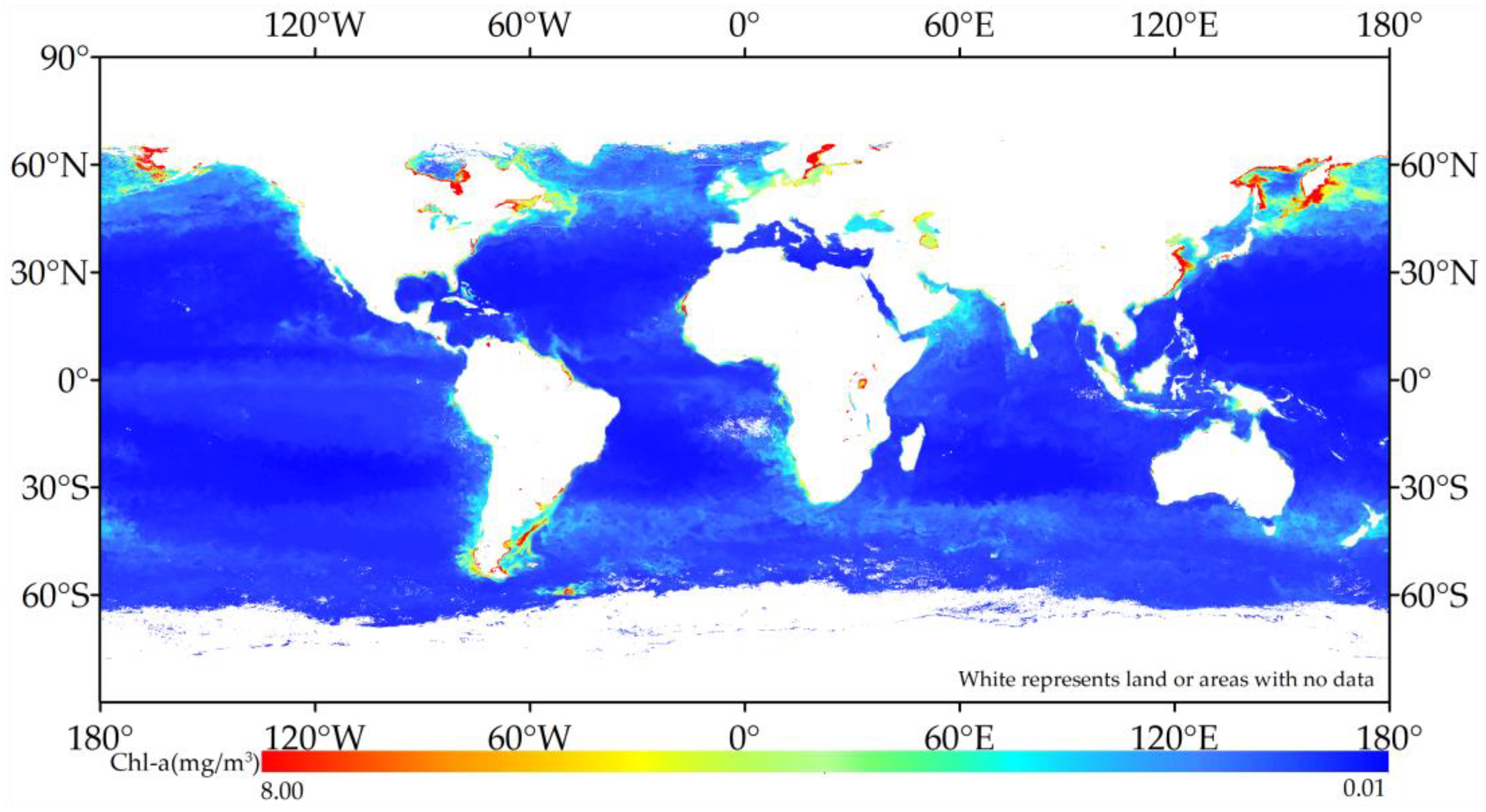
3.3. Global Chlorophyll-a Concentration
3.4. Accuracy Verification
4. Discussion
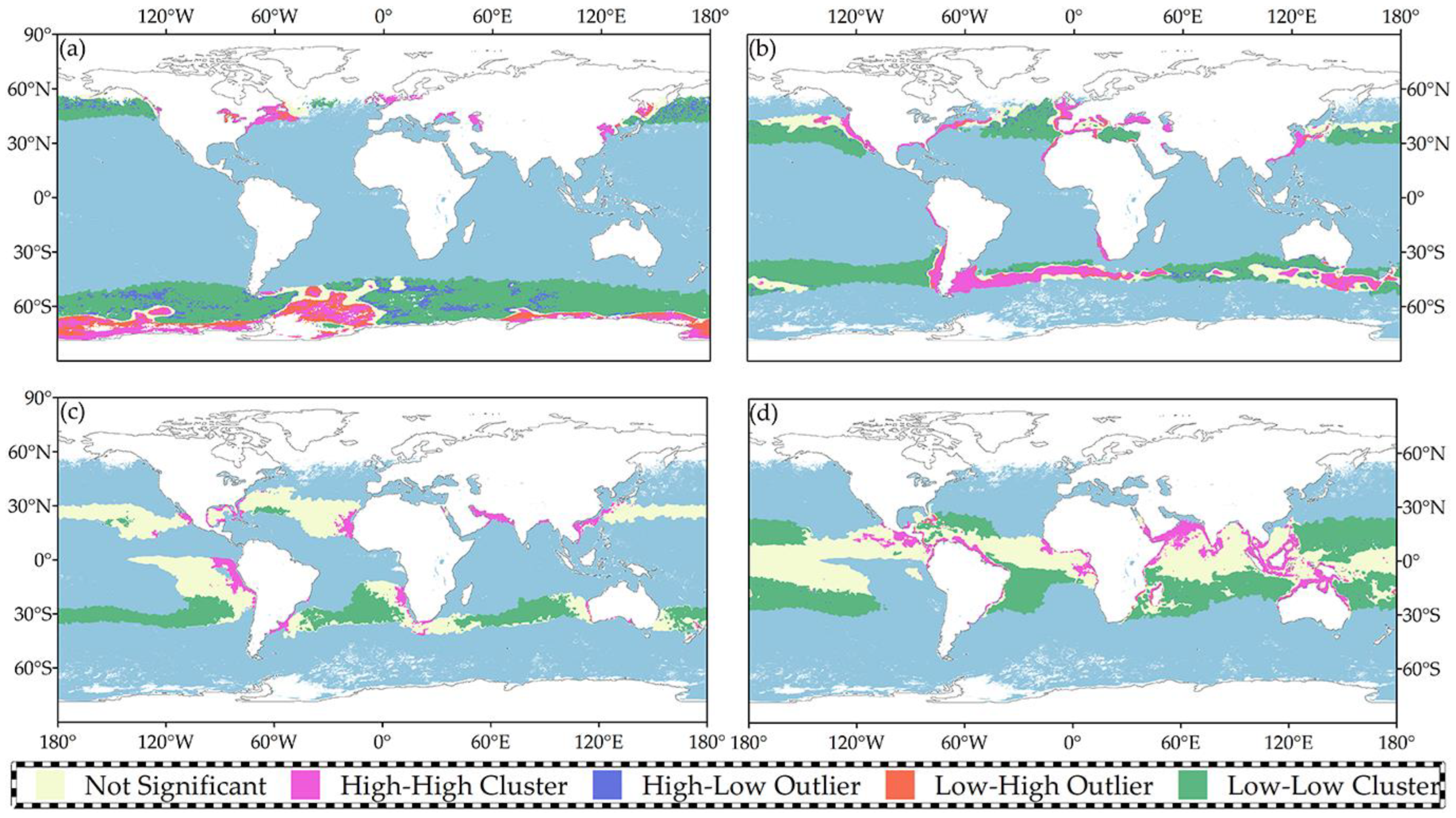
4.1. Spatial Distribution Analysis
4.1.1. Spatial Autocorrelation Analysis
4.1.2. Clustering and Outlier Analysis
4.1.3. Hotspot Analysis
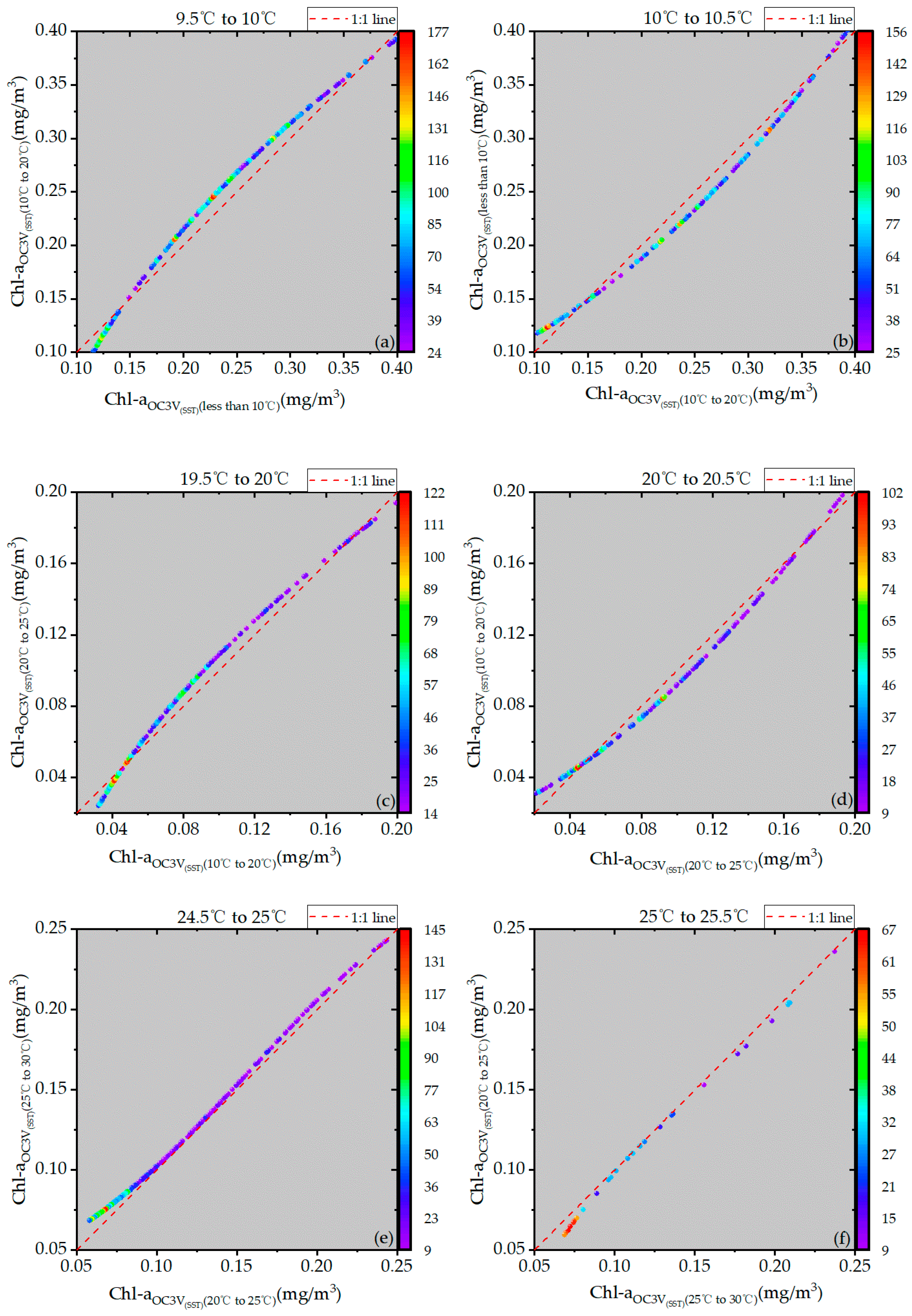
4.2. Continuity Analysis
4.3. Correlation between Temperature and Chlorophyll-a
5. Conclusions
- This study developed a temperature-zoned OC3V algorithm based on global data from October 2018 and validated it using data from January, April, July, and October of 2017, 2018, and 2019, as well as data from all 31 days of October 2018. The results showed that the accuracy of the improved OC3V(SST) model was higher compared to the original OC3V model.
- Based on the temperature zonation of the global ocean, this study conducted a spatial distribution analysis of chlorophyll-a concentrations in various temperature regions for the month of October 2018. Through a systematic and scientific approach, the spatial distribution patterns of chlorophyll-a in the global ocean across different temperature ranges were determined. Additionally, the study explored the continuity of various models and the correlation between temperature and chlorophyll-a.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A

References
- O’Reilly, J.E.; Maritorena, S.; Mitchell, B.G.; Siegel, D.A.; Carder, K.L.; Garver, S.A.; Kahru, M.; McClain, C. Ocean Color Chlorophyll Algorithms for Seawifs. J. Geophys. Res. Ocean. 1998, 103, 24937–24953. [Google Scholar] [CrossRef]
- Clay, S.; Peña, A.; DeTracey, B.; Devred, E. Evaluation of Satellite-Based Algorithms to Retrieve Chlorophyll-a Concentration in the Canadian Atlantic and Pacific Oceans. Remote Sens. 2019, 11, 2609. [Google Scholar] [CrossRef]
- Kahru, M.; Kudela, R.M.; Anderson, C.R.; Manzano-Sarabia, M.; Mitchell, B.G. Evaluation of Satellite Retrievals of Ocean Chlorophyll-a in the California Current. Remote Sens. 2014, 6, 8524–8540. [Google Scholar] [CrossRef]
- Garcia, C.A.E.; Garcia, V.M.T.; McClain, C.R. Evaluation of Seawifs Chlorophyll Algorithms in the Southwestern Atlantic and Southern Oceans. Remote Sens. Environ. 2005, 95, 125–137. [Google Scholar] [CrossRef]
- Al Shehhi, M.R.; Gherboudj, I.; Ghedira, H. Spectral Response of the Arabian Gulf and Sea of Oman Coastal Waters to Bio-Optical Properties. J. Photochem. Photobiol. B-Biol. 2017, 175, 235–243. [Google Scholar] [CrossRef] [PubMed]
- Volpe, G.; Santoleri, R.; Vellucci, V.; D’Alcalà, M.R.; Marullo, S.; D’Ortenzio, F. The Colour of the Mediterranean Sea: Global Versus Regional Bio-Optical Algorithms Evaluation and Implication for Satellite Chlorophyll Estimates. Remote Sens. Environ. 2007, 107, 625–638. [Google Scholar] [CrossRef]
- D’Ortenzio, F.; Marullo, S.; Ragni, M.; d’Alcalà, M.R.; Santoleri, R. Validation of Empirical Seawifs Algorithms for Chlorophyll-A Retrieval in the Mediterranean Sea: A Case Study for Oligotrophic Seas. Remote Sens. Environ. 2002, 82, 79–94. [Google Scholar] [CrossRef]
- Cannizzaro, J.P.; Carder, K.L. Estimating Chlorophyll Concentrations from Remote-Sensing Reflectance in Optically Shallow Waters. Remote Sens. Environ. 2006, 101, 13–24. [Google Scholar] [CrossRef]
- Wang, M.H.; Son, S. Viirs-Derived Chlorophyll-a Using the Ocean Color Index Method. Remote Sens. Environ. 2016, 182, 141–149. [Google Scholar] [CrossRef]
- Korchemkina, E.; Deryagin, D.; Pavlova, M.; Kostyleva, A.; Kozlov, I.E.; Vazyulya, S. Advantage of Regional Algorithms for the Chlorophyll-a Concentration Retrieval from in Situ Optical Measurements in the Kara Sea. J. Mar. Sci. Eng. 2022, 10, 1587. [Google Scholar] [CrossRef]
- Gupta, A.S.; Thomsen, M.; Benthuysen, J.A.; Hobday, A.J.; Oliver, E.; Alexander, L.V.; Burrows, M.T.; Donat, M.G.; Feng, M.; Holbrook, N.J.; et al. Drivers and Impacts of the Most Extreme Marine Heatwaves Events. Sci. Rep. 2020, 10, 19359. [Google Scholar] [CrossRef] [PubMed]
- Tang, W.; Llort, J.; Weis, J.; Perron, M.M.G.; Basart, S.; Li, Z.; Sathyendranath, S.; Jackson, T.; Rodriguez, E.S.; Proemse, B.C.; et al. Widespread Phytoplankton Blooms Triggered by 2019–2020 Australian Wildfires. Nature 2021, 597, 370–375. [Google Scholar] [CrossRef] [PubMed]
- Hughes, T.P.; Kerry, J.T.; Álvarez-Noriega, M.; Álvarez-Romero, J.G.; Anderson, K.D.; Baird, A.H.; Babcock, R.C.; Beger, M.; Bellwood, D.R.; Berkelmans, R.; et al. Global Warming and Recurrent Mass Bleaching of Corals. Nature 2017, 543, 373–377. [Google Scholar] [CrossRef]
- Roxy, M.K.; Modi, A.; Murtugudde, R.; Valsala, V.; Panickal, S.; Prasanna Kumar, S.; Ravichandran, M.; Vichi, M.; Lévy, M. A Reduction in Marine Primary Productivity Driven by Rapid Warming over the Tropical Indian Ocean. Geophys. Res. Lett. 2016, 43, 826–833. [Google Scholar] [CrossRef]
- Trombetta, T.; Vidussi, F.; Mas, S.; Parin, D.; Simier, M.; Mostajir, B. Water Temperature Drives Phytoplankton Blooms in Coastal Waters. PLoS ONE 2019, 14, e0214933. [Google Scholar] [CrossRef]
- Thomas, A.C.; Townsend, D.W.; Weatherbee, R. Satellite-Measured Phytoplankton Variability in the Gulf of Maine. Cont. Shelf Res. 2003, 23, 971–989. [Google Scholar] [CrossRef]
- Blondeau-Patissier, D.; Gower, J.F.; Dekker, A.G.; Phinn, S.R.; Brando, V.E. A Review of Ocean Color Remote Sensing Methods and Statistical Techniques for the Detection, Mapping and Analysis of Phytoplankton Blooms in Coastal and Open Oceans. Prog. Oceanogr. 2014, 123, 123–144. [Google Scholar] [CrossRef]
- Ustaoğlu, F.; Tepe, Y.; Taş, B. Assessment of Stream Quality and Health Risk in a Subtropical Turkey River System: A Combined Approach Using Statistical Analysis and Water Quality Index. Ecol. Indic. 2020, 113, 105815. [Google Scholar] [CrossRef]
- López Martínez, J.; Farach Espinoza, E.B.; Herrera Cervantes, H.; García Morales, R. Long-Term Variability in Sea Surface Temperature and Chlorophyll Concentration in the Gulf of California. Remote Sens. 2023, 15, 4088. [Google Scholar] [CrossRef]
- Tang, D.; Kawamura, H.; Lee, M.A.; Van Dien, T. Seasonal and Spatial Distribution of Chlorophyll-Concentrations and Water Conditions in the Gulf of Tonkin, South China Sea. Remote Sens. Environ. 2003, 85, 475–483. [Google Scholar] [CrossRef]
- Van Vliet, M.T.H.; Zwolsman, J.J.G. Impact of Summer Droughts on the Water Quality of the Meuse River. J. Hydrol. 2008, 353, 1–17. [Google Scholar] [CrossRef]
- Suikkanen, S.; Laamanen, M.; Huttunen, M. Long-Term Changes in Summer Phytoplankton Communities of the Open Northern Baltic Sea. Estuar. Coast. Shelf Sci. 2007, 71, 580–592. [Google Scholar] [CrossRef]
- Tang, D.; Kester, D.R.; Ni, I.H.; Kawamura, H.; Hong, H. Upwelling in the Taiwan Strait During the Summer Monsoon Detected by Satellite and Shipboard Measurements. Remote Sens. Environ. 2002, 83, 457–471. [Google Scholar] [CrossRef]
- Wei, H.; Sun, J.; Moll, A.; Zhao, L. Phytoplankton Dynamics in the Bohai Sea-Observations and Modelling. J. Mar. Syst. 2004, 44, 233–251. [Google Scholar] [CrossRef]
- Schloss, I.R.; Abele, D.; Moreau, S.; Demers, S.; Bers, A.V.; González, O.; Ferreyra, G.A. Response of Phytoplankton Dynamics to 19-Year (1991–2009) Climate Trends in Potter Cove (Antarctica). J. Mar. Syst. 2012, 92, 53–66. [Google Scholar] [CrossRef]
- Schofield, O.; Saba, G.; Coleman, K.; Carvalho, F.; Couto, N.; Ducklow, H.; Finkel, Z.; Irwin, A.; Kahl, A.; Miles, T.; et al. Decadal Variability in Coastal Phytoplankton Community Composition in a Changing West Antarctic Peninsula. Deep-Sea Res. Part I-Oceanogr. Res. Pap. 2017, 124, 42–54. [Google Scholar] [CrossRef]
- Gong, G.-C.; Wen, Y.-H.; Wang, B.-W.; Liu, G.-J. Seasonal Variation of Chlorophyll Concentration, Primary Production and Environmental Conditions in the Subtropical East China Sea. Deep-Sea Res. Part II Top. Stud. Oceanogr. 2003, 50, 1219–1236. [Google Scholar] [CrossRef]
- Cloern, J.E.; Jassby, A.D.; Thompson, J.K.; Hieb, K.A. A Cold Phase of the East Pacific Triggers New Phytoplankton Blooms in San Francisco Bay. Proc. Natl. Acad. Sci. USA 2007, 104, 18561–18565. [Google Scholar] [CrossRef] [PubMed]
- Meerhoff, M.; Clemente, J.M.; de MELLO, F.T.; Iglesias, C.; Pedersen, A.R.; Jeppesen, E. Can Warm Climate-Related Structure of Littoral Predator Assemblies Weaken the Clear Water State in Shallow Lakes? Glob. Chang. Biol. 2007, 13, 1888–1897. [Google Scholar] [CrossRef]
- Hazen, E.L.; Jorgensen, S.; Rykaczewski, R.R.; Bograd, S.J.; Foley, D.G.; Jonsen, I.D.; Shaffer, S.A.; Dunne, J.P.; Costa, D.P.; Crowder, L.B.; et al. Predicted Habitat Shifts of Pacific Top Predators in a Changing Climate. Nat. Clim. Chang. 2013, 3, 234–238. [Google Scholar] [CrossRef]
- Jeppesen, E.; Kronvang, B.; Meerhoff, M.; Søndergaard, M.; Hansen, K.M.; Andersen, H.E.; Lauridsen, T.L.; Liboriussen, L.; Beklioglu, M.; Özen, A.; et al. Climate Change Effects on Runoff, Catchment Phosphorus Loading and Lake Ecological State, and Potential Adaptations. J. Environ. Qual. 2009, 38, 1930–1941. [Google Scholar] [CrossRef]
- Tang, D.L.; Kawamura, H.; Doan-Nhu, H.; Takahashi, W. Remote Sensing Oceanography of a Harmful Algal Bloom Off the Coast of Southeastern Vietnam. J. Geophys. Res. Ocean. 2004, 109, C03014. [Google Scholar] [CrossRef]
- Alvera-Azcárate, A.; Barth, A.; Beckers, J.M.; Weisberg, R.H. Multivariate Reconstruction of Missing Data in Sea Surface Temperature, Chlorophyll, and Wind Satellite Fields. J. Geophys. Res. Ocean. 2007, 112, C03008. [Google Scholar]
- Lin, I.I. Typhoon-Induced Phytoplankton Blooms and Primary Productivity Increase in the Western North Pacific Subtropical Ocean. J. Geophys. Res. Ocean. 2012, 117, C03039. [Google Scholar] [CrossRef]
- Agawin, N.S.; Duarte, C.M.; Agustí, S. Nutrient and Temperature Control of the Contribution of Picoplankton to Phytoplankton Biomass and Production. Limnol. Oceanogr. 2000, 45, 591–600. [Google Scholar] [CrossRef]
- Fitt, W.K.; McFarland, F.K.; Warner, M.E.; Chilcoat, G.C. Seasonal Patterns of Tissue Biomass and Densities of Symbiotic Dinoflagellates in Reef Corals and Relation to Coral Bleaching. Limnol. Oceanogr. 2000, 45, 677–685. [Google Scholar] [CrossRef]
- Carmack, E.; Macdonald, R.; Jasper, S. Phytoplankton Productivity on the Canadian Shelf of the Beaufort Sea. Mar. Ecol. Prog. Ser. 2004, 277, 37–50. [Google Scholar] [CrossRef]
- Leathwick, J.R.; Elith, J.; Francis, M.P.; Hastie, T.; Taylor, P. Variation in Demersal Fish Species Richness in the Oceans Surrounding New Zealand: An Analysis Using Boosted Regression Trees. Mar. Ecol. Prog. Ser. 2006, 321, 267–281. [Google Scholar] [CrossRef]
- Montes-Hugo, M.; Doney, S.C.; Ducklow, H.W.; Fraser, W.; Martinson, D.; Stammerjohn, S.E.; Schofield, O. Recent Changes in Phytoplankton Communities Associated with Rapid Regional Climate Change Along the Western Antarctic Peninsula. Science 2009, 323, 1470–1473. [Google Scholar] [CrossRef]
- Li, W.K.W.; McLaughlin, F.A.; Lovejoy, C.; Carmack, E.C. Smallest Algae Thrive as the Arctic Ocean Freshens. Science 2009, 326, 539. [Google Scholar] [CrossRef]
- Sathyendranath, S.; Brewin, R.J.; Brockmann, C.; Brotas, V.; Calton, B.; Chuprin, A.; Cipollini, P.; Couto, A.B.; Dingle, J.; Doerffer, R.; et al. An Ocean-Colour Time Series for Use in Climate Studies: The Experience of the Ocean-Colour Climate Change Initiative (Oc-Cci). Sensors 2019, 19, 4285. [Google Scholar] [CrossRef]
- Wang, M.; Liu, X.; Tan, L.; Jiang, L.; Son, S.; Shi, W.; Rausch, K.; Voss, K. Impacts of Viirs Sdr Performance on Ocean Color Products. J. Geophys. Res.-Atmos. 2013, 118, 10347–10360. [Google Scholar] [CrossRef]
- Wang, M.; Liu, X.; Jiang, L.; Son, S.; Sun, J.; Shi, W.; Tan, L.; Naik, P.; Mikelsons, K.; Wang, X.; et al. Evaluation of Viirs Ocean Color Products. In Ocean Remote Sensing and Monitoring from Space; SPIE: Bellingham, WA, USA, 2014; p. 9261. [Google Scholar]
- Wang, M.; Jiang, L.; Liu, X.; Son, S.; Sun, J.; Shi, W.; Tan, L.; Mikelsons, K.; Wang, X.; Lance, V. Viirs Ocean Color Products: A Progress Update. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (Igarss), Beijing, China, 10–15 July 2016; pp. 5848–5851. [Google Scholar]
- Wang, M.H.; Wilson, C. Applications of Satellite Ocean Color Products. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 2794–2797. [Google Scholar]
- Barnes, B.B.; Hu, C. Dependence of Satellite Ocean Color Data Products on Viewing Angles: A Comparison between Seawifs, Modis, and Viirs. Remote Sens. Environ. 2016, 175, 120–129. [Google Scholar] [CrossRef]
- Zeng, C.; Xu, H.; Fischer, A.M. Chlorophyll-a Estimation around the Antarctica Peninsula Using Satellite Algorithms: Hints from Field Water Leaving Reflectance. Sensors 2016, 16, 2075. [Google Scholar] [CrossRef]
- Haëntjens, N.; Boss, E.; Talley, L.D. Revisiting Ocean Color Algorithms for Chlorophyll and Particulate Organic Carbon in the Southern Ocean Using Biogeochemical Floats. J. Geophys. Res. Ocean. 2017, 122, 6583–6593. [Google Scholar] [CrossRef]
- Mélin, F.; Vantrepotte, V.; Chuprin, A.; Grant, M.; Jackson, T.; Sathyendranath, S. Assessing the Fitness-for-Purpose of Satellite Multi-Mission Ocean Color Climate Data Records: A Protocol Applied to Oc-Cci Chlorophyll-Data. Remote Sens. Environ. 2017, 203, 139–151. [Google Scholar] [CrossRef]
- Valente, A.; Sathyendranath, S.; Brotas, V.; Groom, S.; Grant, M.; Taberner, M.; Antoine, D.; Arnone, R.; Balch, W.M.; Barker, K.; et al. A Compilation of Global Bio-Optical in Situ Data for Ocean-Colour Satellite Applications. Earth Syst. Sci. Data 2016, 8, 235–252. [Google Scholar] [CrossRef]
- Valente, A.; Sathyendranath, S.; Brotas, V.; Groom, S.; Grant, M.; Taberner, M.; Antoine, D.; Arnone, R.; Balch, W.M.; Barker, K.; et al. A Compilation of Global Bio-Optical in Situ Data for Ocean-Colour Satellite Applications-Version Two. Earth Syst. Sci. Data 2019, 11, 1037–1068. [Google Scholar] [CrossRef]
- Valente, A.; Sathyendranath, S.; Brotas, V.; Groom, S.; Grant, M.; Jackson, T.; Chuprin, A.; Taberner, M.; Airs, R.; Antoine, D.; et al. A Compilation of Global Bio-Optical in Situ Data for Ocean Colour Satellite Applications–Version Three. Earth Syst. Sci. Data 2022, 14, 5737–5770. [Google Scholar] [CrossRef]
- Marullo, S.; Nardelli, B.B.; Guarracino, M.; Santoleri, R. Observing the Mediterranean Sea from Space: 21 Years of Pathfinder-Avhrr Sea Surface Temperatures (1985 to 2005): Re-Analysis and Validation. Ocean Sci. 2007, 3, 299–310. [Google Scholar] [CrossRef]
- Hughes, S.L.; Holliday, N.P.; Colbourne, E.; Ozhigin, V.; Valdimarsson, H.; Østerhus, S.; Wiltshire, K. Comparison of Time-Series of Temperature with Gridded Sea Surface Temperature Datasets in the North Atlantic. ICES J. Mar. Sci. 2009, 66, 1467–1479. [Google Scholar] [CrossRef]
- Fiedler, E.K.; McLaren, A.; Banzon, V.; Brasnett, B.; Ishizaki, S.; Kennedy, J.; Rayner, N.; Roberts-Jones, J.; Corlett, G.; Merchant, C.J.; et al. Intercomparison of Long-Term Sea Surface Temperature Analyses Using the Ghrsst Multi-Product Ensemble (Gmpe) System. Remote Sens. Environ. 2019, 222, 18–33. [Google Scholar] [CrossRef]
- Castro, S.L.; Wick, G.A.; Steele, M. Validation of Satellite Sea Surface Temperature Analyses in the Beaufort Sea Using Uptemp Buoys. Remote Sens. Environ. 2016, 187, 458–475. [Google Scholar] [CrossRef]
- Zabaleta, B.; Achkar, M.; Aubriot, L. Hotspot Analysis of Spatial Distribution of Algae Blooms in Small and Medium Water Bodies. Environ. Monit. Assess. 2021, 193, 221. [Google Scholar] [CrossRef]
- Ghalhari, G.F.; Roudbari, A.D. An Investigation on Thermal Patterns in Iran Based on Spatial Autocorrelation. Theor. Appl. Climatol. 2018, 131, 865–876. [Google Scholar] [CrossRef]
- Ijumulana, J.; Ligate, F.; Bhattacharya, P.; Mtalo, F.; Zhang, C. Spatial Analysis and Gis Mapping of Regional Hotspots and Potential Health Risk of Fluoride Concentrations in Groundwater of Northern Tanzania. Sci. Total Environ. 2020, 735, 139584. [Google Scholar] [CrossRef]
- Sánchez-Martín, J.-M.; Rengifo-Gallego, J.-I.; Blas-Morato, R. Hot Spot Analysis Versus Cluster and Outlier Analysis: An Enquiry into the Grouping of Rural Accommodation in Extremadura (Spain). ISPRS Int. J. Geo-Inf. 2019, 8, 176. [Google Scholar] [CrossRef]
- Mathur, S.; Agrawal, D.; Jajoo, A. Photosynthesis: Response to High Temperature Stress. J. Photochem. Photobiol. B-Biol. 2014, 137, 116–126. [Google Scholar] [CrossRef]
- Reynaud, S.; Leclercq, N.; Romaine-Lioud, S.; Ferrier-Pagés, C.; Jaubert, J.; Gattuso, J. Interacting Effects of Co Partial Pressure and Temperature on Photosynthesis and Calcification in a Scleractinian Coral. Glob. Chang. Biol. 2003, 9, 1660–1668. [Google Scholar] [CrossRef]
- Davis, T.W.; Berry, D.L.; Boyer, G.L.; Gobler, C.J. The Effects of Temperature and Nutrients on the Growth and Dynamics of Toxic and Non-Toxic Strains of During Cyanobacteria Blooms. Harmful Algae 2009, 8, 715–725. [Google Scholar] [CrossRef]
- Montagnes, D.J.S.; Franklin, D.J. Effect of Temperature on Diatom Volume, Growth Rate, and Carbon and Nitrogen Content: Reconsidering Some Paradigms. Limnol. Oceanogr. 2001, 46, 2008–2018. [Google Scholar] [CrossRef]
- Rigosi, A.; Carey, C.C.; Ibelings, B.W.; Brookes, J.D. The Interaction between Climate Warming and Eutrophication to Promote Cyanobacteria Is Dependent on Trophic State and Varies among Taxa. Limnol. Oceanogr. 2014, 59, 99–114. [Google Scholar] [CrossRef]
- Siegel, D.A.; Behrenfeld, M.J.; Maritorena, S.; McClain, C.R.; Antoine, D.; Bailey, S.W.; Bontempi, P.S.; Boss, E.S.; Dierssen, H.M.; Doney, S.C. Yoder. Regional to Global Assessments of Phytoplankton Dynamics from the Seawifs Mission. Remote Sens. Environ. 2013, 135, 77–91. [Google Scholar] [CrossRef]
- Hirst, A.G.; Bunker, A.J. Growth of Marine Planktonic Copepods: Global Rates and Patterns in Relation to Chlorophyll, Temperature, and Body Weight. Limnol. Oceanogr. 2003, 48, 1988–2010. [Google Scholar] [CrossRef]
- Behrenfeld, M.J.; Boss, E.; Siegel, D.A.; Shea, D.M. Carbon-Based Ocean Productivity and Phytoplankton Physiology from Space. Glob. Biogeochem. Cycles 2005, 19, GB1006. [Google Scholar] [CrossRef]



| Algorithm | Band Ratio(R) | Coefficient | ||||
|---|---|---|---|---|---|---|
| a0 | a1 | a2 | a3 | a4 | ||
| OC2V | lg(Rrs486/Rrs551) | 0.3410 | −3.0010 | 2.8110 | −2.0410 | −0.0400 |
| OC3V | lg(max(Rrs443,Rrs486)/Rrs551) | 0.3483 | −2.9959 | 2.9873 | −1.4813 | −0.0597 |
| Inversion Range | OC3V(SST) * |
|---|---|
| Less than 10 °C | |
| 10–20 °C | |
| 20–25 °C | |
| 25–30 °C |
| Temperature Interval | a0 | a1 | a2 | a3 | a4 | Statistics | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Value | Standard Error | Value | Standard Error | Value | Standard Error | Value | Standard Error | Value | Standard Error | Reduced Chi-Sqr | R2 | |
| Less than 10 °C | 0.4616 | 0.00534 | −2.03633 | 0.02842 | −1.85074 | 0.15734 | 2.74338 | 0.1961 | −0.01447 | 0.03645 | 0.00352 | 0.88164 |
| 10–20 °C | 0.06249 | 0.01131 | −1.0274 | 0.11553 | −0.63679 | 0.35079 | −0.97679 | 0.37967 | 0.02511 | 0.00374 | 0.00251 | 0.90911 |
| 20–25 °C | 0.23131 | 0.00576 | −2.842 | 0.06537 | 3.49187 | 0.18816 | −3.20636 | 0.17662 | 0.01044 | 0.00163 | 0.00055 | 0.92509 |
| 25–30 °C | 0.08281 | 0.01873 | −1.00229 | 0.04679 | −1.1894 | 0.1006 | 0.87698 | 0.2711 | −0.03798 | 0.04751 | 0.00122 | 0.89923 |
| Inversion Range | Model Formula | RMSE (mg/m3) | MAE (mg/m3) | MRE |
|---|---|---|---|---|
| All areas | OC3V | 0.062 | 0.030 | 19.8% |
| Less than 10 °C | OC3V(SST) | 0.055 | 0.029 | 12.1% |
| 10–20 °C | OC3V(SST) | 0.048 | 0.029 | 11.0% |
| 20–25 °C | OC3V(SST) | 0.028 | 0.013 | 14.1% |
| 25–30 °C | OC3V(SST) | 0.048 | 0.017 | 11.9% |
| Model Formula | RMSE (mg/m3) | MAE (mg/m3) | MRE |
|---|---|---|---|
| OC3V | 7.479 | 1.175 | 70.1% |
| OC3V(SST) | 0.678 | 0.272 | 37.9% |
| Time | Model Formula | RMSE (mg/m3) | MAE (mg/m3) | MRE |
|---|---|---|---|---|
| January 2017 | OC3V | 0.286 | 0.035 | 21.1% |
| OC3V(SST) (Less than 10 °C) | 0.107 | 0.058 | 18.4% | |
| OC3V(SST) (10–20 °C) | 0.063 | 0.035 | 12.9% | |
| OC3V(SST) (20–25 °C) | 0.022 | 0.011 | 11.1% | |
| OC3V(SST) (25–30 °C) | 0.097 | 0.021 | 13.9% | |
| April 2017 | OC3V | 0.509 | 0.037 | 19.9% |
| OC3V(SST) (Less than 10 °C) | 0.115 | 0.052 | 17.2% | |
| OC3V(SST) (10–20 °C) | 0.101 | 0.050 | 15.8% | |
| OC3V(SST) (20–25 °C) | 1.060 | 0.036 | 17.5% | |
| OC3V(SST) (25–30 °C) | 0.050 | 0.017 | 12.4% | |
| July 2017 | OC3V | 0.095 | 0.029 | 19.4% |
| OC3V(SST) (Less than 10 °C) | 0.147 | 0.079 | 22.4% | |
| OC3V(SST) (10–20 °C) | 0.067 | 0.034 | 12.8% | |
| OC3V(SST) (20–25 °C) | 0.110 | 0.020 | 13.3% | |
| OC3V(SST) (25–30 °C) | 0.046 | 0.019 | 14.9% | |
| October 2017 | OC3V | 0.107 | 0.031 | 19.9% |
| OC3V(SST) (Less than 10 °C) | 0.089 | 0.039 | 12.7% | |
| OC3V(SST) (10–20 °C) | 0.063 | 0.036 | 13.0% | |
| OC3V(SST) (20–25 °C) | 0.061 | 0.014 | 10.4% | |
| OC3V(SST) (25–30 °C) | 0.065 | 0.018 | 12.6% | |
| January 2018 | OC3V | 0.083 | 0.033 | 21.7% |
| OC3V(SST) (Less than 10 °C) | 0.114 | 0.055 | 16.5% | |
| OC3V(SST) (10–20 °C) | 0.060 | 0.035 | 12.5% | |
| OC3V(SST) (20–25 °C) | 0.040 | 0.014 | 11.5% | |
| OC3V(SST) (25–30 °C) | 0.049 | 0.019 | 14.2% | |
| April 2018 | OC3V | 0.095 | 0.032 | 20.0% |
| OC3V(SST) (Less than 10 °C) | 0.110 | 0.052 | 18.2% | |
| OC3V(SST) (10–20 °C) | 0.075 | 0.044 | 15.8% | |
| OC3V(SST) (20–25 °C) | 0.032 | 0.013 | 15.6% | |
| OC3V(SST) (25–30 °C) | 0.042 | 0.016 | 12.0% | |
| July 2018 | OC3V | 0.077 | 0.030 | 20.0% |
| OC3V(SST) (Less than 10 °C) | 0.123 | 0.074 | 22.7% | |
| OC3V(SST) (10–20 °C) | 0.067 | 0.033 | 12.9% | |
| OC3V(SST) (20–25 °C) | 0.097 | 0.019 | 12.2% | |
| OC3V(SST) (25–30 °C) | 0.052 | 0.020 | 15.9% | |
| October 2018 | OC3V | 0.062 | 0.030 | 19.8% |
| OC3V(SST) (Less than 10 °C) | 0.055 | 0.029 | 12.1% | |
| OC3V(SST) (10–20 °C) | 0.048 | 0.029 | 11.0% | |
| OC3V(SST) (20–25 °C) | 0.028 | 0.013 | 14.1% | |
| OC3V(SST) (25–30 °C) | 0.048 | 0.017 | 11.9% | |
| January 2019 | OC3V | 0.226 | 0.038 | 20.7% |
| OC3V(SST) (Less than 10 °C) | 0.105 | 0.058 | 15.4% | |
| OC3V(SST) (10–20 °C) | 0.063 | 0.036 | 12.4% | |
| OC3V(SST) (20–25 °C) | 0.037 | 0.012 | 11.3% | |
| OC3V(SST) (25–30 °C) | 0.342 | 0.027 | 13.8% | |
| April 2019 | OC3V | 0.124 | 0.033 | 18.7% |
| OC3V(SST) (Less than 10 °C) | 0.104 | 0.049 | 17.1% | |
| OC3V(SST) (10–20 °C) | 0.076 | 0.045 | 15.7% | |
| OC3V(SST) (20–25 °C) | 0.078 | 0.015 | 14.0% | |
| OC3V(SST) (25–30 °C) | 0.328 | 0.025 | 12.0% | |
| July 2019 | OC3V | 0.075 | 0.029 | 17.7% |
| OC3V(SST) (Less than 10 °C) | 0.112 | 0.070 | 26.3% | |
| OC3V(SST) (10–20 °C) | 0.079 | 0.039 | 13.9% | |
| OC3V(SST) (20–25 °C) | 0.168 | 0.025 | 13.2% | |
| OC3V(SST) (25–30 °C) | 0.048 | 0.017 | 1.7% | |
| October 2019 | OC3V | 0.090 | 0.032 | 19.2% |
| OC3V(SST) (Less than 10 °C) | 0.121 | 0.042 | 12.5% | |
| OC3V(SST) (10–20 °C) | 0.062 | 0.033 | 11.2% | |
| OC3V(SST) (20–25 °C) | 0.035 | 0.013 | 10.3% | |
| OC3V(SST) (25–30 °C) | 0.037 | 0.015 | 1.5% |
| Time | Model Formula | RMSE (mg/m3) | MAE (mg/m3) | MRE |
|---|---|---|---|---|
| January 2017 | OC-CCI | 1.325 | 0.645 | 108.9% |
| OC3V | 2.584 | 0.867 | 146.4% | |
| OC3V(SST) | 1.242 | 0.524 | 82.6% | |
| April 2017 | OC-CCI | 2.150 | 1.010 | 98.2% |
| OC3V | 2.366 | 1.254 | 166.2% | |
| OC3V(SST) | 2.049 | 0.791 | 72.9% | |
| July 2017 | OC-CCI | 1.363 | 0.666 | 105.1% |
| OC3V | 4.385 | 1.390 | 128.8% | |
| OC3V(SST) | 0.717 | 0.467 | 91.1% | |
| October 2017 | OC-CCI | 2.057 | 0.913 | 74.0% |
| OC3V | 4.882 | 1.953 | 126.2% | |
| OC3V(SST) | 2.496 | 0.936 | 56.7% | |
| January 2018 | OC-CCI | 2.431 | 1.251 | 138.6% |
| OC3V | 3.114 | 1.890 | 221.5% | |
| OC3V(SST) | 2.510 | 1.126 | 92.1% | |
| April 2018 | OC-CCI | 2.286 | 0.921 | 92.8% |
| OC3V | 2.285 | 1.107 | 153.7% | |
| OC3V(SST) | 2.259 | 0.882 | 78.9% | |
| July 2018 | OC-CCI | 0.483 | 0.218 | 32.9% |
| OC3V | 3.146 | 1.138 | 64.3% | |
| OC3V(SST) | 1.518 | 0.600 | 51.8% | |
| October 2018 | OC-CCI | 0.389 | 0.181 | 45.3% |
| OC3V | 0.580 | 0.236 | 59.6% | |
| OC3V(SST) | 0.326 | 0.167 | 43.6% | |
| January 2019 | OC-CCI | 2.059 | 1.228 | 72.4% |
| OC3V | 2.433 | 1.565 | 96.5% | |
| OC3V(SST) | 2.177 | 1.249 | 57.9% | |
| April 2019 | OC-CCI | 1.767 | 0.613 | 59.1% |
| OC3V | 1.985 | 0.724 | 109.1% | |
| OC3V(SST) | 1.849 | 0.627 | 67.5% | |
| July 2019 | OC-CCI | 2.401 | 0.902 | 76.3% |
| OC3V | 2.391 | 0.959 | 106.7% | |
| OC3V(SST) | 2.696 | 1.039 | 88.5% | |
| October 2019 | OC-CCI | 0.016 | 0.008 | 7.2% |
| OC3V | 0.008 | 0.008 | 7.8% | |
| OC3V(SST) | 0.014 | 0.012 | 10.4% |
| Temperature Range | The Moran I Index | z-Score | p-Value |
|---|---|---|---|
| Less than 10 °C | 0.356 | 955.8 | 0.000 |
| 10 °C to 20 °C | 0.591 | 370.1 | 0.000 |
| 20 °C to 25 °C | 0.273 | 536.2 | 0.000 |
| 25 °C to 30 °C | 0.497 | 255.9 | 0.000 |
| Temperature Range | RMSE (mg/m3) | MAE (mg/m3) | MRE |
|---|---|---|---|
| 9.5 °C–10 °C | 0.013 | 0.013 | 5.9% |
| 10 °C–10.5 °C | 0.013 | 0.011 | 5.0% |
| 19.5 °C–20 °C | 0.006 | 0.005 | 7.2% |
| 20 °C–20.5 °C | 0.006 | 0.005 | 7.5% |
| 24.5 °C–25 °C | 0.005 | 0.005 | 5.9% |
| 25 °C–25.5 °C | 0.005 | 0.005 | 5.0% |
| Temperature Range | RMSE (mg/m3) | MAE (mg/m3) | MRE |
|---|---|---|---|
| 9.5 °C–10 °C | 0.064 | 0.041 | 12.9% |
| 10 °C–10.5 °C | 0.068 | 0.040 | 10.9% |
| 19.5 °C–20 °C | 0.046 | 0.019 | 13.1% |
| 20 °C–20.5 °C | 0.027 | 0.013 | 10.2% |
| 24.5 °C–25 °C | 0.022 | 0.012 | 10.2% |
| 25 °C–25.5 °C | 0.097 | 0.020 | 18.0% |
| Temperature Range | RMSE (mg/m3) | MAE (mg/m3) | MRE |
|---|---|---|---|
| 9.5 °C–10 °C | 0.061 | 0.036 | 10.7% |
| 10 °C–10.5 °C | 0.068 | 0.042 | 12.3% |
| 19.5 °C–20 °C | 0.039 | 0.016 | 10.1% |
| 20 °C–20.5 °C | 0.032 | 0.016 | 13.3% |
| 24.5 °C–25 °C | 0.029 | 0.016 | 17.8% |
| 25 °C–25.5 °C | 0.032 | 0.014 | 11.3% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Y.; Leng, L.; Ji, X.; Wang, M.; Huo, Y.; Li, Z. Inversion and Analysis of Global Ocean Chlorophyll-a Concentration Based on Temperature Zoning. Remote Sens. 2024, 16, 2302. https://doi.org/10.3390/rs16132302
He Y, Leng L, Ji X, Wang M, Huo Y, Li Z. Inversion and Analysis of Global Ocean Chlorophyll-a Concentration Based on Temperature Zoning. Remote Sensing. 2024; 16(13):2302. https://doi.org/10.3390/rs16132302
Chicago/Turabian StyleHe, Yanbo, Liang Leng, Xue Ji, Mingchang Wang, Yanping Huo, and Zheng Li. 2024. "Inversion and Analysis of Global Ocean Chlorophyll-a Concentration Based on Temperature Zoning" Remote Sensing 16, no. 13: 2302. https://doi.org/10.3390/rs16132302
APA StyleHe, Y., Leng, L., Ji, X., Wang, M., Huo, Y., & Li, Z. (2024). Inversion and Analysis of Global Ocean Chlorophyll-a Concentration Based on Temperature Zoning. Remote Sensing, 16(13), 2302. https://doi.org/10.3390/rs16132302






