Estimation of the Wind Field with a Single High-Frequency Radar
Abstract
1. Introduction
2. Methods
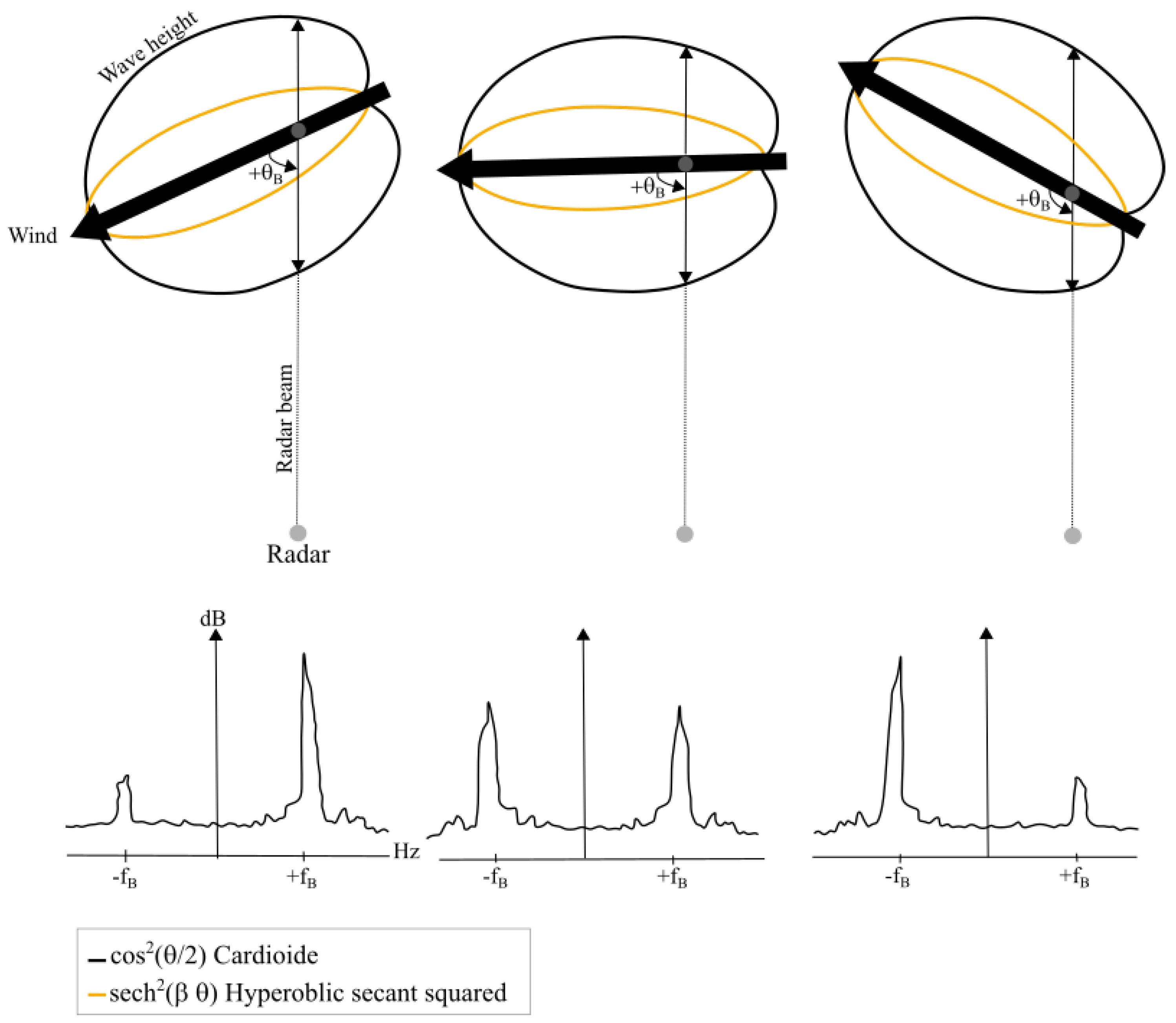
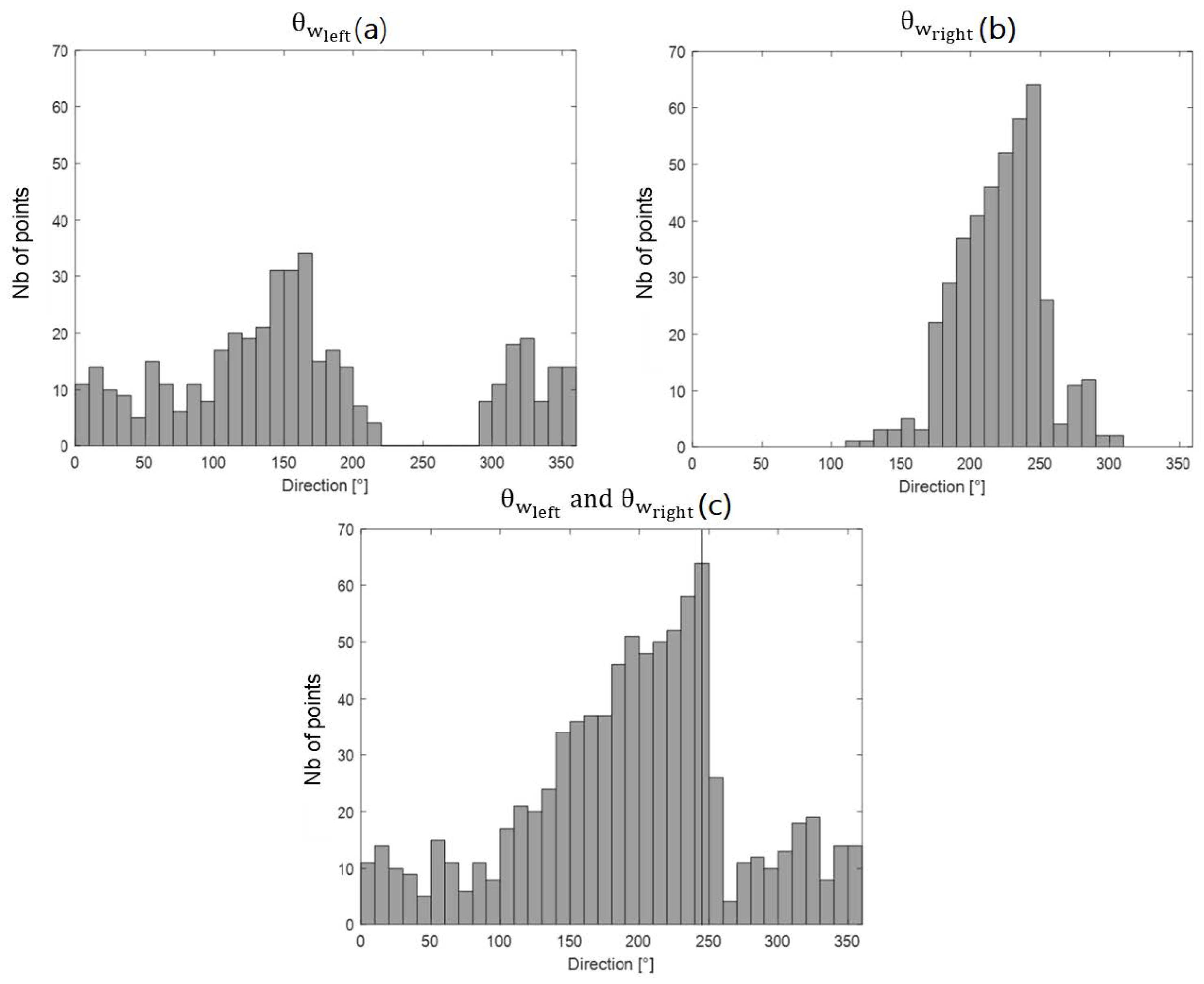
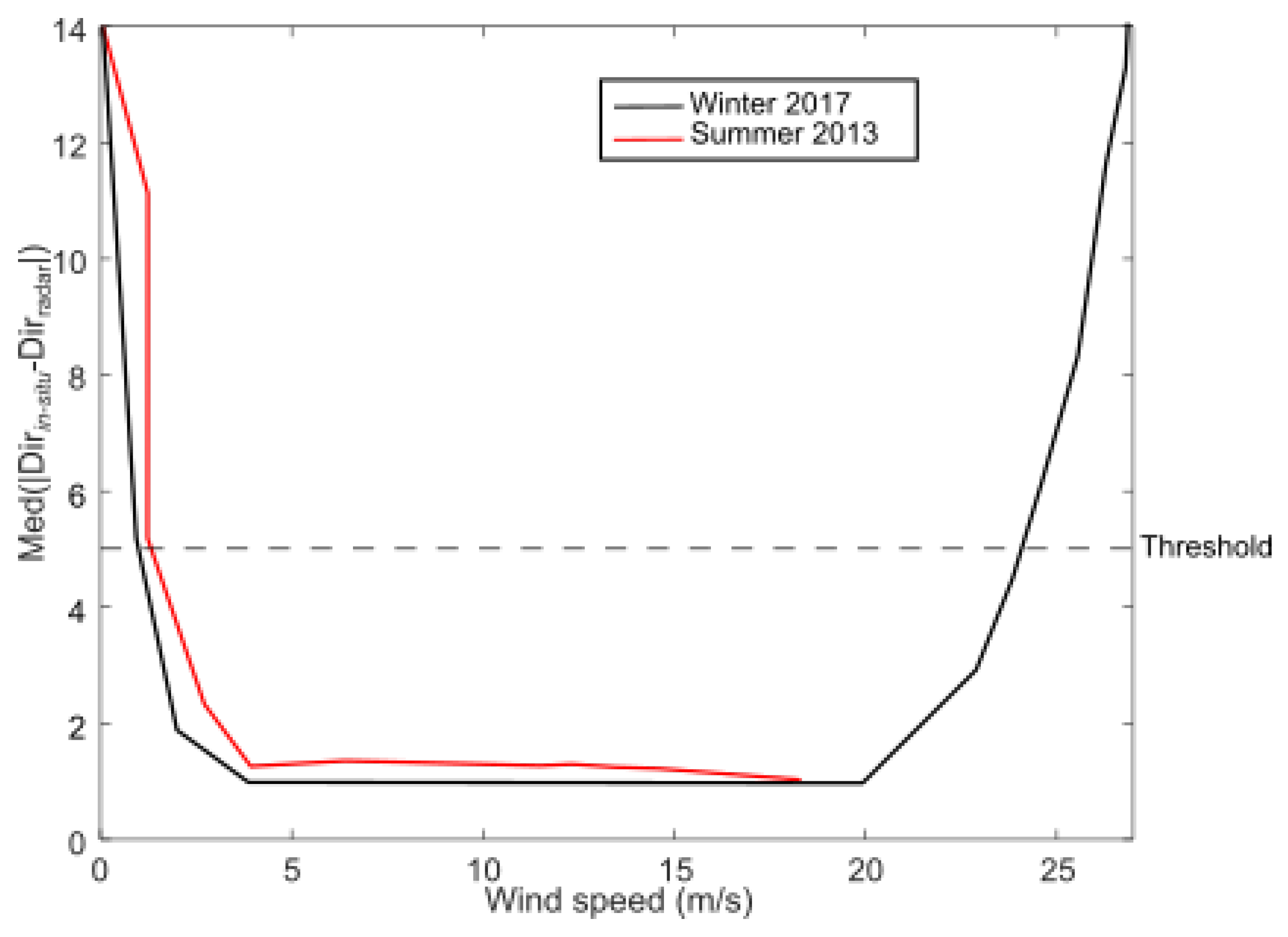
2.1. Wind Direction Estimation by a Single HF Radar
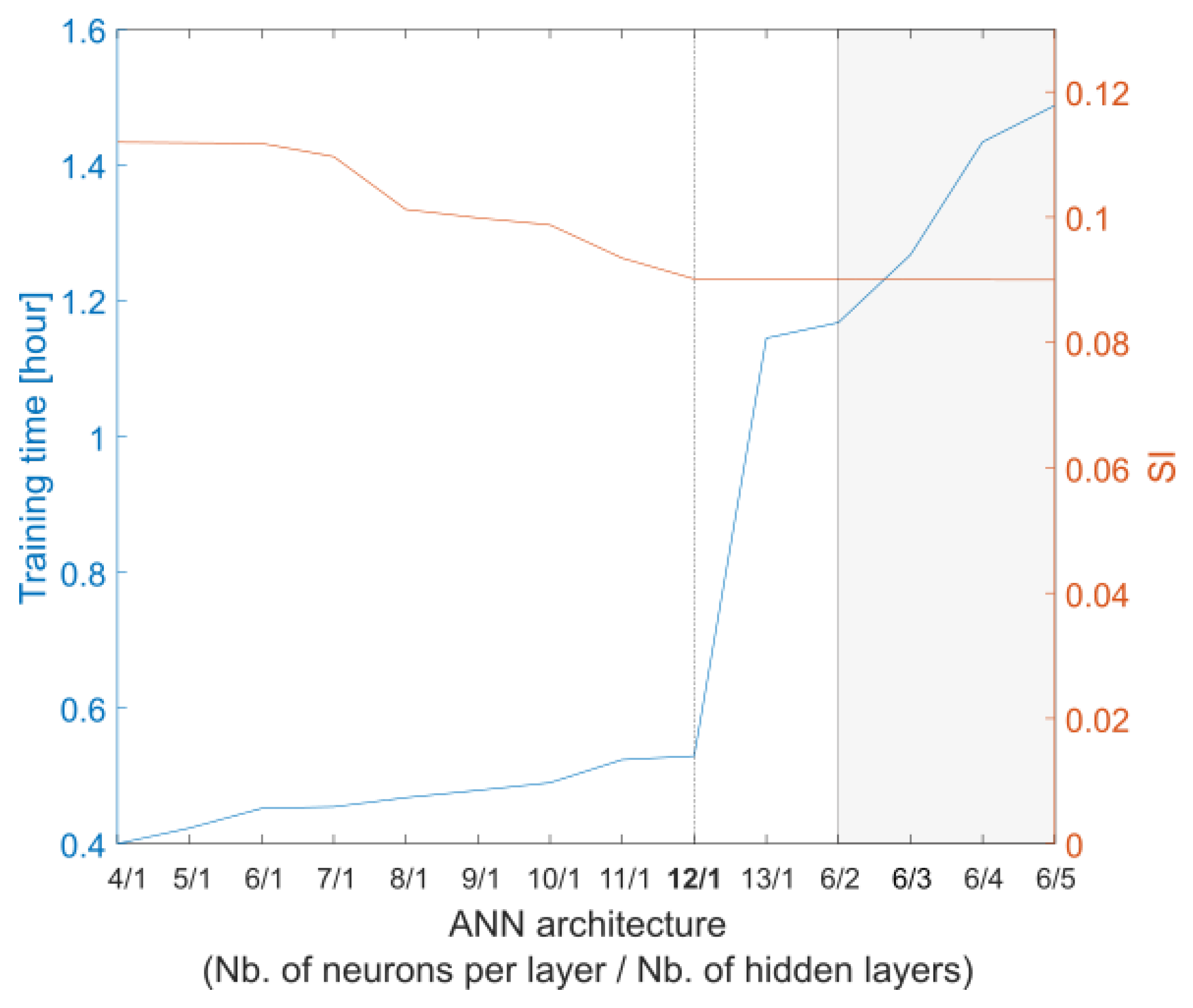
2.2. Wind Speed Estimation by a Single HF Radar
2.3. Statistical Analysis of Data
3. Study Area and Data
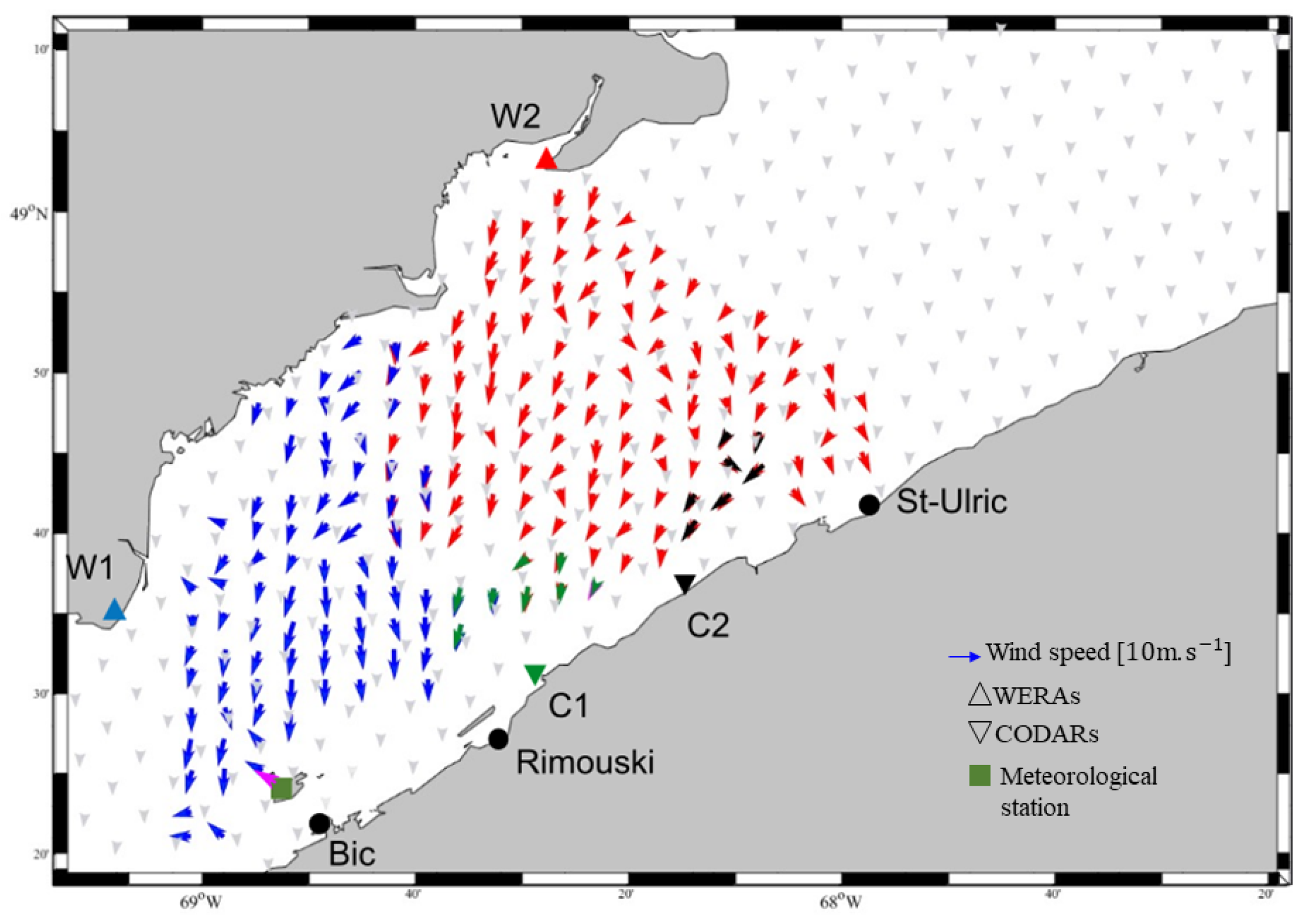
3.1. Study Area
3.2. Data
3.2.1. HF Radars
3.2.2. Meteorological and Model Data
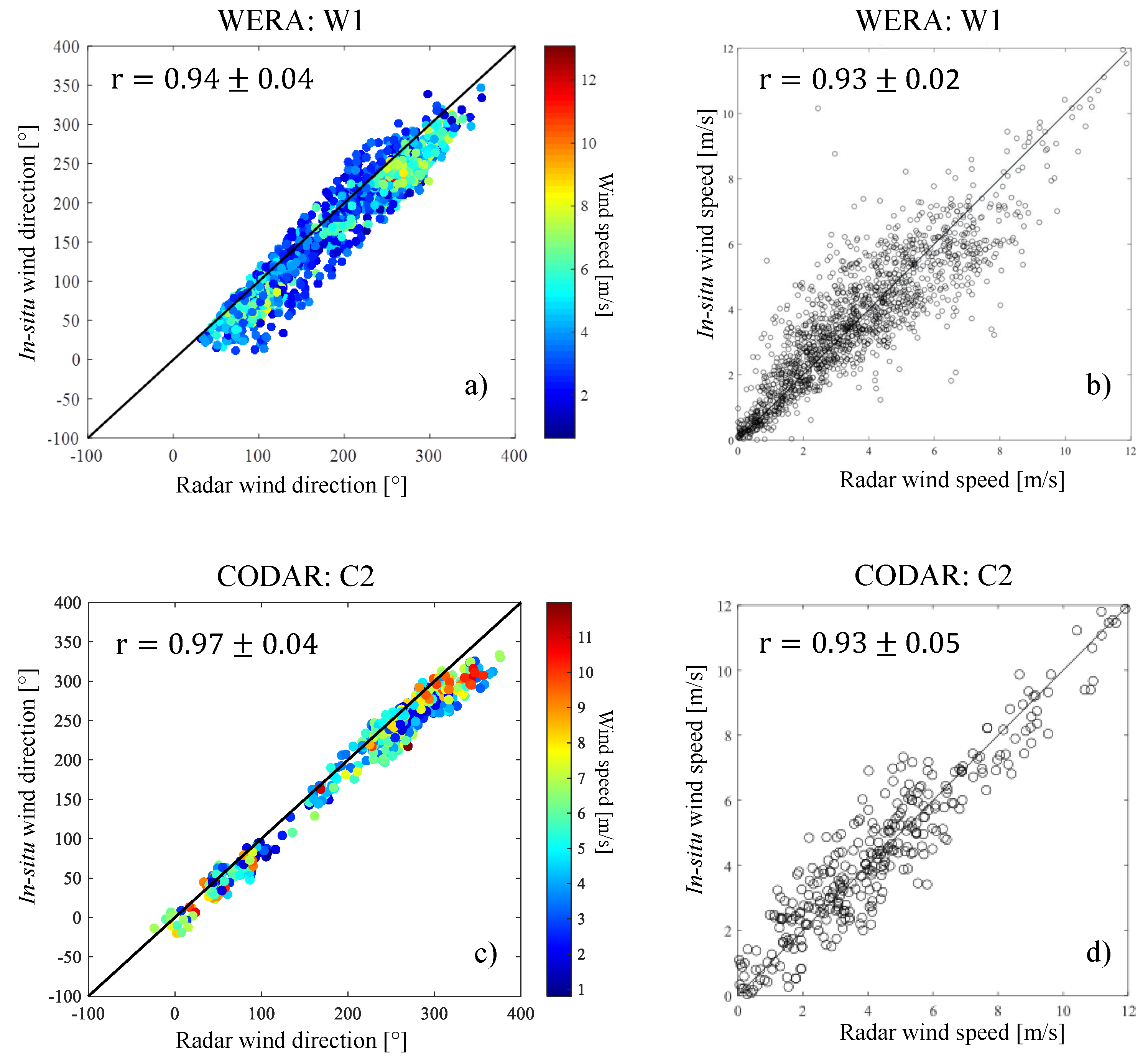
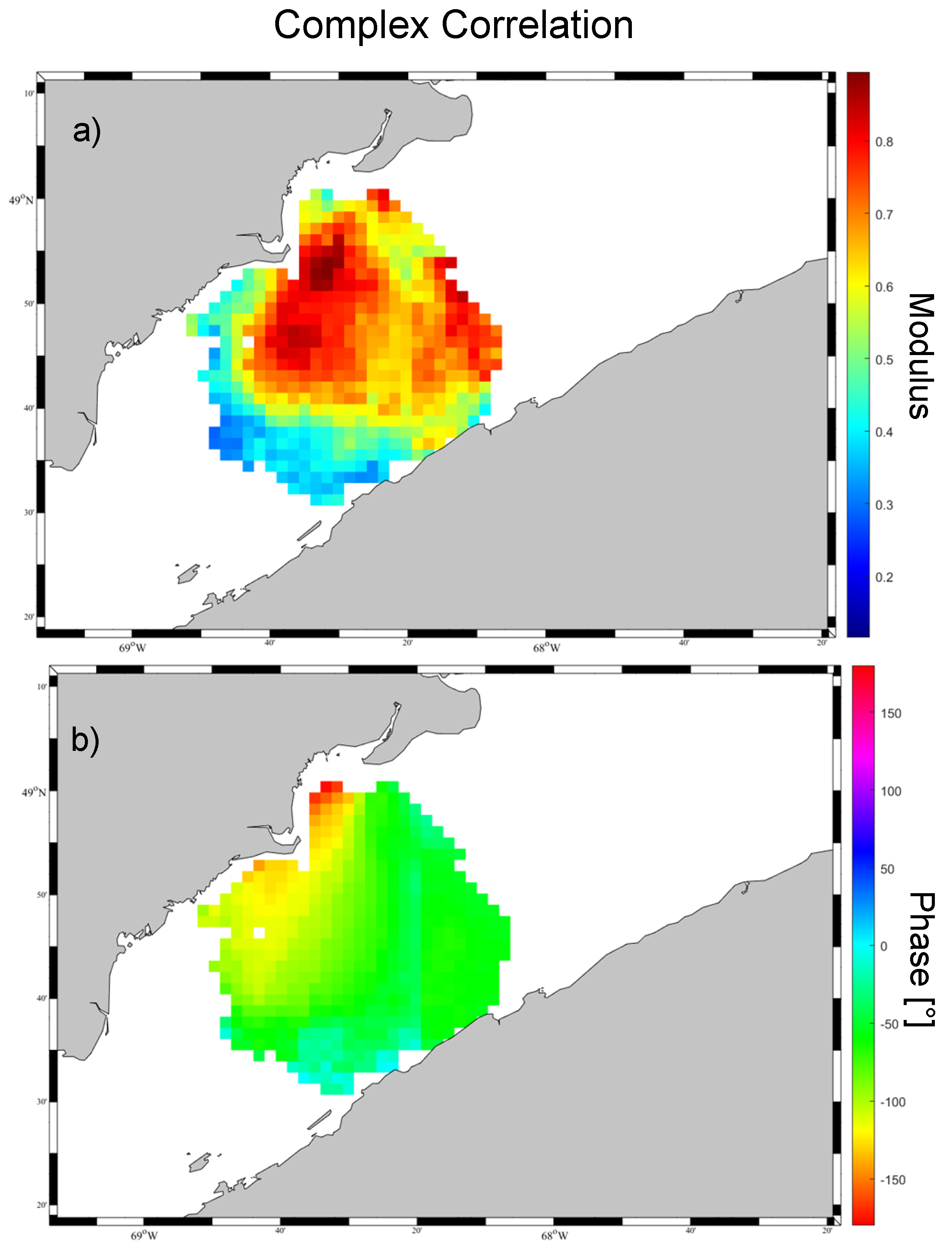
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Long, A.; Trizna, D. Mapping of North Atlantic winds by HF radar sea backscatter interpretation. IEEE Trans. Antennas Propag. 1973, 21, 680–685. [Google Scholar] [CrossRef]
- Heron, M.; Rose, R. On the application of HF ocean radar to the observation of temporal and spatial changes in wind direction. IEEE J. Ocean. Eng. 1986, 11, 210–218. [Google Scholar] [CrossRef]
- Fernandez, D.M.; Graber, H.C.; Paduan, J.D.; Barrick, D.E. Mapping wind direction with HF radar. Oceanography 1997, 10, 93–95. [Google Scholar] [CrossRef]
- Huang, W.; Gill, E.; Wu, S.; Wen, B.; Yang, Z.; Hou, J. Measuring surface wind direction by monostatic HF ground-wave radar at the Eastern China Sea. IEEE J. Ocean. Eng. 2004, 29, 1032–1037. [Google Scholar] [CrossRef]
- Ahearn, J.L.; Curley, S.R.; Headrick, J.M.; Trizna, D. Tests of remote skywave measurement of ocean surface conditions. Proc. IEEE 1974, 62, 681–687. [Google Scholar] [CrossRef]
- Dexter, P.; Theodoridis, S. Surface wind speed extraction from HF sky wave radar Doppler spectra. Radio Sci. 1982, 17, 643–652. [Google Scholar] [CrossRef]
- Huang, W.; Wu, S.; Gill, E.; Wen, B.; Hou, J. HF radar wave and wind measurement over the Eastern China Sea. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1950–1955. [Google Scholar] [CrossRef]
- Stewart, R.H.; Barnum, J.R. Radio measurements of oceanic winds at long ranges: An evaluation. Radio Sci. 1975, 10, 853–857. [Google Scholar] [CrossRef]
- Green, D.; Gill, E.; Huang, W. An inversion method for extraction of wind speed from high-frequency ground-wave radar oceanic backscatter. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3338–3346. [Google Scholar] [CrossRef]
- Vesecky, J.F.; Drake, J.; Laws, K.; Ludwig, F.L.; Teague, C.C.; Paduan, J.D.; Meadows, L. Using multifrequency HF radar to estimate ocean wind fields. In Proceedings of the International Geoscience and Remote Sensing Symposium, Anchorage, AK, USA, 20–24 September 2004; Volume 7, p. 4769. [Google Scholar]
- Shen, W.; Gurgel, K.W.; Voulgaris, G.; Schlick, T.; Stammer, D. Wind-speed inversion from HF radar first-order backscatter signal. Ocean Dyn. 2012, 62, 105–121. [Google Scholar] [CrossRef]
- Wen, C.; Tian, Y.; Wen, B. Wind speed extraction based on high frequency radar retrieved wind-driven current. IEEE Geosci. Remote Sens. Lett. 2020, 18, 1555–1559. [Google Scholar] [CrossRef]
- Wyatt, L.R. Progress towards an HF radar wind speed measurement method using machine learning. Remote Sens. 2022, 14, 2098. [Google Scholar] [CrossRef]
- Donelan, M.A.; Hamilton, J.; Hui, W. Directional spectra of wind-generated ocean waves. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1985, 315, 509–562. [Google Scholar]
- Banner, M.L. Equilibrium spectra of wind waves. J. Phys. Oceanogr. 1990, 20, 966–984. [Google Scholar] [CrossRef]
- Pawlowicz, R.; Beardsley, B.; Lentz, S. Classical tidal harmonic analysis including error estimates in MATLAB using T_TIDE. Comput. Geosci. 2002, 28, 929–937. [Google Scholar] [CrossRef]
- Dussol, A.; Chavanne, C.; Gregorio, S.; Dumont, D. Experimental Confirmation of Stokes Drift Measurement by High-Frequency Radars. J. Atmos. Ocean. Technol. 2022, 39, 1541–1559. [Google Scholar] [CrossRef]
- Kundu, P.K. Ekman veering observed near the ocean bottom. J. Phys. Oceanogr. 1976, 6, 238–242. [Google Scholar] [CrossRef]
- Shevlyakov, G.; Smirnov, P.; Shin, V.I.; Kim, K. Asymptotically minimax bias estimation of the correlation coefficient for bivariate independent component distributions. J. Multivar. Anal. 2012, 111, 59–65. [Google Scholar] [CrossRef]
- Emery, W.J.; Thomson, R.E. Statistical Methods and Error Handling. In Data Analysis Methods in Physical Oceanography; Elsevier Science: Amsterdam, The Netherlands, 2001; Chapter 3; pp. 193–304. [Google Scholar] [CrossRef]
- El-Sabh, M.I. Physical oceanography of the St. Lawrence estuary. In Hydrodynamics of Estuaries, Volume II, Estuarine Case Studies; CRC Press: Boca Raton, FL, USA, 1988; pp. 61–78. [Google Scholar]
- Koutitonsky, V.; Bugden, G. The physical oceanography of the Gulf of St. Lawrence: A review with emphasis on the synoptic variability of the motion. In The Gulf of St. Lawrence: Small Ocean or Big Estuary? Proceedings of a Workshop/Symposium Held at the Maurice Lamontagne Institute, Mont-Joli, QC, Canada, 14–17 March 1989; Therriault, J.C., Ed.; Canadian Special Publication of Fisheries and Aquatic Sciences, 113; Fisheries and Oceans Canada: Ottawa, ON, Canada, 1991; pp. 57–90. [Google Scholar]
- Mertz, G.; Koutitonsky, V.; Gratton, Y.; El-Sabh, M. Wind-induced eddy motion in the lower St. Lawrence Estuary. Estuar. Coast. Shelf Sci. 1992, 34, 543–556. [Google Scholar] [CrossRef]
- Tee, K.T.; Lim, T.H. The freshwater pulse—A numerical model with application to the St. Lawrence Estuary. J. Mar. Res. 1987, 45, 871–909. [Google Scholar] [CrossRef]
- Forrester, W. Internal tides in St. Lawrence estuary. J. Mar. Res. 1974, 32. [Google Scholar]
- Drapeau, G. Dynamique sédimentaire des littoraux de l’estuaire du Saint-Laurent. Géographie Phys. Et Quat. 1992, 46, 233–242. [Google Scholar] [CrossRef]
- Didier, D.; Bernatchez, P.; Augereau, E.; Caulet, C.; Dumont, D.; Bismuth, E.; Cormier, L.; Floc’h, F.; Delacourt, C. LiDAR validation of a video-derived beachface topography on a tidal flat. Remote Sens. 2017, 9, 826. [Google Scholar] [CrossRef]
- Bushnell, M.; Worthington, H. Manual for Real-Time Quality Control of High Frequency Radar Surface Current Data: A Guide to Quality Control and Quality Assurance for High Frequency Radar Surface Current Observations; U.S. Department of Commerce, National Oceanic and Atmospheric Administration, National Ocean Service, Integrated Ocean Observing System: Silver Spring, MD, USA, 2016.
- Emery, B. HFR CS processing toolbox for MATLAB, v1.0. Zendo 2018. [Google Scholar] [CrossRef]
- Gurgel, K.W.; Essen, H.H.; Kingsley, S. High-frequency radars: Physical limitations and recent developments. Coast. Eng. 1999, 37, 201–218. [Google Scholar] [CrossRef]
- Smith, G.C.; Roy, F.; Brasnett, B. Evaluation of an operational ice–ocean analysis and forecasting system for the Gulf of St Lawrence. Q. J. R. Meteorol. Soc. 2013, 139, 419–433. [Google Scholar] [CrossRef]
- Zeng, Y.; Zhou, H.; Roarty, H.; Wen, B. Wind speed inversion in high frequency radar based on neural network. Int. J. Antennas Propag. 2016, 2016, 2706521. [Google Scholar] [CrossRef]
- Kirincich, A. Remote sensing of the surface wind field over the coastal ocean via direct calibration of HF radar backscatter power. J. Atmos. Ocean. Technol. 2016, 33, 1377–1392. [Google Scholar] [CrossRef]
- Emery, B.; Kirincich, A. HF radar observations of nearshore winds. In Ocean Remote Sensing Technologies—High-Frequency, Marine and GNSS-Based Radar; Institution of Engineering and Technology: London, UK, 2021; pp. 191–216. [Google Scholar]
- Teague, C. Multifrequency HF radar observations of currents and current shears. IEEE J. Ocean. Eng. 1986, 11, 258–269. [Google Scholar] [CrossRef]







| Number of Points | r | RMS | SI | ||
|---|---|---|---|---|---|
| Summer 2013 | C1—Training | 317 (Training) 68 (Validation) 68 (Test) | 0.96 ± 0.04 0.92 ± 0.02 | 10 1.6 | - 0.09 |
| C2 | 456 | 0.97 ± 0.04 0.93 ± 0.05 | 16 1.6 | - 0.10 | |
| W2—Training | 1573 (Training) 337 (Validation) 337 (Test) | 0.95 ± 0.04 0.93 ± 0.05 | 8 1.3 | - 0.08 | |
| W1 | 2243 | 0.94 ± 0.04 0.93 ± 0.02 | 12 1.5 | - 0.09 | |
| Winter 2016–2017 | C1—Training | 250 (Training) 54 (Validation) 54 (Test) | 0.81 ± 0.03 0.83 ± 0.05 | 16 3.1 | - 0.12 |
| C2 | 289 | 0.79 ± 0.04 0.81 ± 0.05 | 19 3.9 | - 0.15 | |
| W1—Training | 1494 (Training) 320 (Validation) 320 (Test) | 0.87 ± 0.04 0.91 ± 0.02 | 9 2.2 | - 0.09 | |
| W2 | 1889 | 0.84 ± 0.02 0.89 ± 0.05 | 12 2.3 | - 0.09 |
| Source | Method | Site # | Correlation Coefficient | SImax | Max Speed | Min Speed |
|---|---|---|---|---|---|---|
| Dexter and Theodoridis, 1982 [6] | Inverse wave model | 2 | - | 0.35 | 15 | - |
| Vesecky et al., 2005 [10] | Partial Least Squares | 2 | 0.8 | - | 14 | 4 |
| Shen et al., 2012 [11] | ANN using first-order peaks | 2 | 0.79–0.84 | 0.1 | 20 | 5 |
| Shen et al., 2012 [11] | ANN usins spreading | 2 | 0.65–0.68 | 0.14 | 20 | 5 |
| Zeng et al., 2016 [32] | ANN using ocean parameters | 2 | 0.65–0.68 | 0.13 | 13 | 5 |
| Wen et al., 2020 [12] | ANN using first-order peaks | 2 | 0.80–0.86 | - | 17 * | 0 * |
| Emery and Kirincich, 2021 [34] | First-order peaks [33] | 2 | 0.63–0.75 | 0.19 | 10 | - |
| Wyatt, 2022 [13] | SVR method | 2 | 0.82–0.95 | 0.13–0.20 | 20 | - |
| This study | ANN using first-order peaks | 1 | 0.79–0.97 | 0.08–0.15 | 24 | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dussol, A.; Chavanne, C. Estimation of the Wind Field with a Single High-Frequency Radar. Remote Sens. 2024, 16, 2258. https://doi.org/10.3390/rs16132258
Dussol A, Chavanne C. Estimation of the Wind Field with a Single High-Frequency Radar. Remote Sensing. 2024; 16(13):2258. https://doi.org/10.3390/rs16132258
Chicago/Turabian StyleDussol, Abïgaëlle, and Cédric Chavanne. 2024. "Estimation of the Wind Field with a Single High-Frequency Radar" Remote Sensing 16, no. 13: 2258. https://doi.org/10.3390/rs16132258
APA StyleDussol, A., & Chavanne, C. (2024). Estimation of the Wind Field with a Single High-Frequency Radar. Remote Sensing, 16(13), 2258. https://doi.org/10.3390/rs16132258






