Abstract
In this study, a tropical cyclone or typhoon rainfall forecast model based on Random Forest is developed to forecast the daily rainfall at 133 weather stations in China. The input factors to the model training process include rainfall observations during 1960–2018, typhoon information (position and intensity), station information (position and altitude), and properties of the western Pacific subtropical high. Model evaluation shows that besides the distance between a station and cyclone, the subtropical high properties are ranked very high in the model’s feature importance, especially the subtropical ridgeline, and intensity. These aspects of the subtropical high influence the location and timing of typhoon landfall. The forecast model has a correlation coefficient of about 0.73, an Index of Agreement of nearly 0.8, and a mean bias of 1.28 mm based on the training dataset. Biases are consistently low, with both positive and negative signs, for target stations in the outer rainband (up to 1000 km, beyond which the model does not forecast) of typhoons. The range of biases is much larger for target stations in the inner-core (0–200 km) region. In this region, the model mostly overestimates (underestimates) the small (large) rain rates. Cases study of Typhoon Doksuri and Talim in 2023, as independent cases, shows the high performance of the model in forecasting the peak rain rates and timing of their occurrence of the two impactful typhoons.
1. Introduction
One of the ways for typhoons to cause disasters is the large amount of water content they carry and bring towards the land during landfall [1] (Figure A1), which may trigger heavy rainfall on a large scale [2]. For example, Super Typhoon Doksuri (2023) affected fourteen provinces (autonomous regions and municipalities) during landfall in eastern China, causing serious damage and flooding with torrential rains in many places including many inland regions to the north [3]. And studies have shown that the intensity of typhoons making landfall in East Asia is getting stronger [4].
Although meteorologists and forecasters have committed to improving the accuracy and timeliness of rainfall forecasts, these aspects of forecasts are still difficult to meet the needs of operations and society due to factors such as limitations in the means of detection and insufficient knowledge of the microphysical processes of rainfall [5,6]. Furthermore, rainfall forecasting for typhoon landfall events, especially estimating the affected areas, is a great challenge [7,8]. Dynamical numerical weather prediction (NWP) models have been improving in rainfall forecasts; however, the biases in rain intensity, timing, and patterns are still large [9,10,11].
In recent years, with the application of artificial intelligence (AI) technology in the field of meteorology [12,13], machine learning has been widely used to improve the accuracy and timeliness of various types of weather forecasts [11,14]. Previous studies have used deep learning to calibrate NWP models to forecast weather including rainfall more accurately. For example, a model that predicts very short-term rainfall was developed in South Korea by training on historical rainfall data and achieved critical success indices of 0.6 for moderate rainfall events and 0.4 for strong rainfall events at the 1 h lead time [15]. While models of this kind depend on the large output products from traditional numerical forecasts, AI models trained by observations can operate quickly and independently from NWP forecasts and also avoid their inherent biases [16,17,18,19]. In particular, Random Forest (RF), as an integrated learning model consisting of multiple decision trees, shows excellent performance in dealing with complex systems with high-dimensional and nonlinear relationships. Its insensitivity to outliers and strong generalization ability make it an ideal choice for forecasting complex systems such as the weather [20]. In applying RF, the systematic model training process can establish complex nonlinear relationships. For example, Chen et al. [21] established an accurate correspondence between typhoons, meteorological factors, and regional pollution indices. This and similar studies suggest that it is feasible to establish a correspondence between potential environmental factors and typhoon rainfall, which is the major aim of this study.
The critical part of developing such a forecast model is whether the most important predictors can be identified. The RF-based model that we present learns from a large amount of historical data and can capture the potential relationships between various meteorological variables with relative accuracy [22]. Thus, the model can generate reliable forecasts of rainfall in typhoon-affected areas and at the same time reveal the largest contributing factors to the forecasts for physical interpretation. RF is a meta-estimator that fits several decision tree classifiers and aggregates their regression values to obtain a forecast; thus, the number of decision trees and maximum depth are critical for the forecast accuracy of RF-based models. Incorporating RF into the development of radar-derived rainfall forecasting models for quantitative precipitation forecasting (QPF) is an excellent case study [23]. Huang et al. [24] performed forecasts of typhoon tracks and intensities by incrementally increasing the number of decision trees in their RF model to determine the optimal number of decision trees that make up a Random Forest. Additionally, Uddin et al. [18] integrate the grid search cross-validation method to find the best decision tree number and max depth for a RF-based forecast typhoon rainfall and track model.
The data sources and processing procedures are described in Section 2. Section 3 consists of a discussion on the model development and its evaluation. The performance of the model concerning an independent dataset from the training period is then discussed, followed by a further illustration of its skill in forecasting the rainfall associated with Typhoon Doksuri (2023) and Talim (2023). Bias characteristics of the model are analyzed in Section 3.2. Then, we conclude the study in Section 6.
2. Data Sources and Processing
In this study, data from 133 meteorological stations of the China Meteorological Agency (CMA) were selected during the construction of the model training set (Figure 1b). Selected stations have a long period (from 1960 to the present) and cover most of the coastal and inland areas of China that may be affected by typhoons, in addition to their participation in the global transmission system. The data from the selected stations show good temporal continuity, spatial homogeneity, and high reliability and consistency. The selected typhoon cases, 719 in total, are all those that affected or made direct landfall in China from 1960 to 2018 (Figure 1a and Appendix A.1) [25,26]. The data used include those listed below.
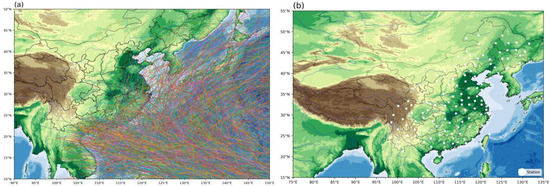
Figure 1.
Overview of the data used in this study. (a) Best tracks of the typhoons that affected or made direct landfall in China during 1960–2018. (b) Locations of the 133 CMA stations (white dots). The different colors of the typhoon tracks are for visualization purposes only.
- The CMA tropical cyclone best track dataset provided by the CMA Tropical Cyclone Data Center is used. The dataset provides the latitude (Lat) and longitude (Long) positions of the centers of the studied typhoons at three or six hourly intervals, the minimum pressure at the center of the typhoon (cap), and the maximum wind speed near the center of the typhoon (mws).
- Typhoon-related rainfall data (PREC) are used. The CMA Tropical Cyclone Data Center has compiled the typhoon daily precipitation dataset, which only includes rain recorded in the 133 stations when there was a typhoon impact. This dataset forms the basis of observations for model training and validation in our study.
- The stations’ longitude (Long_sta), latitude (Lat_sta), and altitude (Alt) based on the data provided by the CMA Tropical Cyclone Data Center are used.
- Environmental parameters are based on the ERA5 reanalysis dataset from 1960 to 2023 provided by the ECMWF. The parameters include the 500 hPa geopotential (Z) and zonal winds (u). From ERA5, the area index, intensity index, ridgeline index, and westernmost point of the subtropical high were also calculated. The domain of consideration was north of 10°N and 90°E to 180°.
As an integral part of the East Asia summer monsoon system, fluctuations in the western Pacific subtropical high (WPSH) exert profound impacts on China’s climatic variability [27,28], thereby inevitably modulating regional typhoon-induced rainfall [2]. Variations in the WPSH can significantly influence the primary track of typhoons or even trigger typhoon events. If the WPSH is stronger and exhibits higher WPSHI values, it can lead to a reduction in the number of typhoon occurrences. A stronger WPSH can create a blocking high-pressure system that redirects or slows the movement of typhoons, resulting in prolonged periods of intense rainfall in certain regions. This blocking effect can increase the convergence of moist air, intensifying precipitation processes [29,30,31]. Rao et al. found that the coupling effect of typhoons and WPSH played an important role in the July 2021 Zhengzhou, Henan extreme rainfall [32].
The National Climate Centre (NCC) of China proposed indices to describe the dynamic evolution of the WPSH [33]. In this study, the western Pacific subtropical high index (WPSHI), a key factor in the typhoon rainfall forecast model, adheres to the definitions provided by the NCC (see Appendix A.2 and Figure A2).
Area index (GM): The area index signifies the cumulative area enclosed by the 5880 gpm isolines spanning from 110°E to 180° longitude and lying above the 10°N latitude.
where dx (dy) is the latitudinal (meridional) distance of a grid cell, i (j) is the ordinal number in the zonal (meridional) direction, is the 500 hPa geopotential height value of a grid point, and is the latitude of a grid point. The summation is over Nx times Ny grid points in the west–east and south–north direction, respectively.
Intensity index (GQ): The intensity index is characterized as the summation of the product of the total area encircled by the 5880 gpm isolines and the surpass of a grid point’s height exceeding 5870 gpm (zero if less than 5870 gpm).
Ridgeline index (GX): The ridgeline index is determined by calculating the average latitude of the zonal wind shear line where the zonal wind (u) equals 0 and the partial derivative of u concerning y is greater than 0, encircled by the 5880 gpm isolines. In cases where the 5880 gpm isolines are absent, the zonal wind shear line (u = 0, ∂u/∂y > 0) encircled by the 5840 gpm isolines are considered. If the 5840 gpm isolines are also absent, the historical minimum value of that month since 1951 will be used as a substitute.
where n is equal to the number of grid points that satisfy the above conditions, i.e., the number of grid points used in the latitude average calculation.
Westernmost point (GD): The westernmost point is defined by the longitude where the westernmost 5880 gpm isolines lie within the range of 90°E to 180° longitude and north of 10°N. If it falls west of 90°E, it is consistently labeled as 90°E. In cases where there are no 5880 gpm isolines in a particular month, the historical maximum value of that month since 1951 is used as a replacement.
Typhoon Talim (ID 2304) and Super Typhoon Doksuri (ID 2305), which made landfall in China in 2023, were selected as case studies to illustrate the capabilities of the model. Seventeen stations were selected to validate the studies. The data also come from CMA.
3. Methods
3.1. Model Development and Forecasting Steps
The model establishment and validation consist of the following three steps.
Step 1: Modeling dataset matching (Figure 2, first box). Based on the date of each data entry in the different datasets described in Section 2, the location of each typhoon center (Long and Lat), the intensity of the typhoon (cap and mws), the WPSHI during the typhoon event, and the daily rainfall at each station during the typhoon event in addition to the geographic information of the station (Long_sta, Lat_sta, and Alt) on the same date are matched to form the dataset [21].
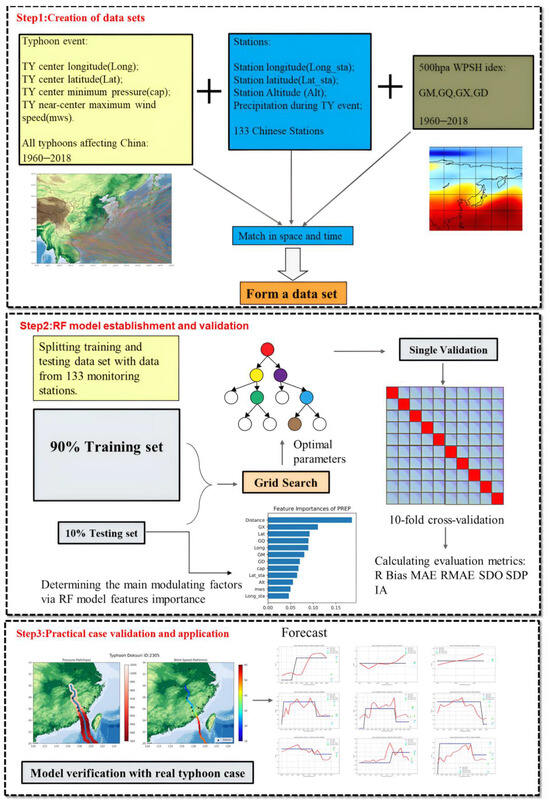
Figure 2.
Model establishment flowchart: The first box is the process of pre-modeling preparation and matching of datasets. The middle box is the process of model algorithm development and evaluating the performance of the model. The third box is an independent case evaluation after the modeling is completed.
Step 2: Model building and validation (Figure 2, middle box). After forming the model dataset in Step 1 above, the dataset is first randomly separated into a 90% training set and a 10% validation set, with the former for training the RF model and the latter for verifying the model performance. Hyperparameters are then identified using the grid search method to determine the optimal hyperparameters for the model in this case [34]. By grid search and minimizing error, the optimal hyperparameter combination can be obtained, thereby improving the accuracy and generalization ability of the RF model (see Appendix A.3). The training set and optimal hyperparameters were then input into the RF model to build the typhoon rainfall forecast model. In addition, this study used the hold-out method, which splits the dataset into mutually exclusive parts. The formal part is the training set and the latter part is used for validation. If different splitting ratios are used, the average evaluation metrics (R = 0.727, bias = 1.283, and IA = 0.792, see Section 3.2) vary between 1% and 9% compared to the 10-fold cross-validation. Therefore, the model performance is not sensitive to the dataset separation method and has good generalization ability. Next, to reduce the bias due to the single division between the training and validation sets, ten multiple divisions are performed such that every typhoon has the chance to enter the training sub-dataset or validation sub-dataset. Practically, the dataset is divided into ten parts, and trials are performed by rotating nine of them as training data and one as validation data. Each trial yields the corresponding model performance evaluation parameters [35]. The average of the evaluation parameters including bias, mean absolute error (MAE), root mean square error (RMSE), correlation (R), standard deviation (SD, for observations and predictions, respectively), and index of agreement (IA) [36] from the 10 trails was used as an estimate of the algorithm’s accuracy.
where is the th predicted value, is the th observed value, N is the total number of samples, the mean of the observed values, is the mean of the predicted values, and is the difference between the th predicted value and the observed value. See Table A1 in Appendix B for the definitions of all the evaluation metrics. According to the above evaluation and validation, the hyperparameters of the RF model are set as the number of decision trees = 200, max_depth = 50, min_samples_leaf = 2, min_samples_split = 5, and max_features = default value. The model performance tends to be unchanged when the number of decision trees exceeds 200 with other parameters held constant. The combination of max_depth, min_samples_leaf, and min_samples_split was determined with the consideration of maintaining the balance between model accuracy and preventing overfitting.
Step 3: Model performance evaluation (Figure 2, third box). After constructing the typhoon rainfall forecast model in Step 2 above, the model is tested using Typhoons Talim (2023) and Doksuri (2023) as case studies. In other words, the forecast factors (Lat, Long, cap, mws, and WPSHI-related parameters) of the two typhoons are input into the model and the resulting outputs are compared with the rainfall records at the 17 stations. The performance of the model for these two typhoons serves as an independent validation of the model development dataset.
The model output consists of the daily (i.e., 24 h accumulated) rainfall after the model initialization time at each of the 133 stations. Once a typhoon enters the alert line designated by the CMA, its path is updated every 3 h. The best track dataset used in this study also employs a 3 h interval for typhoon center updates. Thus, the 3 h interval in our model corresponds to the operational protocol and the interval specified by the dataset for optimal accuracy. The model has a lead time of forecast of 24 h and is initialized every 3 h such that a 3 h time series is output for comparison with station observations. The model stops when it comes to the last record of the typhoon center position in the best (or forecast) track. By default, the model assumes that there is no typhoon rainfall at a station when the typhoon center is not within 1000 km [25,26]. Thus, the model, as well as other machine learning algorithms, is not suitable for forecasting typhoon remote rainfall events whose inducing factors are not fully known [9,37,38,39]. Although the impacts of typhoon remote rainfall events may be huge, they are not very frequent [40] and future work is necessary to develop a specific model for forecasting them.
3.2. Model Evaluation
The evaluation metrics for the model’s validation dataset with a single, random separation of the training and testing dataset are as follows: = 14.09 mm, = 23.81 mm, = 1.28 mm, = 0.727, = 21.82, = 14.28, and = 0.79. The correlation coefficient and IA values are considered high compared with other studies using machine learning on precipitation estimates, e.g., [41]. Given the large range of daily rain rates associated with typhoons (up to hundreds of mm), the error in our model is also considered small [42,43].
The results of calculating the variance inflation factor (VIF) showed that only GM had a VIF greater than 10 (GM = 11.1) and GQ had a VIF between 5 and 10 (GQ = 9.8), while the VIFs of the other factors were between 1 and 5. When GM, GQ, GD, and GX were considered as components of the WPSHI, their average VIF was 5.7 (WPSHI_avg = 5.7). It is generally accepted that a VIF greater than 10 indicates severe multicollinearity, a VIF between 5 and 10 indicates moderate covariance and a VIF less than 5 indicates mild covariance. These results suggest that the factors are relatively independent. Moreover, according to the importance ranking of the model features (Figure 3c), the distance between the typhoon center and the station holds the highest significance with a number of 18.5%, and the ridgeline (GX) in the WPSHI is the second most crucial factor with a number of 11%. The total contribution of the WPSHI is 35.1%. The position of the typhoon center (Lat and Long) is close in importance to the GQ in the WPSHI, making them tie for the third position. Remarkably, the cap and the mws carry comparatively lower weights, implying that the intensity is not a determining factor for rainfall forecast. In the training dataset, the vast majority of the samples (red dots in Figure 3a) cluster at or near the diagonal line. This means that the model makes accurate estimates for most of the samples during training. For a considerable number of samples, the model underestimates. In the testing dataset, the model is quite accurate for the small daily rain rates (which consist of most samples) and slightly overestimates (Figure 3b). For the rest of the testing dataset with higher rain rates, the model both underestimates and overestimates them. Such model predictive ability is comparable to recent applications of RF in precipitation forecast, e.g., [19]. After the 10-fold cross-validation of the typhoon rainfall model (i.e., random shuffling of the training and testing dataset), the mean evaluation metrics become = 14.39 mm, = 24.80 mm, = 1.18 mm, = 0.71,= 34.79, = 20.69, and = 0.85. The consistency of these metrics across multiple folds demonstrates the stability and generalizability of the model.
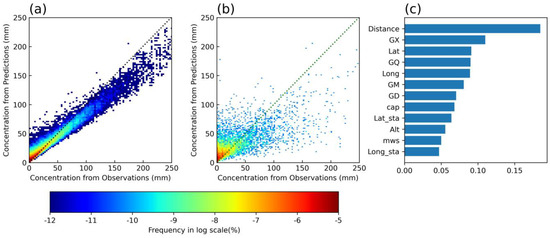
Figure 3.
Characterization of the model and performance of forecasted rainfall. (a) Training and (b) testing dataset performance. The dotted lines are the locations of points where there is no bias between the model’s forecasts and the observations. The warmer color of the region represents the denser points in that interval. (c) Feature importance ranking of the model predictors.
In China, given that most typhoons make landfall from the east and the south, the southeast coasts are the most prone to typhoon landfalls [44,45]. The stations near the coast observe large amounts of typhoon-related rainfall, and other regions are less likely to be so severely affected. Therefore, it is essential to evaluate the regional variation in the performance of our RF rainfall model. This study evaluated the forecast performance of our model by calculating various metrics, including the mean absolute error (MAE), mean absolute percentage error (MAPE), and correlation coefficient (R) for individual stations across the region (Figure 4). It can be seen that for the R and MAE, there is an overall trend of decreasing from southeast to northwest and from coast to inland, while the trend for the MAPE is the opposite. The MAE of some stations along the southeast coast can reach 30 mm/day. The largest MAEs are found in Taiwan island, the Bohai Rim region, then the coastal provinces of the East China Sea and the Northeast China region. For those stations to the northeast, the large MAEs are likely associated with typhoons making the transition to high latitudes and with rainfall patterns under the influences of mid-latitude weather systems. For those stations located on the southeast coast, due to the high frequency of rainfall events caused by typhoons in these regions, the annual rainfall from typhoons is considerable, especially exceeding 100 mm/day at times when typhoons make direct landfall. Conversely, inland areas are less frequently affected by typhoons and consequently receive less annual rainfall from them. Therefore, assuming the consistent forecasting performance of the hypothetical model across these regions, it is reasonable that the MAE for forecasting typhoon-induced rainfall would be higher for the southeastern coastal areas and lower for the inland regions (Figure 4a). Analyzing the MAPE among stations, it was found that in the southeastern coastal areas, where typhoon frequency is higher, the relative error ranged from 75% to 100%. In contrast, inland stations had larger MAPE values, with some reaching up to 200%, indicating significant discrepancies among them (Figure 4b). Thus, the forecast performance of the model seems to be more stable and effective for the typhoon-prone southeastern coastal areas compared to the inland areas. Further analysis showed that the average R for stations in the southeastern coastal areas reached 0.65, which was generally higher than that of inland and northern regions (Figure 4c). In addition, the R values for stations in the southeastern coastal areas were also more consistent. These results suggest, on the one hand, that the model performs better in regions of China frequently affected by typhoons, indicating its strong applicability. The mean values of evaluation metrics for the stations in the representative area were R = 0.58, MAPE = 95%, and MAE = 23.8 mm. On the other hand, they imply that the model also has some predictive ability for regions less frequently affected by typhoons, demonstrating its broad utility. The underlying rationale is that regions with higher typhoon frequencies can provide more training data related to typhoon-induced rainfall, enabling the model to make more accurate predictions; conversely, its forecasting performance may be compromised in regions with lower typhoon frequencies. Therefore, in the future, as the dataset expands, the model’s forecasting performance will continue to improve.

Figure 4.
Distribution of assessment indicators for individual stations: (a) The model’s forecasted MAE (mm/day) on typhoon days at this station. (b) The model’s forecasted MAPE (%) on typhoon days at this station. (c) The model’s mean forecasted result of R. Black inverted triangles represent stations with too little data that the evaluation metrics cannot be calculated.
4. Result
4.1. Cases Study
The first selected typhoon case in this study is Super Typhoon Doksuri (2023). Doksuri was generated in the western North Pacific on the morning of 21 July 2023 and gradually developed into a super typhoon. Doksuri made landfall as a severe typhoon on the coast of Jinjiang City on the morning of 28 July, making it the second strongest typhoon to make landfall in Fujian Province in all available records. The super typhoon had an extraordinary impact in terms of rainfall. Among them, the daily rainfall in Putian even exceeded the historical record of maximum daily rainfall at national observatories in the province [46,47]. Doksuri then continued northward through several provinces, weakened to a tropical depression in Anhui Province, and immediately ceased to be numbered, with the residual circulation of the typhoon triggering exceptionally heavy rainfall over a wide area of northern China (Figure 5a,b).
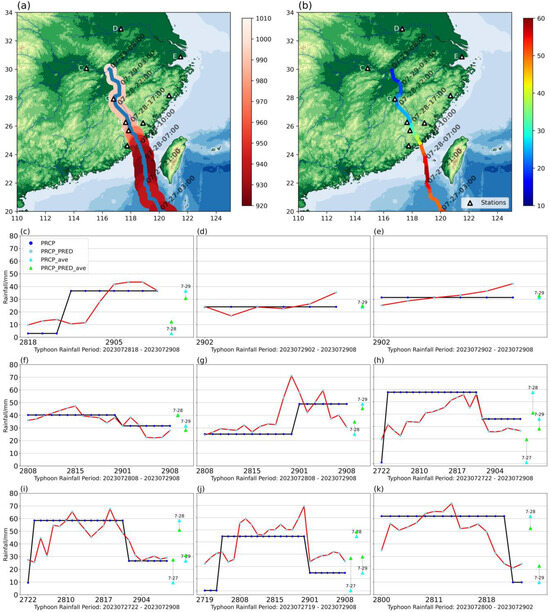
Figure 5.
(a) Track of Typhoon Doksuri (blue line) and its central pressure (hPa; red shading). (b) Track of Typhoon Doksuri and its near-center maximum wind speed (m s−1; color along the track). Comparison between the observed and forecasted daily rainfall at the selected stations: (c) station1, ID: 57499, (30.074N, 114.875E), accuracy(A) = 60%; (d) station2, ID: 58221, (32.844N, 117.304), A = 67%; (e) station3, ID: 58463, (30.887N, 121.496E), A = 100%; (f) station4, ID: 58658, (28.150N, 120.691E), A = 84%; (g) station5, ID: 58712, (27.909N, 116.784E), A = 68%; (h) station6, ID: 58828, (26.274N, 117.642E), A = 48%; (i) station7, ID: 58839, (26.220N, 118.864E), A = 74%; (j) station8, ID: 58923, (25.698N, 117.841E), A = 24%; (k) station9, ID: 59122, (24.624N, 117.753E), A = 65%. The black line and the purple dots above (PRCP) and the blue triangle (PRCP_ave) represent the observed rainfall of the day; the red line and the above light-purple point (PRC_PRED) represent the daily rainfall predicted by the model. The green triangle (PRCP_PRED_ave) represents the average value of the daily rainfall forecast results of the model under different conditions. The letters C–K in (a,b) correspond to the stations represented in the subgraphs below, labeled (c–k).
Model forecasts at nine representative stations affected by Typhoon Doksuri are examined. Among them, four stations were located in Fujian Province, which was directly affected by the typhoon, while one station was located in Zhejiang Province, about 500 km from the center of the typhoon, reflecting its long-range rainfall capability [48]. In addition, two stations are located inland and are affected by the residual circulation of the typhoon (Figure 5c–k). The average results of model forecasts are as follows: accuracy = 61%, R = 0.64, IA = 0.79, MAE = 9.98 mm, and RMSE = 13.36 mm. For comparison, the NCEP Global Forecast System (GFS) 0.25° forecasts (https://doi.org/10.5065/D65D8PWK accessed 28 May 2024) are examined. The average 24 h precipitation forecasts (based on the closest grid points to our stations) have the following values: accuracy = 13%, R = 0.39, IA = 0.43, MAE = 31.62 mm, RMSE = 44.91 mm. The results show that our RF model is satisfactory in forecasting this typhoon and may outperform the global numerical model, although high-resolution regional models may have higher skills than the GFS.
The second selected typhoon case in this study is Typhoon Talim (ID: 2304). Typhoon Talim’s predecessor, a tropical depression, was generated near the Philippines at 11:00 a.m. on 14 July 2023. It made landfall off the coast of Nansandao in Zhanjiang City, Guangdong Province, and then moved along the coasts of Guangdong and Guangxi, becoming the first typhoon to make landfall in China in 2023. During the period from 16 to 19 July 2023, some areas in Guangdong, Hainan, and Guangxi experienced heavy rainfall, with exceptionally heavy rainfall occurring in localities along the southwest coast of Guangdong, the southern coast of Guangxi, and the north-central part of Hainan Island. Talim represents a relatively common type of northwestward-moving typhoon that has caused rainfall mainly in areas along the southeastern coast of China and has stayed over land for quite a long time [47].
The case validation included nine representative stations in Guangdong and Guangxi that were directly affected by Typhoon Talim. Three stations were located along or near the track of the typhoon, another three were located about 200 km from the center of the typhoon in Guangdong, one was located in the eastern part of Guangdong, and two were located in Guangxi, about 500 km from the center of the typhoon (Figure 6a,b). The evaluation of the forecast results for these nine stations is R = 0.87, IA = 0.91, and accuracy = 61%. Compared with the overall evaluation of the model, the forecast results of Typhoon Talim showed a significant increase in R by about 0.14, reaching a strong correlation result of 0.87, and IA increased by 0.12 (from 0.79). However, the MAE (14.83 mm) and RMSE (22.15 mm) are larger than those for Typhoon Doksuri (but still comparable to the model errors concerning the test dataset). Such a difference in the forecast of Typhoon Talim may be caused by the large variability in the rainfall recorded at the stations. The maximum daily rainfall at the selected stations during Typhoon Talim can reach 154 mm, while the minimum daily rainfall is only 0.8 mm. It is a challenge for the model to capture such a large degree of variability. Nevertheless, it can be seen that the peak rainfall rates at the nine stations are quite well predicted and the timing of the peak rainfall events is reasonably captured (Figure 6c–k). Comparing the results of the GFS model for case 2 (accuracy = 22%, R = −0.35, IA = 0.2, MAE = 49.61, and RMSE = 67.31), our model also outperforms the global model in terms of forecasting rainfall for Typhoon Talim.
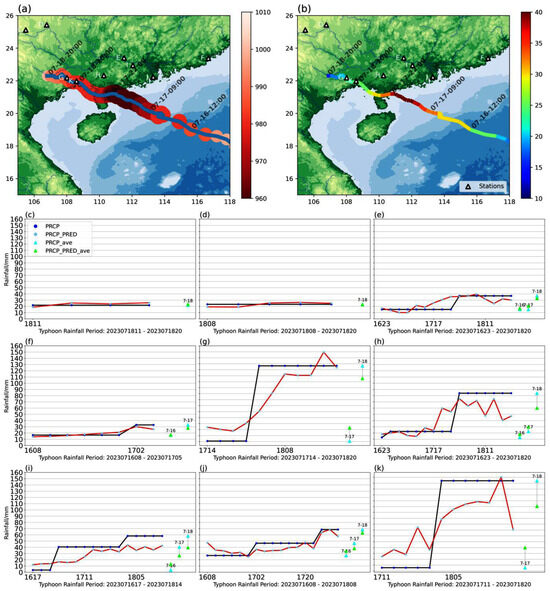
Figure 6.
(a) Track of Typhoon Talim (blue line) and its central pressure (hPa; red shading). (b) Track of Typhoon Talim and its near-center maximum wind speed (m s−1; color along the track). Comparison between the observed and forecasted daily rainfall at the selected stations: (c) station1, ID: 57908, (25.114N, 105.481E), A = 50%; (d) station2, ID: 57916, (25.429N, 106.764E), A = 40%; (e) station3, ID: 59264, (23.397N, 111.508E), A = 75%; (f) station4, ID: 59316, (23.385N, 116.679E), A = 100%; (g) station5, ID: 59429, (22.183N, 108.013E), A = 45%; (h) station6, ID: 59457, (22.323N, 110.269E), A = 62%; (i) station7, ID: 59471, (22.941N, 112.052E), A = 25%. (j) station8, ID: 59487, (22.229N, 113.297E), A = 94%; (k) station9, ID: 59632, (21.980N, 108.595E), A = 42%. The black line and the purple dots above (PRCP) and the blue triangle (PRCP_ave) represent the observed rainfall of the day; the red line and the above light-purple point (PRCP_PRED) represent the daily rainfall predicted by the model. The green triangle (PRCP_PRED_ave) represents the average value of the daily rainfall forecast results of the model under different conditions. The letters C–K in (a,b) correspond to the stations represented in the subgraphs below, labeled (c–k).
4.2. Contribution of the Subtropical High
The feature importance ranking in our model shows that the predictors associated with the subtropical high, i.e., GM, GQ, GX, and GD, are among the most critical to model performance. In particular, GX and GQ are ranked second and third, respectively. To further illustrate the contribution of these factors, we repeat the model training and testing without the WPSHI-related predictors and then calculate evaluation metrics in this situation (Table 1). In addition, predictor denial experiments are performed for Typhoons Doksuri and Talim to examine the impact on forecast performance. When only Lat_sta, Long_sta, Lat, Long, cap, mws, distance, and Alt are entered into the model, the model evaluation metrics are R = 0.52 and IA = 0.64 (compared to R = 0.727 and IA = 0.79 in the model with the WPSHI as a predictor)—both the model correlation and the IA decrease.

Table 1.
Evaluation metrics of the model and case studies without WPSHI.
In the case where the WPSHI was not used as a forecast factor input, the performance of the typhoon rainfall forecast model for the typhoon case deteriorated significantly compared to the original model (Figure A3 and Figure 7a–r). Although the forecasts can still capture the occurrence of the increase in rainfall rates at some stations, there are some large errors. The model with the WPSHI has better generalization performance and its forecasts are more reliable for all stations. In the forecast of Typhoon Doksuri without the WPSHI, the model evaluation indices are R = 0.55, MAE = 13.72 mm, RMSE = 16.93 mm, and IA = 0.26. In the forecast of Talim without the WPSHI, R = 0.82, MAE = 19.03 mm, RMSE = 25.64 mm, and IA = 0.1. It can be seen that R and IA have deteriorated significantly when the WPSHI is not among the model predictors.
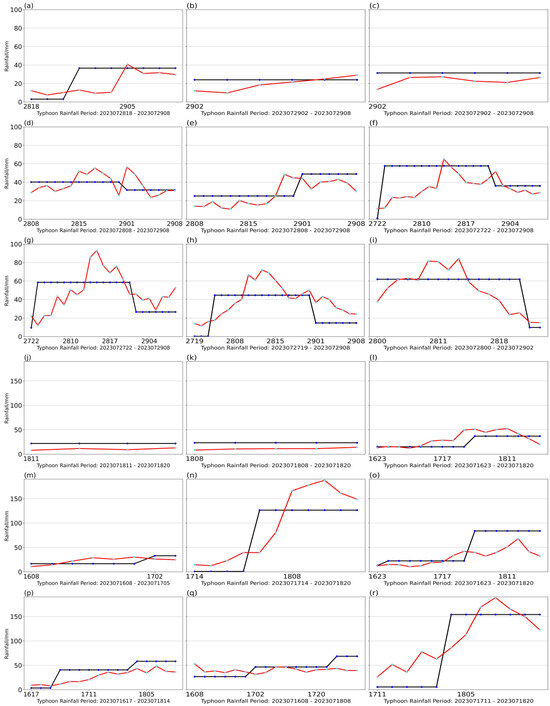
Figure 7.
Observed (blue dots) and forecast (red dots) rainfall for the stations considered for Typhoons Doksuri and Talim, which include (a) ID: 57499, (b) ID: 58221, (c) ID: 58463, (d) ID: 58658, (e) ID: 58712, (f) ID: 58828, (g) ID: 58839, (h) ID: 58923, (i) ID: 59122,(j) ID: 57908, (k) ID: 57916, (l) ID: 59264, (m) ID: 59316, (n) ID: 59429, (o) ID: 59457, (p) ID: 59471, (q) ID: 59487, (r) ID: 59632. The y-axis range is consistent with Figure 5 and Figure 6, respectively; see Figure 5 and Figure 6 for more detailed station information.
These results emphasize the critical contribution of the WPSHI as a forecasting factor and suggest that there is a strong relationship between the WPSHI and typhoon rainfall. Two aspects of the WPSHI have critical influences on the large-scale circulation relevant to typhoon rainfall. The position of the ridge line is known to influence tropical cyclone tracks (especially the direction of motion) and thus the location of landfall. On the other hand, the intensity of the subtropical high influences the steering current of tropical cyclones and thus their speed. Landfall timing would be better predicted if the intensity of the subtropical high could be captured. The intensity of the subtropical high also modifies the vertical wind shear over the coastal Pacific. Although typhoon intensity does not rank high in the model’s feature importance, the intensity of the subtropical high may indirectly contribute to typhoon intensity through its influence on the vertical wind shear change.
5. Discussion
The rainfall pattern of a tropical cyclone concerning its center has a basic structure that follows the vortex circulation. Namely, the eyewall convection is where much of the rain is concentrated. Outside the eyewall, rain is concentrated in the rainbands with largely stratiform rain, but there is great variability in rainband structure among cyclones. For example, many midget tropical cyclones do not have a clear separation between the eyewall convection and the outer rainbands. Given this rainfall pattern, it is important to understand the characteristics, such as the distance, of the typhoon rainfall forecast model concerning forecasting outcomes for a station near the cyclone center or in the outer rainband region.
This study examines the bias distribution of the model as it varies with the distance between the target station and the cyclone center (Figure 8). The density of the sample is also shown in Figure 3. It can be seen that within 0–200 km from the cyclone center (i.e., the inner-core region), the biases are also symmetrically distributed between positive and negative values. A large portion of the samples have low biases (e.g., less than 20 mm); however, large biases of both (up to 100 mm) exist. This implies that when forecasting the convective rain in the inner-core region, the forecast range is large. For moderate distance from the cyclone center (200–600 km), which contains most of our samples, positive and negative biases are more widely distributed. There is an accountable number of large biases beyond the 20 mm boundary, although biases still concentrate within 20 mm. Thus, when forecasting the rainfall outside the inner-core region of cyclones, our model has consistent and promising performance. In the outer region (600–1000 km), typhoon rainbands usually have smaller amounts of rainfall; thus, the biases are mostly less than 20 mm in magnitude with smaller variability. In other words, even when we need to estimate precipitation at stations distant from the tropical cyclone (i.e., in the outer region), our model is generally dependable and able to provide forecasts with consistent performance.
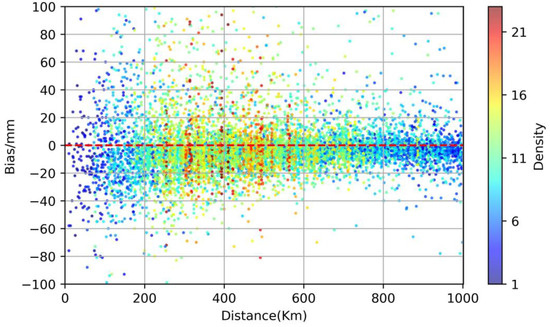
Figure 8.
The distribution of model forecast error (mm) versus distance from the tropical cyclone center (km) regarding the validation dataset. Color shading represents the density of samples.
To further determine the bias characteristics, we examine the correlation between observations and forecasts (i.e., similar to Figure 3a,b), with an indicator of the distance of each sample from the station to the cyclone center (Figure 9). When the model was built using the training dataset, the samples with s small amount of daily rainfall (0–100 mm) had both overestimates and underestimates. However, there is a clear distinction that rainfall is overestimated at stations closer to the cyclone center, while it is underestimated at stations far from the cyclone center (Figure 9a). In contrast, for very large daily rainfall amounts (above 100 mm, which is the CMA definition of a rainfall event), the model overestimates for almost all samples. Such a bias distribution concerning distance is similar in the testing dataset (Figure 9b), except that the samples are more scattered and there are more samples with large bias magnitudes. The bias characteristics shown here, with respect to rain rate and station–cyclone distance, are a valuable reference when the model is applied in a real-time situation.
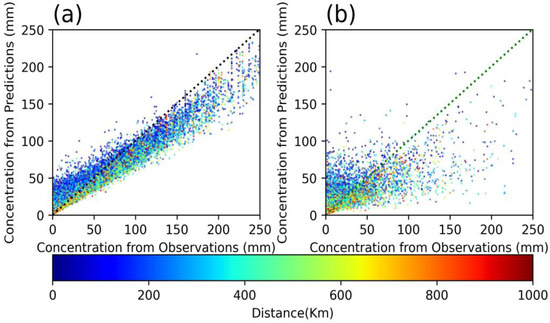
Figure 9.
(a) Results of the training dataset and (b) results of the testing dataset. The distribution of the distances between the observed and forecasted rainfall. The diagonal dotted line represents the same situation of forecast results and observation results. The warmer the color, the farther away from the typhoon center when affected by the typhoon (km).
Currently, the main shortcoming of the model’s performance remains to be the lack of accuracy in forecasting typhoon rainfall, especially for intense typhoons for which the biases of forecasts tend to be large. For example, the long-range and asymmetric distribution of rainbands in a typhoon’s periphery cannot be accurately captured by our model. Real-time and near-real-time radar and satellite data, when included in our model development and forecast scheme, may improve accuracy at typhoon landfall. By combining real-time observational data with modeling, the dynamical processes of typhoon rainfall evolution can be better captured. In addition, extending and increasing the resolution of the typhoon rainfall (e.g., by combining with radar and satellite datasets) would also potentially improve the performance of the model, although the availability of long historical remote sensing datasets for deep learning-based model development is a challenge.
6. Conclusions
In this study, a typhoon rainfall forecast model was developed using Random Forest with typhoon tracking, intensity (surface pressure and maximum wind speed), station position and altitude, and the configuration of the WPSHI as inputs to the predictors. The model achieves the forecast of daily typhoon rainfall by establishing a nonlinear mapping relationship between the forecast factors and rainfall. The importance ranking of the model features shows a strong correlation between the WPSHI (including ridge intensity, ridge line, westward extension, and area) and typhoon rainfall. This indicates that the influences of the WPSHI on typhoon landfall location, motion speed, and thus landfall timing are critical in the development of any statistical and AI-based typhoon rainfall forecast models.
Quantitatively, the evaluation metrics of the model are MAE = 14.09 mm, RMSE = 23.81 mm, Bias = 1.28 mm, R = 0.727, and IA = 0.79 (for a single realization of the training dataset, see Table 1 for the error metrics under other circumstances). The diagnosis of the error characteristics shows that for target stations outside the inner-core (0–200 km) region, the model performs well, with a bias magnitude mostly within 20 mm for daily rain and distributed quite evenly between positive and negative biases. When the target station is in the inner core, however, there is a large range of forecast biases with both signs. Rain at such a station close to the cyclone center is mostly overestimated for low rain rates (<100 mm) and underestimated for large rain rates (>100 mm).
The case study of Super Typhoon Duksuri and Typhoon Talim in 2023 shows that the model has high timeliness and accuracy in forecasting rainfall in the affected areas during typhoons, providing effective support for earlier and more accurate early warnings of typhoon-related disasters and emergency response preparation. The immediate future extension of the current model will be to use rainfall data with higher temporal resolution (e.g., hourly) to train the model so that the output time series can also have higher resolution and better capture the peak rainfall rates. In addition, the current typhoon rainfall dataset is based on an official determination of tropical cyclone-related rainfall. Further investigation is necessary to study if alternate definitions or data of related tropical cyclone rain are applied regarding the accuracy that an RF-based model can model and forecast the rain pattern and magnitude.
Author Contributions
Conceptualization, K.K.W.C. and Y.Y.; methodology, K.K.W.C., Y.Y. and Z.F.; software, Z.F.; validation, Z.F.; formal analysis, Z.F.; investigation, K.K.W.C., Y.Y. and Z.F.; resources, K.K.W.C., Y.Y. and Z.F.; data curation, Z.F.; writing—original draft preparation, Z.F.; writing—review and editing, K.K.W.C., Y.Y. and Z.F.; visualization, Z.F.; supervision, K.K.W.C. and Y.Y.; project administration, K.K.W.C. and Y.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Natural Science Foundation of China (42222503).
Data Availability Statement
The typhoon rainfall forecast model in this paper is based on the Random Forest of the scikit-learn package in Python 3.11.9 [49] and the implementation and analysis code are available upon request to the corresponding author (kevin.cheung@nuist.edu.cn). The historical track, intensity, and rainfall data of the typhoon are publicly available in the China Meteorological Administration Tropical Cyclone Database [25,26]. The historical 500 hPa height for the western Pacific used to build the WPSHI historical dataset is publicly available at the European Centre for Medium-Range Weather Forecasts [50].
Acknowledgments
The authors would like to thank the three anonymous reviewers who have provided insightful comments that have improved the quality of our manuscript substantially. The second author (KKWC) acknowledges support from the Startup Foundation for Introducing Talent of NUIST.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Appendix A.1. Matching of Datasets
The CMA Tropical Cyclone Data Center provides information on the tracking of all typhoons affecting China, with latitude, longitude, barometric pressure, and maximum near-center wind speed of the typhoon center recorded every six hours (after 2017, the recording interval was shortened to three hours during the 24 h before typhoon landfall and land activities). In addition, the center also provides the daily rainfall observed at each observation station due to the typhoon, including the latitude, longitude, and altitude of the station.
In this study, as long as a typhoon rainfall is recorded at a station, and there is an active typhoon during that period, and the distance between the center of the typhoon and the station is less than 1000 km, it is considered that the rainfall of the day at the station is generated by the typhoon, and thus the data are matched. In addition, according to the ERA-5 reanalysis data, the 500 hPa potential height field (z) and wind field values at 6:00, 12:00, 18:00, and 24:00 h are calculated to obtain the WPSHI four times, and the mean value is taken to be the WPSHI for that day, which is the WPSHI for that day during the period of typhoon activity using the above method. According to the above matching principle, the dataset required for model training is obtained. The same rule is followed when selecting typhoon cases and matching datasets in the study.
Appendix A.2. Reliability of the Reconstructed WPSHI Dataset
Since the daily WPSHI data provided by the National Climate Center (NCC) are limited (only up to 1 January 2011) and some data measurements are missing every year, the demand for typhoon data before 2011 could not be met in this study. Therefore, this study reconstructs the WPSHI dataset from 1960 to the present by using the 500 hPa potential height field and meridional wind field data from the ERA5 reanalysis data.
It should be noted that the reanalyzed data are not direct observations, and there are some uncertainties, especially for the historical data with a long period. Therefore, the WPSHI values calculated from the reanalyzed data may differ from the operational monitoring data. To assess the credibility of the reconstructed dataset, the present study uses the annual cycle oscillation of the WPSHI index (which reflects the interannual variability of the western Pacific subtropical high, which is stronger or weaker each year). Specifically, the reconstructed WPSHI dataset in 2021 and the operational monitoring dataset from the NCC in the same year are compared after Z-score normalization [51], and it is found that the interannual variability trends of WPSHI in the two datasets are consistent. Therefore, it can be judged that the results of the reconstructed WPSHI dataset in this study are reasonable (see Figure A2).
Appendix A.3. Determination of Hyperparameters of RF Model
To obtain the best performance of the RF model, this study uses the grid search method to optimize the model hyperparameters. Grid search is a commonly used hyperparameter optimization technique. Its basic principle is to construct a grid composed of multiple hyperparameters and their value ranges and then exhaustively search and evaluate the performance of the model under each hyperparameter combination. Finally, the hyperparameter combination that can generate the minimum validation set error is selected as the optimal combination. Specifically, A denotes the hyperparameter set of the model, and denotes the error of the model for the th sample under the given hyperparameter . Then, the optimal hyperparameter combination can be determined by calculating the Table A1 evaluations and selecting the optimal hyperparameters:
Among them, k is the number of testing set samples. We specify the hyperparameters that need to be optimized and their value ranges and construct a hyperparameter grid; the training set is divided into K subsets by K-fold cross-validation. For each hyperparameter combination, traverse K times, we use K − 1 subsets to train the model each time, and the remaining subset is verified. We calculate the average error of K verifications under this combination. The hyperparameter combination with the minimum average verification error is selected as the optimal combination.
Appendix B
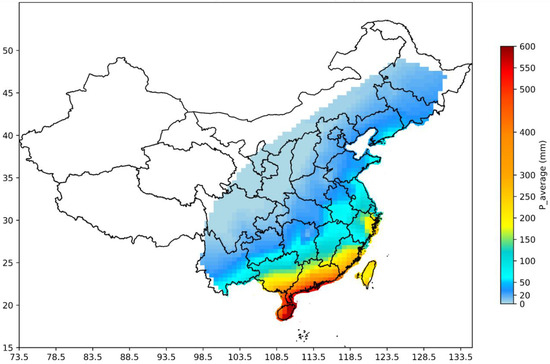
Figure A1.
The average annual rainfall caused by typhoons in each province [18] from 1960 to 2018 within the land area of China. The warmer the color, the greater the annual typhoon rainfall in the region. The maximum value is close to 600 mm/year in Hainan Province. Blank areas represent that the place came out historically unaffected by typhoons.
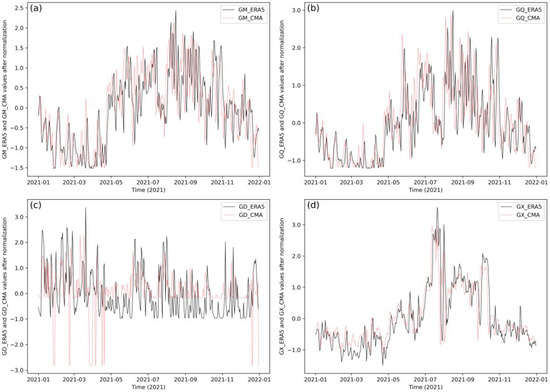
Figure A2.
Standardized time-series comparison plots of the 2021 WPSHI dataset reconstructed in this study and the WPSHI dataset of the NCC (the independent 2021 dataset that does not participate in modeling and case studies is used as a case representative). Comparison of standardized 2021 NCC monitoring (red line) with ERA-5 reanalysis data (black line) for (a) GM, (b) GQ, (c) GD data, and (d) GX.
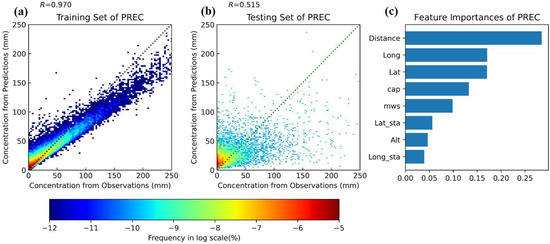
Figure A3.
Characterization of the model without WPSHI and performance of forecasted rainfall. (a) Training and (b) testing dataset performance. The dotted lines are the locations of points where there is no bias between the model’s forecasts and the observations. The warmer color of the region represents the denser the points in that interval. (c) Feature importance ranking of the model predictors.

Table A1.
The definition of evaluation metrics of the model. and represent the correlation and consistency of forecasts made by the model. Other evaluation metrics represent the error of forecasts made by the model.
Table A1.
The definition of evaluation metrics of the model. and represent the correlation and consistency of forecasts made by the model. Other evaluation metrics represent the error of forecasts made by the model.
| Metric | Definition |
|---|---|
| MAE | |
| RMSE | |
| Bias | |
| R | |
| SDO | |
| SDP | |
| IA |
Note: In which is the ith forecast, is the ith observation, N is the total number of samples, is the average of the observations, is the average of the forecasts, and is the difference between the ith forecast and the observation. Among these evaluations, for , and the better, for and , the higher the better, for and , the closer the better, and when the is smaller than the standard deviation of the observed value and the coincidence index IA is higher, and are closer, it means the forecast is better. Bolded fonts mean that this more significant parameter.

Table A2.
The results of model 10-fold cross-validation. Evaluation metrics for 10-fold cross-validation per fold specific validation from Fold_1 to Fold_10, and mean is the average result.
Table A2.
The results of model 10-fold cross-validation. Evaluation metrics for 10-fold cross-validation per fold specific validation from Fold_1 to Fold_10, and mean is the average result.
| MAE (mm) | RMSE (mm) | Bias (mm) | R (Testing Set) * | R (Training Set) | Sdo (mm) | SDo (mm) | IA * | |
|---|---|---|---|---|---|---|---|---|
| Fold_1 | 14.1 | 23.83 | 1.25 | 0.73 | 0.98 | 34.12 | 20.63 | 0.84 |
| Fold_2 | 14.63 | 24.89 | 0.89 | 0.71 | 0.98 | 34.93 | 20.63 | 0.85 |
| Fold_3 | 14.49 | 24.86 | 1.16 | 0.72 | 0.98 | 35.32 | 21.5 | 0.84 |
| Fold_4 | 14.29 | 24.53 | 1.59 | 0.71 | 0.98 | 34.42 | 20.6 | 0.84 |
| Fold_5 | 14.35 | 24.73 | 1.15 | 0.72 | 0.98 | 34.85 | 20.37 | 0.85 |
| Fold_6 | 14.37 | 24.63 | 1.36 | 0.7 | 0.98 | 33.95 | 20.07 | 0.85 |
| Fold_7 | 14.49 | 25.96 | 0.61 | 0.72 | 0.98 | 36.7 | 21.52 | 0.85 |
| Fold_8 | 14.4 | 25.11 | 1.33 | 0.70 | 0.98 | 34.62 | 20.38 | 0.85 |
| Fold_9 | 14.43 | 24.66 | 1.21 | 0.70 | 0.98 | 34.15 | 20.36 | 0.8 |
| Fold_10 | 14.34 | 24.82 | 1.27 | 0.71 | 0.98 | 34.8 | 20.87 | 0.84 |
| Mean | 14.39 | 24.8 | 1.18 | 0.71 | 0.98 | 34.79 | 20.69 | 0.85 |
Note: Bolded fonts mean that these are important parameters. * These metrics are more important in evaluating the model.
References
- Hu, C.; Tam, C.Y.; Loi, C.L.; Cheung, K.K.W.; Li, Y.; Yang, Z.L.; Au-Yeung, Y.M.; Fang, X.; Niyogi, D. Urbanization Impacts on Tropical Cyclone Rainfall Extremes-Inferences from Observations and Convection-Permitting Model Experiments Over South China. JGR Atmos. 2023, 128, e2023JD038813. [Google Scholar] [CrossRef]
- Yang, K.; Cai, W.; Huang, G.; Hu, K.; Ng, B.; Wang, G. Increased variability of the western Pacific subtropical high under greenhouse warming. Proc. Natl. Acad. Sci. USA 2022, 119, e2120335119. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Xiang, C.; Zhang, L.; Xu, Y.; Luo, Q. Analysis on main characteristics of Typhoon Doksuri (2305) and difficulties in its track and intensity forecast. J. Mar. Meteorol. 2023, 43, 1–10. [Google Scholar] [CrossRef]
- Mei, W.; Xie, X.P. Intensification of landfalling typhoons over the northwest Pacific since the late 1970s. Nat. Geosci. 2016, 9, 753–757. [Google Scholar] [CrossRef]
- Allawi, M.F.; Abdulhameed, U.H.; Adham, A.; Sayl, K.N.; Sulaiman, S.O.; Ramal, M.M.; Sherif, M.; El-Shafie, A. Monthly rainfall forecasting modelling based on advanced machine learning methods. Eng. Appl. Comp. Fluid Mech. 2023, 17, 2243090. [Google Scholar] [CrossRef]
- Schauwecker, S.; Schwarb, M.; Rohrer, M.; Stoffel, M. Heavy precipitation forecasts over Switzerland—An evaluation of bias-corrected ECMWF predictions. Weather Clim. Extrem. 2021, 34, 100372. [Google Scholar] [CrossRef]
- Li, Q.; Liu, B.; Wang, Q.; Wang, Y.; Li, G.; Li, T.; Lan, H.; Feng, S.; Liu, C. Operational Forecast of Rainfall Induced by Landfalling Tropical Cyclones Along Guangdong Coast. J. Trop. Meteorol. 2020, 26, 1–13. [Google Scholar] [CrossRef]
- Ren, J.; Xu, N.; Cui, Y. Typhoon Track Prediction Based on Deep Learning. Appl. Sci. 2022, 12, 8028. [Google Scholar] [CrossRef]
- Lin, Y.H.; Wu, C.C. Remote Rainfall of Typhoon Khanun (2017): Monsoon Mode and Topographic Mode. Mon. Weather Rev. 2021, 149, 733–752. [Google Scholar] [CrossRef]
- Ren, X.; Shao, A.; Liu, W.; Li, L. Improvements on short-term precipitation forecast in Northwest China based on regionally optimized moisture adjustment scheme for convective-scale NWP. Atmos. Res. 2022, 273, 106167. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, F.; Sun, P.; Li, X.; Du, Z.; Liu, R. A Spatial Mapping Model for Tropical Cyclone Precipitation Estimation. Appl. Soft Comput. 2022, 124, 109003. [Google Scholar] [CrossRef]
- Wong, C. How AI is improving climate forecasts. Nature 2024, 628, 710–712. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Yang, Y.; Zhan, C.; Zong, L.; Gul, C.; Wang, M. Tropical cyclone-related heatwave episodes in the Greater Bay Area, China: Synoptic patterns and urban-rural disparities. Weather. Clim. Extremes. 2024, 44, 100656. [Google Scholar] [CrossRef]
- Watson-Parris, D.; Rao, Y.; Olivié, D.; Seland, Ø.; Nowack, P.; Camps-Valls, G.; Stier, P.; Bouabid, S.; Dewey, M.; Fons, E.; et al. ClimateBench v1.0: A Benchmark for Data-Driven Climate Projections. J. Adv. Model. Earth SY 2022, 14, e2021MS002954. [Google Scholar] [CrossRef]
- Oh, S.G.; Park, C.; Son, S.W.; Ko, J.; Shin, K.; Kim, S.; Park, J. Evaluation of Deep-Learning-Based Very Short-Term Rainfall Forecasts in South Korea. Source. Asia-Pac. J. Atmos. Sci. 2023, 59, 239–255. [Google Scholar] [CrossRef]
- Tong, X.; Zhou, W.; Xia, J. Improving Boreal Summer Precipitation Predictions from the Global NMME Through Res34-Unet. Geophys. Res. Lett. 2024, 51, e2023GL106391. [Google Scholar] [CrossRef]
- Bochenek, B.; Ustrnul, Z. Machine Learning in Weather Prediction and Climate Analyses–Applications and Perspectives. Atmosphere 2022, 13, 180. [Google Scholar] [CrossRef]
- Uddin, M.J.; Li, Y.; Sattar, M.A.; Nasrin, Z.M.; Lu, C. Effects of Learning Rates and Optimization Algorithms on Forecasting Accuracy of Hourly Typhoon Rainfall: Experiments with Convolutional Neural Network. Earth Space Sci. 2022, 9, e2021EA00216. [Google Scholar] [CrossRef]
- Uddin, M.J.; Li, Y.; Tamim, M.Y.; Miah, M.B.; Ahmed, S.M.S. Extreme Rainfall Indices Prediction with Atmospheric Parameters and Ocean–Atmospheric Teleconnections Using a Random Forest Model. J. Appl. Meteorol. Clim. 2022, 61, 651–667. [Google Scholar] [CrossRef]
- Huang, F.; Chen, J.; Liu, W.; Huang, J.; Hong, H.; Chen, W. Regional rainfall-induced landslide hazard warning based on landslide susceptibility mapping and a critical rainfall threshold. Geomorphology 2022, 408, 108236. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, Y.; Gao, M. Typhoon-associated air quality over the Guangdong–Hong Kong–Macao Greater Bay Area, China: Machine-learning-based prediction and assessment. Atmos. Meas. Tech. 2023, 16, 1279–1294. [Google Scholar] [CrossRef]
- Sarker, I.H. Machine Learning: Algorithms, Real-World Applications and Research Directions. SN Comput. Sci. 2021, 2, 160. [Google Scholar] [CrossRef] [PubMed]
- Yu, P.S.; Yang, T.C.; Chen, S.Y.; Kuo, C.M.; Tseng, H.W. Comparison of random forests and support vector machine for real-time radar-derived rainfall forecasting. J. Hydrol. 2017, 552, 92–104. [Google Scholar] [CrossRef]
- Huang, M.; Wang, Q.; Jing, R.; Lou, W.; Hong, Y.; Wang, L. Tropical cyclone full track simulation in the western North Pacific based on random forests. J. Wind Eng. Ind. Aerodyn. 2022, 228, 105119. [Google Scholar] [CrossRef]
- Ying, M.; Zhang, W.; Yu, H.; Lu, X.; Feng, J.; Fan, Y.; Zhu, Y.; Chen, D. An overview of the China Meteorological Administration tropical cyclone database. J. Atmos. Ocean. Technol. 2014, 31, 287–301. [Google Scholar] [CrossRef]
- Lu, X.; Yu, H.; Ying, M.; Zhao, B.; Zhang, S.; Lin, L.; Bai, L.; Wan, R. Western North Pacific tropical cyclone database created by the China Meteorological Administration. Adv. Atmos. Sci. 2021, 38, 690–699. [Google Scholar] [CrossRef]
- Song, F.; Leung, L.R.; Lu, J.; Dong, L. Seasonally dependent responses of subtropical highs and tropical rainfall to anthropogenic warming. Nat. Clim. Change 2018, 8, 787–792. [Google Scholar] [CrossRef]
- Choi, W.; Kim, K.Y. Summertime variability of the western North Pacific subtropical high and its synoptic influences on the East Asian weather. Sci. Rep. 2019, 9, 7865. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Zhou, T.; Wu, P.; Guo, Z.; Wang, Z. Emergent constraints on future projections of the western North Pacific Subtropical High. Nat. Commun. 2020, 11, 2802. [Google Scholar] [CrossRef]
- Hirata, H.; Kawamura, R. Scale interaction between typhoons and the North Pacific subtropical high and associated remote effects during the Baiu/Meiyu season. JGR Atmos. 2014, 119, 5157–5170. [Google Scholar] [CrossRef]
- Ouyang, S.; Deng, T.; Liu, R.; Chen, J.; He, G.; Leung, J.C.H.; Wang, N.; Liu, S.C. Impact of a subtropical high and a typhoon on a severe ozone pollution episode in the Pearl River Delta, China. Atmos. Chem. Phys. 2022, 22, 10751–10767. [Google Scholar] [CrossRef]
- Rao, C.; Chen, G.; Ran, L. Effects of Typhoon In-Fa (2021) and the western Pacific subtropical high on an extreme heavy rainfall event in central China. JGR Atmos. 2023, 128, e2022JD037924. [Google Scholar] [CrossRef]
- Liu, Y.; Liang, P.; Sun, Y. The Asian Summer Monsoon: Characteristics, Variability, Teleconnections and Projection; Elsevier: Cambridge, MA, USA, 2019; pp. 85–95. [Google Scholar] [CrossRef]
- Bischl, B.; Binder, M.; Lang, M.; Pielok, T.; Richter, J.; Coors, S.; Thomas, J.; Ullmann, T.; Becker, M.; Boulesteix, A.; et al. Hyperparameter optimization: Foundations, algorithms, best practices, and open challenges. WIREs Data Min. Knowl. Discov. 2023, 13, e1484. [Google Scholar] [CrossRef]
- Wang, S.; Li, B.; Li, G.; Li, B.; Li, H.; Jiao, K.; Wang, C. A comprehensive review on the development of data-driven methods for wind power prediction and AGC performance evaluation in wind–thermal bundled power systems. Energy AI 2024, 16, 100336. [Google Scholar] [CrossRef]
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Chen, R.; Zhang, W.; Wang, X. Machine Learning in Tropical Cyclone Forecast Modeling: A Review. Atmosphere 2020, 11, 676. [Google Scholar] [CrossRef]
- Yoshida, N.; Kawamura, R.; Kawano, T.; Mochizuki, T.; Iizuka, S. Remote dynamic and thermodynamic effects of typhoons on Meiyu–Baiu precipitation in Japan assessed with bogus typhoon experiments. Weather Clim. 2023, 41, 100578. [Google Scholar] [CrossRef]
- Zuo, H.; Chen, Y.; Chen, S.; Chen, S.; Li, W.; Zhang, A. The Effect of the Water Tower of Typhoon Mangkhut (2018). Atmosphere 2018, 13, 636. [Google Scholar] [CrossRef]
- Kodama, S.; Satoh, M. Statistical Analysis of Remote Precipitation in Japan Caused by Typhoons in September. J. Meteorol. Soc. Jpn. 2022, 100, 893–911. [Google Scholar] [CrossRef]
- Li, X.; Yang, Y.; Mi, J.; Bi, X.; Zhao, Y.; Huang, Z.; Liu, C.; Zong, L.; Li, W. Leveraging machine learning for quantitative precipitation estimation from Fengyun-4 geostationary observations and ground meteorological measurements. Atmos. Meas. Tech. 2021, 14, 7007–7023. [Google Scholar] [CrossRef]
- Zhao, D.J.; Xu, H.X.; Yu, Y.B.; Chen, L.S. Identification of synoptic patterns for extreme rainfall events associated with landfalling typhoons in China during 1960–2020. Adv. Clim. Chang. Res. 2022, 13, 651–665. [Google Scholar] [CrossRef]
- Yeung, H.Y. “Convective Hot Tower” Signatures and Rapid Intensification of Severe Typhoon Vicente (1208). Trop. Cyclone Res. Rev. 2013, 2, 96–108. [Google Scholar] [CrossRef]
- Liu, L.; Wang, Y. Trends in Landfalling Tropical Cyclone–Induced Precipitation over China. J. Clim. 2020, 33, 2223–2235. [Google Scholar] [CrossRef]
- Su, J.; Ren, G.; Zhang, Y.; Yang, G.; Xue, X.; Lee, R. Changes in extreme rainfall over mainland China induced by landfalling tropical cyclones. Environ. Res. Commun. 2022, 4, 101004. [Google Scholar] [CrossRef]
- Chen, S.; Yang, Y.; Deng, F.; Zhang, Y.; Liu, D.; Liu, C.; Gao, Z. A High-Resolution Monitoring Approach of Canopy Urban Heat Island using Random Forest Model and Multi-platform Observations. Atmos. Meas. Tech. 2022, 15, 735–756. [Google Scholar] [CrossRef]
- Cui, M.; Xiang, C.; Zhang, H.; Xu, Y.; Su, Z. Characteristics of extreme precipitation in Fujian induced by Typhoon Doksuri (2305). J. Mar. Meteorol. 2023, 43, 11–20. [Google Scholar] [CrossRef]
- Xu, H.; Duan, Y.; Li, Y.; Xu, X. Indirect Effects of Binary Typhoons on an Extreme Rainfall Event in Henan Province, China From 19 to 21 July 2021: 1. Ensemble-Based Analysis. J. Geophys. Res.-Atmos. 2022, 127, e2021JD036083. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteor. Soc. 2020, 146, 730. [Google Scholar] [CrossRef]
- Al Shalabi, L.A.; Shaaban, Z.; Kasasbeh, B. Data Mining: A Preprocessing Engine. J. Comput. Sci. 2006, 2, 735–739. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).