Improving Hyperspectral Image Classification with Compact Multi-Branch Deep Learning

Abstract

The progress in hyperspectral image (HSI) classification owes much to the integration of various deep learning techniques. However, the inherent 3D cube structure of HSIs presents a unique challenge, necessitating an innovative approach for the efficient utilization of spectral data in classification tasks. This research focuses on HSI classification through the adoption of a recently validated deep-learning methodology. Challenges in HSI classification encompass issues related to dimensionality, data redundancy, and computational expenses, with CNN-based methods prevailing due to architectural limitations. In response to these challenges, we introduce a groundbreaking model known as “Crossover Dimensionality Reduction and Multi-branch Deep Learning” (CMD) for hyperspectral image classification. The CMD model employs a multi-branch deep learning architecture incorporating Factor Analysis and MNF for crossover feature extraction, with the selection of optimal features from each technique. Experimental findings underscore the CMD model’s superiority over existing methods, emphasizing its potential to enhance HSI classification outcomes. Notably, the CMD model exhibits exceptional performance on benchmark datasets such as Salinas Scene (SC), Pavia University (PU), Kennedy Space Center (KSC), and Indian Pines (IP), achieving impressive overall accuracy rates of 99.35% and 99.18% using only 5% of the training data.

1. Introduction

Hyperspectral imaging (HSI) has revolutionized remote sensing by seamlessly combining imaging with subdivided spectroscopy [1]. This technique provides a unique perspective on surface objects by simultaneously capturing data across numerous small spectral bands over a wide area [1,2]. Despite its wide-ranging applications, including military defense, atmospheric research, urban planning, vegetation ecology, and environmental surveillance [3,4,5], HSI faces challenges like spectral data redundancy, limited annotated examples, and significant within-class variation. Addressing these issues is crucial for unlocking the full potential of HSI data analysis [6].

The classification of HSI stands as a paramount challenge within remote sensing, primarily due to several critical obstacles. To begin with, the paucity of ground truth data or labeled samples poses a significant hindrance to accurate classification endeavors. Acquiring labeled samples for training classifiers proves especially daunting in remote or inaccessible regions, where obtaining ground truth data remains a formidable task. This scarcity not only hampers the development and validation of classification models but also undermines their generalization capabilities, leading to suboptimal performance in real-world scenarios. Additionally, the high dimensionality inherent in HSI data exacerbates classification difficulties, often resulting in sparse data distributions and the curse of dimensionality problem [7]. With an extensive array of spectral bands, effectively modeling the data distribution becomes a daunting challenge, further compounded by the presence of spectral variability influenced by atmospheric conditions and environmental factors. Moreover, the challenge of spectral variability introduces additional complexity, as the spectral response of observed materials can be significantly altered by atmospheric variations, illumination changes, and environmental conditions. Addressing these challenges necessitates innovative approaches that integrate advanced machine learning techniques, such as deep learning architectures, to extract both spectral and spatial features, thereby enhancing the accuracy and reliability of HSI classification for diverse applications in remote sensing and beyond.

Within the rich tapestry of hyperspectral imaging, where each pixel encapsulates a symphony of over 100 spectral bands, lies the intricate challenge of the curse of dimensionality. This enigma, inherent in high-dimensional HSI data, poses significant obstacles to classification tasks, as it leads to sparsity and increased computational complexity. To address this, dimensionality reduction methods such as Linear Discriminant Analysis (LDA) [8], Principal Component Analysis (PCA) [9], and Minimum Noise Fraction (MNF) [10] have been employed. LDA aims to maximize class separability, while PCA extracts orthogonal components capturing the maximum variance in the data. MNF focuses on noise suppression, enhancing the signal-to-noise ratio. However, these methods suffer from limitations such as information loss, especially in the case of PCA which prioritizes variance over class discrimination. Moreover, computational costs associated with these methods can be prohibitive, particularly for large-scale datasets. Hence, the development of efficient dimensionality reduction techniques is imperative, emphasizing the preservation of discriminative information while minimizing computational overhead. Novel approaches integrating machine learning, such as autoencoders and deep neural networks, offer promising avenues for dimensionality reduction in HSI analysis, striving to strike a balance between computational efficiency and preservation of essential spectral characteristics, thus facilitating accurate and scalable HSI classification.

Traditional methods predominantly rely on spectral information, neglecting the incorporation of spatial data, within the dynamic realm of HSI classification. Approaches such as Support Vector Machine (SVM) [11] and Multinomial Logistic Regression (MLR) [12] often restrict their analysis to spectral features, which hinders their ability to capture the comprehensive characteristics of the data. Despite their utility, these techniques exhibit deficiencies in terms of robustness and the completeness of feature extraction. However, the emergence of Convolutional Neural Networks (CNNs), emblematic of deep learning, marked a transformative shift in HSI classification. These intricate algorithms possess an innate capability to autonomously identify intricate patterns from raw data. Various CNN-based architectures, ranging from those equipped with multiple convolutional layers to 2D CNNs [13], 3D CNNs [14], and region-based CNNs, have demonstrated remarkable effectiveness in seamlessly integrating both spectral and spatial dimensions. This fusion has significantly enhanced the accuracy and precision of HSI interpretation, paving the path for revolutionary advancements in remote sensing applications. Nonetheless, challenges persist in the adoption of 2D CNN or 3D CNN architectures in HSI classification. While 2D CNNs excel in capturing spatial information, they often struggle to extract discriminative feature maps from spectral dimensions. Conversely, 3D CNNs, though promising, entail considerable computational costs due to extensive convolution operations. Furthermore, the deep variants necessitate larger training datasets, which are often inaccessible given the limited availability of publicly accessible HSI datasets. Additionally, the widespread use of stacked 3D convolutions in many 3D CNN architectures presents optimization challenges [15], impeding direct estimation loss optimization through such nonlinear structures. These challenges underscore the necessity for ongoing research and innovation in developing more efficient and scalable deep learning architectures tailored to the intricate requirements of HSI classification.

Recent studies underscore the importance of integrating multi-scale spatial characteristics to enhance accuracy, particularly in basic RGB picture segmentation. Models like PSPnet [16] and the Inception Module effectively amalgamate features across dimensions to capture intricate subtleties and bolster overall performance. Building upon this foundation, our investigation introduces the innovative concept of Spectral Dilated Convolutions (SDC) [17], drawing inspiration from the Dilated Residual Network (DRN) [18]. The aim of SDC is to broaden the range of captured wavelengths, while Multiple Spectral Resolution (MSR) [19] incorporates various levels of detail within the spectral dimension. MSR modules employ a series of 3D convolutional branches meticulously tailored for specific spectral widths, extracting sophisticated and high-level spectral information from HSIs. This pioneering approach significantly enhances the efficiency and precision of HSI analysis by enabling the extraction of spectral properties at multiple scales.

While the incorporation of advanced classification techniques like multi-branch CNN models with HSIs undoubtedly signifies a significant leap forward in remote sensing capabilities, it is important to note that these methods still face challenges in training and classification with limited data [20,21]. Despite their effectiveness in combining spectral and spatial information, their performance may be hindered by the scarcity of labeled data available for model training, particularly in real-time applications. As such, while the continuous evolution of HSI technologies underscores the dynamic nature of remote sensing and its pivotal role in enhancing our understanding of the Earth’s surface, ongoing research and advancements in this field must also address the need for more robust methodologies that can effectively extract crucial features and classify data with limited labeled samples.

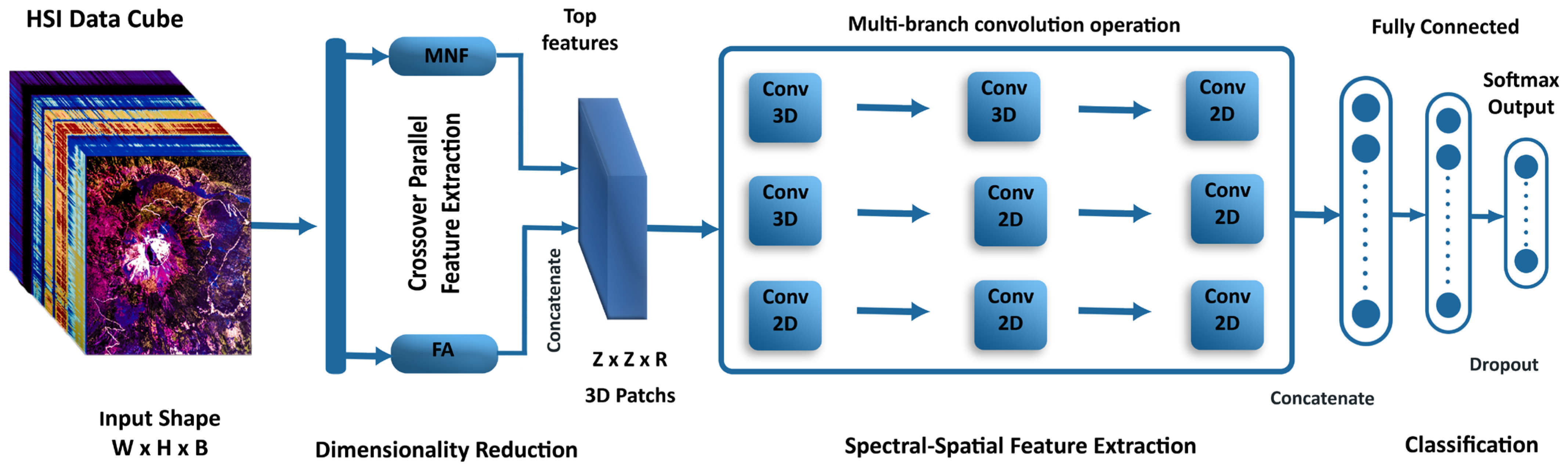
In our dedicated pursuit of overcoming the myriad challenges inherent in HSI classification, we present a groundbreaking model named Compact Multi-Branch Deep Learning (CMD). This meticulously crafted framework signifies a significant departure from conventional approaches, driven by our unwavering commitment to innovation and advancement. At its essence, CMD employs a sophisticated strategy to address the intricacies of HSI analysis, focusing on three key components crucial for enhancing our understanding of HSI data. A pivotal aspect of CMD lies in its innovative approach to simplifying and extracting valuable insights from HSI data through dimensionality reduction. By integrating two prominent methods, Factor Analysis (FA) and Minimum Noise Fraction (MNF), CMD seeks to harness the strengths of each technique to create a comprehensive and informative feature space. This integration allows CMD to leverage spectral features from two distinct dimensions, providing a richer and more informative dataset for classification tasks. By extracting top features from both FA and MNF and integrating them seamlessly, CMD not only streamlines the data but also enhances the discriminative power of the classification model, ultimately leading to improved accuracy and efficiency in HSI classification. This novel approach represents a significant advancement in HSI classification, offering enhanced capabilities for tasks such as remote sensing, environmental monitoring, and beyond.

Building upon this foundational dimensionality reduction synergy, CMD incorporates a meticulously tailored multi-branch deep learning model. This refinement is designed to enhance training efficiency by minimizing trainable parameters, thereby accelerating training durations without compromising classification accuracy. The deep learning model seamlessly integrates spectral and spatial attributes, uncovering intricate data patterns and relationships—a comprehensive approach poised to redefine the essence of HSI classification paradigms. The primary achievements of our study can be outlined as follows:

• Our innovative approach harmonizes FA and MNF methodologies to effectively address high-dimensionality challenges in HSI classification. This transformative process preserves essential features, fostering efficient and accurate classification.
• The CMD model redefines conventional architectures through strategic modification of deep learning, optimizing parameters for swifter training and enhanced capture of intricate HSI patterns. This refinement results in superior classification, marking a significant advancement in the field.
• The CMD framework integrates dimensionality reduction and modified deep learning, culminating in heightened classification precision. Through the prioritization of crucial features and the minimization of noise, our method empowers accurate predictions, contributing to the overall robustness of HSI classification methodologies.

The subsequent structure of this paper unfolds in three key sections. Section 2 elaborates on the methodologies used in the proposed CMD method, providing an in-depth literature review that contextualizes our innovative approach. Moving forward, Section 3 delves into the dataset and experimental analysis, offering thorough descriptions of datasets, meticulous presentation of experimental hyperparameters and configurations, and an extensive analysis and discussion of the obtained results is provided in Section 4. Finally, Section 5 concludes the paper by succinctly summarizing the pivotal outcomes and outlining potential avenues for future research endeavors. This comprehensive structure aims to provide a holistic understanding of the CMD framework’s development, application, and implications in the realm of HSI classification.

2. Materials and Methods

2.1. Minimum Noise Fraction (MNF)

The MNF technique stands out as a crucial dimensionality reduction tool in the realm of hyperspectral imagery, offering a sophisticated approach to enhance data clarity and extract vital signal content [22]. When applied to hyperspectral datasets, MNF serves as an invaluable preprocessing step, particularly due to its ability to mitigate noise interference.

To understand the intricacies of the MNF process, we begin with a hyperspectral data matrix denoted as X, where the dimensions m × n represent spectral bands and pixels, respectively. The initial step involves calculating the mean vector μ across bands for each pixel, resulting in a mean-adjusted data matrix ${\mathit{X}}^t$. This adjustment ensures that the data are centered around their mean, facilitating a clearer representation of the underlying signal patterns. The subsequent step is the derivation of the covariance matrix W from the transformed ${\mathit{X}}^t$, capturing complex interdependencies among spectral bands. The essence of MNF lies in the eigenvalue decomposition of W, expressed as [23]:

$$\mathit{W}=\mathit{V}\mathit{L}{\mathit{V}}^t$$

(1)

Here, W is the covariance matrix, V represents the matrix of eigenvectors, and L is the diagonal matrix of eigenvalues. The transpose of the matrix V is denoted as V^t. The eigenvalues and eigenvectors obtained from this decomposition hold crucial information about the underlying spectral characteristics of the hyperspectral data. To further elaborate, MNF employs a transformation matrix T, defined as:

$$\mathit{T}={\mathit{V}}^t$$

(2)

This transformation matrix is applied to the original hyperspectral data matrix X, yielding a set of transformed data vectors Y:

$$\mathit{Y}=\mathit{T}\mathit{X}$$

(3)

The transformed data vectors Y possess the property that the first few components have maximum variance, effectively highlighting essential signal patterns while suppressing noise. The transformed data can then be expressed as a product of two matrices:

$$\mathit{Y}=\mathit{Q}\surd \Lambda$$

(4)

Here, Q is the matrix of transformed data vectors, and √Λ is the square root of the diagonal matrix of eigenvalues. The inclusion of MNF in the representation is particularly noteworthy due to its effectiveness in reducing noise and enhancing the interpretability of hyperspectral data. MNF’s utilization of eigenvalue decomposition and transformation matrices underscores its sophisticated approach to dimensionality reduction in HSIs, rendering it a potent tool for enhancing data quality and enabling subsequent analyses. MNF stands out for its capability to capture intricate interdependencies among spectral bands and to accentuate crucial signal patterns while mitigating noise, thus addressing the challenges associated with extracting key informative features from hyperspectral datasets. Moreover, the presentation of the MNF algorithm’s pseudocode, along with Equations (1)–(4), in Algorithm 1 offers a comprehensive resource for implementing MNF-based dimensionality reduction for hyperspectral data. This preference for MNF is underscored by its ability to effectively address the complexities inherent in hyperspectral data analysis and its provision of a robust framework for extracting essential features crucial for subsequent analyses.

Algorithm 1: Pseudocode for dimensionality reduction using MNF (Dimensionality Reduction of HSI Data using MNF)

1. Input: Original hyperspectral data matrix $\mathit{X}$ of dimensions $m\times n$, where m represents spectral bands and n represents pixels.

2. Initialization: Calculate the mean vector $\mathit{\mu }$ across bands for each pixel. Compute the mean-adjusted data matrix ${\mathit{X}}^t$ by subtracting μ from each pixel in $$\mathit{X}:{\mathit{X}}^t=\mathit{X}-\mathit{\mu }$$

3. Derive Covariance Matrix: Compute the covariance matrix $\mathit{W}$ capturing complex interdependencies among spectral bands: $$\mathit{W}={\mathit{X}}_{\mathit{t}}{{\mathit{X}}_{\mathit{t}}}^{\mathit{T}}$$

4. Eigenvalue Decomposition: Perform eigenvalue decomposition of $\mathit{W}$ to obtain eigenvectors $\mathbf{V}$ and eigenvalues $\mathsf{\Lambda }:\mathit{W}=\mathbf{V}\mathsf{\Lambda }{\mathbf{V}}^T$

5. Apply Transformation: Compute the matrix product of ${\mathit{V}}^{\mathit{T}}$ and $\mathit{X}$, yielding transformed data vectors $\mathit{Y}:\mathit{Y}={\mathit{V}}^{\mathit{T}}\mathit{X}$

6. Express Transformed Data Vectors: Compute the square root of the diagonal matrix of eigenvalues $\mathsf{\Lambda }:\surd \mathsf{\Lambda }$. Multiply the matrix of transformed data vectors $\mathit{Y}$ by $\surd \mathsf{\Lambda }$, expressing $\mathit{Y}$ as a product of two matrices: $\mathit{Q}$ and $\surd \mathsf{\Lambda }:\mathit{Y}=\mathbf{Q}\surd \mathsf{\Lambda }.$

7. Output: Transformed data vectors $\mathit{Y}$.

2.2. Factor Analysis

Factor Analysis constitutes another statistical methodology that endeavors to reveal the underlying relationships among observed variables by expressing them in terms of latent variables, referred to as factors. The ultimate goal of this method is to reduce a large number of primary variables to a smaller set of components through the strategic transformation of those variables [24]. This process not only captures the most common data variances from the original dataset but also enables a more succinct representation of the underlying structure, thereby enhancing the interpretability and efficiency of subsequent analyses. Fundamentally, FA measures the proportion of data variability attributable to shared factors [25]. To illustrate, consider a collection of observable random variables represented as W = (W₁, W₂………W_n), accompanied by a corresponding mean vector σ = (σ₁, σ₂.……... σ_n). The fundamental equation governing FA takes the form [26]:

$$\mathit{W}=\mathit{\sigma }+\mathit{\delta }\mathit{P}+\mathit{\rho }$$

(5)

In this scenario, P = (P₁, P₂.……...P_n) represents a vector comprising latent factor scores, $\mathit{\rho }$ = ($\rho$₁, $\rho$₂.…….. $\rho$_n) signifies a vector containing latent error terms, and $\mathit{\delta }$ = ($\delta$₁, $\delta$₂, …, $\delta$_n) denotes the factor loadings matrix. For the pursuit of FA, a distinct approach is employed to estimate the covariance matrix of the observable random variable W:

$$Covc\left(\mathit{W}\right)=\mathit{\delta }{\mathit{\delta }}^{\prime }+\mathit{\phi }$$

(6)

Here, φ adopts the structure of a diagonal matrix. The summation of squared loading values within $\mathit{\delta }{\mathit{\delta }}^{\prime }$, forming the Pth diagonal element, is identified as the kth communality. This value signifies the proportion of variability that the common factors account for. Moreover, the Pth diagonal element of φ is recognized as the Pth specific variance, representing distinct characteristics inherent to the variable.

2.3. Proposed Crossover Dimensionality Reduction

In enhancing the effectiveness of machine learning models, our proposed crossover dimensionality reduction method combines the merits of MNF and FA. The motivation behind this integration stems from addressing challenges posed by singular dimensionality reduction approaches, such as PCA, which may encounter difficulties in extracting the most informative features. MNF is proficient in preserving the variance of the data, yet it may face limitations in maintaining correlations among features. Conversely, FA excels in preserving interrelationships among variables but may not be as effective in conserving the inherent variability in the dataset. Our proposed method strategically integrates MNF with FA to harness the complementary strengths of both techniques. Mathematically, this integration can be expressed as follows:

$$\mathit{X}=\mathit{A}\times \mathit{B}+\mathit{E}$$

(7)

Here, X represents the original hyperspectral data matrix, A is the matrix from FA capturing interrelationships, B is the matrix from MNF capturing significant elements explaining data variation, and E represents the residual error matrix. The combination of A and B results in a reduced-dimensional representation that balances the preservation of interrelationships and variability in the dataset.

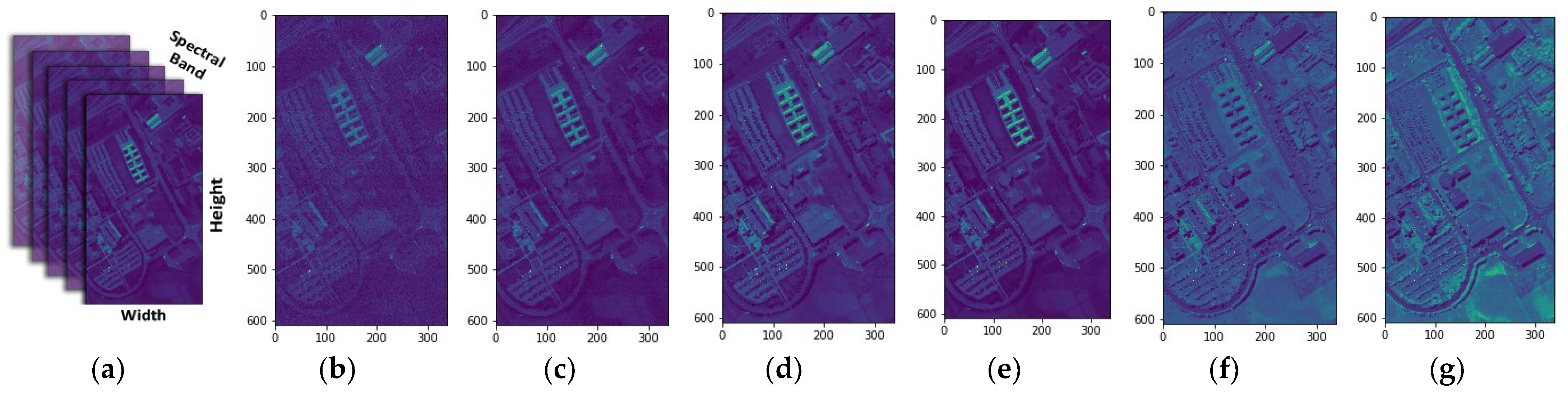
The efficacy of our proposed method has been empirically demonstrated to surpass that of both MNF and FA individually across diverse datasets. This superiority is attributed to the integration of the advantages offered by both MNF and FA. The utilization of a reduced set of characteristics, in comparison to the individual approaches, contributes to the mitigation of overfitting, leading to improved generalization performance. Moreover, the integrated method exhibits greater resilience to noise compared to its individual components, enhancing its robustness in the presence of background noise. The synergistic fusion of MNF and FA thus emerges as a potent strategy for dimensionality reduction in hyperspectral data, paving the way for more effective machine learning models.

2.4. Proposed Multi-Branch Deep Learning Approach

Among the deep learning models, the CNN represents a sophisticated approach to image processing, utilizing a sequence of filters to extract a diverse array of features from images. These features are then processed through multiple layers, enabling the CNN to effectively classify or segment images based on the features it has extracted. In the realm of HSI classification, CNN architectures play a pivotal role. For instance, SpectralNET [27], a notable model, adopts a wavelet CNN architecture with 2D CNN in four levels of decomposition. This architecture aims to extract both spectral and spatial features from the HSI data. While 2D CNNs excel at capturing spatial information, they may not fully leverage the abundant spectral information inherent in HSI data. In contrast, 3D CNNs have the potential to extract both spectral and spatial information simultaneously, which could lead to more comprehensive feature extraction. However, the application of 3D CNNs in HSI classification has its challenges. To address these challenges, a model called Fast and Compact 3D CNN [28] was proposed, integrating incremental PCA for spectral feature reduction. Despite these efforts, both incremental PCA and the 3D CNN architecture were found to be time-consuming and yielded suboptimal results, particularly when trained with limited samples. To mitigate these limitations, a strategy involving the fragmentation of the HSI data cube into overlapping 3D patches has been proposed. This approach enhances the efficiency and effectiveness of feature extraction, thereby improving classification accuracy, especially when dealing with limited training samples. To encompass the $S\times S$ window and all T spectral bands, a collection of 3D contiguous patches $\mathit{Q}\in {\mathit{P}}^{S\times S\times T}$ has been devised. The equation presented illustrates the convolution operation of the 3D CNN across three dimensions:

$${\mathit{Y}}_{x,y,d}^{a,r}=f\left(\sum _m\sum _{i=0}^{I_{a-1}}\sum _{j=0}^{J_{a-1}}\sum _{k=0}^{K_{a-1}}{ὡ}_{i,j,k}^{a,r,m}\times {\mathit{Q}}_{x+i,y+j,d+k}^{a-1,m}+c^{a,r}\right)$$

(8)

$K_i$ represents the size of the spectral dimension for the 3-D kernel, while k denotes the count of kernels in the layer. The convolutional kernel ${ὡ}_{i,j,k}^{a,r,m}$ is linked to the feature map in the rth position of the lth layer.

In a separate investigation, a three-branch Convolutional Neural Network (CNN) termed Tri-CNN was introduced for spectral-spatial feature extraction, coupled with PCA as a feature reduction technique. However, this approach encountered limitations as PCA struggled to effectively handle the nonlinear features present in HSI. Furthermore, within the deep learning architecture, the Tri-CNN model initially extracted spectral features, followed by spatial features, and eventually combined both in the three branches of the CNN. However, relying solely on spectral features proved insufficient to significantly impact classification outcomes. To address these deficiencies, a novel approach was devised, wherein the spatial feature extractor and the spectral-spatial feature extractor were amalgamated with a spectral-only feature extractor, forming a comprehensive three-branch feature fusion network. This architectural enhancement aimed to bolster the extraction of spectral feature characteristics and enhance the overall feature extraction process. Multi-branch CNNs represent a significant advancement from conventional CNNs by incorporating multiple convolutional branches, each specialized in learning distinct features from input images. This integration fosters a more comprehensive understanding of the data, consequently elevating prediction accuracy. As depicted in Figure 1, the CMD model architecture initially captures spectral features and employs multiple convolution layers for subsequent spatial-spectral feature extraction.

Each block consists of three convolution layers with 8, 16, and 32 filters, respectively. The first block incorporates two convolution 3D layers and one convolution 2D layer, featuring kernel sizes of 3 × 3 × 5 and 3 × 3 × 1 for the first two layers and 3 × 3 for the third layer. The second branch comprises one convolution 3D and two convolution 2D layers, with kernel sizes of 3 × 3 × 5 for the first layer and 3 × 3 for the following two layers. The third block is dedicated to spatial features, housing three convolution 2D layers with kernel sizes of 3 × 3 for the initial two layers and 3 × 1 for the last layer.

Efficient feature extraction in the CMD model is achieved by strategically leveraging smaller convolution kernels, as outlined in previous research [29]. Despite their compact size, these kernels play a crucial role in enhancing computational efficiency while capturing intricate patterns within hyperspectral data. As the model progresses through subsequent convolution blocks, outputs from different branches are concatenated and flattened, converting multidimensional features into one-dimensional vectors. This streamlined representation ensures a coherent flow of information, leveraging insights from both spectral and spatial dimensions. To address overfitting concerns, fully connected dense layers incorporate two dropout regularizations, preventing the model from relying too heavily on specific features. The final step in the CMD model’s execution is the classification process, where learned features are utilized to make accurate predictions. This comprehensive approach positions the CMD model as a powerful and efficient tool for HSI analysis, demonstrating its ability to distill complex information into meaningful classifications.

3. Dataset and Experimental Analysis

3.1. Dataset Details

In this study, a diverse set of HSI datasets has been meticulously chosen to ensure a comprehensive evaluation of the proposed CMD model. The Salinas Scene (SA), Pavia University (PU), Kennedy Space Center (KSC), and Indian Pines (IP) datasets collectively contribute to the richness and diversity of the data analyzed [30].

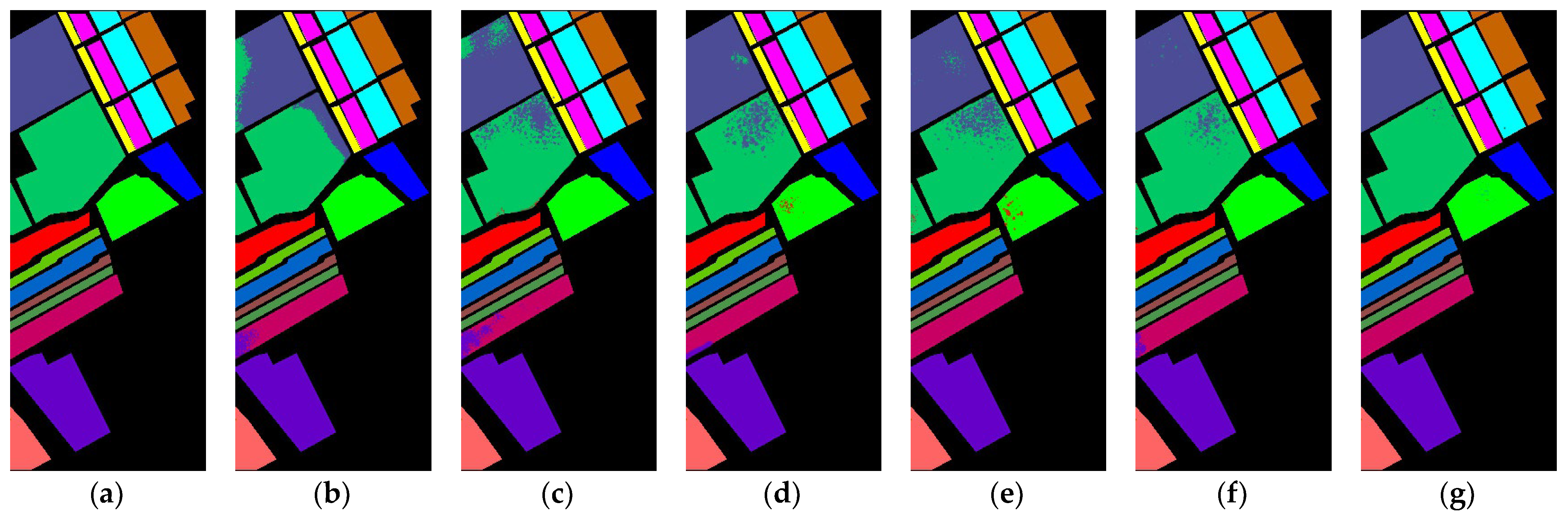
The Salinas Scene dataset (SA) encapsulates a panoramic view with 16 distinct classes, providing detailed spectral information across its spatial dimensions. This dataset facilitates the exploration of various land cover categories, allowing for a thorough characterization and analysis of the scene. The Pavia University dataset (PU) introduces a unique perspective, offering valuable insights into the spectral characteristics of the university environment. With its set of distinct classes, PU contributes to the overall diversity of the study, enabling a nuanced examination of surface features within the university scene. The Kennedy Space Center dataset (KSC) captures the hyperspectral signature of the Kennedy Space Center area and encompasses 13 distinct classes. Each class in the KSC dataset represents different features and materials found within the Kennedy Space Center environment, contributing to a detailed understanding of the spectral signatures associated with various objects and surfaces. The Indian Pines dataset (IP) adds an additional layer of complexity and diversity to the study, featuring a total of 16 distinct classes. This dataset, derived from an agricultural area, provides insights into the spectral variations associated with different crop types and land cover features.

The inclusion of these four diverse datasets—SA, PU, KSC, and IP—ensures a robust evaluation of the proposed model across varying landscapes and class distributions. The comprehensive analysis leveraging these datasets enhances the generalizability and applicability of the study’s findings in the realm of HSI analysis. Further information is elaborated in

Table 1. Brief exposition of datasets used in experiments.

Features	Datasets
	Salinas Scene (SC)	Pavia University (PU)	Kennedy Space Center (KSC)	Indian Pines (IP)
Collected By	AVIRIS sensor	ROSIS Sensor	AVIRIS sensor	AVIRIS sensor
Surface	Salinas Valley, California	University of Pavia, Italy	Kennedy Space Center, Florida	North-western Indiana, Chicago
Spatial Dimension	512 × 217	610 × 340	512 × 614	145 × 145
Spectral Dimension	224	103	176	224
Classes	16	9	13	16

.

3.2. Experimental Hyperparameters and Configuration

In conducting our experiments for HSI classification, we leveraged the powerful computing capabilities of Google Colab, an accessible cloud-based platform. The experiments were conducted within a Python 3.8 environment, with specific attention given to version details for reproducibility. TensorFlow, a leading deep learning framework, was employed with a version of 2.4 to harness its latest features and optimizations. The utilization of GPU acceleration on Google Colab further expedited the model training process, capitalizing on parallel processing capabilities.

To ensure a fair and consistent comparison across experiments, we adhered to a standardized patch extraction process. Three-dimensional patches of uniform dimensions $(11\times 11\times 5)$ were systematically extracted from the input hyperspectral volumes. This spatial-spectral configuration allowed for a comprehensive analysis of local features within the data. The heart of our experimentation lies in a deep learning model crafted specifically for HSI classification. The model architecture featured three branches of convolutional layers, coupled with two fully connected layers. Notably, to optimize pixel-level data retention, we deliberately omitted pooling layers. The total number of trainable parameters for this model was precisely configured to 663,760, striking a balance between model complexity and computational efficiency.

For the intricate process of model training, we adopted the Adam optimizer, a popular choice for its adaptive learning rate capabilities. The mini-batch size was set at 256, striking a balance between memory efficiency and model convergence. A learning rate of 0.001, coupled with a decay rate of 10⁻⁶, ensured the fine-tuning of model parameters over 100 epochs. This epoch count was meticulously chosen to achieve a convergence point while avoiding overfitting on the available data. Execution of the experiments was seamlessly orchestrated on the Google Colab platform, taking advantage of its user-friendly interface and convenient integration with Jupyter notebooks. The TensorFlow framework, optimized for GPU usage, facilitated the efficient execution of the model on the cloud-based environment. A concise overview of the CMD model and its hyperparameters can be found in

Table 2. A succinct summary of the proposed model architecture, focusing on a Salinas dataset with an 11 × 11 window size.

Layer (Type)
Inpt_lyr_1 (InputLayer)	Inpt_lyr_1 (InputLayer)	Inpt_lyr_1 (InputLayer)
Con3d a_1_1	Con3d a_2_1	Con2d b_3_1
Con3d a_1_2	Reshape	Con2d b_3_2
Reshape	Con2d b_2_2	Con2d b_3_3
Con2d b_1_3	Con2d b_2_3	Reshape
Concatenate (Con2d b_1_3, Con2d b_2_3, Con2d b_3_3)
Flatten
Dense (614,656)
Dropout (0.5)
Dense (32,896)
Dropout (0.4)
Dense (2064)
Total Trainable params: 663,760

^a Convolution 3D layer; ^b Convolution 2D layer.

and

Table 3. The hyperparameters utilized in the CMD approach under consideration.

Hyperparameter	Value
Input size	11 × 11 × 5
Optimizer	Adam
Cost function	Categorical cross entropy
Con. 2D layers	6
Con. 3D layers	3
Dense layers	3
Hidden layers drop out	2
Hidden layers activation function	ReLU
Output layers activation function	Softmax
Learning rate	0.001
Batch size	256
Epoch	100
Decay rate	10−6
Momentum	0.9

.

In summary, our experimental setup on Google Colab encapsulated a judicious selection of configurations, encompassing Python version, TensorFlow version, GPU acceleration, patch extraction dimensions, model architecture, and training parameters. These configurations were meticulously chosen to ensure reproducibility, fairness in comparison, and optimal performance in the challenging task of HSI classification.

4. Experiment and Result

4.1. Result Analysis

Before delving into the results, it is imperative to understand the nuances of the original HSI data and its representation. Visual representations of the original HSI data cube and band-to-band images before feature extraction are provided in Figure 2 to enhance interpretation. These visual aids illustrate the artifacts present in HSI images, including ground maps, and shed light on the challenges associated with classifying data with a limited training sample. Notably, while bands 1 and 5 exhibit discernible features, bands 75 and 89 display considerable noise, underscoring the complexity of HSI classification tasks. Conversely, the top five spectral features after extraction by the proposed dimensionality reduction method are presented in Figure 3. Components 3a and 3c belong to the MNF components, while 3b, 3d, and 3e belong to factors, representing the top-ranked features for enhancing the classification. One notable observation is that each of the five components differs from the others, indicating minimal redundancy and less noise. Furthermore, the comprehensive analysis conducted in this study reveals the pivotal influence of the window size on the performance of the proposed CMD model across various HSI datasets. As highlighted in

Table 4. Influence of the size of the 3D patch window on the effectiveness of the proposed approach across all datasets.

Window Size	Salinas Scene			Pavia University			Kennedy Space Center			Indian Pines
	OA	Kappa	AA	OA	Kappa	AA	OA	Kappa	AA	OA	Kappa	AA
7 × 7	98.92	98.13	98.64	97.21	97.05	97.13	98.96	98.64	98.81	96.74	96.47	96.53
9 × 9	99.16	99.04	99.08	98.87	98.68	98.76	98.95	98.69	98.75	96.79	96.55	96.68
11 × 11	99.35	99.29	99.31	99.13	98.78	99.04	99.13	98.98	99.10	97.48	97.32	97.41
13 × 13	99.22	99.06	99.15	97.89	97.46	97.72	99.18	99.10	99.13	98.72	98.66	98.47
15 × 15	99.3	99.18	99.22	98.45	98.33	98.26	99.06	98.99	99.06	98.34	98.13	98.28
17 × 17	99.33	99.23	99.26	98.78	98.73	98.74	99.12	99.13	99.08	97.52	97.39	97.41
19 × 19	99.24	99.21	99.19	98.89	98.68	98.79	99.09	98.95	99.03	98.23	98.05	98.14

, the experimental findings underscore the significance of selecting optimal window sizes tailored to the unique characteristics of each dataset. It is crucial to note that the model’s training utilized only 5% of the available data, making it sensitive to even minor alterations in the setup, resulting in noteworthy fluctuations in performance. The consistent superiority of the 11×11 window size for the SC and PU datasets and the 13 × 13 window size for the KSC and IP datasets underscores the importance of adapting patch window widths to each dataset’s specific characteristics. This adaptability is crucial for optimizing the CMD model’s performance in HSI classification tasks. Despite SC and PU datasets being captured by the same sensor, their differences in spatial resolution result in distinct optimal window sizes, highlighting the need for dataset-specific customization. Additionally, noteworthy fluctuations in performance due to minor alterations in the model setup emphasize the sensitivity of the CMD model to variations in training data and parameter configurations. Therefore, meticulous attention to detail in model training and parameter tuning is essential to ensure consistent and reliable performance across different HSI datasets. Ultimately, adapting patch window widths enhances the CMD approach’s effectiveness, improving classification accuracy, robustness, and generalizability in various remote sensing applications.

The evaluation process of the CMD model involves a comprehensive analysis of its classification accuracy across different fractions of training data. Utilizing a random sampling technique, labeled samples spanning from 1% to 5% of the available data were systematically chosen for training, leaving the remaining data for testing purposes. Figure 4 visually presents the classification results, revealing discernible variations in accuracy relative to different training sample sizes. Strikingly, the CMD model demonstrates unwavering and robust performance across all three datasets, regardless of the size of the training set. This consistent performance suggests that the model generalizes well to varying amounts of training data, indicating its resilience and adaptability. The CMD’s ability to maintain accuracy even with minimal training samples could be attributed to its hierarchical learning approach, which enables the extraction of distinctive features from hyperspectral data, ensuring reliable classification outcomes across different scenarios and dataset sizes.

Table 5. Impact of different combinations of extracted features on the proposed method using two datasets.

MNF:FA	Salinas Scene			Pavia University			Kennedy Space Center			Indian Pines
	OA	Kappa	AA	OA	Kappa	AA	OA	Kappa	AA	OA	Kappa	AA
1:1	98.83	98.51	98.68	96.85	96.38	96.66	97.01	96.76	96.75	93.74	93.58	93.63
1:2	98.82	98.56	98.62	98.43	98.32	98.29	98.34	98.15	98.23	95.42	95.25	95.31
2:1	99.01	98.85	98.88	97.88	97.76	97.82	98.48	98.11	98.38	97.64	97.47	97.53
1:3	99.10	98.97	99.05	98.69	98.61	98.57	98.66	98.27	98.57	96.69	96.57	96.46
3:1	98.99	98.86	98.93	97.74	97.55	97.64	98.63	98.24	97.54	96.95	96.84	96.91
2:3	99.35	99.29	99.31	99.13	98.78	99.04	99.18	99.10	99.13	98.72	98.66	98.47
3:2	99.07	99.04	99.03	99.10	98.67	98.59	98.71	98.49	98.64	98.21	97.89	99.12
MNF (5)	99.05	98.82	98.9	98.36	98.21	98.26	98.65	98.35	99.48	97.34	97.16	97.23
FA (5)	99.03	98.91	98.97	98.81	98.53	98.74	98.59	98.31	98.46	98.14	97.75	98.02

provides a detailed analysis of the proposed model’s performance, delving into various features derived from different methodologies. Notably, the optimal performance is observed when utilizing a 2:3 feature ratio derived from MNF and FA among the different combinations explored, ranging from 1:1 to 3:2. This outcome underscores the synergistic advantages attained by combining features from both MNF and FA, highlighting the model’s adeptness in leveraging the unique strengths of each dimensionality reduction technique. While MNF specializes in capturing correlated features, FA excels in extracting latent ones, resulting in a more comprehensive representation of hyperspectral data. By strategically integrating MNF and FA features, the model enhances its ability to discern and utilize a wide range of spectral and spatial information, ultimately contributing to its superior overall performance in HSI classification. The integration of MNF and FA features allows the model to capture intricate patterns and nuances present in the data, leading to enhanced accuracy and robustness in classification tasks. This holistic approach ensures that the model can effectively handle the complexities inherent in hyperspectral data, making it a valuable tool for various applications in remote sensing and environmental monitoring.

For a comprehensive evaluation of the proposed classification algorithm, we conducted comparisons with several state-of-the-art approaches, including Fast 3D CNN [28], HybridSN [31], SpectralNET [27], MBDA [32], and Tri-CNN [33]. The results, detailed in

Table 6. Time required to train three distinct deep learning models on 5% of the data from three separate benchmark datasets (in seconds).

Methods	Datasets
	Salinas Scene	Pavia University	Kennedy Space Center	Indian Pines
Fast 3D CNN	127.82	131.37	122.31	101.67
HybridSN	85.39	103.48	73.59	80.83
Spectral-NET	84.61	100.04	67.1	79.32
MBDA	109.62	124.35	100.4	93.76
Tri-CNN	80.31	90.73	78.45	72.48
Proposed	75.4	90.15	69.24	70.55

, shed light on the training duration across different datasets, with the CMD model consistently exhibiting minimal training times. Notably, the Fast 3D CNN and MBDA models required the longest training durations due to the complex infrastructure of 3D convolution layers, while other methods averaged comparatively lower times. Impressively, the proposed CMD method recorded the shortest training durations, clocking in at 75.4, 90.15, 69.24, and 70.55 s for the SC, PU, KSC, and IP datasets respectively. Moving to

Table 7. Comparison of classification outcomes using 5% of labeled training samples with various state-of-the-art methods.

Methods	Salinas Scene			Pavia University			Kennedy Space Center			Indian Pines
	OA	Kappa	AA	OA	Kappa	AA	OA	Kappa	AA	OA	Kappa	AA
Fast 3D CNN	98.82	98.62	98.68	97.98	97.84	98.02	98.52	98.33	98.41	97.19	97.02	97.08
HybridSN	99.05	98.92	98.99	98.68	98.53	98.45	98.81	98.42	97.72	96.39	96.27	96.32
Spectral-NET	99.13	99.06	99.09	98.55	98.37	98.47	98.78	98.5	98.64	97.53	97.51	97.44
MBDA	99.11	98.88	98.96	98.95	98.78	98.92	98.83	98.53	99.66	98.29	98.21	98.18
Tri-CNN	99.09	98.97	99.03	98.87	98.74	98.85	98.88	98.69	98.82	98.38	98.23	98.36
Proposed	99.35	99.29	99.31	99.13	98.88	99.04	99.18	99.10	99.13	98.45	98.32	98.37

, we present a comprehensive comparison of three accuracy metrics—overall accuracy, Kappa coefficient, and average accuracy—between the state-of-the-art methods and the proposed CMD model, each trained with only 5% of the available data. The highlighted optimal outcomes underscore the superior performance of the CMD model. Notably, in terms of overall accuracies, SpectralNET and MBDA exhibited better performance compared to other methods. However, the proposed CMD method outshone them all, achieving maximum accuracies of 99.35%, 99.13%, 99.18%, and 98.45% for the SC, PU, KSC, and IP datasets respectively. Despite the complexity of the SpectralNET’s wavelet CNN architecture and the MBDA’s utilization of a multi-branch attention model, their performance was commendable but faltered when dealing with very limited training samples. These findings highlight the robustness and efficacy of the CMD model in achieving high accuracy even with minimal training data, positioning it as a promising solution for HSI classification tasks.

Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 enrich the analysis by providing visual representations of classification accuracy and loss values during each training iteration for the four datasets. In Figure 5, the accuracy and loss during the training process of both training and validation data are presented for the four datasets achieved from the proposed method. Despite utilizing a smaller fraction of training data, the curves exhibit remarkable smoothness, underscoring the robustness of the proposed CMD model. Moving to Figure 6, Figure 7, Figure 8 and Figure 9, these Figures showcase classification maps alongside corresponding ground truth maps for the SC, PU, KSC, and IP datasets, respectively. Upon examination, it is evident that the Fast 3D CNN, HybridSN, and MBDA methods generated classification maps with significant noise, characterized by a large number of incorrectly assigned pixels and low classification accuracy. Conversely, the CMD model excels in accurately defining uniform areas, as evidenced in Figure 6f, Figure 7f, Figure 8f and Figure 9f. While there are some misclassified pixel samples, the CMD method exhibits results closest to the reference ground truth map. These visualizations highlight the prowess of the proposed model in accurately defining uniform areas and reducing instances of isolated noise, further validating its effectiveness in HSI classification tasks.

4.2. Discussion

In summary, the comprehensive experimentation and analysis conducted provide strong validation for the efficacy of the proposed CMD model in hyperspectral image classification. The model’s adaptability to different datasets, its robust performance across varying fractions of training data, and its superior accuracy compared to state-of-the-art approaches firmly position the CMD model as a promising solution for addressing challenges in HSI classification. This study contributes valuable insights to the field by offering a thorough understanding of the factors influencing model performance and presenting a robust methodology for analyzing hyperspectral data. Additionally, the detailed comparison with existing methods underscores the superiority of the CMD model, further cementing its significance in advancing the field of hyperspectral remote sensing image classification.

5. Conclusions and Future Work

The intricate interaction between spectral and spatial redundancy in hyperspectral imaging poses a significant hurdle for effective HSI classification. In order to address this issue, our research presents the Compact Multi-Branch Deep Learning (CMD) model, which is especially made to handle the intricacies of HSI analysis. The model effectively recovers important characteristics from various dimensions while reducing spectral redundancy by combining FA and MNF. In addition, the CMD model enhances CNN-based model construction and integrates a three-branch feature fusion structure to meet existing HSI classification issues. Three branches of a multi-branch CNN are used to analyze the data. Features from each branch are flattened and fused, and fully connected and dropout layers are employed to provide the final classification result.

Future endeavors will focus on refining the CMD model’s architecture to enhance computational efficiency, with attention-based models being explored for improved generalization across varied datasets. Our commitment remains steadfast in advancing the efficiency and reliability of hyperspectral image classification through innovative methodologies and continuous refinement of the CMD model. Addressing the issue of limited labeled samples, we intend to employ data augmentation techniques and explore semi-supervised or unsupervised classification approaches in future HSI classification research. Given the costly and time-consuming nature of labeling HSI pixels, these strategies will be instrumental in overcoming the scarcity of labeled samples.