Abstract
Space plasma turbulence plays a relevant role in several plasma environments, such as solar wind and the Earth’s magnetosphere–ionosphere system, and is essential for describing their complex coupling. This interaction gives rise to various phenomena, including ionospheric irregularities and the amplification of magnetospheric and ionospheric currents. The structure and dynamics of these currents have relevant implications, for example, in studying ionospheric heating and the nature of electric and magnetic field fluctuations in the auroral and polar environments. In this study, we investigate the nature of small-scale fluctuations characterizing the ionospheric magnetic field in response to different geomagnetic conditions. We use high-resolution (50 Hz) magnetic data from the ESA’s Swarm mission, collected during a series of high-latitude crossings, to probe the scaling features of magnetic field fluctuations in auroral and polar cap regions at spatial scales still poorly explored. Our findings reveal that magnetic field fluctuations in field-aligned currents (FACs) and polar cap regions across both hemispheres are characterized by different scaling properties, suggesting a distinct driver of turbulence. Furthermore, we find that geomagnetic activity significantly influences the nature of energy dissipation in FAC regions, leading to more localized filamentary structures toward smaller scales.
1. Introduction
In recent decades, observations of the near-Earth environment have revealed the complex and non-linear coupling between solar activity and phenomena within the Earth’s magnetosphere and ionosphere system. Specifically, variations in the interplanetary magnetic field (IMF) intensity and orientation have a significant impact on plasma circulation, driven by magnetic reconnection events at the magnetopause [1]. High-latitude current systems, such as field-aligned currents (FACs) [2] and the auroral electrojets, which flow parallel and perpendicular to the geomagnetic field, respectively, undergo enhancement [3]. This enhancement leads to an increase in plasma deposition within the auroral oval and, to some extent, in the polar cap regions. These currents are responsible for the geomagnetic field disturbances observed in the high-latitude ionosphere and may have an impact on the atmospheric drag acting on low-Earth orbit satellites [4].
In this context, there has been a growing interest in the statistical analysis of FACs’ properties and topology [5], primarily utilizing in situ measurements from low-orbiting satellites such as Challenging Minisatellite Payload (CHAMP), Active Magnetosphere and Planetary Electrodynamics Response Experiment (AMPERE), Ørsted, Defense Meteorological Satellite Program (DMSP), Iridium and Swarm constellations, and also ground-based magnetometers and the Super Dual Auroral Radar Network (SuperDARN). FACs are known to occur on a variety of scales, ranging from large-scale currents with a breadth of hundreds to thousands of kilometers [6] to scales as small as a few hundred meters [7]. Large-scale FACs exhibit two main regions [6] within the auroral oval, with a structure similar to a double ring centered on the magnetic poles: (i) the inward current sheet (referred to as Region 1) flows upward in the magnetosphere from the evening sector and inward in the ionosphere in the morning sector, while (ii) the outward current sheet (known as Region 2) flows in opposite directions. These two magnetic field-aligned current systems are supplemented by a weaker current system known as Region 0, which is located poleward of the R1 currents and has the opposite polarity, similar to R2 currents.
Research has been conducted to explore the location, intensity, and latitudinal expansion of FACs, examining their relationship with various factors. These factors include seasonal fluctuations and ionospheric conductivity, the substorm cycle, dipole tilt, and solar wind properties such as velocity, density, dynamic pressure, and IMF strength and orientation (see [8] and references therein). Throughout these studies, the orientation of the interplanetary magnetic field has emerged as a critical factor influencing the strength and geometry of FACs [3], with the southward IMF component (Bz < 0) notably contributing to current intensity. A peculiar feature observed by Ritter et al. [9] is an increasing current density at smaller spatial scales with densities ranging from more than 1 mA/m2 at ∼102–103 km scales to some μA/m2 at km scales. These evidences demonstrate the existence of small-scale structures within large-scale currents, even in the cusp and polar cap current systems [10], and pose intriguing implications for the dynamics of magnetosphere–ionosphere coupling. Notably, their high current density and potential filamentary structure [11] could play a significant role in locally heating the ionosphere and thermosphere. Furthermore, the intensity of these currents appears to be influenced by solar wind turbulence [10], highlighting the intricate interplay between external factors and internal processes within the Earth’s magnetosphere–ionosphere system.
Plasma instabilities and turbulence, both fluid and magneto-hydrodynamic, arise as a consequence of large-scale plasma motions [12] and are crucial in the description of their dynamical processes, from the formation and evolution of structures in space to the energy transport and absorption processes. Indeed, turbulence is capable of generating multiscale coherent structures that can be observed as bundles of fluctuations, whose dynamics also lead to the emergence of spatio-temporal intermittency, resulting in an inhomogeneous turbulent energy dissipation pattern [13,14].
Recent years have seen a significant amount of research on the turbulent characteristics of ionospheric plasma and field fluctuations using numerical models, ground stations, rockets, and satellites operating at various scales. For instance, the formation and dynamics of ionospheric irregularities, which characterize active equatorial and polar regions, are linked to the turbulent nature of plasma density. These plasma structures can delay or distort electromagnetic signals, compromising the performance of the Global Navigation Satellite System (GNSS) and Global Positioning System (GPS) [15,16]. As a result, research into turbulence mechanisms that can, under certain situations and spatial scales, exercise significant control over ionospheric dynamics, has become increasingly important. This is especially true in the field of space weather, where a thorough understanding of the ionospheric environment is required for constructing prediction models to mitigate the effects of solar activity on both terrestrial and space-based infrastructures.
Numerous studies have shown that high-latitude magnetic and electric field fluctuations, as well as plasma density, are characterized by power-law spectral densities, scale invariance, and non-Gaussian distribution of small-scale increments, resulting in a complex behavior with intermittent turbulent dynamics [17,18,19,20]. Furthermore, the scaling properties of field fluctuations have also been explored as a function of the different high-latitude regions (auroral oval and polar cap), magnetic local time and the intensity of geomagnetic activity [21,22]. Golovchanskaya and Kozelov [23] observed that, while the amplitude of the electric field fluctuations were significantly smaller at the polar cap than in the auroral zone, their scaling properties were similar, potentially implying the same nature of turbulence in the two regions. These findings may seem counter-intuitive, as the factors influencing turbulent fields on both open and closed magnetic field lines are expected to be different. Specifically, it is presumed that electric field fluctuations in the polar cap are primarily driven by variations in the turbulent solar wind, while fluctuations in the auroral zone are believed to be generated internally by the magnetosphere–ionosphere system. Conversely, examination of the spatial structure of plasma velocities [24] revealed varying degrees of intermittency in the polar cap and auroral areas. The nature and sources of small-scale electric field and plasma velocity fluctuations have been discussed through several theories and models. Some of them associate high-latitude ionospheric turbulence with structures of magnetospheric origin [25], others relate it directly to solar wind turbulence [26] or to shear flow instabilities developing in the large-scale FACs regions [27]. Still, despite the large amount of studies, a clear and unified picture of the origin and properties of high-latitude ionospheric turbulence has yet to emerge. While the intrinsic complexity of the system can be considered the primary cause for our poor understanding, some of it may be due to the difficulty of obtaining adequate in situ measurements. Indeed, most of these studies infer spatial structures and their main features from temporal domain data analysis, for which a good statistic over a wide range of scales is easier to achieve.
In a series of works based on Swarm measurements, De Michelis et al. [17,28] examined the scaling features of the geomagnetic field’s horizontal components. The authors found that different turbulence regimes exist within the regions crossed by satellites, and their scaling properties are influenced by IMF conditions, suggesting that the observed changes could be related to the effect of solar wind–magnetosphere–ionosphere coupling, which drives geomagnetic activity. While most of the previous literature has focused on electric field fluctuations, these studies have shown that the results on the scaling properties of the electric field cannot be directly extended to magnetic field fluctuations. Indeed, a good correlation exists only between the north–south electric field component and the east–west geomagnetic field component [25]. Consolini et al. [11] further investigated the small-scale magnetic field fluctuations in the FACs regions as a function of magnetic local time under disturbed geomagnetic conditions. They observed anomalous scaling invariance, indicating the occurrence of intermittency, which exhibits a dependence on the dayside and nightside sectors.
These studies have highlighted the necessity of investigating the nature and sources of small-scale variability to gain a proper understanding of the turbulent intermittent nature, and the complex filamentary geometries of the current systems associated with magnetic field fluctuations. In this context, our work provides a statistical analysis of the spectral and scaling properties of magnetic field fluctuations under different geomagnetic conditions. We aim to disentangle the small-scale dynamic properties of plasma observed in the polar cap and FAC regions. In detail, we analyze high-resolution measurements from the Swarm A satellite to probe the power density spectra and high-order statistics of magnetic field fluctuations in the auroral and polar cap ionosphere. This paper is organized as follows: In Section 2, we discuss the data sources and the criteria for their selection. Following this, we outline the methods used to evaluate the spectral and scaling properties. Section 3 reports our results for the Northern and Southern Hemispheres, with a comparison of features across various high-latitude regions. Finally, in Section 4, the implications of our findings are discussed in relation to the previous literature.
2. Materials
The ESA’s Swarm mission, launched in 2013 [29], consists of a constellation of three identical satellites: Swarm A and C fly side by side at an altitude of approximately 460 km in a plane with an inclination of 87°, while Swarm B orbits at about 510 km. Thanks to the mission’s high quality and longevity, a large dataset describing the plasma and magnetic field of the topside F-region is available. The scientific payload of the satellites includes an absolute scalar magnetometer (ASM) and a vector field magnetometer (VFM) [30].
In this work, we utilize high-resolution magnetic field observations collected by VFM onboard Swarm A, with a sampling rate of 50 Hz, spanning from June 2015 to February 2023. The magnetic data, expressed in Earth’s spherical coordinates, are extracted from the ESA dissemination server using the oper_maga_HR_1b file type. Additionally, for the same time intervals, we used Swarm Level-2 FAC single product [31] oper_facatms_2f file type, to determine FAC density strength with a sampling rate of 1 Hz. The magnetic field gradients, needed to compute FAC density strength, were detected throughout the Swarm A orbit track.
To designate the satellite position, we adopted the magnetic and non-orthogonal Quasi Dipole (QD) system of magnetic coordinates, commonly utilized in describing processes closely associated with the geomagnetic field and account for the position of the Sun by using Magnetic Local Time (MLT) instead of Coordinated Universal Time (UTC).
In order to examine the effects of geomagnetic activity on the magnetic field fluctuations at high latitude, we divide our dataset into two classes, corresponding to low and high geomagnetic activity, respectively. We identify these periods using the SuperMAG Auroral Electrojet (SME) [32] and the planetary [33] indices. The 1-min SME index [34], which is a generalization of the traditional AE index, provides a proxy of the variation of the electrojet current intensity and, indirectly, of the auroral energy deposition rate. The choice of SME index is due to the fact that the AE-index is not yet available for the entire time period under analysis. Furthermore, the expanded station coverage of the SME index provides better accuracy in the spatial and temporal localization of geomagnetic disturbances. Still, the uneven coverage of geomagnetic observatories between the two hemispheres leads to a bias where the observed disturbances are mostly related to the Northern hemisphere. Given the complexity of magnetosphere–ionosphere coupling, it may not be optimal to simply assume a direct correlation between the presence of disturbances in the two hemispheres, implying that disturbances in the Northern and Southern areas may be limited to a single hemisphere. For this reason, we jointly employ the Kp index, which is utilized to characterize the size of global perturbations in the Earth’s magnetic field with a cadence of 3 h. The two time series were downloaded from the SuperMAG collaboration and GFZ Postdam data facility, respectively.
We select time intervals longer than 15 h that satisfy the average conditions ∩ 75 nT and ∩ 700 nT for quiet and disturbed geomagnetic conditions, respectively. The 15 h time requirement, which roughly corresponds to ten orbits of the Swarm A satellite, is required to obtain good statistics in the high-order analysis. We emphasize that the average conditions as described by the geomagnetic indices are valid for each orbit within the selected time interval. This aspect is crucial as it allows us to study and obtain a statistical measure of magnetic field fluctuations arising from similar geomagnetic conditions. Furthermore, it is important to highlight that the sub-intervals selected within the various periods listed in Table 1, which identify high-latitude passages in both the Northern and Southern hemispheres, have an average duration of approximately 20 min, which is the time required for the satellite to pass over the areas of interest. Within these time intervals, it is reasonable to assume that the level of disturbance remains constant. The SME threshold used to determine low geomagnetic activity corresponds to the 25th percentile of the cumulative distribution throughout the selected time period. The SME threshold for high activity points to the strongest geomagnetic occurrences seen in recent years since it aligns with the 95th percentile. Using our previous selection criterion, we acquired a collection of 11 quiet and 15 disturbed time periods (see Table 1). Considering that the satellite requires approximately 94 min to complete a full orbit around the planet, during which it traverses both high-latitude zones in both hemispheres, the selected periods correspond to multiple passages over the areas of interest.

Table 1.
List of the periods considered for the study of magnetic field fluctuations during disturbed and quiet geomagnetic conditions. The dates of the events (DD day, MM month, and YY year) are listed in the first column, and the time periods in UT for which Swarm A data were evaluated are listed in the second. In some cases, the second column’s time period is provided with a “+1” notation. It shows that the time pertains to the day after the one mentioned in the first column. The third and fourth columns refer to the mean and SME geomagnetic indices, respectively.
3. Methods
3.1. Data Processing
As our interest lies primarily in the analysis of magnetic field fluctuations generated by ionospheric and magnetospheric currents, we subtract from the total magnetic field measured by the VFM instrument onboard Swarm A the magnetic contributions of internal origin, i.e., coming from the Earth’s core and crust, as modeled by CHAOS-7 [35]. CHAOS is a time-dependent model for the near-Earth geomagnetic field based on magnetic field observations collected by low Earth orbit satellites (Swarm, Cryosat-2, CHAMP, SAC-C and Ørsted) and ground observatories. The magnetic data used in the model field estimation satisfy strict geomagnetic quiet-time criteria such as and positive IMF By (see Finlay et al. [35] for further specifications).
A frequent approach in the analysis of plasma dynamics immersed in a magnetic field is to use a reference system with axes parallel and perpendicular to the direction of the magnetic field. In our case, this procedure allows us to separate perturbations generated by FACs in the direction perpendicular to the magnetic field seen by Swarm, i.e., the main field, from those produced by currents flowing horizontally, which are expected to be parallel to the main field [36]. In detail, if B is the external magnetic field and Bi the main geomagnetic field, the projection of B along Bi, i.e., B‖, is
Given the ambiguity in the choice of the vectors in the plane perpendicular to Bi, we decide to rotate B such that the two perpendicular components are directed toward the magnetic North and East, respectively. Introducing the unitary vector parallel to Bi, , the perpendicular unitary vectors in the new reference frame are defined by
where the components of the unitary vector , and are expressed in Earth’s spherical coordinates. Thus, the triad e‖, e⊥1, e⊥2 is a positive defined orthonormal basis. In Figure 1, four examples of the obtained results are shown. In each example, the Swarm A satellite’s magnetic field measurements were adjusted by eliminating the internal and crustal field components, allowing for an examination of only the external magnetic field component. The latter was then projected along the direction parallel to the main geomagnetic field (B‖) and onto the plane orthogonal to it (B⊥1 and B⊥2). Data in the first and second panels of Figure 1 relate to high-latitude crossings that occurred on 27 February 2023, from 00:45:52 to 01:02:01 and 06:13:21 to 06:30:51 UT time in the Northern and Southern Hemispheres, respectively. Similarly, the third and fourth panels show high-latitude crossings that occurred on 29 October 2021, from 01:04:09 to 01:14:48 and 08:08:36 to 08:19:13 UT time. The chosen days correspond to geomagnetic disturbed and quiet conditions, respectively. In all recorded examples, the three magnetic field components show a strong long-term trend, which is punctuated by shorter-period oscillations. This finding emphasizes the non-stationary nature of the signals, revealing temporal variations that fluctuate across time scales.
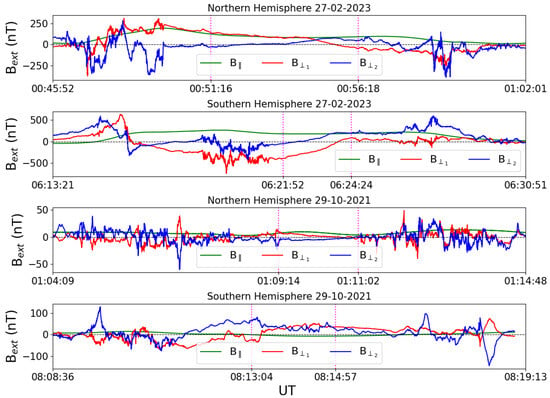
Figure 1.
An example of the magnetic field components of external origin along the main field’s parallel and perpendicular directions during a series of high-latitude crossings. The first and second panels show two Northern and Southern Hemisphere crossings that occurred on 27 February 2023, while the third and fourth panels correspond to crossings that occurred on 29 October 2021. The magenta dotted lines denoted the three distinct regions traversed by the satellite: FACs dayside region, polar cap, and FACs nightside region.
Ascertaining the position of FACs, and more in general the auroral oval boundaries, in each polar crossing of the satellite is a recurrent and crucial problem in high-latitude ionospheric analysis [37]. Such information is necessary in order to separate auroral and polar cap regions, characterized by different physical processes. The time intervals where Swarm A is traversing FAC flows are identified by a standard deviation filter passed on the FAC density data. Specifically, we compute a local of the FAC density data using a moving window, and we label as FAC regions those regions where > 0.03 A/m2 [11]. We then use the MLT and quasi-dipole magnetic latitude of the satellite track to classify dayside (6:00 < MLT < 18:00) and nightside (18:00 < MLT < 6:00) FACs regions and consequently identify the the polar cap as the regions poleward of the FAC, i.e., the magnetic field measurements between their boundaries.
3.2. Empirical Mode Decomposition Detrending
To effectively isolate the prominent long-term trend from the shorter-period oscillations superimposed upon it in all three magnetic field components, we employed the Empirical Mode Decomposition (EMD) [38] method. The EMD method is a powerful data analysis technique designed to capture the complex dynamics of non-stationary signals, such as those seen in geomagnetic field variations. Its primary objective is to break down such signals into a finite set of intrinsic oscillatory modes. This decomposition is achieved through a systematic sifting procedure, which adaptively identifies and extracts various oscillatory components, thereby reconstructing the signal’s behavior at different time scales. Specifically, the EMD method decomposes the signal into a series of empirical modes, denoted as , where n represents the order of the mode. Mathematically, the original signal is expressed as the sum of these empirical modes along with a residual component , which typically exhibits characteristics such as being a constant, a monotonic function, or a function with a single maximum and minimum:
In this process, the criterion adopted to determine the maximum number of empirical modes, denoted by N, is crucial and involves setting a threshold limit for the size of the standard deviation between two consecutive sifting steps. In this context, a threshold value of is commonly employed, ensuring an appropriate balance between capturing signal dynamics and avoiding overfitting [38]. Through this decomposition process, the EMD method provides a comprehensive and insightful framework for analyzing non-stationary signals, allowing us to uncover hidden patterns, extract meaningful information, and gain deeper insights into the underlying dynamics of complex systems.
Our choice in using the EMD was motivated by the the adaptive nature of the method which allows to adjust effectively to variations in signal frequency and amplitude over time without setting a fixed window length. Moreover, EMD offers a data-driven approach to signal decomposition, breaking down the signal into a finite set of intrinsic oscillatory modes without the need for predefined basis functions or filters. These advantages enable the EMD method to capture both short-term oscillations and long-term trends present in the data, providing a comprehensive understanding of the signal dynamics.
We apply the EMD method to the external magnetic field data of each high-latitude crossing. On average, we extract 11 empirical modes plus the residue in the case of both magnetic components (B⊥1, B⊥2) lying in the plane perpendicular to the main magnetic field direction. The consistent number of empirical modes obtained is due to the similar length of the analyzed time series, with their number in each time series decomposition being a function of the logarithm of the number of data points. Upon analyzing each mode, we observe distinct contributions associated with the residue and the last two empirical modes, and , which primarily describe the large-scale magnetic field structure expected from the presence of FACs. Conversely, lower-order modes are attributed to smaller-scale current structures, indicated by their generally higher frequencies. This contribution of different cn modes can be visualized in Figure 2.
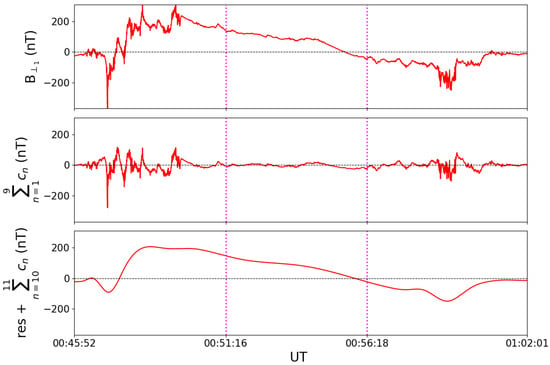
Figure 2.
The upper panel provides an illustration of the Northward magnetic field component originating from external sources, observed during a high-latitude crossing on 27 February 2023. In contrast, the remaining two panels illustrate the signal decomposition using the EMD method. Specifically, the middle panel represents the combination of the first 9 modes, depicting fluctuations of smaller scale within the signal, while the lower panel showcases fluctuations on larger scales. Magenta vertical lines denote the dayside (left) and nightside (right) field-aligned current regions, identified using the standard deviation filter described in Section 3.
The top panel shows the Northward perpendicular component, upon which we applied the empirical mode decomposition. The subsequent two panels display different signals resulting from the combination of various empirical modes. Specifically, the second panel illustrates the summation of the first nine modes, the third panel shows the modes with lower frequencies and the residue. Hence, we subtract the large-scale contributions from Bext, resulting in a residual magnetic field. For simplicity, we will refer to this residual as the filtered external magnetic field moving forward, and continue with our subsequent analysis. Figure 3 shows the filtered magnetic field in the case of a high-latitude crossing on 27 February 2023, between 00:45:42 and 01:02:01. In this case, the EMD and the subsequent removal of the long-term trend within the time series are applied to both magnetic components (B⊥1, B⊥2) lying in the plane perpendicular to the main magnetic field direction (illustrated in the top panel of the figure), as well as the magnetic field component parallel to the main field (depicted in the bottom panel of the figure).
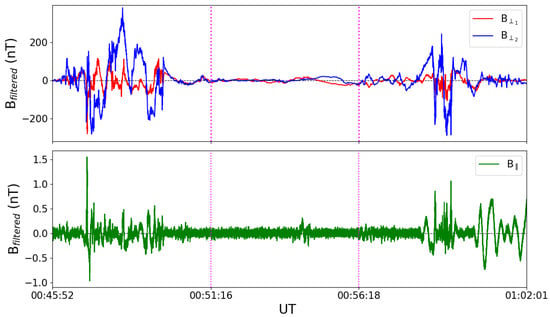
Figure 3.
Example of the three filtered external magnetic field components for the same Northern crossing reported in the first panel of Figure 1. The top panel illustrates the behavior of the filtered perpendicular components, while the bottom panel showcases the behavior of the filtered external magnetic field component aligned parallel to the main field. The vertical lines in magenta highlight the FACs dayside zone (left), polar cap (middle), and FACs nightside region (right), detected by the standard deviation filter defined in Section 3.
3.3. Methods of Analysis
We perform a temporal domain analysis of the selected magnetic field fluctuation data, evaluating their spectral and scaling features. To accomplish this, we first compute the average power spectral density (PSD) for dayside, nightside, and polar cap regions for each event given in Table 1. However, the PSD only provides information on the autocorrelation function, i.e., the second-order momentum of the time series, and is insufficient for investigating turbulence characteristics such as intermittency. For this reason, we use an approach based on the analysis of structure functions to study the scaling features of fluctuations in magnetic fields [39]. The qth-order generalized structure function at scale of magnetic field fluctuations can be written as follows:
where is the j-th component of the external magnetic field and denotes the ensemble average. If the signal is characterized by scale invariance, will scale as a powerlaw with scaling exponent . In the case of a simple global-scale invariant (monofractal) signal, is expected to scale linearly on the moment order q; however in the case of a more complex multifractal system, is typically a non-linear function of q. Further information about the spectral properties of the signals can be inferred using the Wiener–Khinchin theorem [12], which allows us to relate the Fourier power spectral exponent to the second-order structure exponent by = 1 + .
According to Dudok de Wit and Krasnosel’skikh [40], finite sample effects (i.e., the number of points in the time series, Np) have an impact on the accuracy of estimates at order q. In particular, the highest estimable moment order, , is related to the logarithm of Np as . In this scenario, we can investigate statistical moments up to .
Furthermore, to sample each decade in frequency homogeneously, we evaluate increments over a range of timescales equispaced on a logarithmic scale from = 0.02 s to 14 s. The lower boundary is determined by the sampling rate (50 Hz) of the VFM onboard Swarm A, while the greatest scale investigated is 10 times smaller than the time taken by the satellite to cross the shortest region. This procedure ensures a reliable estimation for the fluctuations statistics with a time scale of 14 s. Finally, for the events listed in Table 1, the qth order structure functions of each crossing are normalized by the standard deviation of the increments at the smallest scale in order to properly evaluate the average scaling features.
4. Results
4.1. Spectral Analysis
Following the canonical approach to the study of turbulence, we calculate the average PSD of the filtered external magnetic field for the FACs dayside, polar cap, and FACs nightside zones. The power spectrum reflects the distribution of power fluctuations over frequency and is a commonly used tool for analyzing ionospheric irregularities. PSDs exhibiting a power-law behavior across multiple scales may indicate the presence of inertial range [41]. Figure 4 depicts the average PSD for the three magnetic field components: B∥, B⊥1, and B⊥2, derived from the entire dataset outlined in Table 1. These spectra are analyzed across both quiet and disturbed geomagnetic conditions for each selected sector in the Northern Hemisphere: the FACs region in the dayside, the polar cap, and the FACs region during nighttime. We use different color palettes to illustrate differences between quiet and disturbed geomagnetic conditions in the same regions. In addition, the dashed black line in Figure 4 represents a power-law function with a spectral exponent = 2, which is a common value observed in ionospheric studies [20,25].
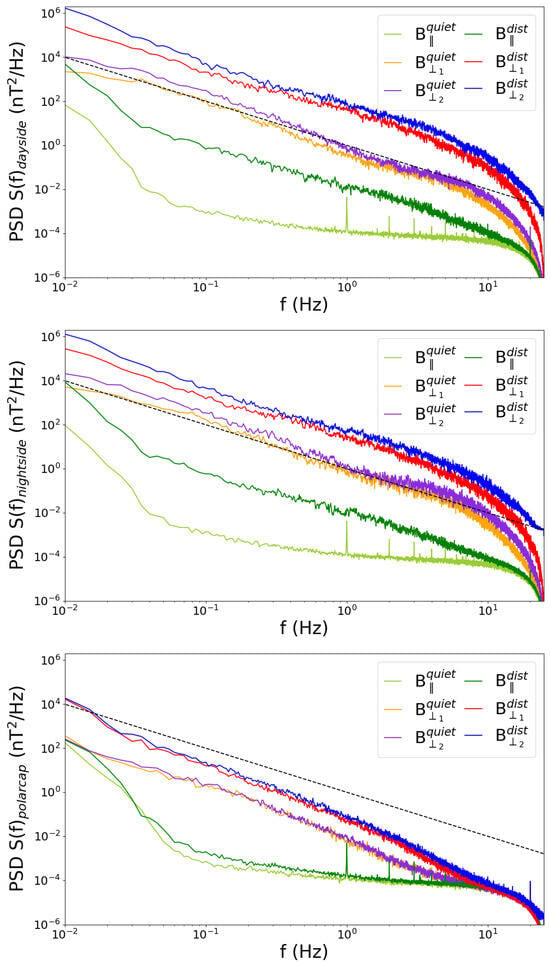
Figure 4.
Average power spectral densities of magnetic field fluctuations along three distinct directions within three chosen sectors in the Northern Hemisphere. The red, blue, and green outlines represent PSDs during disturbed conditions, while orange, violet, and green-lime denote quiet conditions, as explained in the legend. The dashed black line represents a power-law function with an exponent of = 2.
We note that there are no significant differences in the PSD of the Northward and Eastward perpendicular components in the same sector across a wide range of frequencies. More specifically, the spectral shapes are consistent, but the Eastward component seems to be characterized by slightly higher energies in the FAC regions. Figure 4 shows that magnetic fluctuations associated with the parallel component have much lower energy compared to the perpendicular ones. This energy separation can be observed in both quiet and disturbed geomagnetic conditions, suggesting a fluctuation magnetic field that is strongly anisotropic and confined in the plane perpendicular to the main field. This anisotropy supports the view that magnetic field disturbances are mainly due to multiscale field-aligned currents [11].
The spectral features of the perpendicular components are characterized by power-laws (S(f) ∼) over nearly three orders of magnitude with spectral exponents in a range ∈ [1.7, 2.4]. The spectral slope values depend on the analyzed sectors, increasing from dayside and nightside to the polar cap, indicating a more persistent nature of fluctuations, i.e., the sign of fluctuations throughout time tends to remain constant. Similar slopes for magnetic field increments are also reported by Golovchanskaya et al. (2006) [25], although the authors do not differentiate between dayside and nightside. Electric and magnetic field increments, as well as electron density in the high-latitude ionosphere, generally exhibit a spectral break that separates two power-law regimes [19,25]. We also see a steepening of in the FAC regions between 6 Hz and 8 Hz, whereas the spectra above ∼10 Hz are cut off due to the ADC filter. The first break at 8 Hz corresponds to scales of around 1 km, which is consistent with the “cut-off” found by Rother et al. (2007) [5] who argued that the filament nature of FACs at smaller scales may have a relevant role in the high-frequency spectrum behavior. While we limited our earlier explanation to aspects of the Northern Hemisphere, we note that there are no notable changes in spectral behavior or patterns between the two hemispheres.
The primary difference between PSDs for the same selected sector during quiet and disturbed geomagnetic conditions is a spectral energy density increase, as expected from the increase in FACs intensities, although spectral slopes remain the same. The similar may reflect a single physical mechanism responsible for distributing energy onto smaller scales regardless of the energy input provided at larger scales. We underline, however, that an accurate discussion on the interplay between different mechanisms that trigger ionospheric turbulence, which may contribute to understand the nature of this spectral slope similarity, requires further studies taking into account IMF direction, solar wind pressure and more levels of geomagnetic activity. The magnetic field component in the direction parallel to the main field is an exception to the previous case. In quiet geomagnetic conditions, the PSDs exhibit a very steep power-law behavior between 0.01 and 1 Hz, with , and an almost flat behavior at higher frequencies, which can be attributed to instrumental noise. The characteristic frequencies of the knee between these two regimes appear to change according on the selected sector. In fact, the cut-off frequency increases in passing from polar cap to nightside and dayside FAC regions. This shift could be related to the intrinsic higher power associated with fluctuations in the dayside with respect to other regions and underline a difference in their plasma dynamics. Moreover, a series of spikes at 1 Hz and successive harmonics, associated with instrumental sampling frequency, are clearly visible due to the low signal-to-noise ratio in quiet conditions. During disturbed geomagnetic conditions, the increments along the parallel direction to the main magnetic field in FAC regions instead show a power-law behavior similar to the perpendicular components.
The PSDs analysis reveals that, during geomagnetically quiet conditions, the external magnetic field fluctuations in the direction parallel to the main field mainly reflect instrumental noise. Furthermore, attention should be given when studying the parallel component at this altitude. Magnetic fluctuations along the geomagnetic field lines are damped by the strong intensity of the main field [41], which can also be detected in the PSDs presented in Figure 4. As a result, determining the cause of these oscillations is difficult, whether they are directly related to FACs or currents flowing perpendicularly to the main field in lower altitude layers of the ionosphere. Thus, we decide to skip the parallel field component analysis and instead focus on the perpendicular components while performing the structure function analysis.
4.2. Structure Function Analysis
The analysis of qth-order structure functions, Sq, is a useful tool for analysing the occurrence of intermittency in space plasma turbulence and provides information on the scaling behavior of the increment statistics. Kolmogorov and Iroshnikov–Kraichnan theories describe a turbulent fluid/plasma as a mono-fractal system, possessing a global scale invariance with a defined scaling exponent , where h = 1/3 or 1/4. Deviations from a linear dependence of are attributed to a non-homogeneous spatial distribution of energy among scales in the transfer process, implying that dissipation is localized [42]. This is the origin of the so-called intermittency phenomenon.
To investigate the existence of scale invariance and its association with specific regions, we calculated the average structure functions Sq() for each of the three analyzed regions over all our dataset, as listed in Table 1. As explained in the previous section, the single structure function of each crossing is normalized by the value of the increments at the smallest scale, i.e., Sq( = 0.02 s). This approach enabled us to generate average structure functions that effectively characterize the three selected regions based on their geomagnetic activity levels and fixed hemispheric. Figure 5 shows the trace of the qth-order average structure functions for the FACs dayside region during Swarm A satellite’s passing on 27 February 2023, as an example. In detail, Tr() = , where i represents the two perpendicular components and is the ensemble average over the day. The chosen day corresponds to a geomagnetically disturbed day, and the structure functions in the figure were evaluated for the crossings in the Northern Hemisphere. In a double logarithmic scale, the traces of the structure functions of various orders exhibit a clear linear trend with respect to the increment time variable . In order to compute the scaling exponent associated with each structure function, we use the scale interval ranging from 0.1 s to 10 s. The scaling exponent values for each () are estimated in this time interval using a least squares fitting technique. In Figure 5, the dashed red vertical lines delineate the scale interval utilized for fitting, while the resultant fit is depicted in the figure with a dashed black line.
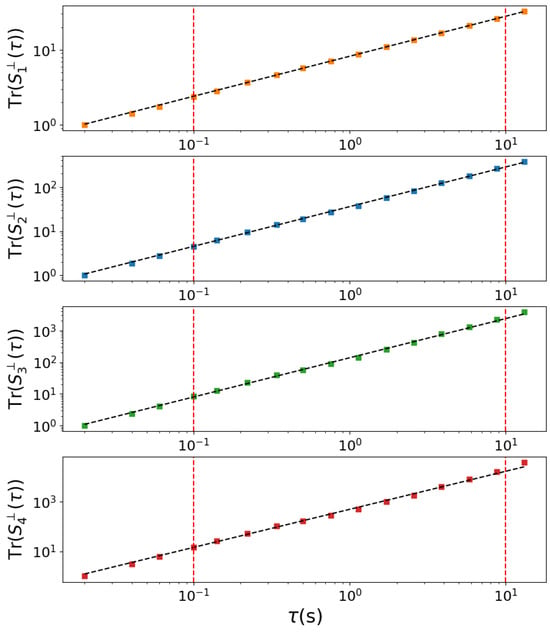
Figure 5.
Example of the trace of qth-order average structure functions Tr(()) = () for the FACs dayside sector, derived from the increments of the external magnetic field perpendicular components recorded by Swarm A satellite during all its transit on 27 February 2023 in the Northern Hemisphere. The panels from top to bottom highlight the behavior of the first, second, third, and fourth moment orders q, respectively. The dashed black lines represent the best linear fit for each moment order. The vertical red lines mark the considered time interval for the fitting process.
Our dataset, consisting of time series of magnetic field increments, can be representative of fluctuations at different spatial scales assuming the validity of Taylor’s hypothesis [43]. This hypothesis is equivalent to assuming that the relative motion of the instrument with respect to the structure it measures is sufficiently fast so that the structures are frozen in and temporal variations can be ignored. In this framework, the frequency measured in the spacecraft reference system is related to the wave number by , where is Swarm spacecraft velocity km/s. With this assumption, which has been shown to be reasonable in auroral and polar regions [44], our analysis of magnetic field fluctuations in the time domain between 0.1 s and 10 s corresponds to probing spatial scales ranging from approximately 1 km to 80 km.
In Figure 6 we show the average scaling exponent behaviors of the Northward perpendicular component in the three MLT sectors for each hemisphere. More in detail, triangles and circles refer to the scaling of quiet and disturbed geomagnetic conditions, respectively. The different colors highlight dayside (red), nightside (blue), and polar cap (green) regions and the related dashed lines are linear interpolation between the q moment orders zero and one scaling exponents during disturbed conditions. The derived values for the first and second order scaling exponents are distributed in ranges between [0.6, 0.8] and [1.0, 1.6], respectively. As observed in the spectral analysis, increases from dayside and nightside to polar cap regions and thus in terms of average properties, the spectral results are consistent with the structure function analysis. Such values are also consistent with the literature [11,28].
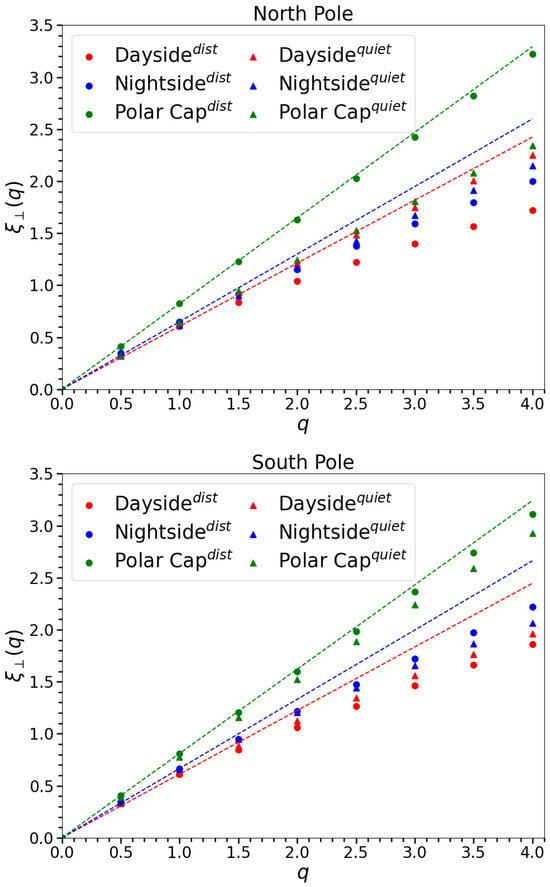
Figure 6.
Scaling exponents relative to the generalized structure functions of the external magnetic field increments for parallel and north directed perpendicular component in the dayside, nightside, and polar cap regions. The triangular markers refers to quiet conditions while the circular ones to disturbed conditions. The dashed lines mark the line passing through the zero and second-order data points for the disturbed geomagnetic conditions.
The dayside perpendicular components show anomalous scaling properties being characterized by a non-linear convex dependency on q (see Figure 6). We observe an increased departure from the linear trend during disturbed conditions with respect to quiet ones in the Northern Hemisphere, which may suggest a more localized energy transfer among different scales during FACs density enhancement. The difference in geomagnetic conditions is less pronounced in the Southern Hemisphere, where both conditions show a significant non-linearity. The scaling exponents of the nightside regions also exhibit non-linearity, albeit to a lesser extent than on the dayside. The trend roughly follows the one observed in the dayside; however, differences between geomagnetic conditions are less evident. These results are in agreement with the idea of intermittent turbulence and support the multifractal character of magnetic field fluctuations in FACs regions. Instead, in the polar cap regions, the magnetic field increments along the perpendicular directions exhibit monofractal behaviors with . The constant coefficient h varies according to geomagnetic conditions with steeper slopes in disturbed periods.
We further highlight differences between the scaling exponents of the two hemispheres in Figure 7. In particular, the top panel displays a scatter plot of the scaling exponents in the Northern and Southern Hemispheres, i.e., and , during disturbed geomagnetic conditions, while the bottom panel shows the same quantities during quiet conditions. The data points are color-coded and shaped in the same manner as in Figure 6. We remark that: (i) if , then the two hemispheres share the same fractal topology, i.e., the same geometrical structure and symmetries; (ii) if , where is a constant coefficient, then the two hemispheres share the same geometrical structures but different symmetries; (iii) if , then they are characterized by different fractal topologies.
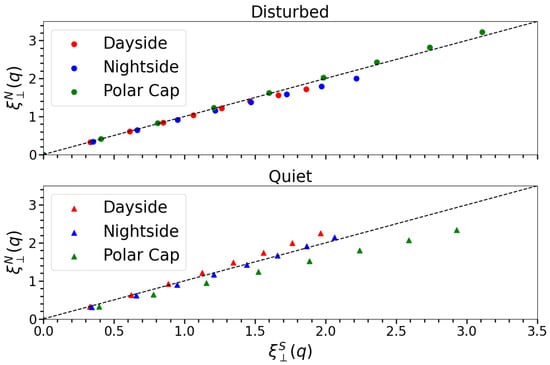
Figure 7.
Comparison between the average scaling exponents for the Northern and Southern Hemispheres in disturbed (top) and quiet (bottom) geomagnetic conditions for each region (dayside: red, nightside: blue, polar cap: green). The dashed line marks the bisector of the plane where .
We observe that, in disturbed conditions, the polar cap exhibits a relation, while the FACs regions , where seems to be consistent for both dayside and nightside regions. Conversely, a non-linear relation holds in FACs regions during quiet geomagnetic conditions. In particular, the Southern Hemisphere exhibits higher intermittency, which can be recognized by the upward convex behavior of the curves in Figure 7. The polar cap region in quiet conditions, on the other end, is characterized by a linear behavior. These results suggest that both hemispheres have roughly the same geometrical structure and symmetries during disturbed geomagnetic conditions, while the Southern Hemisphere exhibits higher intermittency in the FACs regions and fractal topologies during quiet conditions.
To quantify the intermittency of the perpendicular component and its dependence on the geomagnetic conditions, we define the difference between the third-order scaling exponent and three times the first-order one, i.e., . This quantity measures the deviation from linearity and is zero for monofractal signals, while its absolute value increases for other behaviors. We use the relation between (3) and (1) instead of (4) and (2) as the statistics in the former case is more robust. We compute using the scaling exponents of each event reported in Table 1 for dayside, nightside, and polar cap regions, resulting in a set of six distributions for each hemisphere. In Figure 8, the cumulative distributions of for quiet (blue) and disturbed (red) geomagnetic conditions in the three high-latitude regions are shown for both the Northern Hemisphere (, first column) and Southern Hemisphere (, second column). We see significant differences between the two geomagnetic conditions in the FAC regions of the Northern hemisphere, while in the Southern hemisphere, the differences are less pronounced. Specifically, in the dayside region (Figure 8, first row), both hemispheres exhibit higher intermittency during disturbed geomagnetic conditions, as evidenced by the 50th percentile of the cumulative being shifted toward higher values compared to quiet conditions. This separation between intermittency distributions is also found in the nightside region (second row of Figure 8) of the Northern Hemisphere. Instead, the cumulatives associated with quiet and disturbed conditions in the Southern Hemisphere are mostly consistent, suggesting a similar level of intermittency. These results underline the differences between the two FAC zones, as well as their dependence on geomagnetic conditions. In the polar cap region of both hemispheres, the distributions (third row of Figure 8) show values closer to zero, highlighting the quasi-monofractal nature of the perpendicular magnetic field fluctuations in this region. Interestingly, contrary to what is observed in the FAC regions, the distribution associated with disturbed condition exhibits lower intermittency compared to the quiet one.
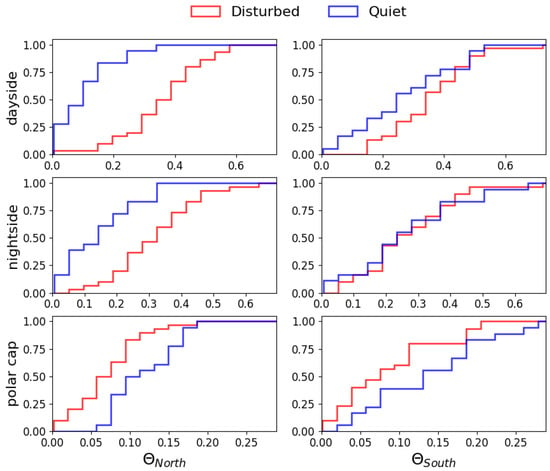
Figure 8.
Cumulative distributions of , which serves as a proxy measure of intermittency, obtained for the Northern () and Southern () Hemispheres. The distributions associated with quiet and disturbed geomagnetic conditions are highlighted in blue and red, respectively, for each high-latitude region.
5. Discussion
We noted variations in the spectral slope value across different regions. Specifically, there was a gradual increase observed from regions hosting FACs during daytime to polar cap areas, and further to regions characterized by the presence of FACs during nighttime. This trend appeared consistent across both quiet and disturbed geomagnetic conditions. De Michelis et al. [28] showed similar results in a statistical study of the horizontal magnetic field component under different interplanetary magnetic field conditions derived from Swarm measurements at 1 Hz. In detail, the spectral slopes observed in all selected regions are steeper than expected from both fluid and MHD 3D isotropic turbulence, typically characterized by and , respectively. The deviation from the theories of Kolmogorov and Iroshnikov–Kraichnan could be attributed to the inherent complexity of our system, which exhibits lower dimensionality in terms of degrees of freedom. This lower dimensionality may arise from various factors, such as the specific characteristics of the magnetohydrodynamic turbulence under investigation or the influence of external perturbations. Moreover, the significant energy gap observed between PSDs along directions parallel and perpendicular to the main field provides further insight. This gap indicates that turbulent fluctuations predominantly occur within the plane perpendicular to the main field, suggesting a quasi-bidimensional nature of turbulence within our system. This quasi-bidimensional behavior could result from physical constraints or the interaction of magnetic field geometry and plasma dynamics, contributing to the deviation from traditional turbulence theories. These results align with previous findings, particularly those highlighted in the case study by Consolini et al. [11]. Additionally, they are corroborated by the observation of low values of the ratio of plasma to magnetic pressure in these regions, as discussed in studies such as that by Biskamp et al. (2003) [41]. This consistency underscores the relevance of our observations and provides further support to the quasi-bidimensional nature of turbulence within the analyzed system.
The observed steepening of the spectral slope around 8 Hz in the FACs dayside and nightside regions is also consistent with previous studies regarding the nature of small-scale FACs [5]. Still, our study is currently limited by the noise cutoff at 12 Hz, which makes difficult to properly ascertain the position and nature of this spectral break.
The scaling of the qth-order structure functions shown in the previous section highlighted the intermittent nature of the magnetic field fluctuations in the plane perpendicular to the main field in the FACs regions of both hemispheres. In particular, the scaling exponents derived for disturbed geomagnetic conditions exhibit a more pronounced non-linearity in both dayside and nightside regions with respect to quiet conditions, although this enhancement is more evident in the Northern Hemisphere. Thus, energy dissipation and its intermittent nature in the high-latitude ionosphere are heavily influenced by geomagnetic conditions and the energy injected in the system. In order to grasp the geometry of dissipative energy burst in day and nightside regions in the Northern Hemisphere, Consolini et al. [11] adopted a simple multifractal model (Cantor set or P-model) and obtained an effective dimension D ≤ 1.6. Intermittent dissipative structures in 3D MHD flows generally manifest as 2D sheets, while in fluid flows, they appear as filamentary structures. Once again, the lower dimensionality of our system compared to MHD models may be attributed to the reduced degrees of freedom and/or the presence of mixed ion and neutral species. Our findings align with those of Consolini et al. [11] and support the idea of an intermittent filamentary energy dissipation pattern in FACs regions during disturbed geomagnetic conditions.
Intuition suggests that distinct behaviors should be expected in day and nightside regions, as they are connected through FACs to the dayside magnetosphere and magnetotail, respectively. Studies regarding the dissipated power density and electron temperature variation as a function of magnetic latitude and geomagnetic activity at Swarm altitudes [45] highlight an asymmetric profile between day and nightside. In particular, climatological maps derived in both quiet and disturbed geomagnetic conditions display a higher dissipated power in the region corresponding to the dayside auroral region. The geometry and symmetry of the FACs structure may be connected to the intensity of the dissipated power. Albeit the cited work is based on 1 Hz measurements, the higher intermittency and consequently the more localized nature of energy dissipation in the dayside may be one of the reason for the observed asymmetry.
The magnetic field fluctuations along the plane perpendicular to the main field in the polar cap regions display monofractal behaviors during disturbed geomagnetic conditions. These findings suggest that the drivers of turbulence in FACs regions and the polar cap differ, aligning with previous studies on the spatial structure of plasma velocities [24]. Additionally, we note that the scaling properties of the polar cap region resemble those observed in the magnetic field fluctuations of the solar wind [46] at kinetic scales. While a connection between the solar wind and polar cap magnetic field fluctuations exist due to the open nature of the magnetic field lines, other physical ionospheric processes, such as convection or shear flows, may also be relevant.
In this study, we also examine similarities and asymmetries in the scaling properties of magnetic field fluctuations between the Northern and Southern Hemispheres. It is important to note that directly comparing observations from both hemispheres presents challenges. Swarm A requires more than 30 min to transition from high-latitude regions in the North to those in the South, resulting in asynchronous observations. This temporal offset could be crucial, particularly in the auroral regions, where plasma dynamics, especially during geomagnetic disturbances, may operate on timescales shorter than 30 min. Therefore, the conditions observed during successive passes over the two hemispheres could vary and may result from processes activated at different times. Given these considerations, in the ensuing discussion, we will assume that it is still possible to compare the dynamics of the two hemispheres by considering the level of disturbance indicated by the SME index, thus hypothesizing that the activated processes are the same under equivalent geomagnetic activity. Within this framework, we can analyze the activity in both the Northern and Southern Hemispheres concurrently. The kernel density estimates of obtained for the Northern () and Southern () Hemispheres are shown in Figure 9 for quiet (blue) and disturbed (red) geomagnetic conditions in the three high-latitude regions. The innermost contours correspond to the regions where 90% of the probability mass of the distribution lies into, while increasingly outward outlines refer to 80%, 70%, 60%, 50%, 40%, and 30% levels, respectively. The absolute value of the versus distributions in the plane provides information on the degree of intermittency, while their position with respect to the bisector of the plane, shown as a dashed black line in Figure 9, suggests hemispheric asymmetries. The scaling exponents (see Figure 7) and intermittency levels (see Figure 9) obtained in disturbed geomagnetic conditions for each high-latitude region show similar behaviors in the two hemispheres, as evidenced by the distribution of intermittency degree with respect to the bisector. However, during quiet geomagnetic conditions, the relationship between the two hemisphere scaling exponents is nonlinear, with the Southern Hemisphere exhibiting higher intermittency in the FACs regions. In particular, we have shown that quiet and disturbed conditions are associated with two distinct intermittency distributions in the Northern Hemisphere, but not in the Southern one. The asymmetric response to varying geomagnetic conditions may stem from the inherently more intricate structure of geomagnetic field lines in the Southern Hemisphere. The pronounced non-dipolar configuration of the magnetic field in the Southern Hemisphere is likely to have a significant impact on the topology of FACs and the manner in which energy is dissipated. Conversely, the magnetic field fluctuations in the two polar caps appear to have the same general properties, with non-homogeneous intermittency distributions and values close to zero.
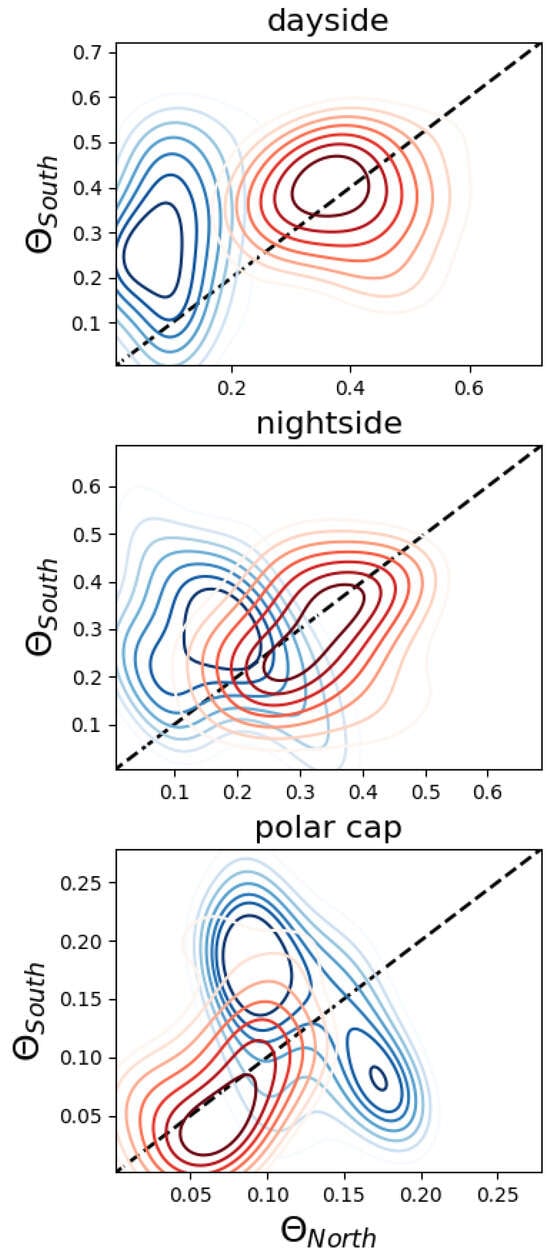
Figure 9.
Kernel density estimates comparing the values of , i.e., the proxy measure of intermittency, obtained for the Northern () and Southern () Hemispheres. The distribution associated with quiet and disturbed geomagnetic conditions are denoted in blue and red for each high-latitude region, respectively. The innermost contours depict the regions containing 90% of the probability mass of the distribution, while subsequent outward contours correspond to 80%, 70%, 60%, 50%, 40%, and 30% probability levels. The dashed black line indicates the bisector of the plane where equals .
6. Conclusions
In this work, we took advantage of the high-quality and high-resolution measurements (50 Hz) provided by the ESA Swarm A satellite to explore the spectral and scaling properties of small-scale (<100 km) magnetic field fluctuations. This examination encompassed two hemispheres, high-latitude regions and geomagnetic conditions, with a particular focus on their power density spectra and high-order statistics. We presented evidence of different turbulent regimes characterizing each region with a clear dependence on geomagnetic activity.
In the first part of our study, namely the spectral analysis, we found the following:
- An evident anisotropy in energy content between magnetic field fluctuations in the plane perpendicular and parallel to the geomagnetic field;
- The energy associated with magnetic field fluctuations in each region greatly increases during disturbed geomagnetic conditions but retain spectral behavior similar to quiet conditions;
- Power-law-like spectra in the plane perpendicular to the geomagnetic field for over two decades in frequency, with spectral indices being dependent on the region.
While we recognize a slight steepening of the FAC spectra around 8 Hz, which could suggest a transition to a different turbulent regime toward smaller scales, we lack the required resolution to higher frequencies to properly prove this transition. In this scenario, what could provide a better understanding of the observed spectral features, in addition to higher resolution measurements, is an interactions model between ion–ion and ion–neutral species in the high-latitude ionosphere and should be further investigated in future studies.
In the second part of the work, we investigated the turbulence characteristic of our dataset using a method based on structure function analysis. We concluded that:
- Turbulent energy dissipation pattern in FAC regions is a function of both MLT sector and geomagnetic activity. In particular, the latter considerably alters the nature of magnetic field fluctuations, leading to enhanced intermittent turbulent dynamics in disturbed geomagnetic conditions;
- Polar cap regions are characterized by distinct scaling properties with respect to FAC regions, which suggests a different driver of turbulence;
- Asymmetries in the measure of intermittency between hemispheres are mainly observed in quiet conditions, whereas consistent results are obtained in disturbed conditions.
Therefore we provided evidence that the enhancement of FACs greatly affects the dynamics on scales <100 km in the auroral regions, leading to regimes where energy is preferentially dissipated through localized filamentary structures instead of more symmetric 2D-layer structures.
While our results are statistically significant in understanding the role of FACs in the high-latitude ionosphere turbulent dynamics, further analysis and the investigation of other physical quantities are necessary to identify the exact turbulent mechanism at the origin of the observed scaling features. In particular, a comprehensive understanding of turbulent structure formations also has to consider other dynamic processes, such as traveling ionospheric disturbances. These disturbances are frequently associated with energetic processes such as Joule heating and particles precipitation in the auroral region, ultimately generating gravity waves which also affect magnetic field fluctuations. Although the examination of the processes is beyond the scope of this paper, it may be interesting to consider how the filamentary and intermittent nature of FACs may impact the formation of wave structures in different geomagnetic conditions.
Author Contributions
Conceptualization, S.M., F.G., and G.C.; methodology, S.M., P.D.M. and G.C.; formal analysis, S.M.; data curation, S.M.; writing—original draft preparation, S.M.; writing—review and editing, all authors; supervision, F.G. and F.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received funding from the CAESAR project, supported by the Italian Space Agency and the National Institute of Astrophysics.
Data Availability Statement
Swarm satellite data can be accessed at https://swarm-diss.eo.esa.int/, accessed on 15 November 2023. SuperMAG data are available at https://supermag.jhuapl.edu/, accessed on 20 November 2023. Kp date are freely available at https://kp.gfz-potsdam.de/en/data, accessed on 22 November 2023.
Acknowledgments
The results presented rely on data collected by the ESA’s Swarm mission. We thank the European Space Agency that supports the Swarm mission. We acknowledge the SuperMAG collaborators and the Data Working Group of the International Association of Geomagnetism and Aeronomy (IAGA Div.V). S.M. acknowledges the Ph.D. course in Astronomy, Astrophysics and Space Science of the University of Rome “Sapienza”, University of Rome “Tor Vergata” and Istituto Nazionale di Geofisica e Vulcanologia, Italy. S.M. acknowledges fruitful discussion with Tommaso Alberti and Roberta Tozzi. This research has been carried out in the framework of the CAESAR project, supported by the Italian Space Agency and the National Institute of Astrophysics through the ASI-INAF n. 2020-35-HH.0 agreement for the development of the ASPIS prototype of scientific data centre for Space Weather.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| IMF | Interplanetary Magnetic Field |
| FAC | Field-Aligned Current |
| GPS | Global Positioning System |
| GNSS | Global Navigation Satellite System |
| ASM | Absolute Scalar Magnetometer |
| VFM | Vector Field Magnetometer |
| QD | Quasi Dipole |
| MLT | Magnetic Local Time |
| UTC | Coordinated Universal Time |
| SME | SuperMag Auroral Electrojet |
| EMD | Empirical Mode Decomposition |
| PSD | Power Spectral Density |
References
- Dungey, J.W. Interplanetary Magnetic Field and the Auroral Zones. Phys. Rev. Lett. 1961, 6, 47–48. [Google Scholar] [CrossRef]
- Zmuda, A.J.; Martin, J.H.; Heuring, F.T. Transverse magnetic disturbances at 1100 kilometers in the auroral region. J. Geophys. Res. 1966, 71, 5033–5045. [Google Scholar] [CrossRef]
- Weimer, D.R. Maps of ionospheric field-aligned currents as a function of the interplanetary magnetic field derived from Dynamics Explorer 2 data. J. Geophys. Res. 2001, 106, 12889–12902. [Google Scholar] [CrossRef]
- Liu, H.; Lühr, H. Strong disturbance of the upper thermospheric density due to magnetic storms: CHAMP observations. J. Geophys. Res. (Space Phys.) 2005, 110, A09S29. [Google Scholar] [CrossRef]
- Rother, M.; Schlegel, K.; Lühr, H. CHAMP observation of intense kilometer-scale field-aligned currents, evidence for an ionospheric Alfvén resonator. Ann. Geophys. 2007, 25, 1603–1615. [Google Scholar] [CrossRef]
- Iijima, T.; Fujii, R.; Potemra, T.A.; Saflekos, N.A. Field-aligned currents in the south polar cusp and their relationship to the interplanetary magnetic field. J. Geophys. Res. 1978, 83, 5595–5603. [Google Scholar] [CrossRef]
- Lühr, H.; Warnecke, J.; Zanetti, L.J.; Lindqvist, P.A.; Hughes, T.J. Fine structure of field-aligned current sheets deduced from spacecraft and ground-based observations: Initial FREJA results. Geophys. Res. Lett. 1994, 21, 1883–1886. [Google Scholar] [CrossRef]
- Holappa, L.; Robinson, R.; Pulkkinen, A.; Asikainen, T.; Mursula, K. Explicit IMF by-dependence in geomagnetic activity: Quantifying ionospheric electrodynamics. J. Geophys. Res. Space Phys. 2021, 126, e2021JA029202. [Google Scholar] [CrossRef]
- Ritter, P.; Lühr, H. Curl-B technique applied to Swarm constellation for determining field-aligned currents. Earth Planets Space 2006, 58, 463–476. [Google Scholar] [CrossRef]
- Neubert, T.; Christiansen, F. Small-scale, field-aligned currents at the top-side ionosphere. Geophys. Res. Lett. 2003, 30, 2010. [Google Scholar] [CrossRef]
- Consolini, G.; De Michelis, P.; Alberti, T.; Giannattasio, F.; Coco, I.; Tozzi, R.; Chang, T.T.S. On the Multifractal Features of Low-Frequency Magnetic Field Fluctuations in the Field-Aligned Current Ionospheric Polar Regions: Swarm Observations. J. Geophys. Res. (Space Phys.) 2020, 125, e27429. [Google Scholar] [CrossRef]
- Kintner, P.M., Jr. Observations of velocity shear driven plasma turbulence. J. Geophys. Res. 1976, 81, 5114–5122. [Google Scholar] [CrossRef]
- Chang, T.; Tam, S.W.Y.; Wu, C.C. Complexity induced anisotropic bimodal intermittent turbulence in space plasmas. Phys. Plasmas 2004, 11, 1287–1299. [Google Scholar] [CrossRef]
- Bruno, R.; Carbone, V. Turbulence in the Solar Wind; Springer: Cham, Switzerland, 2016; Volume 928. [Google Scholar] [CrossRef]
- Pezzopane, M.; Pignalberi, A.; Coco, I.; Consolini, G.; De Michelis, P.; Giannattasio, F.; Marcucci, M.F.; Tozzi, R. Occurrence of GPS Loss of Lock Based on a Swarm Half-Solar Cycle Dataset and Its Relation to the Background Ionosphere. Remote Sens. 2021, 13, 2209. [Google Scholar] [CrossRef]
- De Michelis, P.; Consolini, G.; Pignalberi, A.; Lovati, G.; Pezzopane, M.; Tozzi, R.; Giannattasio, F.; Coco, I.; Marcucci, M.F. Ionospheric Turbulence: A Challenge for GPS Loss of Lock Understanding. Space Weather 2022, 20, e2022SW003129. [Google Scholar] [CrossRef]
- De Michelis, P.; Consolini, G.; Tozzi, R. Magnetic field fluctuation features at Swarm’s altitude: A fractal approach. Geophys. Res. Lett. 2015, 42, 3100–3105. [Google Scholar] [CrossRef]
- Kozelov, B.V.; Golovchanskaya, I.V. Scaling of electric field fluctuations associated with the aurora during northward IMF. Geophys. Res. Lett. 2006, 33, L20109. [Google Scholar] [CrossRef]
- Spicher, A.; Miloch, W.J.; Clausen, L.B.N.; Moen, J.I. Plasma turbulence and coherent structures in the polar cap observed by the ICI-2 sounding rocket. J. Geophys. Res. (Space Phys.) 2015, 120, 10959–10978. [Google Scholar] [CrossRef]
- Tam, S.W.Y.; Chang, T.; Kintner, P.M.; Klatt, E. Intermittency analyses on the SIERRA measurements of the electric field fluctuations in the auroral zone. Geophys. Res. Lett. 2005, 32, L05109. [Google Scholar] [CrossRef]
- De Michelis, P.; Tozzi, R.; Consolini, G.; Coco, I.; Marcucci, M.F.; Giannattasio, F. Dependence of Polar Ionosphere Electron Density Features on IMF Orientation: Swarm Observations. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 9–13 December 2019; Volume 2019, p. SM41A-02. [Google Scholar]
- Consolini, G.; Tozzi, R.; De Michelis, P.; Coco, I.; Giannattasio, F.; Pezzopane, M.; Marcucci, M.F.; Balasis, G. High-latitude polar pattern of ionospheric electron density: Scaling features and IMF dependence. J. Atmos. Sol.-Terr. Phys. 2021, 217, 105531. [Google Scholar] [CrossRef]
- Golovchanskaya, I.V.; Kozelov, B.V. On the origin of electric turbulence in the polar cap ionosphere. J. Geophys. Res. (Space Phys.) 2010, 115, A09321. [Google Scholar] [CrossRef]
- Abel, G.A.; Freeman, M.P.; Chisham, G.; Watkins, N.W. Investigating turbulent structure of ionospheric plasma velocity using the Halley SuperDARN radar. Nonlinear Process. Geophys. 2007, 14, 799–809. [Google Scholar] [CrossRef]
- Golovchanskaya, I.V.; Ostapenko, A.A.; Kozelov, B.V. Relationship between the high-latitude electric and magnetic turbulence and the Birkeland field-aligned currents. J. Geophys. Res. (Space Phys.) 2006, 111, A12301. [Google Scholar] [CrossRef]
- Abel, G.A.; Freeman, M.P.; Chisham, G. IMF clock angle control of multifractality in ionospheric velocity fluctuations. Geophys. Res. Lett. 2009, 36, L19102. [Google Scholar] [CrossRef]
- Kozelov, B.V.; Golovchanskaya, I.V.; Ostapenko, A.A.; Fedorenko, Y.V. Wavelet analysis of high-latitude electric and magnetic fluctuations observed by the Dynamic Explorer 2 satellite. J. Geophys. Res. (Space Phys.) 2008, 113, A03308. [Google Scholar] [CrossRef]
- De Michelis, P.; Consolini, G.; Tozzi, R.; Marcucci, M.F. Scaling Features of High-Latitude Geomagnetic Field Fluctuations at Swarm Altitude: Impact of IMF Orientation. J. Geophys. Res. (Space Phys.) 2017, 122, 10548–10562. [Google Scholar] [CrossRef]
- Friis-Christensen, E.; Lühr, H.; Hulot, G. Swarm: A constellation to study the Earth’s magnetic field. Earth Planets Space 2006, 58, 351–358. [Google Scholar] [CrossRef]
- Knudsen, D.J.; Burchill, J.K.; Buchert, S.C.; Eriksson, A.I.; Gill, R.; Wahlund, J.E.; Öhlen, L.; Smith, M.; Moffat, B. Thermal ion imagers and Langmuir probes in the Swarm electric field instruments. J. Geophys. Res. (Space Phys.) 2017, 122, 2655–2673. [Google Scholar] [CrossRef]
- Ritter, P.; Lühr, H.; Rauberg, J. Determining field-aligned currents with the Swarm constellation mission. Earth Planets Space 2013, 65, 1285–1294. [Google Scholar] [CrossRef]
- Gjerloev, J.W. The SuperMAG data processing technique. J. Geophys. Res. (Space Phys.) 2012, 117, A09213. [Google Scholar] [CrossRef]
- Matzka, J.; Stolle, C.; Yamazaki, Y.; Bronkalla, O.; Morschhauser, A. The Geomagnetic Kp Index and Derived Indices of Geomagnetic Activity. Space Weather 2021, 19, e2020SW002641. [Google Scholar] [CrossRef]
- Newell, P.; Gjerloev, J. Substorm and Magnetosphere Characteristic Scales Inferred from the SuperMAG Auroral Electrojet Indices. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 22–27 April 2012; p. 1381. [Google Scholar]
- Finlay, C.C.; Kloss, C.; Olsen, N.; Hammer, M.D.; Tøffner-Clausen, L.; Grayver, A.; Kuvshinov, A. The CHAOS-7 geomagnetic field model and observed changes in the South Atlantic Anomaly. Earth Planets Space 2020, 72, 156. [Google Scholar] [CrossRef] [PubMed]
- Olsen, N. A new tool for determining ionospheric currents from magnetic satellite data. Geophys. Res. Lett. 1996, 23, 3635–3638. [Google Scholar] [CrossRef]
- Papini, E.; Piersanti, M.; D’Angelo, G.; Cicone, A.; Bertello, I.; Parmentier, A.; Diego, P.; Ubertini, P.; Consolini, G.; Zhima, Z. Detecting the Auroral Oval through CSES-01 Electric Field Measurements in the Ionosphere. Remote Sens. 2023, 15, 1568. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A 1998, 454, 903–998. [Google Scholar] [CrossRef]
- Frisch, U. Turbulence. The Legacy of A.N. Kolmogorov; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Dudok de Wit, T.; Krasnosel’skikh, V.V. Non-Gaussian statistics in space plasma turbulence: Fractal properties and pitfalls. Nonlinear Process. Geophys. 1996, 3, 262–273. [Google Scholar] [CrossRef]
- Biskamp, D. Magnetohydrodynamic Turbulence; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Anselmet, F.; Gagne, Y.; Hopfinger, E.J.; Antonia, R.A. High-order velocity structure functions in turbulent shear flows. J. Fluid Mech. 1984, 140, 63–89. [Google Scholar] [CrossRef]
- Taylor, G.I. The Spectrum of Turbulence. Proc. R. Soc. Lond. Ser. A 1938, 164, 476–490. [Google Scholar] [CrossRef]
- Chaston, C.C.; Salem, C.; Bonnell, J.W.; Carlson, C.W.; Ergun, R.E.; Strangeway, R.J.; McFadden, J.P. The Turbulent Alfvénic Aurora. Phys. Rev. Lett. 2008, 100, 175003. [Google Scholar] [CrossRef] [PubMed]
- Giannattasio, F.; Consolini, G.; Coco, I.; De Michelis, P.; Pezzopane, M.; Pignalberi, A.; Tozzi, R. Dissipation of field-aligned currents in the topside ionosphere. Sci. Rep. 2022, 12, 17202. [Google Scholar] [CrossRef] [PubMed]
- Alberti, T.; Benella, S.; Carbone, V.; Consolini, G.; Quattrociocchi, V.; Stumpo, M. Contrasting Scaling Properties of Near-Sun Sub-Alfvénic and Super-Alfvénic Regions. Universe 2022, 8, 338. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).