Disaggregating National Statistical Data to Assess the Sub-National SDG 6.4.2 Water Stress Indicator by Integrating Satellite Observations and Model Data
Abstract
1. Introduction
2. Methods
2.1. Definition of Water Stress Indicator and Overall Approach of This Study
2.1.1. Definition of Water Stress Indicator
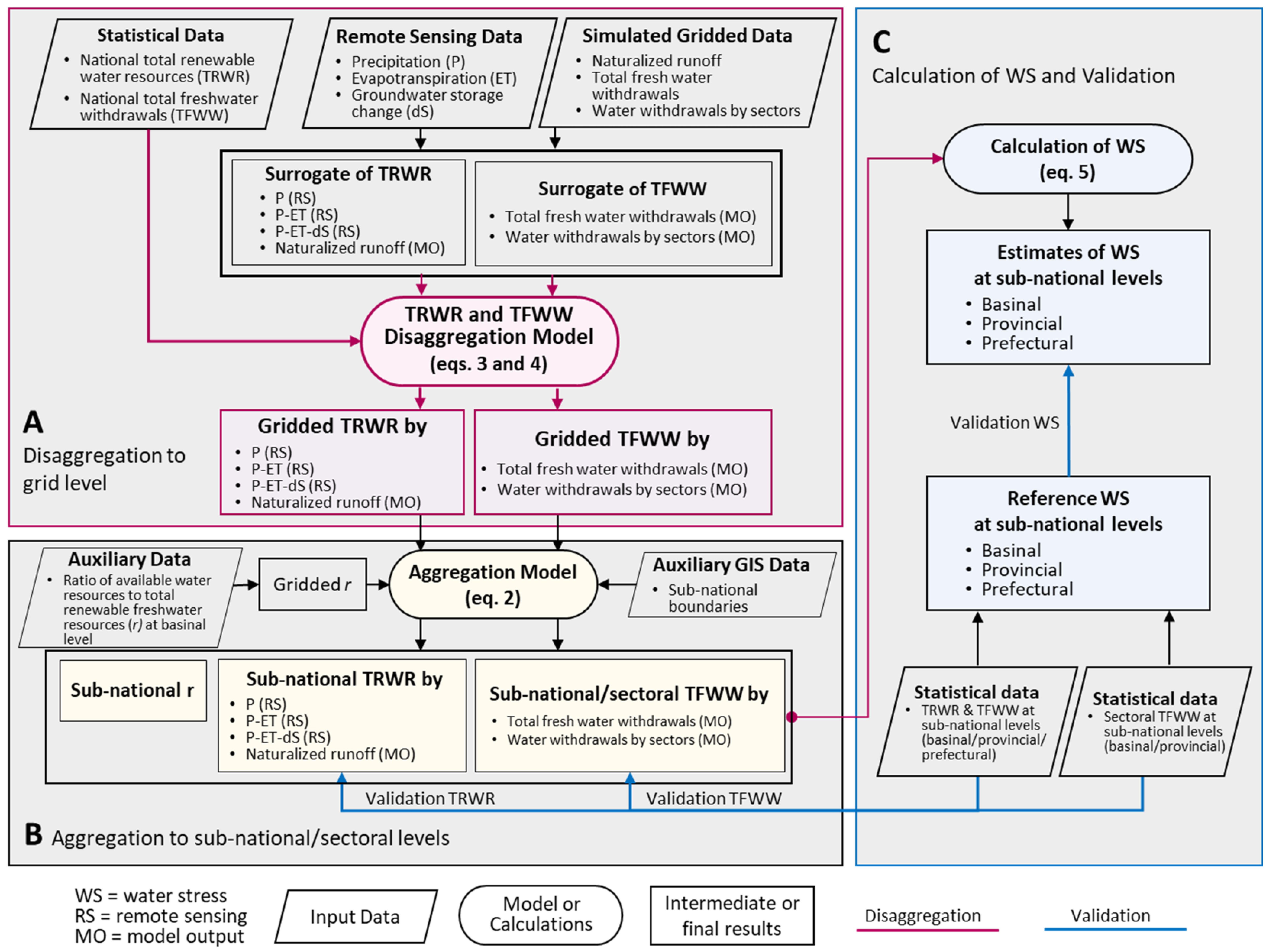
2.1.2. Overall Approach
2.2. Spatial Disaggregation of TRWR and TFWW
2.2.1. Surrogate Variables of TRWR
2.2.2. Surrogate Variables of TFWW
2.3. Temporal Disaggregation of TRWR and TFWW
2.4. Estimation of Environmental Flow Requirement
2.5. Validation Methods
2.5.1. Validation Scheme
2.5.2. Performance Metrics
3. Data Sources and Data Processing
3.1. Statistical Data
3.2. Remote Sensing Data
3.3. Model Simulation Data
4. Results
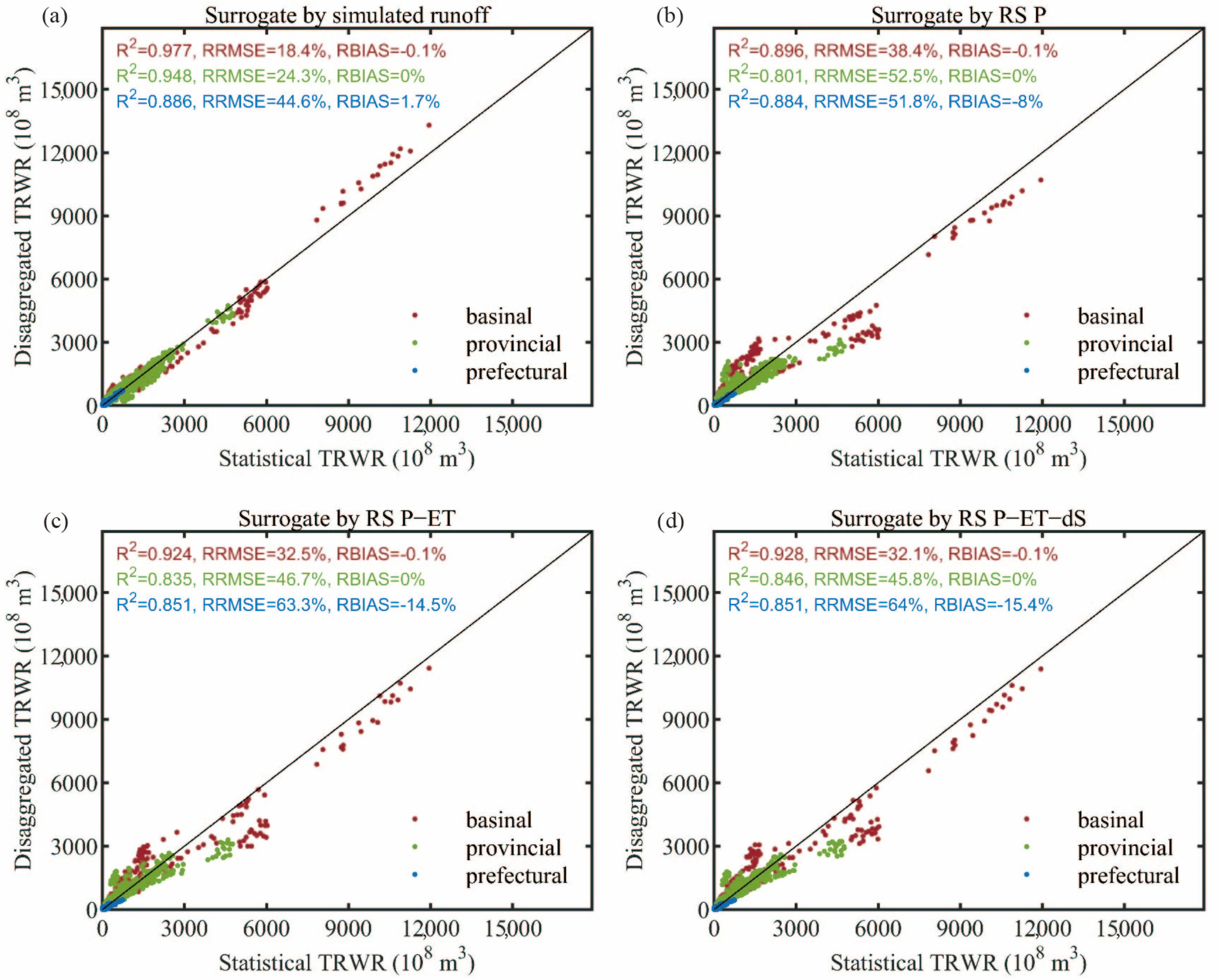
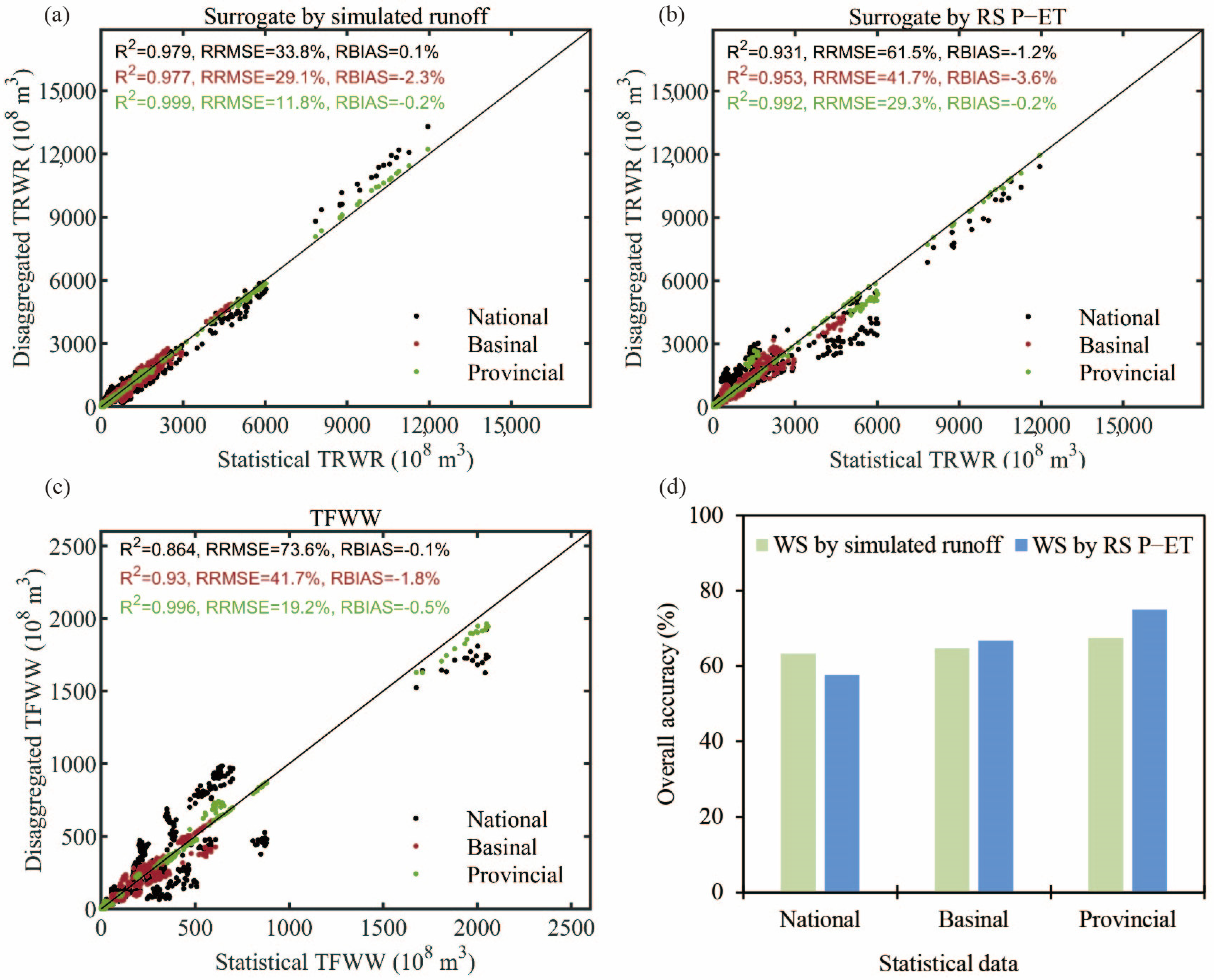
4.1. Evaluation of Spatial Disaggregation of TRWR
4.2. Evaluation of Spatial Disaggregation of TFWW
4.3. Evaluation of Spatial Disaggregation of WS
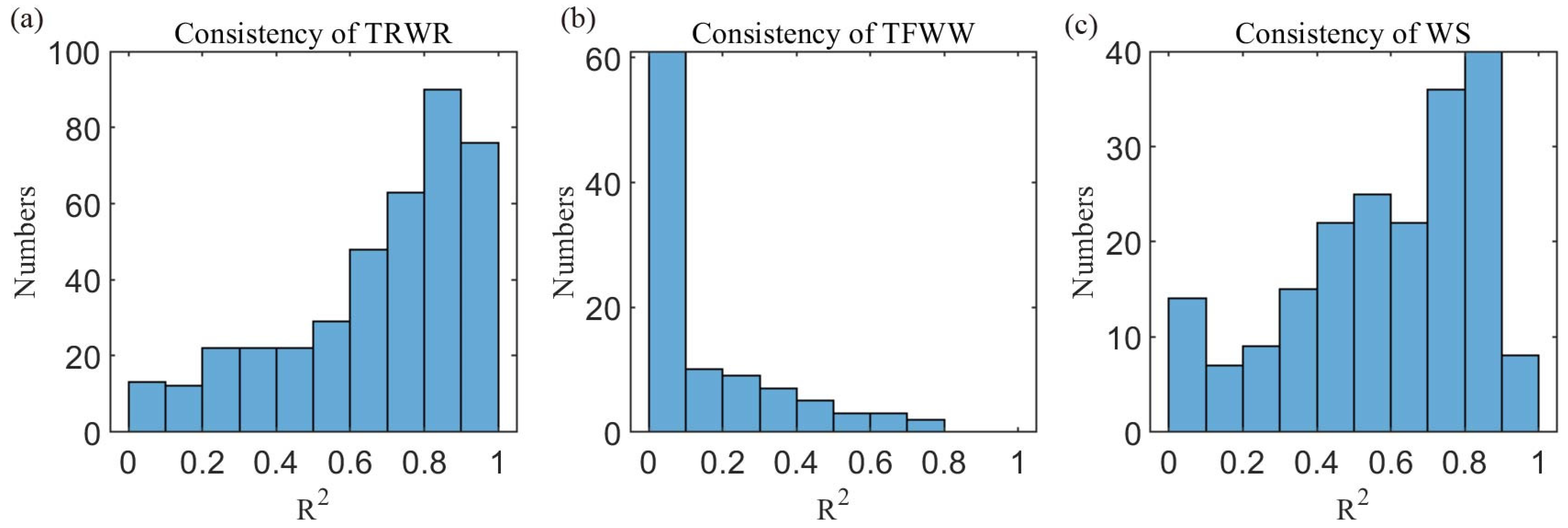
4.4. Consistency of Temporal Evolution of Disaggregated Variables
5. Discussion
5.1. Improvement by Using Sub-National Statistical Data for Disaggregation
5.2. Impact of Water Stress Level Classification on Disaggregation Accuracy
5.3. Determination of Environmental Flow Requirements
5.4. Consideration of External Renewable Freshwater Resources
5.5. Uncertainties from Surrogate Variables
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- UNESCO (United Nations Educational, Scientific, and Cultural Organization). UN World Water Development Report 2021: Valuing Water. 2021. Available online: https://www.unwater.org/publications/un-world-water-development-report-2021 (accessed on 29 April 2024).
- WMO (World Meteorological Organisation). State of Global Water Resources 2021; WMO: Geneva, Switzerland, 2022; Volume 1308, ISBN 978-92-63-11308-5. [Google Scholar]
- UN (United Nations). Transforming Our World: The 2030 Agenda for Sustainable Development. Resolution adopted by the General Assembly on 25 September 2015. Available online: https://digitallibrary.un.org/record/3923923?v=pdf (accessed on 29 April 2024).
- Dolan, F.; Lamontagne, J.; Link, R.; Hejazi, M.; Reed, P.; Edmonds, J. Evaluating the economic impact of water scarcity in a changing world. Nat. Commun. 2021, 12, 1915. [Google Scholar] [CrossRef] [PubMed]
- UN-Water. Summary Progress Update 2021: SDG 6—Water and Sanitation for All. 2021. Available online: https://www.unwater.org/publications/summary-progress-update-2021-sdg-6-water-and-sanitation-all (accessed on 29 April 2024).
- Liu, J.; Liu, Q.; Yang, H. Assessing water scarcity by simultaneously considering environmental flow requirements, water quantity, and water quality. Ecol. Indic. 2016, 60, 434–441. [Google Scholar] [CrossRef]
- Liu, J.; Yang, H.; Gosling, S.N.; Kummu, M.; Florke, M.; Pfister, S.; Hanasaki, N. Water scarcity assessments in the past, present and future. Earth’s Future 2017, 5, 545–559. [Google Scholar] [CrossRef] [PubMed]
- Rodell, M.; Famiglietti, J.S.; Wiese, D.N.; Reager, J.T.; Beaudoing, H.K.; Landerer, F.W.; Lo, M.H. Emerging Trends in Global Freshwater Availability. Nature 2018, 557, 651–659. [Google Scholar] [CrossRef] [PubMed]
- FAO (Food and Agriculture Organization of the United Nations). Progress on level of water stress—Global baseline for SDG 6 Indicator 6.4.2. 2018. Available online: https://www.unwater.org/publications/progress-level-water-stress-global-baseline-sdg-indicator-642 (accessed on 29 April 2024).
- UN-Water. Progress on Level of Water Stress—Global Status and Acceleration Needs for SDG Indicator 6.4.2. 2021. Available online: https://www.unwater.org/publications/progress-level-water-stress-2021-update (accessed on 29 April 2024).
- Biancalani, R.; Michela, M. Assessing SDG indicator 6.4.2 ‘level of water stress’ at major basins level. UCL Open Environ. 2021, 3, e026. [Google Scholar] [CrossRef] [PubMed]
- Mekonnen, M.M.; Hoekstra, A.Y. Four billion people facing severe water scarcity. Sustainability 2016, 2, e1500323. [Google Scholar] [CrossRef] [PubMed]
- Vanham, D.; Hoekstra, A.Y.; Wada, Y.; Bouraoui, F.; de Roo, A.; Mekonnen, M.M.; van de Bund, W.J.; Batelaa, O.; Pavelic, P.; Bastiaanssen, W. Physical water scarcity metrics for monitoring progress towards SDG target 6.4: An evaluation of indicator 6.4.2 Level of water stress. Sci. Total Environ. 2018, 613–614, 218–232. [Google Scholar] [CrossRef] [PubMed]
- Fehri, R.; Khlifi, S.; Vanclooster, M. Disaggregating SDG-6 water stress indicator at different spatial and temporal scales in Tunisia. Sci. Total Environ. 2019, 694, 133766. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Tang, Q.; Cui, H.; Mu, M.; Gerten, D.; Gosling, S.N.; Masaki, Y.; Satoh, Y.; Wada, Y. Multimodel uncertainty changes in simulated river flows induced by human impact parameterizations. Environ. Res. Lett. 2017, 12, 025009. [Google Scholar] [CrossRef]
- Schewe, J.; Heinke, J.; Gerten, D.; Haddeland, I.; Arnell, N.W.; Clark, D.B.; Dankers, R. Multimodel assessment of water scarcity under climate change. Proc. Natl. Acad. Sci. USA 2014, 111, 3245–3250. [Google Scholar] [CrossRef]
- Ndehedehe, C. Remote Sensing Hydrology. In Satellite Remote Sensing of Terrestrial Hydrology; Springer: Cham, Switzerland, 2022. [Google Scholar] [CrossRef]
- Piao, S.; Ciais, P.; Huang, Y.; Shen, Z.; Peng, S.; Li, J.; Zhou, L. The impacts of climate change on water resources and agriculture in China. Nature 2010, 467, 43–51. [Google Scholar] [CrossRef] [PubMed]
- Konapala, G.; Mishra, A.K.; Wada, Y.; Mann, M.E. Climate change will affect global water availability through compounding changes in seasonal precipitation and evaporation. Nat. Commun. 2020, 11, 3044. [Google Scholar] [CrossRef]
- Liu, W.; Lim, W.; Sun, F.; Mitchell, D.; Wang, H.; Chen, D.; Bethke, I.; Shiogama, H.; Fischer, E. Global Freshwater Availability Below Normal Conditions and Population Impact Under 1.5 and 2 °C Stabilization Scenarios. Geophys. Res. Lett. 2018, 45, 9803–9813. [Google Scholar] [CrossRef]
- Lu, J.; Jia, L.; Zheng, C.; Hu, G. Potential of remote sensing-based water budget for the estimation of regional water resources. Remote Sens. Technol. Appl. 2019, 34, 630–638. (In Chinese) [Google Scholar]
- Zhang, Y.; He, B.; Guo, L.; Liu, J.; Xie, X. The Relative Contributions of Precipitation, Evapotranspiration, and Runoff to Terrestrial Water Storage Changes across 168 River Basins. J. Hydrol. 2019, 579, 124194. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Karimi, P.; Rebelo, L.; Duan, Z.; Senay, G.; Muthuwatte, L.; Smakhti, V. Earth Observation Based Assessment of the Water Production and Water Consumption of Nile Basin Agro-Ecosystems. Remote Sens. 2014, 6, 10306–10334. [Google Scholar] [CrossRef]
- Müller Schmied, H.; Cáceres, D.; Eisner, S.; Flörke, M.; Herbert, C.; Niemann, C.; Peiris, T.A. The global water resources and use model WaterGAP v2.2d: Model description and evaluation. Geosci. Model Dev. 2021, 14, 1037–1079. [Google Scholar] [CrossRef]
- Wu, B.; Tian, F.; Zhang, M.; Piao, S.; Zeng, H.; Zhu, W.; Liu, J.; Elnashar, A.; Lu, Y. Quantifying Global Agricultural Water Appropriation with Data Derived from Earth Observations. J. Clean. Prod. 2022, 358, 131891. [Google Scholar] [CrossRef]
- Liu, X.; Liu, W.; Liu, L.; Tang, Q.; Liu, J.; Yang, H. Environmental flow requirements largely reshape global surface water scarcity assessment. Environ. Res. Lett. 2021, 16, 104029. [Google Scholar] [CrossRef]
- Pastor, A.V.; Ludwig, F.; Biemans, H.; Hoff, H.; Kabat, P. Accounting for Environmental Flow Requirements in Global Water Assessments. Hydrol. Earth Syst. Sci. 2014, 18, 5041–5059. [Google Scholar] [CrossRef]
- Tennant, D. Instream flow regimens for fish, wildlife, recreation, and related environmental resources. Fisheries 1976, 1, 6–10. [Google Scholar]
- Jia, S.; Liu, W. Tracing and thinking about 40% threshold value of water resources development and utilization ratio. Water Resour. Prot. 2021, 37, 87–89. (In Chinese) [Google Scholar] [CrossRef]
- Wang, J.S.; Zhong, H.; Geng, L.; Xu, P.; Liu, C. Available water resources in China. Adv. Water Sci. 2006, 17, 549–553. (In Chinese) [Google Scholar]
- Alberg, A.J.; Park, J.W.; Hager, B.W.; Brock, M.V.; Diener-West, M. The use of ‘overall accuracy’ to evaluate the validity of screening or diagnostic tests. J. Gen. Intern. Med. 2004, 19, 460–465. [Google Scholar] [CrossRef] [PubMed]
- Landis, J.R.; Koch, G.G. The measurement of observer agreement for categorical data. Biometrics 1977, 33, 159–174. [Google Scholar] [CrossRef] [PubMed]
- Zheng, C.; Jia, L.; Hu, G. Global Land Surface Evapotranspiration Monitoring by ETMonitor Model Driven by Multi-source Satellite Earth Observations. J. Hydrol. 2022, 613, 128444. [Google Scholar] [CrossRef]
- Müller Schmied, H.; Cáceres, D.; Eisner, S.; Flörke, M.; Herbert, C.; Niemann, C.; Peiris, T.A. The global water resources and use model WaterGAP v2.2d—Standard model output. PANGAEA. 2020. Available online: https://doi.org/10.1594/PANGAEA.918447 (accessed on 29 April 2024).
- Hu, B.; Wang, L.; Li, X.; Zhou, J.; Pan, Y. Divergent Changes in Terrestrial Water Storage across Global Arid and Humid Basins. Geophys. Res. Lett. 2021, 48, e2020GL091069. [Google Scholar] [CrossRef]
- Liu, X.; Tang, Q.; Liu, W.; Veldkamp, T.; Boulange, J.; Liu, J.; Wada, Y.; Huan, Z.; Yang, H. A Spatially Explicit Assessment of Growing Water Stress in China from the Past to the Future. Earth’s Future 2019, 7, 1027–1043. [Google Scholar] [CrossRef]
- Ma, T.; Sun, S.; Fu, G.; Hall, J.W.; Ni, Y.; He, L.; Yi, J.; Zhao, N. Pollution exacerbates China’s water scarcity and its regional inequality. Nat. Commun. 2020, 11, 650. [Google Scholar] [CrossRef]
- Vanham, D.; Alfieri, L.; Florke, M.; Grimaldi, S.; Lorini, V.; de Roo, A.; Feyen, L. The Number of People Exposed to Water Stress in Relation to How Much Water Is Reserved for the Environment: A Global Modelling Study. Lancet Planet. Health. 2021, 5, e766–e774. [Google Scholar]
- Vanham, D.; Alfieri, L.; Feyen, L. National Water Shortage for Low to High Environmental Flow Protection. Sci. Rep. 2022, 12, 3037. [Google Scholar] [CrossRef] [PubMed]
- FAO (Food and Agriculture Organization of the United Nations). Incorporating Environmental Flows into Water Stress Indicator 6.4.2—Guidelines for a Minimum Standard Method for Global Reporting. 2019. Available online: https://www.unwater.org/publications/incorporating-environmental-flows-water-stress-indicator-642 (accessed on 29 April 2024).
- Wang, J.Y.; Huang, J.; Li, Y.; Yan, T.; Sun, T. Growing water scarcity, food security and government responses in China. Glob. Food Sec. 2017, 14, 9–17. [Google Scholar] [CrossRef]
- Gohari, A.; Eslamian, S.; Mirchi, A.; Abedi-Koupaei, J.; Bavani, A.M.; Madani, K. Water transfer as a solution to water shortage: A fix that can backfire. J. Hydrol. 2013, 491, 23–39. [Google Scholar] [CrossRef]
- Rising, J.; Josset, L.; Troy, T.; Lall, U. The importance of infrastructure and national demand to represent constraints on water supply in the United States. Glob. Environ. Change 2022, 73, 102468. [Google Scholar] [CrossRef]
- Shumilova, O.; Tockner, K.; Thieme, M.; Koska, A.; Zarfl, C. Global water transfer megaprojects: A potential solution for the water-food-energy nexus? Front. Environ. Sci. 2018, 6, 11. [Google Scholar] [CrossRef]
- Sun, S.; Tang, Q.; Kona, M.; Fang, C.; Liu, H.; Li, X.; Fu, G. Water transfer infrastructure buffers water scarcity risks to supply chains. Water Res. 2022, 22, 119442. [Google Scholar] [CrossRef]
- Long, D.; Yang, W.; Scanlon, B.; Zhao, J.; Liu, D.; Burek, P.; Pan, Y.; You, L.; Wada, Y. South-to-North Water Diversion stabilizing Beijing’s groundwater levels. Nat. Commun. 2020, 11, 3665. [Google Scholar] [CrossRef] [PubMed]
- Yin, Y.; Wang, L.; Wang, Z.; Tang, Q.; Piao, S.; Chen, D.; Xia, J. Quantifying Water Scarcity in northern China within the context of Climatic and Societal Changes and South-to-North Water Diversion. Earth’s Future 2020, 8, e2020EF001492. [Google Scholar] [CrossRef]
- Xie, J.; You, J.; Ma, Z.; Deng, X.; Lin, P.; Gao, J. Methodology for Including Reservoir Regulation in Water Scarcity Evaluation. J. Clean. Prod. 2022, 365, 132657. [Google Scholar] [CrossRef]
- Du, Y.; Zhao, D.; Qiu, S.; Zhou, F.; Peng, J. How can virtual water trade reshape water stress pattern? A global evaluation based on the metacoupling perspective. Ecol. Indic. 2022, 145, 109712. [Google Scholar] [CrossRef]
- Bernauer, T.; Böhmelt, T. International conflict and cooperation over freshwater resources. Nat. Sustain. 2020, 3, 350–356. [Google Scholar] [CrossRef]
- Rajani, K.P.; Markonis, Y.; Godoy, M.R.V.; Villalba-Pradas, A.; Andreadis, K.M.; Nikolopoulos, E.I.; Papalexiou, S.M.; Rahim, A.; Tapiador, F.J.; Hanel, M. Review of GPM IMERG performance: A global perspective. Remote Sens. Environ. 2022, 268, 112754. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Zhang, Z.; Save, H.; Wiese, D.N.; Landerer, F.W.; Long, D.; Longuevergne, L.; Chen, J. Global evaluation of new GRACE mascon products for hydrologic applications. Water Resour. Res. 2016, 52, 9412–9429. [Google Scholar] [CrossRef]




| Range of Water Stress | Water Stress Levels |
|---|---|
| (0, 25%] | No stress |
| (25%, 50%] | Low |
| (50%, 75%] | Medium |
| (75%, 100%] | High |
| >100% | Critical |
| Level | Regions/Spatial Scales | Source | Variables | Temporal Resolution |
|---|---|---|---|---|
| National | Whole country | China Water Resources Bulletin (CWRB) (www.mwr.gov.cn/sj/tjgb/szygb/, accessed on 29 April 2024) |
| Yearly |
| Provincial | 31 provincial administrative units, excluding Hong Kong, Macau, and Taiwan | |||
| Basinal | 10 first-level water resource regions:
| |||
| Prefectural | 60 prefectures from 4 provinces of Zhejiang (ZJ), Hubei (HB), Sichuan (SC), and Gansu (GS) | Local Water Resources Bulletin |
| Data Types | Variables | Spatial Resolution | Temporal Resolution | Sources |
|---|---|---|---|---|
| Remote sensing data | Precipitation | 0.1° | Monthly | GPM data https://gpm1.gesdisc.eosdis.nasa.gov/data/GPM_L3/GPM_3IMERGM.07 (accessed on 29 April 2024) |
| Evapotranspiration | 1 km | Daily | ETMonitor model output https://data.casearth.cn/thematic/GWRD_2023/272 (accessed on 29 April 2024) | |
| Terrestrial water storage change | 0.5° | Monthly | GRACE JPL Mascon products https://grace.jpl.nasa.gov/data/get-data/jpl_global_mascons (accessed on 29 April 2024) | |
| Model simulation data | Naturalized runoff; potential withdrawal water uses for irrigation, livestock, household, manufacturing, and thermal power cooling. | 0.5° | Monthly | WaterGAP 2.2d model output https://doi.org/10.1594/PANGAEA.918447 (accessed on 29 April 2024) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, J.; Jia, L. Disaggregating National Statistical Data to Assess the Sub-National SDG 6.4.2 Water Stress Indicator by Integrating Satellite Observations and Model Data. Remote Sens. 2024, 16, 1654. https://doi.org/10.3390/rs16101654
Lu J, Jia L. Disaggregating National Statistical Data to Assess the Sub-National SDG 6.4.2 Water Stress Indicator by Integrating Satellite Observations and Model Data. Remote Sensing. 2024; 16(10):1654. https://doi.org/10.3390/rs16101654
Chicago/Turabian StyleLu, Jing, and Li Jia. 2024. "Disaggregating National Statistical Data to Assess the Sub-National SDG 6.4.2 Water Stress Indicator by Integrating Satellite Observations and Model Data" Remote Sensing 16, no. 10: 1654. https://doi.org/10.3390/rs16101654
APA StyleLu, J., & Jia, L. (2024). Disaggregating National Statistical Data to Assess the Sub-National SDG 6.4.2 Water Stress Indicator by Integrating Satellite Observations and Model Data. Remote Sensing, 16(10), 1654. https://doi.org/10.3390/rs16101654






