Neighborhood Selection Synchronization Mechanism-Based Moving Source Localization Using UAV Swarm

Abstract

To obtain the accurate time difference of arrival (TDOA) and frequency difference of arrival (FDOA) for passive localization in an unmanned aerial vehicle (UAV) swarm, UAV swarm network synchronization is necessary. However, most of the traditional distributed time synchronization protocols are based on iteration, which hinders efficiency improvement. High communication costs and long convergence times are often required in large-scale UAV swarm networks. This paper presents a neighborhood selection-all selection (NS-AS) synchronization mechanism-based moving source localization method for UAV swarms. First, the NS-AS synchronization mechanism is introduced, to model the UAV swarm network synchronization process. Specifically, the UAV neighbors are first grouped by sector, and the most representative neighbors are selected from each sector for the state update calculation. When the UAV swarm network reaches a fully connected state, the synchronization mechanism is switched to select all neighbors, to improve the convergence speed. Then, the TDOA-FDOA joint localization algorithm is employed to locate the moving radiation source. Through simulation, the effectiveness of the proposed method is verified by the system convergence and localization performance under different parameters. Experimental results show that the synchronization mechanism based on NS-AS effectively improves the convergence speed of the system while ensuring the accuracy of moving radiation source localization.

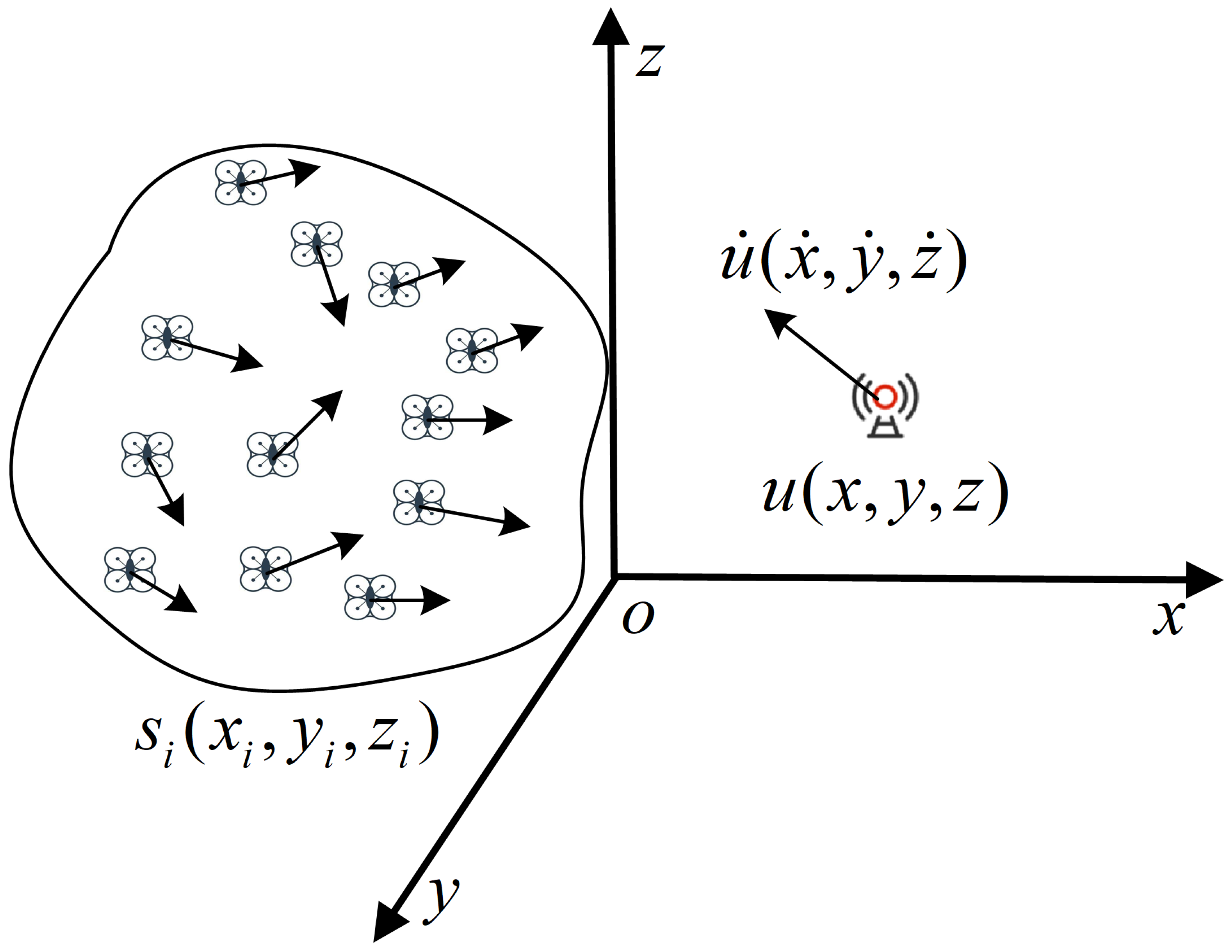
1. Introduction

In recent years, unmanned aerial vehicles (UAVs) have been widely used in electronic reconnaissance due to their high mobility [1]. As traditional radiation source localization technologies mostly rely on fixed base stations on the ground to receive signals, the geometric positions of the base stations render it impossible to complete the localization task in remote areas, with only a few base stations. Compared with large active localization systems, small and light passive localization systems are more suitable for UAV platforms [2,3]. UAV passive localization systems can improve positioning flexibility and solve the problem of poor positioning accuracy at long distances from the fixed base stations.

At present, the measurement information for passive localization is mainly acquired from the air domain, frequency domain, and time domain. Direction cosine intersection localization locates targets based on information in the air domain, where target localization is achieved by measuring the angle of arrival (AOA) of the received signal [4,5,6,7]. However, this method has high requirements for measuring the attitude of the moving platform. With the information in the frequency domain, the Doppler frequency difference of arrival (FDOA) related to the frequency modulation of the signal [8,9] is measured for target positioning. Yet, the adaptability of the signal is often poor. Compared with localization algorithms based on air and frequency domain information, time difference of arrival (TDOA) localization has better performance in stationary target localization [10,11,12,13]. When there are relative motions between the UAV and the maneuvering target, FDOA and TDOA can be combined to improve localization accuracy and estimate the target speed [14,15,16,17]. As time synchronization among UAV swarm nodes is essential for TDOA passive localization [18,19], various algorithms have been developed.

The existing time synchronization algorithms can be divided into centralized and distributed ones. Centralized time synchronization algorithms include the timing-sync protocol for sensor networks (TPSN) [20], coefficient exchange synchronization protocol (CESP) [21], and cluster-based consensus time synchronization [22,23,24]. When applied to large-scale cluster networks, centralized time synchronization has the disadvantages of a large accumulation of synchronization errors, poor scalability, and poor invulnerability. The emergence of distributed time synchronization protocols has addressed some of the above problems, where each node uses the local information, synchronized with its neighbors, to reach a global consensus, and no master or global clock is assumed. Distributed time synchronization algorithms include distributed consensus time synchronization (DCTS) [25] and average time synchronization (ATS) [26,27,28], where no reference is required. With the DCTS algorithm, all network nodes agree on a virtual time through information fusion between neighboring nodes. However, DCTS relies on diffusion to deliver synchronization messages, resulting in slower convergence. The ATS method can only be realized asymptotically, and too many calculation and communication iterations are required in practice. Therefore, convergence speed and synchronization accuracy improvements are necessary. Meanwhile, most distributed clock synchronization methods utilize the global positioning system (GPS) direct timing method. An accurate time reference is obtained by the GPS receivers of the UAV swarm. Although this method has a small synchronization error and a wide coverage area, it is easy to lose the lock due to the influence of the external environment, e.g., forests, high-rise buildings. After the GPS loses lock, the synchronization error reaches the millisecond level or worse, which cannot meet the requirements of TDOA localization.

Traditional distributed communication protocols will establish a large number of communication connections during communication. Extensive studies have shown that higher numbers of communication connections of the agent are not conducive to accelerating system synchronization convergence [29], while selecting representative neighbors for the synchronization evolution can improve the synchronization convergence speed [30,31]. A control protocol for selecting neighbors with minimum state differences is designed in [32] for first-order linear multi-agent systems, based on undirected topological graphs. The auction algorithm is applied in [33,34] to delete the safe edge in the network according to the state information of the agent, and a simpler connected topology is used to update the state. The circumcenter algorithm, based on the proximity graph, is studied in [35]. Delaunary graphs, Gabriel graphs, and other graph construction methods are used to select neighbors for communication and calculation. 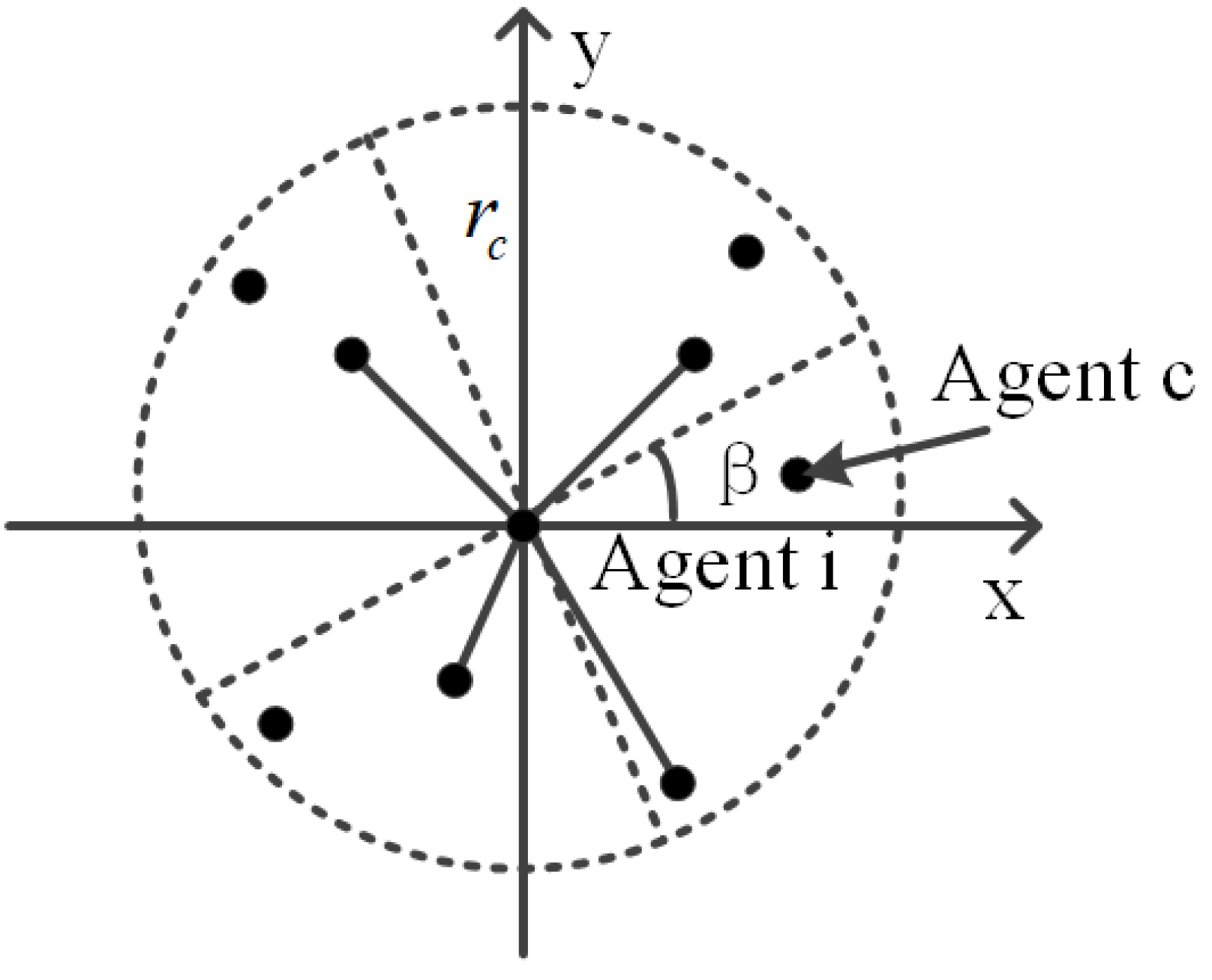In [36], nodes with the smallest differences from their neighbors are selected from the fixed 120-degree fan-shaped communication area centered on agent i. The method of selecting neighbors with large differences to improve system convergence to a cluster is investigated in [37]. Reference broadcast synchronization (RBS) is a traditional synchronization method based on the neighborhood all selection (AS) mechanism, where the state of an agent is determined by the states of all its neighbors [38]. With non-neighboring nodes A and B sending reference messages, the receiving nodes within the communication radius can perform time synchronization. However, in a large-scale UAV swarm network, each UAV can have a large number of neighbors. Thus, AS-based synchronization increases the amount of calculations and the energy consumption of the system, and agents having more communication connections cannot accelerate system convergence.

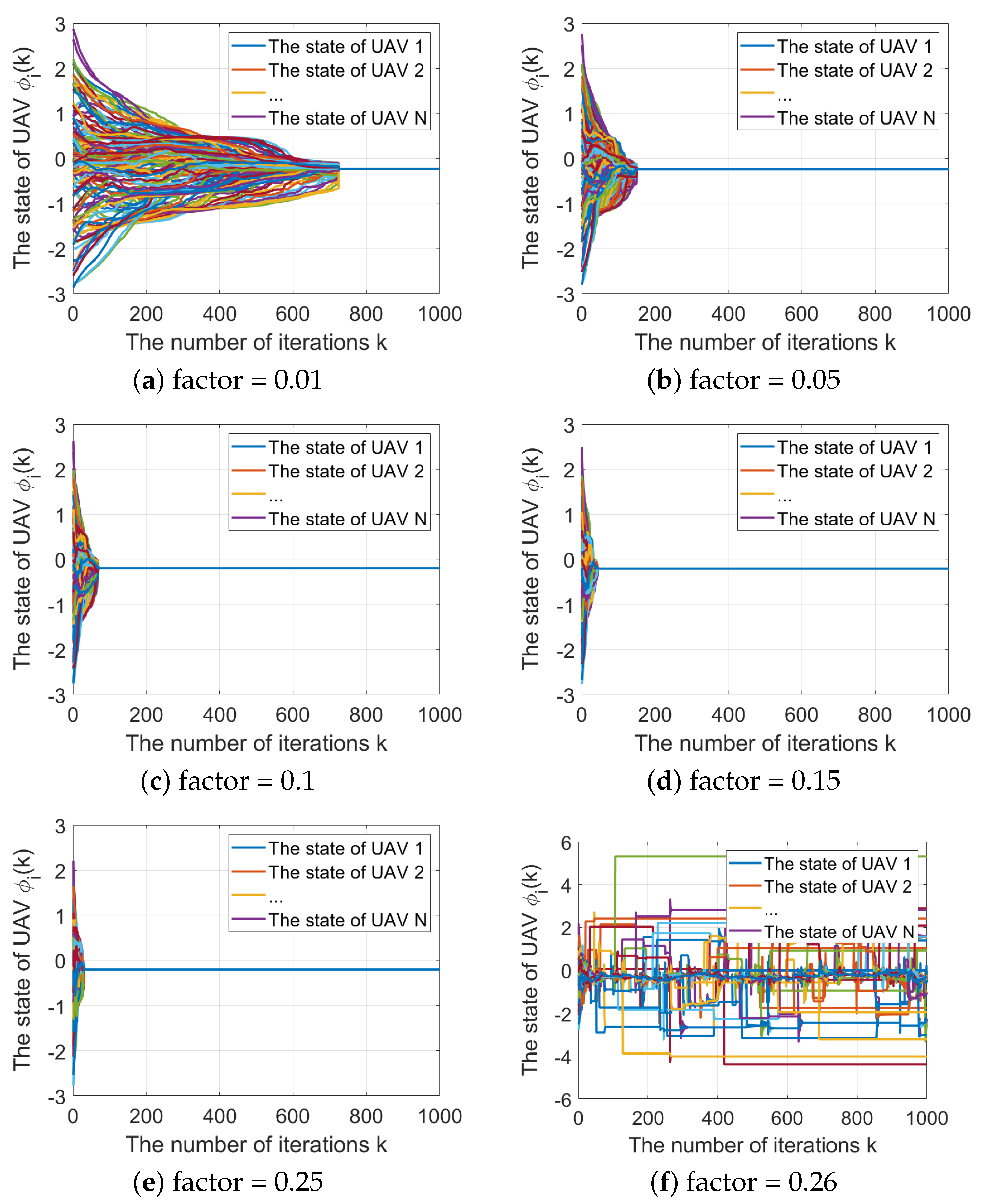
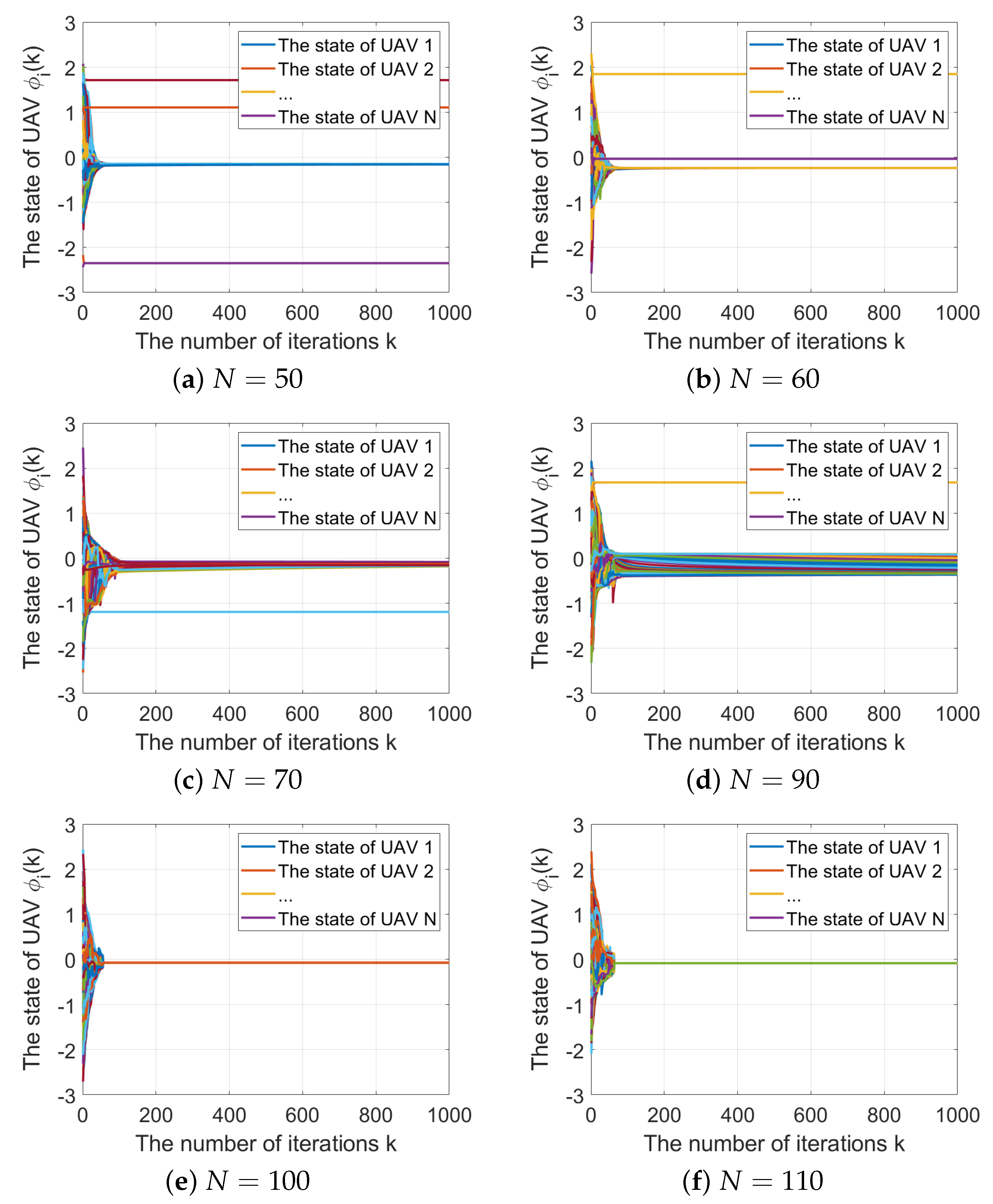
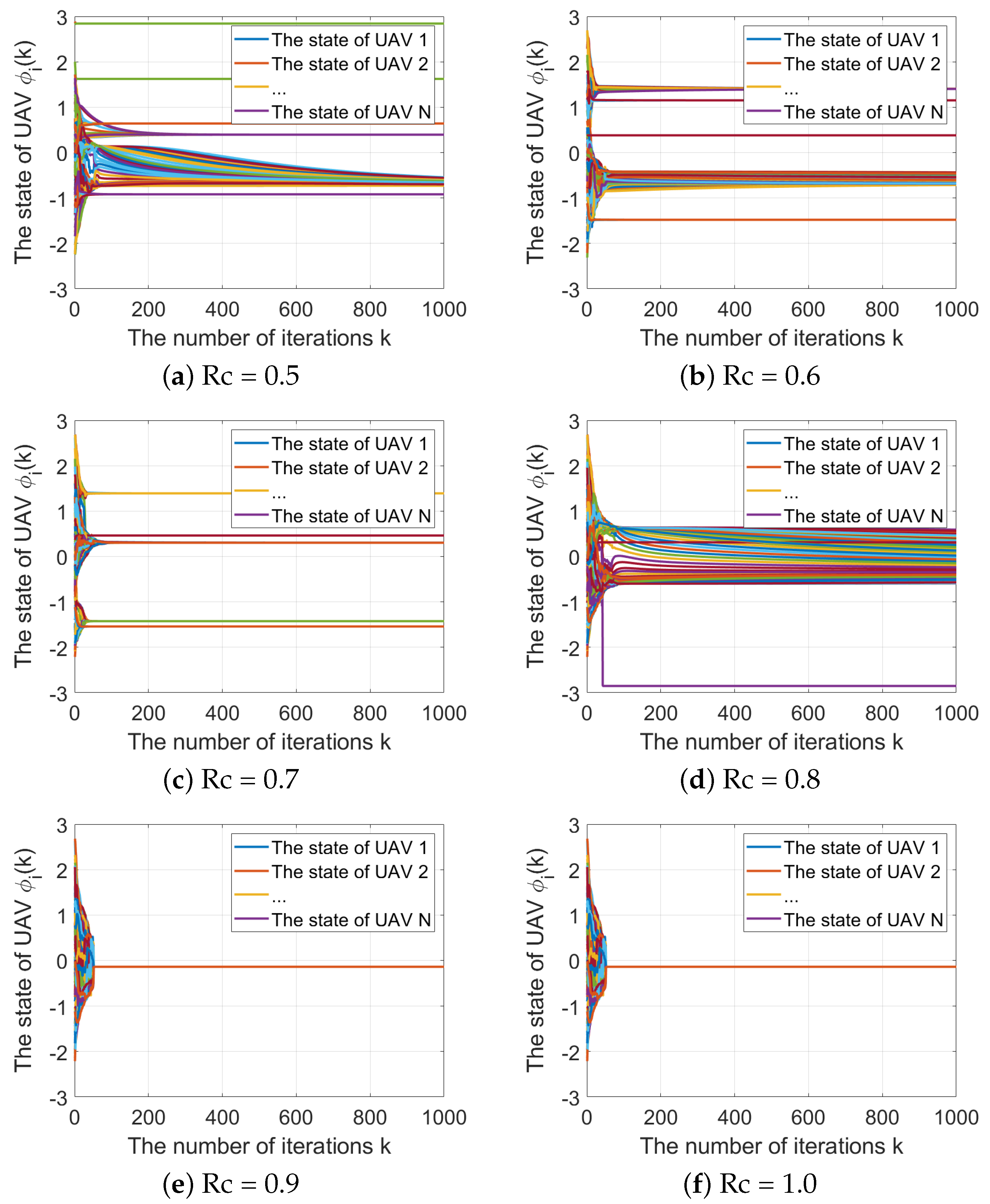
The neighborhood selection (NS) strategy has been shown to enhance the convergence speed and stability of the system [30]. As each UAV only requires some neighbors for updating its own state information, NS synchronization can achieve faster convergence. To facilitate convergence and improve system consistency, agents with the smallest state differences in each sector are selected to form the backbone network topology. This paper presents an NS-AS synchronization mechanism-based moving source localization method for UAV swarms. The most representative individuals are selected from each sector for state update calculation. When the UAV swarm network reaches full connectivity, the synchronization algorithm switches to the AS strategy.

Compared with the existing research, the main contributions of this study are summarized as follows:

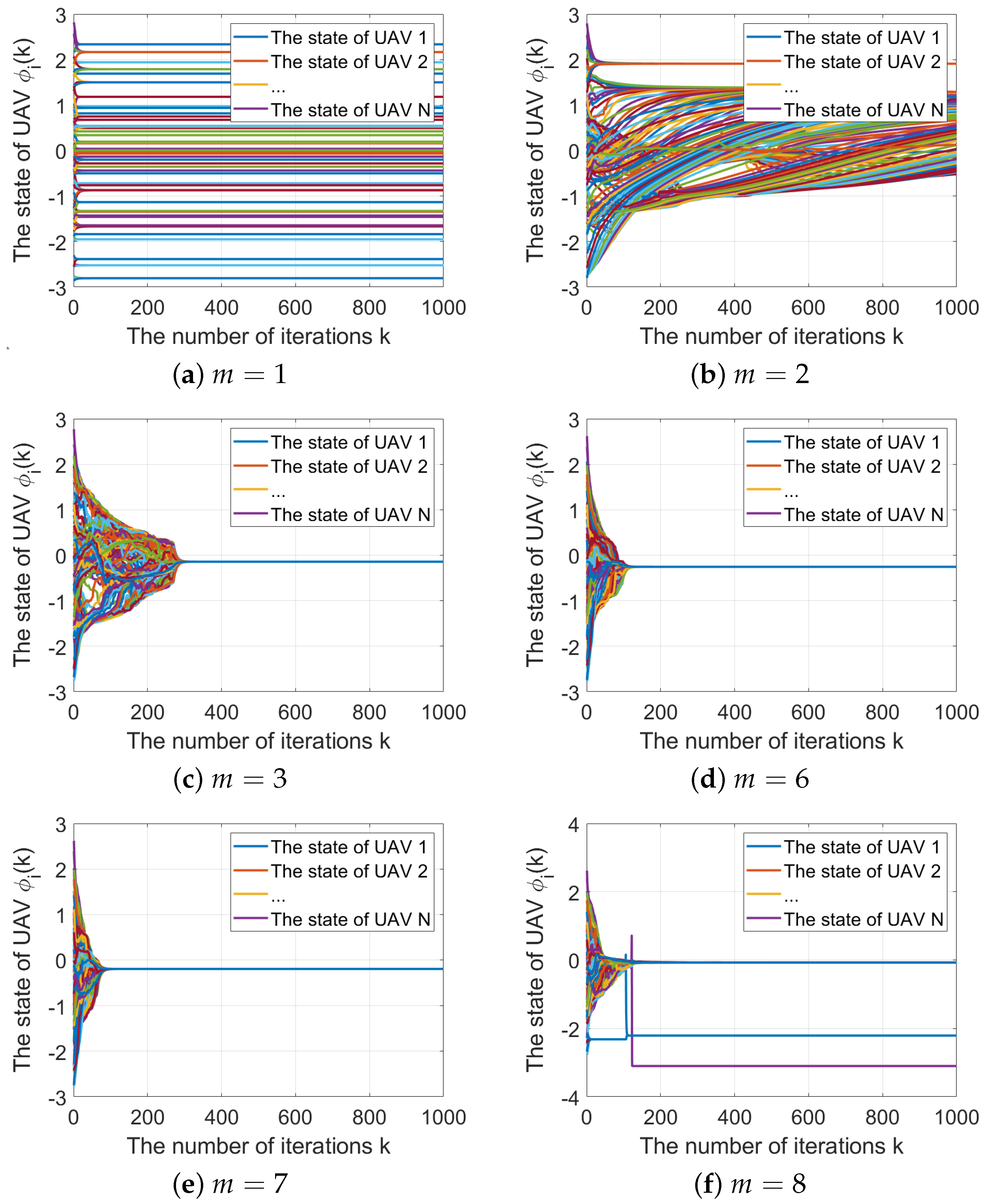
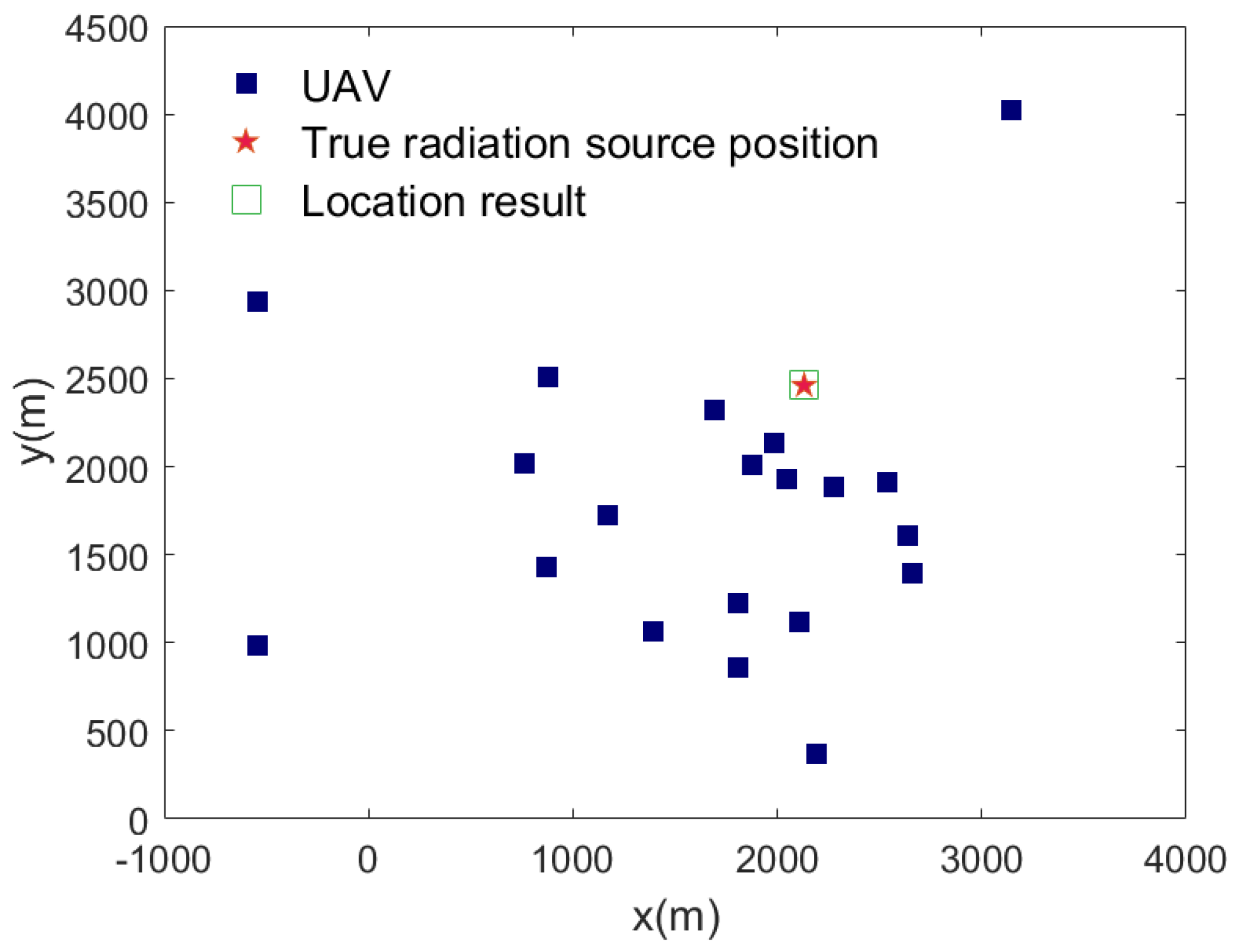
(a) The NS-AS synchronization mechanism is introduced to improve system synchronization convergence. (b) The TDOA-FDOA joint localization algorithm is utilized to achieve passive localization of moving radiation sources. (c) The convergence performance of different synchronization algorithms and their related parameters are analyzed. (d) The effects of different passive localization parameters, e.g., the synchronization errors and the number of UAVs, on localization accuracy are analyzed.

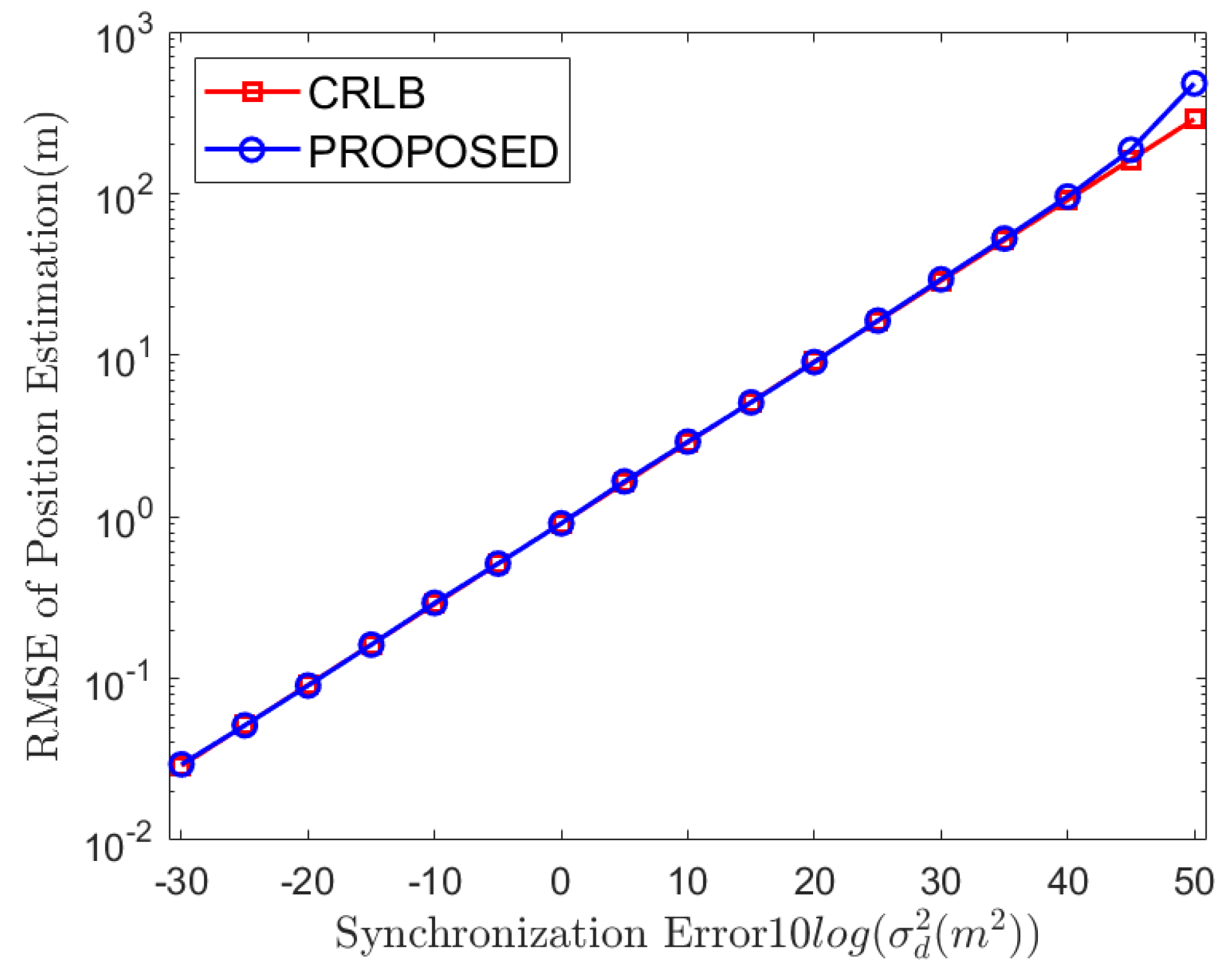
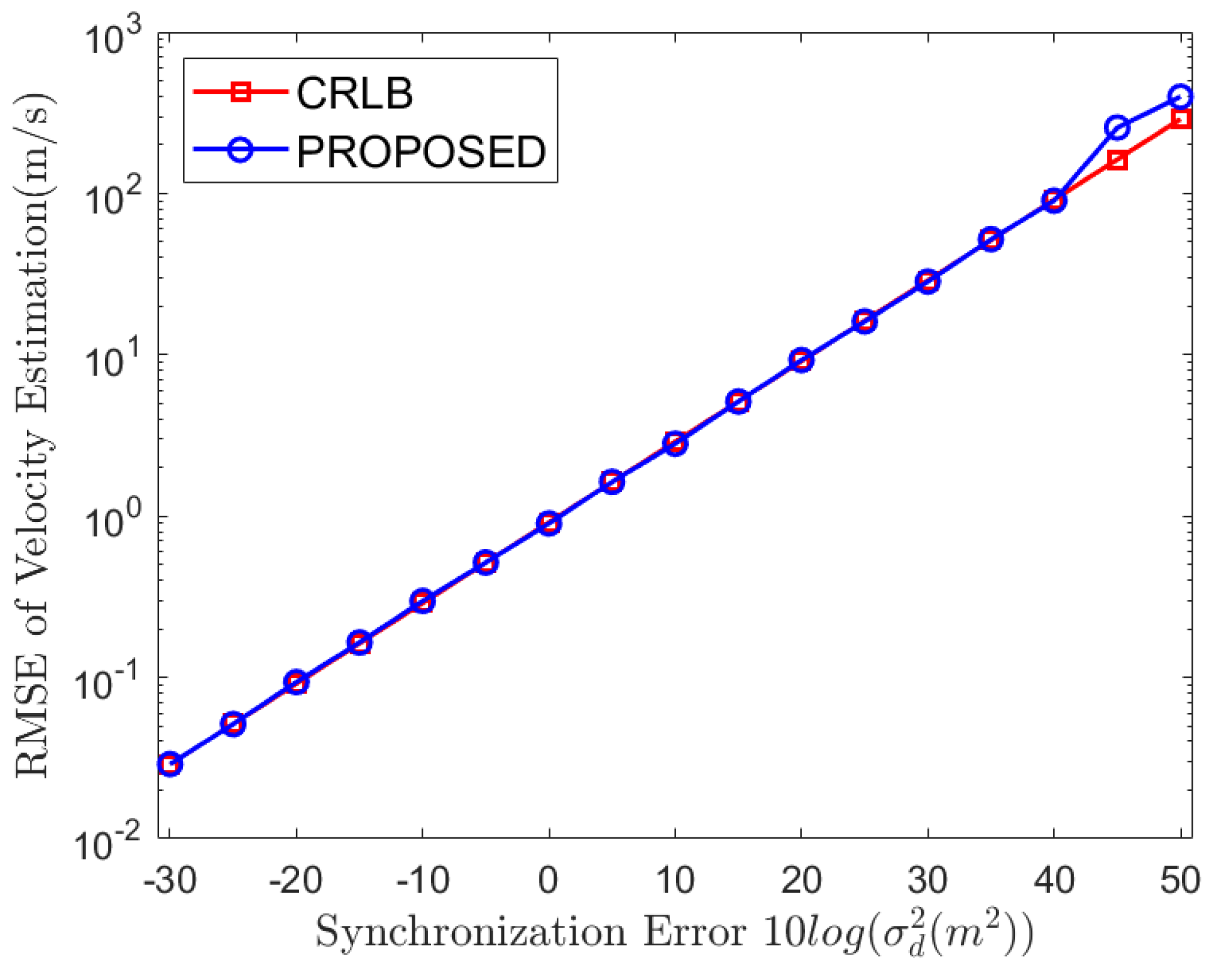
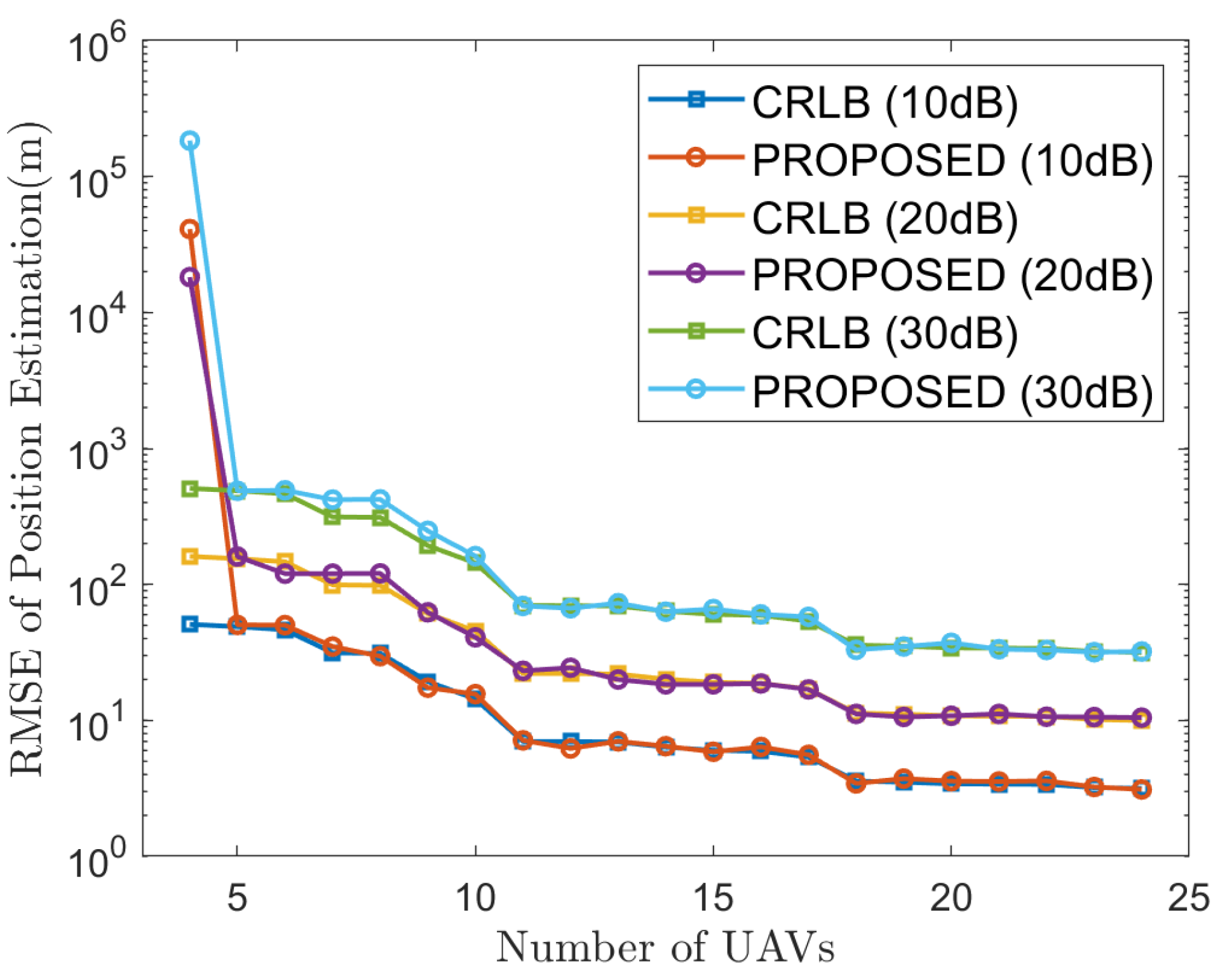
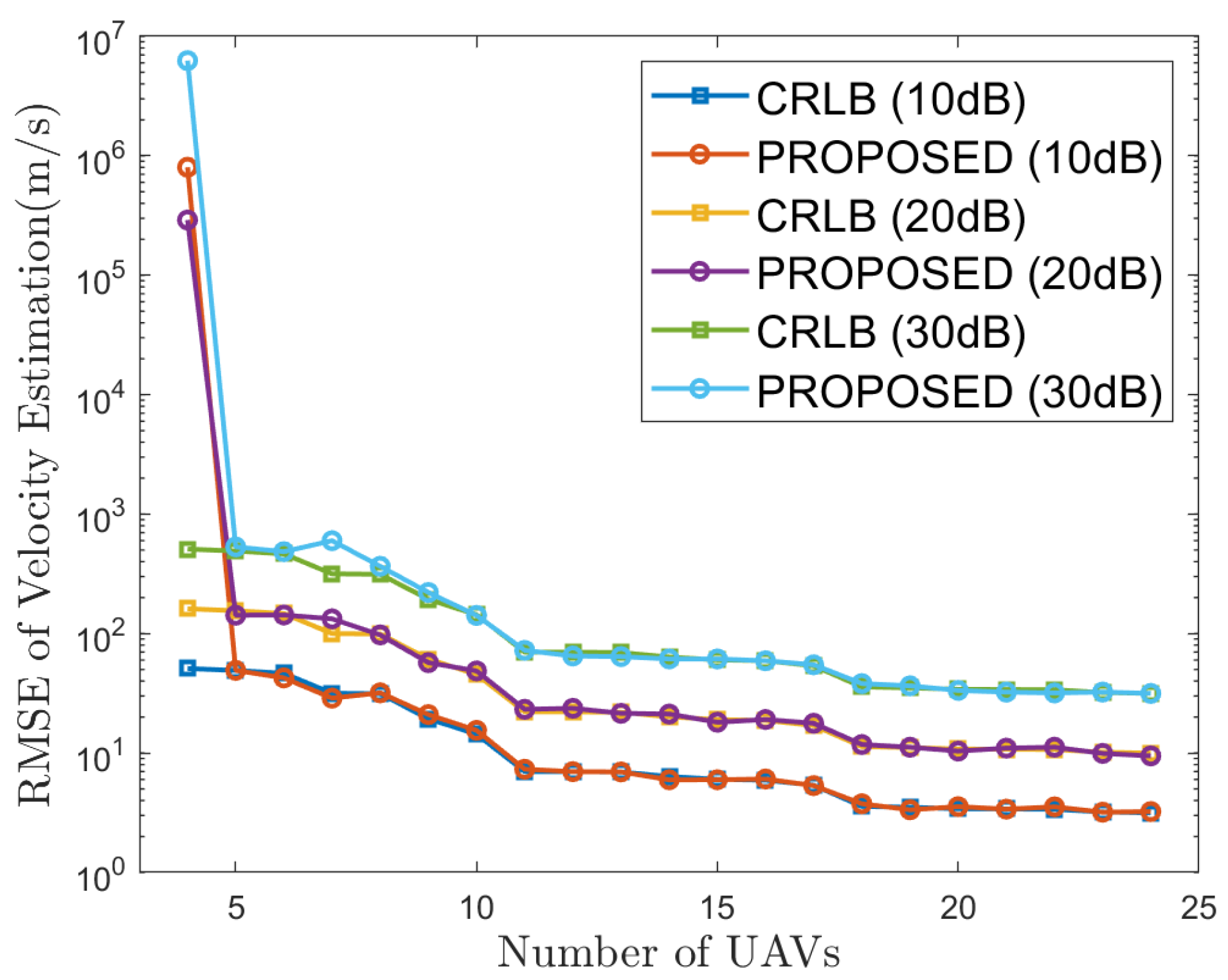
The rest of this paper is organized as follows. Section 2 formulates the passive localization problem of UAV swarms; Section 3 presents the proposed algorithm; Section 4 discusses the relevant simulation results; Section 5 concludes the paper.

2. Problem Description and Modeling

UAV swarm network synchronization is the prerequisite for moving radiation source localization. This subsection analyzes the synchronization model and the passive localization scenario.

2.1. The Time Synchronization Model

The UAV swarm network is modeled as graph $G(V,ϵ)$, where $V=\left\{1,2,\cdots ,n\right\}$ represents the nodes of the UAV swarm network, and $ϵ$ defines the available communication links. The set of neighbors of $v_i$ is $N_i=\left\{j,(i,j)\in ϵ,i\ne j\right\}$.

The time synchronization algorithm has two time concepts, i.e., the hardware clock $C_i\left(t\right)$ and software clock $L_i\left(t\right)$. $C_i\left(t\right)$ is defined as follows:

$$C_i\left(t\right)=\frac{1}{f_0}{\int }_{t_0}^t{f}_i\left(t\right)dt+C_i\left(t_0\right)$$

(1)

where $f_0$ is the nominal frequency of the crystal oscillator, $f_i\left(t\right)$ is the crystal frequency of node i at time t, t is the actual time, and $C_i\left(t_0\right)$ denotes the local time at time $t_0$.

Equation (1) can also be written as:

$$C_i\left(t\right)={\alpha }_{i}t+{\beta }_i$$

(2)

where ${\alpha }_i$ and ${\beta }_i$ represent the local time drift and offset, respectively.

Based on the hardware clock, the software clock of a node, also known as the logical clock, can be constructed as follows:

$$L_i\left(t\right)={\int }_{t_0}^t{\omega }_i\left(t\right)dt+L_i\left(t_0\right)$$

(3)

where $\omega$ denotes the software clock frequency, and $L_i\left(t_0\right)$ represents the initial value at time $t_0$.

The UAV swarm synchronization process can be described by the Kuramoto model [39]. The differential equation model of UAV state quantity and time is as follows:

$$\begin{array}{ccc}\hfill {\dot{\varphi }}_i\left(t\right)& =& \sum _{j\in N_i}{m}_i{a}_{ij}\left({\varphi }_j\left(t\right)-{\varphi }_i\left(t\right)\right)\hfill \end{array}$$

(4)

where ${\dot{\varphi }}_{\mathrm{i}}$ represents the UAV state. $m_i$ is the synchronization factor. $a_{ij}$ denotes the element value corresponding to the adjacency matrix, and ${\varphi }_i$ and ${\varphi }_j$ represent the states of the i-th and j-th UAV, respectively.

The system achieves synchronization when all nodes of the UAV swarm network satisfy $\underset{t\to \infty }{lim}\left|x_l\left(t\right)-x_j\left(t\right)\right|=0$.

After the discretization of Equation (4), we have:

$$\begin{array}{ccc}\hfill {\varphi }_i(k+1)& =& {\varphi }_i\left(k\right)+\epsilon \sum _{j\in N_i}{m}_j{a}_{ij}\left({\varphi }_j\left(k\right)-{\varphi }_i\left(k\right)\right)\hfill \end{array}$$

(5)

where $ϵ$ denotes the weight, and ${\varphi }_i\left(k\right)$ represents the time parameter of UAV i at the k-th iteration.

Rewriting Equation (5) into vector form, we have:

$$\begin{array}{ccc}\hfill \varphi (k+1)& =& (I-\epsilon L)\varphi \left(k\right)\hfill \end{array}$$

(6)

where $\varphi \left(k\right)={\left({\varphi }_1\left(0\right),\dots ,{\varphi }_n\left(0\right)\right)}^T$. Considering $(I-\epsilon L)$ as a Peron matrix with parameter L, the iterative model can be expressed as:

$$\begin{array}{ccc}\hfill x\left(k\right)& =& P^{k}x\left(0\right)\hfill \end{array}$$

(7)

where $x\left(0\right)={\left({\varphi }_1\left(0\right),{\varphi }_1\left(0\right),\dots ,{\varphi }_n\left(0\right)\right)}^T$ represents the initial value of the node time parameter. When $P^k$ converges to a consistent value, the time of the UAV node can also be synchronized.

2.2. The Moving Radiation Source Localization Scenario

The moving radiation source localization model based on UAV swarms is depicted in Figure 1. Assuming that the task is performed by N UAVs, the position vector of the i-th UAV can be denoted by $s_i={\left[x_i,y_i,z_i\right]}^T$, where $i=0,1,\dots ,N-1$. The position vector of the radiation source can be expressed as $u={[x,y,z]}^T$. The velocity vectors of the UAV and the radiation source can be expressed as $\dot{s_i}=\left[\dot{x_i},\dot{y_i},\dot{z_i}\right]$ and $\dot{u}=\left[\dot{x},\dot{y},\dot{z}\right]$, respectively.

The distance difference between the i-th UAV and the first UAV to the signal source is defined as:

$$r_{i1}=c{t}_{i1}=r_i-r_1$$

(8)

where c is the signal propagation speed. The distance between the i-th UAV and the radiation source is expressed as:

$$\begin{array}{ccc}\hfill r_i& =& ∥u-s_i∥=\sqrt{{(u-s_i)}^T(u-s_i)}\hfill \end{array}$$

(9)

By integrating Equations (8) and (9), the TDOA localization equation can be obtained as follows:

$$r_{i1}+2r_{i1}{r}_1=s_i^T{s}_i-s_1^T{s}_1-2{(s_i-s_1)}^{T}u.$$

(10)

The FDOA equation can be derived from Equation (10) as follows:

$$\begin{array}{ccc}\hfill 2\left({\dot{r}}_{i1}{r}_{i1}+{\dot{r}}_{i1}{r}_1+r_{i1}{\dot{r}}_1\right)& =& 2\left({\dot{\mathbf{s}}}_i^T{\mathbf{s}}_i-{\dot{\mathbf{s}}}_1^T{\mathbf{s}}_1-{\left({\dot{\mathbf{s}}}_i-{\dot{\mathbf{s}}}_1\right)}^T\mathbf{u}-{\left({\mathbf{s}}_i-{\mathbf{s}}_1\right)}^T\dot{\mathbf{u}}\right)\hfill \end{array}$$

(11)

where $\dot{r_i}$ is the derivative of $r_i$, which can be written as:

$$\begin{array}{c}\hfill {\dot{r}}_i=\frac{{\left(\dot{\mathbf{u}}-{\dot{\mathbf{s}}}_i\right)}^T\left(\mathbf{u}-{\mathbf{s}}_i\right)}{r_i}\end{array}$$

(12)

2.3. The Root Mean Square Error

The TDOA localization error $n_{i1}$ mainly includes range measurement noise error $n_{di}$ and synchronization error $n_{si}$. The range measurement noise $n_{di},i=1,2,\cdots ,N$ is independent and follows a Gaussian distribution with zero mean and variance ${\sigma }_{di}^2$. In this paper, the state value of UAV ${\varphi }_i\left(k\right)$ is defined as the clock period deviated from the time reference, where the state value is 0 to represent the time reference. The variance of synchronization error ${\sigma }_{si}^2$ can be given by

$$\begin{array}{c}\hfill {\sigma }_{si}^2=\frac{{\sum }_{i=1}^N{\left({\varphi }_i\left(k\right)-{\varphi }_0\left(k\right)\right)}^2}{N}\end{array}$$

(13)

where ${\varphi }_i\left(k\right)$ represents the state value of the i-th UAV at time k, and ${\varphi }_0\left(k\right)$ is the time reference.

By combining Equations (8) and (9), the TDOA equation can be obtained as:

$$\begin{array}{c}\hfill d_{i1}=c{t}_{i1}=∥u-s_i∥-∥u-s_1∥+n_{i1},i=2,\dots ,N\end{array}$$

(14)

The TDOA equation can be rewritten in the following matrix form:

$$d=Gh+\Delta n$$

(15)

where $d={[d_{21},d_{31},\cdots ,d_{N1}]}^T$, $G=[-1_{N-1},I_{n-1}]$, $h=[∥u-s_1∥,∥u-s_2∥,\cdots ,∥u-s_N∥]$. The equation can be rewritten as $\Delta n=d-Gh=[n_{21},n_{31},\cdots ,n_{N1}]$. Since the noise satisfies the Gaussian distribution, the likelihood function can be obtained as

$$\begin{array}{ccc}\hfill f(\tilde{d}\mid u)& =& \frac{1}{{\left(2\pi \right)}^{\frac{N}{2}}{\left|Q\right|}^{\frac{1}{2}}}{e}^{-\frac{1}{2}{(\tilde{d}-Gh)}^T{Q}^{-1}(\tilde{d}-Gh)}\hfill \end{array}$$

(16)

The value of the maximized likelihood function is used as the estimated value of the target position, and the maximum likelihood problem can be written as:

$$\begin{array}{ccc}\hfill \underset{u}{min}f(u)& =& {(\tilde{d}-Gh)}^T{Q}^{-1}(\tilde{d}-Gh)\hfill \end{array}$$

(17)

The problem of solving the likelihood function is transformed into the problem of finding the minimum function. The optimal solution can be obtained by iterating the estimated value of the target position using the gradient descent method. In unbiased estimation problems, CRLB is usually used to measure the validity of an estimate. If the root mean square error of an estimate is smaller, then it is closer to the value obtained by CRLB, which means that the estimate is more effective. Through the TDOA measurement model, the estimated CRLB of the radiation source can be given by:

$$\begin{array}{ccc}\hfill CRL{B}_{\mathrm{tdoa}}\left(u\right)& =& {\left({\tilde{H}}^T{\tilde{Q}}^{-1}\tilde{H}\right)}^{-1}\hfill \end{array}$$

(18)

where

$$\begin{array}{c}\hfill \tilde{H}=\frac{\partial \left(Gh\right)}{\partial u^T}=\left[\begin{array}{c}\frac{{\left(u-s_2\right)}^T}{∥u-s_2∥}-\frac{{\left(u-s_1\right)}^T}{∥u-s_1∥}\\ \frac{{\left(u-s_3\right)}^T}{∥u-s_3∥}-\frac{{\left(u-s_3\right)}^T}{∥u-s_3∥}\\ \cdots \\ \frac{{\left(u-s_N\right)}^T}{∥u-s_N∥}-\frac{{\left(u-s_N\right)}^T}{∥u-s_N∥}\end{array}\right]\end{array}$$

(19)

The covariance matrix $\tilde{Q}$ of $\Delta n$ is as follow:

$$\begin{array}{c}\hfill \tilde{Q}=E\left[\Delta n\Delta n^T\right]=diag\left\{{\sigma }_2^2,\dots ,{\sigma }_N^2\right\}+1_{N-1}{1}_{N-1}^T{\sigma }_1^2\end{array}$$

(20)

The relationship between the RMSE of the radiation source position estimate $\widehat{u}={[\widehat{x},\widehat{y}]}^T$ and the CRLB is as follows:

$$\begin{array}{ccc}\hfill RMSE& =& \sqrt{E\left[{(x-\widehat{x})}^2+{(y-\widehat{y})}^2\right]}\ge \sqrt{CRLB(1,1)+CRLB(2,2)}\hfill \end{array}$$

(21)

3. The Proposed Method

3.1. The NS-AS Synchronization Mechanism

The circular area within the sensing distance $r_c$ of agent i is the communication range $R_c,R_c\in R^2$. The communication range is evenly divided into m fan-shaped communication sectors, forming a set $V=\left\{1,2,\cdots ,m\right\}$. Figure 2 displays the optimized distribution of communication sectors [30]. By rotating the two-dimensional coordinate axis of agent i clockwise, the number of neighbors distributed in each fan-shaped area is reduced to a minimum standard deviation. The rotation angle $\beta$ can be expressed as:

$$\beta =R_{array}\left\{min(\left(std\left(N_n\right)\right)\right\}$$

(22)

where $R_{array}$ denotes the rotation angles set, $std\left(N_n\right)$ represents the standard deviation of the neighbor set, and $N_n$ is the number of UAVs in each sector.

During the k-th evolution cycle, the set of neighbors of agent i in the $\mathrm{v}$-th fan-shaped communication sector is expressed as:

$$\begin{array}{ccc}\hfill N_i^{\mathrm{v}}\left(k\right)& =& \left\{\begin{array}{c}j:∥s_j^k-s_i^k∥\le r_c\\ 2\pi \left({\mathrm{v}}^{-}1\right)/\mathrm{m}<\theta 〈\overrightarrow{ij},x^{+}〉\le 2\pi \mathrm{v}/m\\ i,j\in Agent,i\ne j,\mathrm{v}\in V\end{array}\right\}\hfill \end{array}$$

(23)

where the angle between agent i and its neighbor j in the two-dimensional space is referred to as $\theta 〈\overrightarrow{ij},x^{+}〉$, and $s_i^k$ and $s_j^k$ represent the position vectors of the i-th and j-th UAV at time k, respectively.

Under this network configuration, all potential neighbors of agent i are involved in its state update calculation. The state transition equation can be written as follows:

$${\varphi }_i(k+1)={\varphi }_i\left(k\right)+{\gamma }_i\left(k\right)$$

(24)

where ${\gamma }_i\left(k\right)$ denotes the control input, which can be expressed as:

$$\begin{array}{c}{\gamma }_i\left(k\right)=\lambda (\sum _{v=1}^m\left({\varphi }_{min\left(i^v\right)}\left(k\right)-{\varphi }_i\left(k\right)\right)\\ +\sum _{c\in P_i\left(k\right),c\notin A_i\left(k\right)}\left({\varphi }_c\left(k\right)-{\varphi }_i\left(k\right)\right))\end{array}$$

(25)

where $\lambda$ is the adjustment factor of the model, m is the number of communication sectors, and $i^u$ indicates that agent i actively selects a neighbor from the u-th sector $i^u$ and adds it into the candidate set $H_i\left(t\right)$. $x_{min\left(i^u\right)}\left(k\right)$ is the state information of agent $i^u$ at k time with the smallest u sector state difference. $P_i\left(k\right)$ and $A_i\left(k\right)$ denote the set of neighbors from which agent i receives the cooperation signal and the set of agents to which agent i sends the cooperation signal, respectively.

To enhance the convergence speed of the system, the proposed method optimizes the previously mentioned NS algorithm. When the system reaches a fully connected state, meaning that agent i has $n-1$ neighbors, it switches to the AS algorithm for updates. This approach is referred to as the NS-AS algorithm, and its implementation process is outlined in Algorithm 1.

The status information of the UAV at the next moment [31] can be re-expressed as:

$$\begin{array}{c}\forall i,N_i\left(k\right)<n-1:\\ {\varphi }_i(k+1)={\varphi }_i\left(k\right)+\alpha 1\{\sum _{u=1}{\varphi }_{min\left(i^u\right)}\left(t\right)-{\varphi }_i\left(k\right)\\ +\sum _{c\in P_i\left(k\right),c\notin A_i\left(k\right)}\left({\varphi }_{ii}\left(k\right)-{\varphi }_i\left(k\right)\right)\};\end{array}$$

(26)

$$\begin{array}{c}\forall i,N_i\left(k\right)=n-1:\\ {\varphi }_i(k+1)={\varphi }_i\left(k\right)+\alpha 2\sum _{j\in N_i\left(k\right)}\left({\varphi }_j\left(k\right)-{\varphi }_i\left(k\right)\right).\end{array}$$

(27)

where ${\alpha }_1$ and ${\alpha }_2$ represent the adjustment factors under different conditions.

Algorithm 1. The NS-AS synchronization algorithm.

Step1: Initialize UAV swarm network topology and UAV state ${\varphi }_i\left(k\right)$.

Step2: If the UAV swarm network is not fully connected, the NS algorithm is used for synchronization. Neighboring agents are selected into the candidate set $A_i\left(k\right)$. The UAV state ${\varphi }_i\left(k\right)$ is updated by the candidate set $A_i\left(k\right)$.

Step3: When the UAV swarm network reaches full connectivity, it switches to the AS synchronization mechanism. All agents in the domain are selected to update the UAV state ${\varphi }_i\left(k\right)$.

3.2. The TDOA-FDOA Joint Localization Algorithm

The TDOA-FDOA joint localization algorithm utilizes the signals received by the UAV swarms to estimate the time difference and frequency difference, thereby locating the radiation source [40]. The algorithm consists of two main steps: (a) processing the received signal to obtain the estimated time difference and frequency difference, and (b) analyzing the TDOA and FDOA values to estimate the position of the target source.

Suppose $\mathbf{r}={\left[r_{21},r_{31},\dots ,r_{M1}\right]}^T$ and $\dot{\mathbf{r}}={\left[{\dot{r}}_{21},{\dot{r}}_{31},\dots ,{\dot{r}}_{M1}\right]}^T$ are the distance difference and speed difference with noise, respectively, we have:

$$\begin{array}{ccc}\hfill {\mathbf{r}}^o& =& \mathbf{r}+c\Delta {\sigma }_n\hfill \end{array}$$

(28)

$$\begin{array}{ccc}\hfill \dot{{\mathbf{r}}^o}& =& \dot{\mathbf{r}}+c\Delta \dot{{\sigma }_n}\hfill \end{array}$$

(29)

where ${(*)}^o$ is the measured value with actual noise, and $\Delta {\sigma }_n$ and $\Delta \dot{{\sigma }_n}$ represent the noise in TDOA and FDOA, respectively. The covariance matrix Q of noise can be obtained as:

$$\begin{array}{c}\hfill \frac{1}{c^2}\mathbf{Q}=E\left[{\left[\begin{array}{cc}\Delta {\sigma }_n^T\hfill & \dot{\Delta {\sigma }_n^T}\hfill \end{array}\right]}^T\left[\begin{array}{cc}\Delta {\sigma }_n^T\hfill & \Delta {\dot{{\sigma }_n}}^T\hfill \end{array}\right]\right]\end{array}$$

(30)

Thus, the error equations for TDOA and FDOA are obtained as follows:

$$\begin{array}{cc}\hfill {\delta }_1=[{\delta }_t& {\delta }_f{]}^T={\mathbf{F}}_1-{\mathbf{H}}_1{\xi }_1\end{array}$$

(31)

where ${\xi }_1={\left[{\mathbf{u}}^T,r_1,{\dot{\mathbf{u}}}^T,{\dot{r}}_1\right]}^T$ denotes the auxiliary vector defined for the solution.

$$\begin{array}{ccc}\hfill {\mathbf{F}}_1& =& \left[\begin{array}{c}{r}_{2,1}^2-{\mathbf{s}}_2^T{\mathbf{s}}_2+{\mathbf{s}}_1^T{\mathbf{s}}_1\\ ⋮\\ r_{M,1}^2-{\mathbf{s}}_M^T{\mathbf{s}}_M+{\mathbf{s}}_1^T{\mathbf{s}}_1\\ 2\left({\dot{r}}_{2,1}{r}_{2,1}-{\dot{\mathbf{s}}}_2^T{\mathbf{s}}_2+{\dot{\mathbf{s}}}_1^T{\mathbf{s}}_1\right)\\ ⋮\\ 2\left({\dot{r}}_{M,1}{r}_{M,1}-{\dot{\mathbf{s}}}_M^T{\mathbf{s}}_M+{\dot{\mathbf{s}}}_1^T{\mathbf{s}}_1\right)\end{array}\right]\hfill \end{array}$$

(32)

$$\begin{array}{ccc}\hfill {\mathbf{H}}_1& =& -2\left[\begin{array}{cccc}{\left({\mathbf{s}}_2-{\mathbf{s}}_1\right)}^T& r_{21}& 0^T& 0\\ ⋮& ⋮& ⋮& ⋮\\ {\left({\mathbf{s}}_M-{\mathbf{s}}_1\right)}^T& r_{M1}& 0^T& 0\\ {\left({\dot{\mathbf{s}}}_2-{\dot{\mathbf{s}}}_1\right)}^T& r_{2,1}& {\left({\mathbf{s}}_2-{\mathbf{s}}_1\right)}^T& r_{2,1}\\ ⋮& ⋮& ⋮& ⋮\\ {\left({\dot{\mathbf{s}}}_M-{\dot{\mathbf{s}}}_1\right)}^T& {\dot{r}}_{M,1}& {\left({\mathbf{s}}_M-{\mathbf{s}}_1\right)}^T& r_{M,1}\end{array}\right]\hfill \end{array}$$

(33)

where $\mathbf{0}$ is a $3\times 1$ column vector of zero. The purpose of incorporating the nuisance variables is to transform Equation (31) into a set of linear equations in terms of ${\xi }_1$. Therefore, the weighted least squares (WLS) estimation result of Equation (31) is:

$$\begin{array}{ccc}\hfill {\xi }_1& =& {\left({\mathbf{H}}_1^T{\mathbf{W}}_1{\mathbf{H}}_1\right)}^{-1}{\mathbf{H}}_1^T{\mathbf{W}}_1{\mathbf{F}}_1\hfill \end{array}$$

(34)

where ${\mathbf{W}}_1={\mathbf{D}}_1^{-T}{\mathbf{Q}}^{-1}{\mathbf{D}}_1^{-1}$, ${\mathbf{D}}_1=\left[\begin{array}{cc}\mathbf{D}\hfill & \mathbf{O}\hfill \\ \dot{\mathbf{D}}\hfill & \mathbf{D}\hfill \end{array}\right]$, $\mathbf{D}=2diag\left\{r_2,r_3,\dots ,r_M\right\}$. $\dot{\mathbf{D}}=2diag\left\{\dot{r_2},\dot{r_3},\dots ,\dot{r_M}\right\}$. The covariance matrix of ${\xi }_1$ can be expressed as:

$$\begin{array}{ccc}\hfill \mathbf{cov}\left({\xi }_{\mathbf{1}}\right)& =& {\left({\mathbf{H}}_1^T{\mathbf{W}}_1{\mathbf{H}}_1\right)}^{-1}{\mathbf{H}}_1^T{\mathbf{W}}_1{\mathbf{F}}_1\hfill \end{array}$$

(35)

The two constraints of TDOA and FDOA are as follows:

$$\begin{array}{c}\hfill \begin{array}{c}{r}_1^2={\left(\mathbf{u}-{\mathbf{s}}_1\right)}^T\left(\mathbf{u}-{\mathbf{s}}_1\right)\\ {\dot{r}}_1{r}_1={\left(\dot{\mathbf{u}}-{\dot{\mathbf{s}}}_1\right)}^T\left(\mathbf{u}-{\mathbf{s}}_1\right)\end{array}\end{array}$$

(36)

The new system of equations can be obtained as:

$$\begin{array}{ccc}\hfill {\delta }_2& =& {\mathbf{F}}_2-{\mathbf{H}}_2{\xi }_2\hfill \end{array}$$

(37)

where

$$\begin{array}{ccc}\hfill {\mathbf{F}}_2& =& \left[\begin{array}{c}\left({\xi }_{1,\mathrm{u}}-{\mathbf{s}}_1\right)\odot \left({\xi }_{1,\mathrm{u}}-{\mathbf{s}}_1\right)\\ {\xi }_1{\left(4\right)}^2\\ \left({\xi }_{1,\mathrm{u}}-{\dot{\mathbf{s}}}_1\right)\odot \left({\xi }_{1,\mathrm{u}}-{\mathbf{s}}_1\right)\\ {\xi }_1\left(8\right){\xi }_1\left(4\right)\end{array}\right]\hfill \end{array}$$

(38)

$$\begin{array}{ccc}\hfill {\mathbf{H}}_2& =& {\left[\begin{array}{cccc}\mathbf{I}& {\mathbf{1}}^T& \mathbf{0}& {\mathbf{0}}^{{}^{\prime }T}\\ \mathbf{0}& {\mathbf{0}}^{{}^{\prime }T}& \mathbf{I}& {\mathbf{1}}^T\end{array}\right]}^T\hfill \end{array}$$

(39)

$$\begin{array}{ccc}\hfill {\xi }_2& =& \left[\begin{array}{c}\left(\mathbf{u}-{\mathbf{s}}_1\right)\odot \left(\mathbf{u}-{\mathbf{s}}_1\right)\hfill \\ \left(\dot{\mathbf{u}}-{\dot{\mathbf{s}}}_1\right)\odot \left(\mathbf{u}-{\mathbf{s}}_1\right)\hfill \end{array}\right]\hfill \end{array}$$

(40)

where $\mathbf{I}$ is the identity matrix, $\mathbf{0}$ is a $3\times 3$ zero matrix, $\mathbf{1}$ is a matrix whose elements are all 1, ${\mathbf{0}}^{{}^{\prime }\mathbf{T}}$ is a $3\times 1$ zero matrix, and ⊙ denotes the dot product of the matrix.

The WLS optimal estimation result of Equation (37) can be expressed as:

$$\begin{array}{ccc}\hfill {\xi }_2& =& {\left({\mathbf{H}}_2^T{\mathbf{W}}_2{\mathbf{H}}_2\right)}^{-1}{\mathbf{H}}_2^T{\mathbf{W}}_2{\mathbf{F}}_2\hfill \end{array}$$

(41)

where

$$\begin{array}{ccc}\hfill {\mathbf{W}}_2& =& {\mathbf{D}}_2^{-T}cov{\left({\xi }_1\right)}^{-1}{\mathbf{D}}_2^{-1}\hfill \end{array}$$

(42)

$$\begin{array}{ccc}\hfill {\mathbf{D}}_2& =& \left[\begin{array}{cccc}2diag\left\{\mathbf{u}-{\mathbf{s}}_1\right\}& \mathbf{0}& \mathbf{0}& \mathbf{0}\\ {\mathbf{0}}^T& 2r_1& {\mathbf{0}}^T& 0\\ diag\left\{\dot{\mathbf{u}}-{\dot{\mathbf{s}}}_1\right\}& \mathbf{0}& diag\left\{\mathbf{u}-{\mathbf{s}}_1\right\}& \mathbf{0}\\ {\mathbf{0}}^T& {\dot{r}}_1& {\mathbf{0}}^T& r_1^{\circ }\end{array}\right]\hfill \end{array}$$

(43)

The position and velocity information of the moving radiation source can be solved by:

$$\begin{array}{ccc}\hfill \mathbf{u}& =& \mathbf{U}{\left[\sqrt{{\xi }_2\left(1\right)},\sqrt{{\xi }_2\left(2\right)},\sqrt{{\xi }_2\left(3\right)}\right]}^T+{\mathrm{s}}_1\hfill \end{array}$$

(44)

$$\begin{array}{ccc}\hfill \dot{\mathbf{u}}& =& \mathbf{U}{\left[\frac{{\xi }_2\left(4\right)}{\sqrt{{\xi }_2\left(1\right)}}\frac{{\xi }_2\left(5\right)}{\sqrt{{\xi }_2\left(2\right)}}\frac{{\xi }_2\left(6\right)}{\sqrt{{\xi }_2\left(3\right)}}\right]}^T+{\dot{\mathrm{s}}}_1\hfill \end{array}$$

(45)

where $\mathbf{U}=diag\left\{sgn\left({\xi }_{1,\mathrm{u}}-{\mathbf{s}}_1\right)\right\}$. The process of the TDOA-FDOA joint localization algorithm is summarized in Algorithm 2.

Algorithm 2. The TDOA-FDOA joint localization algorithm.

Step1: The error equations are constructed as (31), let ${\mathbf{W}}_1=\mathbf{I}$.

Step2: The rough estimation of $\xi$ is provided by Equation (34), which is used to recalculate ${\mathbf{D}}_{\mathbf{1}}$ and ${\mathbf{W}}_{\mathbf{1}}$.

Step3: Iterate Steps 1 to 2 until either the estimated difference meets the threshold or the maximum number of iterations is reached. The covariance matrix $\mathbf{cov}\left({\xi }_{\mathbf{1}}\right)$ can be calculated with Equation (35).

Step4: The new set of error equations is constructed as (37). ${\xi }_1$ is calculated through iteration to obtain ${\mathbf{D}}_{\mathbf{2}}$ and ${\mathbf{W}}_{\mathbf{2}}$.

Step5: The estimated value of ${\xi }_2$ is then calculated with Equation (41), which is used to determine the position and velocity of the radiation source.

Step6: Iterate Steps 4 to 5 until either the estimated difference meets the threshold or the maximum number of iterations is reached. The position and velocity of the radiation source are finally determined.

4. Simulation Results

In this section, numerical simulations are conducted to illustrate the performance of the proposed method. The convergence of the proposed NS-AS method is compared with that of other synchronization algorithms. The relevant parameters affecting the synchronization of the systems are studied. The moving source is located using the TDOA-FDOA localization algorithm. The localization performance under different synchronization errors and different numbers of UAVs is simulated.

4.1. System Convergence

4.1.1. Different Synchronization Algorithms

Figure 3 shows the convergence performance using different synchronization algorithms. When the AS synchronization algorithm is adopted, the system diverges after iteration. The UAV swarm diverges to multiple local central values, and the NS synchronization algorithm selects the most representative individual from each sector for synchronization. Despite the improved convergence performance of the system compared with the AS algorithm, it still cannot achieve convergence. Then, an improved NS algorithm is proposed, which adjusts the angle of the sectors so that the number of UAVs in each sector is evenly distributed, thus improving the convergence of the system. An NS-AS strategy is proposed to further improve the convergence performance of the system.

As shown in

Table 1. The convergence performance comparison under different communication sectors.

Synchronization Algorithm	Whether to Converge	Running Time (s)
AS algorithm	No	7.7350
NS synchronization algorithm	No	5.4784
Optimized NS synchronization algorithm	Yes	74.5223
NS-AS synchronization algorithm	Yes	9.5636

, this section counts the number of times and running time required for different synchronization algorithms to reach system convergence. The traditional AS synchronization algorithm and NS-1 synchronization algorithm did not realize the convergence of the system, but diverged to multiple local centers. Although the NS-2 synchronization algorithm finally realized system convergence, the time required for convergence was 74.5223 s, and this chapter The time required for the proposed NS-AS synchronization algorithm to reach system convergence is 9.5836 s, which greatly improves the convergence speed of the system compared with the traditional synchronization algorithm.

4.1.2. System Parameters

The above simulation results indicate that the NS-AS algorithm can achieve faster synchronization convergence compared with other synchronization algorithms. In this section, we simulate the relevant parameters affecting system synchronization performance, such as the number of communication sectors, synchronization factor, number of UAVs, and communication radius.

(a)

The Number of Communication Sectors

The simulated synchronization convergence performance with different communication sectors is shown in Figure 4. With one communication sector, the system synchronously selects one UAV from the neighbors for evolution, resulting in the divergence of the system. An increased number of communication sectors improves the convergence performance of the system while increasing the amount of calculations. Therefore, the selected number of communication sectors should reduce the amount of calculations as much as possible while ensuring good convergence performance.

In order to further verify the relationship between the number of communication sectors and the system convergence performance, a comparative experiment is performed, trying to find the appropriate number of sectors to enable the system to converge quickly. The number of communication sectors is set from 1 to 8. The convergence and running times of the systems are shown in

Table 2. The convergence performance comparison under different communication sectors.

Number of Communication Sectors	Whether to Converge	Running Time (s)
$m=1$	No	25.4000
$m=2$	No	33.3513
$m=3$	Yes	12.2104
$m=4$	Yes	8.5606
$m=5$	Yes	6.5740
$m=6$	Yes	6.4967
$m=7$	Yes	5.7435
$m=8$	No	46.9694

.

It can be seen from the simulation results, that when the number of sectors is too small or too large, the system will not converge. When the number of sectors ranges from 3 to 7, the convergence speed of the system will gradually become faster. Therefore, in order to ensure the convergence speed of the system, the number of sectors can be set to between 4 and 7.

(b)

The Synchronization Factor

The synchronization factor is used to adjust the step value of the state between two UAVs. As shown in Figure 5, the synchronization factor is positively correlated with the system synchronization convergence speed. If the synchronization factor is too small, the system will diverge to multiple local centers, and the synchronization will fail.

In order to further verify the relationship between synchronization factor and system convergence performance, a comparative experiment is performed. The value range of the optimal adjustment factor can be determined by the results of the comparative experiment, as shown in

Table 3. The convergence performance comparison under different communication sectors.

Synchronization Factor	Whether to Converge	Running Time (s)
$\alpha$ = 0.01	Yes	25.4000
$\alpha$ = 0.05	Yes	33.3513
$\alpha$ = 0.1	Yes	12.2104
$\alpha$ = 0.15	Yes	8.5606
$\alpha$ = 0.2	Yes	6.5740
$\alpha$ = 0.25	Yes	6.4967
$\alpha$ = 0.26	No	5.7435

.

It can be seen from the simulation results that when the value range of the synchronization factor is 0.01–0.25, the overall convergence speed of the system gradually becomes faster. When the synchronization factor is 0.26, the system begins to diverge. The value range of the synchronization factor can be roughly determined from the simulation results.

(c)

The Number of UAVs

In order to verify the relationship between the number of communication sectors and the system convergence performance, a comparative experiment is performed, the number of UAVs is set to 50–120. The convergence and running time of the system are shown in Figure 6 and

Table 4. The convergence performance comparison under different communication sectors.

Number of UAVs	Whether to Converge	Running Time (s)
$N=50$	No	20.1960
$N=60$	No	30.3420
$N=70$	No	34.4473
$N=80$	No	42.4709
$N=90$	No	53.1091
$N=100$	Yes	8.4407
$N=110$	Yes	9.0300
$N=120$	Yes	10.2648

.

It can be seen from the simulation results that when the number of UAVs is less than 100, the system cannot converge. The amount of computational complexity gradually increases, and the computational time shows an upward trend. When the number of unmanned vehicles is greater than 100, the system can achieve convergence, but too many unmanned aerial vehicles will also increase the amount of calculations. In actual scenarios, the appropriate number of unmanned aerial vehicles should be set according to the task requirements.

(d)

The Communication Radius

In order to verify the relationship between the communication radius and the system convergence performance, a comparative experiment is performed. The communication radius is set to 0.5∼1.1. The convergence and running time of the system are shown in Figure 7 and

Table 5. The convergence performance comparison under different communication radius.

Number of UAVs	Whether to Converge	Running Time (s)
Rc = 0.5	No	44.0695
Rc = 0.6	No	47.6577
Rc = 0.7	No	48.8751
Rc = 0.8	No	55.8752
Rc = 0.9	Yes	11.7280
Rc = 1.0	Yes	12.0460
Rc = 1.1	Yes	12.1298

.

It can be seen from the simulation results that when the communication radius is less than 0.8, the system cannot achieve convergence. When the communication radius is 0.9∼1.1, the system can achieve convergence. The increase in the communication radius will increase the amount of calculations, so the time required for convergence shows an increasing trend.

4.2. Localization Performance

The simulation scenario of moving source localization based on UAV swarms is shown in Figure 8. The actual target is placed at (2130, 2460) m. A total of 20 UAVs are randomly distributed in an area of 5000 × 4500 m. The number of Monte Carlo cycles is set to 1000. In the experimental scene, we use the Cramereau lower bound (CRLB) and the root mean square error (RMSE) as the standards to measure the localization performance with different parameters.

The position estimation RMSE and velocity estimation RMSE under different synchronization errors are presented in Figure 9 and Figure 10. Both position RMSE and velocity RMSE are very close to the CRLB as the synchronization error increases.

The localization performance with different numbers of UAVs is shown in Figure 11 and Figure 12. The RMSEs of target orientation and velocity estimations gradually decrease with the number of UAVs.

5. Conclusions

To solve the synchronization problem in the passive localization of UAV swarms, an NS synchronization mechanism-based source localization method for UAV swarms was proposed in this paper. Firstly, the synchronization of the UAV swarm network was achieved using the NS-AS mechanism. The current UAV state was updated by selecting the most representative individual from each sector. Once the UAV swarm network was fully connected, the system switched to the AS algorithm to enhance the convergence speed. Then, the TDOA-FDOA joint localization algorithm was utilized to locate the moving radiation source. Finally, the convergence performance of the system was analyzed through simulations. The proposed synchronization algorithm was compared with other algorithms. The localization performance was simulated with different synchronization errors and numbers of UAVs to verify the effectiveness of the proposed method.