Comparison of Different Remotely Sensed Data Sources for Detection of Presence of Standing Dead Trees Using a Tree-Based Approach
Abstract
1. Introduction
- comparing the performance of ALS and optical data to identify trees;
- comparing the performance of aerial and satellite images with different spatial and spectral resolution to determine tree status, i.e., dead or living.
2. Materials and Methods
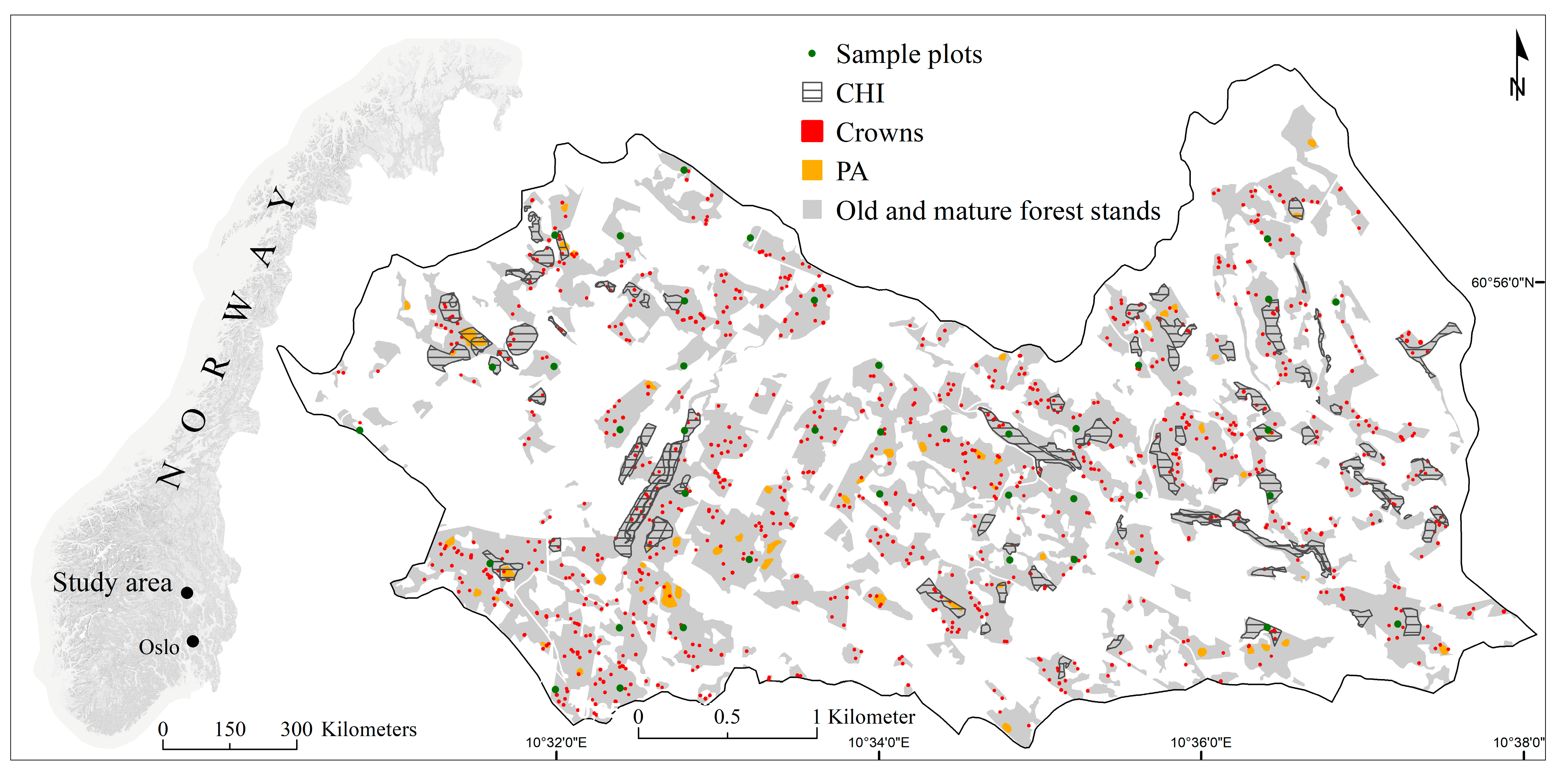
2.1. Study Area
2.2. Reference and Validation Data
2.2.1. Sample Plot Data
2.2.2. Crown Dataset
2.2.3. Complementary Hotspot Inventory Dataset
2.2.4. Presence/Absence Dataset
2.3. Remotely Sensed Data
2.4. Methodology
2.4.1. Overview
2.4.2. Tree Identification
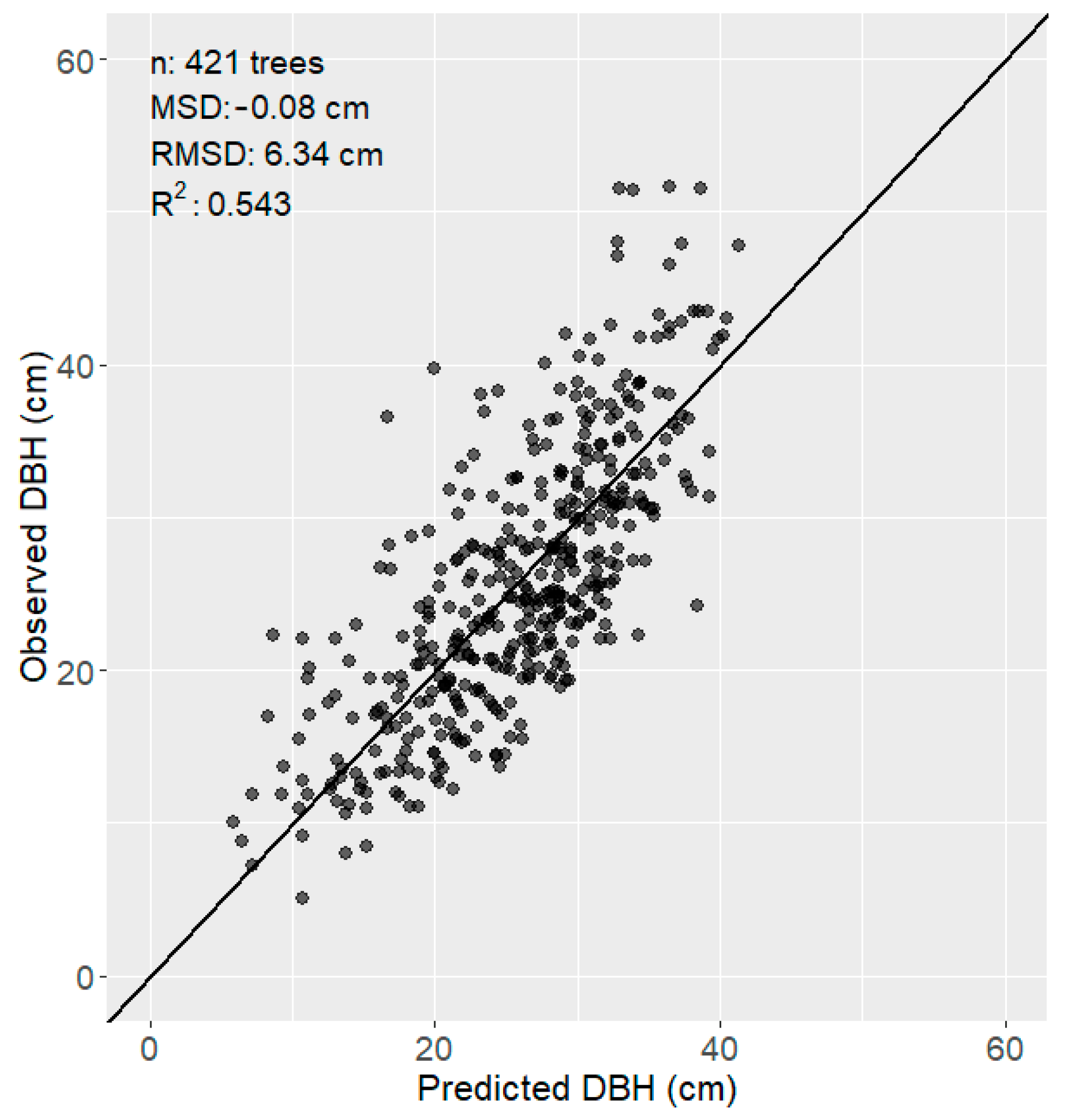
2.4.3. DBH-Height Model
2.4.4. Status Identification
2.4.5. Validation
3. Results
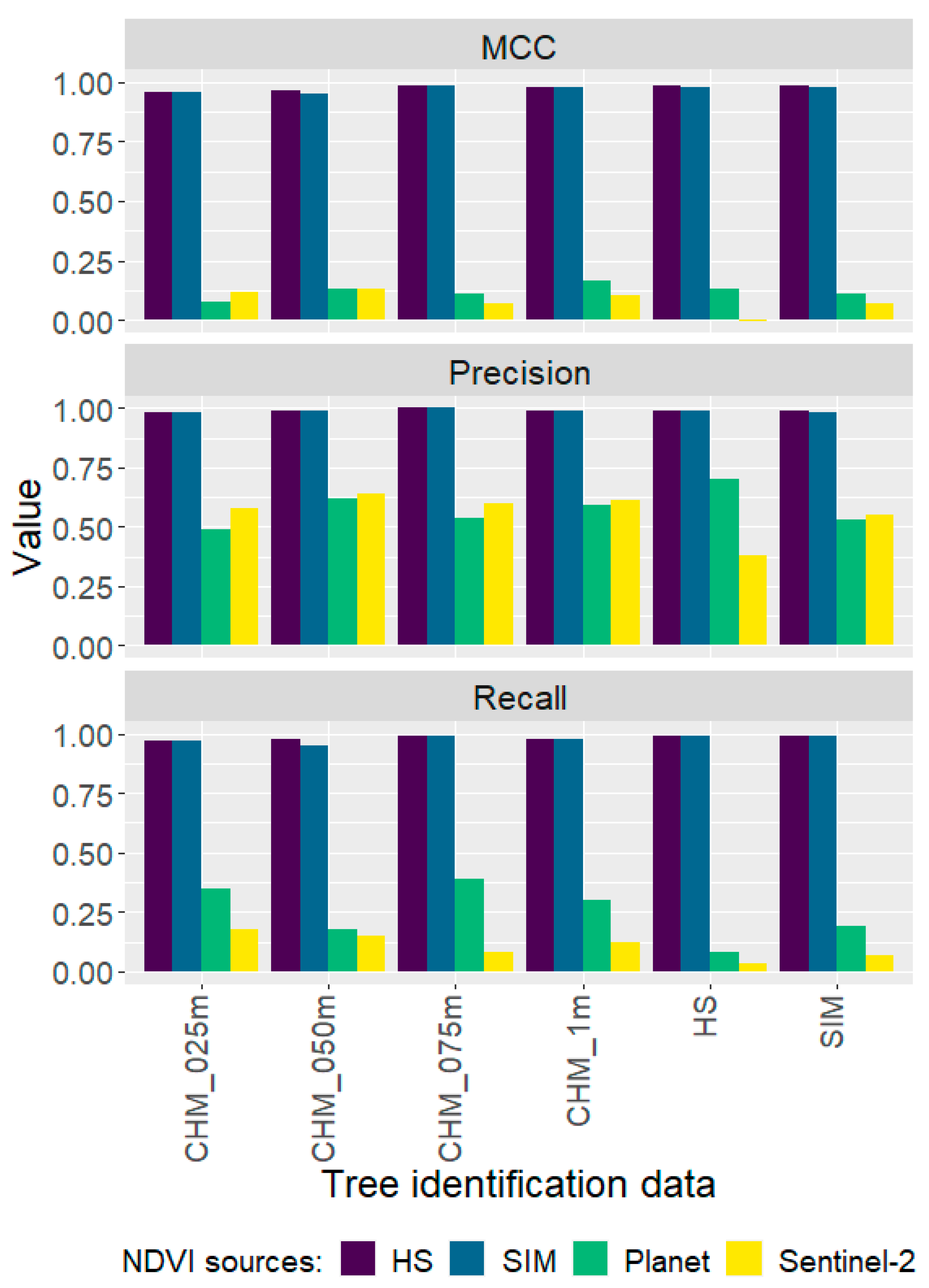
3.1. Tree Identification
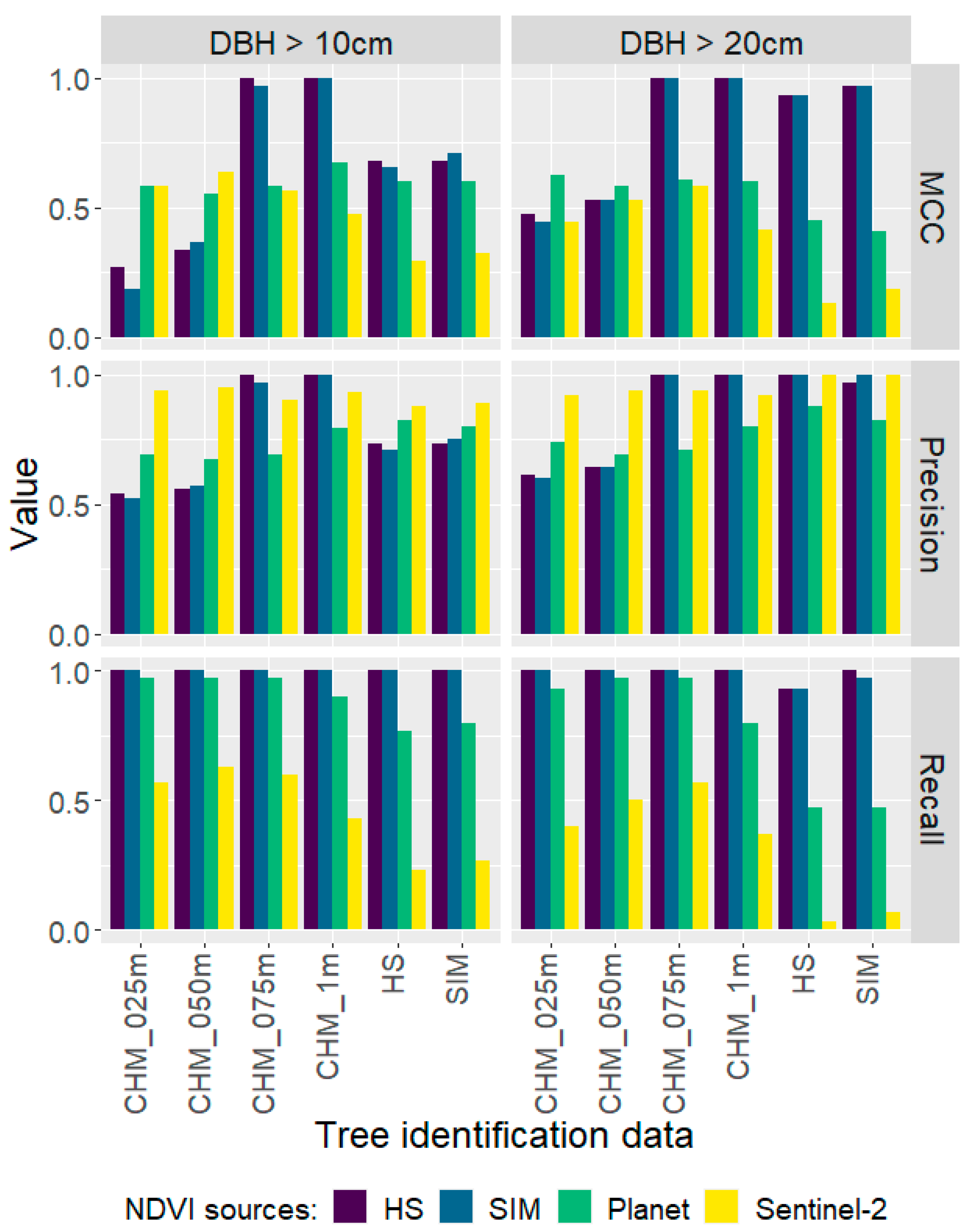
3.2. Status Identification
3.3. Validation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Costanza, R.; de Groot, R.; Braat, L.; Kubiszewski, I.; Fioramonti, L.; Sutton, P.; Farber, S.; Grasso, M. Twenty years of ecosystem services: How far have we come and how far do we still need to go? Ecosyst. Serv. 2017, 28, 1–16. [Google Scholar] [CrossRef]
- IPBES. Summary for Policymakers of the Global Assessment Report on Biodiversity and Ecosystem Services of the Intergovernmental Science-Policy Platform on Biodiversity and Ecosystem Services; Díaz, S., Settele, J., Brondizio, E.S., Eds.; IPBES Secretariat: Bonn, Germany, 2019; p. 56. [Google Scholar] [CrossRef]
- Lonsdale, D.; Pautasso, M.; Holdenrieder, O. Wood-decaying fungi in the forest: Conservation needs and management options. Eur. J. For. Res. 2008, 127, 1–22. [Google Scholar] [CrossRef]
- Siitonen, J. Forest Management, Coarse Woody Debris and Saproxylic Organisms: Fennoscandian Boreal Forests as an Example. Ecol. Bull. 2001, 49, 11–41. [Google Scholar]
- Bradshaw, C.J.A.; Warkentin, I.G.; Sodhi, N.S. Urgent preservation of boreal carbon stocks and biodiversity. Trends Ecol. Evol. 2009, 24, 541–548. [Google Scholar] [CrossRef]
- Stokland, J.N.; Tomter, S.M.; Söderberg, U. Development of dead wood indicators for biodiversity monitoring: Experiences from Scandinavia. Monit. Indic. For. Biodivers. Eur.—Ideas Oper. 2004, 51, 207–226. [Google Scholar]
- Harmon, M.E.; Franklin, J.F.; Swanson, F.J.; Sollins, P.; Gregory, S.V.; Lattin, J.D.; Anderson, N.H.; Cline, S.P.; Aumen, N.G.; Sedell, J.R.; et al. Ecology of Coarse Woody Debris in Temperate Ecosystems. Adv. Ecol. Res. 1986, 15, 133–302. [Google Scholar]
- Stokland, J.N.; Siitonen, J.; Jonsson, B.G. Biodiversity in Dead Wood; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Esseen, P.-A.; Ehnström, B.; Ericson, L.; Sjöberg, K. Boreal Forests. Ecol. Bull. 1997, 46, 16–47. [Google Scholar]
- Franklin, J.F.; Shugart, H.H.; Harmon, M.E. Tree Death as an Ecological Process. BioScience 1987, 37, 550–556. [Google Scholar] [CrossRef]
- Hansen, A.J.; Spies, T.A.; Swanson, F.J.; Ohmann, J.L. Conserving Biodiversity in Managed Forests. BioScience 1991, 41, 382–392. [Google Scholar] [CrossRef]
- Kuuluvainen, T. Natural variability of forests as a reference for restoring and managing biological diversity in boreal Fennoscandia. Silva Fenn. 2002, 36, 97–125. [Google Scholar] [CrossRef]
- Gjerde, I.; Sætersdal, M.; Blom, H.H. Complementary Hotspot Inventory—A method for identification of important areas for biodiversity at the forest stand level. Biol. Conserv. 2007, 137, 549–557. [Google Scholar] [CrossRef]
- Timonen, J.; Siitonen, J.; Gustafsson, L.; Kotiaho, J.S.; Stokland, J.N.; Sverdrup-Thygeson, A.; Mönkkönen, M. Woodland key habitats in northern Europe: Concepts, inventory and protection. Scand. J. For. Res. 2010, 25, 309–324. [Google Scholar] [CrossRef]
- Lindenmayer, D.B.; Franklin, J.F. Conserving Forest Biodiversity: A Comprehensive Multiscaled Approach; Island Press: Washington, DC, USA, 2002. [Google Scholar]
- Gjerde, I.; Sætersdal, M.; Rolstad, J.; Blom, H.H.; Storaunet, K.O. Fine-scale diversity and rarity hotspots in northern forests. Conserv. Biol. 2004, 18, 1032–1042. [Google Scholar] [CrossRef]
- Hansson, L. Key Habitats in Swedish Managed Forests. Scand. J. For. Res. 2001, 16, 52–61. [Google Scholar] [CrossRef]
- Baumann, C.; Gjerde, I.; Blom, H.H.; Sætersdal, M.; Nilsen, J.-E.; Løken, B.; Ekanger, I. Environmental Inventories in Forests—Biodiversity. Part 1: Background and Principles; Skogforsk and Norwegian Ministry of Agriculture: Uppsala, Sweden, 2002. [Google Scholar]
- PEFC Norway. Norwegian PEFC Forest Standard; PEFC Norway: Oslo, Norway, 2015; p. 31. [Google Scholar]
- Baumann, C.; Gjerde, I.; Blom, H.H.; Sætersdal, M.; Nilsen, J.-E.; Løken, B.; Ekanger, I. Environmental Inventories in Forests—Biodiversity. Part 2: Forest Habitats; Skogforsk and the Norwegian Ministry of Agriculture: Uppsala, Sweden, 2002. [Google Scholar]
- Haga, H.E.; Nilsen, A.B.; Ullerud, H.A.; Bryn, A. Quantification of accuracy in field-based land cover maps: A new method to separate different components. Appl. Veg. Sci. 2021, 24, e12578. [Google Scholar] [CrossRef]
- Eriksen, E.L.; Ullerud, H.A.; Halvorsen, R.; Aune, S.; Bratli, H.; Horvath, P.; Volden, I.K.; Wollan, A.K.; Bryn, A. Point of view: Error estimation in field assignment of land-cover types. Phytocoenologia 2018, 49, 135–148. [Google Scholar] [CrossRef]
- Ørka, H.O.; Jutras-Perreault, M.-C.; Candelas-Bielza, J.; Gobakken, T. Delineation of Geomorphological Woodland Key Habitats Using Airborne Laser Scanning. Remote Sens. 2022, 14, 1184. [Google Scholar] [CrossRef]
- Magnussen, S.; Boudewyn, P. Derivations of stand heights from airborne laser scanner data with canopy-based quantile estimators. Can. J. For. Res. 1998, 28, 1016–1031. [Google Scholar] [CrossRef]
- Maltamo, M.; Packalen, P. Species-specific management inventory in Finland. In Forestry Applications of Airborne Laser Scanning; Springer: Dordrecht, The Netherlands, 2014; pp. 241–252. [Google Scholar]
- Næsset, E. Accuracy of forest inventory using airborne laser scanning: Evaluating the first nordic full-scale operational project. Scand. J. For. Res. 2004, 19, 554–557. [Google Scholar] [CrossRef]
- Næsset, E. Practical large-scale forest stand inventory using a small-footprint airborne scanning laser. Scand. J. For. Res. 2004, 19, 164–179. [Google Scholar] [CrossRef]
- Næsset, E. Area-based inventory in Norway—From innovation to an operational reality. In Forestry Applications of Airborne Laser Scanning; Springer: Dordrecht, The Netherlands, 2014; pp. 215–240. [Google Scholar]
- Kim, Y.; Yang, Z.; Cohen, W.B.; Pflugmacher, D.; Lauver, C.L.; Vankat, J.L. Distinguishing between live and dead standing tree biomass on the North Rim of Grand Canyon National Park, USA using small-footprint lidar data. Remote Sens. Environ. 2009, 113, 2499–2510. [Google Scholar] [CrossRef]
- Martinuzzi, S.; Vierling, L.A.; Gould, W.A.; Falkowski, M.J.; Evans, J.S.; Hudak, A.T.; Vierling, K.T. Mapping snags and understory shrubs for a LiDAR-based assessment of wildlife habitat suitability. Remote Sens. Environ. 2009, 113, 2533–2546. [Google Scholar] [CrossRef]
- Pesonen, A.; Maltamo, M.; Eerikäinen, K.; Packalèn, P. Airborne laser scanning-based prediction of coarse woody debris volumes in a conservation area. For. Ecol. Manag. 2008, 255, 3288–3296. [Google Scholar] [CrossRef]
- Bekkar, M.; Djemaa, H.K.; Alitouche, T.A. Evaluation measures for models assessment over imbalanced data sets. J. Inf. Eng. Appl. 2013, 3, 27–38. [Google Scholar]
- Chicco, D.; Jurman, G. The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation. BMC Genom. 2020, 21, 6. [Google Scholar] [CrossRef]
- Jutras-Perreault, M.-C.; Næsset, E.; Gobakken, T.; Ørka, H.O. Detecting the presence of standing dead trees using airborne laser scanning and optical data. under revision.
- Li, W.; Guo, Q.; Jakubowski, M.K.; Kelly, M. A new method for segmenting individual trees from the lidar point cloud. Photogramm. Eng. Remote Sens. 2012, 78, 75–84. [Google Scholar] [CrossRef]
- Rahman, M.Z.A.; Gorte, B.; Bucksch, A.K. A new method for individual tree measurement from airborne LiDAR. In Proceedings of the Silvilaser, College Station, TX, USA, 14–16 October 2009; pp. 14–16. [Google Scholar]
- Solberg, S.; Naesset, E.; Bollandsas, O.M. Single tree segmentation using airborne laser scanner data in a structurally heterogeneous spruce forest. Photogramm. Eng. Remote Sens. 2006, 72, 1369–1378. [Google Scholar] [CrossRef]
- Popescu, S.C.; Wynne, R.H. Seeing the Trees in the Forest: Using Lidar and Multispectral Data Fusion with Local Filtering and Variable Window Size for Estimating Tree Height. Photogramm. Eng. Remote Sens. 2004, 70, 589–604. [Google Scholar] [CrossRef]
- Ene, L.; Næsset, E.; Gobakken, T. Single tree detection in heterogeneous boreal forests using airborne laser scanning and area-based stem number estimates. Int. J. Remote Sens. 2012, 33, 5171–5193. [Google Scholar] [CrossRef]
- Wang, L.; Gong, P.; Biging, G.S. Individual tree-crown delineation and treetop detection in high-spatial-resolution aerial imagery. Photogramm. Eng. Remote Sens. 2004, 70, 351–357. [Google Scholar] [CrossRef]
- Korpela, I.; Anttila, P.; Pitkänen, J. The performance of a local maxima method for detecting individual tree tops in aerial photographs. Int. J. Remote Sens. 2006, 27, 1159–1175. [Google Scholar] [CrossRef]
- Wulder, M.; Niemann, K.O.; Goodenough, D.G. Local maximum filtering for the extraction of tree locations and basal area from high spatial resolution imagery. Remote Sens. Environ. 2000, 73, 103–114. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Cohen, W.B.; Acker, S.A.; Parker, G.G.; Spies, T.A.; Harding, D. Lidar Remote Sensing of the Canopy Structure and Biophysical Properties of Douglas-Fir Western Hemlock Forests. Remote Sens. Environ. 1999, 70, 339–361. [Google Scholar] [CrossRef]
- Wing, B.M.; Ritchie, M.W.; Boston, K.; Cohen, W.B.; Olsen, M.J. Individual snag detection using neighborhood attribute filtered airborne lidar data. Remote Sens. Environ. 2015, 163, 165–179. [Google Scholar] [CrossRef]
- Bütler, R.; Schlaepfer, R. Spruce snag quantification by coupling colour infrared aerial photos and a GIS. For. Ecol. Manag. 2004, 195, 325–339. [Google Scholar] [CrossRef]
- Pasher, J.; King, D.J. Mapping dead wood distribution in a temperate hardwood forest using high resolution airborne imagery. For. Ecol. Manag. 2009, 258, 1536–1548. [Google Scholar] [CrossRef]
- Haara, A.; Nevalainen, S. Detection of dead or defoliated spruces using digital aerial data. For. Ecol. Manag. 2002, 160, 97–107. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; Latifi, H.; Ghosh, A.; Joshi, P.K.; Koch, B. Assessing the potential of hyperspectral imagery to map bark beetle-induced tree mortality. Remote Sens. Environ. 2014, 140, 533–548. [Google Scholar] [CrossRef]
- Lausch, A.; Heurich, M.; Gordalla, D.; Dobner, H.-J.; Gwillym-Margianto, S.; Salbach, C. Forecasting potential bark beetle outbreaks based on spruce forest vitality using hyperspectral remote-sensing techniques at different scales. For. Ecol. Manag. 2013, 308, 76–89. [Google Scholar] [CrossRef]
- Zielewska-Büttner, K.; Adler, P.; Kolbe, S.; Beck, R.; Ganter, L.M.; Koch, B.; Braunisch, V. Detection of Standing Deadwood from Aerial Imagery Products: Two Methods for Addressing the Bare Ground Misclassification Issue. Forests 2020, 11, 801. [Google Scholar] [CrossRef]
- Maltamo, M.; Kallio, E.; Bollandsås, O.M.; Næsset, E.; Gobakken, T.; Pesonen, A. Assessing Dead Wood by Airborne Laser Scanning. In Forestry Applications of Airborne Laser Scanning; Springer: Dordrecht, The Netherlands, 2014; pp. 375–395. [Google Scholar]
- Landbruksdirektoratet. Veileder for Kartlegging av MiS-Livsmiljøer Etter NiN (Guide for Mapping MiS Habitats According to NiN); Landbruksdirektoratet: Oslo, Norway, 2017; p. 26. [Google Scholar]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Shepard, D. A two-dimensional interpolation function for irregularly-spaced data. In Proceedings of the 1968 23rd ACM National Conference, New York, NY, USA, 27–29 August 1968; pp. 517–524. [Google Scholar] [CrossRef]
- Baldi, P.; Brunak, S.; Chauvin, Y.; Andersen, C.A.; Nielsen, H. Assessing the accuracy of prediction algorithms for classification: An overview. Bioinformatics 2000, 16, 412–424. [Google Scholar] [CrossRef] [PubMed]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?–Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Lindberg, E.; Hollaus, M. Comparison of methods for estimation of stem volume, stem number and basal area from airborne laser scanning data in a hemi-boreal forest. Remote Sens. 2012, 4, 1004–1023. [Google Scholar] [CrossRef]
- Heinzel, J.N.; Weinacker, H.; Koch, B. Prior-knowledge-based single-tree extraction. Int. J. Remote Sens. 2011, 32, 4999–5020. [Google Scholar] [CrossRef]
- Dalponte, M.; Ørka, H.O.; Ene, L.T.; Gobakken, T.; Næsset, E. Tree crown delineation and tree species classification in boreal forests using hyperspectral and ALS data. Remote Sens. Environ. 2014, 140, 306–317. [Google Scholar] [CrossRef]
- Dalponte, M.; Reyes, F.; Kandare, K.; Gianelle, D. Delineation of individual tree crowns from ALS and hyperspectral data: A comparison among four methods. Eur. J. Remote Sens. 2015, 48, 365–382. [Google Scholar] [CrossRef]
- Clark, M.L.; Roberts, D.A.; Clark, D.B. Hyperspectral discrimination of tropical rain forest tree species at leaf to crown scales. Remote Sens. Environ. 2005, 96, 375–398. [Google Scholar] [CrossRef]
- Bi, H.; Fox, J.C.; Li, Y.; Lei, Y.; Pang, Y. Evaluation of nonlinear equations for predicting diameter from tree height. Can. J. For. Res. 2012, 42, 789–806. [Google Scholar] [CrossRef]
- Ryu, J.-H.; Na, S.-I.; Cho, J. Inter-Comparison of normalized difference vegetation index measured from different footprint sizes in cropland. Remote Sens. 2020, 12, 2980. [Google Scholar] [CrossRef]
- Van Leeuwen, W.J.; Orr, B.J.; Marsh, S.E.; Herrmann, S.M. Multi-sensor NDVI data continuity: Uncertainties and implications for vegetation monitoring applications. Remote Sens. Environ. 2006, 100, 67–81. [Google Scholar] [CrossRef]
- Norwegian Mapping Authority. The N50 Topographic Map Series of Norway. Scale 1:50,000; Updated in 2007; Norwegian Mapping Authority: Hønefoss, Norway, 2017. [Google Scholar]
- Huang, C.; Davis, L.; Townshend, J. An assessment of support vector machines for land cover classification. Int. J. Remote Sens. 2002, 23, 725–749. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Khosravipour, A.; Skidmore, A.K.; Wang, T.; Isenburg, M.; Khoshelham, K. Effect of slope on treetop detection using a LiDAR Canopy Height Model. ISPRS J. Photogramm. Remote Sens. 2015, 104, 44–52. [Google Scholar] [CrossRef]



| n | Range (m2) | Mean (m2) | SD | |
|---|---|---|---|---|
| Crowns | ||||
| Living | 500 | [0.8–66.4] | 8.0 | 5.3 |
| Dead | 500 | [0.3–18.6] | 3.4 | 2.7 |
| CHI | ||||
| Density of SDT | 43 | [750–36380] | 8893 | 7904 |
| PA * | ||||
| Living | 30 | [304–2187] | 1022 | 454 |
| Dead | 30 | [43–6645] | 1424 | 1534 |
| Optical Data | Spatial Resolution (m) | Spectral Resolution Red Band (nm) | Spectral Resolution NIR Band (nm) |
|---|---|---|---|
| HS | 0.3 | 660–667 | 830–836 |
| Sim | 0.3 | 600–680 | 680–850 |
| Planet | 3 | 590–670 | 780–860 |
| Sentinel-2 | 10 | 650–680 | 785–899 |
| Reference | ||||||||
|---|---|---|---|---|---|---|---|---|
| ws | n | M | SD | MSD | SE | t | p | |
| Reference | 1016 | 25 | 9.5 | |||||
| CHM_025m | 5 | 1355 | 34 | 9.4 | 8.5 | 1.7 | 4.9 | <0.001 |
| 7 | 641 | 16 | 4.5 | −9.4 | 1.1 | −8.7 | <0.001 | |
| 9 | 492 | 12 | 3.4 | −13.1 | 1.1 | −12.2 | <0.001 | |
| CHM_050m | 3 | 1055 | 26 | 7.2 | 1.0 | 1.5 | 0.6 | 0.529 |
| 5 | 455 | 11 | 3.1 | −14.0 | 1.2 | −12.1 | <0.001 | |
| CHM_075m | 3 | 508 | 13 | 3.1 | −12.7 | 1.1 | −11.5 | <0.001 |
| CHM_1m | 3 | 381 | 10 | 2.2 | −15.9 | 1.3 | −12.3 | <0.001 |
| SIM | 5 | 1194 | 30 | 7.5 | 4.5 | 1.4 | 3.2 | 0.003 |
| 7 | 706 | 18 | 4.0 | −7.8 | 1.2 | −6.3 | <0.001 | |
| 9 | 539 | 13 | 3.7 | −11.9 | 1.2 | −9.7 | <0.001 |
| Living Crowns | Dead Crowns | |||||
|---|---|---|---|---|---|---|
| Omitted | Detected | Detected > 1 Tree | Omitted | Detected | Detected > 1 Tree | |
| CHM_025m | 1 | 351 | 148 | 17 | 389 | 94 |
| (0.00) | (0.70) | (0.30) | (0.03) | (0.78) | (0.19) | |
| CHM_050m | 2 | 393 | 105 | 30 | 402 | 68 |
| (0.00) | (0.79) | (0.21) | (0.06) | (0.80) | (0.14) | |
| CHM_075m | 8 | 477 | 15 | 70 | 416 | 14 |
| (0.02) | (0.95) | (0.03) | (0.14) | (0.83) | (0.03) | |
| CHM_1m | 22 | 474 | 4 | 123 | 374 | 3 |
| (0.04) | (0.95) | (0.01) | (0.25) | (0.75) | (0.01) | |
| HS | 13 | 271 | 216 | 78 | 303 | 119 |
| (0.03) | (0.54) | (0.43) | (0.16) | (0.61) | (0.24) | |
| SIM | 12 | 266 | 222 | 73 | 310 | 117 |
| (0.02) | (0.53) | (0.44) | (0.15) | (0.62) | (0.23) | |
| DBH > 10 cm | DBH > 20 cm | ||||||||
| RMSD | MSD | RMSD | MSD | ||||||
| Tree Datasets | NDVI | n ha−1 | % mean | n ha−1 | % mean | n ha−1 | % mean | n ha−1 | % mean |
| CHM_025m | HS | 289 | 520 | 231 | 416 | 169 | 304 | 111 | 200 |
| SIM | 305 | 548 | 250 | 449 | 181 | 326 | 124 | 224 | |
| Planet | 332 | 597 | 221 | 397 | 249 | 449 | 144 | 259 | |
| S2 | 101 | 181 | −1 | −2 | 70 | 126 | −33 | −59 | |
| CHM_050m | HS | 196 | 352 | 153 | 276 | 115 | 208 | 73 | 131 |
| SIM | 185 | 332 | 141 | 253 | 108 | 195 | 64 | 115 | |
| Planet | 275 | 495 | 183 | 329 | 223 | 402 | 132 | 237 | |
| S2 | 91 | 163 | 0 | 1 | 69 | 124 | −23 | −41 | |
| CHM_075m | HS | 48 | 87 | 17 | 31 | 35 | 63 | −4 | −8 |
| SIM | 49 | 89 | 20 | 37 | 34 | 62 | −2 | −4 | |
| Planet | 126 | 227 | 76 | 137 | 107 | 192 | 56 | 102 | |
| S2 | 62 | 112 | −16 | −29 | 55 | 99 | −29 | −51 | |
| CHM_1m | HS | 36 | 66 | −14 | −26 | 36 | 65 | −23 | −41 |
| SIM | 36 | 65 | −14 | −25 | 36 | 65 | −23 | −41 | |
| Planet | 61 | 109 | 7 | 13 | 58 | 104 | 3 | 5 | |
| S2 | 56 | 100 | −41 | −74 | 56 | 101 | −45 | −81 | |
| HS | HS | 113 | 203 | 68 | 122 | 49 | 88 | −7 | −13 |
| SIM | 116 | 208 | 72 | 130 | 49 | 89 | −6 | −11 | |
| Planet | 127 | 229 | 35 | 63 | 65 | 117 | −22 | −39 | |
| S2 | 89 | 160 | −35 | −63 | 64 | 116 | −48 | −86 | |
| SIM | HS | 104 | 187 | 64 | 115 | 47 | 85 | −9 | −16 |
| SIM | 107 | 192 | 68 | 122 | 47 | 85 | −8 | −15 | |
| Planet | 137 | 247 | 41 | 74 | 69 | 124 | −20 | −35 | |
| S2 | 87 | 157 | −32 | −58 | 64 | 116 | −47 | −85 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jutras-Perreault, M.-C.; Gobakken, T.; Næsset, E.; Ørka, H.O. Comparison of Different Remotely Sensed Data Sources for Detection of Presence of Standing Dead Trees Using a Tree-Based Approach. Remote Sens. 2023, 15, 2223. https://doi.org/10.3390/rs15092223
Jutras-Perreault M-C, Gobakken T, Næsset E, Ørka HO. Comparison of Different Remotely Sensed Data Sources for Detection of Presence of Standing Dead Trees Using a Tree-Based Approach. Remote Sensing. 2023; 15(9):2223. https://doi.org/10.3390/rs15092223
Chicago/Turabian StyleJutras-Perreault, Marie-Claude, Terje Gobakken, Erik Næsset, and Hans Ole Ørka. 2023. "Comparison of Different Remotely Sensed Data Sources for Detection of Presence of Standing Dead Trees Using a Tree-Based Approach" Remote Sensing 15, no. 9: 2223. https://doi.org/10.3390/rs15092223
APA StyleJutras-Perreault, M.-C., Gobakken, T., Næsset, E., & Ørka, H. O. (2023). Comparison of Different Remotely Sensed Data Sources for Detection of Presence of Standing Dead Trees Using a Tree-Based Approach. Remote Sensing, 15(9), 2223. https://doi.org/10.3390/rs15092223







