Reconstruction of Global Long-Term Gap-Free Daily Surface Soil Moisture from 2002 to 2020 Based on a Pixel-Wise Machine Learning Method
Abstract
1. Introduction
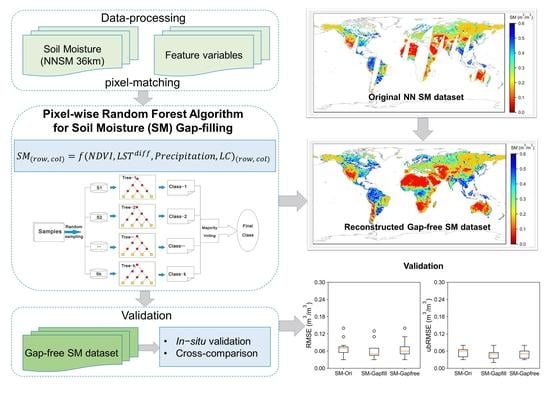
2. Methods
2.1. Gap-Filling Method Based on Random Forest Algorithm
2.1.1. Principle of Random Forest
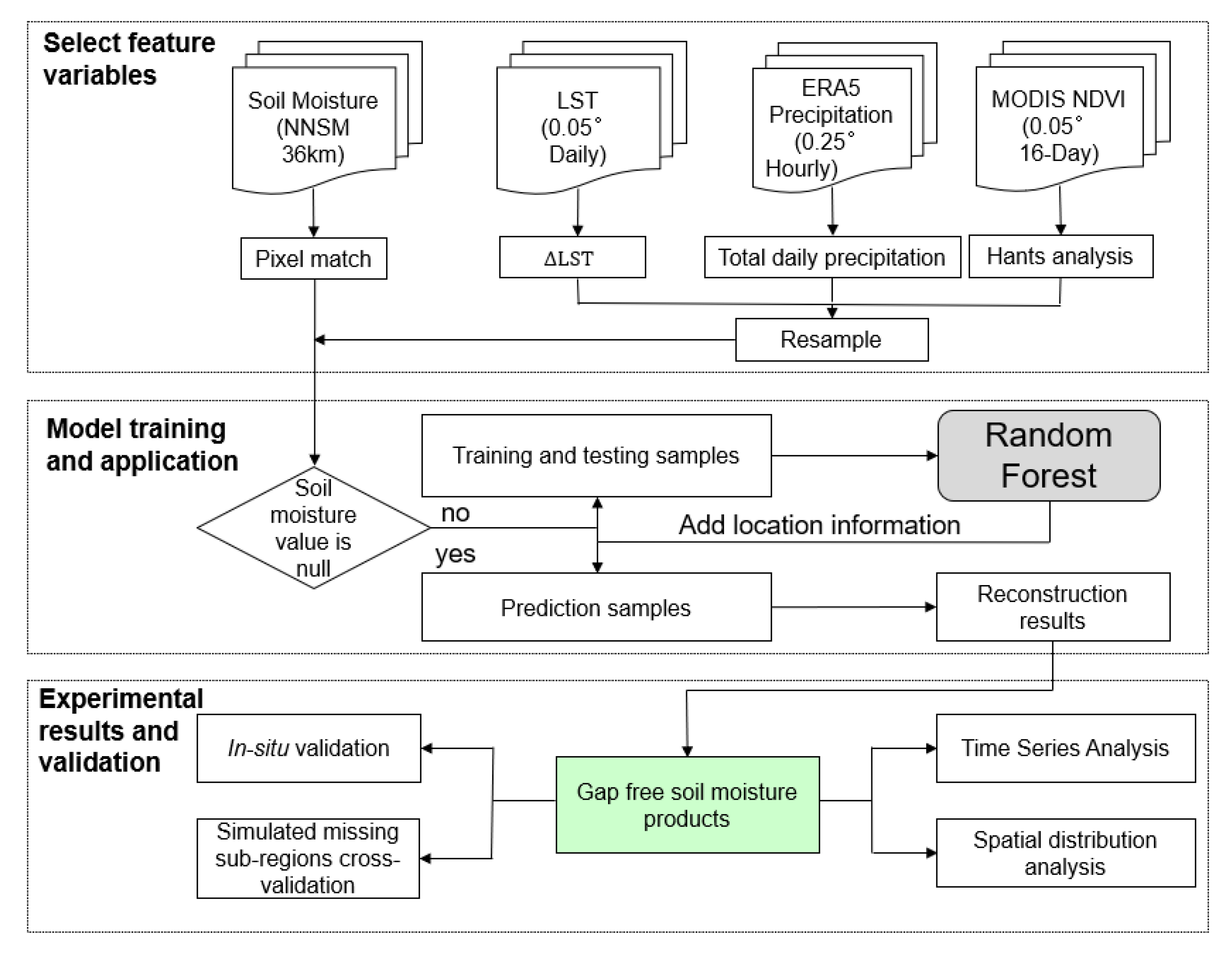
2.1.2. Selection of Feature Variables
2.1.3. RF Model Establishment for SM Gap-Filling
2.2. Evalution Metrics
3. Data
3.1. Surface Soil Moisture Product
3.2. Feature Variables Data
- (a)
- Normalized Difference Vegetation Index
- (b) Land surface temperature
- (c) ERA 5 Precipitation
- (d) Land Cover Type
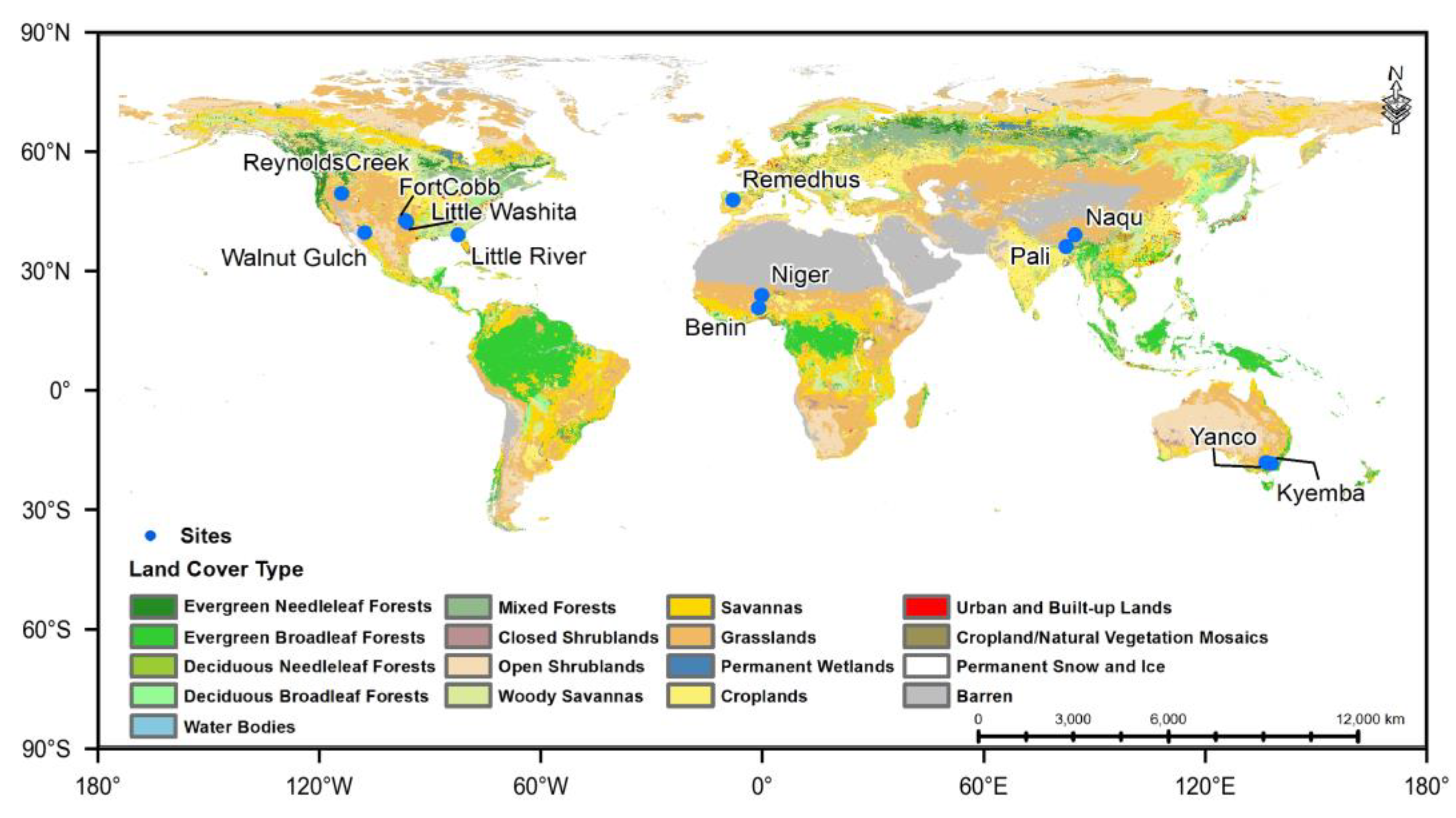
3.3. In Situ Observations Data
4. Results
4.1. RF Training Results
4.1.1. Importance of Feature Variables in RF Model Construction
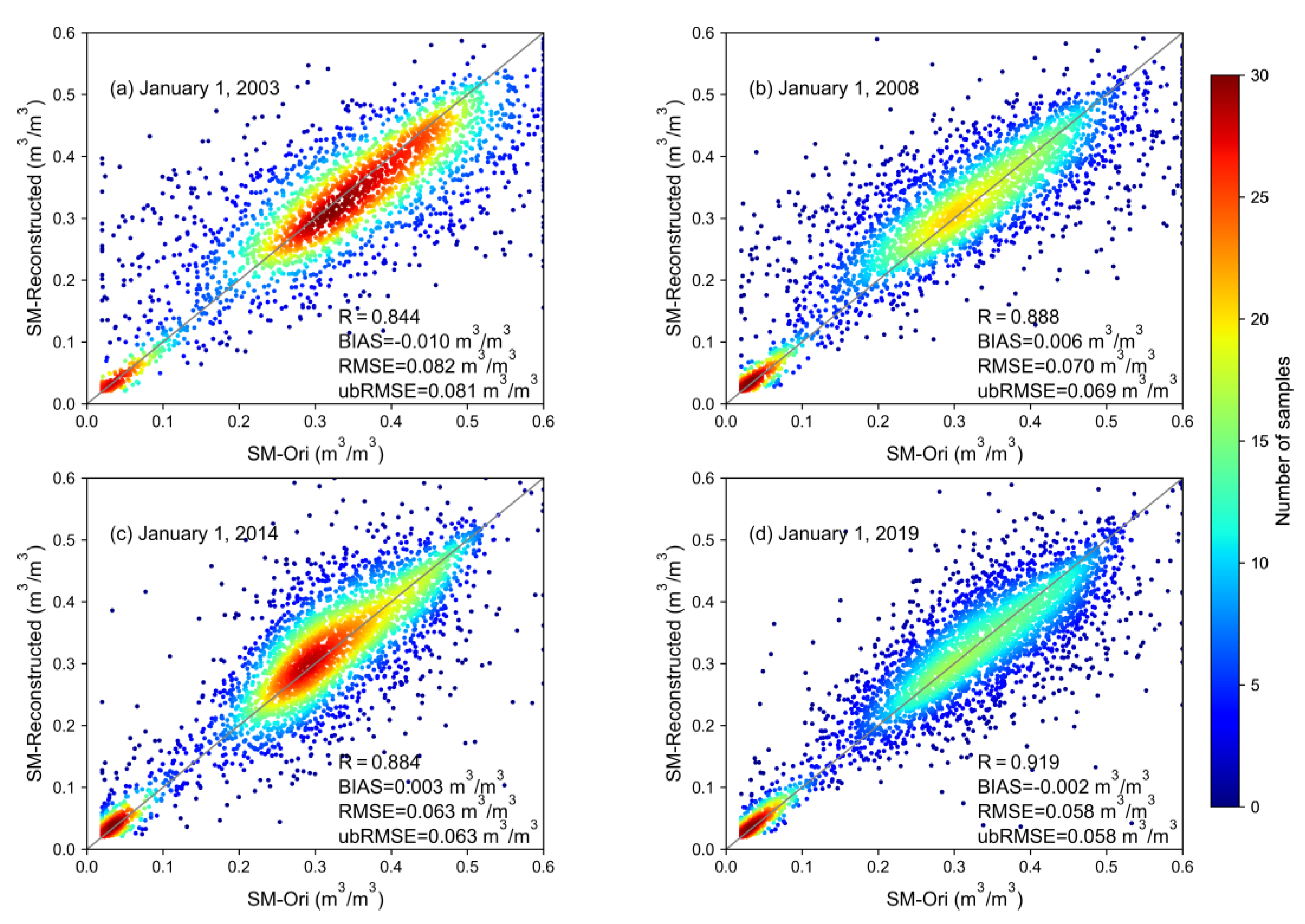
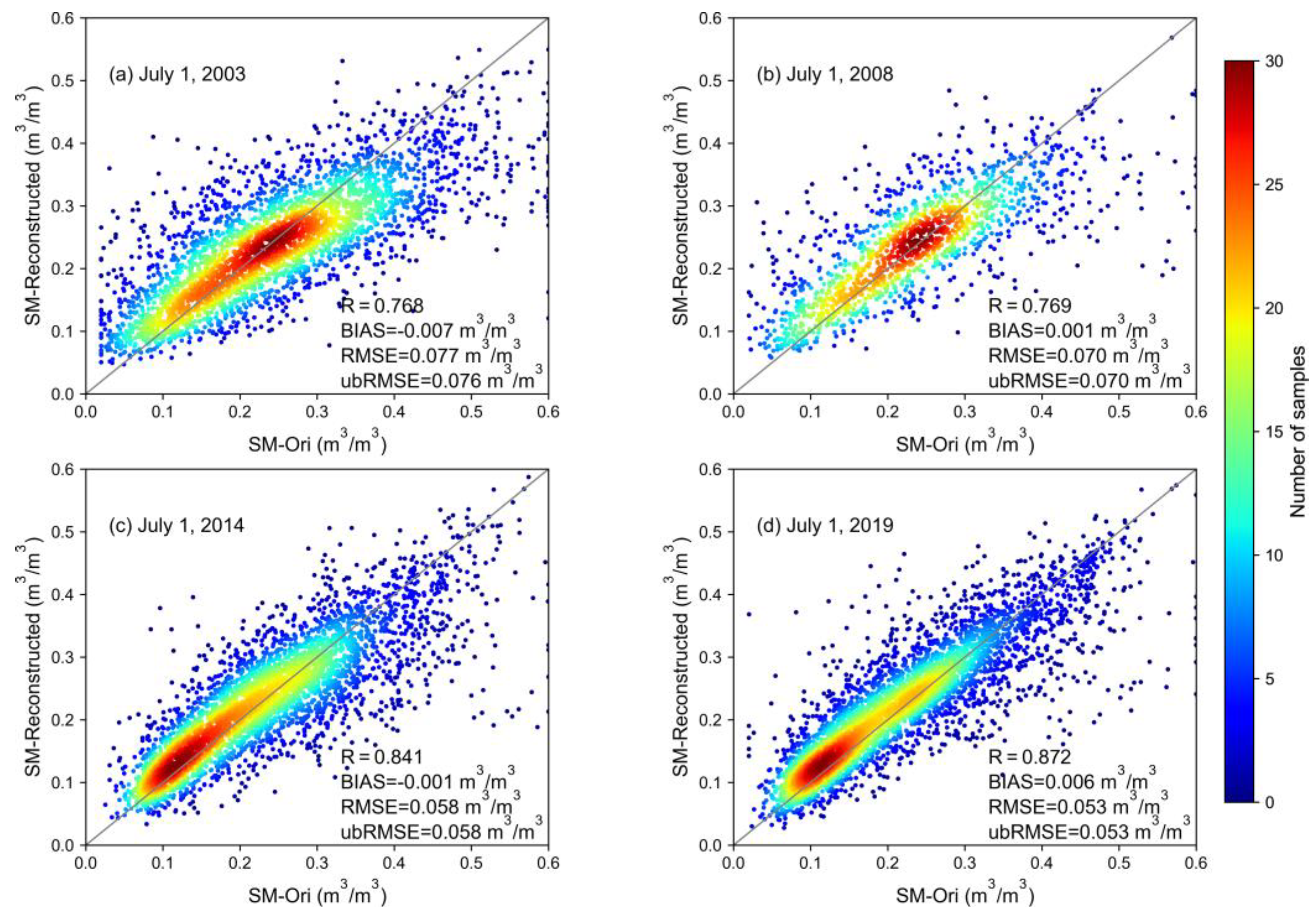
4.1.2. Evaluation of Model Performance
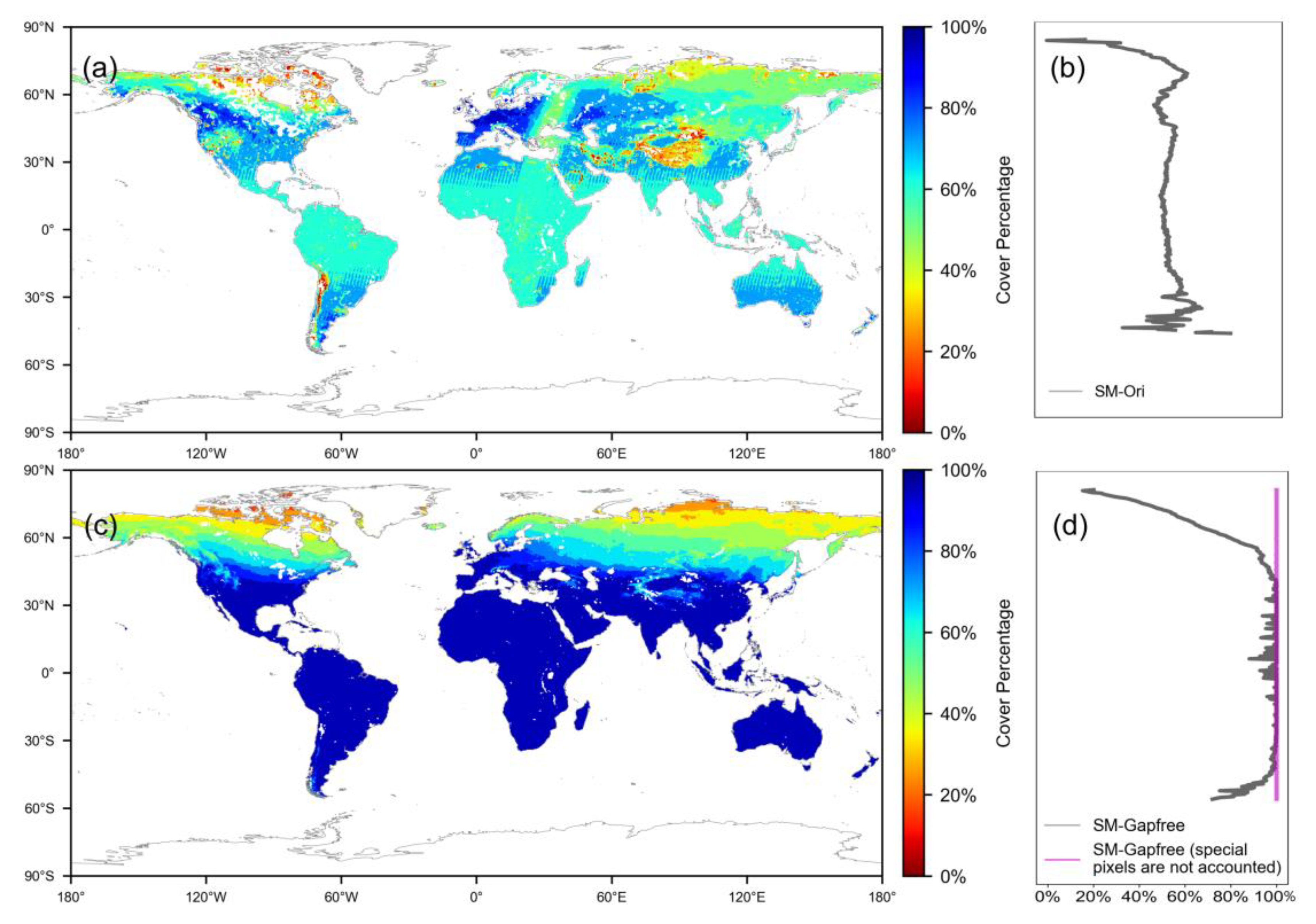
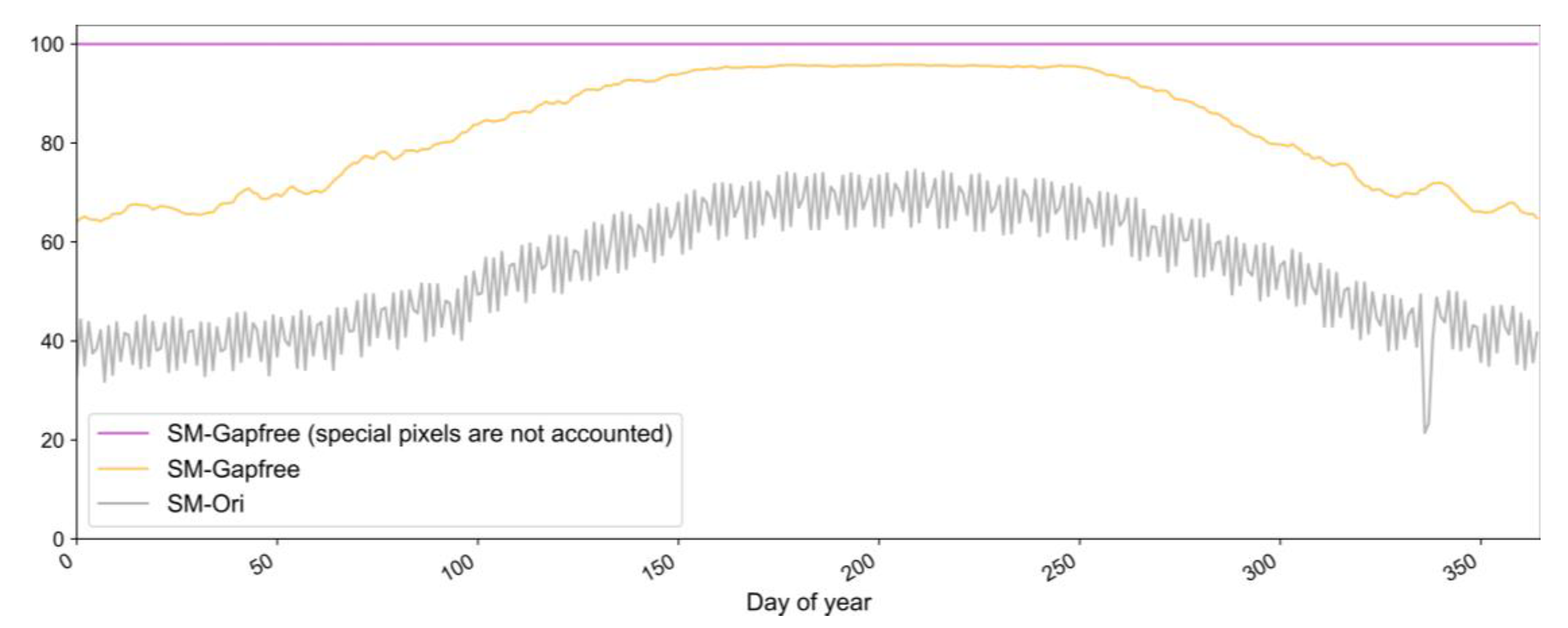
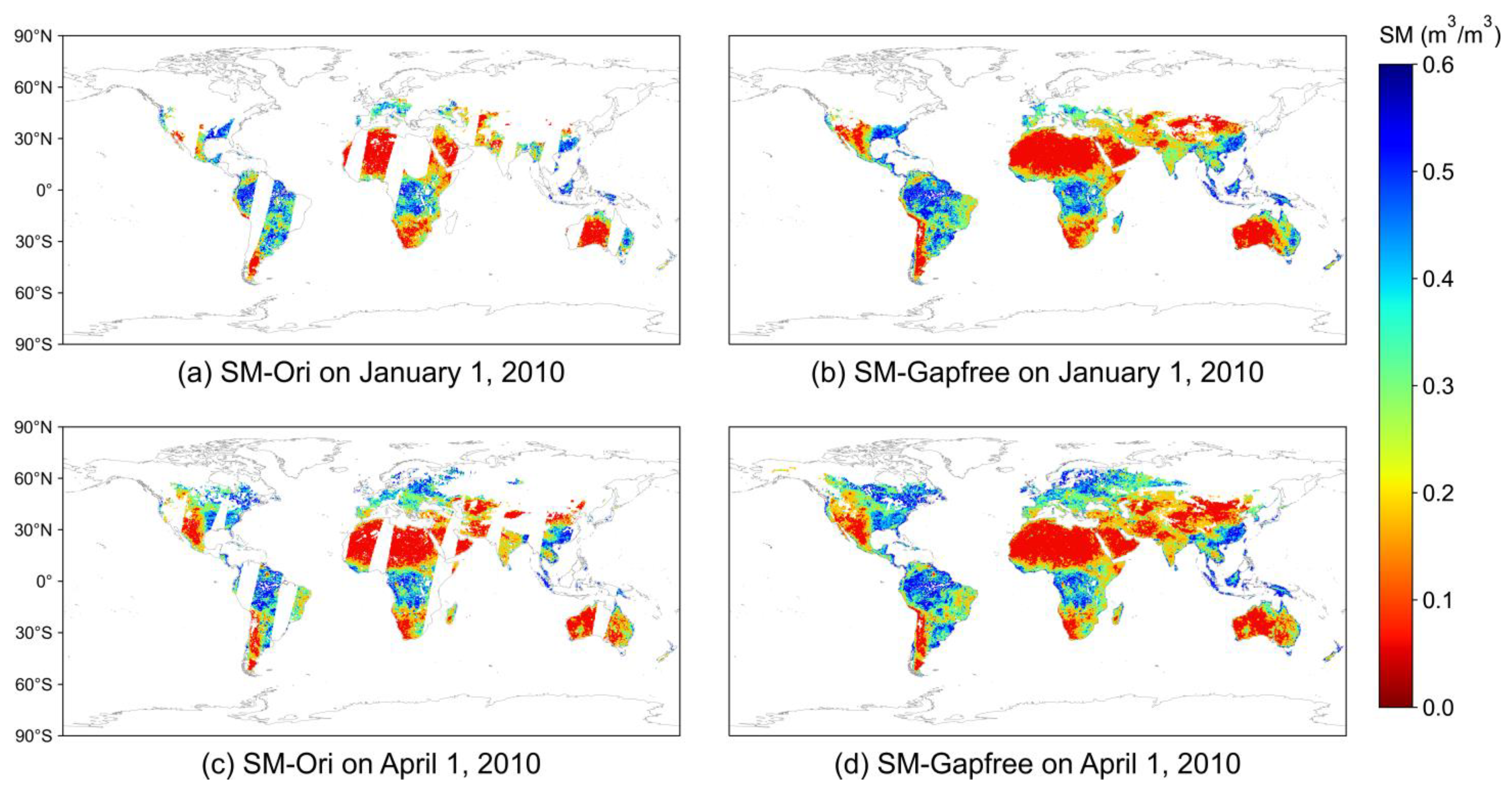
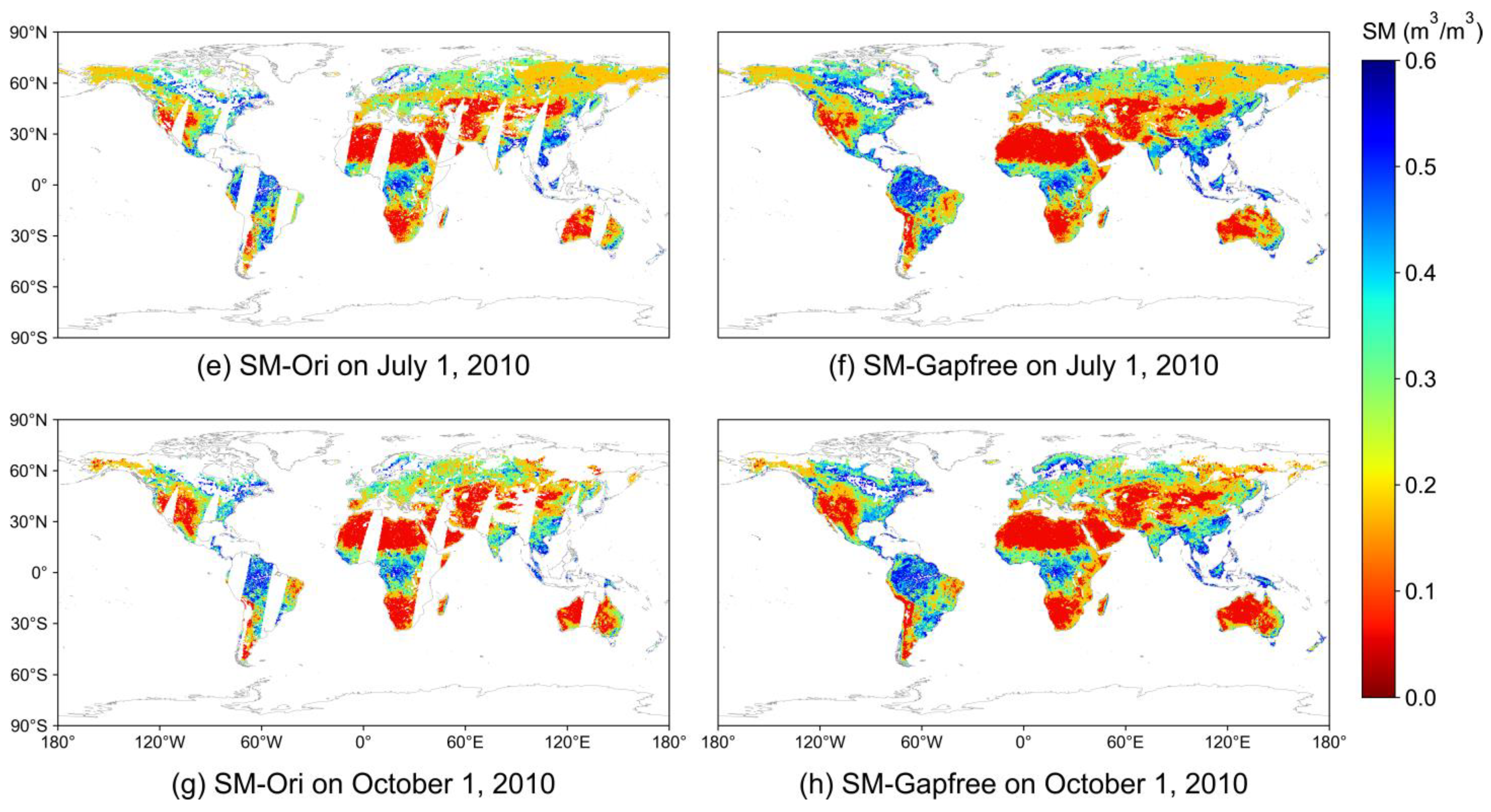
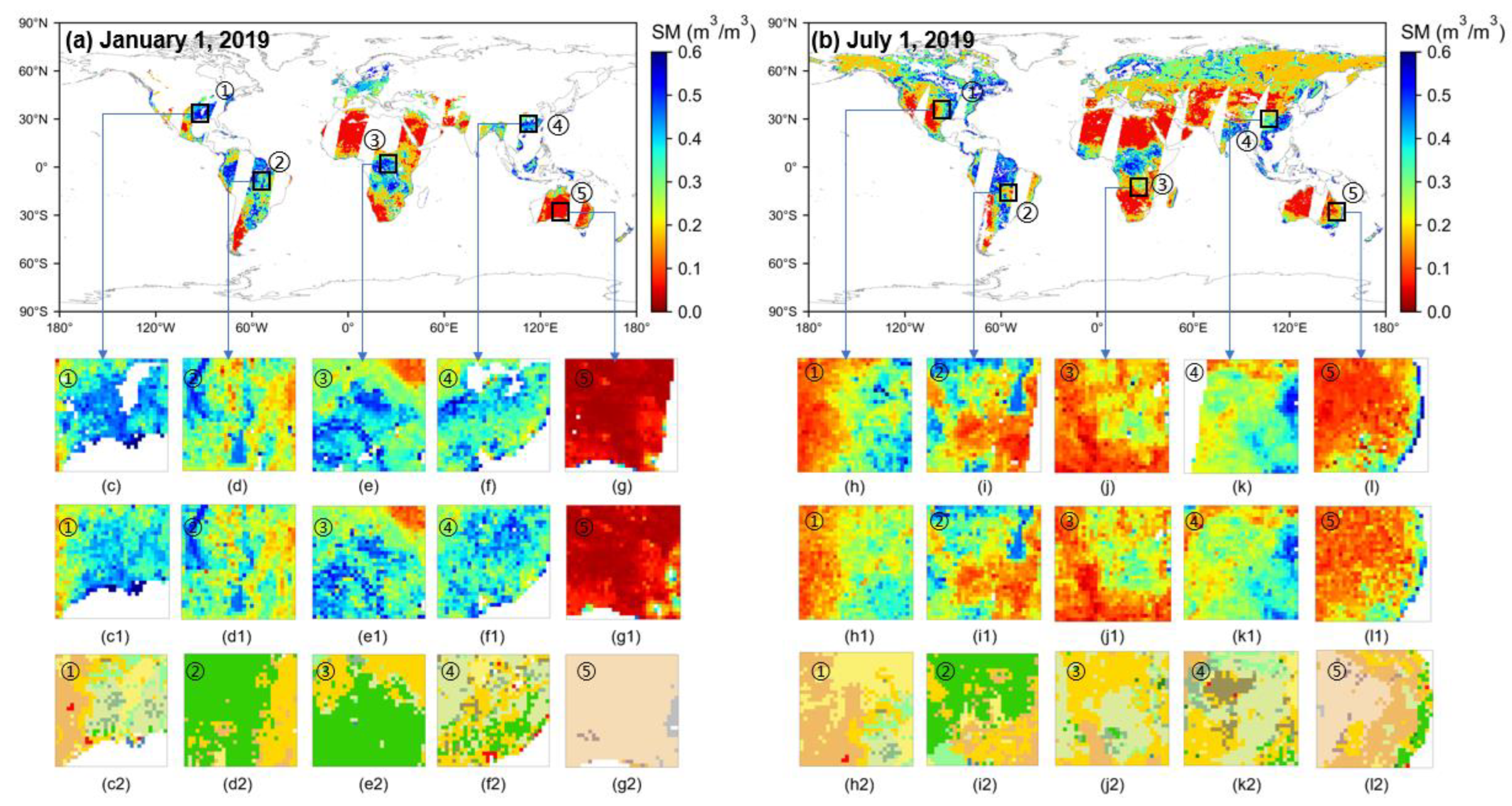
4.2. Reconstruction Results and Cross-Comparison
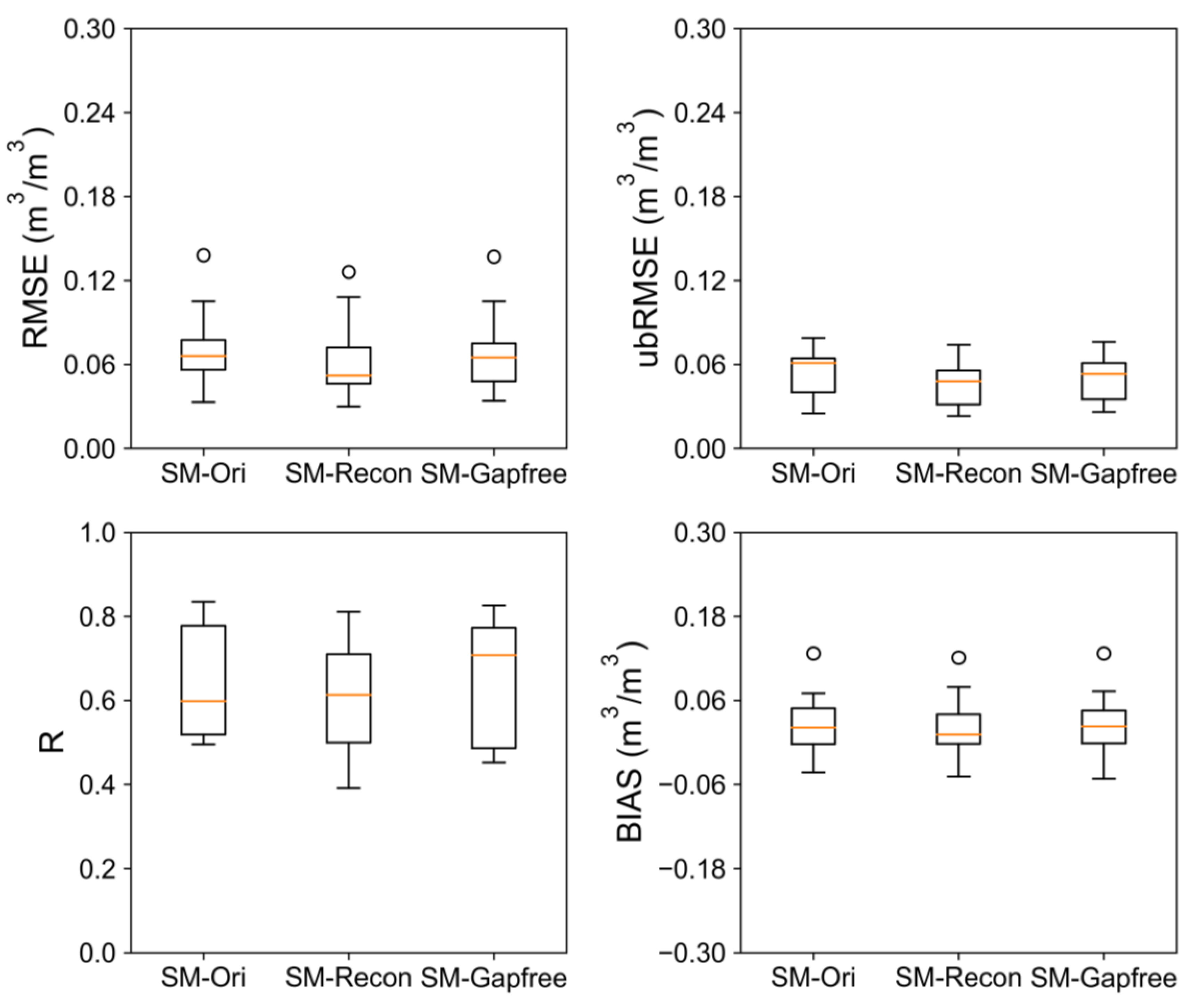
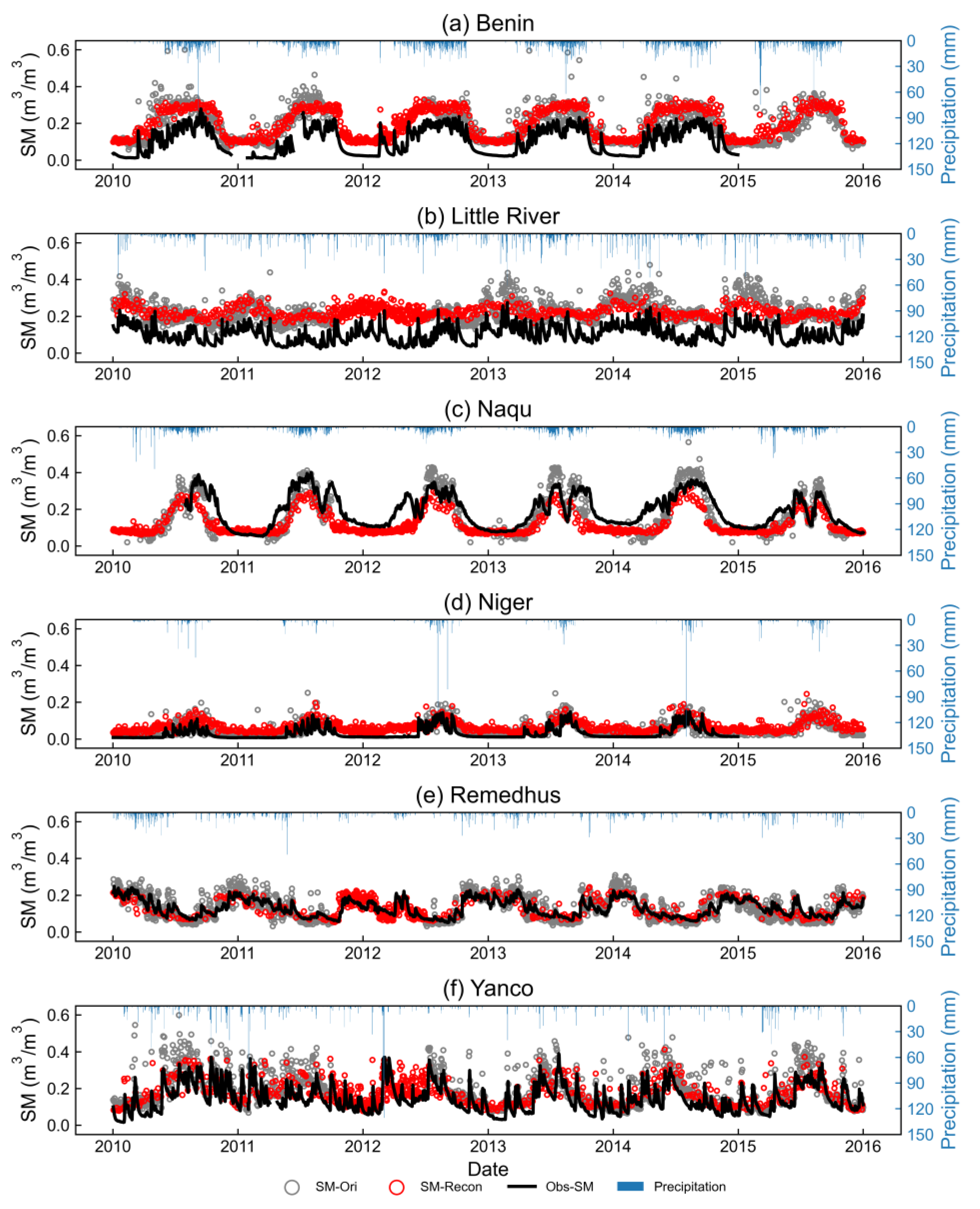
4.3. Validation Using the In Situ Observations
5. Discussion
5.1. The Proposed Pixel-Wise RF Method and the Gap-Filling Results
5.2. Uncertainty Analysis of the Gap-Free Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gianotti, D.J.S.; Akbar, R.; Feldman, A.F.; Salvucci, G.D.; Enthekabi, D. Terrestrial Evaporation and Moisture Drainage in a Warmer Climate. Geophys. Res. Lett. 2020, 47, e2019GL086498. [Google Scholar] [CrossRef]
- Oki, T.; Kanae, S.; Musiake, K. Global hydrological cycle and world water resources. Membrane 2003, 28, 206–214. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, Y.; Zhang, L.Q.; Ren, L.L.; Yuan, F.; Yang, X.L.; Jiang, S.H. Flash droughts characterization over China: From a perspective of the rapid intensification rate. Sci. Total Environ. 2020, 704, 135373. [Google Scholar] [CrossRef] [PubMed]
- Wei, L.Y.; Jiang, S.H.; Ren, L.L.; Yuan, F.; Zhang, L.Q. Performance of Two Long-Term Satellite-Based and GPCC 8.0 Precipitation Products for Drought Monitoring over the Yellow River Basin in China. Sustainability 2019, 11, 4969. [Google Scholar] [CrossRef]
- Zhang, L.Q.; Liu, Y.; Ren, L.L.; Jiang, S.H.; Yang, X.L.; Yuan, F.; Wang, M.H.; Wei, L.Y. Drought Monitoring and Evaluation by ESA CCI Soil Moisture Products Over the Yellow River Basin. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3376–3386. [Google Scholar] [CrossRef]
- Teuling, A.J. CLIMATE HYDROLOGY A hot future for European droughts. Nat. Clim. Chang. 2018, 8, 364–365. [Google Scholar] [CrossRef]
- Laiolo, P.; Gabellani, S.; Campo, L.; Silvestro, F.; Delogu, F.; Rudari, R.; Pulvirenti, L.; Boni, G.; Fascetti, F.; Pierdicca, N.; et al. Impact of different satellite soil moisture products on the predictions of a continuous distributed hydrological model. Int. J. Appl. Earth Obs. Geoinf. 2016, 48, 131–145. [Google Scholar] [CrossRef]
- Collow, T.W.; Robock, A.; Wu, W. Influences of soil moisture and vegetation on convective precipitation forecasts over the United States Great Plains. J. Geophys. Res. Atmos. 2014, 119, 9338–9358. [Google Scholar] [CrossRef]
- Dirmeyer, P.A.; Guo, Z.C.; Gao, X. Comparison, validation, and transferability of eight multiyear global soil wetness products. J. Hydrometeorol. 2004, 5, 1011–1033. [Google Scholar] [CrossRef]
- Njoku, E.G.; Jackson, T.J.; Lakshmi, V.; Chan, T.K.; Nghiem, S.V. Soil moisture retrieval from AMSR-E. IEEE Trans. Geosci. Remote Sens. 2003, 41, 215–229. [Google Scholar] [CrossRef]
- Robock, A.; Vinnikov, K.Y.; Srinivasan, G.; Entin, J.K.; Hollinger, S.E.; Speranskaya, N.A.; Liu, S.X.; Namkhai, A. The Global Soil Moisture Data Bank. Bull. Am. Meteorol. Soc. 2000, 81, 1281–1299. [Google Scholar] [CrossRef]
- Al-Yaari, A.; Wigneron, J.P.; Ducharne, A.; Kerr, Y.; de Rosnay, P.; de Jeu, R.; Govind, A.; Al Bitar, A.; Albergel, C.; Munoz-Sabater, J.; et al. Global-scale evaluation of two satellite-based passive microwave soil moisture datasets (SMOS and AMSR-E) with respect to Land Data Assimilation System estimates. Remote Sens. Environ. 2014, 149, 181–195. [Google Scholar] [CrossRef]
- Raoult, N.; Delorme, B.; Ottle, C.; Peylin, P.; Bastrikov, V.; Maugis, P.; Polcher, J. Confronting Soil Moisture Dynamics from the ORCHIDEE Land Surface Model with the ESA-CCI Product: Perspectives for Data Assimilation. Remote Sens. 2018, 10, 1786. [Google Scholar] [CrossRef]
- Loew, A.; Ludwig, R.; Mauser, W. Derivation of surface soil moisture from ENVISAT ASAR wide swath and image mode data in agricultural areas. IEEE Trans. Geosci. Remote Sens. 2006, 44, 889–899. [Google Scholar] [CrossRef]
- Zeng, J.Y.; Li, Z.; Chen, Q.; Bi, H.Y.; Qiu, J.X.; Zou, P.F. Evaluation of remotely sensed and reanalysis soil moisture products over the Tibetan Plateau using in-situ observations. Remote Sens. Environ. 2015, 163, 91–110. [Google Scholar] [CrossRef]
- Du, J.Y.; Kimball, J.S.; Jones, L.A.; Kim, Y.; Glassy, J.; Watts, J.D. A global satellite environmental data record derived from AMSR-E and AMSR2 microwave Earth observations. Earth Syst. Sci. Data 2017, 9, 791–808. [Google Scholar] [CrossRef]
- Du, J.Y.; Kimball, J.S.; Shi, J.C.; Jones, L.A.; Wu, S.L.; Sun, R.J.; Yang, H. Inter-Calibration of Satellite Passive Microwave Land Observations from AMSR-E and AMSR2 Using Overlapping FY3B-MWRI Sensor Measurements. Remote Sens. 2014, 6, 8594–8616. [Google Scholar] [CrossRef]
- Feng, X.M.; Li, J.X.; Cheng, W.; Fu, B.J.; Wang, Y.Q.; Lu, Y.H.; Shao, M.A. Evaluation of AMSR-E retrieval by detecting soil moisture decrease following massive dryland re-vegetation in the Loess Plateau, China. Remote Sens. Environ. 2017, 196, 253–264. [Google Scholar] [CrossRef]
- Kim, H.; Parinussa, R.; Konings, A.G.; Wagner, W.; Cosh, M.H.; Lakshmi, V.; Zohaib, M.; Choi, M. Global-scale assessment and combination of SMAP with ASCAT (active) and AMSR2 (passive) soil moisture products. Remote Sens. Environ. 2018, 204, 260–275. [Google Scholar] [CrossRef]
- Kim, S.; Liu, Y.Y.; Johnson, F.M.; Parinussa, R.M.; Sharma, A. A global comparison of alternate AMSR2 soil moisture products: Why do they differ? Remote Sens. Environ. 2015, 161, 43–62. [Google Scholar] [CrossRef]
- Tuttle, S.E.; Salvucci, G.D. A new approach for validating satellite estimates of soil moisture using large-scale precipitation: Comparing AMSR-E products. Remote Sens. Environ. 2014, 142, 207–222. [Google Scholar] [CrossRef]
- van der Velde, R.; Su, Z.B.; van Oevelen, P.; Wen, J.; Ma, Y.M.; Salama, M.S. Soil moisture mapping over the central part of the Tibetan Plateau using a series of ASAR WS images. Remote Sens. Environ. 2012, 120, 175–187. [Google Scholar] [CrossRef]
- Yang, H.; Weng, F.Z.; Lv, L.Q.; Lu, N.M.; Liu, G.F.; Bai, M.; Qian, Q.Y.; He, J.K.; Xu, H.X. The FengYun-3 Microwave Radiation Imager On-Orbit Verification. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4552–4560. [Google Scholar] [CrossRef]
- Chan, S.K.; Bindlish, R.; O’Neill, P.E.; Njoku, E.; Jackson, T.; Colliander, A.; Chen, F.; Burgin, M.; Dunbar, S.; Piepmeier, J.; et al. Assessment of the SMAP Passive Soil Moisture Product. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4994–5007. [Google Scholar] [CrossRef]
- Colliander, A.; Jackson, T.J.; Bindlish, R.; Chan, S.; Das, N.; Kim, S.B.; Cosh, M.H.; Dunbar, R.S.; Dang, L.; Pashaian, L.; et al. Validation of SMAP surface soil moisture products with core validation sites. Remote Sens. Environ. 2017, 191, 215–231. [Google Scholar] [CrossRef]
- Xie, Q.; Jia, L.; Menenti, M.; Hu, G. Global soil moisture data fusion by Triple Collocation Analysis from 2011 to 2018. Sci. Data 2022, 9, 687. [Google Scholar] [CrossRef] [PubMed]
- Yao, P.; Shi, J.; Zhao, T.; Lu, H.; Al-Yaari, A. Rebuilding long time series global soil moisture products using the neural network adopting the microwave vegetation index. Remote Sens. 2017, 9, 35. [Google Scholar] [CrossRef]
- Yao, P.; Lu, H.; Shi, J.; Zhao, T.; Yang, K.; Cosh, M.H.; Gianotti, D.J.S.; Entekhabi, D. A long term global daily soil moisture dataset derived from AMSR-E and AMSR2 (2002–2019). Sci. Data 2021, 8, 143. [Google Scholar] [CrossRef]
- Cho, E.S.; Su, C.H.; Ryu, D.; Kim, H.; Choi, M. Does AMSR2 produce better soil moisture retrievals than AMSR-E over Australia? Remote Sens. Environ. 2017, 188, 95–105. [Google Scholar] [CrossRef]
- Long, D.; Bai, L.L.; Yan, L.; Zhang, C.J.; Yang, W.T.; Lei, H.M.; Quan, J.L.; Meng, X.Y.; Shi, C.X. Generation of spatially complete and daily continuous surface soil moisture of high spatial resolution. Remote Sens. Environ. 2019, 233, 111364. [Google Scholar] [CrossRef]
- Guo, G.; Zhao, B. Monitoring soil moisture content with modis data. Soil 2004, 36, 219–221. [Google Scholar]
- Llamas, R.M.; Guevara, M.; Rorabaugh, D.; Taufer, M.; Vargas, R. Spatial Gap-Filling of ESA CCI Satellite-Derived Soil Moisture Based on Geostatistical Techniques and Multiple Regression. Remote Sens. 2020, 12, 665. [Google Scholar] [CrossRef]
- Sandholt, I.; Rasmussen, K.; Andersen, J. A simple interpretation of the surface temperature/vegetation index space for assessment of surface moisture status. Remote Sens. Environ. 2002, 79, 213–224. [Google Scholar] [CrossRef]
- Wang, G.J.; Garcia, D.; Liu, Y.; de Jeu, R.; Dolman, A.J. A three-dimensional gap filling method for large geophysical datasets: Application to global satellite soil moisture observations. Environ. Model. Softw. 2012, 30, 139–142. [Google Scholar] [CrossRef]
- Ahmad, S.; Kalra, A.; Stephen, H. Estimating soil moisture using remote sensing data: A machine learning approach. Adv. Water Resour. 2010, 33, 69–80. [Google Scholar] [CrossRef]
- Liu, Y.X.Y.; Yang, Y.P.; Jing, W.L.; Yue, X.F. Comparison of Different Machine Learning Approaches for Monthly Satellite-Based Soil Moisture Downscaling over Northeast China. Remote Sens. 2018, 10, 31. [Google Scholar] [CrossRef]
- Zhang, Q.; Yuan, Q.Q.; Li, J.; Wang, Y.; Sun, F.J.; Zhang, L.P. Generating seamless global daily AMSR2 soil moisture (SGD-SM) long-term products for the years 2013–2019. Earth Syst. Sci. Data 2021, 13, 1385–1401. [Google Scholar] [CrossRef]
- Chan, J.C.-W.; Paelinckx, D. Evaluation of Random Forest and Adaboost tree-based ensemble classification and spectral band selection for ecotope mapping using airborne hyperspectral imagery. Remote Sens. Environ. 2008, 112, 2999–3011. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Ghimire, B.; Rogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J.P. An assessment of the effectiveness of a random forest classifier for land-cover classification. ISPRS J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
- Hutengs, C.; Vohland, M. Downscaling land surface temperatures at regional scales with random forest regression. Remote Sens. Environ. 2016, 178, 127–141. [Google Scholar] [CrossRef]
- Sun, H.; Xu, Q. Evaluating Machine Learning and Geostatistical Methods for Spatial Gap-Filling of Monthly ESA CCI Soil Moisture in China. Remote Sens. 2021, 13, 2848. [Google Scholar] [CrossRef]
- Rahmati, O.; Falah, F.; Dayal, K.S.; Deo, R.C.; Mohammadi, F.; Biggs, T.; Moghaddam, D.D.; Naghibi, S.A.; Bui, D.T. Machine learning approaches for spatial modeling of agricultural droughts in the south-east region of Queensland Australia. Sci. Total Environ. 2020, 699, 134230. [Google Scholar] [CrossRef]
- Didan, K. MOD13C1 MODIS/Terra Vegetation Indices 16-Day L3 Global 0.05Deg CMG V006. Distributed by NASA EOSDIS Land Processes DAAC. 2015. Available online: https://doi.org/10.5067/MODIS/MOD13C1.006 (accessed on 5 February 2023).
- Yu, P.; Zhao, T.; Shi, J.; Ran, Y.; Jia, L.; Ji, D.; Xue, H. Global spatiotemporally continuous MODIS land surface temperature dataset. Sci. Data 2022, 9, 143. [Google Scholar] [CrossRef] [PubMed]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Friedl, M.; Sulla-Menashe, D. MCD12C1 MODIS/Terra+Aqua Land Cover Type Yearly L3 Global 0.05Deg CMG V006. distributed by NASA EOSDIS Land Processes DAAC. 2015. Available online: https://doi.org/10.5067/MODIS/MCD12C1.006 (accessed on 5 February 2023).
- Zhou, J.; Jia, L.; Menenti, M.; Liu, X. Optimal Estimate of Global Biome—Specific Parameter Settings to Reconstruct NDVI Time Series with the Harmonic ANalysis of Time Series (HANTS) Method. Remote Sens. 2021, 13, 4251. [Google Scholar] [CrossRef]
- Menenti, M.; Azzali, S.; Verhoef, W.; Vanswol, R. Mapping agroecological zones and time lag in vegetation growth by means of fourier analysis of time series of NDVI images. In Proceedings of the Symp on Remote Sensing for Oceanography, Hydrology and Agriculture, at the Cospar 29th Plenary Meeting, Washington, DC, USA, 28 August–5 September 1992; pp. 233–237. [Google Scholar]
- Zhou, J.; Jia, L.; van Hoek, M.; Menenti, M.; Lu, J.; Hu, G.; Ieee. An optimization of parameter settings in HANTS for global NDVI time series reconstruction. In Proceedings of the 36th IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 3422–3425. [Google Scholar]
- Roerink, G.J.; Menenti, M.; Verhoef, W. Reconstructing cloudfree NDVI composites using Fourier analysis of time series. Int. J. Remote Sens. 2000, 21, 1911–1917. [Google Scholar] [CrossRef]
- Verhoef, W. Application ofHarmonic Analysis ofNDVI Time Series (HANTS). In Fourier Analysis of Temporal NDVI in the Southern African and American Continents; DLOWinand Staring Centre: Wageningen, The Netherlands, 1996; pp. 19–24. [Google Scholar]
- Dorigo, W.A.; Wagner, W.; Hohensinn, R.; Hahn, S.; Paulik, C.; Xaver, A.; Gruber, A.; Drusch, M.; Mecklenburg, S.; van Oevelen, P.; et al. The International Soil Moisture Network: A data hosting facility for global in situ soil moisture measurements. Hydrol. Earth Syst. Sci. 2011, 15, 1675–1698. [Google Scholar] [CrossRef]
- Smith, A.B.; Walker, J.P.; Western, A.W.; Young, R.I.; Ellett, K.M.; Pipunic, R.C.; Grayson, R.B.; Siriwardena, L.; Chiew, F.H.S.; Richter, H. The Murrumbidgee soil moisture monitoring network data set. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Dorigo, W.A.; Xaver, A.; Vreugdenhil, M.; Gruber, A.; Hegyiova, A.; Sanchis-Dufau, A.D.; Zamojski, D.; Cordes, C.; Wagner, W.; Drusch, M. Global Automated Quality Control of In Situ Soil Moisture Data from the International Soil Moisture Network. Vadose Zone J. 2013, 12. [Google Scholar] [CrossRef]
- Yang, K.; Qin, J.; Zhao, L.; Chen, Y.; Tang, W.; Han, M.; Chen, Z.; Lv, N.; Ding, B.; Wu, H.; et al. A multiscale soil moisture and freeze-thaw monitoring network on the third pole. Bull. Am. Meteorol. Soc. 2013, 94, 1907–1916. [Google Scholar] [CrossRef]
- Rudiger, C.; Hancock, G.; Hemakumara, H.M.; Jacobs, B.; Kalma, J.D.; Martinez, C.; Thyer, M.; Walker, J.P.; Wells, T.; Willgoose, G.R. Goulburn River experimental catchment data set. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Sanchez, N.; Martinez-Fernandez, J.; Scaini, A.; Perez-Gutierrez, C. Validation of the SMOS L2 Soil Moisture Data in the REMEDHUS Network (Spain). IEEE Trans. Geosci. Remote Sens. 2012, 50, 1602–1611. [Google Scholar] [CrossRef]
- Pellarin, T.; Laurent, J.P.; Cappelaere, B.; Decharme, B.; Descroix, L.; Ramier, D. Hydrological modelling and associated microwave emission of a semi-arid region in South-western Niger. J. Hydrol. 2009, 375, 262–272. [Google Scholar] [CrossRef]
- Cappelaere, B.; Descroix, L.; Lebel, T.; Boulain, N.; Ramier, D.; Laurent, J.P.; Favreau, G.; Boubkraoui, S.; Boucher, M.; Moussa, I.B.; et al. The AMMA-CATCH experiment in the cultivated Sahelian area of south-west Niger—Investigating water cycle response to a fluctuating climate and changing environment. J. Hydrol. 2009, 375, 34–51. [Google Scholar] [CrossRef]
- de Rosnay, P.; Gruhier, C.; Timouk, F.; Baup, F.; Mougin, E.; Hiernaux, P.; Kergoat, L.; LeDantec, V. Multi-scale soil moisture measurements at the Gourma meso-scale site in Mali. J. Hydrol. 2009, 375, 241–252. [Google Scholar] [CrossRef]
- Mougin, E.; Hiernaux, P.; Kergoat, L.; Grippa, M.; de Rosnay, P.; Timouk, F.; Le Dantec, V.; Demarez, V.; Lavenu, F.; Arjounin, M.; et al. The AMMA-CATCH Gourma observatory site in Mali: Relating climatic variations to changes in vegetation, surface hydrology, fluxes and natural resources. J. Hydrol. 2009, 375, 14–33. [Google Scholar] [CrossRef]
- Bosch, D.D.; Sheridan, J.M.; Lowrance, R.R.; Hubbard, R.K.; Strickland, T.C.; Feyereisen, G.W.; Sullivan, D.G. Little river experimental watershed database. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Cosh, M.H.; Jackson, T.J.; Starks, P.; Heathman, G. Temporal stability of surface soil moisture in the Little Washita River watershed and its applications in satellite soil moisture product validation. J. Hydrol. 2006, 323, 168–177. [Google Scholar] [CrossRef]
- Moran, M.S.; Emmerich, W.E.; Goodrich, D.C.; Heilman, P.; Collins, C.D.H.; Keefer, T.O.; Nearing, M.A.; Nichols, M.H.; Renard, K.G.; Scott, R.L.; et al. Preface to special section on fifty years of research and data collection: US Department of Agriculture Walnut Gulch Experimental Watershed. Water Resour. Res. 2008, 44, W05S01. [Google Scholar] [CrossRef]
- Seyfried, M.S.; Murdock, M.D.; Hanson, C.L.; Flerchinger, G.N.; Van Vactor, S. Long-term soil water content database, Reynolds Creek Experimental Watershed, Idaho, United States. Water Resour. Res. 2001, 37, 2847–2851. [Google Scholar] [CrossRef]
- Sullivan, D.G.; Batten, H.L.; Bosch, D.; Sheridan, J.; Strickland, T. Little river experimental watershed, Tifton, Georgia, United States: A geographic database. Water Resour. Res. 2007, 43, W09475. [Google Scholar] [CrossRef]
- Chen, T.; de Jeu, R.A.M.; Liu, Y.Y.; van der Werf, G.R.; Dolman, A.J. Using satellite based soil moisture to quantify the water driven variability in NDVI: A case study over mainland Australia. Remote Sens. Environ. 2014, 140, 330–338. [Google Scholar] [CrossRef]
- Wang, S.; Li, R.; Wu, Y.; Zhao, S.; Wang, X. Soil Moisture Inversion Based on Environmental Variables and Machine Learning. Trans. Chin. Soc. Agric. Mach. 2022, 53, 332–341. [Google Scholar]
- Zheng, C.; Jia, L.; Zhao, T. A 21-year dataset (2000–2020) of gap-free global daily surface soil moisture at 1-km grid resolution. Sci. Data 2023, 10, 139. [Google Scholar] [CrossRef]
- Dorigo, W.; Wagner, W.; Albergel, C.; Albrecht, F.; Balsamo, G.; Brocca, L.; Chung, D.; Ertl, M.; Forkel, M.; Gruber, A.; et al. ESA CCI Soil Moisture for improved Earth system understanding: State-of-the art and future directions. Remote Sens. Environ. 2017, 203, 185–215. [Google Scholar] [CrossRef]
- Xiao, Z.Q.; Jiang, L.M.; Zhu, Z.L.; Wang, J.D.; Du, J.Y. Spatially and Temporally Complete Satellite Soil Moisture Data Based on a Data Assimilation Method. Remote Sens. 2016, 8, 49. [Google Scholar] [CrossRef]
- Zhang, L.X.; Zhao, T.J.; Jiang, L.M.; Zhao, S.J. Estimate of Phase Transition Water Content in Freeze-Thaw Process Using Microwave Radiometer. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4248–4255. [Google Scholar] [CrossRef]
- Zhao, T.J.; Zhang, L.X.; Jiang, L.M.; Zhao, S.J.; Chai, L.N.; Jin, R. A new soil freeze/thaw discriminant algorithm using AMSR-E passive microwave imagery. Hydrol. Process. 2011, 25, 1704–1716. [Google Scholar] [CrossRef]
- James, S.R.; Minsley, B.J.; McFarland, J.W.; Euskirchen, E.S.; Edgar, C.W.; Waldrop, M.P. The Biophysical Role of Water and Ice Within Permafrost Nearing Collapse: Insights from Novel Geophysical Observations. J. Geophys. Res. Earth Surf. 2021, 126, e2021JF006104. [Google Scholar] [CrossRef]
- Su, Z.; Wen, J.; Dente, L.; van der Velde, R.; Wang, L.; Ma, Y.; Yang, K.; Hu, Z. The Tibetan Plateau observatory of plateau scale soil moisture and soil temperature (Tibet-Obs) for quantifying uncertainties in coarse resolution satellite and model products. Hydrol. Earth Syst. Sci. 2011, 15, 2303–2316. [Google Scholar] [CrossRef]
- Van der Vliet, M.; van der Schalie, R.; Rodriguez-Fernandez, N.; Colliander, A.; de Jeu, R.; Preimesberger, W.; Scanlon, T.; Dorigo, W. Reconciling Flagging Strategies for Multi-Sensor Satellite Soil Moisture Climate Data Records. Remote Sens. 2020, 12, 3439. [Google Scholar] [CrossRef]
- Roy, D.P.; Borak, J.S.; Devadiga, S.; Wolfe, R.E.; Zheng, M.; Descloitres, J. The MODIS Land product quality assessment approach. Remote Sens. Environ. 2002, 83, 62–76. [Google Scholar] [CrossRef]
- Wu, X.D.; Wen, J.G.; Xiao, Q.; You, D.Q.; Dou, B.; Lin, X.; Hueni, A. Accuracy Assessment on MODIS (V006), GLASS and MuSyQ Land-Surface Albedo Products: A Case Study in the Heihe River Basin, China. Remote Sens. 2018, 10, 2045. [Google Scholar] [CrossRef]
- Hossain, F.; Anagnostou, E.N. Numerical investigation of the impact of uncertainties in satellite rainfall estimation and land surface model parameters on simulation of soil moisture. Adv. Water Resour. 2005, 28, 1336–1350. [Google Scholar] [CrossRef]





| Variable Name | Data Name | Temporal Resolution | Spatial Resolution | Reference |
|---|---|---|---|---|
| Surface soil moisture | NN-SM | Daily | 36 km | [28] |
| NDVI | MOD13C1 | 16 days | 0.05° | [43] |
| LST | Global daily 0.05° spatiotemporal continuous land surface temperature dataset | Daily | 0.05° | [44] |
| Precipitation | ERA5 | Hourly | 0.25° | [45] |
| Land Cover Type | MCD12C1 | Yearly | 0.05° | [46] |
| Networks | Sites Names | Stations | Climate Regime | IGBP Land Cover | Measured Depth | Reference |
|---|---|---|---|---|---|---|
| Tibetan Plateau (Asia) | Pali | 24 | Arid | Barren/sparse | 5 cm | [55] |
| Naqu | 57 | Polar | Grasslands | |||
| OZNET (Australia) | Yanco | 12 | Semi-arid | Croplands/Grasslands | 5–8 cm | [56] |
| Kyeamba | 8 | Temperate | Croplands | |||
| REMEDHUS (Europe) | REMEDHUS | 23 | Temperate | Croplands | 5 cm | [57] |
| AMMA (Africa) | Benin | 4 | Arid | Savannas | 5 cm | [58,59,60,61] |
| Niger | 3 | Arid | Grasslands | |||
| USDA (North America) | Little River | 33 | Temperate | Croplands | 5 cm | [62,63,64,65,66] |
| Little Washita | 20 | Temperate | Grasslands | |||
| Walnut Gulch | 19 | Arid | Shrub open rangeland | |||
| Fort Cobb | 15 | Temperate | Croplands | |||
| Reynolds Creek | 20 | Arid | Grasslands |
| R | RMSE (m3/m3) | ubRMSE (m3/m3) | Bias (m3/m3) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sites | SM -Ori | SM -Recon | SM -Gapfree | SM -Ori | SM -Recon | SM -Gapfree | SM -Ori | SM -Recon | SM -Gapfree | SM -Ori | SM -Recon | SM -Gapfree |
| Benin | 0.800 | 0.853 | 0.818 | 0.120 | 0.112 | 0.117 | 0.058 | 0.042 | 0.052 | 0.105 | 0.104 | 0.104 |
| Fort Cobb | 0.495 | 0.447 | 0.453 | 0.061 | 0.049 | 0.061 | 0.061 | 0.048 | 0.061 | −0.004 | −0.006 | −0.002 |
| Kyemba | 0.740 | 0.613 | 0.708 | 0.105 | 0.108 | 0.105 | 0.079 | 0.074 | 0.076 | 0.070 | 0.079 | 0.073 |
| Little River | 0.539 | 0.552 | 0.505 | 0.138 | 0.126 | 0.137 | 0.054 | 0.037 | 0.051 | 0.127 | 0.121 | 0.127 |
| Little Washita | 0.498 | 0.391 | 0.452 | 0.066 | 0.052 | 0.065 | 0.062 | 0.051 | 0.061 | 0.024 | 0.011 | 0.023 |
| Naqu | 0.810 | 0.751 | 0.809 | 0.075 | 0.072 | 0.074 | 0.071 | 0.054 | 0.053 | −0.025 | −0.049 | −0.052 |
| Niger | 0.786 | 0.669 | 0.708 | 0.033 | 0.044 | 0.038 | 0.025 | 0.023 | 0.026 | 0.021 | 0.037 | 0.029 |
| Pali | 0.598 | 0.811 | 0.811 | 0.051 | 0.03 | 0.038 | 0.028 | 0.029 | 0.032 | −0.043 | −0.009 | −0.02 |
| Remedhus | 0.835 | 0.76 | 0.826 | 0.036 | 0.034 | 0.034 | 0.036 | 0.034 | 0.034 | −0.001 | 0.002 | −0.001 |
| Reynolds Creek | 0.497 | 0.423 | 0.468 | 0.069 | 0.057 | 0.07 | 0.067 | 0.057 | 0.067 | 0.016 | 0.003 | 0.018 |
| Walnut Gulch | 0.574 | 0.553 | 0.572 | 0.065 | 0.051 | 0.058 | 0.044 | 0.028 | 0.036 | 0.047 | 0.043 | 0.046 |
| Yanco | 0.770 | 0.628 | 0.737 | 0.080 | 0.072 | 0.076 | 0.062 | 0.062 | 0.061 | 0.050 | 0.036 | 0.045 |
| all | 0.662 | 0.621 | 0.656 | 0.075 | 0.067 | 0.073 | 0.054 | 0.045 | 0.051 | 0.032 | 0.031 | 0.033 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mi, P.; Zheng, C.; Jia, L.; Bai, Y. Reconstruction of Global Long-Term Gap-Free Daily Surface Soil Moisture from 2002 to 2020 Based on a Pixel-Wise Machine Learning Method. Remote Sens. 2023, 15, 2116. https://doi.org/10.3390/rs15082116
Mi P, Zheng C, Jia L, Bai Y. Reconstruction of Global Long-Term Gap-Free Daily Surface Soil Moisture from 2002 to 2020 Based on a Pixel-Wise Machine Learning Method. Remote Sensing. 2023; 15(8):2116. https://doi.org/10.3390/rs15082116
Chicago/Turabian StyleMi, Pei, Chaolei Zheng, Li Jia, and Yu Bai. 2023. "Reconstruction of Global Long-Term Gap-Free Daily Surface Soil Moisture from 2002 to 2020 Based on a Pixel-Wise Machine Learning Method" Remote Sensing 15, no. 8: 2116. https://doi.org/10.3390/rs15082116
APA StyleMi, P., Zheng, C., Jia, L., & Bai, Y. (2023). Reconstruction of Global Long-Term Gap-Free Daily Surface Soil Moisture from 2002 to 2020 Based on a Pixel-Wise Machine Learning Method. Remote Sensing, 15(8), 2116. https://doi.org/10.3390/rs15082116