Analysis of Spatial–Temporal Variability of PM2.5 Concentrations Using Optical Satellite Images and Geographic Information System
Abstract
1. Introduction
2. Study Area and Datasets
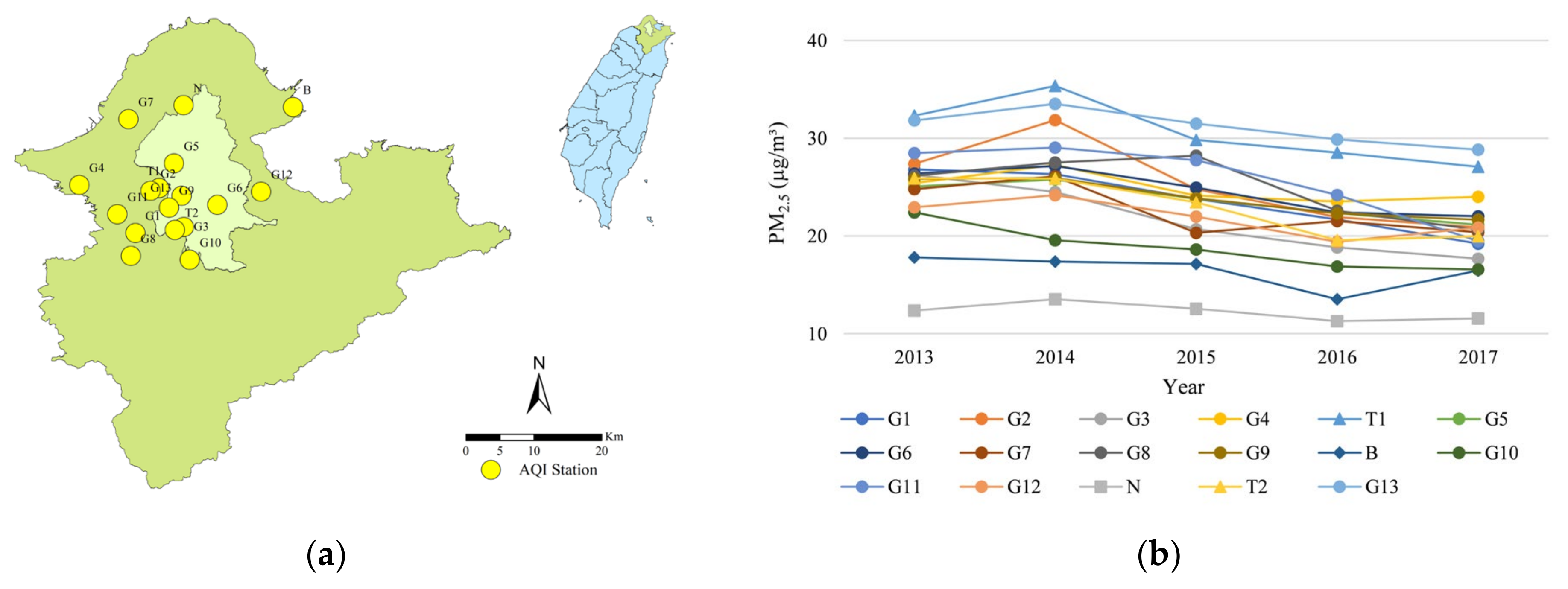
2.1. Taipei Metropolis and Air Quality Dataset
2.2. Geographic Dataset
2.3. Satellite Image Data
3. Methodology
3.1. Generation of Cloud-Free Image for Classification
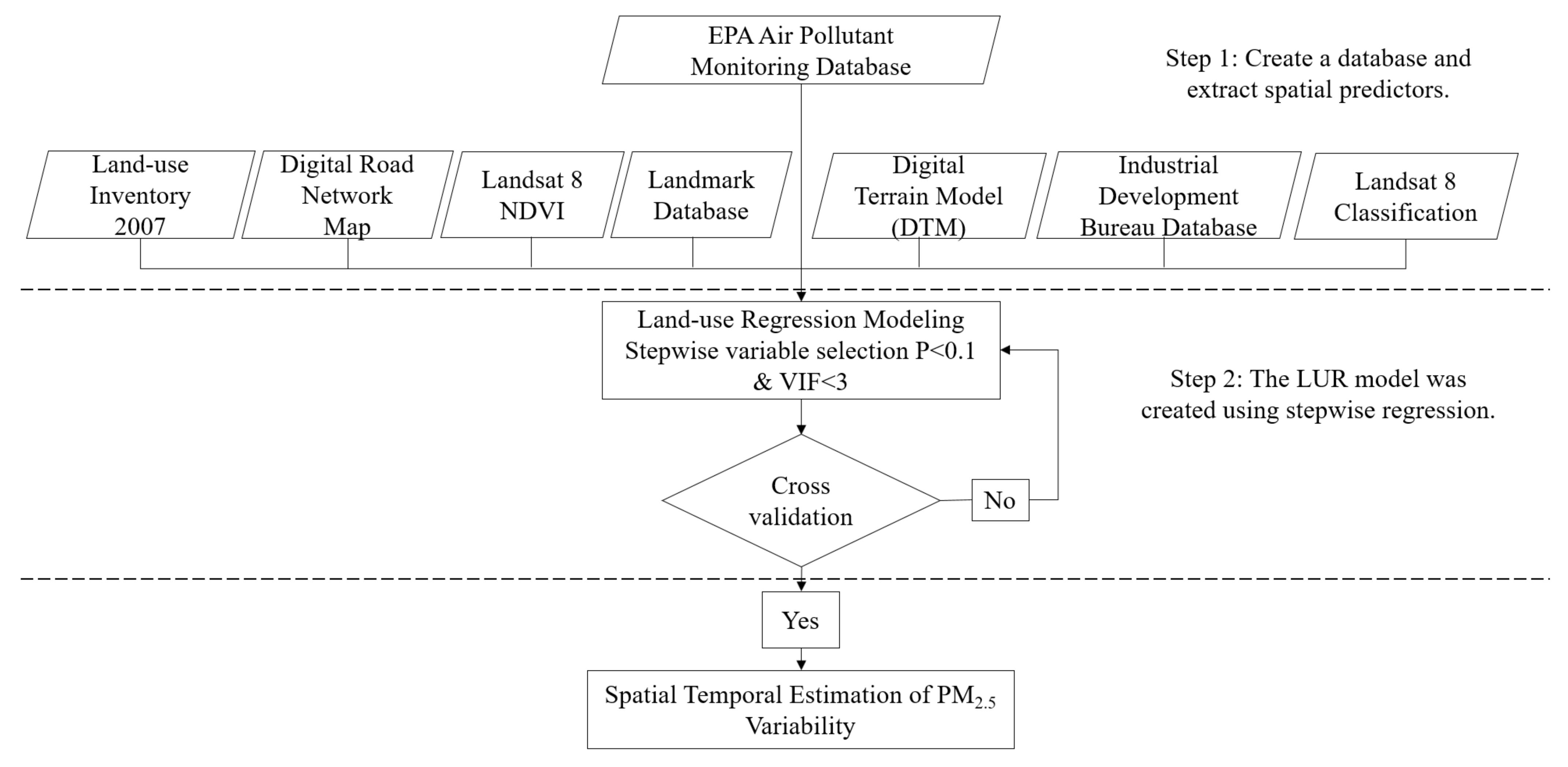
3.2. PM2.5 Concentration Model Development
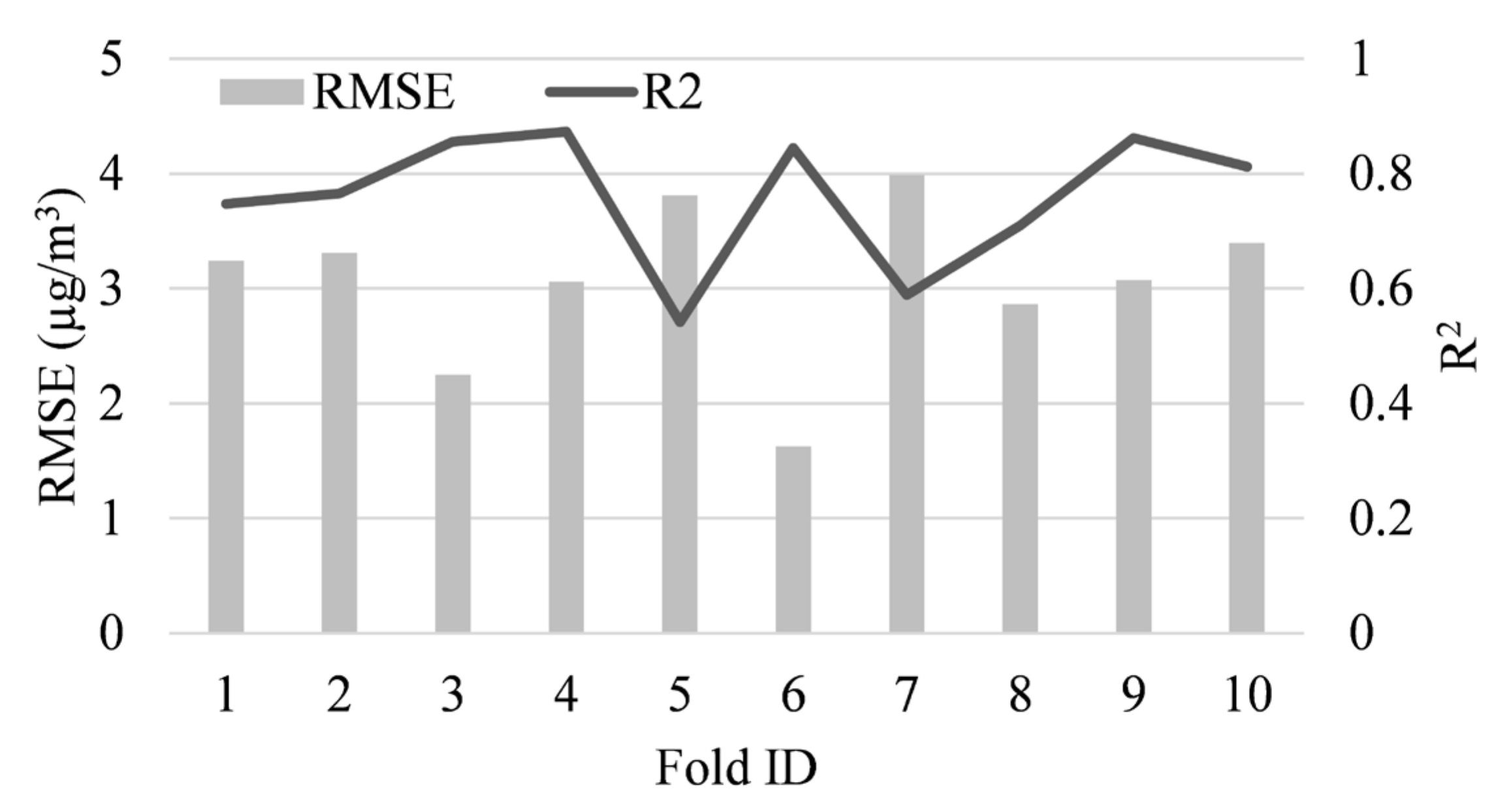
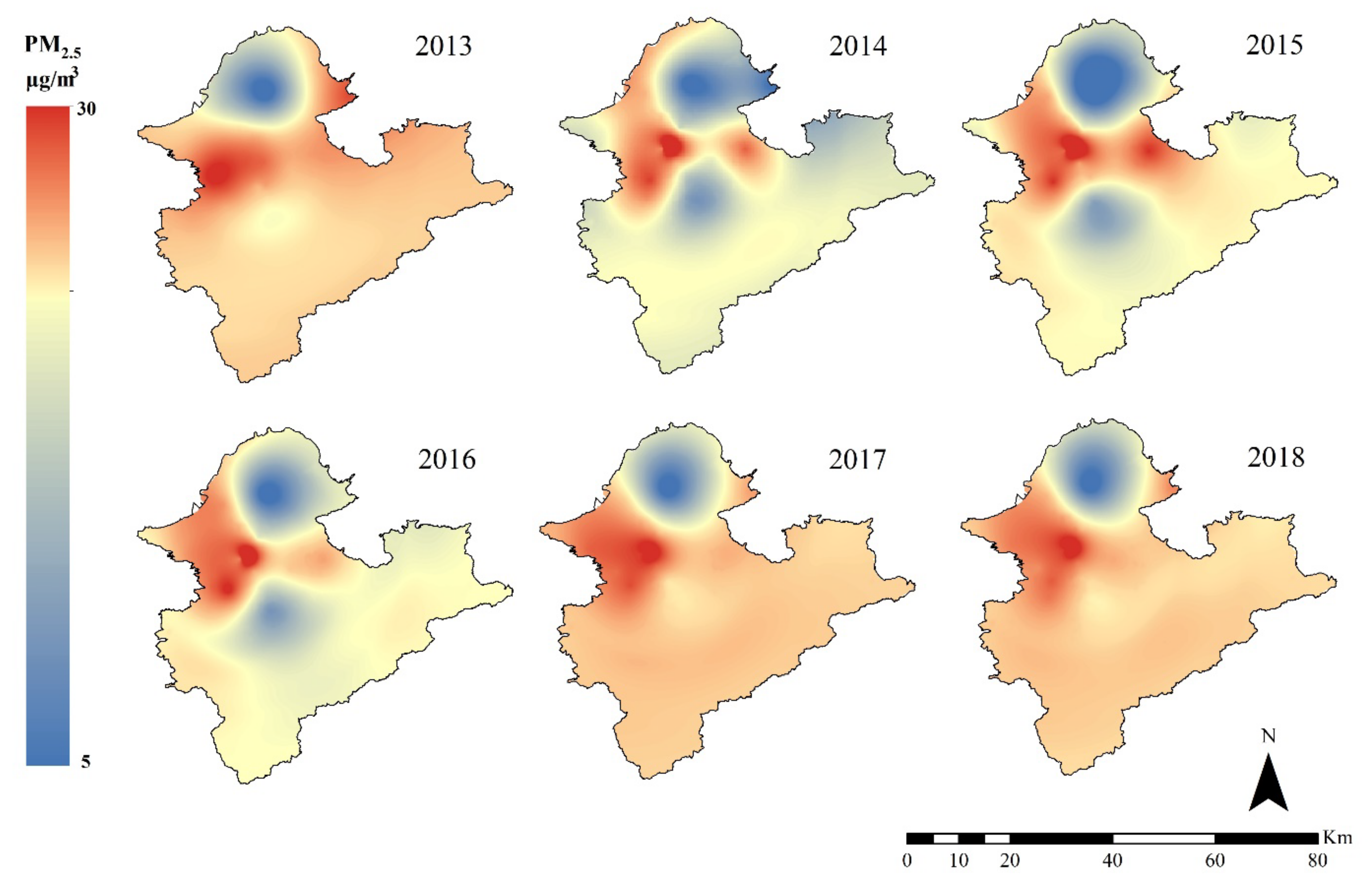
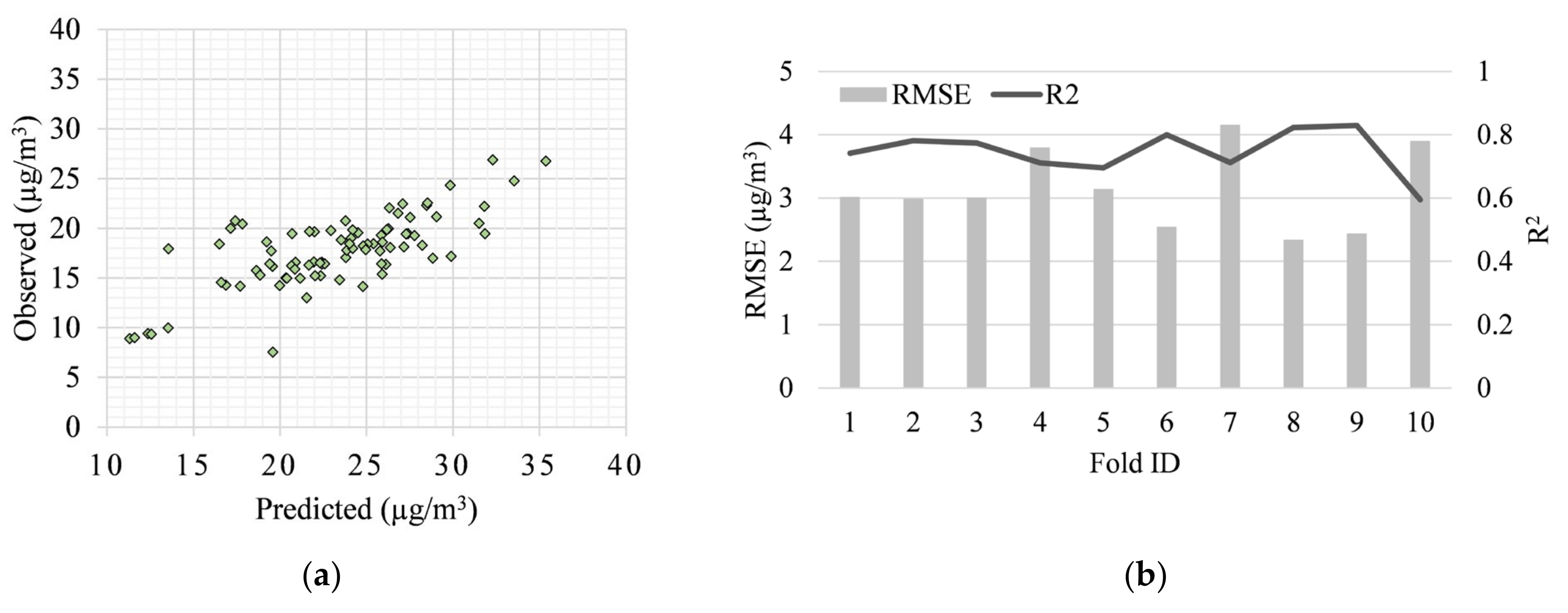
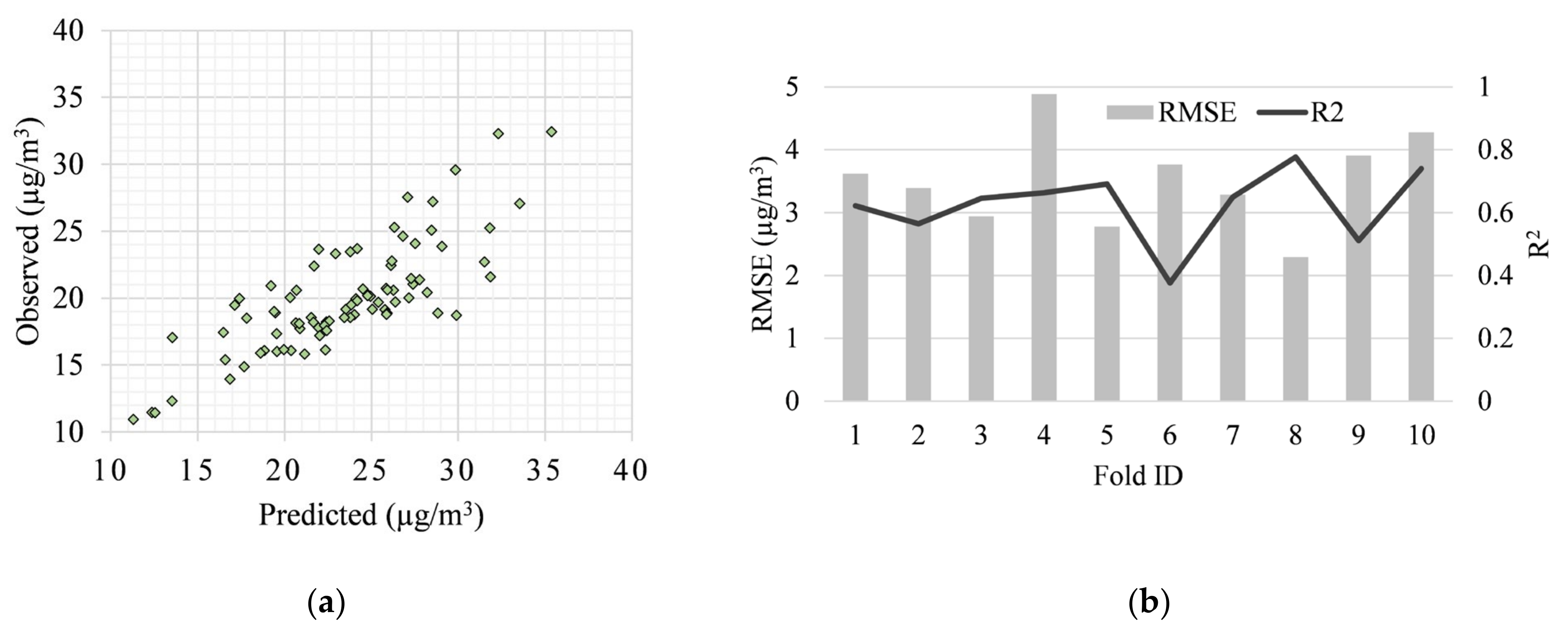
4. Experimental Result and Discussion
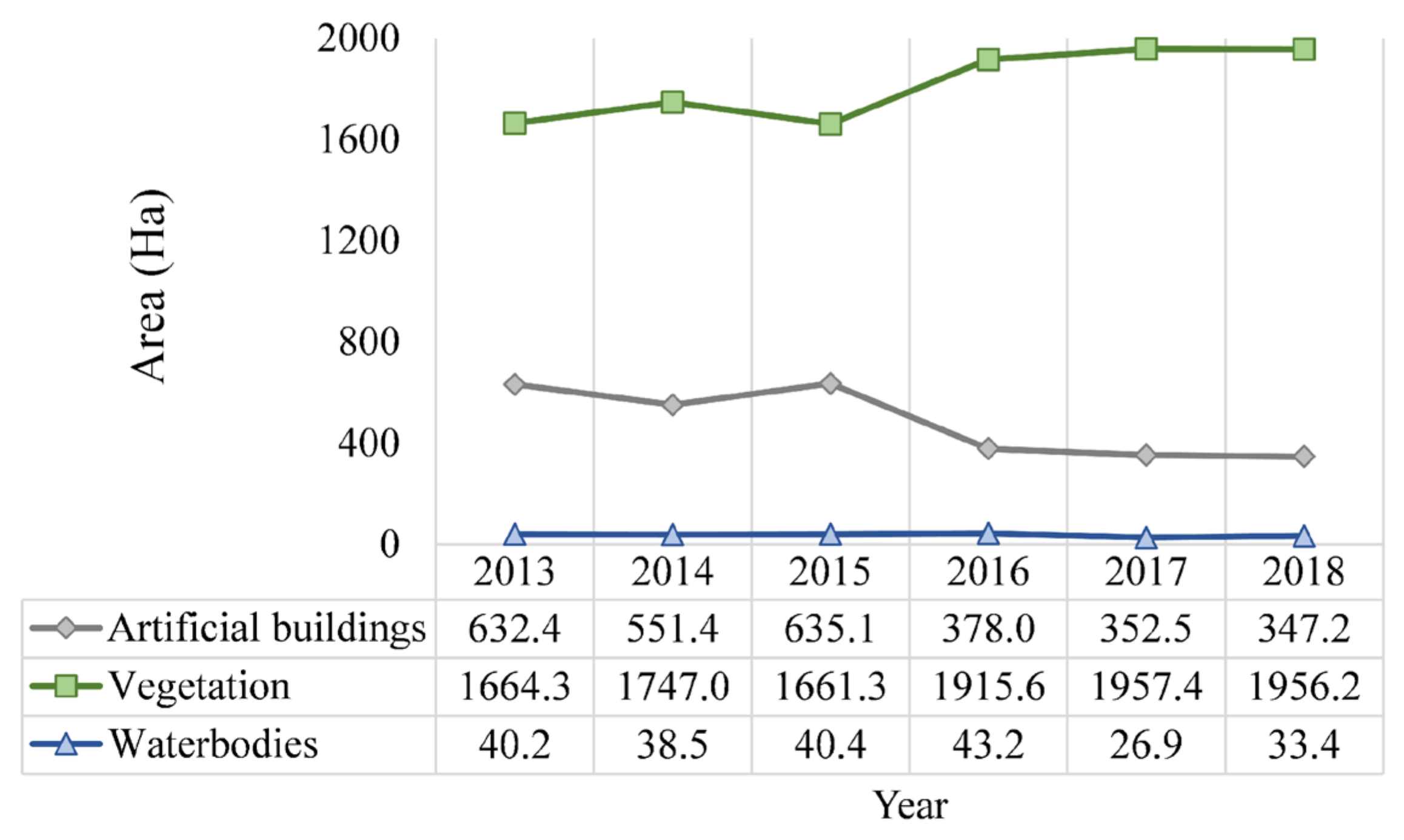
4.1. Cloud-Free Image and Classification
4.2. PM2.5 Concentration Model with Geographic and Satellite Image Integration
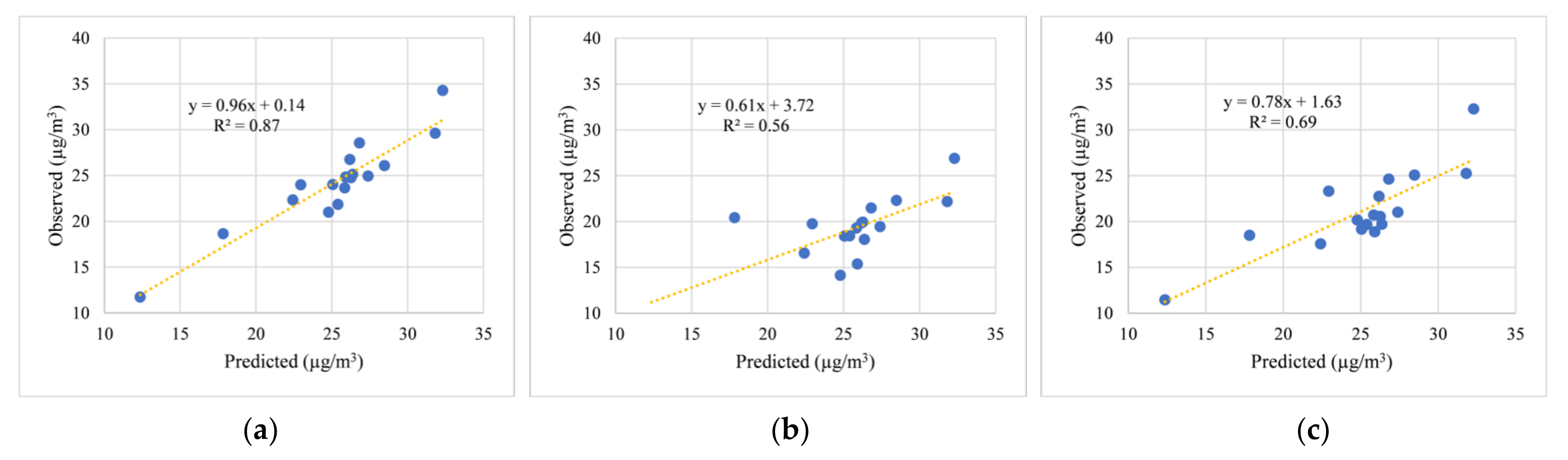
4.3. Comparison with Related Models
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Greenwell, L.L.; Moreno, T.; Jones, T.P.; Richards, R.J. Particle-induced oxidative damage is ameliorated by pulmonary antioxidants. Free Radic. Biol. Med. 2002, 32, 898–905. [Google Scholar] [CrossRef] [PubMed]
- Eze, I.C.; Schaffner, E.; Fischer, E.; Schikowski, T.; Adam, M.; Imboden, M.; Tsai, M.; Carballo, D.; von Eckardstein, A.; Künzli, N.; et al. Long-term air pollution exposure and diabetes in a population-based Swiss cohort. Environ. Int. 2014, 70, 95–105. [Google Scholar] [CrossRef]
- Manisalidis, I.; Stavropoulou, E.; Stavropoulos, A.; Bezirtzoglou, E. Environmental and Health Impacts of Air Pollution: A Review. Front. Public Health 2020, 8, 14. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Yang, Y.; Li, Y.; Qian, Z.; Xiao, W.; Wang, X.; Rolling, C.A.; Liu, E.; Xiao, J.; Zeng, W.; et al. Short-term and long-term effects of PM2.5 on acute nasopharyngitis in 10 communities of Guangdong, China. Sci. Total. Environ. 2019, 688, 136–142. [Google Scholar] [CrossRef]
- Shang, J.; Zhang, Y.; Schauer, J.J.; Tian, J.; Hua, J.; Han, T.; Fang, D.; An, J. Associations between source-resolved PM2.5 and airway inflammation at urban and rural locations in Beijing. Environ. Int. 2020, 139, 105635. [Google Scholar] [CrossRef]
- Xing, Y.-F.; Xu, Y.-H.; Shi, M.-H.; Lian, Y.-X. The impact of PM2.5 on the human respiratory system. J. Thorac. Dis. 2016, 8, E69–E74. [Google Scholar] [CrossRef]
- Song, Y.; Huang, B.; He, Q.; Chen, B.; Wei, J.; Mahmood, R. Dynamic assessment of PM2.5 exposure and health risk using remote sensing and geo-spatial big data. Environ. Pollut. 2019, 253, 288–296. [Google Scholar] [CrossRef]
- Slama, R.; Morgenstern, V.; Cyrys, J.; Zutavern, A.; Herbarth, O.; Wichmann, H.-E.; Heinrich, J. Traffic-related atmospheric pollutants levels during pregnancy and offspring’s term birth weight: A study relying on a land-use regression exposure model. Environ. Health Perspect. 2007, 115, 1283–1292. [Google Scholar] [CrossRef] [PubMed]
- Briggs, D.J.; Collins, S.; Elliott, P.; Fischer, P.; Kingham, S.; Lebret, E.; Pryl, K.; van Reeuwijk, H.; Smallbone, K.; van der Veen, A. Mapping urban air pollution using GIS: A regression-based approach. Int. J. Geogr. Inf. Sci. 1997, 11, 699–718. [Google Scholar] [CrossRef]
- Aguilera, I.; Eeftens, M.; Meier, R.; Ducret-Stich, R.E.; Schindler, C.; Ineichen, A.; Phuleria, H.C.; Probst-Hensch, N.; Tsai, M.-Y.; Künzli, N. Land use regression models for crustal and traffic-related PM2.5 constituents in four areas of the SAPALDIA study. Environ. Res. 2015, 140, 377–384. [Google Scholar] [CrossRef] [PubMed]
- Beelen, R.; Hoek, G.; Vienneau, D.; Eeftens, M.; Dimakopoulou, K.; Pedeli, X.; Tsai, M.-Y.; Künzli, N.; Schikowski, T.; Marcon, A.; et al. Development of NO2 and NOx land use regression models for estimating air pollution exposure in 36 study areas in Europe—The ESCAPE project. Atmos. Environ. 2013, 72, 10–23. [Google Scholar] [CrossRef]
- Hoek, G.; Beelen, R.; de Hoogh, K.; Vienneau, D.; Gulliver, J.; Fischer, P.; Briggs, D. A review of land-use regression models to assess spatial variation of outdoor air pollution. Atmos. Environ. 2008, 42, 7561–7578. [Google Scholar] [CrossRef]
- Lee, J.-H.; Wu, C.-F.; Hoek, G.; de Hoogh, K.; Beelen, R.; Brunekreef, B.; Chan, C.-C. LUR models for particulate matters in the Taipei metropolis with high densities of roads and strong activities of industry, commerce and construction. Sci. Total. Environ. 2015, 514, 178–184. [Google Scholar] [CrossRef] [PubMed]
- Eeftens, M.; Beelen, R.; de Hoogh, K.; Bellander, T.; Cesaroni, G.; Cirach, M.; Declercq, C.; Dėdelė, A.; Dons, E.; de Nazelle, A.; et al. Development of land use regression models for PM2.5, PM2.5 absorbance, PM10 and PMcoarse in 20 European study areas; Results of the ESCAPE project. Environ. Sci. Technol. 2012, 46, 11195–11205. [Google Scholar] [CrossRef] [PubMed]
- Lui, K.; Bandowe, B.A.M.; Ho, S.S.H.; Chuang, H.-C.; Cao, J.-J.; Chuang, K.-J.; Lee, S.; Hu, D.; Ho, K. Characterization of chemical components and bioreactivity of fine particulate matter (PM2.5) during incense burning. Environ. Pollut. 2016, 213, 524–532. [Google Scholar] [CrossRef]
- Yu, K.-P.; Yang, K.R.; Chen, Y.C.; Gong, J.Y.; Shih, H.-C.; Lung, S.-C.C. Indoor air pollution from gas cooking in five Taiwanese families. Build. Environ. 2015, 93, 258–266. [Google Scholar] [CrossRef]
- Tunno, B.J.; Dalton, R.; Cambal, L.; Holguin, F.; Lioy, P.; Clougherty, J.E. Indoor source apportionment in urban communities near industrial sites. Atmos. Environ. 2016, 139, 30–36. [Google Scholar] [CrossRef]
- Atkinson, R.W.; Fuller, G.W.; Anderson, H.R.; Harrison, R.M.; Armstrong, B. Urban ambient particle metrics and health: A time-series analysis. Epidemiology 2010, 21, 501–511. [Google Scholar] [CrossRef]
- Kim, K.-H.; Kabir, E.; Kabir, S. A review on the human health impact of airborne particulate matter. Environ. Int. 2015, 74, 136–143. [Google Scholar] [CrossRef] [PubMed]
- Araki, S.; Yamamoto, K.; Kondo, A. Application of regression kriging to air pollutant concentrations in Japan with high spatial resolution. Aerosol Air Qual. Res. 2015, 15, 234–241. [Google Scholar] [CrossRef]
- Chung, C.-J.; Wu, C.-D.; Hwang, B.-F.; Wu, C.-C.; Huang, P.-H.; Ho, C.-T.; Hsu, H.-T. Effects of ambient PM2.5 and particle-bound metals on the healthy residents living near an electric arc furnace: A community- based study. Sci. Total. Environ. 2020, 728, 138799. [Google Scholar] [CrossRef]
- Wu, C.-D.; Zeng, Y.-T.; Lung, S.-C.C. A hybrid kriging/land-use regression model to assess PM2.5 spatial-temporal variability. Sci. Total Environ. 2018, 645, 1456–1464. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.-D.; Chen, Y.-C.; Pan, W.-C.; Zeng, Y.-T.; Chen, M.-J.; Guo, Y.L.; Lung, S.-C.C. Land-use regression with long-term satellite-based greenness index and culture-specific sources to model PM2.5 spatial-temporal variability. Environ. Pollut. 2017, 224, 148–157. [Google Scholar] [CrossRef]
- Burkhardt, J. Hygroscopic particles on leaves: Nutrients or desiccants? Ecol. Monogr. 2010, 80, 369–399. [Google Scholar] [CrossRef]
- McDonald, J.D.; Reed, M.D.; Campen, M.J.; Barrett, E.G.; Seagrave, J.; Mauderly, J.L. Health Effects of Inhaled Gasoline Engine Emissions. Inhal. Toxicol. 2007, 19, 107–116. [Google Scholar] [CrossRef] [PubMed]
- Sæbø, A.; Popek, R.; Nawrot, B.; Hanslin, H.M.; Gawronska, H.; Gawroński, S.W. Plant species differences in particulate matter accumulation on leaf surfaces. Sci. Total Environ. 2012, 427–428, 347–354. [Google Scholar] [CrossRef]
- DGB (Directorate General of Budget). National Statistics—Current Index. 2011. Available online: http://www.stat.gov.tw/point.asp?index=4 (accessed on 27 July 2020).
- NLSMC (National Land Surveying and Mapping Center). Land Use Investigation of Taiwan. 2009. Available online: http://lui.nlsc.gov.tw/LUWeb/eng/AboutLU.aspx (accessed on 27 July 2020).
- Morris, P.; Therivel, R. Methods of Environmental Impact Assessment, 3rd ed.; Taylor & Francis: Abingdon, UK, 2009. [Google Scholar]
- Algarni, D.A.; El Hassan, I.M. Comparison of thin plate spline, polynomial, C1-function and Shepard’s interpolation techniques with GPS-derived DEM. Int. J. Appl. Earth Obs. Geoinf. 2001, 3, 155–161. [Google Scholar] [CrossRef]
- Gascon, F.; Bouzinac, C.; Thépaut, O.; Jung, M.; Francesconi, B.; Louis, J.; Lonjou, V.; Lafrance, B.; Massera, S.; Gaudel-Vacaresse, A.; et al. Copernicus Sentinel-2A calibration and products validation status. Remote Sens. 2017, 9, 584. [Google Scholar] [CrossRef]




| Geographic Datasets | Types | Predictor Notations |
|---|---|---|
| National land use inventory | Pure residential (pR), commercial residential (cR), industrial–commercial residential (iR), agricultural (A) | , , , |
| Map of industrial park | Industrial parks in the year of 2010 (iP) | |
| Landmark | 0.25 million landmarks including Chinese restaurant (CR), night market (NM), temple (Te) | , , |
| Digital road network | Local roads (LR), major roads (MR), and expressways (EW) | , , , |
| DTM | DTM with the 20 m spatial resolution (DTM) |
| Land Use Type | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P.A. | U.A. | P.A. | U.A. | P.A. | U.A. | P.A. | U.A. | P.A. | U.A. | P.A. | U.A. | |
| in Percentage (%) | ||||||||||||
| Artificial buildings | 99.9 | 89.3 | 99.6 | 94.9 | 99.9 | 91.7 | 96.8 | 97.5 | 93.2 | 88.9 | 97.4 | 84.1 |
| Vegetation | 96.3 | 99.9 | 98.5 | 99.9 | 97.2 | 99.9 | 99.4 | 98.8 | 96.7 | 98.0 | 94.8 | 99.2 |
| Water bodies | 98.7 | 100.0 | 98.2 | 100.0 | 98.7 | 100.0 | 98.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 |
| Overall acc. | 97.4 | 98.70 | 98 | 98.70 | 96 | 95.5 | ||||||
| Kappa coef. | 95 | 98 | 96 | 98 | 90 | 90 | ||||||
| Class | Potential Predictors | r | |
|---|---|---|---|
| Radius in BA | Notation | ||
| Artificial buildings | 250 m | 0.57 | |
| 500 m | 0.63 | ||
| 750 m | 0.65 | ||
| 1000 m | 0.67 | ||
| 1250 m | 0.66 | ||
| 1500 m | 0.65 | ||
| 1750 m | 0.66 | ||
| 2000 m | 0.66 | ||
| Water bodies | 250 m | −0.19 | |
| 500 m | −0.02 | ||
| 750 m | −0.04 | ||
| 1000 m | 0.06 | ||
| 1250 m | 0.16 | ||
| 1500 m | 0.05 | ||
| 1750 m | −0.19 | ||
| 2000 m | −0.02 | ||
| Vegetation | 250 m | −0.56 | |
| 500 m | −0.63 | ||
| 750 m | −0.66 | ||
| 1000 m | −0.69 | ||
| 1250 m | −0.55 | ||
| 1500 m | −0.70 | ||
| 1750 m | −0.71 | ||
| 2000 m | −0.71 | ||
| Predictor | p-Value | VIF | Part. R2 | R2 | Adj. R2 | RMSE | |
|---|---|---|---|---|---|---|---|
| (Intercept) | 2.03 | 0.26 | - | - | 0.85 | 0.72 | 3.06 |
| PM10 | 0.28 | <0.001 | 1.67 | 70.7% | |||
| 0.01 × 10−3 | <0.001 | 1.41 | 21.2% | ||||
| Wind speed | 1.00 | <0.01 | 1.01 | 12.2% | |||
| SO2 | 1.86 | <0.01 | 1.82 | 7.4% | |||
| 0.71 × 10−4 | <0.1 | 1.01 | 0.7% |
| Predictor | p-Value | VIF | Part. R2 | R2 | Adj. R2 | RMSE | |
|---|---|---|---|---|---|---|---|
| (Intercept) | 1.29 | 0.43 | - | - | 0.68 | 0.7 | 3.14 |
| PM10 | 0.29 | <0.001 | 1.80 | 59.0% | |||
| 0.01 × 10−3 | <0.001 | 1.56 | 13.0% | ||||
| SO2 | 1.75 | <0.01 | 1.82 | 8.0% | |||
| 0.01 × 10−2 | <0.01 | 1.18 | 0.7% |
| Predictor | p-Value | VIF | Part. R2 | R2 | Adj. R2 | RMSE | |
|---|---|---|---|---|---|---|---|
| (Intercept) | 0.55 | 0.8 | - | - | 0.79 | 0.62 | 3.47 |
| PM10 | 0.33 | 0.001 | 1.62 | 33.2% | |||
| SO2 | 3.25 | 0.001 | 1.61 | 16.9% | |||
| Wind Speed | 1.12 | 0.002 | 1.02 | 7.4% | |||
| 0.01 × 10−1 | 0.01 | 1.04 | 5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heriza, D.; Wu, C.-D.; Syariz, M.A.; Lin, C.-H. Analysis of Spatial–Temporal Variability of PM2.5 Concentrations Using Optical Satellite Images and Geographic Information System. Remote Sens. 2023, 15, 2009. https://doi.org/10.3390/rs15082009
Heriza D, Wu C-D, Syariz MA, Lin C-H. Analysis of Spatial–Temporal Variability of PM2.5 Concentrations Using Optical Satellite Images and Geographic Information System. Remote Sensing. 2023; 15(8):2009. https://doi.org/10.3390/rs15082009
Chicago/Turabian StyleHeriza, Dewinta, Chih-Da Wu, Muhammad Aldila Syariz, and Chao-Hung Lin. 2023. "Analysis of Spatial–Temporal Variability of PM2.5 Concentrations Using Optical Satellite Images and Geographic Information System" Remote Sensing 15, no. 8: 2009. https://doi.org/10.3390/rs15082009
APA StyleHeriza, D., Wu, C.-D., Syariz, M. A., & Lin, C.-H. (2023). Analysis of Spatial–Temporal Variability of PM2.5 Concentrations Using Optical Satellite Images and Geographic Information System. Remote Sensing, 15(8), 2009. https://doi.org/10.3390/rs15082009







