Stratospheric Temperature Observations by Narrow Bands Ultra-High Spectral Resolution Sounder from Nadir-Viewing Satellites
Abstract
1. Introduction
2. Spectral Consideration
3. Simulation Analysis on the Sounding Capability of Narrow Band
3.1. The Main Influence Factors of Sounding Capability
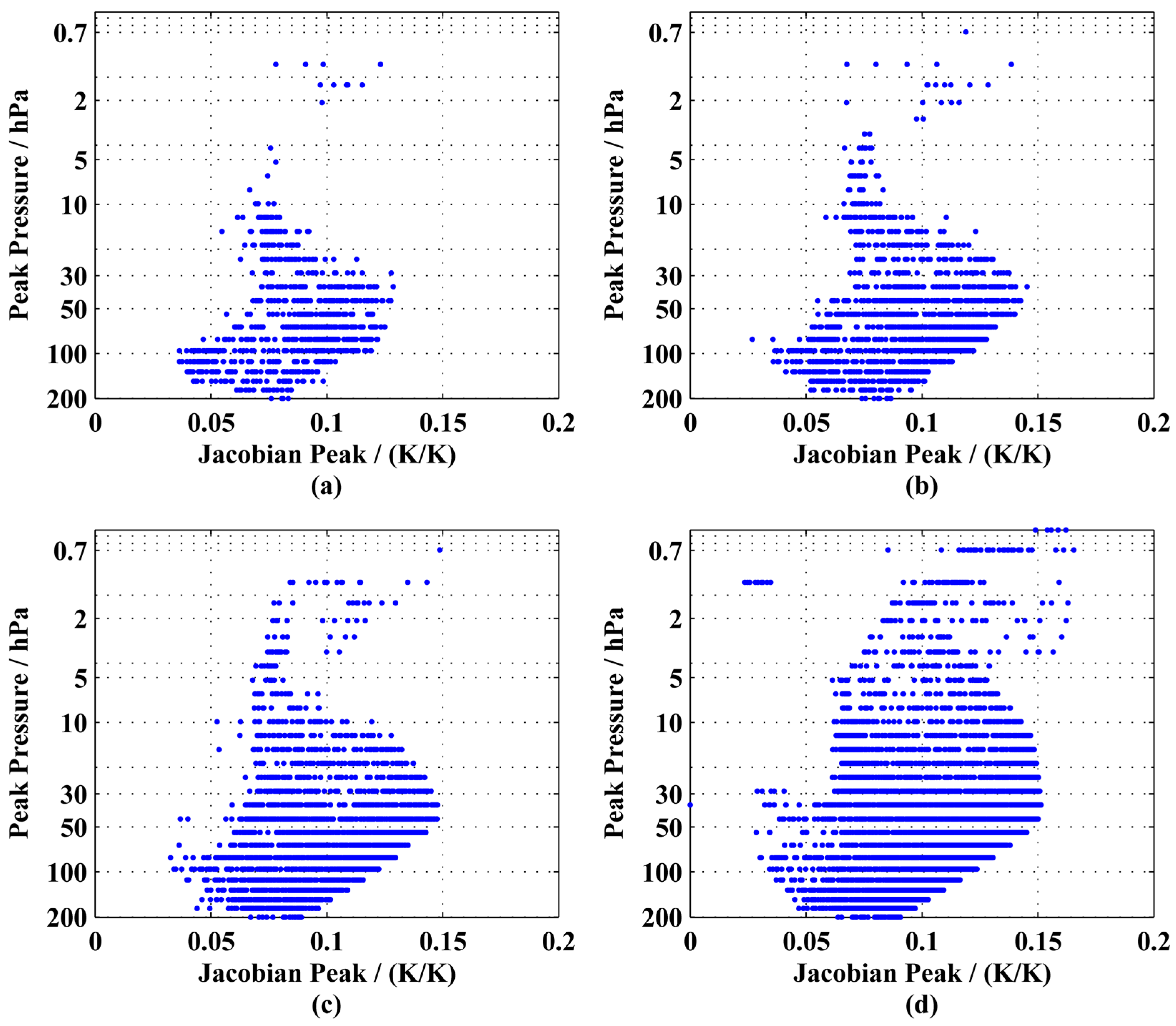
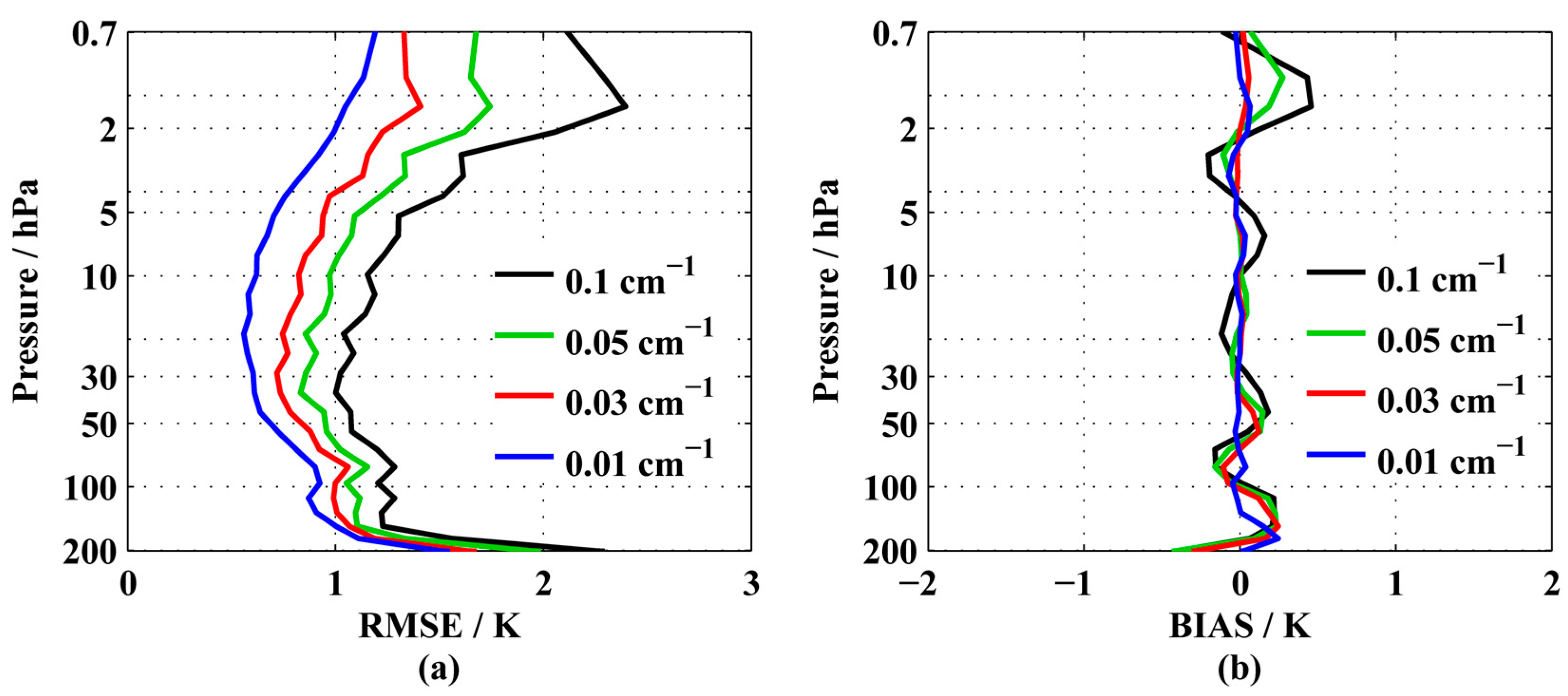
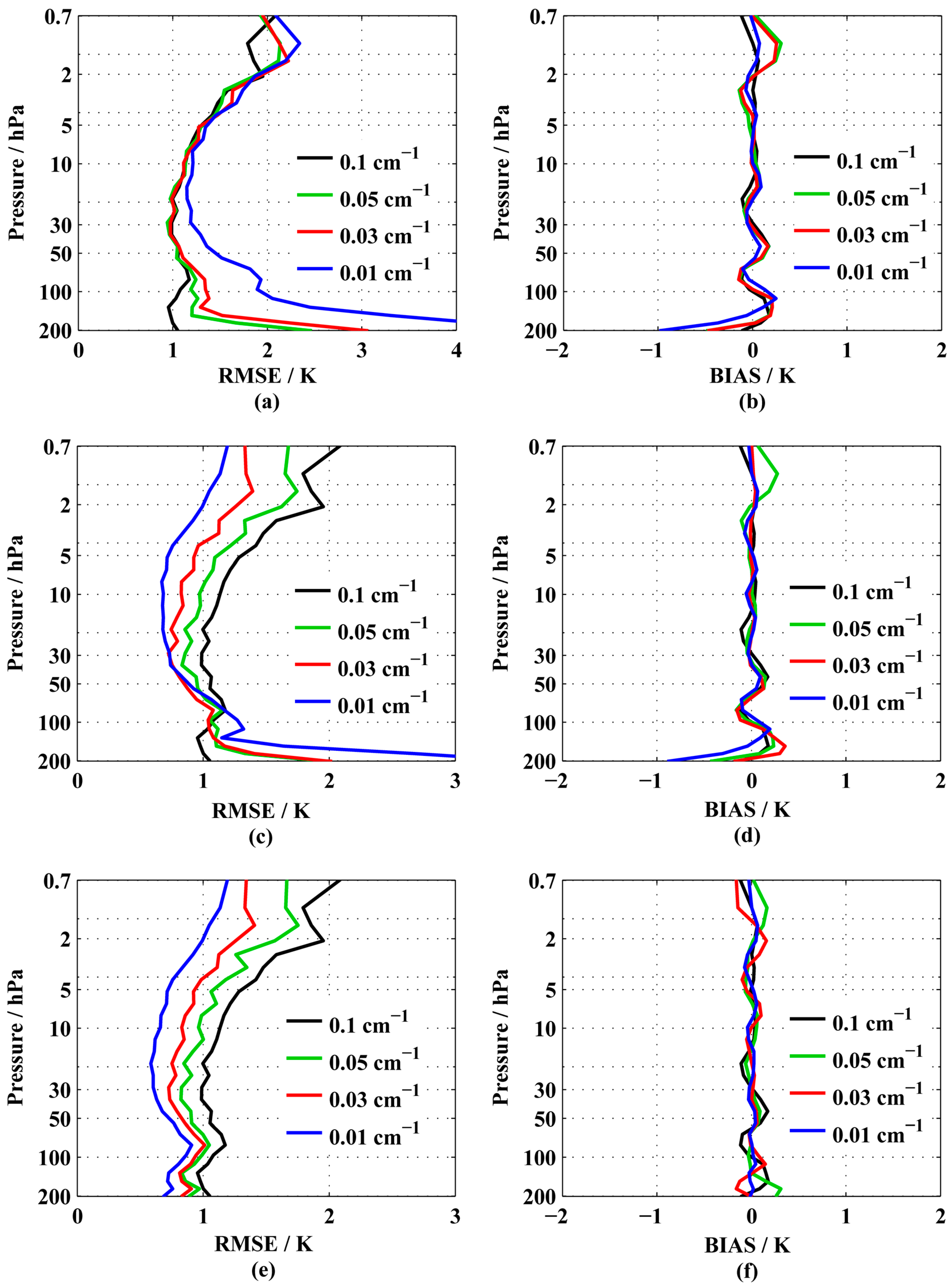
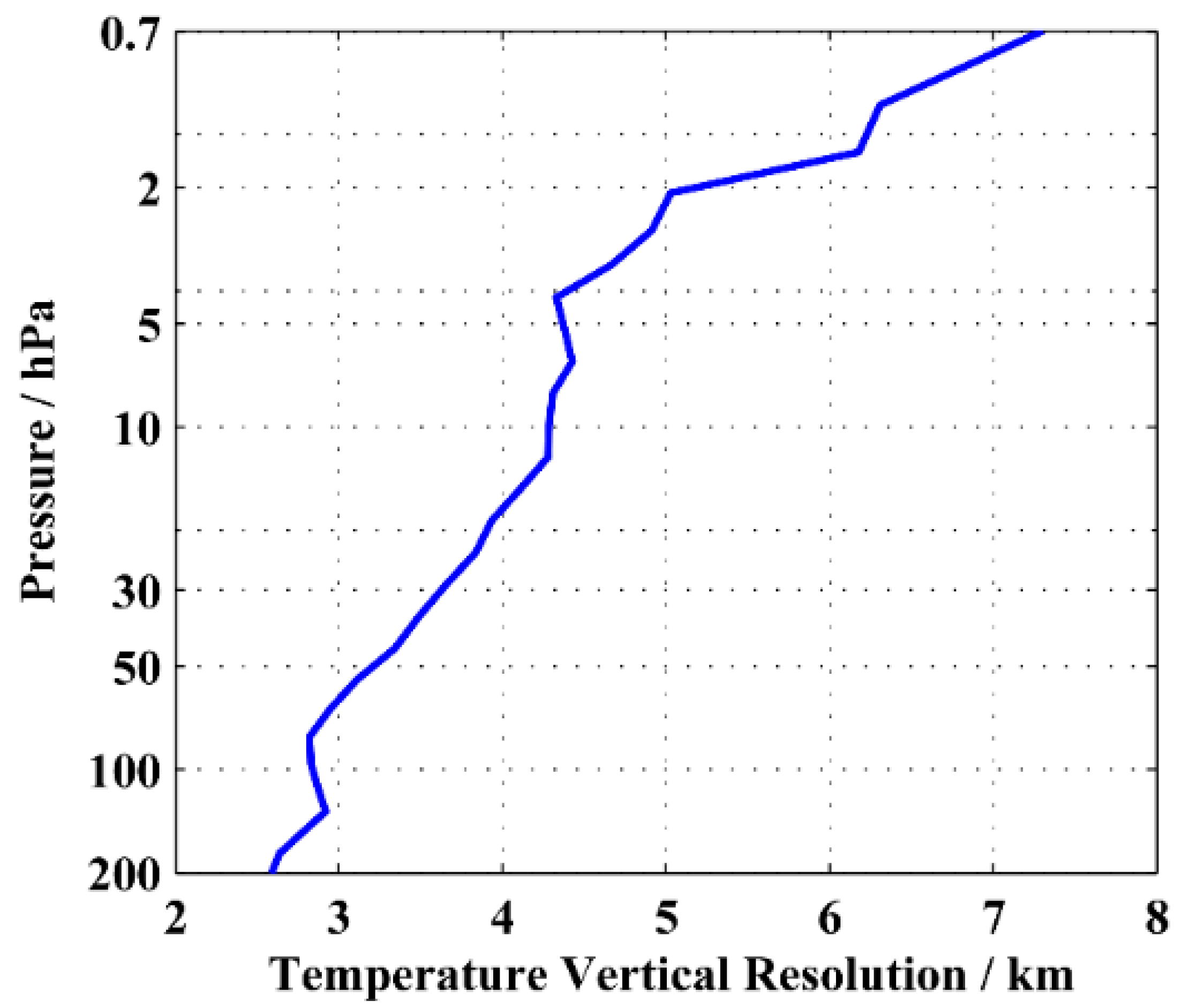
3.1.1. Spectral Resolution
3.1.2. Spectral Range
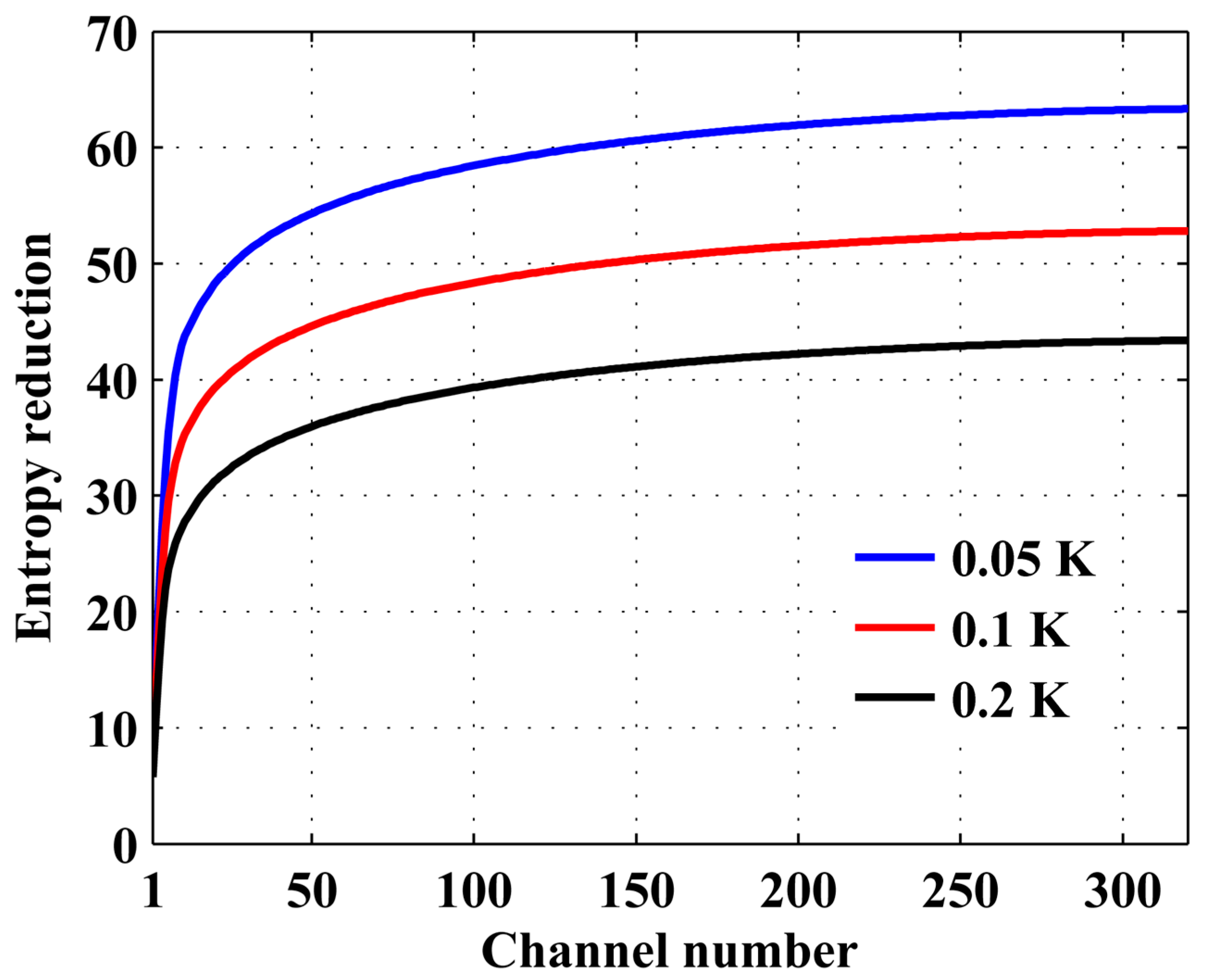
3.1.3. Instrumental Noise
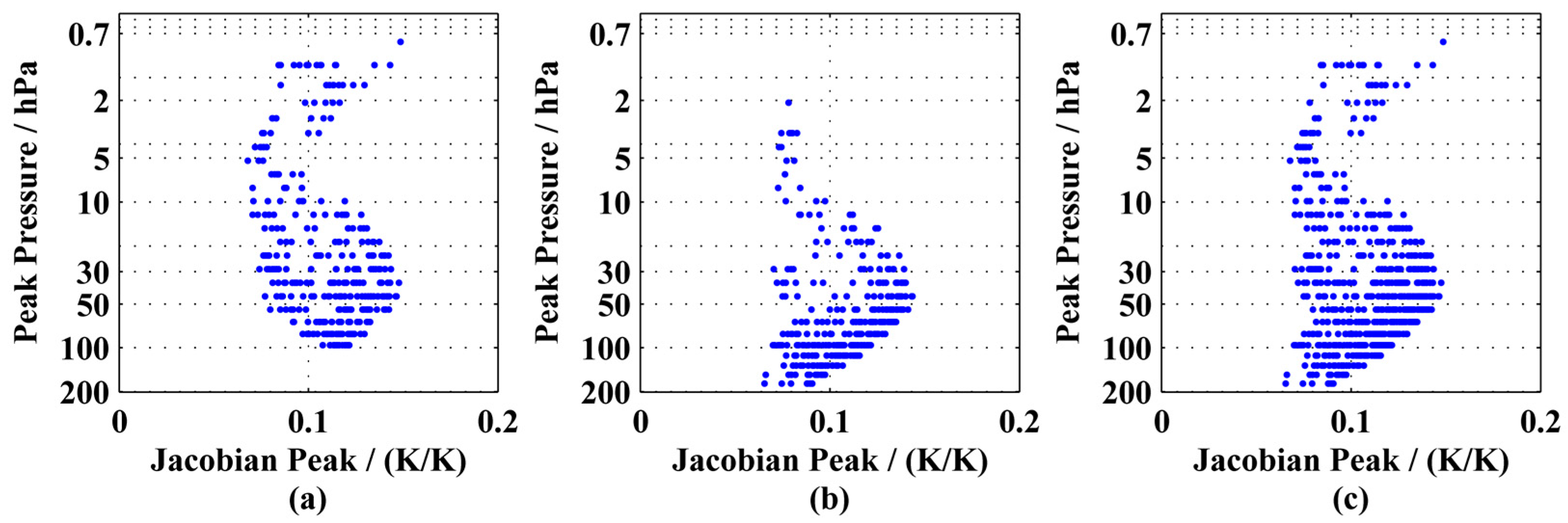
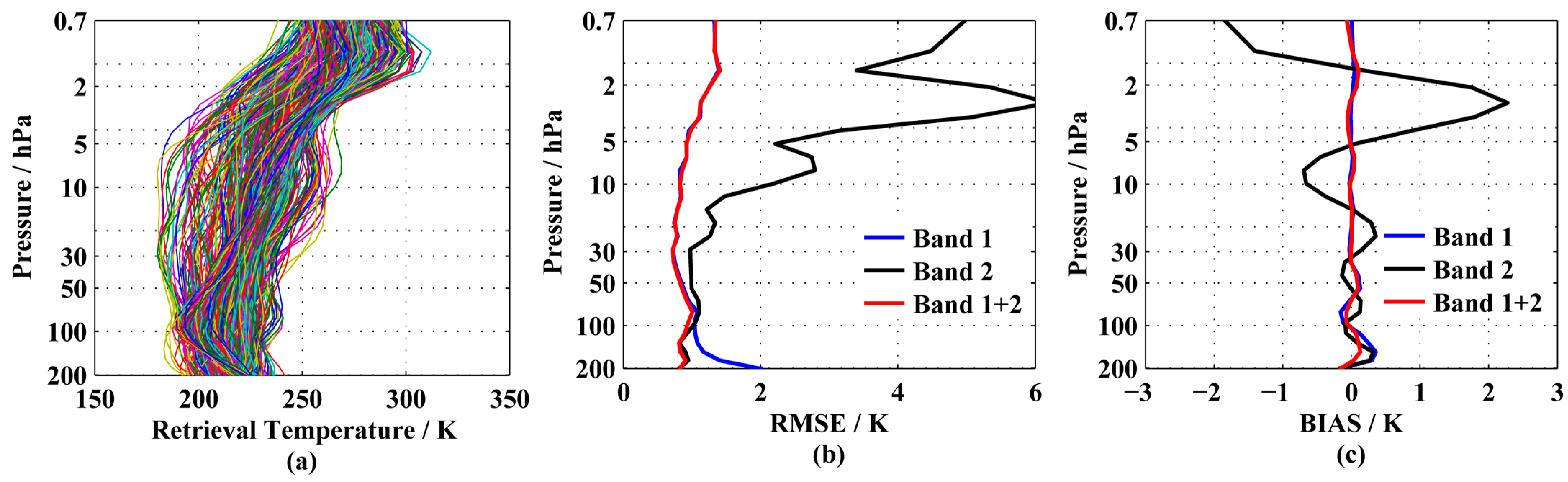
3.2. The Soundings of the Single Spectral Band and Multiple Spectral Bands
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chung, E.S.; Soden, B.J. Investigating the influence of carbon dioxide and the stratosphere on the long-term tropospheric temperature monitoring from HIRS. Am. Meteorol. Soc. 2010, 49, 1927–1937. [Google Scholar] [CrossRef]
- Holton, J.R.; Haynes, P.H.; Mclntyre, M.E.; Douglass, A.R.; Rood, R.B.; Pfister, L. Stratosphere-Troposphere Exchange. Rev. Geophys. 1995, 33, 403–439. [Google Scholar] [CrossRef]
- Meriwether, J.W.; Gerrard, A.J. Mesosphere inversion layers and stratosphere temperature enhancements. Rev. Geophys. 2004, 42, 133. [Google Scholar] [CrossRef]
- Fan, Z.Q.; Sheng, Z.; Shi, H.Q.; Zhang, X.H.; Zhou, C.J. A Characterization of the Quality of the Stratospheric Temperature Distributions from SABER based on Comparisons with COSMIC Data. J. Atmos. Ocean. Technol. 2016, 33, 2401–2413. [Google Scholar] [CrossRef]
- Ramaswamy, V.; Chanin, M.L.; Angell, J.; Barnett, J.; Gaffen, D.; Gelman, M.; Keckhut, P.; Koshelkov, Y.; Labitzke, K.; Lin, J.J.R.; et al. Stratospheric temperature trends: Observations and model simulations. Rev. Geophys. 2001, 39, 71–122. [Google Scholar] [CrossRef]
- Baldwin, M.P.; Thompson, D.W.; Shuckburgh, E.F.; Norton, W.A.; Gillett, N.P. Weather from the stratosphere? Science 2003, 301, 317–319. [Google Scholar] [CrossRef] [PubMed]
- He, M.; Chau, J.L.; Forbes, J.M.; Thorsen, D.; Li, G.; Siddiqui, T.A.; Yamazaki, Y.; Hocking, W.K. Quasi-10-Day Wave and Semidiurnal Tide Nonlinear Interactions During the Southern Hemispheric SSW 2019 Observed in the Northern Hemispheric Mesosphere. Geophys. Res. Lett. 2020, 47, 1453. [Google Scholar] [CrossRef]
- Ma, Z.; Gong, Y.; Zhang, S.; Zhou, Q.; Huang, C.; Huang, K.; Luo, J.; Yu, Y.; Li, G. Study of a Quasi 4-Day Oscillation During the 2018/2019 SSW Over Mohe, China. J. Geophys. Res.-Space 2020, 125, 27687. [Google Scholar] [CrossRef]
- Keckhut, P.; Claud, C.; Funatsu, B.; Hauchecorne, A.; Maury, P.; Khaykin, S.; Pichon, A.L.; Steinbrecht, W. Temperature Trends Observed in the Middle Atmosphere and Future Directions. In Infrasound Monitoring for Atmospheric Studies; Springer: Berlin/Heidelberg, Germany, 2019; pp. 805–823. [Google Scholar]
- Dou, X.; Han, Y.; Sun, D.; Xia, H.; Shu, Z.; Zhao, R.; Shangguan, M.; Guo, J. Mobile Rayleigh Doppler lidar for wind and temperature measurements in the stratosphere and lower mesosphere. Opt. Express 2014, 22, A1203–A1221. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Q.; Hua, D. Preliminary exploration of atmospheric water vapor, liquid water and ice water by ultraviolet Raman lidar. Opt. Express 2019, 27, 36311–36328. [Google Scholar]
- Dudhia, A. Satellites and Satellite Remote Sensing|Temperature Soundings. In Encyclopedia of Atmospheric Sciences; Elsevier: Amsterdam, The Netherlands, 2015; pp. 145–156. [Google Scholar]
- Dong, C.; Li, J.; Zhang, P. The Principle and Application of Satellite Hyperspectral Infrared Atmospheric Remote Sensing, 1st ed.; Science Press: Beijing, China, 2013; pp. 2–9. [Google Scholar]
- Zou, C.Z.; Qian, H. Stratospheric Temperature Climate Data Record from Merged SSU and AMSU-A Observations. J. Atmos. Ocean. Technol. 2016, 33, 1967–1984. [Google Scholar] [CrossRef]
- Li, J.; Wolf, W.W.; Menzel, W.P.; Zhang, W.; Huang, H.L.; Achtor, T.H. Global soundings of the atmosphere from ATOVS measurements: The algorithm and validation. J. Appl. Meteorol. 2000, 39, 1248–1268. [Google Scholar] [CrossRef]
- Irion, F.W.; Kahn, B.H.; Schreier, M.M.; Fetzer, E.J.; Fishbein, E.; Fu, D.; Kalmus, P.; Wilson, R.C.; Wong, S.; Yue, Q. Single-footprint retrievals of temperature, water vapor and cloud properties from AIRS. Atmos. Meas. Technol. 2018, 11, 971–995. [Google Scholar] [CrossRef]
- Grieco, G.; Masiello, G.; Matricardi, M.; Serio, C. Partially scanned interferogram methodology applied to IASI for the retrieval of CO, CO2, CH4 and N2O. Opt. Express 2013, 21, 24753–24769. [Google Scholar] [CrossRef]
- Nalli, N.R.; Gambacorta, A.; Liu, Q.; Barnet, C.D.; Tan, C.; Iturbide-Sanchez, F.; Reale, T.; Sun, B.; Wilson, M.; Borg, L.; et al. Validation of Atmospheric Profile Retrievals from the SNPP NOAA-Unique Combined Atmospheric Processing System. Part 1: Temperature and Moisture. IEEE Trans. Geosci. Remote Sens. 2018, 56, 180–190. [Google Scholar] [CrossRef]
- Coopmann, O.; Fourrie, N.; Guidard, V. Analysis of MTG-IRS observations and general channel selection for numerical weather prediction models. Q. J. R. Meteorol. Soc. 2022, 148, 1864–1885. [Google Scholar] [CrossRef]
- Li, S.; Hu, H.; Fang, C.; Wang, S.; Xun, S.; He, B.; Wu, W.; Huo, Y. Hyperspectral Infrared Atmospheric Sounder (HIRAS) atmospheric sounding system. Remote Sens. 2022, 14, 3882. [Google Scholar] [CrossRef]
- Cai, X.; Bao, Y.; Petropoulos, G.P.; Lu, F.; Lu, Q.; Zhu, L.; Wu, Y. Temperature and humidity profile retrieval from FY4-GIIRS hyperspectral data using artificial neural networks. Remote Sens. 2020, 12, 1872. [Google Scholar] [CrossRef]
- Olsen, E.T. AIRS/AMSU/HSB Version 5 CalVal Status Summary. 2007. Available online: https://docserver.gesdisc.eosdis.nasa.gov/repository/Mission/AIRS/3.7_ScienceDataProductValidation/V5_CalVal_Status_Summary.pdf (accessed on 1 September 2022).
- Schluessel, P. IASI instrument performances just before the launch of MetOp. In Proceedings of the ESA Atmospheric Science Conference, Frascati, Italy, 8–12 May 2006. [Google Scholar]
- Wu, H.; Ni, L.; Wang, N.; Qian, Y.; Tang, B.H.; Li, Z.L. Estimation of Atmospheric Profiles from Hyperspectral Infrared IASI Sensor. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1485–1494. [Google Scholar] [CrossRef]
- Wu, X.; Yao, Z.; Han, Z.; Zhao, Z. Retrieval of Stratospheric Temperature from Radiance Measurements by Infrared Atmospheric Sounding Interferometer. Infrared 2016, 37, 11–17. [Google Scholar]
- Song, C.; Yin, Q. Research on vertical spatial characteristic of satellite infrared hyperspectral atmospheric sounding data. Front. Earth Sci. 2021, 16, 265–276. [Google Scholar] [CrossRef]
- Huang, P.; Guo, Q.; Han, C.; Zhang, C.; Yang, T.; Huang, S. An improved method combining ANN and 1D-Var for the retrieval of atmospheric temperature profiles from FY-4A/GIIRS hyperspectral data. Remote Sens. 2021, 13, 481. [Google Scholar] [CrossRef]
- Aires, F.; Chédin, A.; Scott, N.A.; Rossow, W.B. A regularized neural net approach for retrieval of atmospheric and surface temperatures with the IASI instrument. J. Appl. Meteorol. 2002, 41, 144–159. [Google Scholar] [CrossRef]
- Chang, S.; Sheng, Z.; Du, H.; Ge, W.; Zhang, W. A channel selection method for hyperspectral atmospheric infrared sounders based on layering. Atmos. Meas. Technol. 2020, 13, 629–644. [Google Scholar] [CrossRef]
- Serio, C.; Standfuss, C.; Masiello, G.; Liuzzi, G.; Dufour, E.; Tournier, B.; Stuhlmann, R.; Tjemkes, S.; Antonelli, P. Infrared atmospheric sounder interferometer radiometric noise assessment from spectral residuals. Appl. Opt. 2015, 54, 5924–5936. [Google Scholar] [CrossRef]
- Yang, Y.H.; Yin, Q.; Shu, J. Channel selection of atmosphere vertical sounder (GIIRS) onboard the FY-4A geostationary satellite. J. Infrared Millim. Waves 2018, 37, 545–552. [Google Scholar]
- Yang, X. Retrieval of Temperature for Near Space Atmoshpere Based on Oxygen A-Band Emission Spectrum. Ph.D. Thesis, University of Chinese Academy of Sciences, Beijing, China, 2020. [Google Scholar]
- Zeng, Q. The Principle of Atmospheric Infrared Remote Sensing; Science Press: Beijing, China, 1974; pp. 13–36. [Google Scholar]
- Coopmann, O.; Guidard, V.; Fourrié, N.; Josse, B.; Marécal, V. Update of Infrared Atmospheric Sounding Interferometer (IASI) channel selection with correlated observation errors for numerical weather prediction (NWP). Atmos. Meas. Technol. 2020, 13, 2659–2680. [Google Scholar] [CrossRef]
- Masiello, G.; Matricardi, M.; Serio, C. The use of IASI data to identify systematic errors in the ECMWF forecasts of temperature in the upper stratosphere. Atmos. Chem. Phys. 2011, 11, 1009–1021. [Google Scholar] [CrossRef]
- López-Puertas, M.; Zaragoza, G.; López-Valverde, M.Á.; Taylor, F.W. Non local thermodynamic equilibrium (LTE) atmospheric limb emission at 4.6 μm: 1. An update of the CO2 non-LTE radiative transfer model. J. Geophys. Res. Atmos. 1998, 103, 8499–8513. [Google Scholar] [CrossRef]
- Liu, D.; Dai, C.; Wei, H. CO2 limb radiation in the middle and upper atmosphere: Comparison analysis of simulation and measurement. Infrared Laser Eng. 2016, 45, 154–160. [Google Scholar]
- Barnet, C.D.; Smith, N.; Ide, K.; Garrett, K.; Jones, E. Evaluating the Value of CrIS Shortwave-Infrared Channels in Atmospheric-Sounding Retrievals. Remote Sens. 2023, 15, 547. [Google Scholar] [CrossRef]
- Gordon, I.E.; Rothman, L.S.; Hargreaves, R.J.; Hashemi, R.; Karlovets, E.V.; Skinner, F.M.; Conway, E.K.; Hill, C.; Kochanov, R.V.; Tan, Y.; et al. The HITRAN2020 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2022, 277, 107949. [Google Scholar] [CrossRef]
- Bormann, N.; Collard, A.; Bauer, P. Estimates of spatial and interchannel observation-error characteristics for current sounder radiances for numerical weather prediction. II: Application to AIRS and IASI data. Q. J. R. Meteorol. Soc. 2010, 136, 1051–1063. [Google Scholar] [CrossRef]
- Chu, Q.; Li, X.; Jirigalantu; Sun, C.; Chen, J.; Wang, J.; Sun, Y.; Bayanheshig. Design study of a cross-dispersed spatial heterodyne spectrometer. Opt. Express 2022, 30, 10547–10562. [Google Scholar] [CrossRef]
- Nemeth, G.; Pekker, A. New design and calibration method for a tunable single-grating spatial heterodyne spectrometer. Opt. Express 2020, 28, 22720–22731. [Google Scholar] [CrossRef]
- Englert, C.R.; Babcock, D.D.; Harlander, J.M. Doppler asymmetric spatial heterodyne spectroscopy (DASH): Concept and experimental demonstra. Appl. Opt. 2007, 46, 7297–7307. [Google Scholar] [CrossRef]
- Clough, S.A.; Shephard, M.W.; Mlawer, E.J.; Delamere, J.S.; Iacono, M.J.; Cady-Pereira, K.; Boukabara, S.; Brown, P.D. Atmospheric radiative transfer modeling: A summary of the AER codes. J. Quant. Spectros. Radiat. Transf. 2005, 91, 233–244. [Google Scholar] [CrossRef]
- Wu, X. Study on the Methodology and Applications of Retrieving Atmospheric Parameter Profiles Using Infrared High-Resolution Spectra. Ph.D. Thesis, University of Science and Technology of China, Hefei, China, 2019. [Google Scholar]
- LBLRTM Specification File. Available online: http://rtweb.aer.com/lblrtm_frame.html (accessed on 1 September 2019).
- Lerner, J.A.; Weisz, E.; Kirchengast, G. Temperature and humidity retrieval from simulated Infrared Atmospheric Sounding Interferometer (IASI) measurements. J. Geophys. Res. 2002, 107, 4189–4199. [Google Scholar] [CrossRef]
- Rodgers, C.D. Inverse Methods for Atmospheres: Theory and Practice; World Scientific: Singapore, 2000; pp. 81–85. [Google Scholar]
- Feng, J.; Huang, Y.; Qu, Z. A simulation-experiment-based assessment of retrievals of above-cloud temperature and water vapor using a hyperspectral infrared sounder. Atmos. Meas. Technol. 2021, 14, 5717–5734. [Google Scholar] [CrossRef]
- Fineschi, S.; Watchorn, S.; Fennelly, J.A.; Noto, J.; Waldrop, L.S. 8446-Angstrom observations of neutral oxygen with the Spatial Heterodyne Spectrometer at Millstone Hill. Proc. SPIE 2009, 7438, 111–120. [Google Scholar]
- Wang, F.; Li, J.; Schmit, T.J.; Ackerman, S.A. Trade-off studies of a hyperspectral infrared sounder on a geostationary satellite. Appl. Opt. 2007, 46, 200–209. [Google Scholar] [CrossRef] [PubMed]
- Griffiths, P.R.; Haseth, J.A. Fourier Transform Infrared Spectrometry, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007; pp. 161–176. [Google Scholar]
- Davis, S.P.; Abrams, M.C.; Brault, J.W. Fourier Transform Spectrometry; Academic Press: San Diego, CA, USA, 2001; pp. 119–142. [Google Scholar]
- Solheim, B.; Brown, S.; Sioris, C.; Shepherd, G. SWIFT-DASH: Spatial Heterodyne Spectroscopy Approach to Stratospheric Wind and Ozone Measurement. Atmos. Ocean 2013, 53, 50–57. [Google Scholar] [CrossRef]
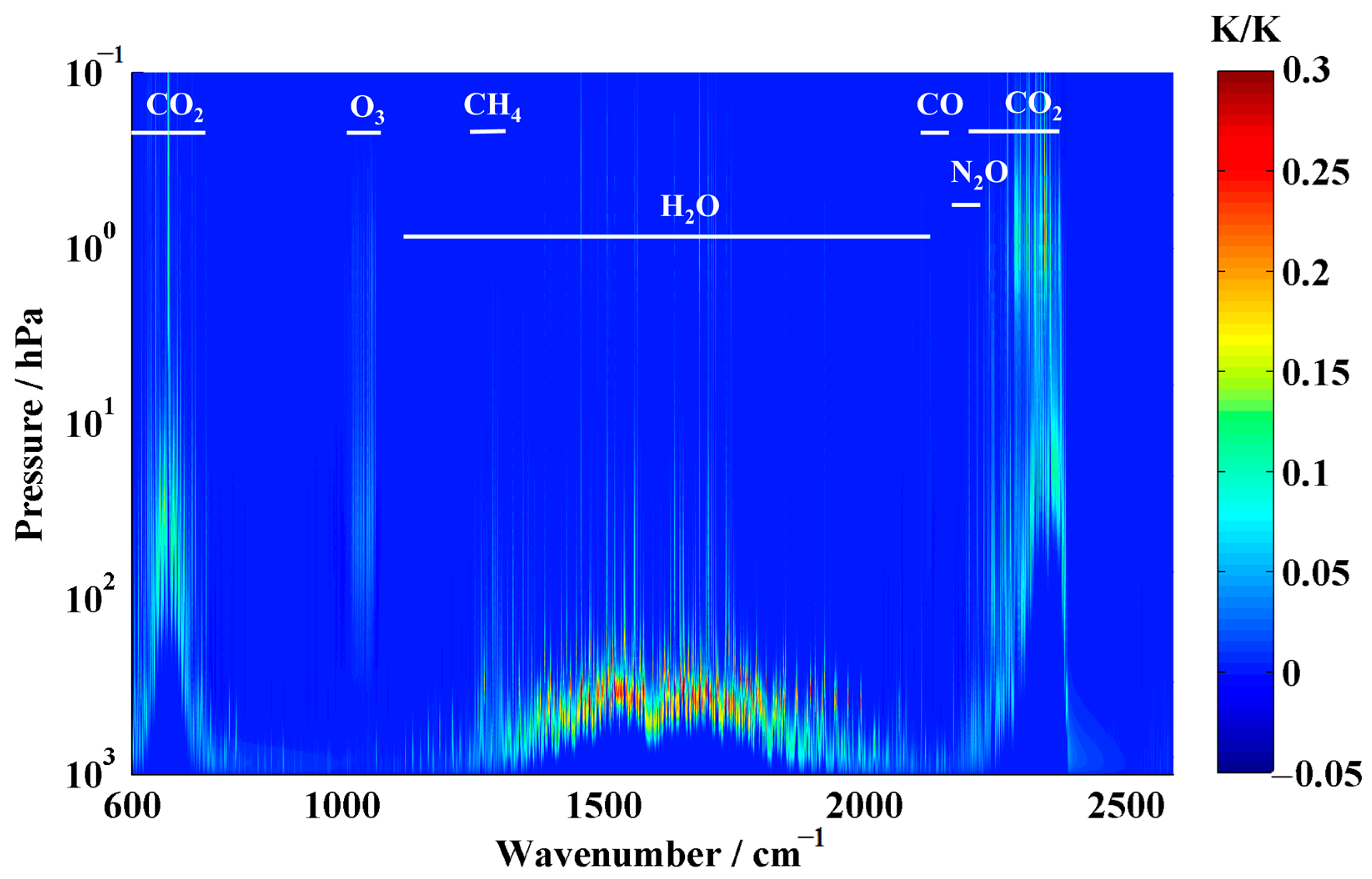


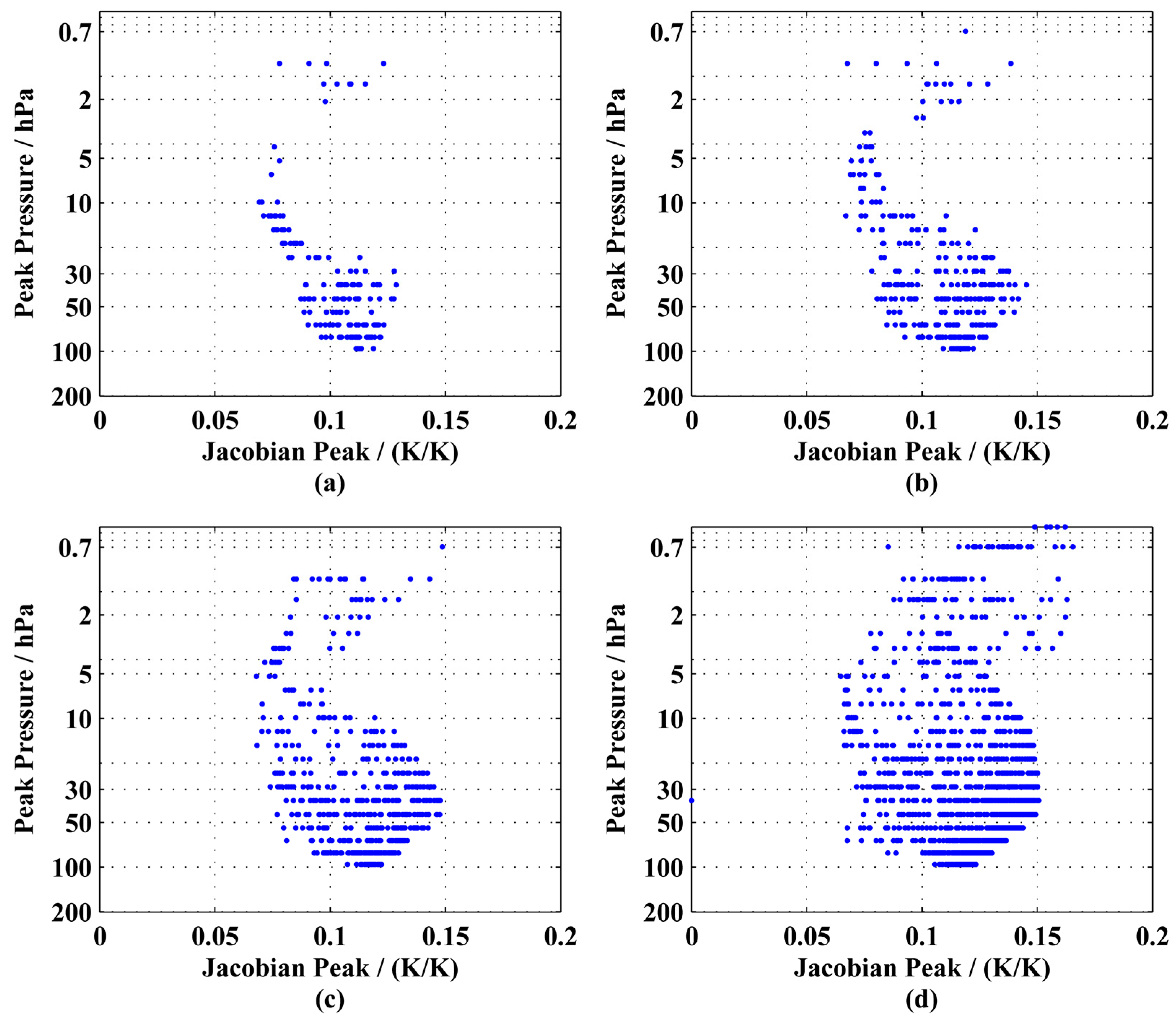

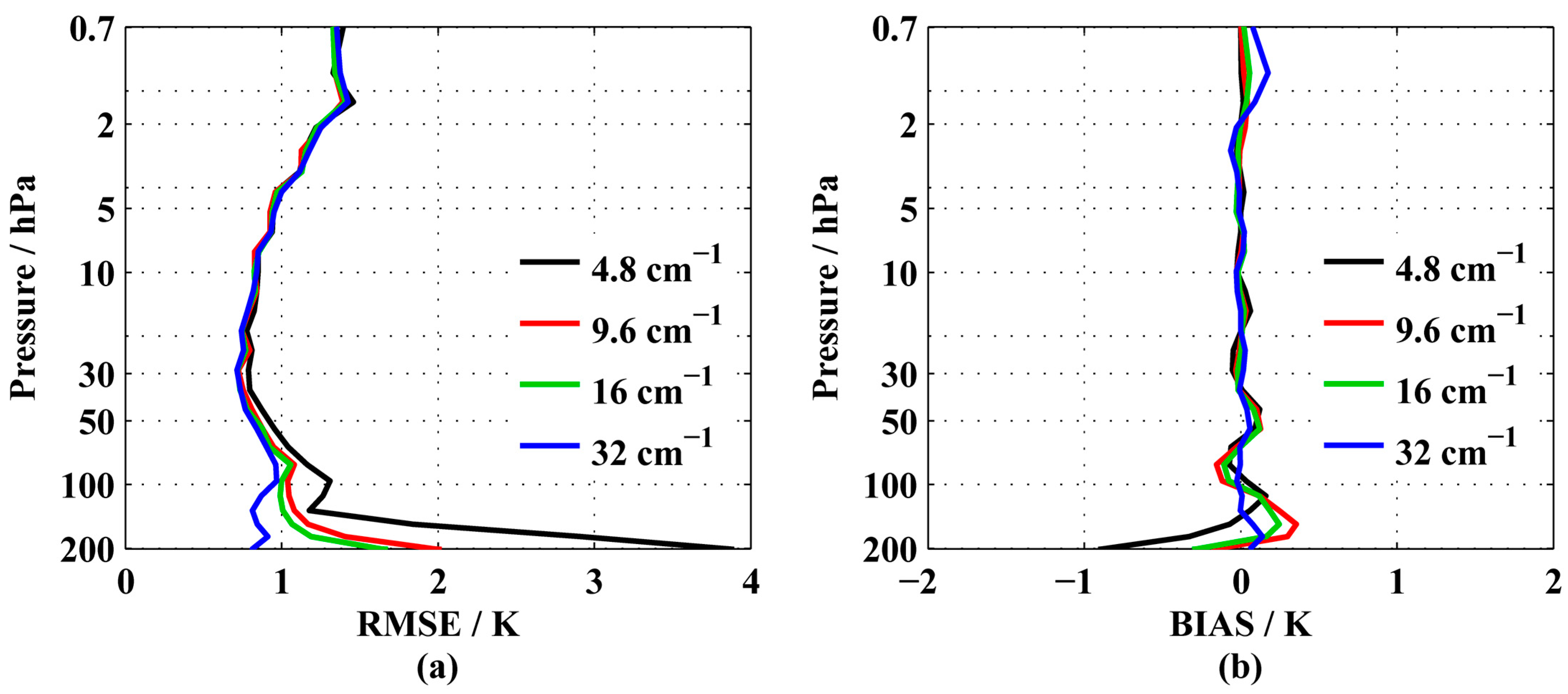
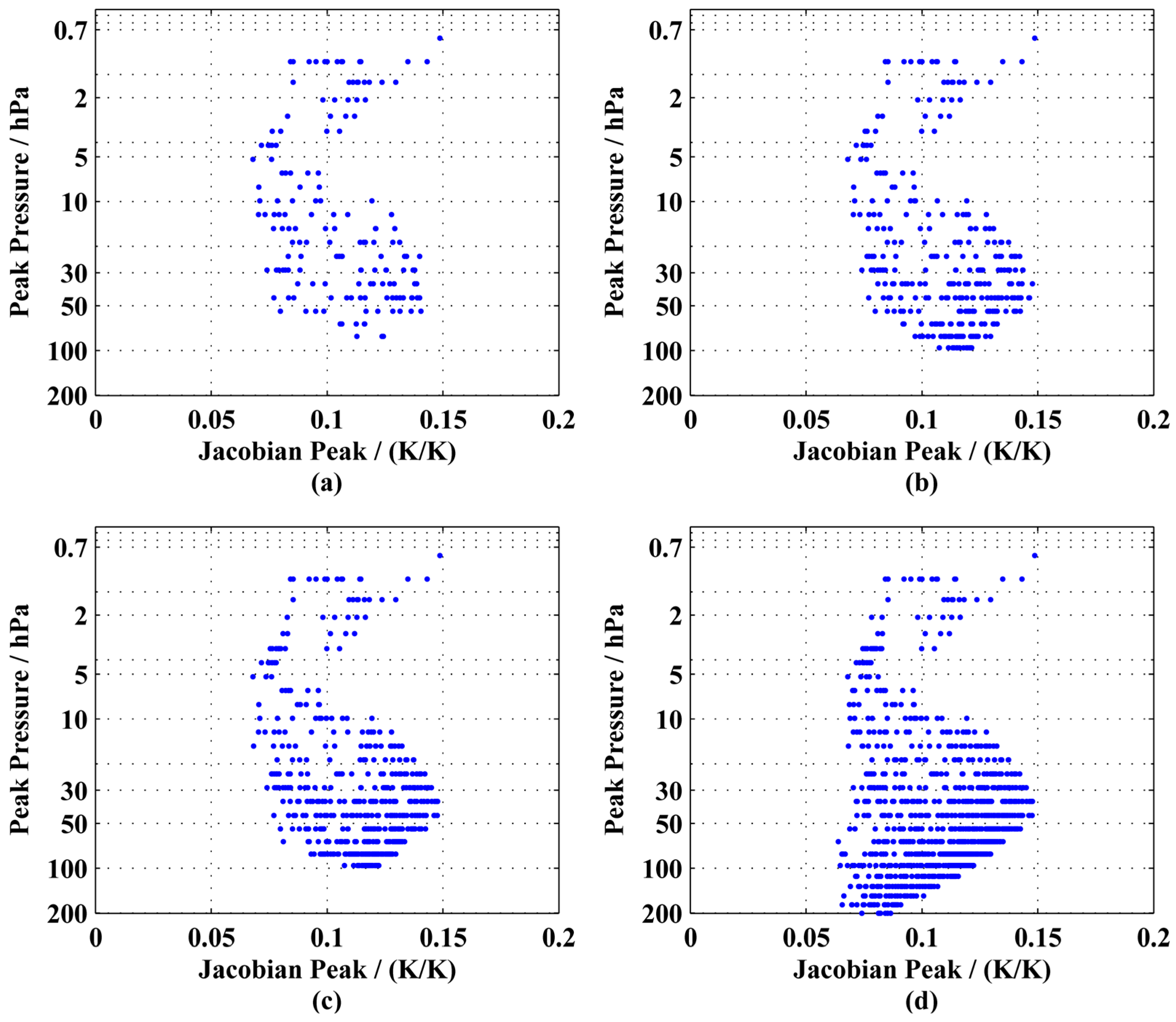
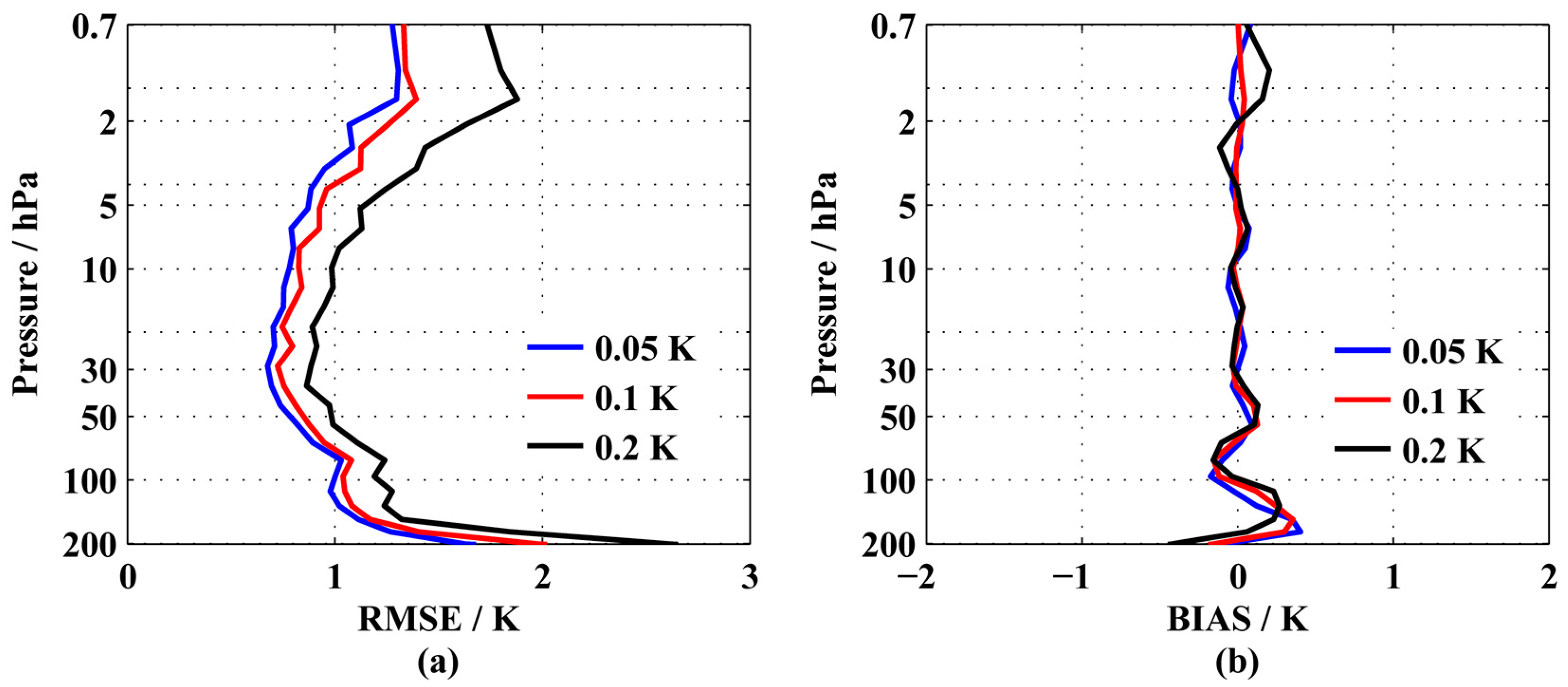
| Satellite | Instrument | Technique | Spectral Range/cm−1 | Spectral Resolution/cm−1 | Channels | NeDT/NeDR |
|---|---|---|---|---|---|---|
| EOS-Aqua | AIRS | GS | 650–1135 1215–1615 2180–2665 | 0.5 1.2 2 | 2378 | 0.15–0.35 K @280 K |
| MetOp | IASI | MI | 645–1210 1210–2000 2000–2760 | 0.5 (a spectral sampling of 0.25) | 8461 | 0.2–0.3 K@280 K 0.2–0.5 K@280 K 0.5–2 K@280 K |
| SNPP | CrIS | MI | 650–1095 1210–1750 2155–2550 | 0.625 1.25 2.5 | 1305 | 0.1–0.5 K@250 K |
| MTG | IRS | MI | 680–1210 1600–2250 | ~0.625 | 1960 | 0.17 K @280 K |
| FY-3 | HIRAS | MI | 667–1136 1210–1750 2155–2550 | 0.625 1.25 2.5 | 1343 | 0.15 K@250 K 0.2 K@250 K 0.3 K@250 K |
| FY-4 | GIIRS | MI | 680–1130 1650–2250 | 0.625 | 1682 | 0.5 mW/m2 srcm−1 0.1 mW/m2 srcm−1 |
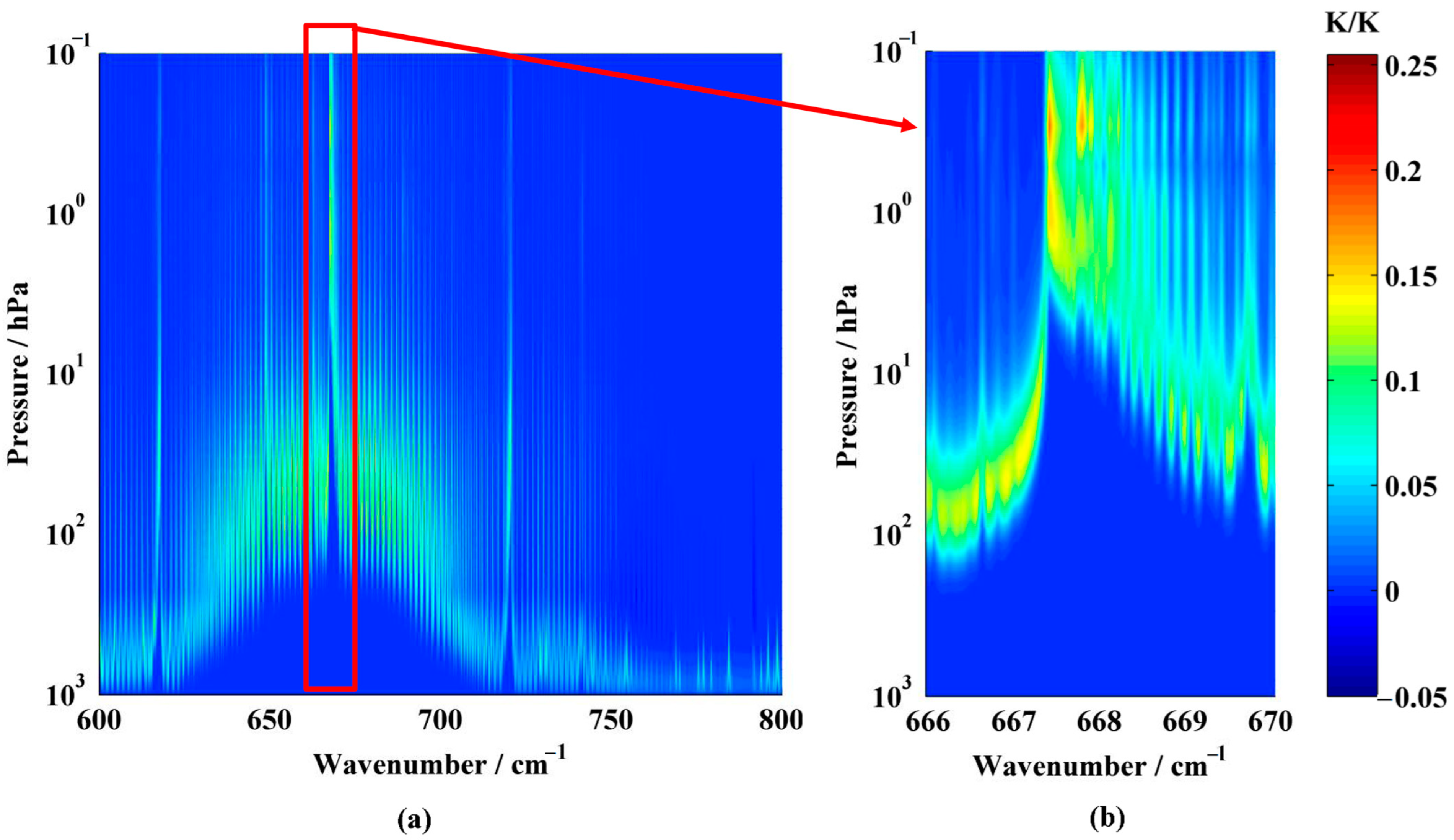
| Spectral Resolution/cm−1 | Spectral Region/cm−1 | Spectral Range/cm−1 |
|---|---|---|
| 0.1 | 659.60–691.50 | 32 |
| 0.05 | 666.70–682.65 | 16 |
| 0.03 | 666.87–676.44 | 9.6 |
| 0.01 | 667.32–670.51 | 3.2 |
| Spectral Resolution/cm−1 | Spectral Region/cm−1 | Spectral Range/cm−1 | Pressure Range/Height |
|---|---|---|---|
| 0.1 | 659.60–691.50 | 32 | 200–0.7 hPa/11.5–50 km |
| 0.05 | 666.70–682.65 | 16 | 80–0.7 hPa/17.5–50 km |
| 682.70–698.65 | 200–80 hPa/11.5–17.5 km | ||
| 0.03 | 666.87–676.44 | 9.6 | 80–0.7 hPa/17.5–50 km |
| 683.58–693.15 | 200–80 hPa/11.5–17.5 km | ||
| 0.01 | 638.98–642.17 | 3.2 | 200–80 hPa/11.5–17.5 km |
| 658.09–661.28 | 80–10 hPa/17.5–31 km | ||
| 667.32–670.51 | 10–0.7 hPa/31–50 km |
| Parameters | Value |
|---|---|
| Spectral region | Band 1: 666.87–676.44 cm−1 Band 2: 683.58–693.15 cm−1 |
| Spectral resolution | 0.03 cm−1 |
| Horizontal pixel number | 640 |
| Vertical pixel number | 512 |
| Pixel pitch | 30 μm |
| NeDT | ~0.1 K@ 226 K |
| Exposure time | 1.15 s |
| F number | 1.2 |
| Transmittance | 0.2 |
| Detectivity | 2.8 × 1011 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Feng, Y.; Fu, D.; Kong, L.; Li, H.; Han, B.; Lu, F. Stratospheric Temperature Observations by Narrow Bands Ultra-High Spectral Resolution Sounder from Nadir-Viewing Satellites. Remote Sens. 2023, 15, 1967. https://doi.org/10.3390/rs15081967
Wang S, Feng Y, Fu D, Kong L, Li H, Han B, Lu F. Stratospheric Temperature Observations by Narrow Bands Ultra-High Spectral Resolution Sounder from Nadir-Viewing Satellites. Remote Sensing. 2023; 15(8):1967. https://doi.org/10.3390/rs15081967
Chicago/Turabian StyleWang, Sufeng, Yutao Feng, Di Fu, Liang Kong, Hongbo Li, Bin Han, and Feng Lu. 2023. "Stratospheric Temperature Observations by Narrow Bands Ultra-High Spectral Resolution Sounder from Nadir-Viewing Satellites" Remote Sensing 15, no. 8: 1967. https://doi.org/10.3390/rs15081967
APA StyleWang, S., Feng, Y., Fu, D., Kong, L., Li, H., Han, B., & Lu, F. (2023). Stratospheric Temperature Observations by Narrow Bands Ultra-High Spectral Resolution Sounder from Nadir-Viewing Satellites. Remote Sensing, 15(8), 1967. https://doi.org/10.3390/rs15081967






