Learning-Based Traffic Scheduling in Non-Stationary Multipath 5G Non-Terrestrial Networks
Abstract
1. Introduction
- We provide a learning-based method for selecting an optimal MPR-based policy according to the time-varying satellite elevation angle. We also provide a mechanism for reliable estimation of the non-stationary LOS probability.
- By including MPR capabilities in our transmission policy, we allow the UE to transmit on multiple satellite links to improve link availability and data rates and minimize end-to-end (E2E) loss.
- The novelty in this work is that we provide a self-learning-based LOS tracking mechanism that can work in scenarios with non-stationary link state transition probabilities, which is a challenge in NTN mobile systems.
1.1. Related Work
1.1.1. Multipath Traffic Scheduling and Protection
1.1.2. RL-Based Traffic Scheduling
1.1.3. LOS Prediction and Tracking
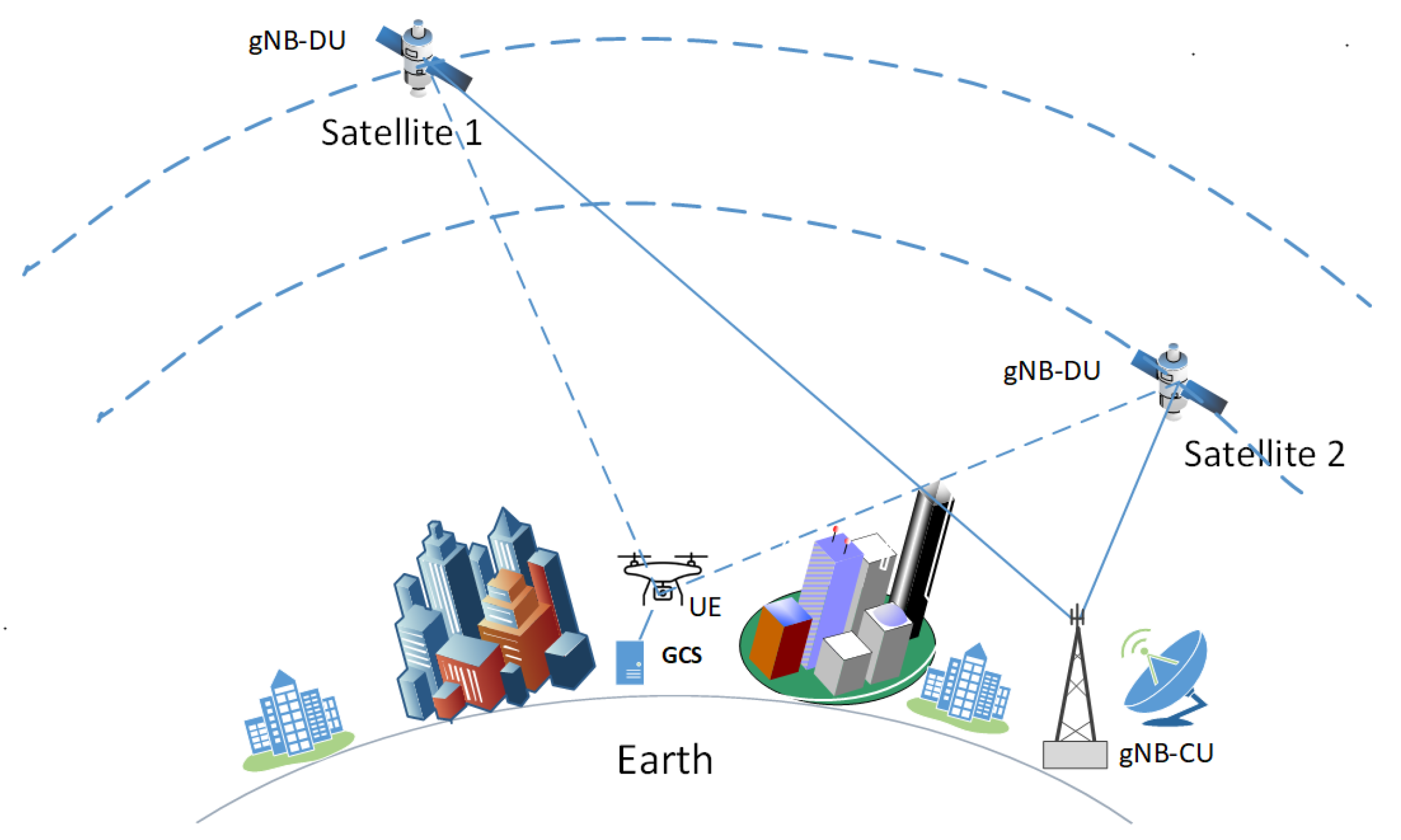
2. Materials and Methods
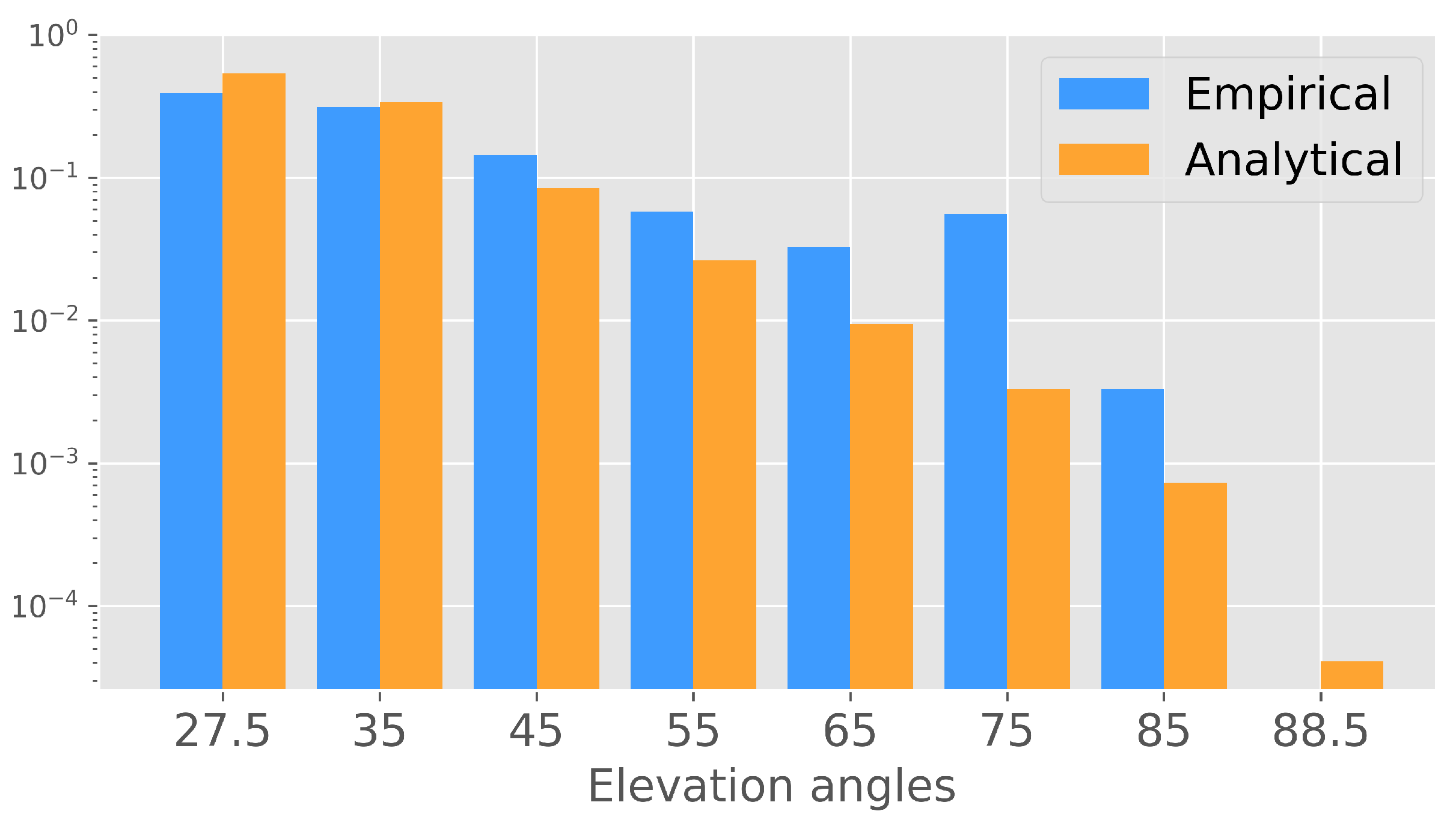
2.1. Channel Model
2.2. Problem Formulation
- State space: We assumed the state of each selected channel to be a binary variable with values in so that we could formally define the state of the link at time t as follows:Each of the N links dynamically changes its state between LOS and NLOS according to its own transition matrix as defined in [28]. In our use case, we assumed that the number of available links was so that we could define the link state space as the set of vectors , which generates a state space .
- : An action constitutes the choice of the appropriate transmission pattern (i.e., a subset of the N links). The action space is the set of vectors , where indicates that the nth link is selected and it is otherwise for . In this case study, we assumed that we had a pair of radio interfaces (i.e., ), which led to having an action space .
- : The immediate reward is defined as a penalty to the agent and is proportional to the E2E loss rate above the threshold calculated over an episode, as in the following equation:where is the E2E loss, is the E2E loss threshold and is the number of transmission links used in the previous episode. The first term in the equation encourages the use of double transmissions when there are losses, while the second term conserves bandwidth in favorable link conditions.
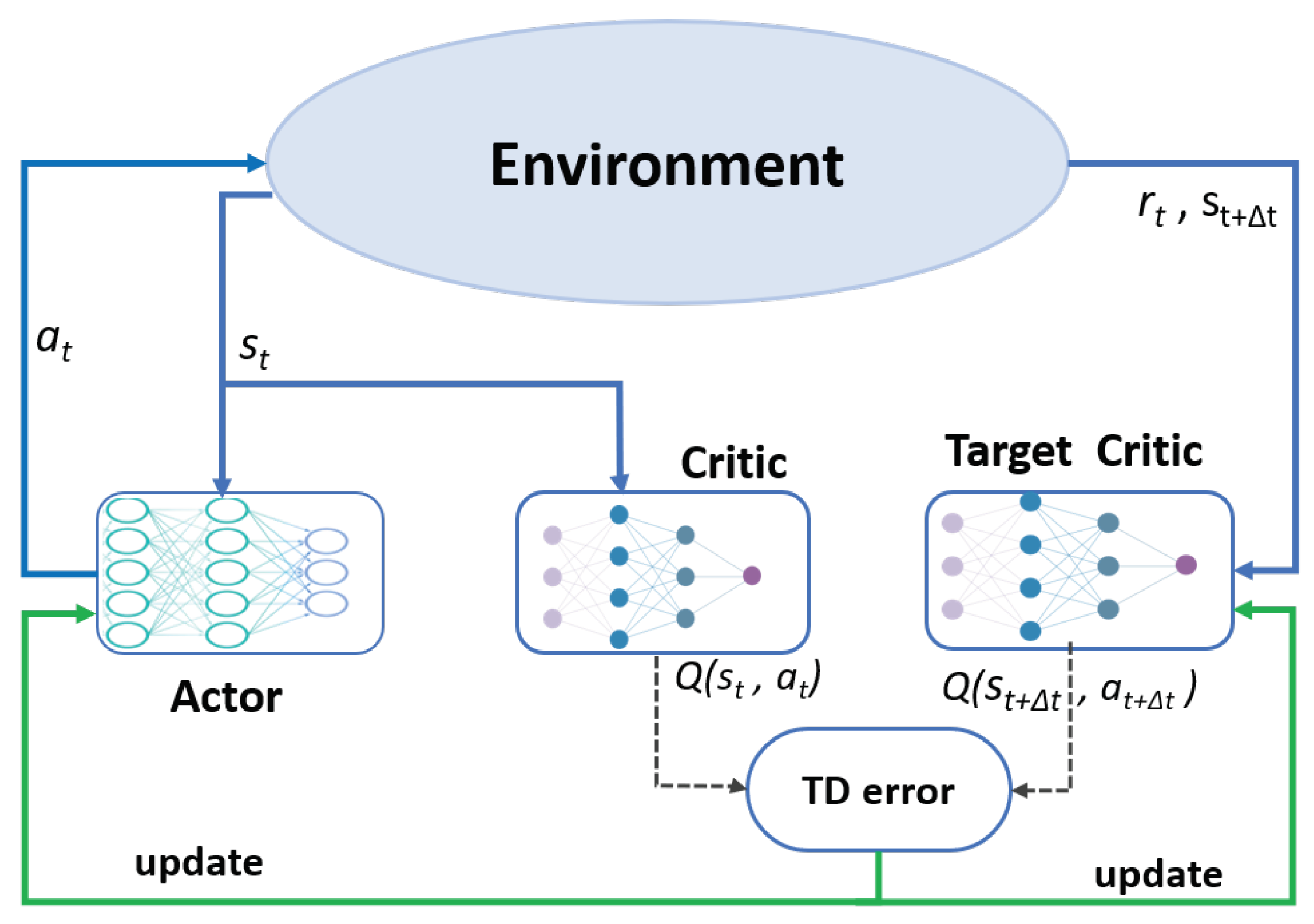
2.3. Actor-Critic RL Architecture
- Actor: The actor explores a policy that maps the agent’s observation of the state to the action space using the mapping policy which is the function of the state:. To explore the optimal policy , the actor selects actions from the action space and optimizes its selection policy in order to maximize the long-term rewards. The selected action is given byThe agent’s optimization goal of the long-term rewards can be represented bywhere is the discounting factor.
- Critic: The critic is used to estimate the state-action value , which gives the goodness of the action selected by the actor at time t and state and is used to optimize the agent’s selection policy in the direction of maximizing future rewards.
- Target-Critic: To overcome the instability problem of the critic due to frequent updates, we use a third network, the target-critic network, to perform the Bellman’s estimation of the future state-action values. When the action is taken at time t and executed by the agent by transmitting the traffic over the network, the received feedback from the environment is sent to the target critic to estimate the future state-action value. The feedback includes the instant reward and the next state of the environment (transmission paths). The future state-action values are estimated as follows:
Updating the Networks
2.4. The Learning Process of the AC Agent
| Algorithm 1 The training procedure for the AC-DRL agent for traffic scheduling |
|
2.5. Simulation Set-Up
3. Results
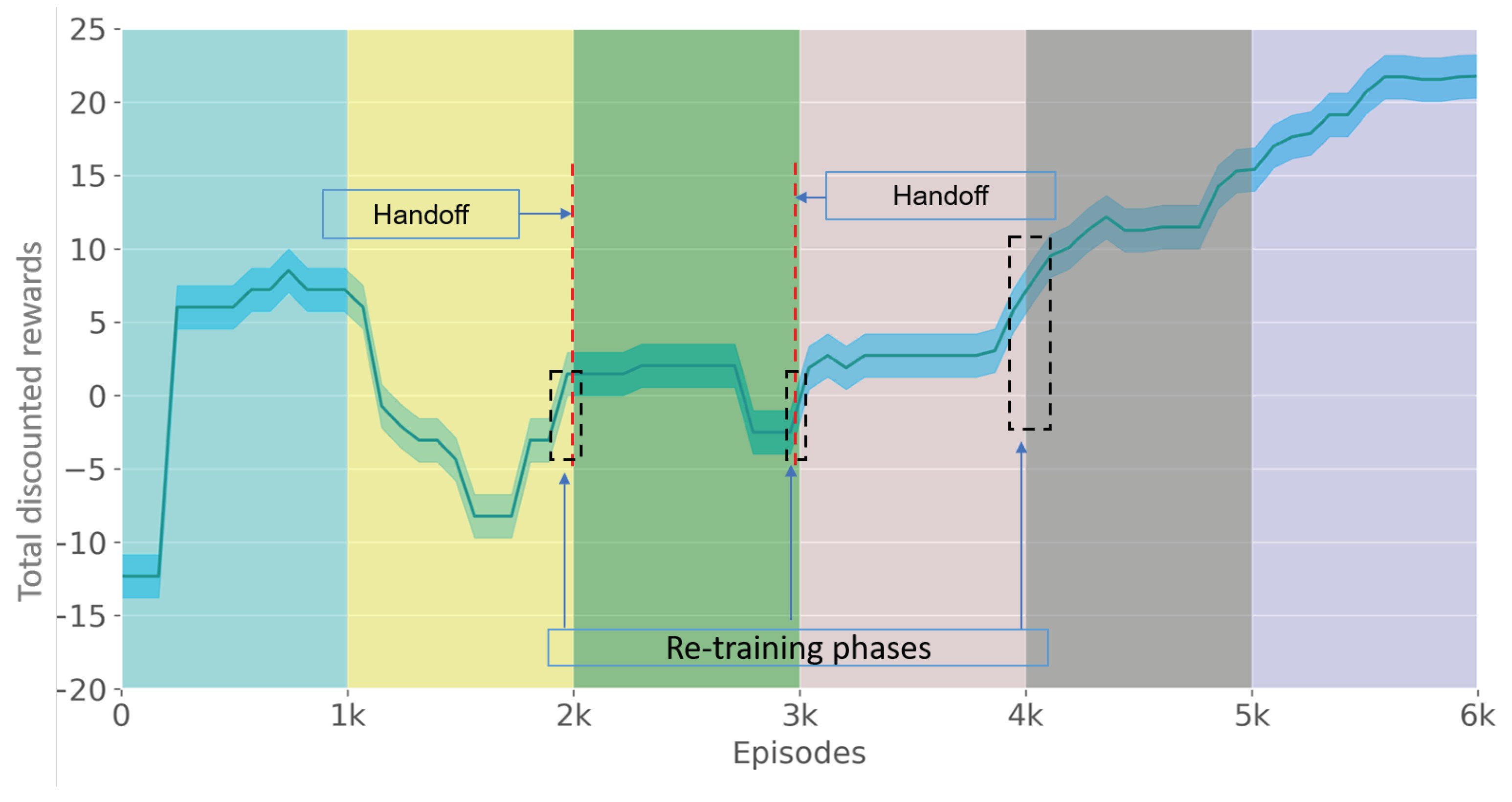
3.1. The AC Agent Learning Performance
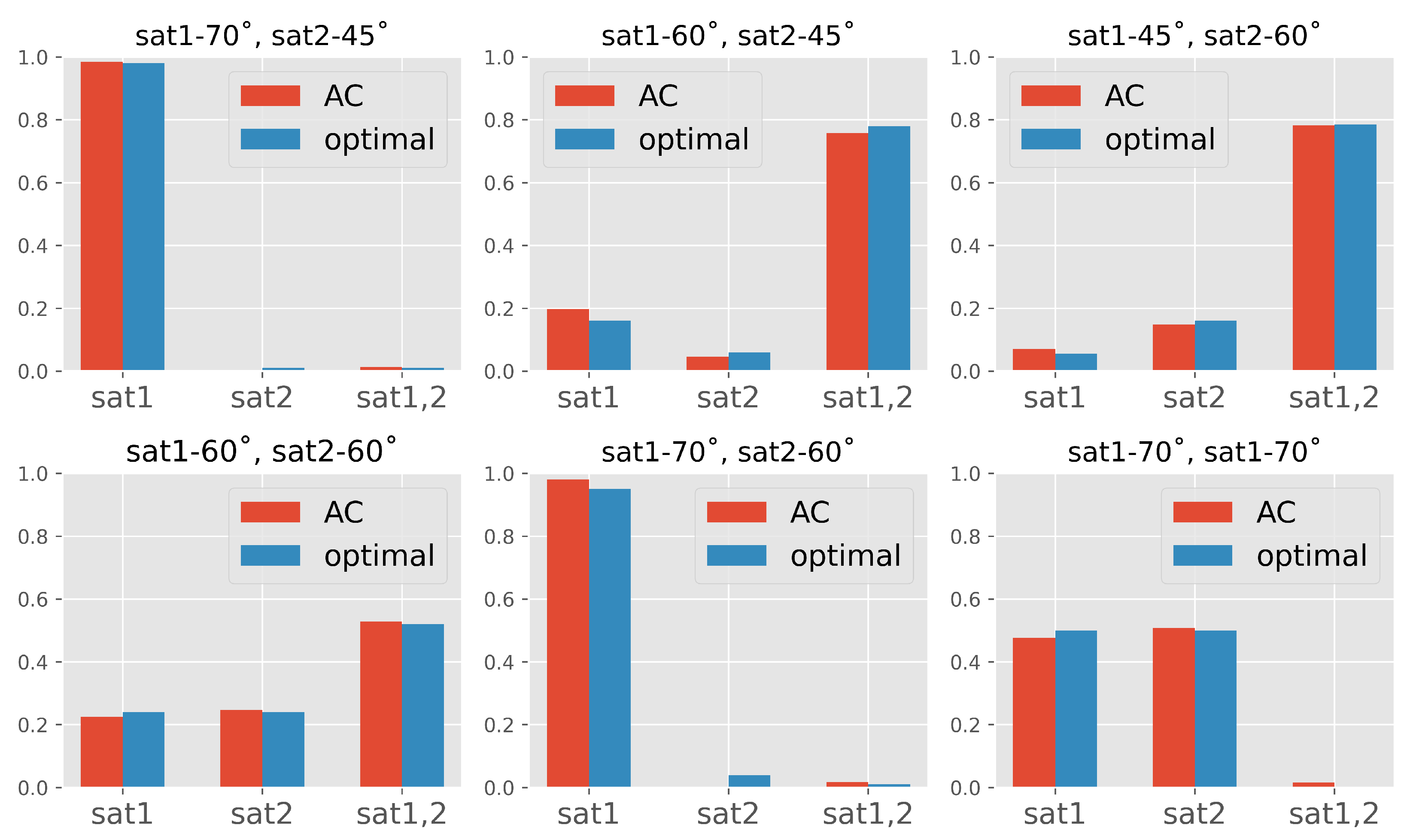
3.2. Path Selection
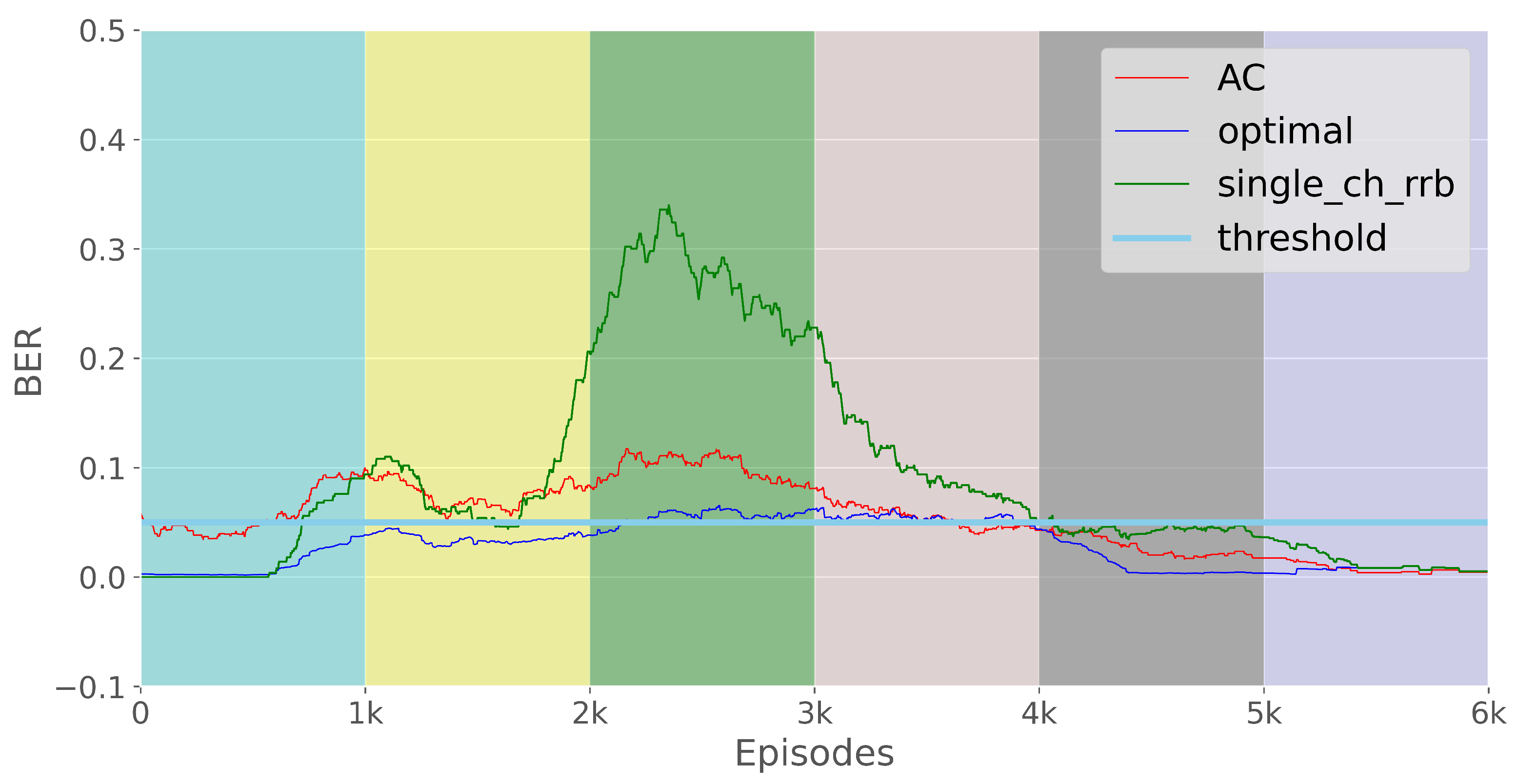
3.3. E2E Loss Rate
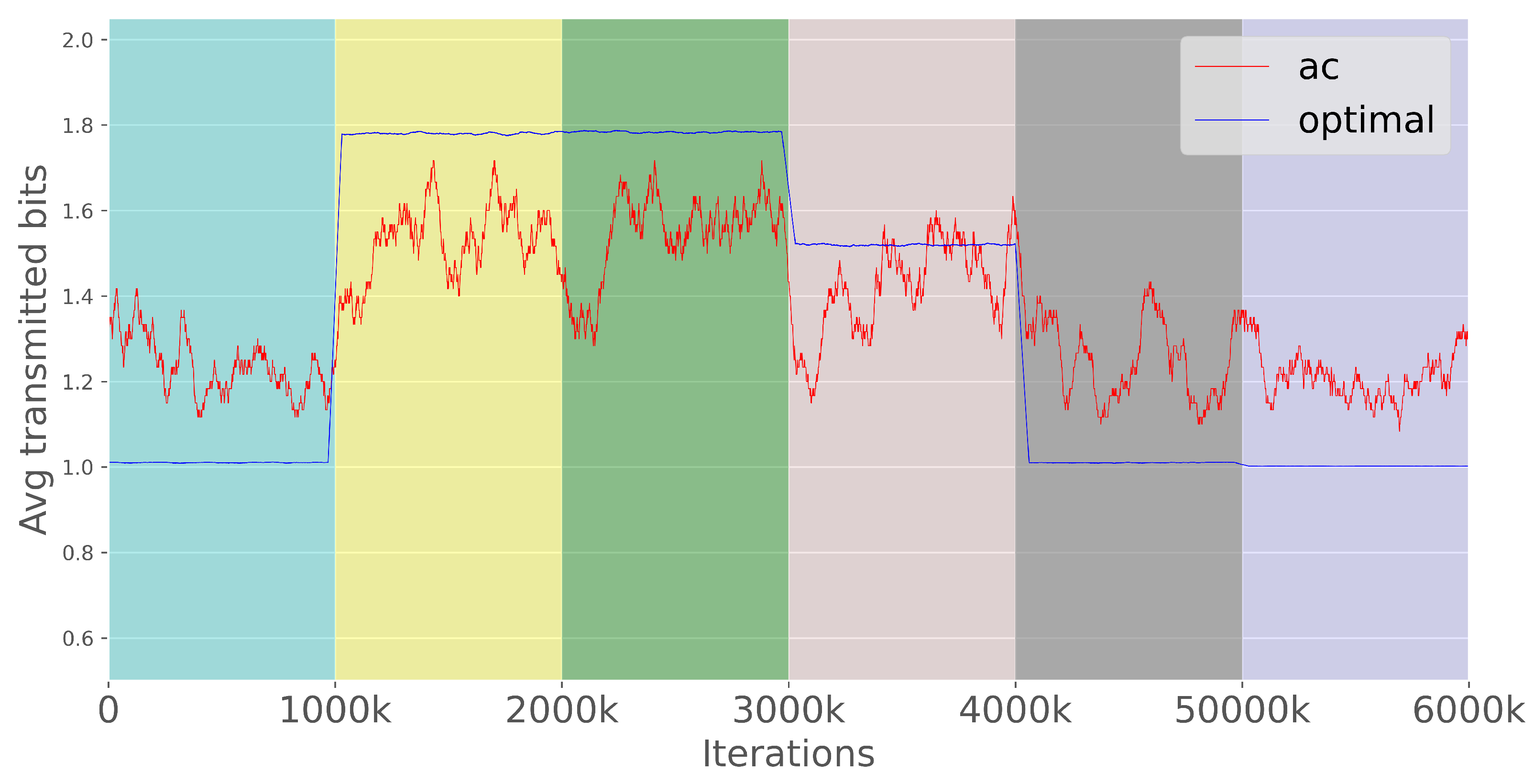
3.4. Bandwidth Utilization
4. Discussion
4.1. Learning Performance
4.2. Path Selection Performance
4.3. Tracking the E2E Loss Threshold
4.4. Bandwidth Utilization
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bacco, M.; Davoli, F.; Giambene, G.; Gotta, A.; Luglio, M.; Marchese, M.; Patrone, F.; Roseti, C. Networking Challenges for Non-Terrestrial Networks Exploitation in 5G. In Proceedings of the IEEE 2nd 5G World Forum (5GWF), Dresden, Germany, 30 September–2 October 2019; pp. 623–628. [Google Scholar]
- 3GPP. Technical Specification Group Radio Access Network; Solutions for NR to Support Non-Terrestrial Networks (NTN): TR 38.821 V16.1.0 (2021-05), (Release 16). Available online: https://portal.3gpp.org/desktopmodules/Specifications/SpecificationDetails.aspx?specificationId=3525 (accessed on 5 January 2023).
- Machumilane, A.; Gotta, A.; Cassarà, P.; Bacco, M. A Path-Aware Scheduler for Air-to-Ground Multipath Multimedia Delivery in Real Time. IEEE Commun. Mag. 2022, 60, 54–58. [Google Scholar] [CrossRef]
- Bacco, M.; Cassará, P.; Gotta, A.; Pellegrini, V. Real-Time Multipath Multimedia Traffic in Cellular Networks for Command and Control Applications. In Proceedings of the 2019 IEEE 90th Vehicular Technology Conference (VTC2019-Fall), Honolulu, HI, USA, 22–25 September 2019; pp. 1–5. [Google Scholar]
- Recommendation, I. Propagation Data Required for The design of Earth-Space Land Mobile Telecommunication Systems; International Telecommunication Union: Geneva, Switzerland, 2017; pp. 681–710. [Google Scholar]
- Paasch, C.; Ferlin, S.; Alay, O.; Bonaventure, O. Experimental Evaluation of Multipath TCP Schedulers. In Proceedings of the ACM SIGCOMM Workshop on Capacity Sharing Workshop, Chicago, IL, USA, 18 August 2014; pp. 27–32. [Google Scholar]
- Wu, J.; Yuen, C.; Cheng, B.; Shang, Y.; Chen, J. Goodput-Aware Load Distribution for Real-Time Traffic over Multipath Networks. IEEE Trans. Parallel Distrib. Syst. 2014, 26, 2286–2299. [Google Scholar] [CrossRef]
- Houze, P.; Mory, E.; Texier, G.; Simon, G. Applicative-Layer Multipath for Low-Latency Adaptive Live Streaming. In Proceedings of the International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 22–27 May 2016; pp. 1–7. [Google Scholar]
- Afzal, S.; Rothenberg, C.E.; Testoni, V.; Kolan, P.; Bouazizi, I. Multipath MMT-based Approach for Streaming High Quality Video over Multiple Wireless Access Networks. Comput. Netw. 2021, 185, 1–18. [Google Scholar] [CrossRef]
- Mao, S.; Bushmitch, D.; Narayanan, S.; Panwar, S.S. MRTP: A Multiflow Real-Time Transport Protocol for Ad Hoc Networks. IEEE Trans. Multimed. 2006, 8, 356–369. [Google Scholar]
- Hodroj, A.; Ibrahim, M.; Hadjadj-Aoul, Y. A Survey on Video Streaming in Multipath and Multihomed Overlay Networks. IEEE Access 2021, 9, 66816–66828. [Google Scholar] [CrossRef]
- Bacco, M.; Gotta, A.; Roseti, C.; Zampognaro, F. A study on TCP error recovery interaction with Random Access satellite schemes. In Proceedings of the 2014 7th Advanced Satellite Multimedia Systems Conference and the 13th Signal Processing for Space Communications Workshop (ASMS/SPSC), Livorno, Italy, 8–10 September 2014; pp. 405–410. [Google Scholar] [CrossRef]
- Kazemi, M.; Shirmohammadi, S.; Sadeghi, K.H. A Review of Multiple Description Coding Techniques for Error-Resilient Video Delivery. Multimed. Syst. 2014, 20, 283–309. [Google Scholar] [CrossRef]
- Wang, Q.; Nguyen, T.; Bose, B. Towards Adaptive Packet Scheduler with Deep-Q Reinforcement Learning. In Proceedings of the 2020 International Conference on Computing, Networking and Communications (ICNC), Big Island, HI, USA, 17–20 February 2020; pp. 118–123. [Google Scholar]
- Wu, H.; Alay, Ö.; Brunstrom, A.; Ferlin, S.; Caso, G. Peekaboo: Learning-based multipath scheduling for dynamic heterogeneous environments. IEEE J. Sel. Areas Commun. 2020, 38, 2295–2310. [Google Scholar] [CrossRef]
- Zhong, C.; Lu, Z.; Gursoy, M.C.; Velipasalar, S. A deep actor-critic reinforcement learning framework for dynamic multichannel access. IEEE Trans. Cogn. Commun. Netw. 2019, 5, 1125–1139. [Google Scholar] [CrossRef]
- Yang, H.; Xie, X. An actor-critic deep reinforcement learning approach for transmission scheduling in cognitive internet of things systems. IEEE Syst. J. 2019, 14, 51–60. [Google Scholar] [CrossRef]
- Machumilane, A.; Gotta, A.; Cassará, P.; Gennaro, C.; Amato, G. Actor-Critic Scheduling for Path-Aware Air-to-Ground Multipath Multimedia Delivery. In Proceedings of the 2022 IEEE 95th Vehicular Technology Conference: (VTC2022-Spring), Helsinki, Finland, 19–22 June 2022; pp. 1–5. [Google Scholar]
- Badr, A.; Khisti, A.; Tan, W.T.; Apostolopoulos, J. Perfecting Protection for Interactive Multimedia: A survey of forward error correction for low-delay interactive applications. IEEE Signal Process. Mag. 2017, 34, 95–113. [Google Scholar] [CrossRef]
- Sun, Y.; Fu, L. Stacking Ensemble Learning for Non-Line-of-Sight Detection of Global Navigation Satellite System. IEEE Trans. Instrum. Meas. 2022, 71, 1–10. [Google Scholar] [CrossRef]
- Aydın, V.; Çavdar, İ.H.; Hasirci, Z. Line of sight (los) probability prediction for satellite and haps communication in trabzon, turkey. Int. J. Appl. Math. Electron. Comput. 2016, 1, 155–160. [Google Scholar] [CrossRef]
- Granelli, F. Network slicing. In Computing in Communication Networks; Elsevier: Amsterdam, The Netherlands, 2020; pp. 63–76. [Google Scholar]
- Li, S.Y.; Liu, C. An analytical model to predict the probability density function of elevation angles for LEO satellite systems. IEEE Commun. Lett. 2002, 6, 138–140. [Google Scholar] [CrossRef]
- Lutz, E.; Cygan, D.; Dippold, M.; Dolainsky, F.; Papke, W. The land mobile satellite communication channel-recording, statistics, and channel model. IEEE Trans. Veh. Technol. 1991, 40, 375–386. [Google Scholar] [CrossRef]
- Bischel, H.; Werner, M.; Lutz, E. Elevation-dependent channel model and satellite diversity for NGSO S-PCNs. In Proceedings of the Proceedings of Vehicular Technology Conference-VTC, Atlanta, GA, USA, 28 April–1 May 1996; Volume 2, pp. 1038–1042.
- Celandroni, N.; Gotta, A. Performance analysis of systematic upper layer FEC codes and interleaving in land mobile satellite channels. IEEE Trans. Veh. Technol. 2011, 60, 1887–1894. [Google Scholar] [CrossRef]
- Monahan, G.E. State of the art—A survey of partially observable Markov decision processes: Theory, models, and algorithms. Manag. Sci. 1982, 28, 1–16. [Google Scholar] [CrossRef]
- Juan, E.; Rodriguez, I.; Lauridsen, M.; Wigard, J.; Mogensen, P. Time-correlated Geometrical Radio Propagation Model for LEO-to-Ground Satellite Systems. In Proceedings of the 2021 IEEE 94th Vehicular Technology Conference (VTC2021-Fall), Norman, OK, USA, 27–30 September 2021; pp. 1–5. [Google Scholar]
- Grondman, I.; Busoniu, L.; Lopes, G.A.D.; Babuska, R. A Survey of Actor-Critic Reinforcement Learning: Standard and Natural Policy Gradients. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2012, 42, 1291–1307. [Google Scholar] [CrossRef]

| Elevation | |||
|---|---|---|---|
| 2.0042, 3.6890 | 1.2049, 0.9796 | 3.9889, 10.3114 | |
| 2.7332, 2.7582 | 1.1030, 1.2210 | 7.3174, 5.7276 | |
| 3.0639, 2.9108 | 1.6980, 1.2602 | 10.0, 6.0 | |
| 2.8135, 2.0211 | 1.9595, 0.6568 | 10.0, 1.9126 | |
| 4.2919, 2.1012 | 2.4703, 1.0341 | 118.3312, 4.8569 |
| Elevation | (g) | (b) |
|---|---|---|
| 0.00014310 | 0.00047466 | |
| 0.00024460 | 0.00027570 | |
| 0.00020318 | 0.00007556 | |
| 0.00105161 | 0.00010797 | |
| 0.00052923 |
| Name | Value |
|---|---|
| Number of hidden layers | 3 |
| Number of neurons for hidden layer | 64 |
| Discount factor () | 0.96 |
| Learning rate for the actor () | 0.001 |
| Learning rate for the critic () | 0.005 |
| Optimizer | ADAM |
| UAV velocity ( | 10 m/s |
| Packet length (l) | 1000 bits |
| Context | Satellite 1 | Satellite 2 |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | (handoff) | |
| 4 | (handoff) | |
| 5 | ||
| 6 |
| Model | E2E Loss Rate (BER) | Bandwidth (Mbps) |
|---|---|---|
| Actor-critic | 2.1 | |
| Optimal policy | 2.1 | |
| Round-robin | 8% | 1.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Machumilane, A.; Gotta, A.; Cassará, P.; Amato, G.; Gennaro, C. Learning-Based Traffic Scheduling in Non-Stationary Multipath 5G Non-Terrestrial Networks. Remote Sens. 2023, 15, 1842. https://doi.org/10.3390/rs15071842
Machumilane A, Gotta A, Cassará P, Amato G, Gennaro C. Learning-Based Traffic Scheduling in Non-Stationary Multipath 5G Non-Terrestrial Networks. Remote Sensing. 2023; 15(7):1842. https://doi.org/10.3390/rs15071842
Chicago/Turabian StyleMachumilane, Achilles, Alberto Gotta, Pietro Cassará, Giuseppe Amato, and Claudio Gennaro. 2023. "Learning-Based Traffic Scheduling in Non-Stationary Multipath 5G Non-Terrestrial Networks" Remote Sensing 15, no. 7: 1842. https://doi.org/10.3390/rs15071842
APA StyleMachumilane, A., Gotta, A., Cassará, P., Amato, G., & Gennaro, C. (2023). Learning-Based Traffic Scheduling in Non-Stationary Multipath 5G Non-Terrestrial Networks. Remote Sensing, 15(7), 1842. https://doi.org/10.3390/rs15071842









