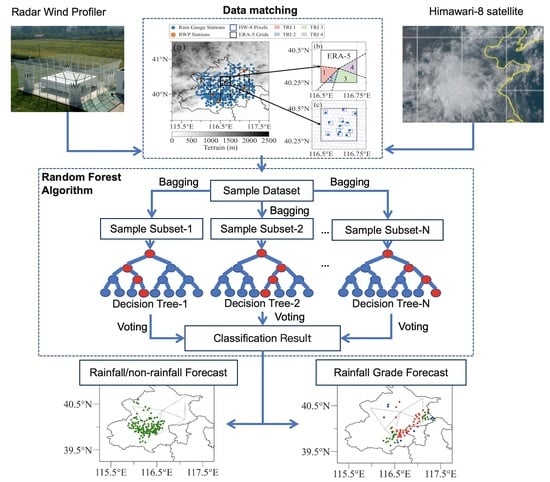
Forecasting Precipitation from Radar Wind Profiler Mesonet and Reanalysis Using the Random Forest Algorithm
Abstract
1. Introduction
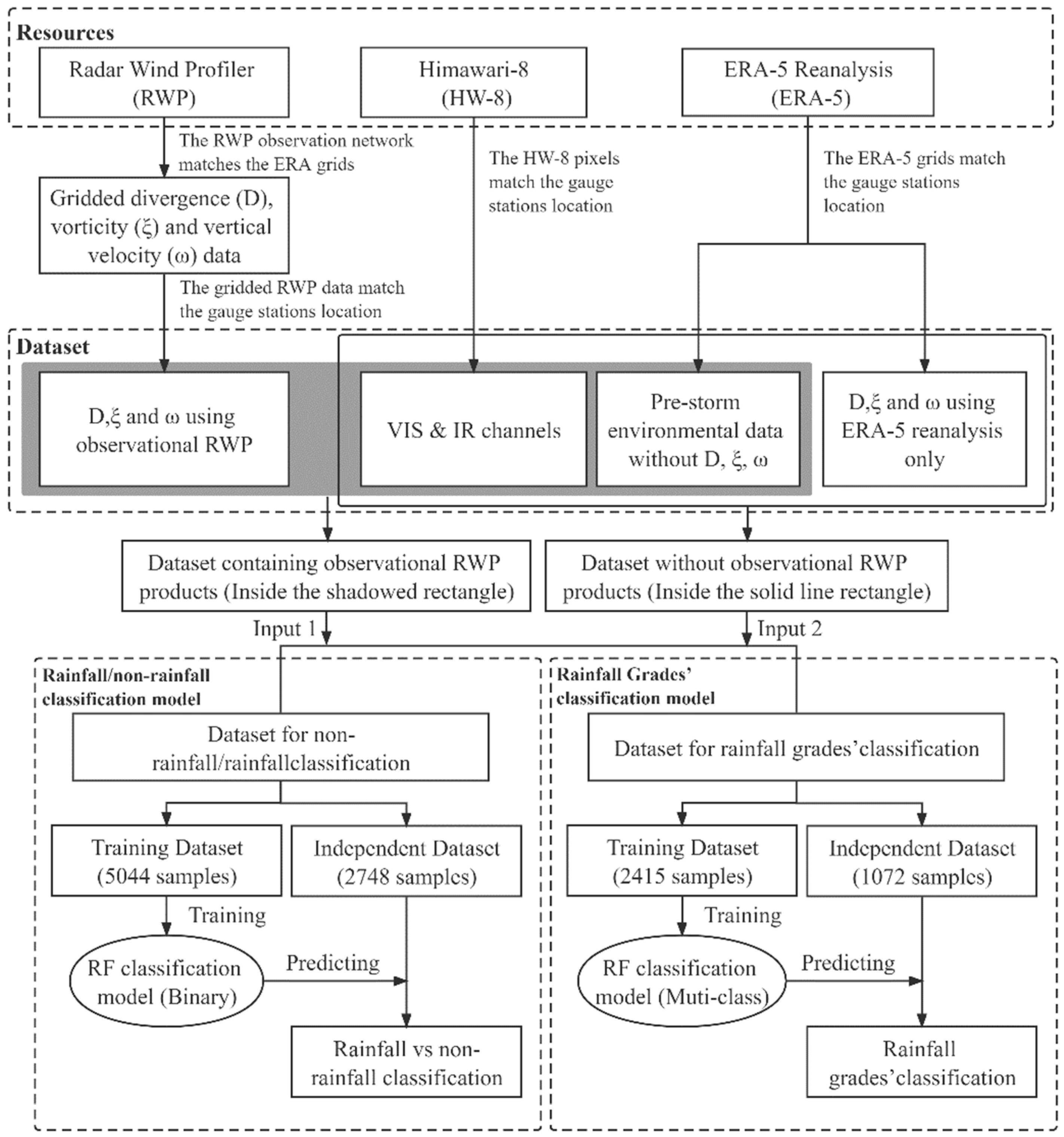
2. Data and Methods
2.1. Atmospheric Dynamic Variables from RWP
2.2. Variables from Himawari-8 Satellite, ERA-5 Reanalysis and Rain Gauge
2.3. Data Processing and Matching
2.4. The Random Forest Classification Algorithm
2.4.1. Random Forest Classifier
2.4.2. Training Process
2.5. Accuracy Evaluation
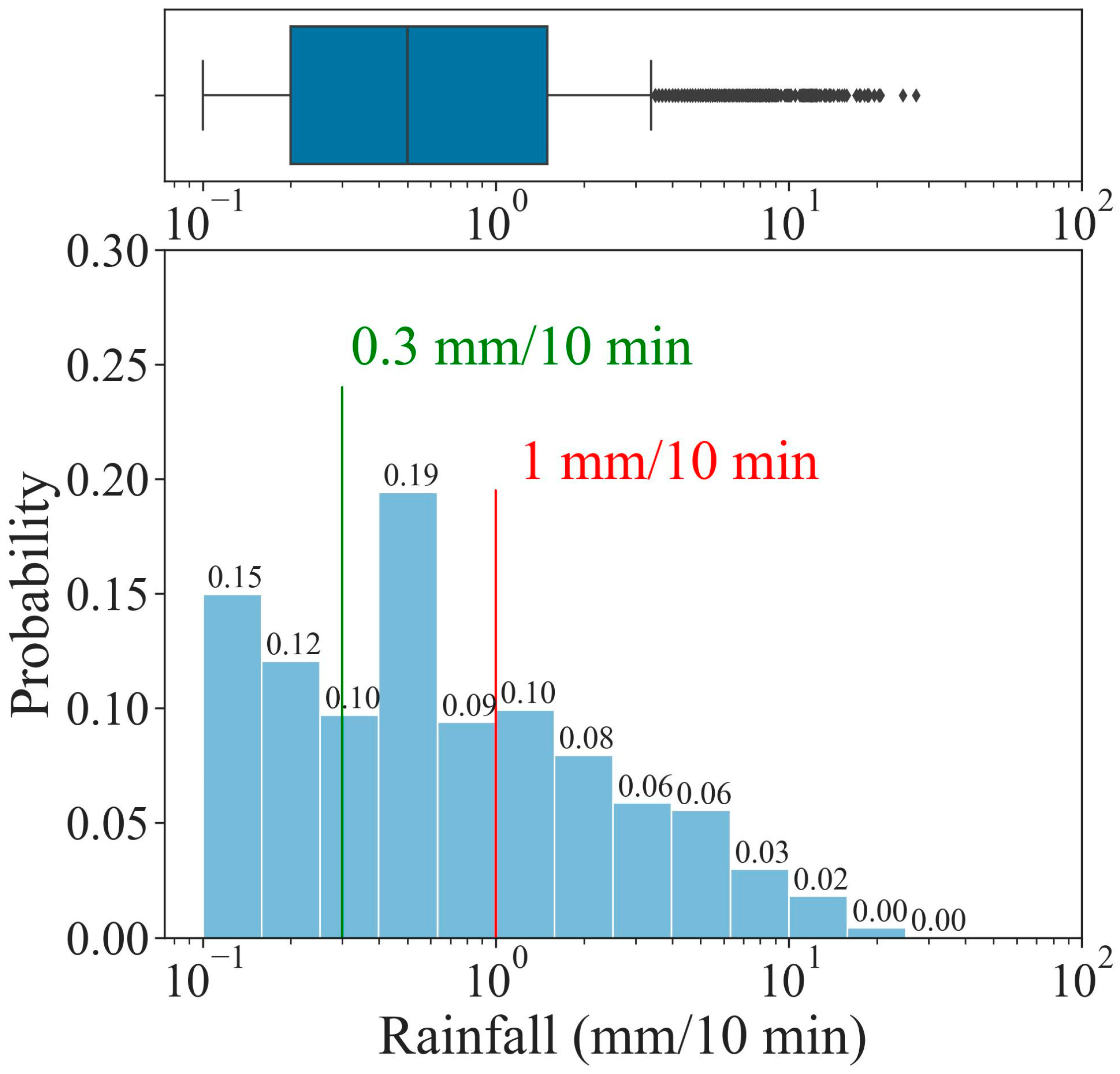
3. Results and Discussion
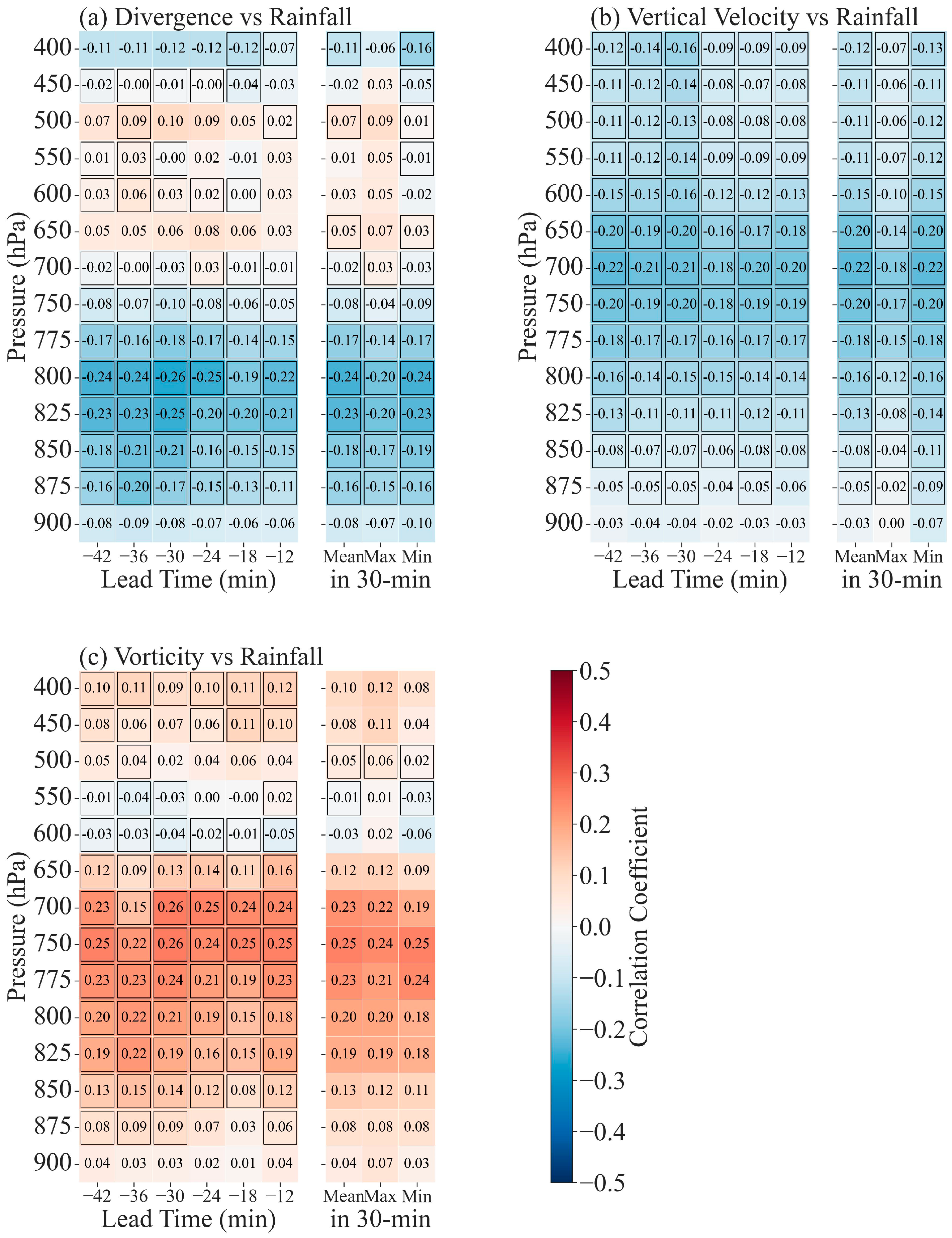
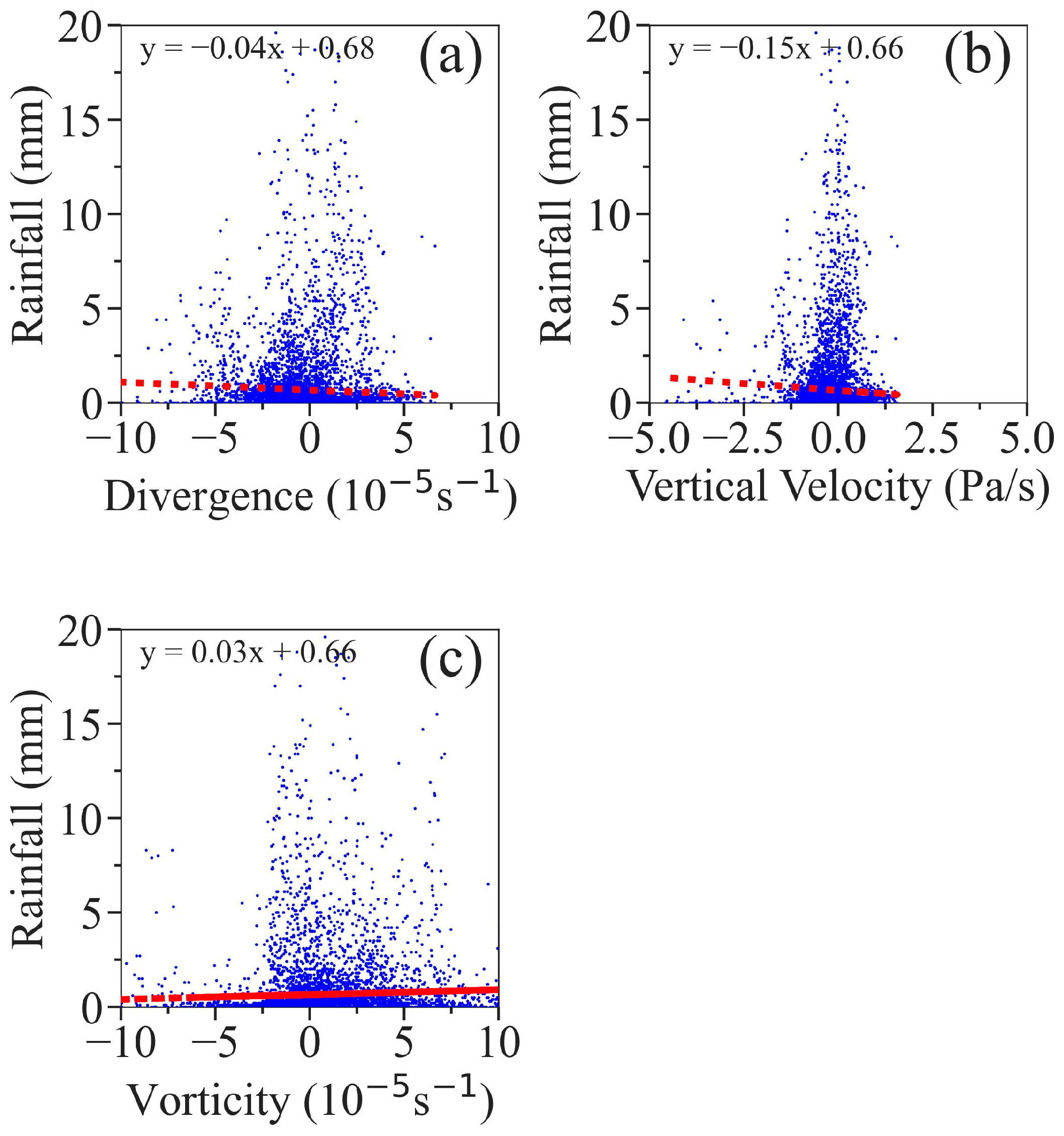
3.1. Correlation Analysis between Atmospheric Dynamic Variables from RWP and Rainfall
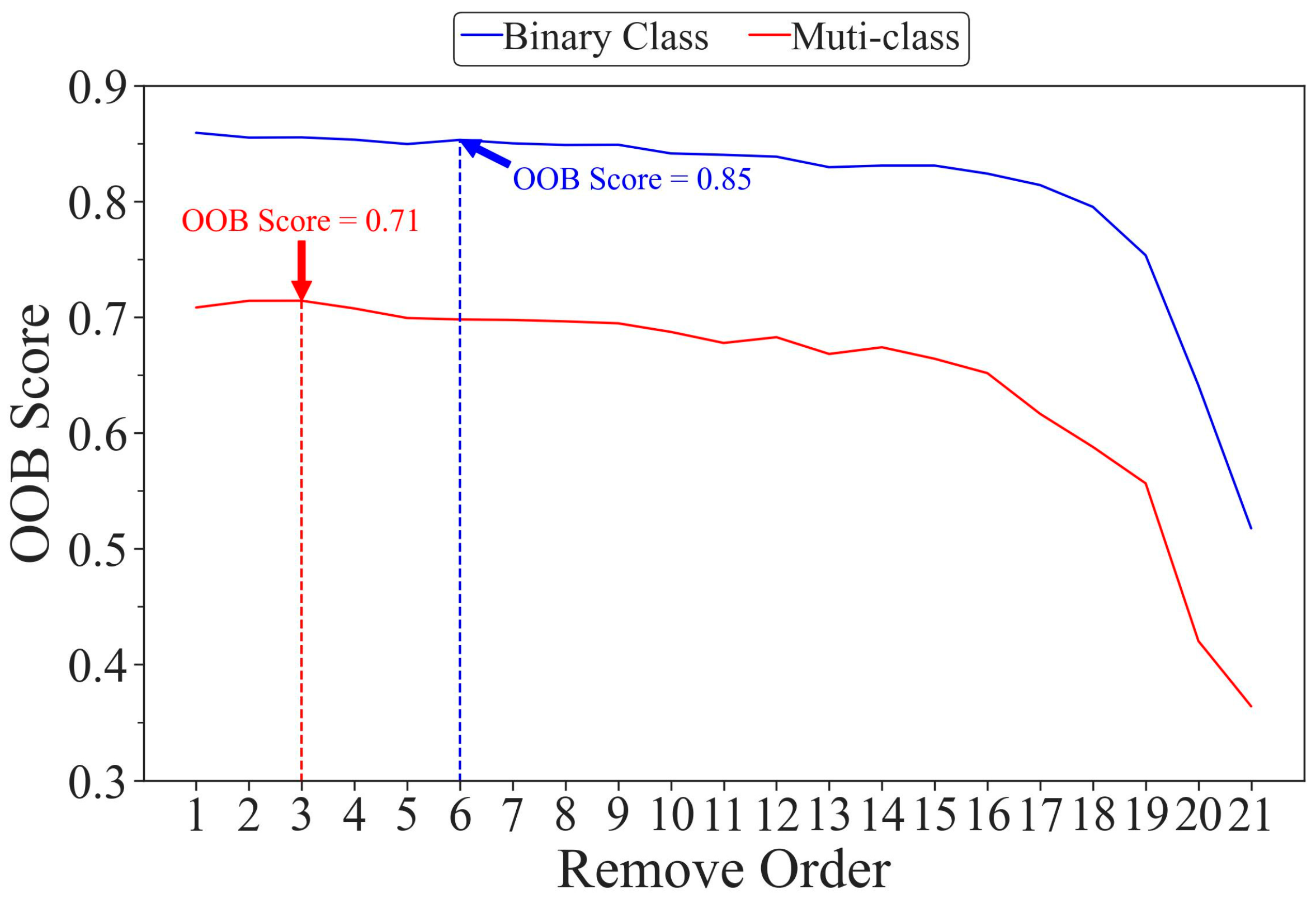
3.2. Influence of Different Input Features on RF Model Performance
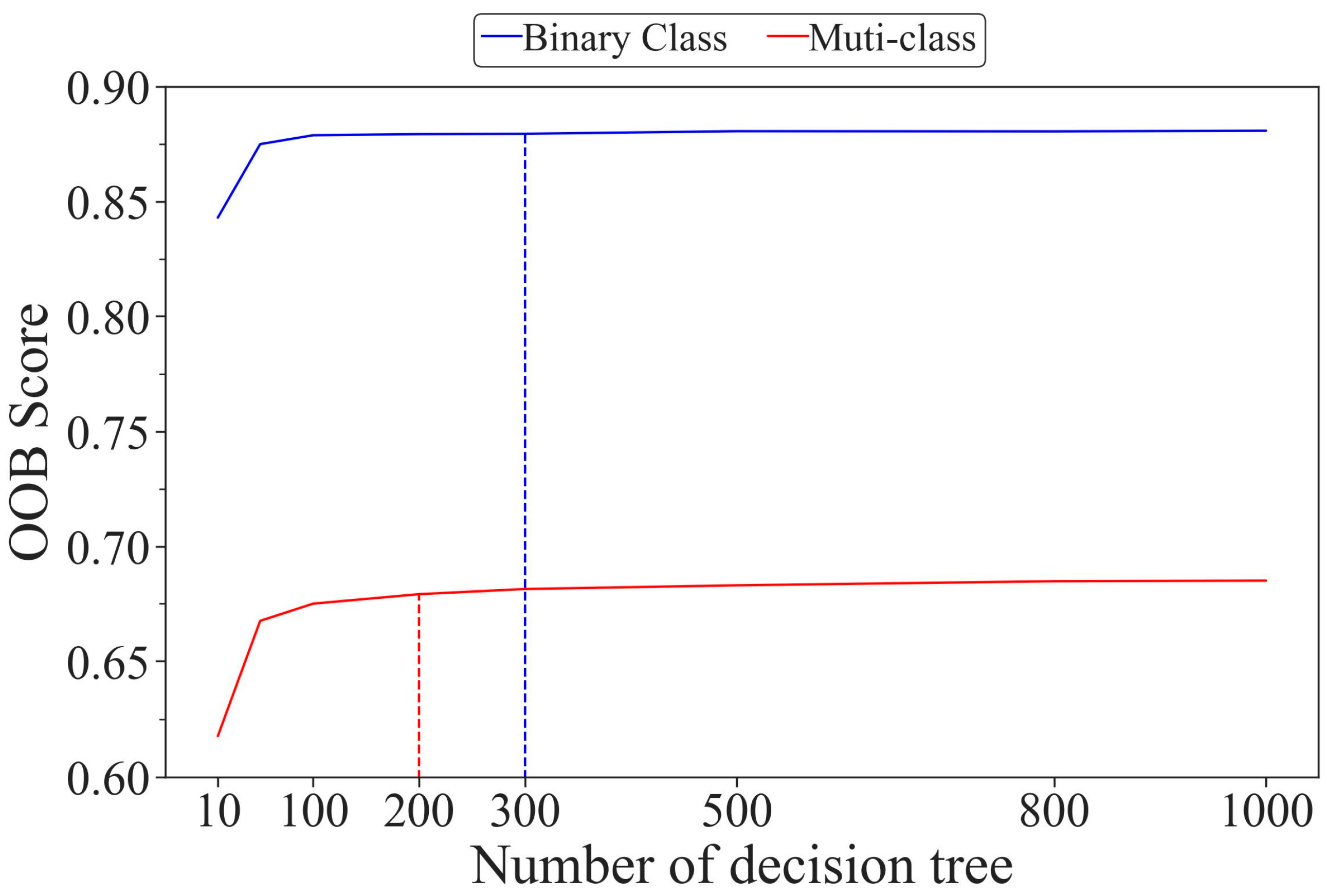
3.3. Hyperparameter Optimization
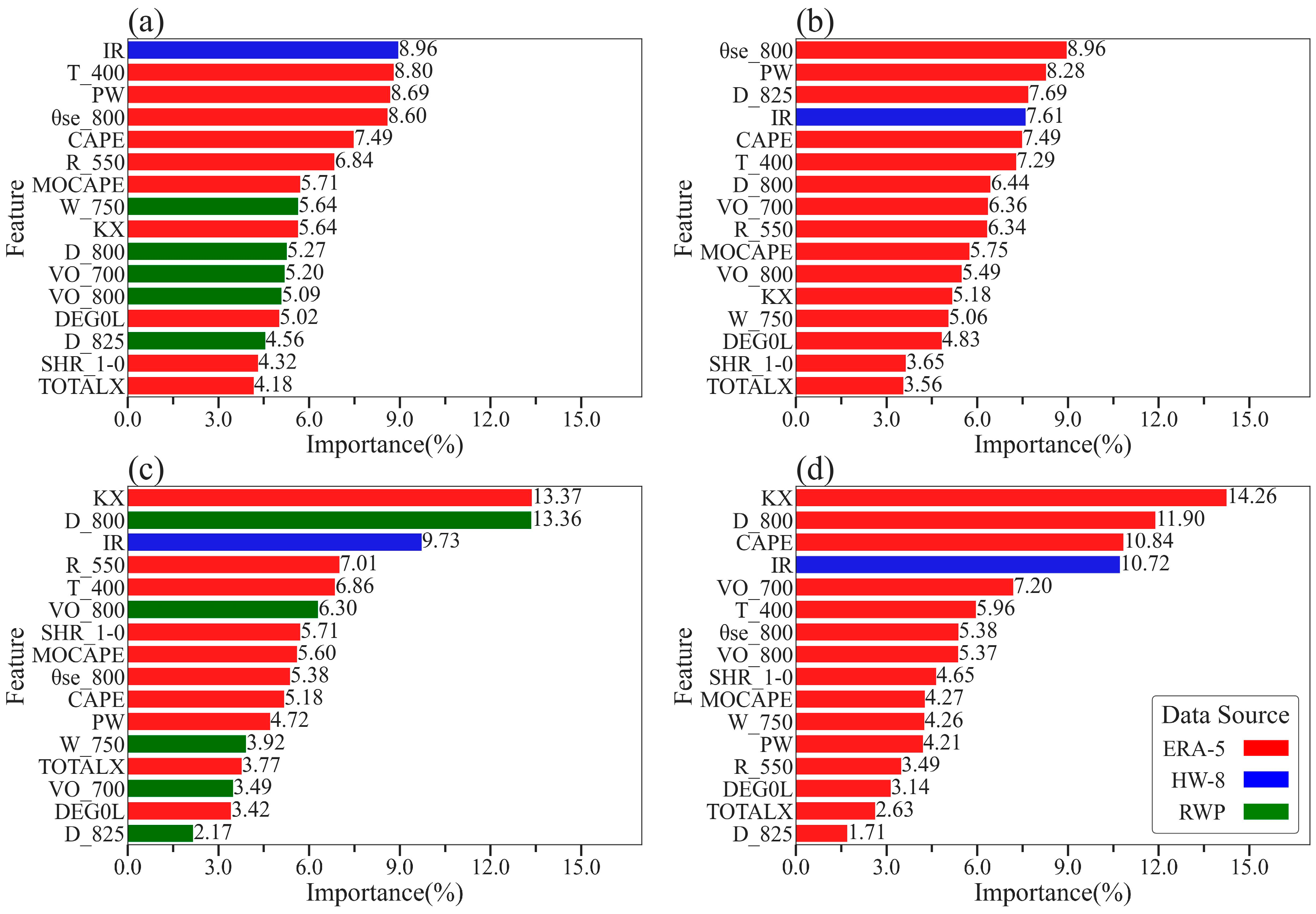
3.4. The Feature Importance Scores of the Input Features from Different Data Sources
3.5. Independent Dataset Evaluate Results
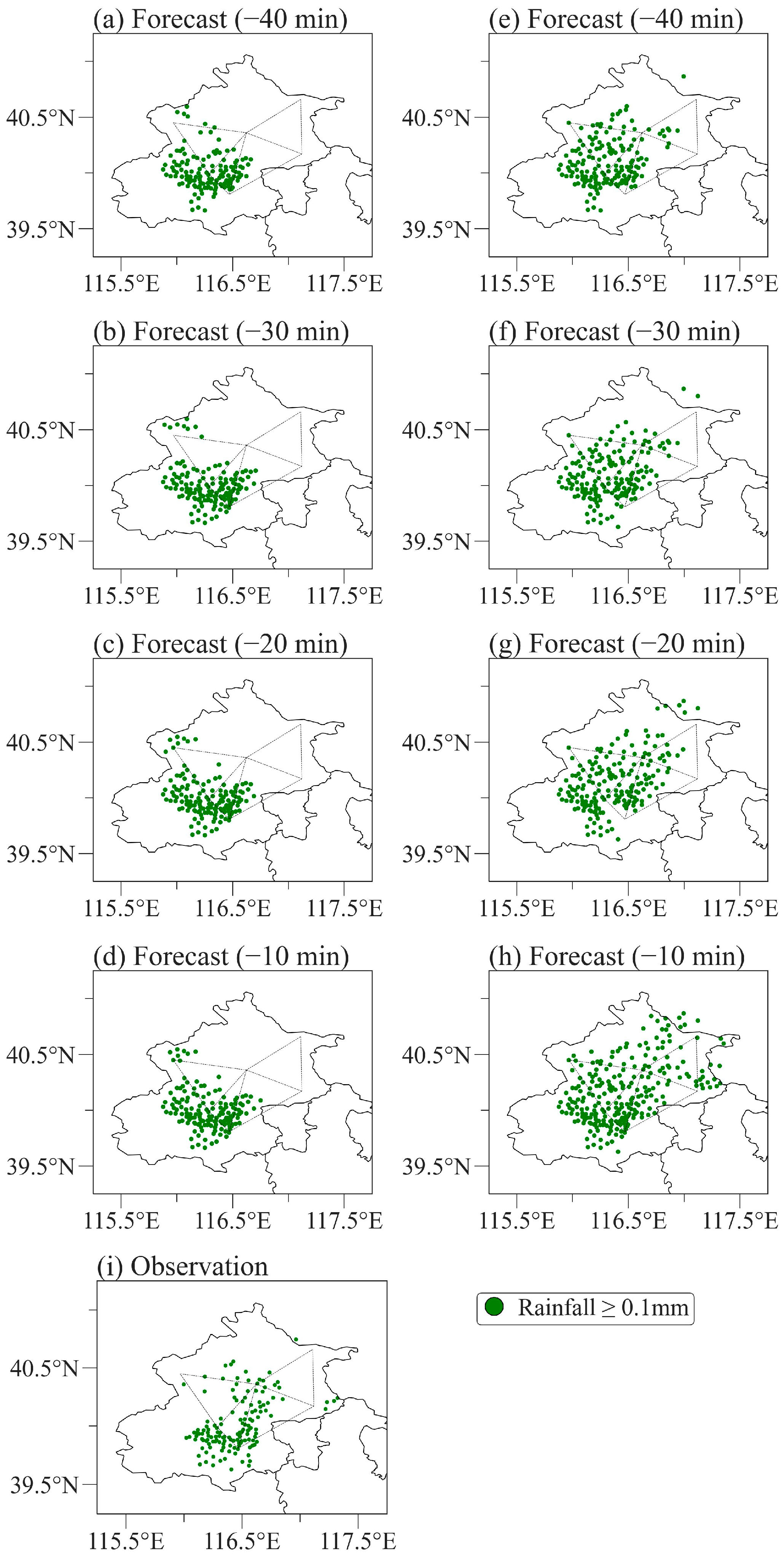
3.5.1. Evaluation of Rainfall/Non-Rainfall Forecast
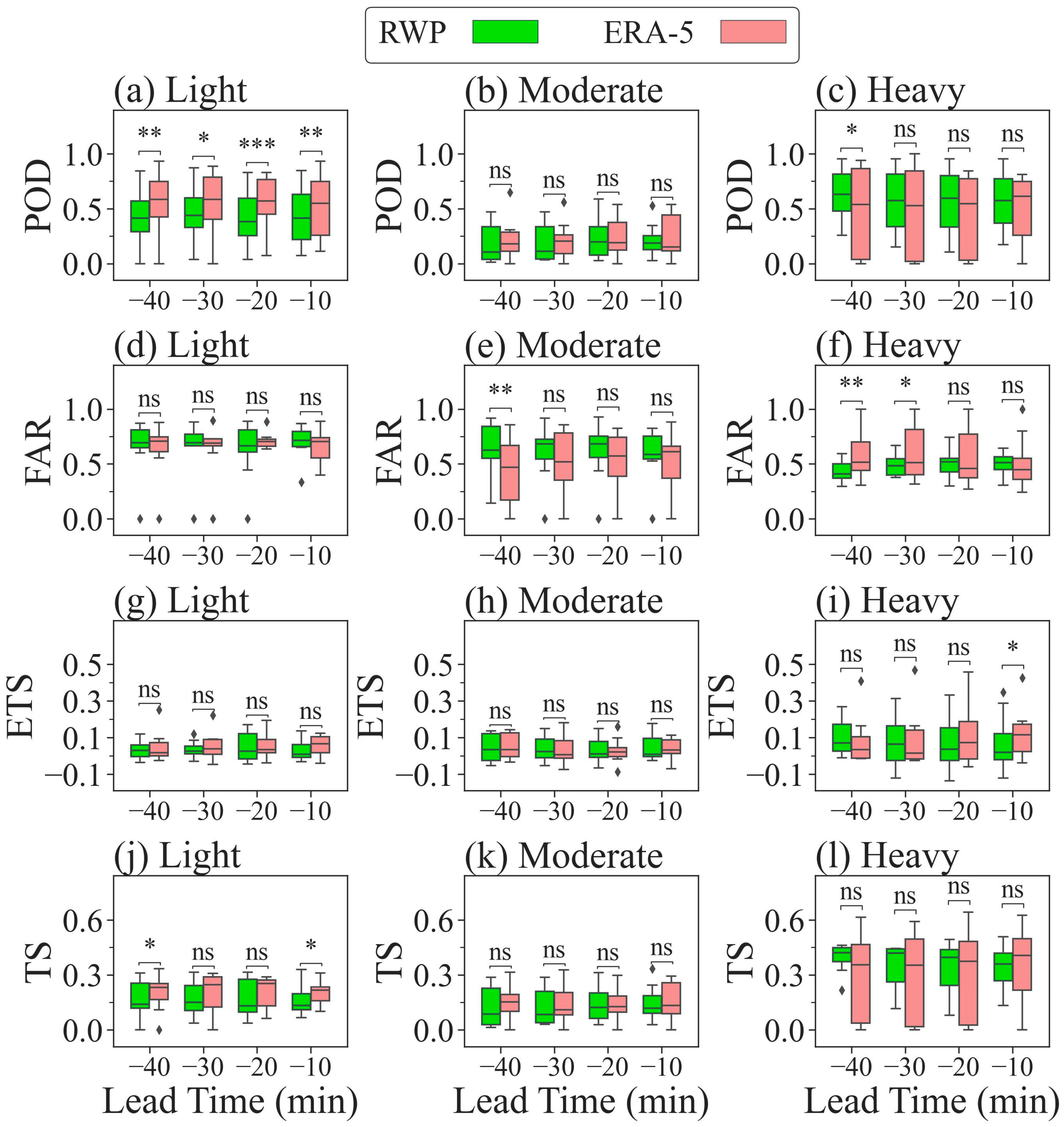
3.5.2. Evaluation of Rainfall Grade Forecast
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ravuri, S.; Lenc, K.; Willson, M.; Kangin, D.; Lam, R.; Mirowski, R.; Fitzsimons, M.; Athanassiadou, M.; Kashem, S.; Madge, S.; et al. Skilful precipitation nowcasting using deep generative models of radar. Nature 2021, 597, 672–677. [Google Scholar] [CrossRef] [PubMed]
- Jonassen, M.O.; Ólafsson, H.; Ágústsson, H.; Rögnvaldsson, Ó.; Reuder, J. Improving High-Resolution Numerical Weather Simulations by Assimilating Data from an Unmanned Aerial System. Mon. Weather Rev. 2012, 140, 3734–3756. [Google Scholar] [CrossRef]
- Li, Z. Impact of assimilating Mode-S EHS winds in the Met Office’s high-resolution NWP model. Meteorol. Appl. 2021, 28, e1989. [Google Scholar] [CrossRef]
- Mueller, C.K.; Saxen, T.; Roberts, R.; Wilson, J.; Betancourt, T.; Dettling, S.; Oien, N.; Yee, J. NCAR Auto-Nowcast System. Weather Forecast. 2003, 18, 545–561. [Google Scholar] [CrossRef]
- Wilson, J.W.; Feng, Y.R.; Chen, M.; Roberts, R.D. Nowcasting challenges during the Beijing Olympics: Successes, failures, and implications for future nowcasting systems. Weather Forecast. 2010, 25, 1691–1714. [Google Scholar] [CrossRef]
- Ballard, S.; Li, Z.; Davud, S.; Helen, B.; Cristina, C.P.; Nicolas, G.; Lee, H.S. Use of radar data in NWP-based nowcasting in the Met Office. In Proceedings of the Weather Radar and Hydrology Symposium, Exeter, UK, 18 April 2011. [Google Scholar]
- Pulkkinen, S.; Chandrasekar, V.; Lerber, A.V.; Harri, A.M. Nowcasting of Convective Rainfall Using Volumetric Radar Observations. IEEE Trans. Geosci. Remote Sens. 2020, 58, 7845–7859. [Google Scholar] [CrossRef]
- Mecikalski, J.R.; Li, X.L.; Carey, L.D.; McCaul, E.W.; Coleman, T.A. Regional comparison of GOES cloud-top properties and radar characteristics in advance of first-flash lightning initiation. Mon. Weather Rev. 2013, 141, 55–74. [Google Scholar] [CrossRef]
- Bedka, M.; Wang, C.; Rogers, R.; Carey, L.D.; Feltz, W.; Kanak, J. Examining deep convective cloud evolution using total lightning, WSR-88D, and GOES-14 super rapid scan datasets. Weather Forecast. 2015, 30, 571–590. [Google Scholar] [CrossRef]
- Gravelle, C.M.; Mecikalski, J.R.; Line, W.E.; Bedka, K.M.; Petersen, R.A.; Sieglaff, J.M.; Stano, G.T.; Goodman, S.J. Demonstration of a GOES-R satellite convective toolkit to “bridge the gap” between severe weather watches and warnings: An example from the 20 May 2013 Moore, Oklahoma, tornado outbreak. Bull. Am. Meteorol. Soc. 2016, 97, 69–84. [Google Scholar] [CrossRef]
- Baker, N.L.; Daley, R. Observation and background adjoint sensitivity in the adaptive observation-targeting problem. Quart. J. R. Meteorol. Soc. 2000, 126, 1431–1454. [Google Scholar] [CrossRef]
- Majumdar, S.J. A Review of Targeted Observations. Bull. Am. Meteorol. Soc. 2016, 97, 2287–2303. [Google Scholar] [CrossRef]
- Chiara, G.D.; Bonavita, M.; English, S.J. Improving the Assimilation of Scatterometer Wind Observations in Global NWP. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2415–2423. [Google Scholar] [CrossRef]
- Janisková, M.; Fielding, M.D. Direct 4D-Var assimilation of space-borne cloud radar and lidar observations. Part II: Impact on analysis and subsequent forecast. Q. J. R. Meteorol. Soc. 2020, 146, 3877–3899. [Google Scholar] [CrossRef]
- Caumont, O.; Cimini, D.; Löhnert, U.; Lucas, A.A.; Bleisch, R.; Buffa, F.; Ferrario, M.E.; Haefele, A.; Huet, T.; Madonna, F.; et al. Assimilation of humidity and temperature observations retrieved from ground-based microwave radiometers into a convective-scale NWP model. Q. J. R. Meteorol. Soc. 2016, 142, 2692–2704. [Google Scholar] [CrossRef]
- Wang, C.; Chen, M.; Chen, Y. Impact of Combined Assimilation of Wind Profiler and Doppler Radar Data on a Convective-Scale Cycling Forecasting System. Mon. Weather Rev. 2022, 150, 431–450. [Google Scholar] [CrossRef]
- Wang, D.; Giangrande, S.E.; Feng, Z.; Hardin, J.C.; Prein, A.F. Updraft and Downdraft Core Size and Intensity as Revealed by Radar Wind Profilers: MCS Observations and Idealized Model Comparisons. J. Geophys. Res. Atmos. 2020, 125, e2019JD031774. [Google Scholar] [CrossRef]
- Zhang, Y.; Gou, J.; Yang, Y.J.; Wang, Y.; Yim, S. Vertical Wind Shear Modulates Particulate Matter Pollutions: A Perspective from Radar Wind Profiler Observations in Beijing, China. Remote Sens. 2020, 12, 546. [Google Scholar] [CrossRef]
- Giangrande, S.E.; Biscaro, T.; Peters, J.M. Seasonal Controls on Isolated Convective Storm Drafts, Precipitation Intensity, and Life Cycle as Observed During GoAmazon2014/5. EGUsphere, 2022; manuscript in preparation. [Google Scholar]
- Liu, B.; Gou, J.; Gong, W.; Zhang, Y.; Ma, Y. Characteristics and performance of wind profiles as observed by the radar wind profiler network of China. Atmos. Meas. Tech. 2020, 13, 4589–4600. [Google Scholar] [CrossRef]
- Guo, X.; Guo, J.; Zhang, D.L.; Yun, Y. Vertical Divergence Profiles as Detected by a Wind Profiler Mesonet over East China: Implications for Nowcasting Convective Storms. Q. J. 2023; manuscript in preparation. [Google Scholar]
- Akdi, Y.; Ünlü, K.D. Periodicity in precipitation and temperature for monthly data of Turkey. Theor. Appl. Climatol. 2021, 143, 957–968. [Google Scholar] [CrossRef]
- Han, L.; Sun, J.; Zhang, W. Convolutional Neural Network for Convective Storm Nowcasting Using 3-D Doppler Weather Radar Data. IEEE Trans. Geosci. Remote Sens. 2019, 58, 1487–1495. [Google Scholar] [CrossRef]
- Han, L.; Zhao, Y.; Chen, H.; Chandrasekar, V. Advancing Radar Nowcasting Through Deep Transfer Learning. IEEE Trans. Geosci. Remote Sens. 2021, 60, 4100609. [Google Scholar] [CrossRef]
- Mecikalski, J.R.; Williams, J.K.; Jewett, C.P.; Ahijevych, D.; LeRoy, A.; Walker, J.R. Probabilistic 0–1-h convective initiation nowcasts that combine geostationary satellite observations and numerical weather prediction model data. J. Appl. Meteorol. Climatol. 2015, 54, 1039–1059. [Google Scholar] [CrossRef]
- Gao, H.; Shen, C.; Zhou, Y.; Wang, X.; Chan, P.; Hon, K.; Zhou, D.; Li, J. A Spatio-Temporal Neural Network for Fine-Scale Wind Field Nowcasting Based on Lidar Observation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 5596–5606. [Google Scholar] [CrossRef]
- Han, L.; Sun, J.; Zhang, W.; Xiu, Y.; Feng, H.; Lin, Y. A machine learning nowcasting method based on real-time reanalysis data. J. Geophys. Res. Atmos. 2017, 122, 4038–4051. [Google Scholar] [CrossRef]
- Zhou, K.; Zheng, Y.; Li, B.; Dong, W.; Zhang, X. Forecasting Different Types of Convective Weather: A Deep Learning Approach. J. Meteorol. Res. 2019, 33, 797–809. [Google Scholar] [CrossRef]
- Zhou, K.; Sun, J.; Zheng, Y.; Zhang, Y. Quantitative Precipitation Forecast Experiment Based on Basic NWP Variables Using Deep Learning. Adv. Atmos. Sci. 2020, 39, 1472–1486. [Google Scholar] [CrossRef]
- Ahijevych, D.; Pinto, J.; Willliams, J.K.; Steiner, M. Probabilistic forecasts of mesoscale convective system initiation using the random forest data mining technique. Weather Forecast. 2016, 31, 581–599. [Google Scholar] [CrossRef]
- Leinonen, J.; Hamann, U.; Germann, U.; Mecikalski, J.R. Nowcasting thunderstorm hazards using machine learning: The impact of data sources on performance. Nat. Hazards Earth Syst. Sci. 2021, 22, 577–597. [Google Scholar] [CrossRef]
- Liu, X.; Chen, H.; Han, L.; Ge, Y. A Machine Learning Approach for Convective Initiation Detection Using Multi-Source Data. In Proceedings of the IGARSS 2022—2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Hill, A.J.; Schumacher, R.S.; Jirak, I.L. A New Paradigm for Medium-range Severe Weather Forecasts: Probabilistic Random Forest-based Predictions. Weather Forecast. 2022, 38, 251–272. [Google Scholar] [CrossRef]
- McCandless, T.; Gagne, D.; Kosović, B.; Haupt, S.E.; Yang, B.; Becker, C.; Schreck, J. Machine Learning for Improving Surface-Layer-Flux Estimates. Bound. Layer Meteorol. 2021, 185, 199–228. [Google Scholar] [CrossRef]
- Bellamy, J.C. Objective calculations of divergence, vertical velocity and vorticity. Bull. Am. Meteorol. Soc. 1949, 30, 45–49. [Google Scholar] [CrossRef]
- Bessho, K.; Date, K.; Hayashi, M.; Ikeda, A.; Imai, T.; Inoue, H.; Kumagai, Y.; Miyakawa, T.; Murata, H.; Ohno, T.; et al. An introduction to Himawari-8/9-Japan’s new generation geostationary meteorological satellites. J. Meteorol. Soc. Jpn. 2016, 94, 151–183. [Google Scholar] [CrossRef]
- Mecikalski, J.R.; Bedka, K.M. Forecasting Convective Initiation by Monitoring the Evolution of Moving Cumulus in Daytime GOES Imagery. Mon. Weather Rev. 2006, 134, 49–78. [Google Scholar] [CrossRef]
- Chen, D.; Guo, J.; Yao, D.; Lin, Y.; Zhao, C.; Min, M.; Xu, H.; Liu, L.; Huang, X.; Chen, T.; et al. Mesoscale convective systems in the Asian monsoon region from advanced Himawari imager: Algorithms and preliminary results. J. Geophys. Res. Atmos. 2019, 124, 2210–2234. [Google Scholar] [CrossRef]
- Chen, D.; Guo, J.; Yao, D.; Feng, Z.; Lin, Y. Elucidating the life cycle of warm-season mesoscale convective systems in eastern China from the Himawari-8 geostationary satellite. Remote Sens. 2020, 12, 2307. [Google Scholar] [CrossRef]
- Hoffmann, L.; Günther, G.; Li, D.; Stein, O.; Wu, X.; Griessbach, S.; Heng, Y.; Konopka, P.; Müller, R.; Vogel, B.; et al. From ERA-Interim to ERA5: The considerable impact of ECMWF’s next-generation reanalysis on Lagrangian transport simulations. Atmos. Chem. Phys. 2019, 19, 3097–3124. [Google Scholar] [CrossRef]
- Altman, N.; Krzywinski, M. Ensemble methods: Bagging and random forests. Nat. Methods 2017, 14, 933–935. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Zhang, T.H.; Zhang, R.; Zhu, Z.M.; Yang, J.; Chen, P.Y.; Ou, C.Q.; Guo, Y. Extreme gradient boosting model to estimate PM 2.5 concentrations with missing-filled satellite data in China. Atmos. Environ. 2019, 202, 180–189. [Google Scholar] [CrossRef]
- Di, Q.; Amin, H.; Shi, L.; Kloog, I.; Silvern, R.; Kelly, J.; Sabath, M.B.; Choirat, C.; Koutrakis, P.; Lyapustin, A.; et al. An ensemble-based model of PM2.5 concentration across the contiguous United States with high spatiotemporal resolution. Environ. Int. 2019, 130, 104909. [Google Scholar] [CrossRef] [PubMed]
- Genuer, R.; Poggi, J.M.; Christine, T.M. Variable selection using random forests. Pattern Recognit. Lett. 2010, 31, 2225–2236. [Google Scholar] [CrossRef]




| Data Source | Temporal Resolution | Feature Name | Units |
|---|---|---|---|
| ERA-5 reanalysis | 60 min | Convective Available Potential Energy | J·kg−1 |
| Convective Inhibition | J·kg−1 | ||
| K Index | °C | ||
| Surface Pressure | hPa | ||
| Temperature | °C | ||
| 2 m Dewpoint Temperature | °C | ||
| Zero Degree Level | m | ||
| Total Totals Index | °C | ||
| Precipitable Water | mm | ||
| u-component and v-component wind | m/s | ||
| Relative Humidity | % | ||
| Radar wind profiler (RWP) | 6 min | Vorticity | s−1 |
| Divergence | s−1 | ||
| Vertical Velocity | Pa·s−1 | ||
| Himawari-8 (HW-8) | 10 min | 10.4 μm Brightness Temperature | K |
| 0.64 μm Albedo | non-dimensional | ||
| Rain gauge | 10 min | Precipitation | mm |
| Data Source | Feature Name | Descriptions | Remove Order | |
|---|---|---|---|---|
| Binary | Multi-Class | |||
| ERA-5 reanalysis | CAPE | Convective Available Potential Energy | 18 | 18 |
| DEG0L | Zero Degree Level | 7 | 10 | |
| KX | K Index | 14 | 21 | |
| LI | Lifting Index | 1 * | 2 * | |
| MUCAPE | Most Unstable Convective Available Potential Energy | 13 | 5 | |
| PW | Precipitable Water | 20 | 20 | |
| R_550 | Relative Humidity on 550 hPa | 17 | 15 | |
| θse_800 | Potential Pseudo-Equivalent Temperature on 800 hPa | 22 | 19 | |
| SHR_1-0 | 0–1 km Wind Shear | 8 | 12 | |
| T_400 | Temperature on 400 hPa | 19 | 14 | |
| TOTALX | Total Totals Index | 9 | 13 | |
| Himawari-8 (HW-8) | IR | 10.4μm Brightness Temperature | 21 | 17 |
| VIS | 0.64μm Albedo | 5 * | 1 * | |
| Radar wind profiler (RWP) | D_800 | Divergence on 800 hPa | 12 | 22 |
| D_825 | Divergence on 825 hPa | 10 | 9 | |
| VO_700 | Vorticity on 700 hPa | 16 | 11 | |
| VO_750 | Vorticity on 750 hPa | 4 * | 3 * | |
| VO_775 | Vorticity on 775 hPa | 2 * | 7 | |
| VO_800 | Vorticity on 800 hPa | 11 | 16 | |
| W_650 | Vertical Velocity on 650 hPa | 3 * | 8 | |
| W_700 | Vertical Velocity on 700 hPa | 6 * | 4 | |
| W_750 | Vertical Velocity on 750 hPa | 15 | 6 | |
| Hyperparameter Name | Descriptions | Adjusting Range | Values of Selected Parameters | |
|---|---|---|---|---|
| Binary | Muti-Class | |||
| n_estimators | The number of trees in the forest. | 10, 50, 90, 100, 200, 300, 500, 800, 1000 | 300 | 200 |
| max_depth | The maximum depth of the tree. | 5, 8, 15, 25, 30, None | 8 | 5 |
| min_samples_leaf | The minimum number of samples required to be at a leaf node. | 1, 2, 5, 10 | 5 | 1 |
| min_samples_split | The minimum number of samples required to split an internal node. | 2, 5, 10, 15 | 2 | 5 |
| max_features | The number of features to consider when looking for the best split. | sqrt, log, None | sqrt | None |
| Data Source | Lead Time (min) | FAR | POD | Accuracy | AUC | TS | ETS |
|---|---|---|---|---|---|---|---|
| RWP | −40 | 0.42 | 0.56 | 0.65 | 0.64 | 0.40 | 0.16 |
| −30 | 0.38 | 0.62 | 0.68 | 0.68 | 0.45 | 0.21 | |
| −20 | 0.40 | 0.62 | 0.67 | 0.66 | 0.44 | 0.20 | |
| −10 | 0.41 | 0.63 | 0.63 | 0.66 | 0.44 | 0.19 | |
| ERA-5 | −40 | 0.46 | 0.64 | 0.63 | 0.63 | 0.42 | 0.15 |
| −30 | 0.44 | 0.69 | 0.65 | 0.66 | 0.45 | 0.18 | |
| −20 | 0.46 | 0.70 | 0.63 | 0.64 | 0.43 | 0.15 | |
| −10 | 0.49 | 0.89 | 0.60 | 0.64 | 0.48 | 0.15 |
| Metrics | Grades | Lead Time (min) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| −40 | −30 | −20 | −10 | ||||||
| RWP | ERA-5 | RWP | ERA-5 | RWP | ERA-5 | RWP | ERA-5 | ||
| Accuracy | All | 0.49 | 0.25 | 0.46 | 0.22 | 0.32 | 0.26 | 0.33 | 0.24 |
| POD | Light | 0.50 | 0.600 | 0.45 | 0.60 | 0.30 | 0.75 | 0.35 | 0.75 |
| Mod. | 0.17 | 0.28 | 0.17 | 0.22 | 0.22 | 0.22 | 0.17 | 0.11 | |
| Heavy | 0.63 | 0.05 | 0.61 | 0.03 | 0.37 | 0.03 | 0.40 | 0.03 | |
| FAR | Light | 0.67 | 0.733 | 0.69 | 0.73 | 0.79 | 0.72 | 0.77 | 0.72 |
| Mod. | 0.62 | 0.808 | 0.7 | 0.86 | 0.75 | 0.79 | 0.77 | 0.88 | |
| Heavy | 0.37 | 0.6 | 0.38 | 0.75 | 0.55 | 0.75 | 0.53 | 0.8 | |
| TS | Light | 0.25 | 0.226 | 0.23 | 0.23 | 0.14 | 0.26 | 0.16 | 0.25 |
| Mod. | 0.13 | 0.128 | 0.12 | 0.09 | 0.13 | 0.12 | 0.11 | 0.06 | |
| Heavy | 0.46 | 0.049 | 0.44 | 0.02 | 0.26 | 0.02 | 0.27 | 0.02 | |
| ETS | Light | 0.07 | 0.01 | 0.04 | 0.01 | −0.04 | 0.02 | −0.03 | 0.02 |
| Mod. | 0.05 | −0.04 | 0.03 | −0.07 | 0.01 | −0.02 | −0.01 | −0.07 | |
| Heavy | 0.15 | −0.01 | 0.13 | −0.03 | −0.04 | −0.03 | −0.03 | −0.04 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Guo, J.; Chen, T.; Chen, A. Forecasting Precipitation from Radar Wind Profiler Mesonet and Reanalysis Using the Random Forest Algorithm. Remote Sens. 2023, 15, 1635. https://doi.org/10.3390/rs15061635
Wu Y, Guo J, Chen T, Chen A. Forecasting Precipitation from Radar Wind Profiler Mesonet and Reanalysis Using the Random Forest Algorithm. Remote Sensing. 2023; 15(6):1635. https://doi.org/10.3390/rs15061635
Chicago/Turabian StyleWu, Yizhi, Jianping Guo, Tianmeng Chen, and Aijun Chen. 2023. "Forecasting Precipitation from Radar Wind Profiler Mesonet and Reanalysis Using the Random Forest Algorithm" Remote Sensing 15, no. 6: 1635. https://doi.org/10.3390/rs15061635
APA StyleWu, Y., Guo, J., Chen, T., & Chen, A. (2023). Forecasting Precipitation from Radar Wind Profiler Mesonet and Reanalysis Using the Random Forest Algorithm. Remote Sensing, 15(6), 1635. https://doi.org/10.3390/rs15061635