Spectral Mixing Theory-Based Double-Branch Network for Spectral Super-Resolution
Abstract
1. Introduction
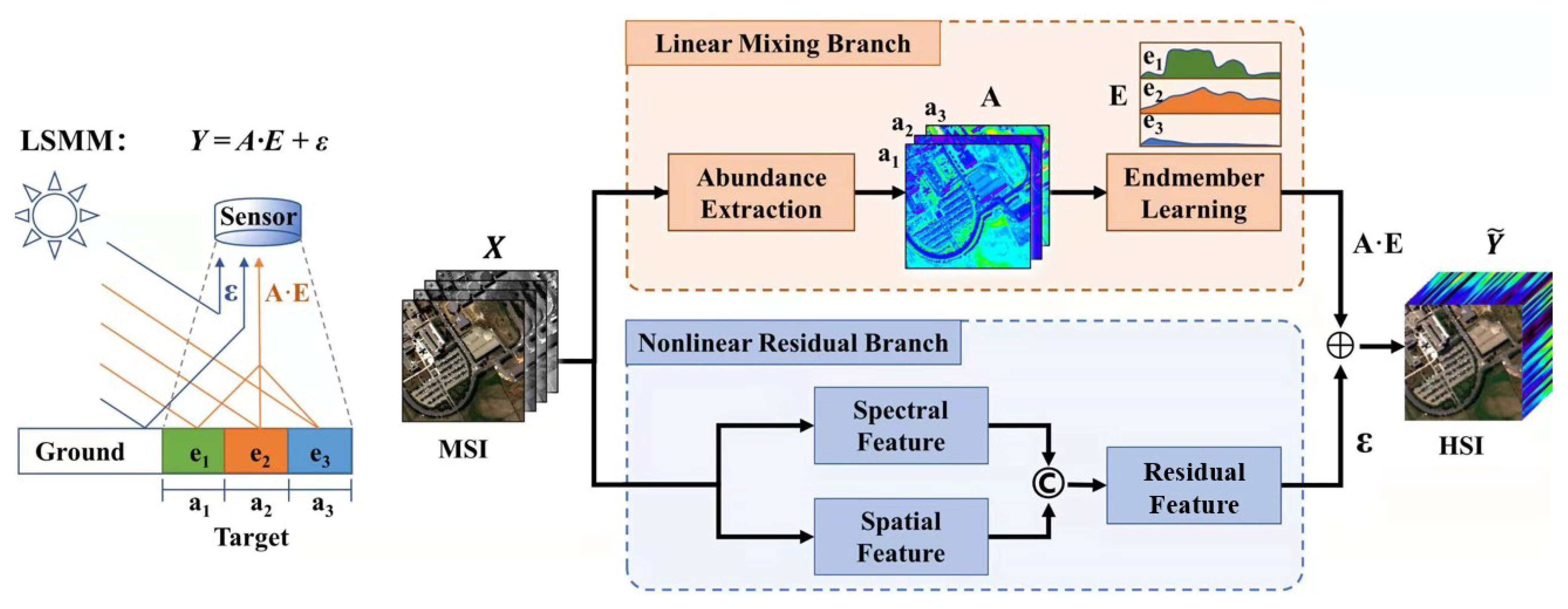
- It is an early attempt to introduce the spectral mixing theory into the SSR deep learning model construction. Inspired by the linear mixing part and the nonlinear residual part of the LSMM, the proposed method improves the interpretability of the network, through which the endmembers and abundance can be extracted and visualized for detailed analysis.
- A double-branch network structure is built in order to completely represent the linear and nonlinear mixed processes in HSIs. The linear mixing branch focuses on recovering rough HSIs with linear combinations of endmembers and abundance, consisting of a series of convolutions. The nonlinear residual branch supplements the rough HSIs with fine-scale residuals, including spatial textures and spectral details extracted by and convolutions. By combining these two branches, precise HSIs can be generated from corresponding MSIs with wide coverage.
- According to the physical significance of LSMM, our network is constrained at different stages, which form the joint loss function. In this way, the linear branch can provide a solid foundation for a nonlinear branch. Unlike the previous simulation dataset, a real MSI–HSI dataset with larger coverage is employed in the experiment, which demonstrates the robustness of our model in practical applications.
2. Materials and Methods
2.1. Theoretical Foundation
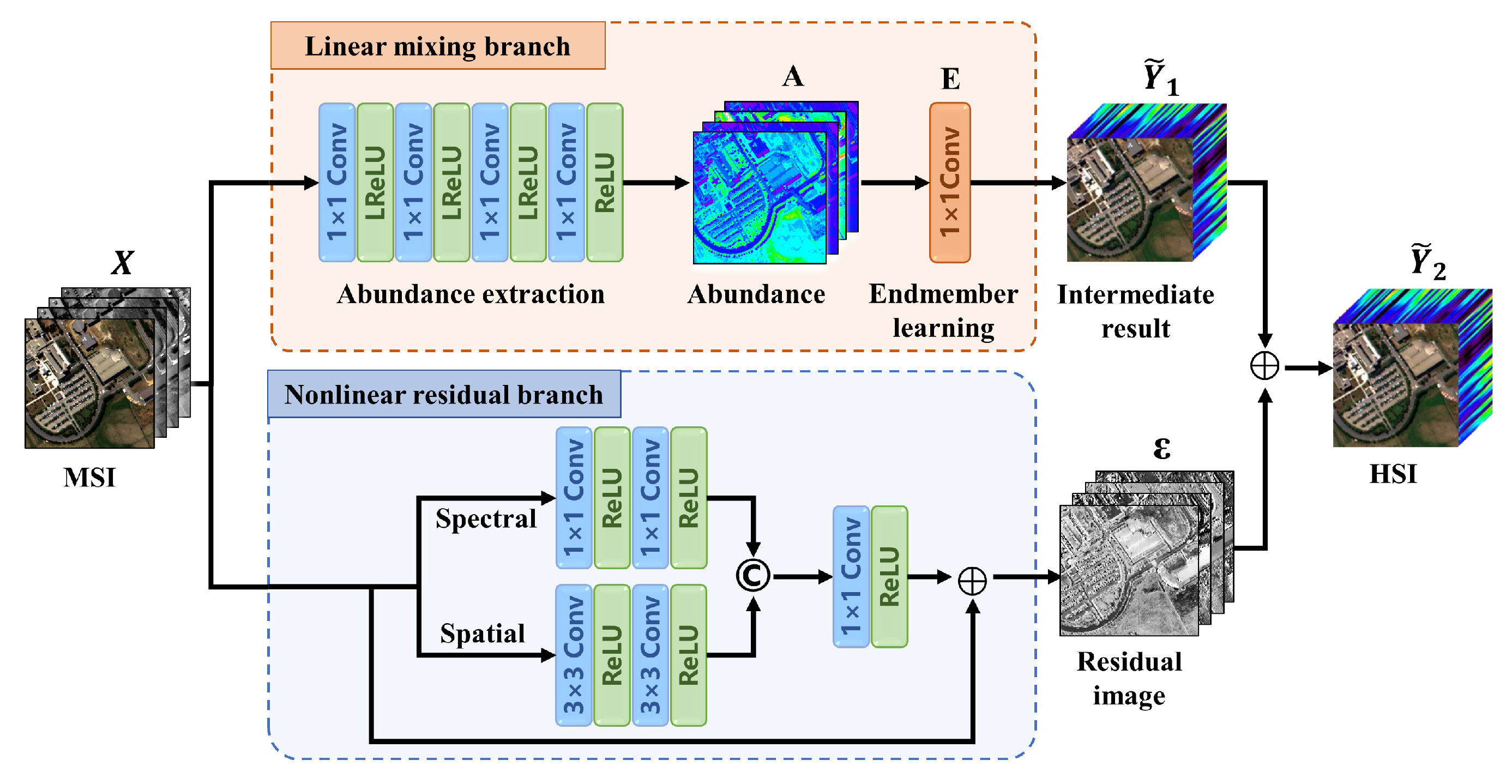
2.2. Linear Mixing Branch
2.2.1. Abundance Extraction Module
2.2.2. Endmember Adaptive Learning
2.3. Nonlinear Residual Branch
2.4. Feature Fusion
2.5. Joint Loss Function
- Abundance sum-to-one error: As mentioned in the abundance extraction module, the abundance needs to meet the sum-to-one constraint, which means that the sum of an abundance of all endmembers in the pixel is 1. Therefore, we create a sum2one loss function to make the extracted abundance reasonable and efficient. To be specific, we sum the channel of the abundance image and calculate the difference between each pixel value and 1. The formula is as follows:where i indicates the ith band of the abundance matrix A.
- HSI estimation error of intermediate result: The final result of this network is the fusion of linear and nonlinear branches. If we constrain the final result but not the intermediate result , each branch may fail to learn the desired result. Moreover, in traditional spectral unmixing, the error of image reconstruction is minimized to obtain the optimal endmembers and abundances. Therefore, it is necessary to constrain the intermediate result. In this way, when the model converges, the intermediate result could be approximate to the real HSI Y and ensure the accuracy of endmember and abundance. The formula is as follows:
- HSI estimation error of final result: The above two loss functions drive the gradient updating of the linear branch. In order to drive the nonlinear branch, the last HSI estimated loss function is added to the final result . This loss promotes the learning of residual features and enhances the precision of super-resolution. The formula is as follows:
3. Results
3.1. Datasets
3.1.1. Simulated Dataset
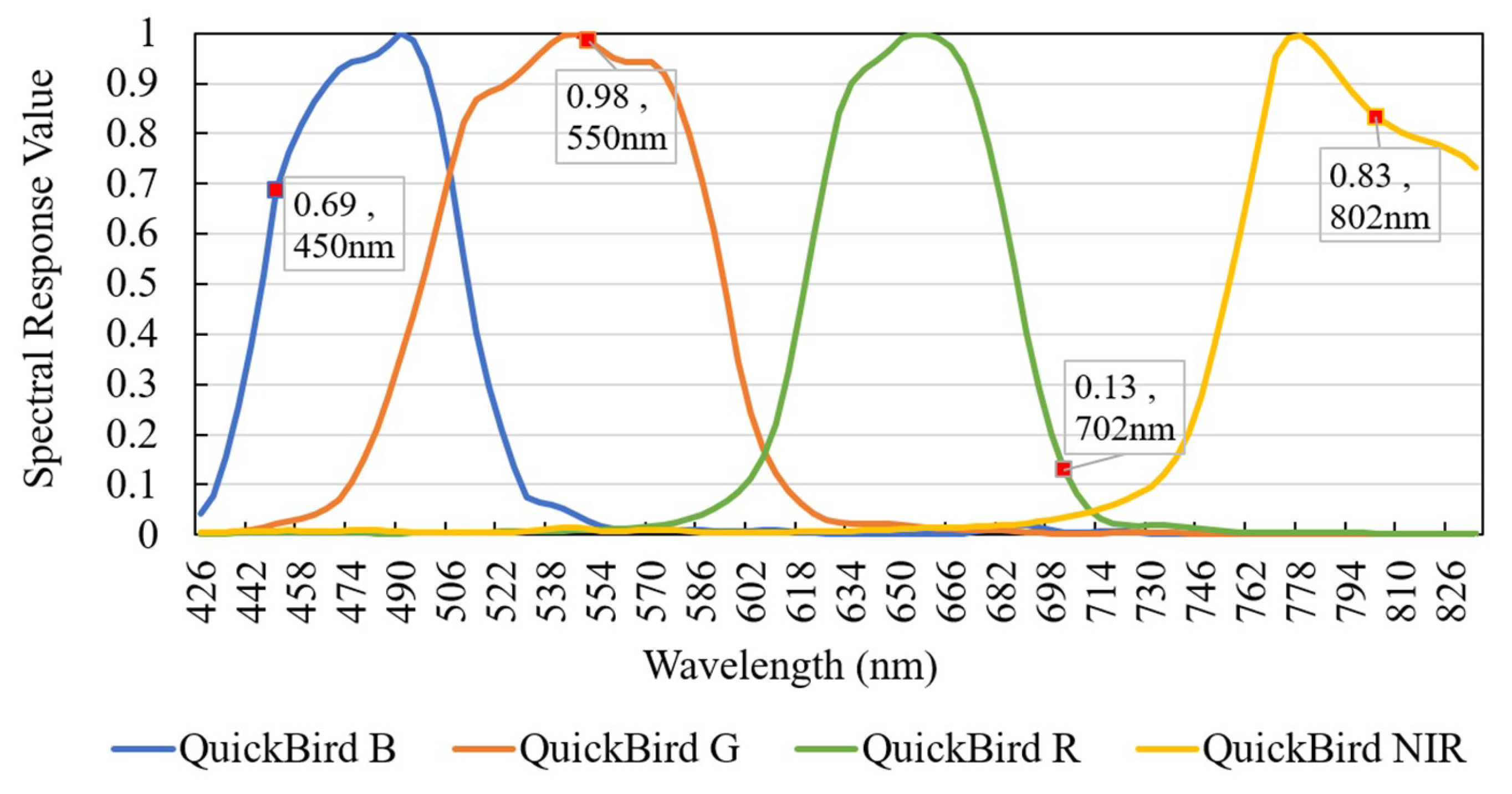
3.1.2. Real Satellite Dataset
3.2. Implementation Details
3.3. Comparison with the State of the Art
3.3.1. Results Using Pavia University Dataset
3.3.2. Results Using Indian Pines Dataset
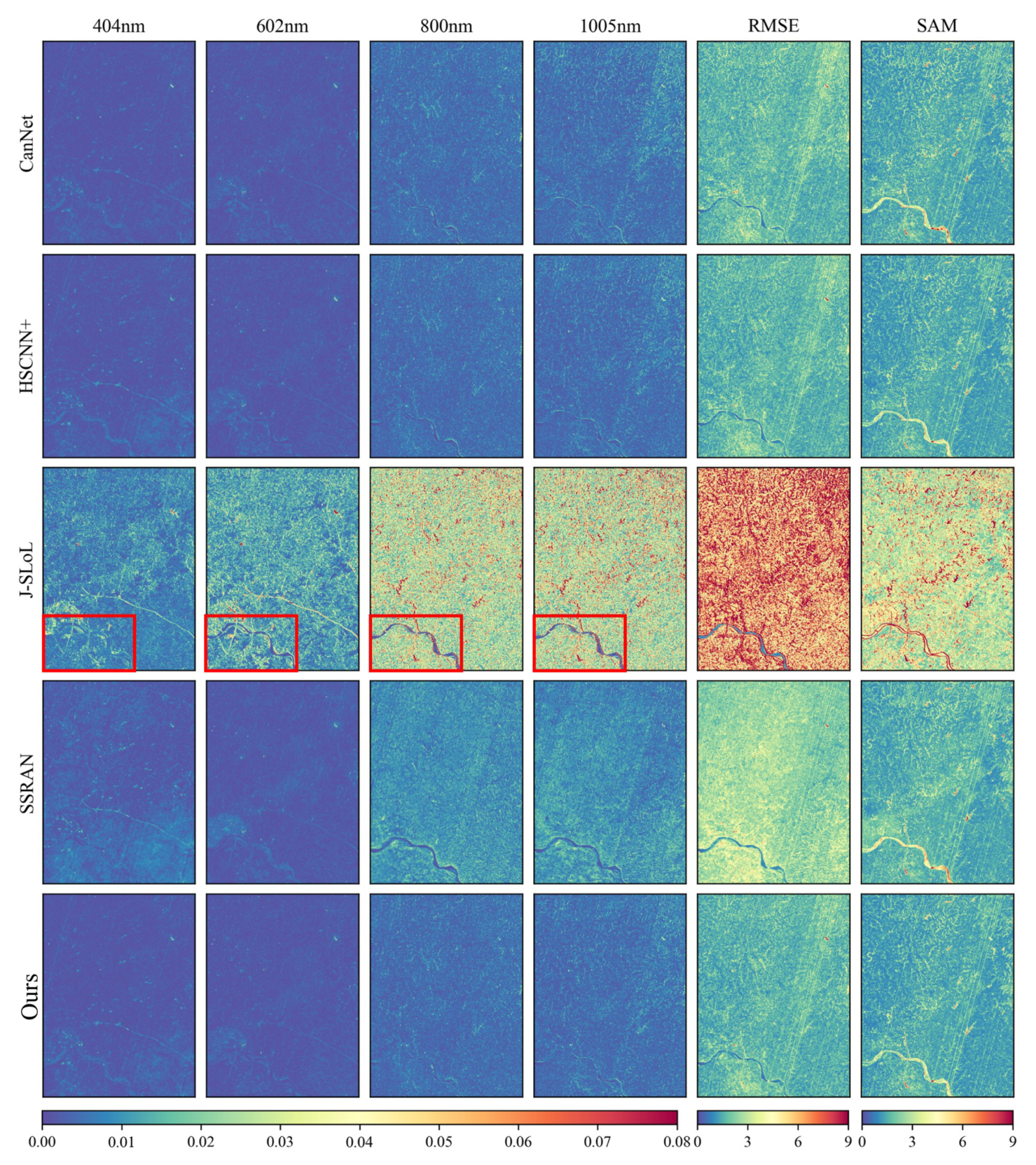
3.3.3. Results on ZY1-02D Dataset
3.4. Visualization Results
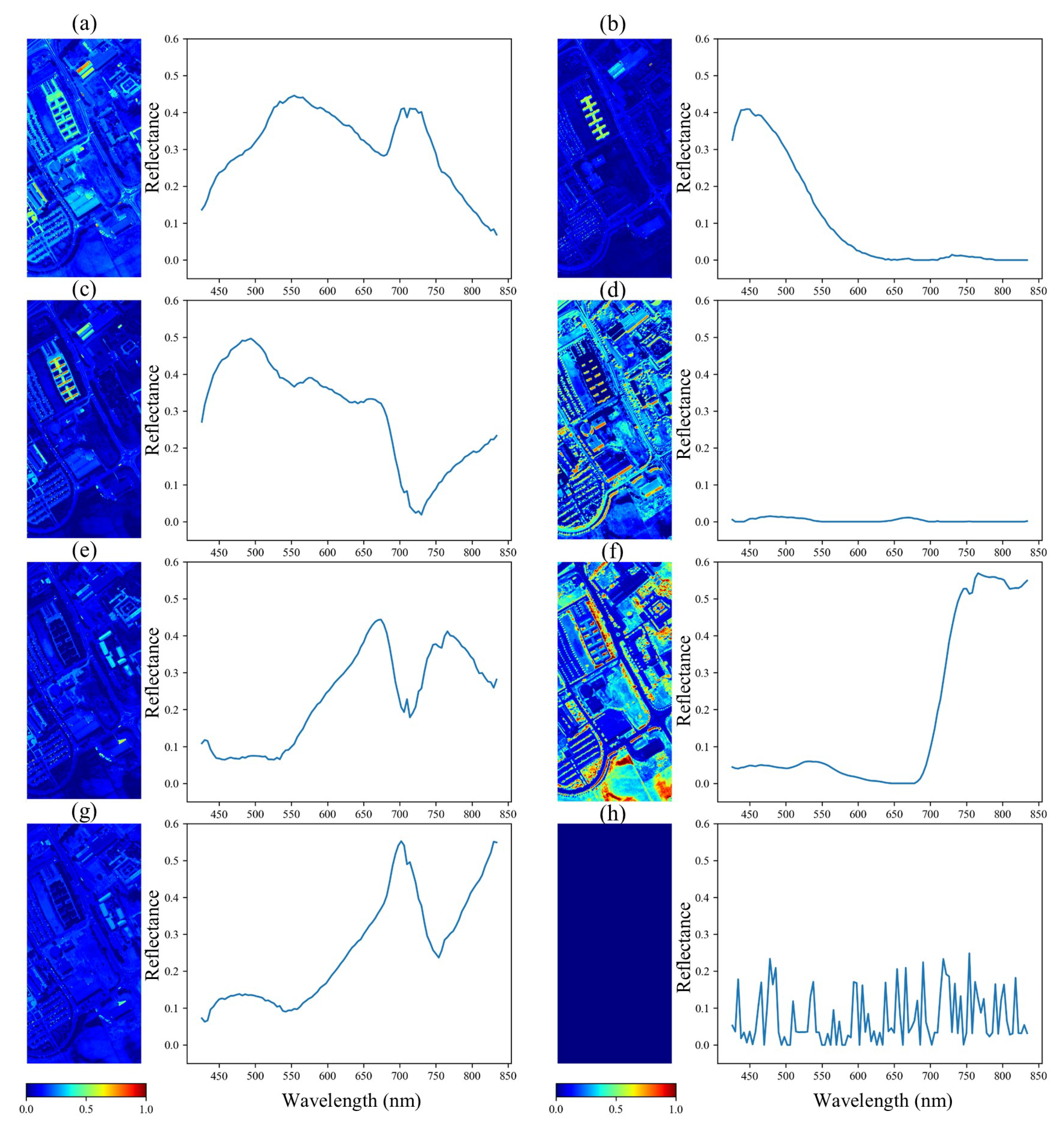
3.4.1. Endmembers and Abundances
3.4.2. Results of Two Branches
3.5. Ablation Study
3.6. Time Cost
4. Discussion
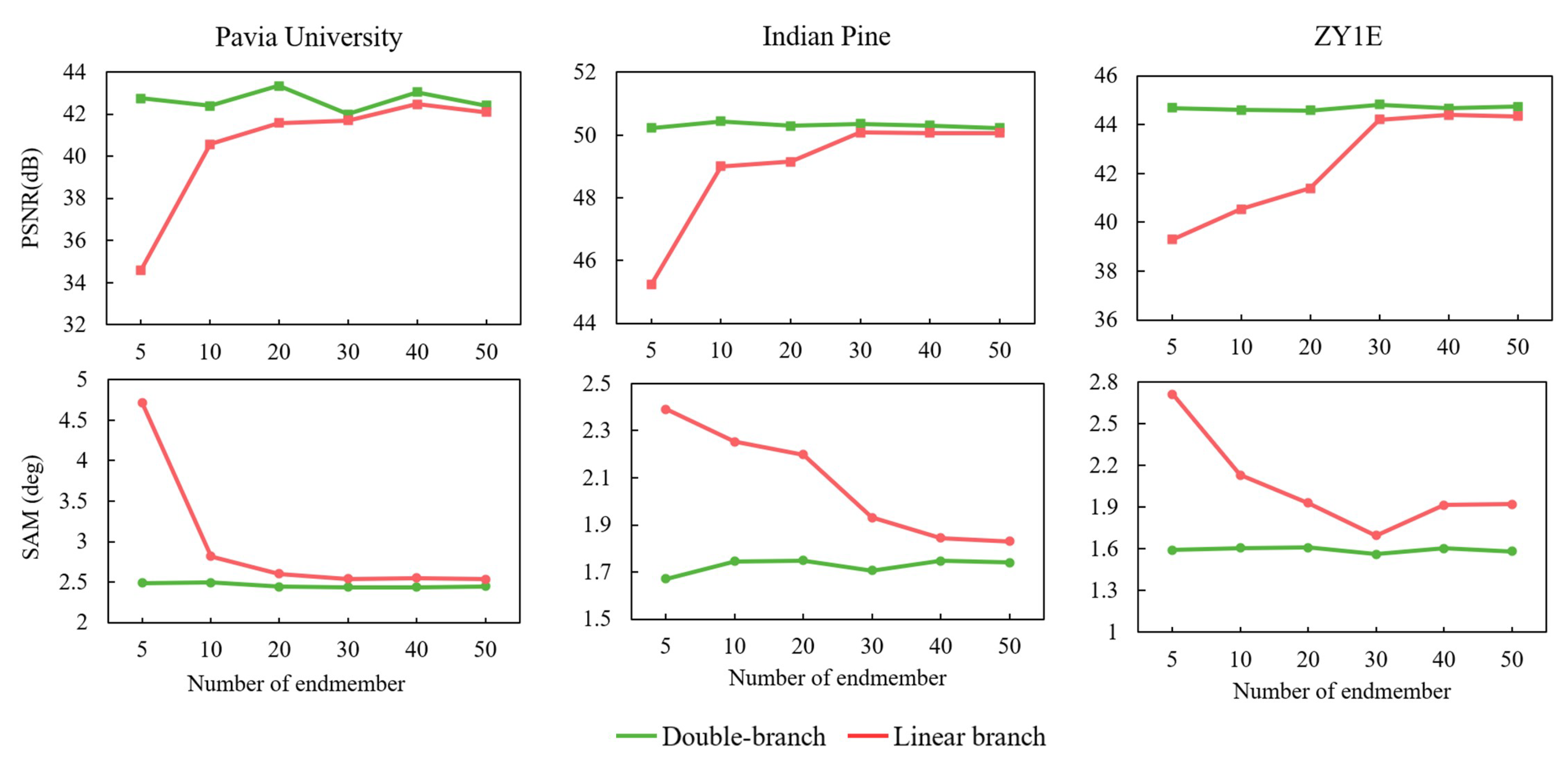
4.1. Number of Endmembers
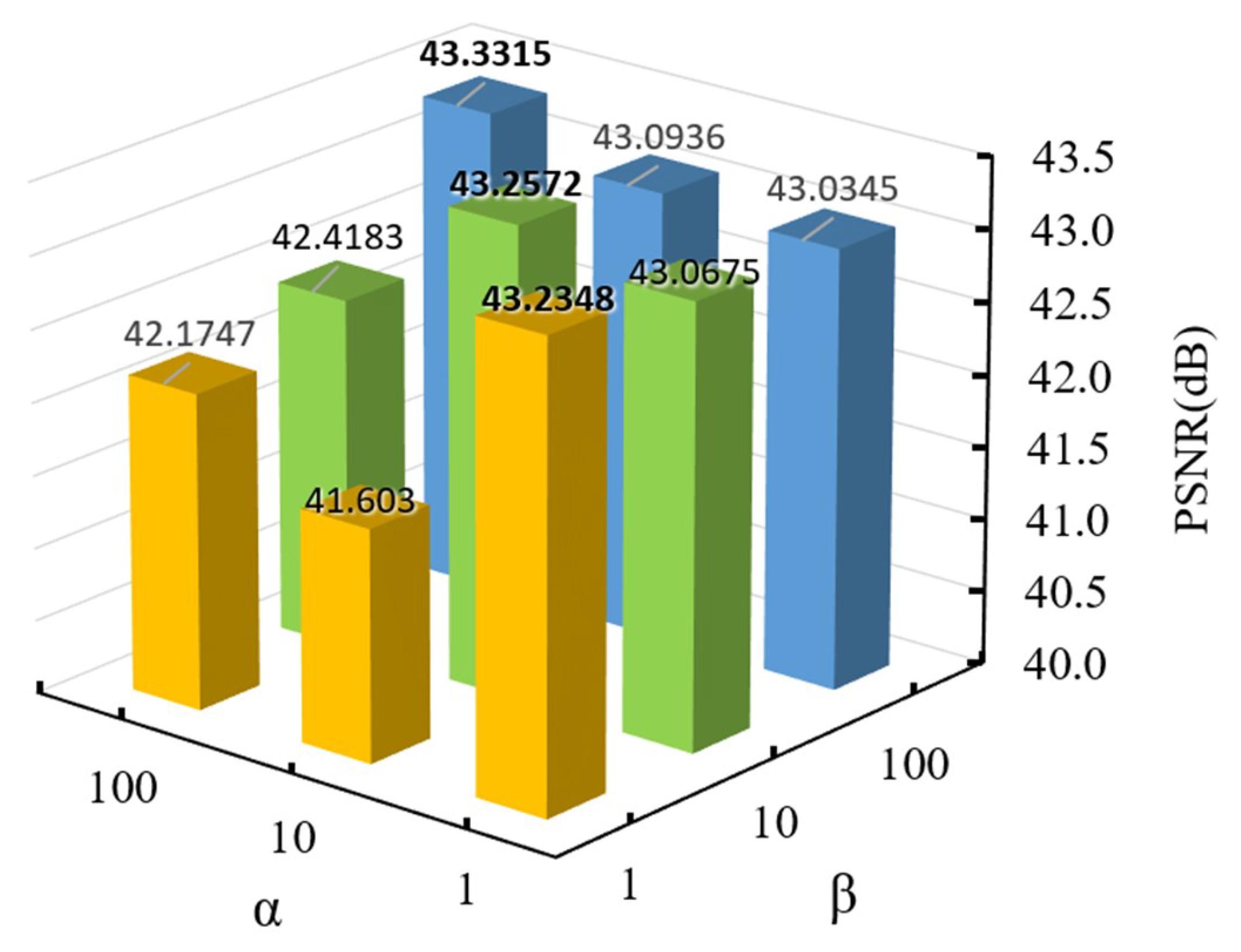
4.2. Loss Function Weight Coefficients
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, L.; Li, J. Development and Prospect of Sparse Representation-Based Hyperspectral Image Processing and Analysis. J. Remote Sens. 2016, 20, 1091. [Google Scholar] [CrossRef]
- Goetz, A.F.H.; Vane, G.; Solomon, J.E.; Rock, B.N. Imaging Spectrometry for Earth Remote Sensing. Science 1985, 228, 1147–1153. [Google Scholar] [CrossRef] [PubMed]
- Siebels, K.; Goïta, K.; Germain, M. Estimation of Mineral Abundance From Hyperspectral Data Using a New Supervised Neighbor-Band Ratio Unmixing Approach. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6754–6766. [Google Scholar] [CrossRef]
- Thiemann, S.; Kaufmann, H. Lake water quality monitoring using hyperspectral airborne data—A semiempirical multisensor and multitemporal approach for the Mecklenburg Lake District, Germany. Remote Sens. Environ. 2002, 81, 228–237. [Google Scholar] [CrossRef]
- Yuan, Q.; Shen, H.; Li, T.; Li, Z.; Li, S.; Jiang, Y.; Xu, H.; Tan, W.; Yang, Q.; Wang, J.; et al. Deep learning in environmental remote sensing: Achievements and challenges. Remote Sens. Environ. 2020, 241, 111716. [Google Scholar] [CrossRef]
- Zhang, N.; Yang, G.; Pan, Y.; Yang, X.; Chen, L.; Zhao, C. A Review of Advanced Technologies and Development for Hyperspectral-Based Plant Disease Detection in the Past Three Decades. Remote Sens. 2020, 12, 3188. [Google Scholar] [CrossRef]
- Yu, H.; Zhang, H.; Liu, Y.; Zheng, K.; Xu, Z.; Xiao, C. Dual-Channel Convolution Network with Image-Based Global Learning Framework for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Yokoya, N.; Yairi, T.; Iwasaki, A. Coupled non-negative matrix factorization (CNMF) for hyperspectral and multispectral data fusion: Application to pasture classification. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 1779–1782. [Google Scholar] [CrossRef]
- Manolakis, D.; Shaw, G. Detection algorithms for hyperspectral imaging applications. IEEE Signal Process. Mag. 2002, 19, 29–43. [Google Scholar] [CrossRef]
- Nielsen, A.A. The Regularized Iteratively Reweighted MAD Method for Change Detection in Multi- and Hyperspectral Data. IEEE Trans. Image Process. 2007, 16, 463–478. [Google Scholar] [CrossRef]
- Xu, Y.; Wu, Z.; Chanussot, J.; Comon, P.; Wei, Z. Nonlocal Coupled Tensor CP Decomposition for Hyperspectral and Multispectral Image Fusion. IEEE Trans. Geosci. Remote Sens. 2020, 58, 348–362. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, Y.Q.; Chan, J.C.W. Hyperspectral and Multispectral Image Fusion via Deep Two-Branches Convolutional Neural Network. Remote Sens. 2018, 10, 800. [Google Scholar] [CrossRef]
- Li, J.; Bioucas-Dias, J.M.; Plaza, A. Spectral–Spatial Hyperspectral Image Segmentation Using Subspace Multinomial Logistic Regression and Markov Random Fields. IEEE Trans. Geosci. Remote Sens. 2012, 50, 809–823. [Google Scholar] [CrossRef]
- Zhong, Y.; Wang, X.; Wang, S.; Zhang, L. Advances in spaceborne hyperspectral remote sensing in China. Geo-Spat. Inf. Sci. 2021, 24, 95–120. [Google Scholar] [CrossRef]
- Mei, S.; Jiang, R.; Li, X.; Du, Q. Spatial and Spectral Joint Super-Resolution Using Convolutional Neural Network. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4590–4603. [Google Scholar] [CrossRef]
- Chen, W.; Zheng, X.; Lu, X. Semisupervised Spectral Degradation Constrained Network for Spectral Super-Resolution. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- He, J.; Li, J.; Yuan, Q.; Shen, H.; Zhang, L. Spectral Response Function-Guided Deep Optimization-Driven Network for Spectral Super-Resolution. IEEE Trans. Neural Networks Learn. Syst. 2022, 33, 4213–4227. [Google Scholar] [CrossRef] [PubMed]
- Arad, B.; Ben-Shahar, O. Sparse Recovery of Hyperspectral Signal from Natural RGB Images. In Proceedings of the Computer Vision, ECCV 2016, Amsterdam, The Netherlands, 11–14 October 2016; Leibe, B., Matas, J., Sebe, N., Welling, M., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 19–34. [Google Scholar]
- Rubinstein, R.; Zibulevsky, M.; Elad, M. Efficient Implementation of the K-SVD Algorithm Using Batch Orthogonal Matching Pursuit; Technical report; Computer Science Department, Technion: Haifa, Israel, 2008. [Google Scholar]
- Gao, L.; Hong, D.; Yao, J.; Zhang, B.; Gamba, P.; Chanussot, J. Spectral Superresolution of Multispectral Imagery with Joint Sparse and Low-Rank Learning. IEEE Trans. Geosci. Remote Sens. 2021, 59, 2269–2280. [Google Scholar] [CrossRef]
- Huang, Z.; Chen, Q.; Chen, Q.; Liu, X.; He, H. A Novel Hyperspectral Image Simulation Method Based on Nonnegative Matrix Factorization. Remote Sens. 2019, 11, 2416. [Google Scholar] [CrossRef]
- Nguyen, R.M.H.; Prasad, D.K.; Brown, M.S. Training-Based Spectral Reconstruction from a Single RGB Image. In Proceedings of the Computer Vision, ECCV 2014, Zurich, Switzerland, 6–12 September 2014; Fleet, D., Pajdla, T., Schiele, B., Tuytelaars, T., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 186–201. [Google Scholar]
- Alvarez-Gila, A.; van de Weijer, J.; Garrote, E. Adversarial Networks for Spatial Context-Aware Spectral Image Reconstruction from RGB. CoRR 2017, arXiv:1709.00265. [Google Scholar]
- Jégou, S.; Drozdzal, M.; Vazquez, D.; Romero, A.; Bengio, Y. The One Hundred Layers Tiramisu: Fully Convolutional DenseNets for Semantic Segmentation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 21–26 July 2017; pp. 1175–1183. [Google Scholar] [CrossRef]
- Galliani, S.; Lanaras, C.; Marmanis, D.; Baltsavias, E.; Schindler, K. Learned Spectral Super-Resolution. CoRR 2017, arXiv:1703.09470. [Google Scholar]
- Can, Y.B.; Timofte, R. An efficient CNN for spectral reconstruction from RGB images. CoRR 2018, arXiv:1804.04647. [Google Scholar]
- Shi, Z.; Chen, C.; Xiong, Z.; Liu, D.; Wu, F. HSCNN+: Advanced CNN-Based Hyperspectral Recovery from RGB Images. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Salt Lake City, UT, USA, 18–22 June 2018; pp. 1052–10528. [Google Scholar] [CrossRef]
- Li, J.; Wu, C.; Song, R.; Li, Y.; Xie, W.; He, L.; Gao, X. Deep Hybrid 2-D-3-D CNN Based on Dual Second-Order Attention with Camera Spectral Sensitivity Prior for Spectral Super-Resolution. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 623–634. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Wu, C.; Song, R.; Xie, W.; Ge, C.; Li, B.; Li, Y. Hybrid 2-D–3-D Deep Residual Attentional Network with Structure Tensor Constraints for Spectral Super-Resolution of RGB Images. IEEE Trans. Geosci. Remote Sens. 2021, 59, 2321–2335. [Google Scholar] [CrossRef]
- Ji, S.; Xu, W.; Yang, M.; Yu, K. 3D Convolutional Neural Networks for Human Action Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 221–231. [Google Scholar] [CrossRef] [PubMed]
- Mei, S.; Ji, J.; Hou, J.; Li, X.; Du, Q. Learning Sensor-Specific Spatial-Spectral Features of Hyperspectral Images via Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4520–4533. [Google Scholar] [CrossRef]
- Arun, P.V.; Herrmann, I.; Budhiraju, K.M.; Karnieli, A. Convolutional network architectures for super-resolution/sub-pixel mapping of drone-derived images. Pattern Recognit. 2019, 88, 431–446. [Google Scholar] [CrossRef]
- Zheng, X.; Chen, W.; Lu, X. Spectral Super-Resolution of Multispectral Images Using Spatial–Spectral Residual Attention Network. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Zhang, B. Advancement of Hyperspectral Image Processing and Information Extraction. J. Remote Sens. 2016, 20, 1062–1090. [Google Scholar] [CrossRef]
- Chen, W.; Lu, X. Unregistered Hyperspectral and Multispectral Image Fusion with Synchronous Nonnegative Matrix Factorization. In Proceedings of the Pattern Recognition and Computer Vision, Nanjing, China, 16–18 October 2020; Peng, Y., Liu, Q., Lu, H., Sun, Z., Liu, C., Chen, X., Zha, H., Yang, J., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 602–614. [Google Scholar]
- Ghamisi, P.; Yokoya, N.; Li, J.; Liao, W.; Liu, S.; Plaza, J.; Rasti, B.; Plaza, A. Advances in Hyperspectral Image and Signal Processing: A Comprehensive Overview of the State of the Art. IEEE Geosci. Remote Sens. Mag. 2017, 5, 37–78. [Google Scholar] [CrossRef]
- Zheng, K.; Gao, L.; Liao, W.; Hong, D.; Zhang, B.; Cui, X.; Chanussot, J. Coupled Convolutional Neural Network with Adaptive Response Function Learning for Unsupervised Hyperspectral super-resolution. IEEE Trans. Geosci. Remote Sens. 2021, 59, 2487–2502. [Google Scholar] [CrossRef]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep sparse rectifier neural networks. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 11–13 April 2011; pp. 315–323. [Google Scholar]
- Maas, A.L.; Hannun, A.Y.; Ng, A.Y. Rectifier nonlinearities improve neural network acoustic models. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; Volume 30, p. 3. [Google Scholar]
- Li, J.; Du, S.; Song, R.; Wu, C.; Li, Y.; Du, Q. HASIC-Net: Hybrid Attentional Convolutional Neural Network with Structure Information Consistency for Spectral Super-Resolution of RGB Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Dong, W.; Fu, F.; Shi, G.; Cao, X.; Wu, J.; Li, G.; Li, X. Hyperspectral Image Super-Resolution via Non-Negative Structured Sparse Representation. IEEE Trans. Image Process. 2016, 25, 2337–2352. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Wei, W.; Bai, C.; Gao, Y.; Zhang, Y. Exploiting Clustering Manifold Structure for Hyperspectral Imagery Super-Resolution. IEEE Trans. Image Process. 2018, 27, 5969–5982. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Lang, Z.; Wang, P.; Wei, W.; Liao, S.; Shao, L.; Zhang, Y. Pixel-aware Deep Function-mixture Network for Spectral Super-Resolution. CoRR 2019, arXiv:1903.10501. [Google Scholar] [CrossRef]
- Licciardi, G.; Pacifici, F.; Tuia, D.; Prasad, S.; West, T.; Giacco, F.; Thiel, C.; Inglada, J.; Christophe, E.; Chanussot, J.; et al. Decision Fusion for the Classification of Hyperspectral Data: Outcome of the 2008 GRS-S Data Fusion Contest. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3857–3865. [Google Scholar] [CrossRef]
- Niu, C.; Tan, K.; Wang, X.; Han, B.; Ge, S.; Du, P.; Wang, F. Radiometric Cross-Calibration of the ZY1-02D Hyperspectral Imager Using the GF-5 AHSI Imager. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–12. [Google Scholar] [CrossRef]
- Yokoya, N.; Grohnfeldt, C.; Chanussot, J. Hyperspectral and Multispectral Data Fusion: A comparative review of the recent literature. IEEE Geosci. Remote Sens. Mag. 2017, 5, 29–56. [Google Scholar] [CrossRef]
- Arad, B.; Ben-Shahar, O.; Timofte, R.; Van Gool, L.; Zhang, L.; Yang, M.H.; Xiong, Z.; Chen, C.; Shi, Z.; Liu, D.; et al. NTIRE 2018 Challenge on Spectral Reconstruction from RGB Images. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Salt Lake City, UT, USA, 18–22 June 2018; pp. 1042–104209. [Google Scholar] [CrossRef]




| Method | Model | Datasets | Characteristics and Limitations |
|---|---|---|---|
| Sparse representation | Arad [18] | RGB natural images | specific physical significance; limited feature extraction ability |
| J-SLoL [20] | simulated MSIs in small area (Pavia University; Indian Pines; Jasper Ridge data) | ||
| Linear mixing | Huang [21] | real MSIs in small area (Hyperion and ALI data) | |
| Deep learning | Nguyen [22] | RGB natural images | powerful nonlinear mapping ability; few of prior knowledge |
| Alvaretz-Gila [23] | |||
| CanNet [26] | |||
| HSCNN+ [27] | |||
| HSRnet [17] | |||
| HSACS [33] | |||
| Galliani [25] SSRAN [29] | simulated MSIs in small area (Pavia University; WDCM; Hyperion data) |
| Model | SAM↓ | mPSNR↑ | mSSIM↑ | RMSE↓ | ERGAS↓ |
|---|---|---|---|---|---|
| CanNet | 2.7033 | 41.4423 | 0.981 | 2.6965 | 7.5656 |
| HSCNN+ | 2.5827 | 41.9854 | 0.9821 | 2.5681 | 7.5035 |
| J-SLoL | 3.1975 | 41.2597 | 0.9779 | 3.0937 | 8.9397 |
| SSRAN | 3.0921 | 40.2035 | 0.9815 | 3.3208 | 7.7943 |
| proposed | 2.4404 | 43.3315 | 0.9839 | 2.2573 | 6.4855 |
| Model | SAM↓ | mPSNR↑ | mSSIM↑ | RMSE↓ | ERGAS↓ |
|---|---|---|---|---|---|
| CanNet | 2.0264 | 45.224 | 0.9592 | 2.9174 | 3.4896 |
| HSCNN+ | 1.6546 | 46.4107 | 0.9733 | 2.6456 | 3.0362 |
| J-SLoL | 2.1402 | 48.0629 | 0.9605 | 3.1001 | 3.5629 |
| SSRAN | 1.7582 | 45.8878 | 0.9691 | 2.5511 | 3.1053 |
| proposed | 1.7065 | 50.3618 | 0.9737 | 2.5436 | 2.8286 |
| Model | SAM↓ | mPSNR↑ | mSSIM↑ | RMSE↓ | ERGAS↓ |
|---|---|---|---|---|---|
| CanNet | 1.6647 | 44.2458 | 0.9836 | 2.1065 | 4.4467 |
| HSCNN+ | 1.5805 | 44.6401 | 0.9851 | 1.9874 | 4.2816 |
| J-SLoL | 3.2446 | 35.0172 | 0.8836 | 5.913 | 11.8999 |
| SSRAN | 1.7480 | 41.9410 | 0.9835 | 2.8180 | 5.4941 |
| proposed | 1.5605 | 44.8206 | 0.9851 | 1.9707 | 4.1625 |
| Dataset | Model | SAM↓ | mPSNR↑ | mSSIM↑ | RMSE↓ | ERGAS↓ |
|---|---|---|---|---|---|---|
| Pavia university | Linear branch | 2.5513 | 42.7637 | 0.9832 | 2.401 | 6.8618 |
| Noninear branch | 2.4841 | 42.9299 | 0.9834 | 2.4256 | 7.0207 | |
| Double-branch | 2.4404 | 43.3315 | 0.9839 | 2.2573 | 6.4855 | |
| Indian pine | Linear branch | 2.2036 | 49.6509 | 0.9626 | 3.1763 | 3.5063 |
| Noninear branch | 1.7154 | 50.0954 | 0.9728 | 2.6155 | 2.8442 | |
| Double-branch | 1.7065 | 50.3618 | 0.9737 | 2.5436 | 2.8286 | |
| ZY1-02D | Linear branch | 1.8944 | 41.4519 | 0.9658 | 2.8046 | 5.7678 |
| Noninear branch | 1.5963 | 44.553 | 0.9846 | 2.0042 | 4.2992 | |
| Double-branch | 1.5605 | 44.8206 | 0.9851 | 1.9707 | 4.1625 |
| Model | Time Cost (mins) | mPSNR |
|---|---|---|
| CanNet | 23.50 | 44.2458 |
| HSCNN+ | 33.06 | 44.6401 |
| J-SLoL | 41.92 | 35.0172 |
| SSRAN | 24.17 | 41.9410 |
| proposed | 28.25 | 44.8206 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sha, L.; Zhang, W.; Zhang, B.; Liu, Z.; Li, Z. Spectral Mixing Theory-Based Double-Branch Network for Spectral Super-Resolution. Remote Sens. 2023, 15, 1308. https://doi.org/10.3390/rs15051308
Sha L, Zhang W, Zhang B, Liu Z, Li Z. Spectral Mixing Theory-Based Double-Branch Network for Spectral Super-Resolution. Remote Sensing. 2023; 15(5):1308. https://doi.org/10.3390/rs15051308
Chicago/Turabian StyleSha, Lingyu, Wenjuan Zhang, Bing Zhang, Zhiqiang Liu, and Zhen Li. 2023. "Spectral Mixing Theory-Based Double-Branch Network for Spectral Super-Resolution" Remote Sensing 15, no. 5: 1308. https://doi.org/10.3390/rs15051308
APA StyleSha, L., Zhang, W., Zhang, B., Liu, Z., & Li, Z. (2023). Spectral Mixing Theory-Based Double-Branch Network for Spectral Super-Resolution. Remote Sensing, 15(5), 1308. https://doi.org/10.3390/rs15051308







