An ADMM-qSPICE-Based Sparse DOA Estimation Method for MIMO Radar
Abstract
1. Introduction
2. Materials and Methods
2.1. MIMO Signal Model
2.2. qSPICE
2.3. ADMM
2.4. Proposed Method
2.4.1. ADMM-qSPICE
| Algorithm 1 ADMM-qSPICE |
|
2.4.2. Computational Complexity Analysis
3. Results
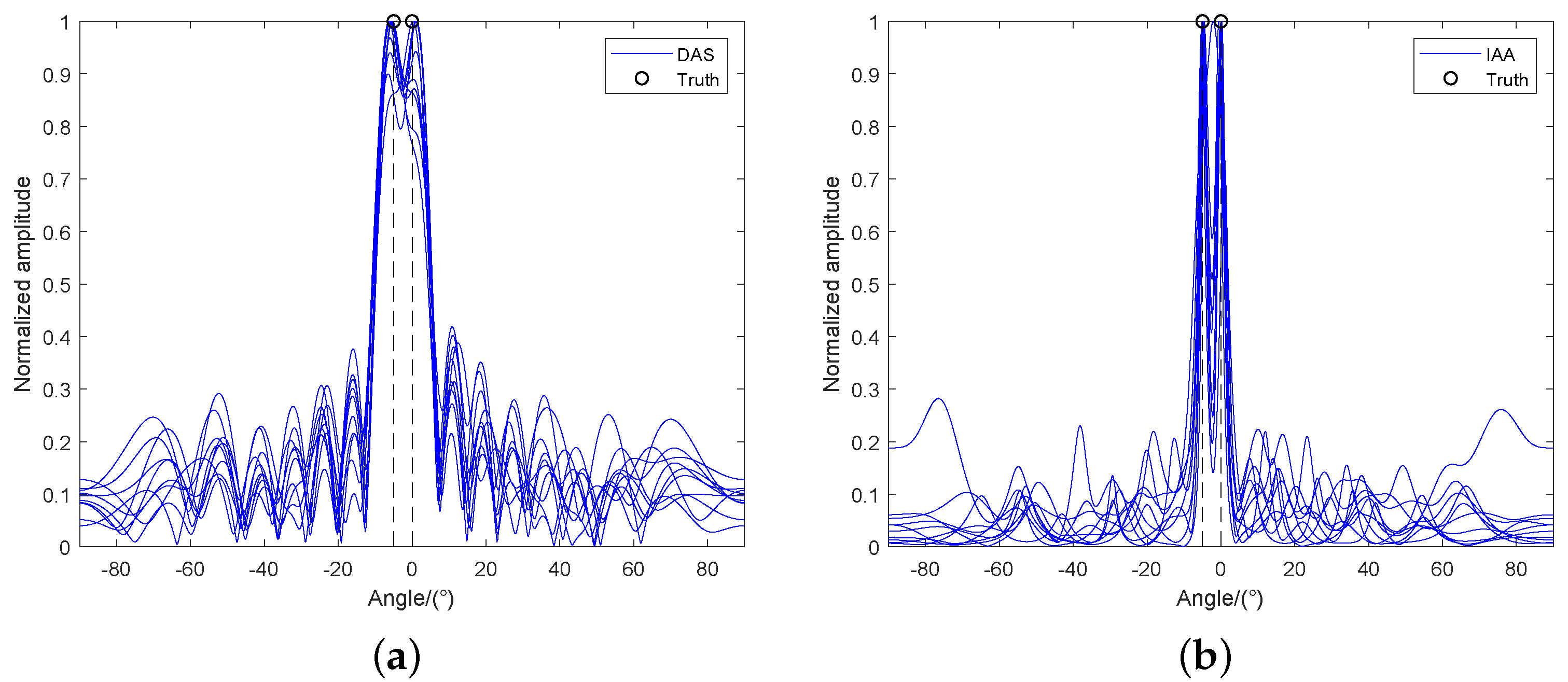
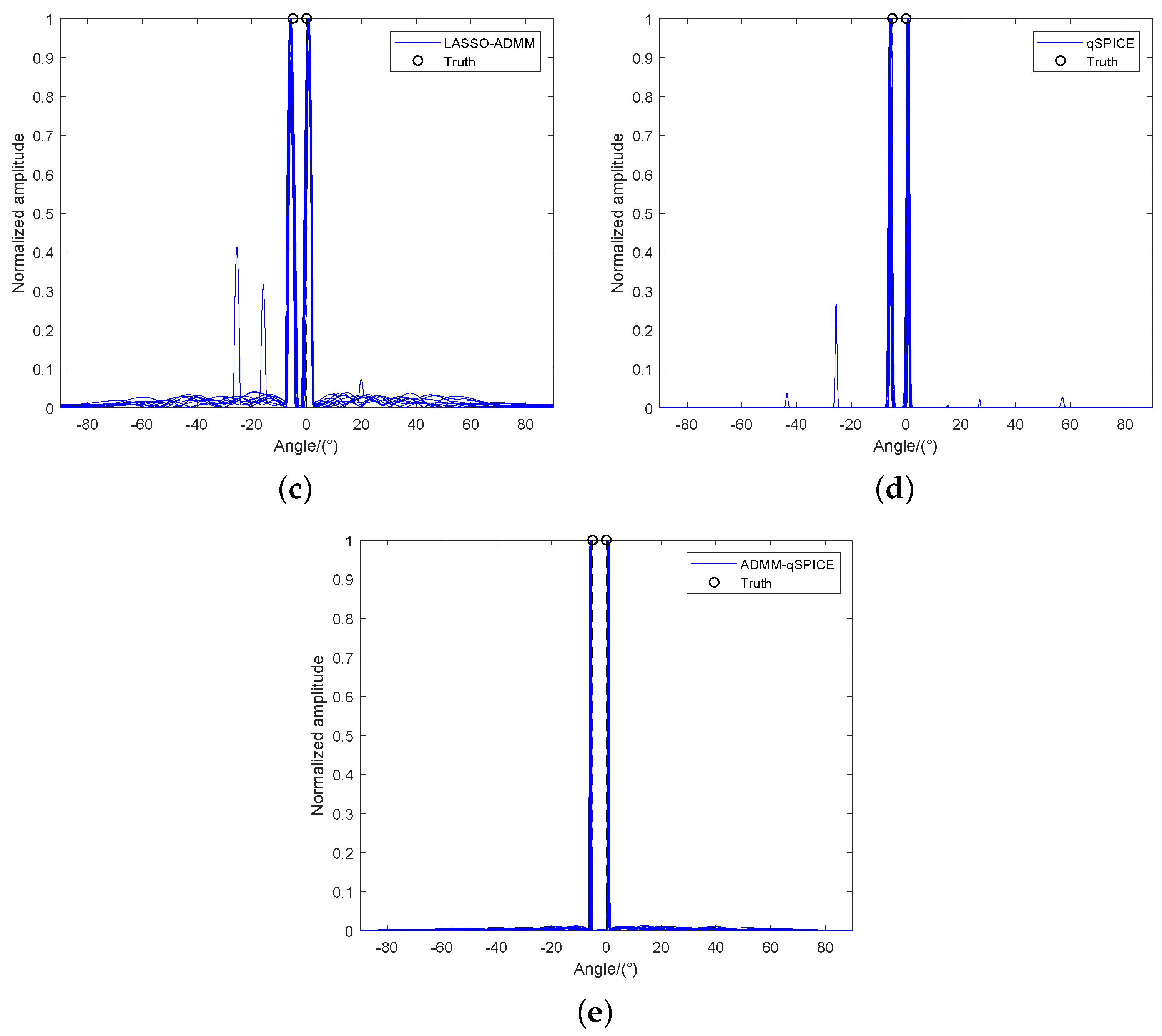
3.1. Simulation Results
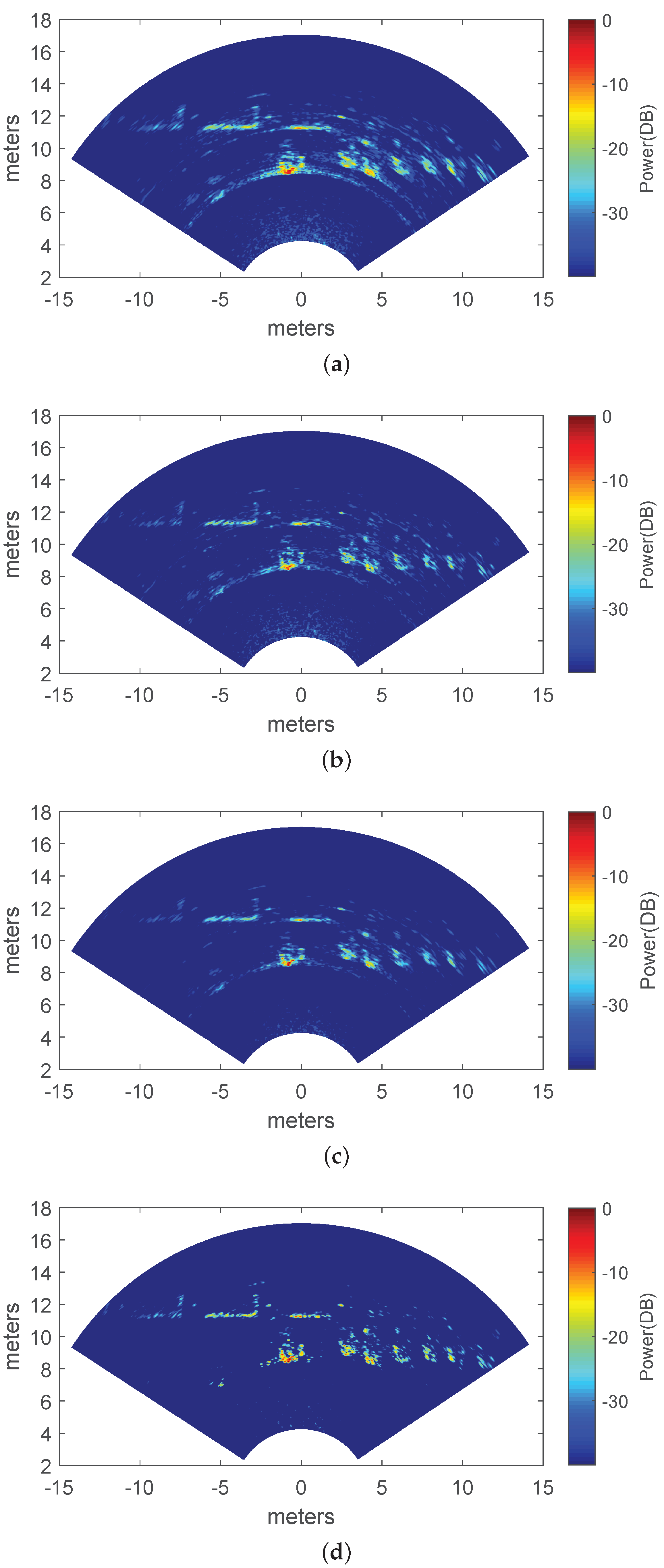
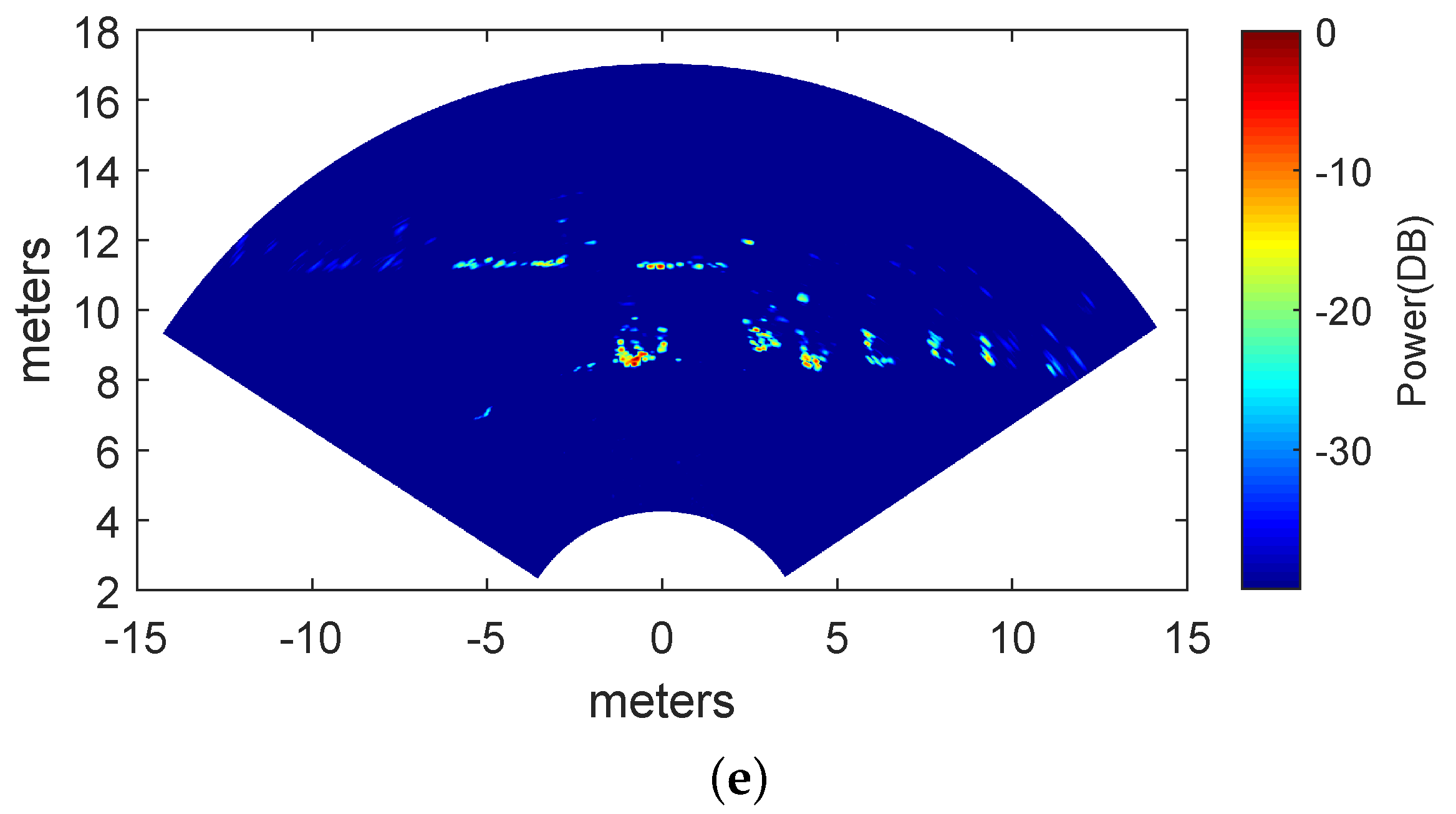
3.2. Measured Results
4. Discussion
4.1. Results Analysis and Limitations
4.2. Extended Applications
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DOA | directions of arrival |
| MIMO | multiple-input multiple-output |
| LASSO | least absolute shrinkage and selection operator |
| ADMM | alternating-direction method of multipliers |
| qSPICE | generalized SParse Iterative Covariance-based Estimation |
| DAS | delay-and-sum |
| FFT | fast Fourier transform |
| SIMO | single-input multiple-output |
| ESPRIT | estimation of signal parameters via rotational invariance techniques |
| MUSIC | multiple signal classification |
| PARAFAC | parallel factor analysis |
| MVDR | Minimum variance distortionless response |
| IAA | iterative adaptive method |
| SLIM | sparse learning via iterative minimization |
| SPICE | sparse Iterative Covariance-based Estimation |
| NS | Neumann series |
| MIA | matrix inversion approximation |
| CS | compressed sensing |
| IPM | interior point method |
| ALM | augmented Lagrange multiplier |
| ULA | uniform linear array |
| RMSE | root mean square error |
| CRB | Cramer-Rao bound |
| UAV | unmanned aerial vehicle |
| SNR | signal-to-noise ratio |
| IE | Image entropy |
References
- Sharma, P.; Tiwari, R.N.; Singh, P.; Kumar, P.; Kanaujia, B.K. MIMO Antennas: Design Approaches, Techniques and Applications. Sensors 2022, 22, 7813. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Tong, N.; Wang, J.; Ding, S.; Zhao, X. Matrix completion-based MIMO radar imaging with sparse planar array. Signal Process. 2017, 131, 49–57. [Google Scholar] [CrossRef]
- Fishler, E.; Haimovich, A.; Blum, R.; Chizhik, D.; Cimini, L.; Valenzuela, R. MIMO radar: An idea whose time has come. In Proceedings of the 2004 IEEE Radar Conference (IEEE Cat. No. 04CH37509), Philadelphia, PA, USA, 29 April 2004; pp. 71–78. [Google Scholar]
- Dai, J.; So, H.C. Real-valued sparse Bayesian learning for DOA estimation with arbitrary linear arrays. IEEE Trans. Signal Process. 2021, 69, 4977–4990. [Google Scholar] [CrossRef]
- Liang, Y.; Liu, W.; Shen, Q.; Cui, W.; Wu, S. A review of closed-form Cramér-Rao bounds for DOA estimation in the presence of Gaussian noise under a unified framework. IEEE Access 2020, 8, 175101–175124. [Google Scholar] [CrossRef]
- Zhang, Y.; Luo, J.; Zhang, Y.; Huang, Y.; Cai, X.; Yang, J.; Mao, D.; Li, J.; Tuo, X.; Zhang, Y. Resolution Enhancement for Large-Scale Real Beam Mapping Based on Adaptive Low-Rank Approximation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5116921. [Google Scholar] [CrossRef]
- Zhang, Y.; Luo, J.; Li, J.; Mao, D.; Zhang, Y.; Huang, Y.; Yang, J. Fast inverse-scattering reconstruction for airborne high-squint radar imagery based on Doppler centroid compensation. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5205517. [Google Scholar] [CrossRef]
- Qiu, S.; Ma, X.; Zhang, R.; Han, Y.; Sheng, W. A dual-resolution unitary ESPRIT method for DOA estimation based on sparse co-prime MIMO radar. Signal Process. 2023, 202, 108753. [Google Scholar] [CrossRef]
- Meng, F.X.; Li, Z.T.; Xu-Tao, Y.; Zhang, Z.C. Quantum algorithm for MUSIC-based DOA estimation in hybrid MIMO systems. Quantum Sci. Technol. 2022, 7, 025002. [Google Scholar] [CrossRef]
- Ruan, N.J.; Wen, F.q.; Ai, L.; Xie, K. A PARAFAC decomposition algorithm for DOA estimation in colocated MIMO radar with imperfect waveforms. IEEE Access 2019, 7, 14680–14688. [Google Scholar] [CrossRef]
- Hassanien, A.; Vorobyov, S.A. Transmit energy focusing for DOA estimation in MIMO radar with colocated antennas. IEEE Trans. Signal Process. 2011, 59, 2669–2682. [Google Scholar] [CrossRef]
- Huang, H.; Yang, J.; Huang, H.; Song, Y.; Gui, G. Deep learning for super-resolution channel estimation and DOA estimation based massive MIMO system. IEEE Trans. Veh. Technol. 2018, 67, 8549–8560. [Google Scholar] [CrossRef]
- Roberts, W.; Stoica, P.; Li, J.; Yardibi, T.; Sadjadi, F.A. Iterative adaptive approaches to MIMO radar imaging. IEEE J. Sel. Top. Signal Process. 2010, 4, 5–20. [Google Scholar] [CrossRef]
- Shang, X.; Liu, J.; Li, J. Multiple object localization and vital sign monitoring using IR-UWB MIMO radar. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 4437–4450. [Google Scholar] [CrossRef]
- Tan, X.; Roberts, W.; Li, J.; Stoica, P. Sparse learning via iterative minimization with application to MIMO radar imaging. IEEE Trans. Signal Process. 2010, 59, 1088–1101. [Google Scholar] [CrossRef]
- Stoica, P.; Babu, P.; Li, J. New method of sparse parameter estimation in separable models and its use for spectral analysis of irregularly sampled data. IEEE Trans. Signal Process. 2010, 59, 35–47. [Google Scholar] [CrossRef]
- Luo, J.; Zhang, Y.; Yang, J.; Zhang, D.; Zhang, Y.; Zhang, Y.; Huang, Y.; Jakobsson, A. Online Sparse DOA Estimation Based on Sub–Aperture Recursive LASSO for TDM–MIMO Radar. Remote Sens. 2022, 14, 2133. [Google Scholar] [CrossRef]
- Swärd, J.; Adalbjörnsson, S.I.; Jakobsson, A. Generalized sparse covariance-based estimation. Signal Process. 2018, 143, 311–319. [Google Scholar] [CrossRef]
- Khan, I.; Al-Wesabi, F.N.; Obayya, M.; Hilal, A.M.; Hamza, M.A.; Rizwanullah, M.; Al-Zahrani, F.A.; Amano, H.; Mostafa, S.M. An Optimized Algorithm for CR-MIMO Wireless Networks. CMC Comput. Mater. Contin. 2022, 71, 697–715. [Google Scholar]
- Khan, I.; Rodrigues, J.J.; Al-Muhtadi, J.; Khattak, M.I.; Khan, Y.; Altaf, F.; Mirjavadi, S.S.; Choi, B.J. A robust channel estimation scheme for 5G massive MIMO systems. Wirel. Commun. Mob. Comput. 2019, 2019, 3469413. [Google Scholar] [CrossRef]
- Karad, K.V.; Hendre, V.S. Review of Antenna Array for 5G Technology Using mmWave Massive MIMO. In Recent Trends in Electronics and Communication; Springer: Singapore, 2022; pp. 775–787. [Google Scholar]
- Al-Tarifi, M.A.; Sharawi, M.S.; Shamim, A. Massive MIMO antenna system for 5G base stations with directive ports and switched beamsteering capabilities. IET Microwaves Antennas Propag. 2018, 12, 1709–1718. [Google Scholar] [CrossRef]
- Alja’Afreh, S.S.; Altarawneh, B.; Alshamaileh, M.H.; E’qab, R.A.; Hussain, R.; Sharawi, M.S.; Xing, L.; Xu, Q. Ten antenna array using a small footprint capacitive-coupled-shorted loop antenna for 3.5 GHz 5G smartphone applications. IEEE Access 2021, 9, 33796–33810. [Google Scholar] [CrossRef]
- Jaglan, N.; Gupta, S.D.; Kanaujia, B.K.; Sharawi, M.S. 10 element sub-6-GHz multi-band double-T based MIMO antenna system for 5G smartphones. IEEE Access 2021, 9, 118662–118672. [Google Scholar] [CrossRef]
- Elbir, A.M.; Mishra, K.V.; Chatzinotas, S. Terahertz-band joint ultra-massive MIMO radar-communications: Model-based and model-free hybrid beamforming. IEEE J. Sel. Top. Signal Process. 2021, 15, 1468–1483. [Google Scholar] [CrossRef]
- Li, X.; Wang, B. Coherence optimised subarray partition for hybrid MIMO phased array radar. IET Microwaves Antennas Propag. 2021, 15, 1441–1457. [Google Scholar] [CrossRef]
- Zhu, D.; Li, B.; Liang, P. On the matrix inversion approximation based on Neumann series in massive MIMO systems. In Proceedings of the 2015 IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015; pp. 1763–1769. [Google Scholar]
- Albreem, M.A. Approximate matrix inversion methods for massive mimo detectors. In Proceedings of the 2019 IEEE 23rd International Symposium on Consumer Technologies (ISCT), Ancona, Italy, 19–21 June 2019; pp. 87–92. [Google Scholar]
- Zhang, X.; Zeng, H.; Ji, B.; Zhang, G. Low Complexity Implicit Detection for Massive MIMO Using Neumann Series. IEEE Trans. Veh. Technol. 2022, 71, 9044–9049. [Google Scholar] [CrossRef]
- Prabhu, H.; Rodrigues, J.; Edfors, O.; Rusek, F. Approximative matrix inverse computations for very-large MIMO and applications to linear pre-coding systems. In Proceedings of the 2013 IEEE Wireless Communications and Networking Conference (WCNC), Shanghai, China, 7–10 April 2013; pp. 2710–2715. [Google Scholar]
- Song, W.; Chen, X.; Wang, L.; Lu, X. Joint conjugate gradient and Jacobi iteration based low complexity precoding for massive MIMO systems. In Proceedings of the 2016 IEEE/CIC International Conference on Communications in China (ICCC), Chengdu, China, 27–29 July 2016; pp. 1–5. [Google Scholar]
- Kouni, V.; Paraskevopoulos, G.; Rauhut, H.; Alexandropoulos, G.C. ADMM-DAD net: A deep unfolding network for analysis compressed sensing. In Proceedings of the ICASSP 2022—2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 23–27 May 2022; pp. 1506–1510. [Google Scholar]
- Qu, W.; Xiu, X.; Zhang, H.; Fan, J. An efficient semi-proximal ADMM algorithm for low-rank and sparse regularized matrix minimization problems with real-world applications. J. Comput. Appl. Math. 2022, 424, 115007. [Google Scholar] [CrossRef]
- Li, X.; Bai, X.; Zhou, F. High-resolution ISAR imaging and autofocusing via 2d-ADMM-net. Remote Sens. 2021, 13, 2326. [Google Scholar] [CrossRef]
- Shang, F.; Xu, T.; Liu, Y.; Liu, H.; Shen, L.; Gong, M. Differentially private ADMM algorithms for machine learning. IEEE Trans. Inf. Forensics Secur. 2021, 16, 4733–4745. [Google Scholar] [CrossRef]
- Elgabli, A.; Elghariani, A.; Al-Abbasi, A.O.; Bell, M. Two-stage LASSO ADMM signal detection algorithm for large scale MIMO. In Proceedings of the 2017 51st Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 29 October–1 November 2017; pp. 1660–1664. [Google Scholar]
- Wang, Q.; Zhao, Z.; Chen, Z. Fast compressive sensing DOA estimation via ADMM solver. In Proceedings of the 2017 IEEE International Conference on Information and Automation (ICIA), Macao, China, 18–20 July 2017; pp. 53–57. [Google Scholar]
- Chen, J.; Zhang, C.; Fu, S.; Li, J. Robust Reweighted ℓ2,1-Norm Based Approach for DOA Estimation in MIMO Radar Under Array Sensor Failures. IEEE Sens. J. 2021, 21, 27858–27867. [Google Scholar] [CrossRef]
- Hashempour, H.R. Sparsity-driven ISAR imaging based on two-dimensional ADMM. IEEE Sens. J. 2020, 20, 13349–13356. [Google Scholar] [CrossRef]
- Li, J.; Stoica, P. MIMO Radar Signal Processing; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Wang, X.; Wang, L.; Li, X.; Bi, G. Nuclear norm minimization framework for DOA estimation in MIMO radar. Signal Process. 2017, 135, 147–152. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends® Mach. Learn. 2011, 3, 1–122. [Google Scholar]
- Rojas, C.R.; Katselis, D.; Hjalmarsson, H. A note on the SPICE method. IEEE Trans. Signal Process. 2013, 61, 4545–4551. [Google Scholar] [CrossRef]
- Stoica, P.; Zachariah, D.; Li, J. Weighted SPICE: A unifying approach for hyperparameter-free sparse estimation. Digit. Signal Process. 2014, 33, 1–12. [Google Scholar] [CrossRef]
- Wright, S.J.; Nowak, R.D.; Figueiredo, M.A. Sparse reconstruction by separable approximation. IEEE Trans. Signal Process. 2009, 57, 2479–2493. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Y.; Mao, D.; Bu, Y.; Yang, H.; Shi, J. Sparse Reconstruction for Synthetic Aperture Radar VIA Generalized Sparse Covariance Fitting. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 767–770. [Google Scholar]
- Ali, E.; Ismail, M.; Nordin, R.; Abdulah, N.F. Beamforming techniques for massive MIMO systems in 5G: Overview, classification, and trends for future research. Front. Inf. Technol. Electron. Eng. 2017, 18, 753–772. [Google Scholar] [CrossRef]


| Method | Number of Multiplication and Division Operations | Computational Complexity | Computational Time () |
|---|---|---|---|
| DAS (FFT) | s | ||
| IAA [13] | 4.88 s | ||
| ADMM-LASSO [36] | 0.03 s | ||
| qSPICE [18] | 11.41 s | ||
| Proposed method | 0.13 s |
| Method | 3 dB Width (Degrees) | RMSE (dB) |
|---|---|---|
| DAS | 16.80 | 12.79 |
| IAA | 2.26 | 0.15 |
| ADMM-LASSO | 3.22 | 3.791 |
| qSPICE | 1.32 | −2.269 |
| ADMM-SPICE | 0.98 | −1.791 |
| Parameter | Value |
|---|---|
| Carrier frequency | 77 GHz |
| Bandwidth | 3.75 GHz |
| Beam width | 1.4 |
| Pulse width | 1 ms |
| Pulse recurrence interval | 512 s |
| Number of transmitting array elements | 12 |
| Number of receiving array elements | 16 |
| Range sampling points | 261 |
| Methods | IE |
|---|---|
| DAS | 4.03 |
| IAA | 3.70 |
| ADMM-LASSO | 1.55 |
| qSPICE | 1.08 |
| ADMM-SPICE | 0.97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Zhang, Y.; Luo, J.; Huang, Y.; Yan, J.; Zhang, Y.; Yang, J. An ADMM-qSPICE-Based Sparse DOA Estimation Method for MIMO Radar. Remote Sens. 2023, 15, 446. https://doi.org/10.3390/rs15020446
Zhang Y, Zhang Y, Luo J, Huang Y, Yan J, Zhang Y, Yang J. An ADMM-qSPICE-Based Sparse DOA Estimation Method for MIMO Radar. Remote Sensing. 2023; 15(2):446. https://doi.org/10.3390/rs15020446
Chicago/Turabian StyleZhang, Yongwei, Yongchao Zhang, Jiawei Luo, Yulin Huang, Jianan Yan, Yin Zhang, and Jianyu Yang. 2023. "An ADMM-qSPICE-Based Sparse DOA Estimation Method for MIMO Radar" Remote Sensing 15, no. 2: 446. https://doi.org/10.3390/rs15020446
APA StyleZhang, Y., Zhang, Y., Luo, J., Huang, Y., Yan, J., Zhang, Y., & Yang, J. (2023). An ADMM-qSPICE-Based Sparse DOA Estimation Method for MIMO Radar. Remote Sensing, 15(2), 446. https://doi.org/10.3390/rs15020446









