Abstract
Based on various velocity fields from Global Positioning System (GPS) data over nearly 20 years in the Sichuan–Yunnan region, this paper calculated the strain rate field and its spatiotemporal characteristics by using an improved least squares collocation method. We evaluated the calculated strain field by extensively discussing the impact of non-tectonic factors on the calculation. Subsequently, we described the present-day strain rate features and their spatiotemporal variations. The results indicate the necessity of considering the influence of non-tectonic factors when calculating the strain rate field by using GPS velocity data. Widespread strain accumulation is observed in the Sichuan–Yunnan region, and significant second strain rate invariant with an average value of 33.1 nanostrain/yr primarily occurs along the eastern boundary faults of the Sichuan–Yunnan rhomboid block, specifically the Xianshuihe–Anninghe–Zemuhe–Xiaojiang fault systems. These fault systems also demarcate the zones with negative and positive dilation strain. According to the spatiotemporal variations of strain rate fields, the northern and southern segments of the Xianshuihe Fault, the Anninghe Fault and its eastern adjacent faults, and the Xiaojiang Fault are undergoing intensifying strain. Consequently, these zones should be paid more attention due to their relatively higher seismic risk in the Sichuan–Yunnan region.
1. Introduction
The Sichuan–Yunnan region is located in the southwest of mainland China and is one of six subblocks in the Qinghai–Tibetan Plateau, adjoining the stable South China Block in the east (Figure 1) [1]. The ongoing northward collision of the India Plate with the Eurasia Plate has led to eastward crustal movement within the Qinghai–Tibetan Plateau Block and a clockwise rotation around the eastern Himalayan syntaxis, forming a series of large boundary fault systems, including the Xianshuihe–Aninghe–Zemuhe–Xiaojiang sinistral strike-slip faults and the Jinsha River–Red River dextral strike-slip faults [2]. The complex fault systems indicate the complicated tectonic deformation in the Sichuan–Yunnan region, making it one of the most seismically active regions in mainland China, in which tens of M 7.0+ earthquakes occur, including two M 8.0 earthquakes, the 1833 Songming earthquake and the 2008 Wenchuan earthquake [3,4,5,6,7,8,9,10,11]. Therefore, it is of great significance to carry out research on the tectonic movement and deformation in the Sichuan–Yunnan region in order to explore the deformation pattern and future seismic risk in this region.
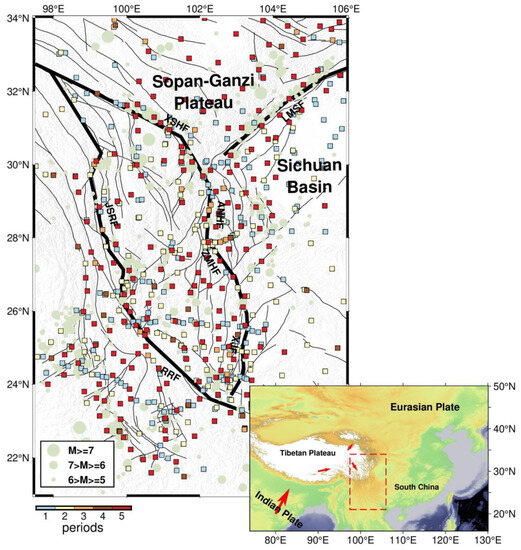
Figure 1.
Distribution of GPS stations in the Sichuan–Yunnan region. Colored squares indicate the station location with different periods (1-, 2-, 3-, 4-, and 5- periods are displayed using different colors); pale green circles represent historical earthquakes from 1976 to 2016, provided by the U.S. Geological Survey website (https://earthquake.usgs.gov/earthquakes/search/, (accessed on 1 July 2023)); the black solid lines represent active faults; the thick black solid lines highlight the boundary faults, including the Longmenshan Fault (LMSF), Xianshuihe Fault (XSHF), Anninghe Fault (ANHF), Zemuhe Fault (ZMHF), Xiaojiang Fault (XJF), Jinsha River Fault (JSRF), and Red River Fault (RRF). In the inset, the red dashed lines show the limits of the study area and the red arrows indicate motion directions of the Indian Plate and Tibetan Plateau.
Previous studies have discussed the relationship between crustal deformation, seismic activity, and stress field in the 1980s [6,7]. Since the first crustal deformation monitoring was carried out in the western Yunnan experimental field in 1988, Global Positioning System (GPS) technology has been extensively applied in studies on the crustal deformation of the Tibetan Plateau and its neighboring regions, leading to the accumulation of GPS observations and several deformation fields with various periods [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18]. In the early stages of research, although the GPS data were relatively insufficient, the overall characteristics of crustal deformation in the Tibetan Plateau were clearly revealed by the GPS crustal motion velocity field [9,10,11,12,13,14,15]. Thus, the GPS velocity field has gradually become essential for the study of crustal deformation, especially with the continuous improvement in GPS positioning precision and spatiotemporal resolution. The GPS velocity field can reflect crustal deformation features at different scales in the Tibetan Plateau and provide a more reliable reference for scholars to discuss the patterns and mechanisms of crustal deformation. Moreover, the strain field derived from the GPS velocity field can visually display the characteristics of crustal deformation and provide the quantitative parameters of shear, rotational, expansion, and compression deformation. To a certain extent, it reflects the tectonic stress field and has been widely discussed in many relevant studies [19,20,21,22,23,24,25,26,27,28,29,30]. There are several methods to calculate strain rate fields, among which mathematical methods based on continuum assumptions can better display the overall spatial distribution of strain rate trends, such as least squares collocation [23], spherical harmonic function [24], and multi-surface function [25]. Compared with other calculation methods, the improved least squares collocation based on station density proposed by Shen et al. [29,30] has advantages in reliability, applicability, and robustness [31] since it determines the smoothing factor that can maximize the utilization of GPS observations, thereby presenting more refined features for the strain rate field. Recently, some researchers have employed strain rate fields to investigate changes in crustal deformation before and after earthquakes [32,33,34,35,36,37,38,39]; however, studies examining variations in the strain rate field over a long timescale and in multiple periods are still limited. Furthermore, previous studies have been mostly based on the average GPS velocity field within a specific period. However, crustal deformation during different phases of that period may vary spatially. For example, Jiang et al. [20] analyzed the strain rate field and found that the relative motion between the Longmenshan Fault zone and the South China Block intensified after 2004. Therefore, the spatiotemporal characteristics of horizontal crustal deformation in the Sichuan–Yunnan region have significant implications for understanding the stress–strain evolution in this region. The availability of multi-period GPS data over a long timescale offers the possibility to conduct such studies.
In this study, we collect five periods of GPS velocity fields within two decades in the Sichuan–Yunnan region and adopt improved least squares collocation to solve for the velocity field and strain rate field at different periods in this region. By evaluating the influence of non-tectonic factors such as station density and data processing strategy on the strain rate field calculation, we present the spatiotemporal characteristics of horizontal crustal deformation in the Sichuan–Yunnan region and further analyze and discuss the stress–strain state and trend in this region.
2. Data and Methods
2.1. GPS Velocity Field
In this paper, we collected GPS velocity fields over five distinct periods from 1999 to 2016, defined as V0, V1, V2, V3, and V4, respectively. Among these velocity field datasets, V0 is regarded as the reference version to calculate the changes between it and the other versions. Their sources and quality statistics are presented in Table 1, whereas their distribution is illustrated in Figure 1. These GPS velocity fields are primarily originated from the Crustal Movement Observation Network of China (CMONOC) and some local GPS networks operated by different agencies [2]. Since the first data acquisition of base stations from CMONOC in 1999, at least eight periods of repeated campaign surveys of the base network have been conducted, with each station observed for at least four consecutive days in each campaign survey [11,12,13,14]. The stations are mainly deployed near the major fault zones in the Sichuan–Yunnan region. From the earliest version of velocity field V0 to the latest version V4, the number of stations has increased from 181 to 400, with the mean length of the sides of Delaunay triangulations decreasing from 42.8 km to 28.1 km, indicating that the station density is greatly improved. The precision of the velocity field has also been also significantly improved, with uncertainties from 2–3 mm/yr in velocity field V0 to 0.5 mm/yr in velocity field V4. The improvement in the precision results from many factors, including the better refined models adopted in the data processing and the longer time periods in the following versions compared with version V0. In order to mitigate the effects of varying station distributions from the aforementioned velocity fields, about 172 common stations in these fields were utilized to study the spatiotemporal characteristics of horizontal deformation in the Sichuan–Yunnan region (Figure 1).

Table 1.
GPS Velocity Field Sources and Statistics Used in the Study.
In addition to differences in periods, these velocity fields also exhibit disparities in data processing and postseismic deformation corrections. Regarding data processing, GPS observation data are processed into coordinate time series using software such as Bernese 5.0 or GAMIT/GLOBK. Subsequently, annual velocity values are computed using functional modeling [14]. Although data fitting or constraints from coseismic rupture models eliminate coseismic effects to some extent, corrections for postseismic effects induced by strong earthquakes are approximate [2,3,4,5,6,7,8,9,10,11,12,13,14]. The velocity fields V0 and V1 ignore the postseismic effects associated with the 2001 Mw 7.8 Kunlun earthquake [10,11], whereas the velocity fields V2 and V3 are based on the removal of the postseismic observations from the near-field stations [12,14]. As for the velocity field V4, it applies logarithmic function fittings to remove the postseismic effects of earthquakes with magnitudes larger than 6.0 [2].
2.2. The Improved Least Squares Collocation Method
In addition to the velocity field, the strain rate field is another common method to describe crustal movement and deformation. In contrast to the velocity field, it is independent of the reference frame and can reflect the intensity and dominant direction of stress accumulation. In this study, the strain rate field and changes in the Sichuan–Yunnan region were calculated using the velocity interpolation to strain rates (VISR) program, based on the improved least squares collocation method and proposed by Shen et al. [29,30]. This method ensures the comparability of strain rates across regions with various station densities and accommodates stability and resolution to maximize the utilization of GPS data, ensuring solution continuity through incremental iterations. The GPS-derived horizontal velocity () has a linear relationship with the parameters at interpolation points (), as represented by the following equations:
where is the coefficient matrix of , is error matrix, ~N(0, ), is the covariance matrix of GPS velocity, and are the east and north velocities at station , respectively, and are the components of distance between the station and interpolation point (), and are the east and north velocities of the interpolation point, and , , , and are components of rotation and strain rate. To enhance the weight of the GPS stations near the interpolation points, function () was introduced into by Shen et al. [30] using the Gaussian function for distance weighting and Voronoi cell for areal weighting. On the basis of , , and , the dilation rate (abbreviated as ), the second strain rate invariant (abbreviated as ), and the maximum shear strain rate were calculated for further depiction of crustal deformation, as expressed by:
From Equations (1)–(4), the reliability of strain parameters is determined by the accuracy of velocities at the interpolated stations; thus, it is necessary to evaluate the modeled velocity field by the method adopted in this study. Based on the various versions of velocity fields at common stations, direct validation and cross-validation methods were employed to evaluate the consistency among these fields by two evaluation metrics, the mean absolute error (MAE) and root mean squared error (RMSE) of the velocity residuals. The MAE and RMSE are calculated by:
where is twice the number of stations and is the residual between the modeled and observed velocity.
3. Results
In order to mitigate the impact of variations in station quantity and distribution among different versions of velocity fields on the computation of strain rate fields, this study selected the velocity values of common stations from various versions of velocity fields to calculate the respective strain rate fields and the velocity values at regular grid points with a 0.5° × 0.5° resolution by using the improved least squares collocation method. In the calculation, the weighting was considered by following the study of Shen et al. [30]. Finally, a weighting coefficient of 12 was employed in this study to achieve a favorable compromise between the RMSE and the smoothing distance. Furthermore, the spatiotemporal characteristics of the strain rate fields were discussed.
3.1. Regular Grid Velocity Variations
Based on the velocity field V0, we computed the velocity differences at the grid points between it and the other velocity fields including V1, V2, V3, and V4, referred to as dV1, dV2, dV3, and dV4, respectively. The corresponding mean values of these differences are 0.9, 1.2, 2.0, and 2.2 mm/yr. The obvious difference is bounded by 26.5°N, especially for the dominant directions of NE in the north and NW in the south, as illustrated in Figure 2. When in the timeline view, the magnitudes and directions of velocity differences at the grid points show great distinctions, indicating the variation in velocity fields is not uniform over time.
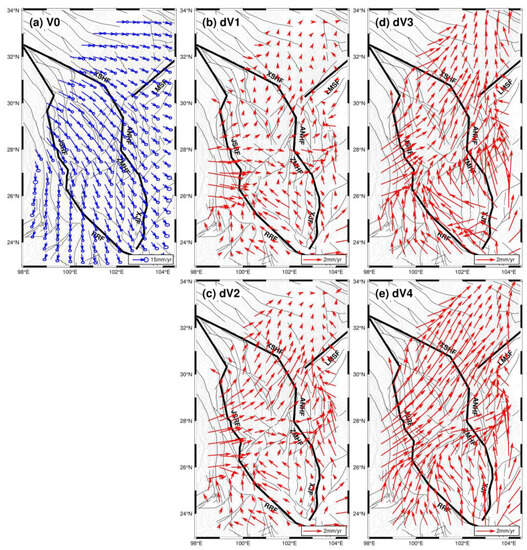
Figure 2.
Velocity field in a regular grid of 0.5° × 0.5° in the Sichuan–Yunnan region interpolated from the velocity field V0 (a) and the differential velocity fields between the interpolated velocity fields from V1, V2, V3, and V4 and V0, labelled as dV1 (b), dV2 (c), dV3 (d), and dV4 (e), respectively.
3.2. Strain Rate Changes
The strain rate field derived from the GPS velocity field is independent of the reference frame and directly reflects the characteristics of crustal deformation in the Sichuan–Yunnan region. The strain rate fields from the velocity fields V0, V1, V2, V3, and V4 were calculated, as well as their differences relative to the strain rate field from the V0 field. The changes in the second strain rate invariant and dilation rate in the Sichuan–Yunnan region are illustrated in Figure 3 and Figure 4, respectively, and detailed in Table 2. It should be noted that if the strain rate fields are calculated from the GPS velocity fields with a constant period of 2 or 4 years, we would likely observe more pronounced fluctuations in the spatiotemporal characteristics. However, the published GPS velocity fields [2,10,11,12,14] typically provide the average velocity during the observation period for each station based on the collected station observation data. This leads to the derived strain rate field missing the high-frequency variations of the spatiotemporal characteristics; however, the low-frequency or first-order variations are accurately obtained and used for further analysis.
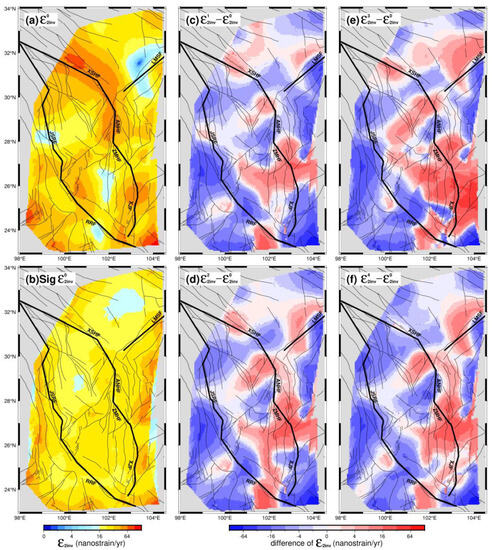
Figure 3.
The second strain rate invariant in the Sichuan–Yunnan region calculated from the velocity field V0 (a) and its 1-sigma uncertainty (b). The difference distributions between the second strain rate invariants calculated from the velocity fields V1, V2, V3, and V4 and V0, shown in (c–f), respectively.
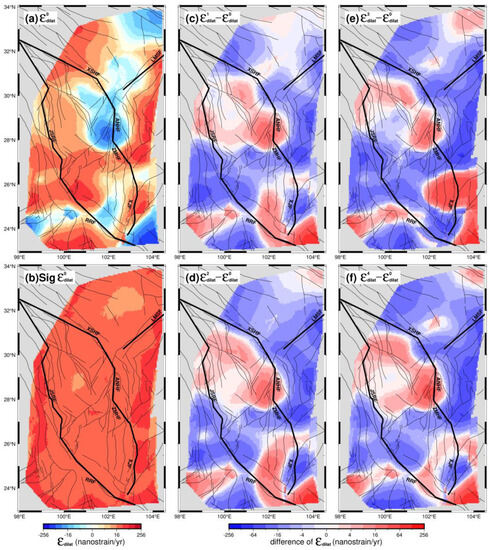
Figure 4.
Dilation rate in the Sichuan–Yunnan region calculated from the velocity field V0 (a) and its 1-sigma uncertainty (b). The difference distributions between the dilation rates calculated from the velocity fields V1, V2, V3, and V4 and V0 shown in (c–f), respectively.

Table 2.
Statistics of the second strain rate invariant and dilation rate.
The second strain rate invariant calculated from the V0 field displays the overall strain accumulation characteristics (Figure 3a), with an average value of 33.1 nanostrain/yr (equals to 10−9 strain/yr) and a mean uncertainty of 25.8 nanostrain/yr (Figure 3b and Table 2). Their differences are shown in Figure 3c–f, with average values of −4.8, −3.8, −1.2, and −3.5 nanostrain/yr, respectively. The corresponding variation ratios decrease with magnitudes of −14.5%, −11.5%, −3.6%, and −10.6%, respectively. Moreover, the areas with large values are mostly located along the boundary faults (Figure 3a). Although changes in strain accumulation vary spatially, the positive changes are concentrated at the Zemuhe Fault and in northern segment of the Xiaojiang Fault zone (Figure 3c–f), indicating that the strain accumulation increased in these zones, whereas the overall accumulation decreased in the study area over time.
Similar to the strain rate fields, the dilation rate fields and their differences were also calculated, as illustrated in Figure 4a–f, respectively. Except for the XSHF-ANHF-LMSF junction zone, other zones generally undergo dilation strains, and the average value for the dilation strain was 7.8 ± 26.0 nanostrain/yr in the study area (Figure 4a,b and Table 2). The difference distributions of dilation rates are rather complicated (Figure 4c–f); the dilation rate decreases, with average values of −4.7, −5.5, −6.7, and −7.0 nanostrain/yr, respectively. However, the difference images exhibit two zones with distinct increasing dilation strains, one zone to the west of XSHF-ANHF and the other zone surrounding the XJF (Figure 4c−f), indicating that the dilation strain is accumulating in the ANHF zone, whereas it is releasing in the XJF zone over time.
Moreover, we also calculated the statistical values of the second strain rate invariant and dilation rate from various fields, as detailed in Table 2. The mean uncertainties of the second strain rate invariants and dilation rates derived from the five fields became smaller, from ~26, ~17, ~12, and ~10 to ~4 nanostrain/yr, respectively, which corresponds to the better precision of velocity fields from V0 to V4 (Table 1). Considering the average values and their uncertainties, the second strain rate invariants have better signal-to-noise ratios (SNRs), from 1.3, 1.7, 2.4, and 3.2 to 8.7 for various fields, and the maximum values have higher SNRs, ranging from 3.8 to 21.6, indicating that the results with maximum values are reliable. By comparison, the variations in the second strain rate invariants have lower SNRs but the results with extremums are acceptable since their SNRs are generally larger than 3.0. As for dilation rate fields, the averages have relatively low SNRs for their small values but both dilation rates and their variations with extremums are reliable for their much higher SNRs. Thus, we will analyze the spatiotemporal characteristics of strain rate fields mainly according to those extremums.
4. Discussion
4.1. Validation of the Strain Rate Field Calculation in the Sichuan–Yunnan Region
Although the improved least squares collocation method has proven to be effective to calculate the strain rate [29,30], it is still necessary to validate whether it is appropriate to implement such a calculation constrained by the velocity field in the Sichuan–Yunnan region. Therefore, we adopted both direct validation and cross-validation methods to evaluate the effectiveness of the calculation.
Firstly, the direct validation method was used to fit the velocity at all stations under the constraint of each velocity field, resulting in the RMSE values for various versions of the velocity fields. Taking the example of the fitting results in the V4 field, the average residual velocity was 0.01 mm/yr, the MAE was 0.10 mm/yr (Figure 5a), and the error limit of velocity residuals (taking three times the RMSE) was 0.72 mm/yr. For other velocity fields, all MAEs were less than 0.3 mm/yr and the error limits were 1.21, 0.55, 0.61, and 1.05 mm/yr, respectively. Secondly, the cross-validation method involved randomly selecting 30% of the stations as the validation group, then using the remaining 70% of stations to interpolate the velocities at the stations in the validation group and calculating the external fitting accuracy of the model by comparing the interpolated and measured velocities for the validation group stations. For the cross-validation in the V4 field, the average residual velocity was 0.13 mm/yr (Figure 5b), the MAE was 0.74 mm/yr, and the error limit was 2.70 mm/yr. The MAEs were 1.79, 0.92, 0.75, and 1.20 mm/yr and the error limits were 6.48, 3.19, 2.93, and 4.14 mm/yr for other velocity fields, respectively. Finally, compared with the mean velocity uncertainties in each velocity field, both direct validation and cross-validation MAEs are smaller, indicating that the fitted velocity fields and strain rate fields are reliable by using the improved least squares collocation method in this study.
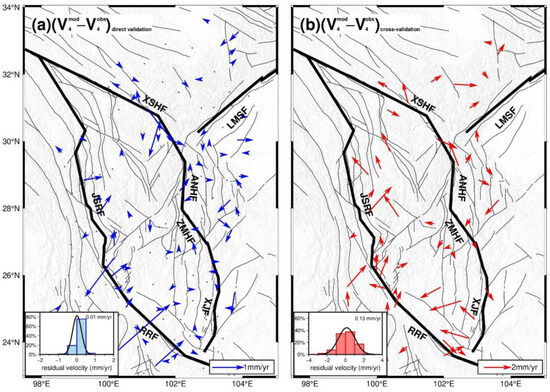
Figure 5.
Residual velocity in direct validation (a) and cross-validation (b) based on velocity field V4. The blue and red histograms denote the distribution of residuals in magnitude.
4.2. Influence of Non-Tectonic Deformation on the Strain Rate Field Calculation
The spatiotemporal characteristics of crustal deformation in the study area were mainly obtained by using the crustal velocity fields over various time spans to calculate them. However, the velocity field datasets were from different studies [2,10,11,12,14] and there may disparities due to non-tectonic factors, such as data processing strategy, station spacing, and uncertainty of the velocity field. Thus, their influences need to be analyzed.
- (1)
- Systematic Bias between Velocity Fields
If there is a systematic bias between velocity fields, it will cause a large deviation in the calculated strain rate, so the existence of systematic biases needs to be verified. This study selected four common stations for the assessment. These stations were located in the South China Block and away from the strong earthquake epicenters, thus their velocities are relatively stable over time. If significant variations are observed in the velocities of these stations, it would indicate substantial systematic bias between the velocity fields. The information of selected stations is described in Table 3. Among these stations, JB25 exhibits the largest change in velocity value, with a value of 1.9 mm/yr; SNMX has the largest change in the velocity direction, with a value of 16.9°. Compared with their uncertainties in velocity magnitude and azimuth, the velocity changes at the four stations were less than twice their uncertainties (Figure 6). This implies that there was no large change in velocity, suggesting the absence of systematic biases between various velocity fields.

Table 3.
Velocity Statistics of Stations in the South China Block.
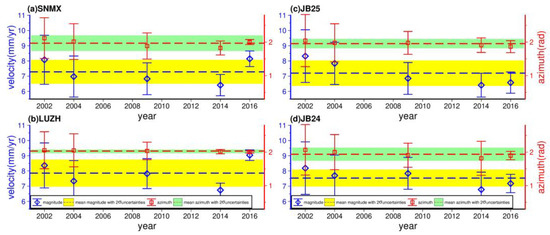
Figure 6.
The velocity variation of stations in the South China Block. The blue diamond and red square represent the magnitude and azimuth of station velocity with 1-sigma uncertainty, respectively. The blue and red dashed lines denote the mean magnitude and azimuth of station velocity, respectively. The thick yellow and green lines indicate the range of the 2-sigma uncertainty of the mean magnitude and azimuth, respectively.
- (2)
- Station Spacing
Previous studies have examined the effect of changing station spacing on the computed strain rate fields using both simulated data and actual measurements, revealing that variation in station spacing will impact the stability of the calculations [26,38]. Smaller station spacing can show details of the local strain rate field, whereas larger station spacing yields an averaged strain rate influenced by the smoothing factor. This can lead to strain rate results at different station spacings that may not objectively reflect the actual crustal strain. Therefore, a quantitative assessment of the impact of station spacing on the computed strain rate fields is required. To exclude the influence of other factors on this assessment, the stable South China Block (region range: 105°–117°E, 24°–31°N) was selected as the experimental area; the measured velocities of all stations in this area are holistic and consecutive [2]. The velocity field V4, which has a relatively small uncertainty, was selected to calculate the variation in the strain rate field during the alteration of station spacing. By randomly subsampling stations to increase the station spacing, this study evaluates the resulting changes in the strain rate field. Due to the inability to compute results after subsampling beyond 48% of the stations, the assessment was only performed for the schemes shown in Table 4.

Table 4.
List of information in different schemes based on the V4 velocity field in the South China Block.
The differences in the strain rate field are shown in Table 5, and the distribution of the second strain rate invariant is shown in Figure 7. As the station spacing gradually increased, the mean and RMSE values of differences increased accordingly, which agrees well with the previous studies [31]. In the worst case of scheme F–A, the mean and RMSE values of differences in the second strain rate invariant reached 2.5 and 4.3 nanostrain/yr, respectively, whereas for the dilation strain rate, the values were 0.9 and 4.3 nanostrain/yr, respectively. Comparing the effects of station spacing variation with the average values of strain rate differences in Figure 3, we found the impact caused by changes in station spacing was roughly equivalent to the magnitude of strain rate differences. This indicates that the influence of station spacing cannot be neglected when analyzing the spatiotemporal characteristics of strain rate field. Therefore, we used a velocity field with a denser distribution of common stations to calculate the strain rate field compared with a previous similar study [24]. Additionally, we carried out subsequent analysis of the spatiotemporal characteristics.

Table 5.
Difference statistics of strain rate in the South China Block.
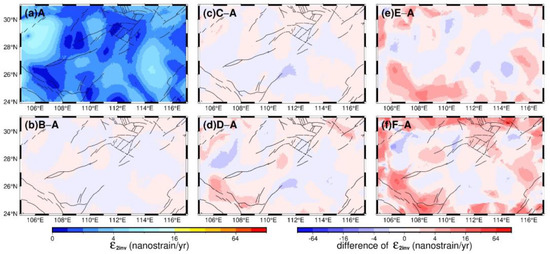
Figure 7.
The second strain rate invariant in the South China Block calculated from scheme A (a) and the difference distributions between the second strain rate invariant calculated from schemes B, C, D, E, and F and A, shown as (b), (c), (d), (e), and (f), respectively.
- (3)
- Other Non-tectonic Deformations
Regarding the effects of other non-tectonic deformations, such as atmospheric loading, tidal ocean loading, and continental water loading, we treated them as an overall deviation and conducted a quantitative evaluation in the South China Block interior. Previous studies have demonstrated that crustal deformation changes within the South China Block are extremely weak [1,2], so we assume changes in the strain rate field within the block are collectively caused by other non-tectonic deformations. Due to the sparse distribution of GPS stations within the South China Block in the V0 and V1 fields, we selected the common stations from three other velocity fields for the strain rate field computation and comparative analysis. Prior to computation, the velocity fields of the common stations were interpolated and densified to match the station spacing of common stations in the Sichuan–Yunnan region. The strain rate differences between the strain rate fields calculated from V3, V4, and V2 (Figure 8) indicated that other non-tectonic deformations can impact the calculation results. The maximum average differences in the second strain rate invariant and dilation rate were −0.9 and −2.14 nanostrain/yr, respectively. Nevertheless, the calculation results in the Sichuan–Yunnan region show that the second strain rate invariant differences were between −0.8 and −4.8 nanostrain/yr and the dilation rate differences were between −7.0 and 0.8 nanostrain/yr. Similar to the station spacing, the changes in the strain rate fields caused by other non-tectonic deformations were comparable to the calculation results. Thus, it is challenging to directly deduct them from the calculation results in order to improve the accuracy of the results. However, for the sake of enhancing the reliability of spatiotemporal characteristics of the strain rate fields, this study assumes that when the strain rate changes are greater than three times the mean strain rate variation caused by non-tectonic factors, the strain rate changes can be considered significant.
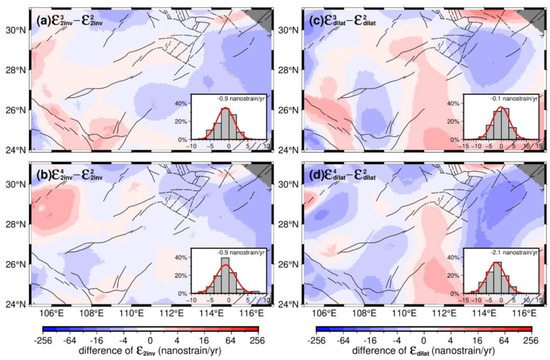
Figure 8.
The difference distributions between the second strain rate invariant (a,b) calculated from the velocity fields V3, V4, and V2 and the dilation rate (c,d). The histogram in each subfigure denotes the distribution of differences between two second strain rate invariants or dilation rates.
4.3. Spatiotemporal Characteristics of the Strain Rate Field in the Sichuan–Yunnan Region
Constrained by various GPS velocity fields (Table 1 and Figure 2), the corresponding strain rate fields are computed by the improved least squares collocation method, as illustrated in Figure 3 and Figure 4. Due to the similar trends intrinsic to various GPS velocity fields (Figure 2), the calculated second strain rate invariant and dilation rate fields exhibit similar first-order characteristics (Figure 9 and Figure 10). The strain accumulation is pervasive in the Sichuan–Yunnan region, especially in the zones along the boundary faults, such as XSHF-ANHF-ZMHF-XJF. The largest values for the second strain rate invariant appeared in the northern segment of XSHF, ANHF, and the northern segment of XJF, indicating high seismic risk in these zones (Figure 3 and Figure 9). These results are in accordance with the qualitative or semi-quantitative findings that a high seismic hazard or an approximately 10–20% probability of a strong earthquake occurring along XSHF, ANHF, XJF, and other faults that were derived from seismic geological data, tectonic movement data, historical seismic actively data, and GPS data [40,41,42,43,44,45]. The obvious small values of the second strain rate invariant occurred in the LMSF zone, especially before the 2008 Wenchuan earthquake (Figure 9a,c); these values increased after the earthquake, implying that the strain status in the LMSF zone was adjusted by the 2008 Wenchuan earthquake. The Sichuan–Yunnan rhomboid block, bounded on its eastern boundary by XSHF-ANHF-ZMHF-XJF and its western boundary by JSRF-RRF, had a positive dilation rate in its interior, whereas the exterior zone adjacent to its eastern boundary had a negative dilation rate, indicating that XSHF-ANHF-ZMHF-XJF plays an important role in adjusting the crustal deformation between the Qinghai–Tibetan plateau and the Sichuan basin. This feature is also observed in the GPS velocity field (Figure 4a), where there was an obvious clockwise rotation within the block and a rapidly decreased velocity field across the eastern boundary, suggesting that the eastward flow of material from the Qinghai–Tibetan plateau is obstructed by the stable South China Block and results in clockwise movement [1,2,9,10].
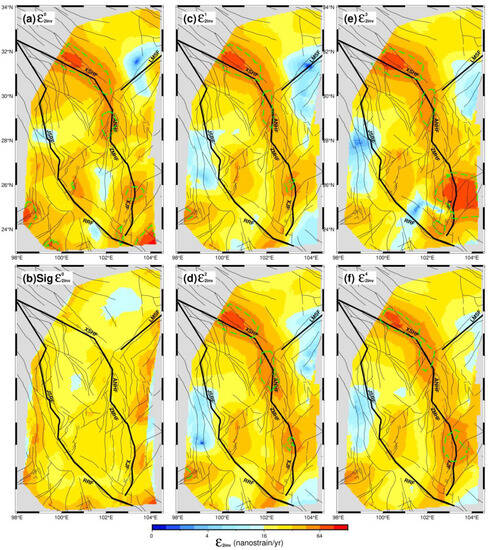
Figure 9.
The second strain rate invariant calculated from the velocity fields V0 (a), V1 (c), V2 (d), V3 (e), and V4 (f). The 1-sigma uncertainty of the second strain rate invariant from the V0 field (b). The green dashed lines encircle the zones where the magnitudes exceed twice the 2-sigma uncertainty of .
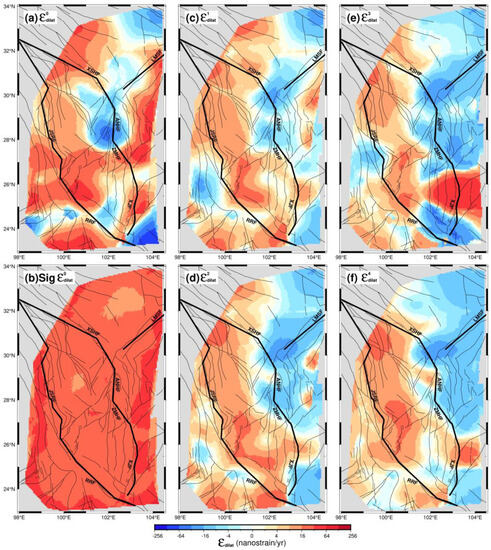
Figure 10.
The dilation rate fields calculated from the velocity fields V0 (a), V1 (c), V2 (d), V3 (e) and V4 (f). The 1-sigma uncertainty of the dilation rate from V0 field (b).
Furthermore, in order to show variations over time, we further calculated the differences in the second strain rate invariant and dilation rate fields (Figure 3 and Figure 4). Although there was no continuous and stable spatial change over time, the zones with a high strain rate were mainly distributed along the boundary faults of the Sichuan–Yunnan rhomboid block. There are many zones with increasing second strain rate invariants, such as the northern and southern segments of XSHF, the Mabian Fault and Daliangshan Fault zones to the east of ANHF, zones along ZMHF and XJF, and the southern segment of RRF, suggesting higher seismic risk in these zones. This was evidenced by the 2014 Mw 6.2 Ludian earthquake and the Mw 6.2 Jinggu earthquake, which occurred in the east of ANHF and the vicinity of the southern segment of RRF [40]. Within the Sichuan–Yunnan rhomboid block, its northern part experienced the intensifying extensional strain over time, whereas the XSHF-ANHF-LMSF junction zone experienced increasing compressional strain, suggesting a high seismic risk in the southern segment of XSHF.
5. Conclusions
In this paper, constrained by GPS velocity fields covering several periods over nearly 20 years, we employed an improved least squares collocation method to successfully calculate the strain rate field and its spatiotemporal variations in the Sichuan–Yunnan region.
We thoroughly discussed and assessed the impact of non-tectonic deformation on the calculated strain rate field. Changes in station spacing will significantly impact the strain rate field, whereas other non-tectonic factors also contribute to the results to a certain extent. This underscores the importance of considering the influence of non-tectonic deformation when calculating and analyzing the strain rate field from the GPS velocity field.
The Sichuan–Yunnan region is undergoing widespread strain accumulation. The significant second strain rate invariant mainly concentrates at the boundary faults of the Sichuan–Yunnan rhomboid block. Its eastern boundary, XSHF-ANHF-ZMHF-XJF, demarcates the extensional and compressional strain zones. Among these boundary faults, the northern and southern segments of XSHF, ANHF and its eastern adjacent faults, and XJF, exhibit relatively higher seismic risk due to intensifying strain.
Author Contributions
Conceptualization, K.D. and Q.Z.; methodology, K.D.; validation, Q.Z. and S.P.; formal analysis, Q.Z., Y.L. and Y.W.; data curation, Q.Z.; writing—original draft preparation, Q.Z.; writing—review and editing, G.L., S.P., T.L. and Y.W.; visualization, G.L., S.P., T.L. and Q.Z.; supervision, K.D.; funding acquisition, K.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Natural Science Foundation of China (Grant No. 42174012).
Data Availability Statement
The GPS velocity data used in this study are available in the Supplementary Materials of studies [2,10,11,12,14].
Acknowledgments
We sincerely thank Zhengkang Shen for sharing the VSIR code. We also thank editors and three anonymous reviewers for their valuable comments to improve the manuscript. Some of the Figures were prepared using the GMT graphics package [46].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Deng, Q.D.; Zhang, P.Z. Basic characteristics of active tectonics of China. Sci. China Ser. D Earth Sci. 2003, 46, 356–372. (In Chinese) [Google Scholar]
- Wang, M.; Shen, Z.K. Present-day crustal deformation of continental China derived from GPS and its tectonic implications. J. Geophys. Res. Solid Earth 2020, 125, e2019JB018774. [Google Scholar] [CrossRef]
- Cheng, J.; Xu, X.W.; Chen, G.H. A new prediction model of seismic hazard for the Sichuan-Yunnan region based on the occurrence rate of large earthquakes. Chin. J. Geophys. 2020, 63, 1170–1182. (In Chinese) [Google Scholar]
- Wang, Q.X.; Xu, X.W. Strain characteristics of north-south seismic zone and the analysis of earthquake risk. J. Geod. Geodyn. 2020, 40, 23–39. (In Chinese) [Google Scholar]
- Wei, W.X.; Jiang, Z.S. Distribution and variation characteristics of strain rate field in Sichuan-Yunnan region. Earthquake 2015, 35, 11–20. (In Chinese) [Google Scholar]
- Zhao, B. Crustal deformation on the Chinese mainland during 1998–2014 based on GPS data. Geod. Geodyn. 2015, 6, 7–15. [Google Scholar] [CrossRef]
- McKenzie, D.P.; Parker, R.L. The North Pacific: An example of tectonics on a sphere. Nature 1967, 216, 1276–1280. [Google Scholar] [CrossRef]
- England, P.; McKenzie, D.P. A thin viscous sheet model for continental deformation. Geophys. J. Int. 1982, 70, 295–321. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, P.Z. Present-day crustal deformation in China constrained by Global Positioning System measurements. Science 2001, 294, 574–577. [Google Scholar] [CrossRef]
- Zhang, P.Z.; Shen, Z.K. Kinematics of present-day tectonic deformation of the Tibetan plateau and its vicinities. Seismol. Geol. 2014, 26, 367–377. [Google Scholar]
- Gan, W.J.; Zhang, P.Z. Present-day crustal motion within the Tibetan Plateau inferred from GPS measurements. J. Geophys. Res. Solid Earth 2007, 112, 416. [Google Scholar] [CrossRef]
- Zhang, Z.Q.; McCaffrey, R. Relative motion across the eastern Tibetan plateau: Contributions from faulting, internal strain and rotation rates. Tectonophysics 2013, 584, 240–256. [Google Scholar] [CrossRef]
- Liang, S.M.; Gan, W.J. Three-dimensional velocity field of present-day crustal motion of the Tibetan Plateau derived from GPS measurements. J. Geophys. Res. Solid Earth 2013, 118, 5722–5732. [Google Scholar] [CrossRef]
- Wang, W.; Qiao, X. Present-day velocity field and block kinematics of Tibetan Plateau from GPS measurements. Geophys. J. Int. 2017, 208, 1088–1102. [Google Scholar] [CrossRef]
- Rui, X.; Stamps, D.S. A geodetic strain rate and tectonic velocity model for China. Geochem. Geophys. Geosyst. 2018, 20, 1280–1297. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, P.Z. Present-day crustal movement and tectonic deformation in China continent. Sci. China Ser. D Earth Sci. 2001, 45, 865–874. [Google Scholar] [CrossRef]
- Zheng, G.; Wang, H. Crustal deformation in the India-Eurasia collision zone from 25 years of GPS measurements. J. Geophys. Res. Solid Earth 2017, 122, 9290–9312. [Google Scholar] [CrossRef]
- Wang, M.; Shen, Z.K. Present-day tectonic deformation in continental China: Thirty years of GPS Observation and research. Earthq. Res. China 2020, 36, 660–683. (In Chinese) [Google Scholar]
- Xiang, Y.F.; Wang, H. GNSS imaging of strain rate changes and vertical crustal motions over the Tibetan Plateau. Remote Sens. 2021, 13, 4397. [Google Scholar] [CrossRef]
- Jiang, Z.S.; Fang, Y. The dynamic process of regional crustal movement and deformation before Wenchuan Ms8.0 earthquake. Chin. J. Geophys. 2009, 52, 505–518. (In Chinese) [Google Scholar]
- Savage, J.C.; Gan, W.J. Strain accumulation and rotation in the Eastern California Shear Zone. J. Geophys. Res. Solid Earth 2001, 106, 21995–22007. [Google Scholar] [CrossRef]
- Arnoso, J.; Riccardi, U. Strain Pattern and Kinematics of the Canary Islands from GNSS Time Series Analysis. Remote Sens. 2020, 12, 3297. [Google Scholar] [CrossRef]
- Jiang, Z.S.; Liu, J.N. The method of establishing strain field and velocity field of crustal movement using least square collocation. Chin. J. Geophys. 2010, 53, 1116–1117. (In Chinese) [Google Scholar] [CrossRef]
- Wu, Y.Q.; Jiang, Z.S. Research on the method for entire calculation of GPS strain field by using spherical harmonic function. J. Geod. Geodyn. 2009, 29, 68–73. (In Chinese) [Google Scholar]
- Wu, Y.Q.; Jiang, Z.S. Application and method of GPS strain Calculating in whole mode using multi-surface function. Geomat. Inf. Sci. Wuhan Univ. 2009, 34, 1085–1089. (In Chinese) [Google Scholar]
- Wu, Y.Q.; Jiang, Z.S. The application and method of GPS strain calculation in whole mode using least square collocation in sphere surface. Chin. J. Geophys. 2009, 52, 1707–1714. (In Chinese) [Google Scholar] [CrossRef]
- Su, X.N.; Meng, G.J. Methodology and application of GPS strain field estimation based on multi-scale spherical wavelet. Chin. J. Geophys. 2016, 59, 1585–1595. (In Chinese) [Google Scholar]
- Kreemer, C.; Holt, W.E. An integrated global model of present-day plate motions and plate boundary deformation. Geophys. J. Int. 2003, 154, 8–34. [Google Scholar] [CrossRef]
- Shen, Z.K.; Jackson, D.D. Crustal deformation across and beyond the Los Angeles basin from geodetic measurements. J. Geophys. Res. Solid Earth 1996, 1012, 27957–27980. [Google Scholar] [CrossRef]
- Shen, Z.K.; Wang, M. Optimal Interpolation of Spatially Discretized Geodetic Data. Bull. Seismol. Soc. Am. 2016, 105, 2117–2127. [Google Scholar] [CrossRef]
- Wu, Y.Q.; Jiang, Z.S. Comparison of GPS strain rate computing methods and their reliability. Geophys. J. Int. 2011, 185, 703–717. [Google Scholar] [CrossRef]
- Han, Z.J.; Xu, J. Active blocks and strong earthquakes in North China. Sci. China Ser. D Earth Sci. 2003, 33, 108–118. (In Chinese) [Google Scholar]
- Dang, Y.M.; Yang, Q. Block Movement and Strain Characteristics Effected by Earthquake in Sichuan-Yunnan Region. Acta Geod. Cartogr. Sin. 2018, 47, 559–566. (In Chinese) [Google Scholar]
- Jiang, Z.S.; Yang, G.H. Research on crustal movement in China continent and its relationship with strong earthquakes. J. Geod. Geodyn. 2006, 3, 1–9. (In Chinese) [Google Scholar]
- Yu, J.S.; Zhao, B. Analysis of GNSS postseismic deformation of Wenchuan earthquake. Acta Geod. Cartogr. Sin. 2018, 47, 1196–1206. (In Chinese) [Google Scholar]
- Zhang, P.Z.; Deng, Q.D. Strong earthquake activity and active blocks in mainland China. Sci. China Ser. D Earth Sci. 2003, 33, 12–20. [Google Scholar]
- Li, L.; Wu, Y. Dynamic deformation and fault locking of the Xianshuihe Fault Zone, Southeastern Tibetan Plateau: Implications for seismic hazards. Earth Planets Space 2022, 74, 35. [Google Scholar] [CrossRef]
- Deng, W.B.; Lan, M. Analysis of dynamic crustal deformation in Xinjiang by least squares collocation. Chin. J. Geol. 2022, 57, 958–974. (In Chinese) [Google Scholar]
- Bian, W.W.; Wu, J.C. Recent Crustal Deformation Based on Interpolation of GNSS Velocity in Continental China. Remote Sens. 2020, 12, 3753. [Google Scholar] [CrossRef]
- Wang, F.; Wang, M.; Wang, Y.; Shen, Z.K. Earthquake potential of the Sichuan-Yunnan region, western China. J. Asian. Earth. Sci. 2015, 107, 232–243. [Google Scholar] [CrossRef]
- Liu, X.; Ma, J.; Du, X.S.; Zhu, S.; Li, L.Y.; Sun, D.Y. Recent movement changes of main fault zones in the Sichuan-Yunnan region and their relevance to seismic activity. Sci. China Ser. D Earth Sci. 2016, 46, 706–719. (In Chinese) [Google Scholar] [CrossRef]
- Wang, Y.Z.; Wang, E.N.; Shen, Z.K.; Gan, W.J.; Qiao, X.N.; Meng, G.J. GPS-constrained inversion of present-day slip rates along major faults of the Sichuan-Yunnan region, China. Sci. China Ser. D Earth Sci. 2008, 38, 582–597. (In Chinese) [Google Scholar] [CrossRef]
- Xu, X.W.; Cheng, J.; Xu, C.; Li, X.; Yu, G.H.; Chen, G.H.; Tan, X.B.; Wu, X.Y. Discussion on block kinematic model and future themed areas for earthquake occurrence in the Tibetan plateau: Inspiration from the Ludian and Jinggu earthquakes. Seismol. Geol. 2014, 36, 1116–1134. (In Chinese) [Google Scholar]
- Zhao, J.; Jiang, Z.S.; Niu, A.F.; Liu, J.; Wu, Y.Q.; Wei, W.X.; Liu, X.X.; Yan, W. Study on dynamic characteristics of fault locking and fault slip deficit in the eastern boundary of the Sichuan-Yunnan rhombic block. Chin. J. Geophys. 2015, 58, 872–885. (In Chinese) [Google Scholar]
- Yin, D.; Dong, P.Y.; Cao, J.L.; Shi, Y.L. Numerical analysis of the seismic hazard in Sichuan-Yunnan region. Chin. J. Geophys. 2022, 65, 1612–1627. (In Chinese) [Google Scholar]
- Wessel, P.; Luis, J.F.; Uieda, L.; Scharroo, R.; Wobbe, F.; Smith, W.H.F.; Tian, D. The Generic Mapping Tools version 6. Geochem. Geophys. Geosyst. 2019, 20, 5556–5564. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).