Robust Loop Closure Selection Based on Inter-Robot and Intra-Robot Consistency for Multi-Robot Map Fusion
Abstract
1. Introduction
- 1
- We present a novel consistency score that considers both pairwise-loop and loop-odometry consistency for loop closure selection;
- 2
- We propose an efficient consistency-based loop closure selection strategy to provide an initial relative pose estimate between robots;
- 3
- To the best of our knowledge, this work is the first to conduct experiments to demonstrate the impact of accumulative noise on multi-robot map fusion problem, and our experimental result shows that the existing loop selection method relies on the quality of single-robot odometry and degenerates significantly under severe accumulative noise.
2. Related Work
2.1. Robust Optimization in SLAM
2.2. Robust Optimization in Multi-Robot SLAM
3. Preliminaries
3.1. Multiple Robot Pose Graph Optimization
3.2. Loop Closure Selection Problem
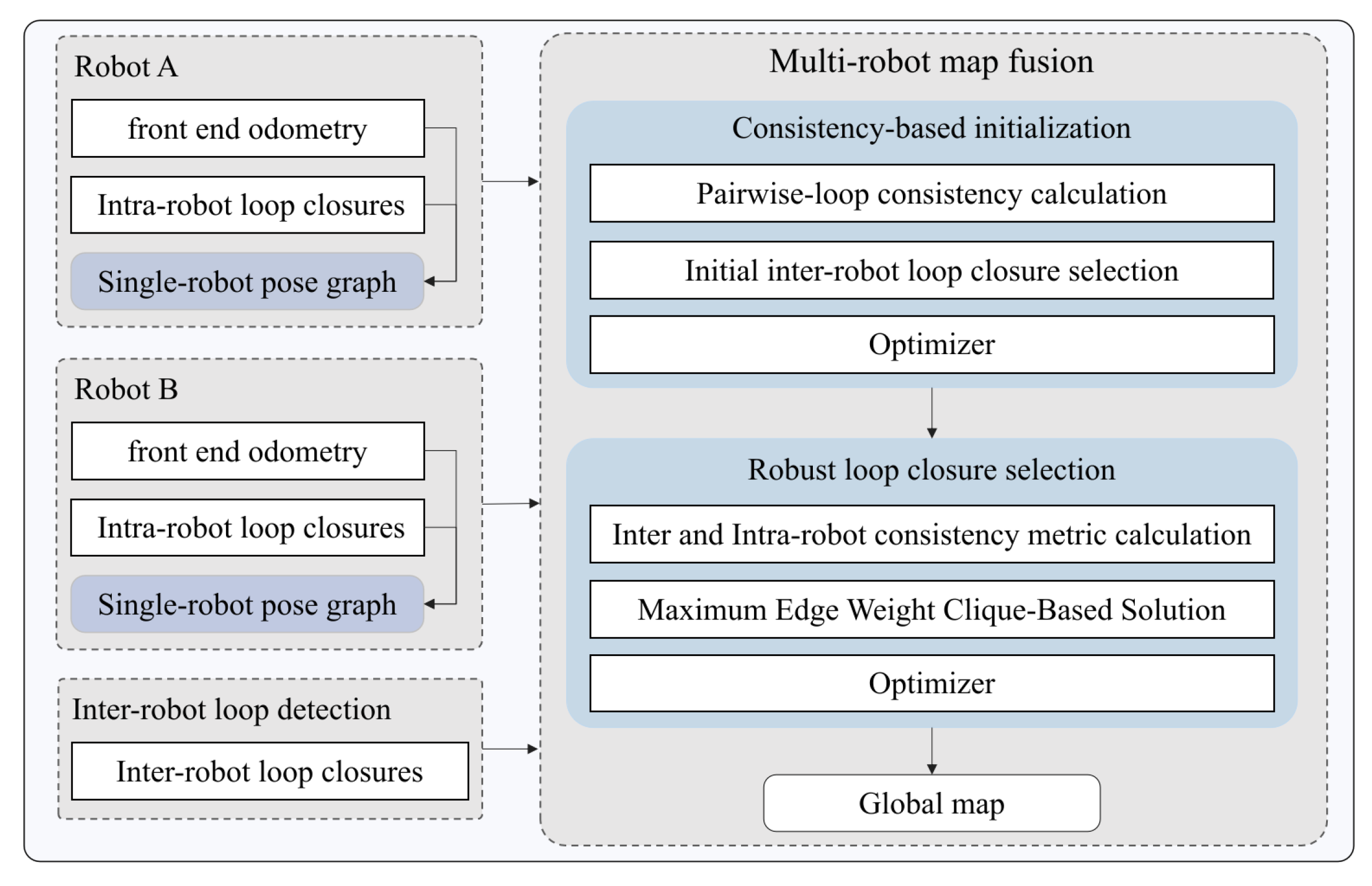
4. Methodology
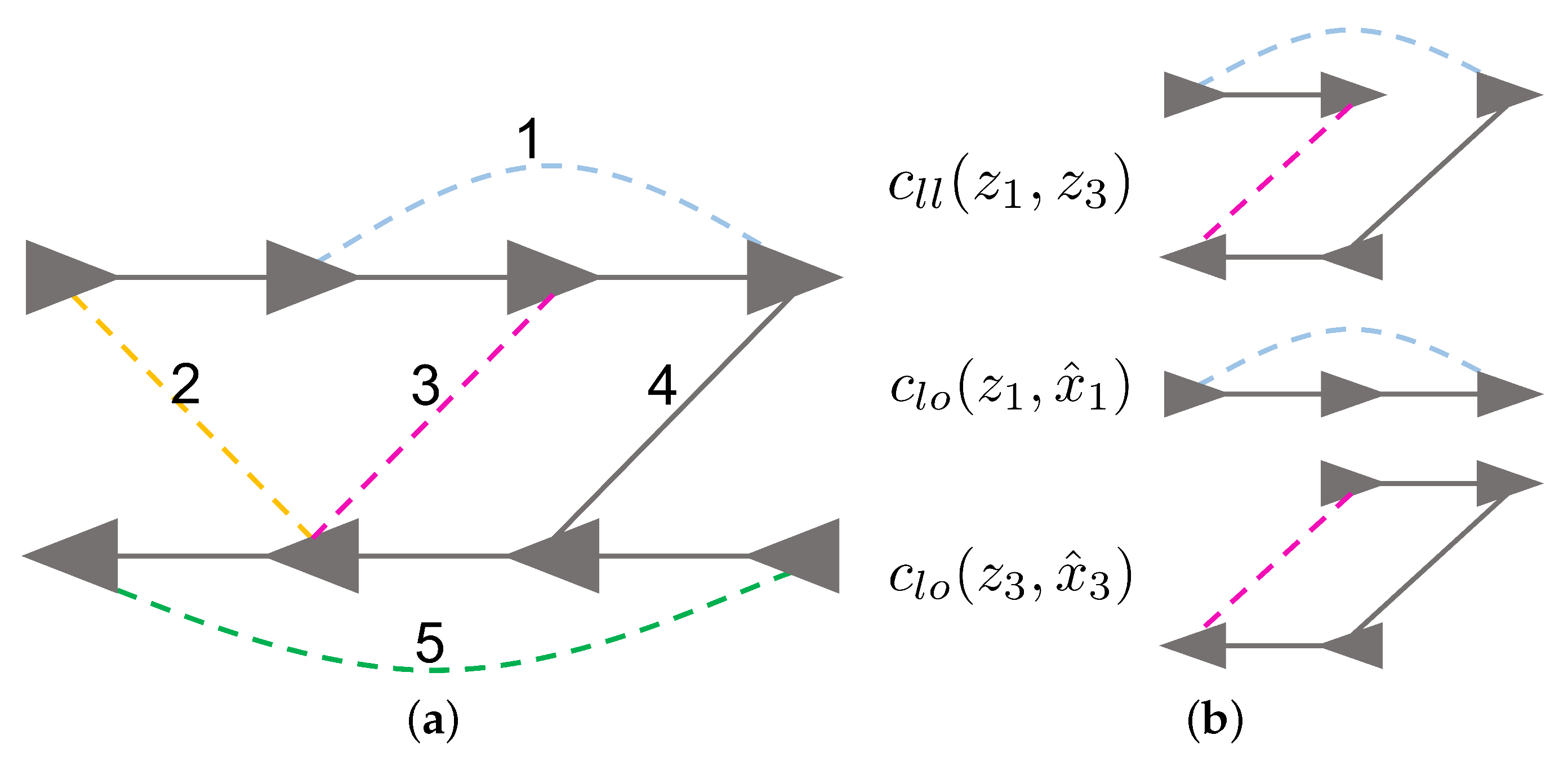
4.1. Inter and Intra-Robot Consistency Metric
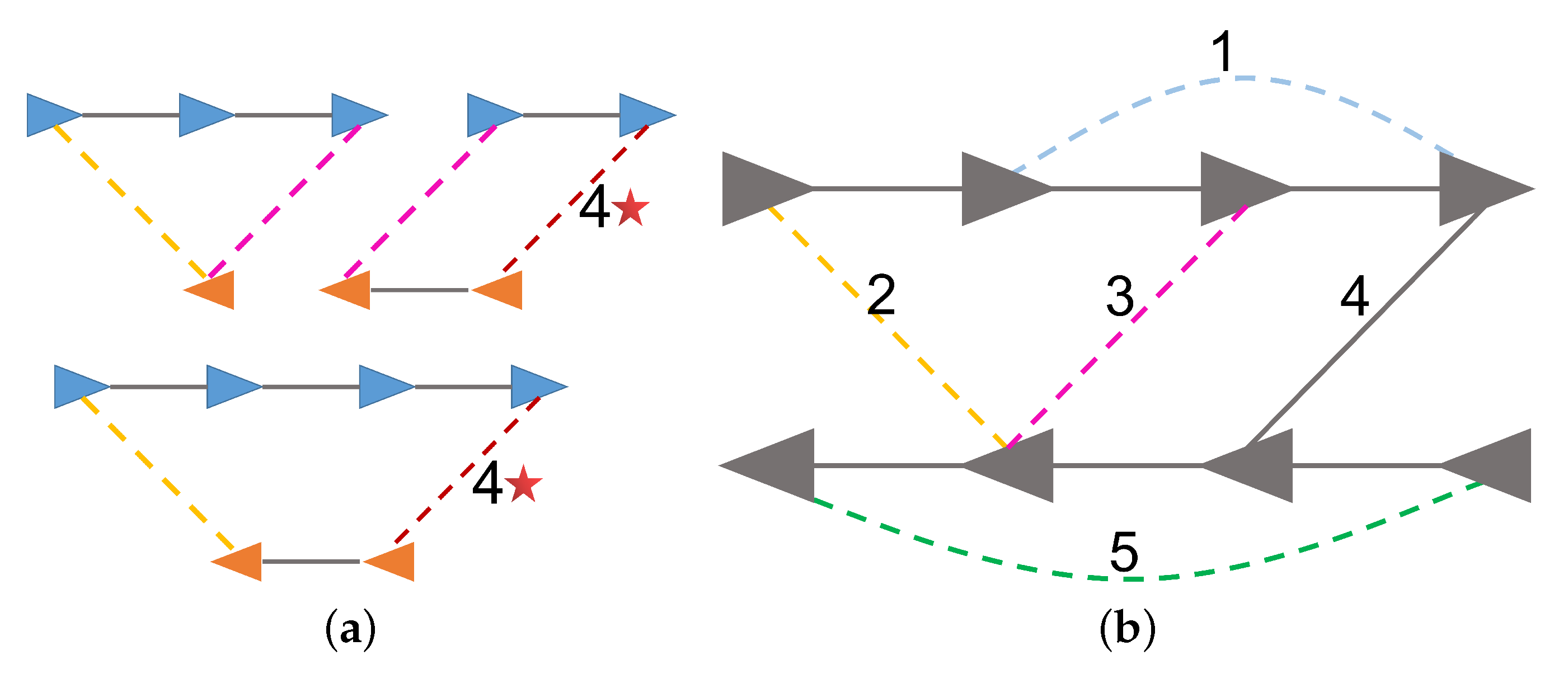
4.2. Consistency-Based Initialization
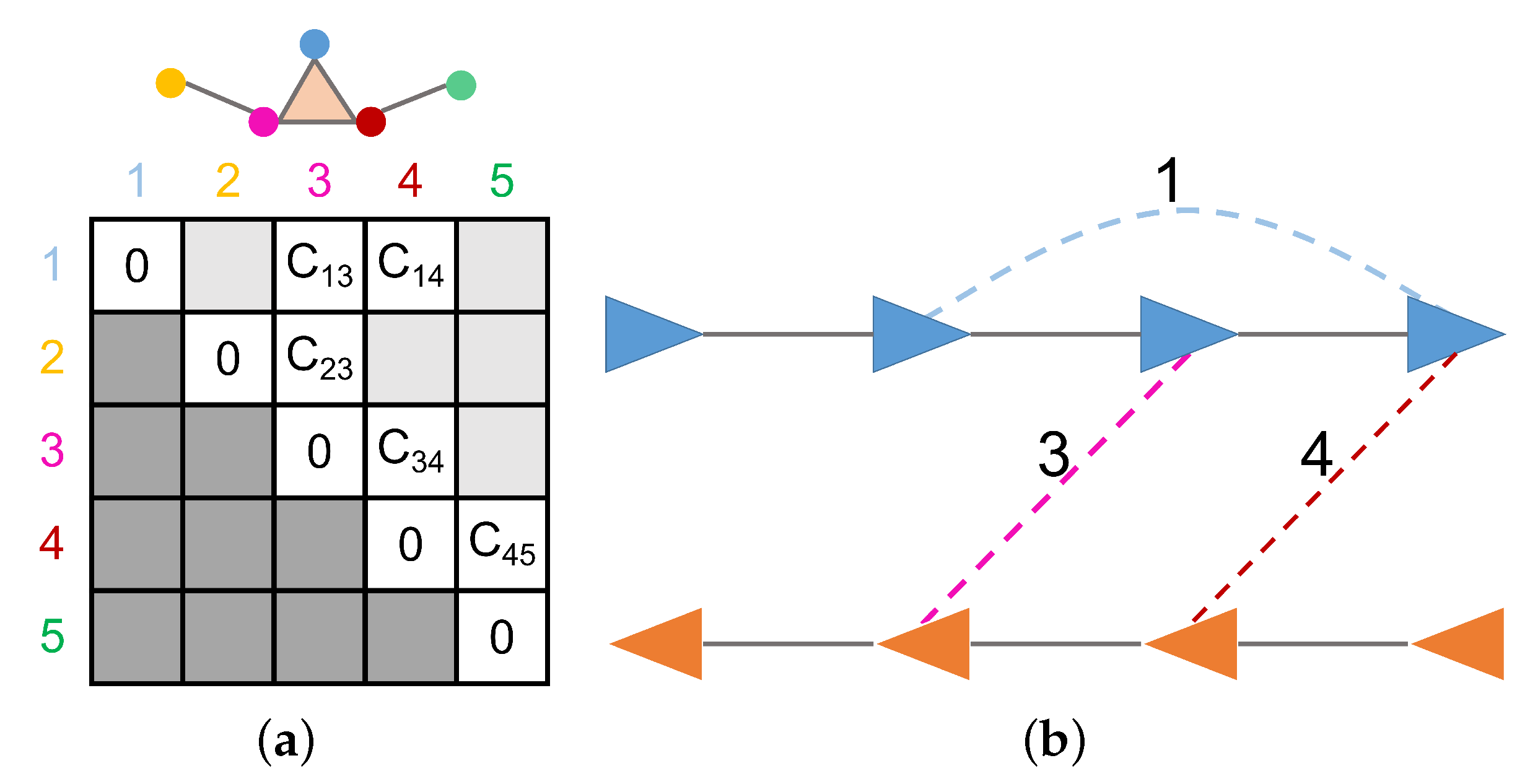
4.3. Maximum Edge Weight Clique-Based Solution
5. Experimental Results
5.1. MEWCP Cutoff Time Experiment
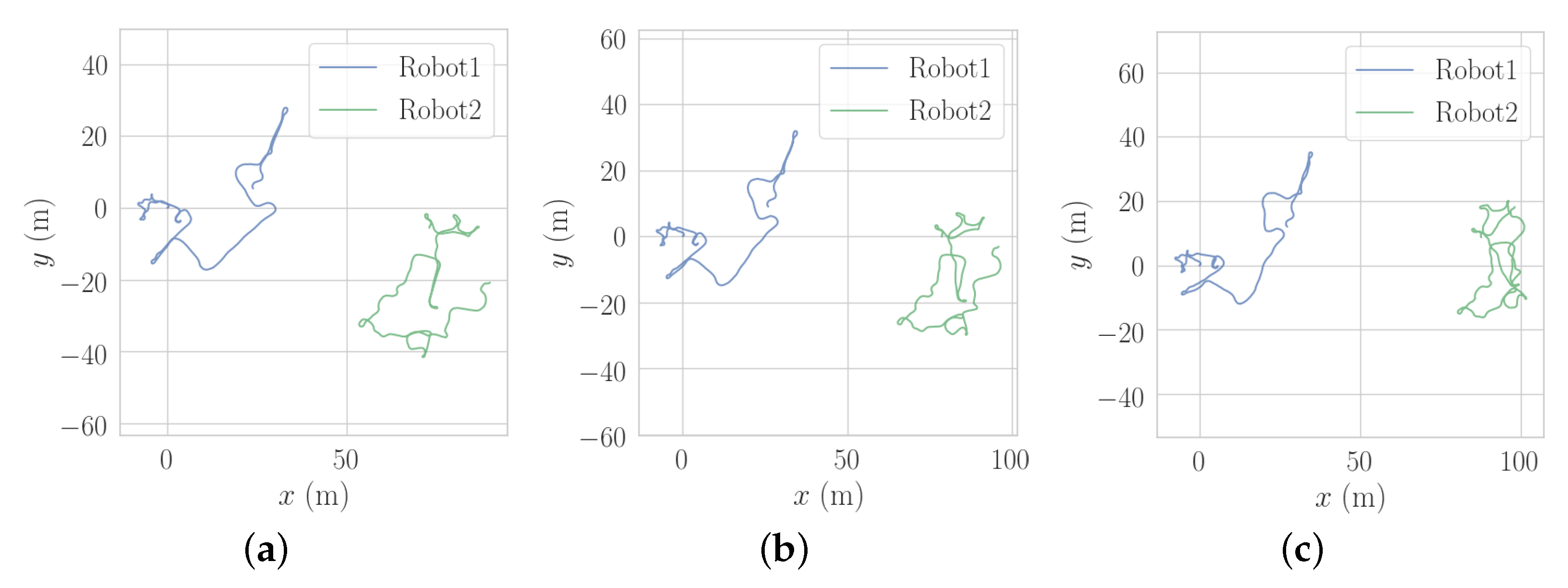
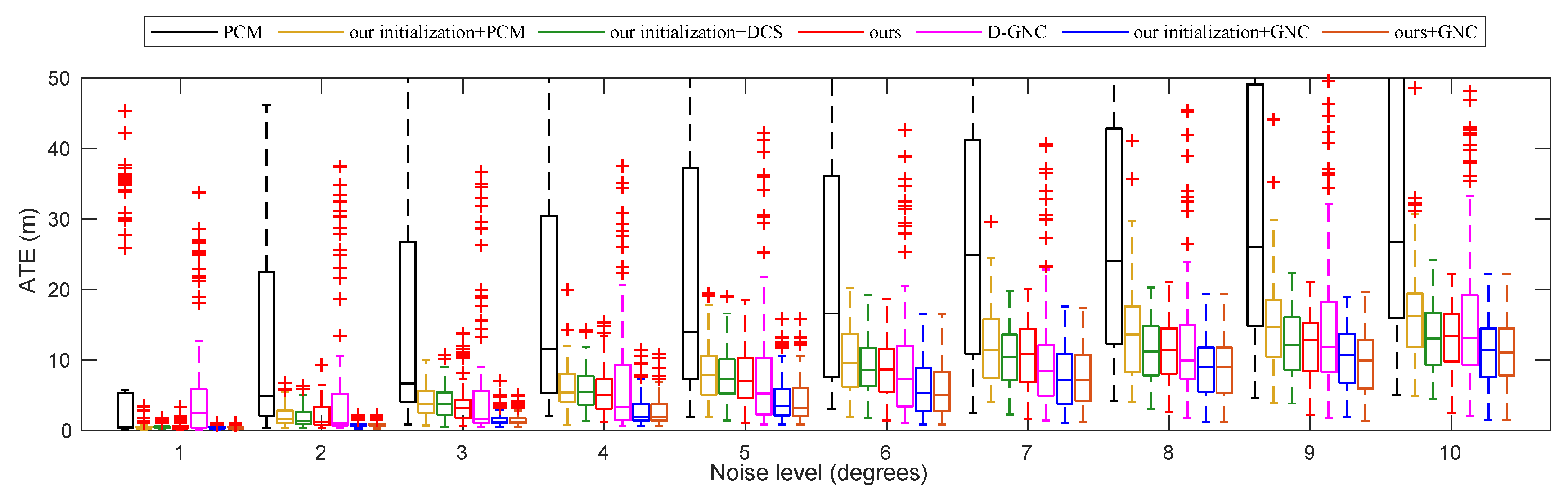
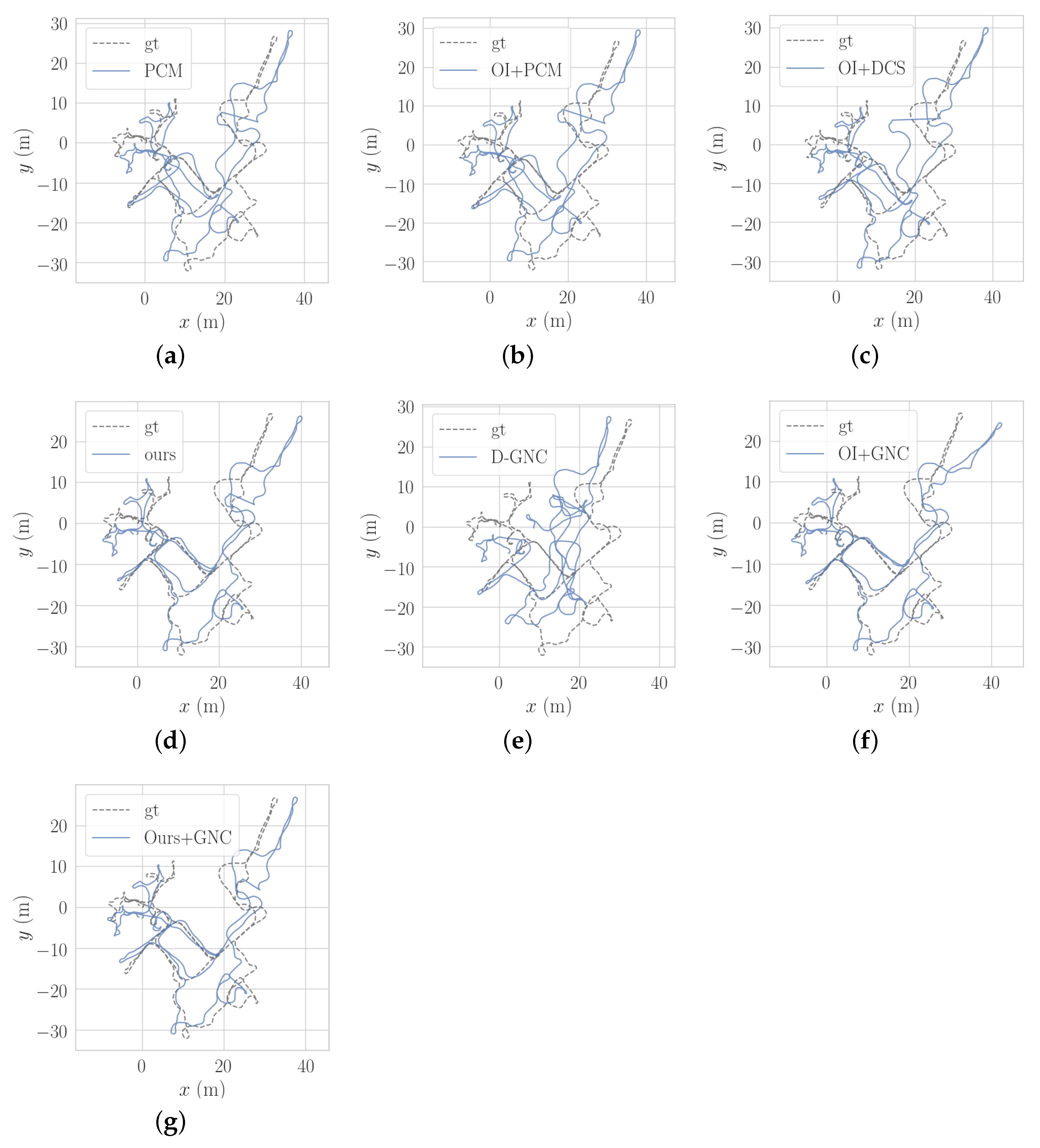
5.2. Modified CSAIL Datasets
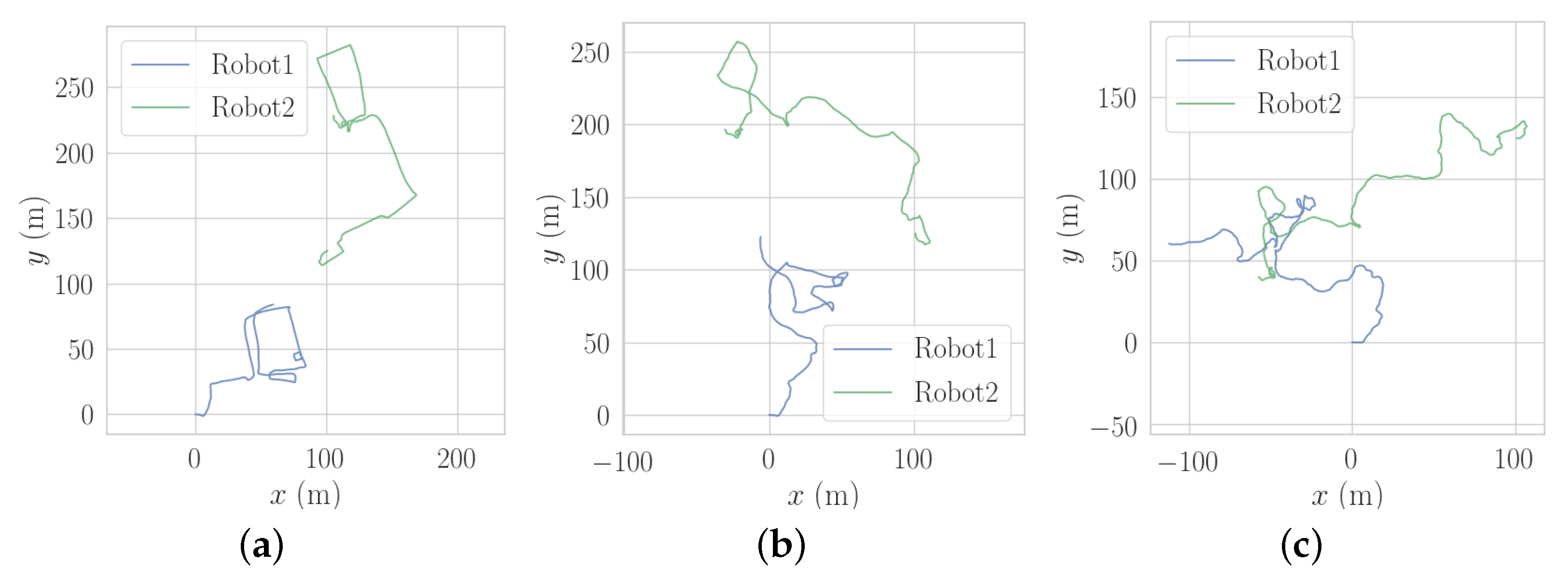
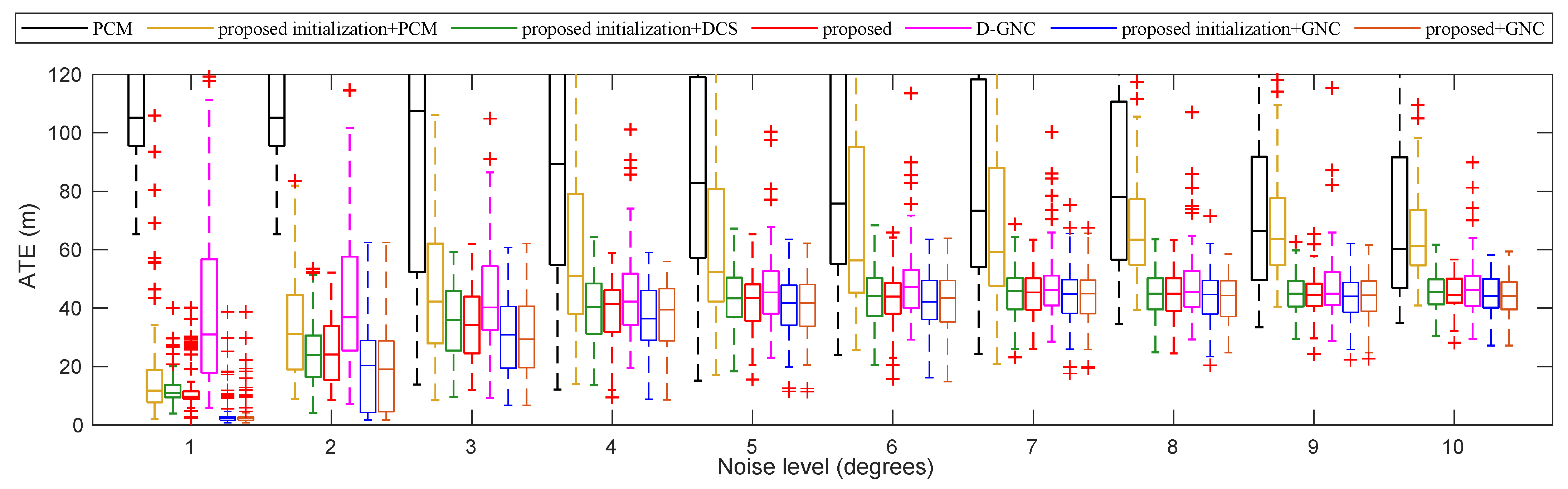
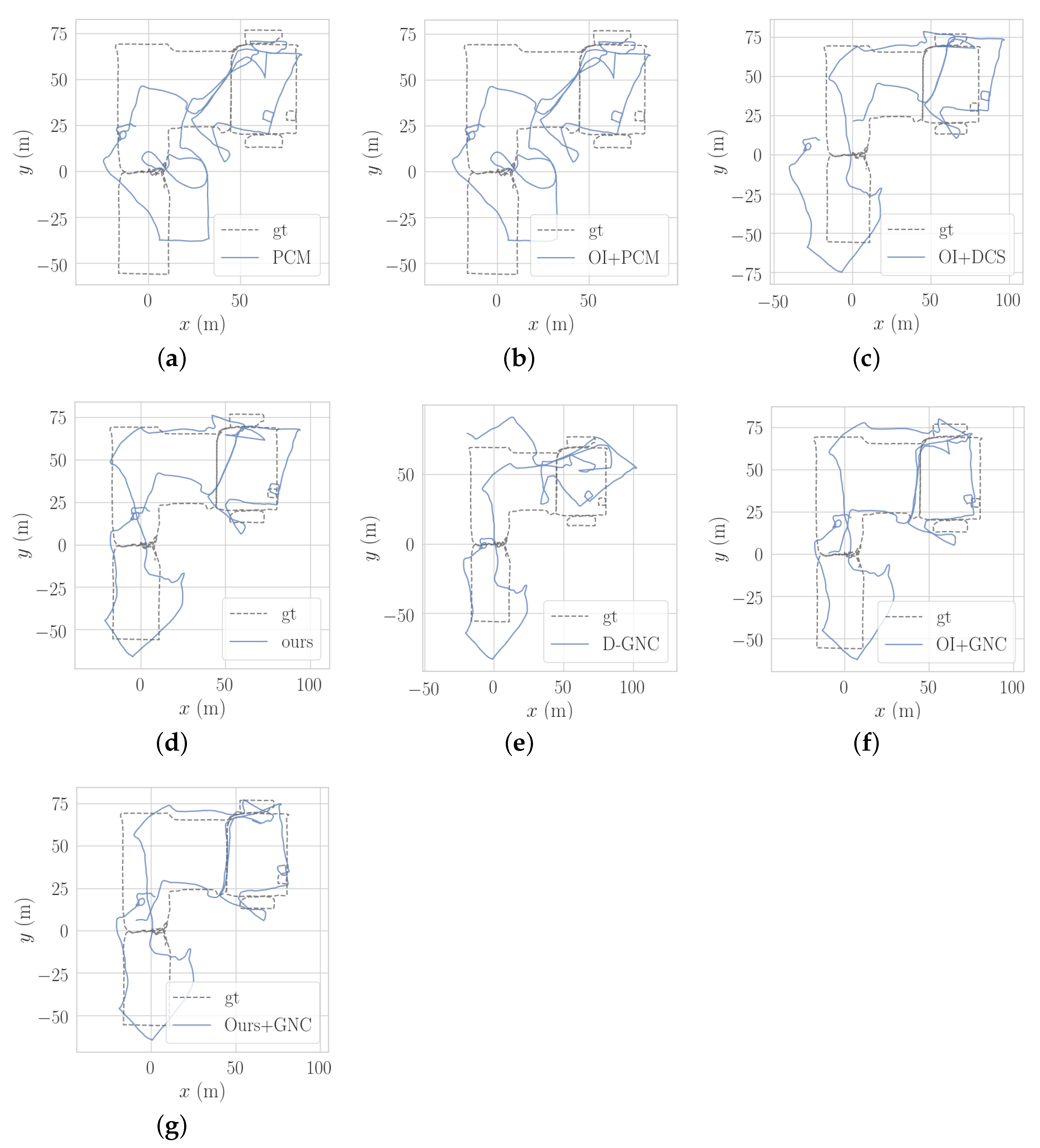
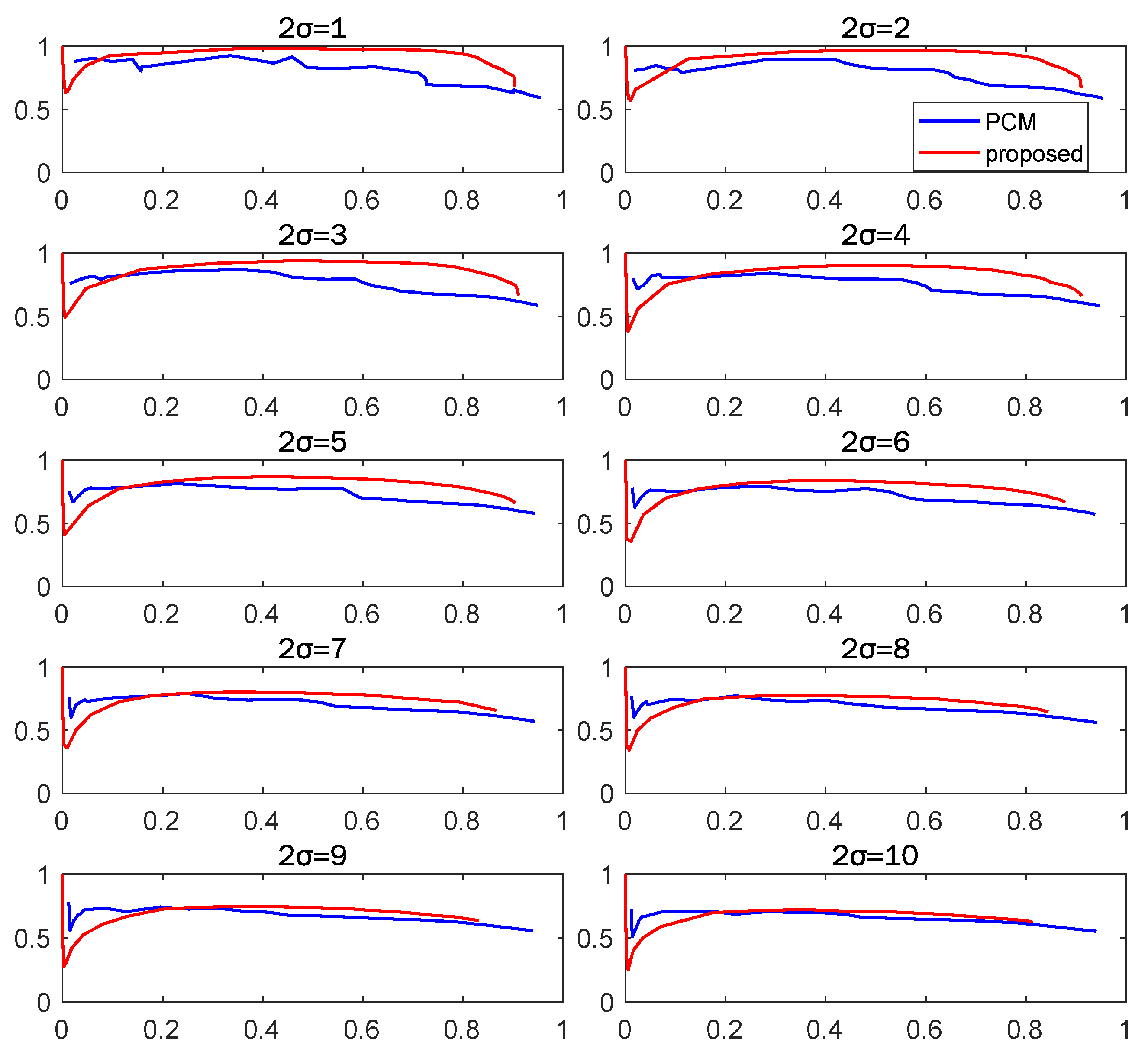
5.3. Modified Bicocca Dataset
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Noise Level () | PCM | OI + PCM | OI + DCS | Ours | D-GNC | OI + GNC | Ours + GNC | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ATE (m) | Std | ATE (m) | Std | ATE (m) | Std | ATE (m) | Std | ATE (m) | Std | ATE (m) | Std | ATE (m) | Std | |
| 1 | 8.090 | 2.782 | 0.641 | 0.371 | 0.519 | 0.283 | 0.591 | 0.356 | 5.932 | 2.238 | 0.4235 | 0.2275 | 0.4218 | 0.2261 |
| 2 | 11.824 | 5.774 | 2.096 | 1.200 | 1.892 | 1.042 | 2.090 | 1.166 | 5.577 | 2.220 | 0.8429 | 0.4520 | 0.8428 | 0.4519 |
| 3 | 15.502 | 7.512 | 4.205 | 2.285 | 4.027 | 2.177 | 3.753 | 2.104 | 5.928 | 2.307 | 1.6510 | 0.9477 | 1.5759 | 0.9139 |
| 4 | 20.083 | 9.375 | 6.048 | 3.213 | 5.926 | 3.178 | 5.816 | 3.132 | 7.336 | 3.046 | 3.0158 | 1.7602 | 2.7889 | 1.6560 |
| 5 | 22.497 | 10.311 | 8.358 | 4.461 | 7.662 | 4.065 | 7.285 | 8.528 | 9.205 | 3.908 | 4.5247 | 2.6030 | 4.5200 | 2.6065 |
| 6 | 25.692 | 11.320 | 10.092 | 5.294 | 9.158 | 4.892 | 8.348 | 9.805 | 11.038 | 4.577 | 6.0605 | 3.4220 | 5.8896 | 3.3359 |
| 7 | 28.991 | 12.861 | 11.988 | 6.117 | 10.566 | 5.549 | 9.391 | 11.019 | 11.004 | 5.194 | 7.8708 | 4.4807 | 7.7653 | 4.3847 |
| 8 | 30.760 | 12.699 | 14.012 | 7.067 | 11.544 | 6.059 | 10.067 | 11.829 | 13.233 | 6.228 | 9.0729 | 4.9996 | 9.0393 | 4.9747 |
| 9 | 34.161 | 14.332 | 15.364 | 7.946 | 12.342 | 6.426 | 10.705 | 12.549 | 15.728 | 7.104 | 10.3245 | 5.6425 | 9.8986 | 5.4318 |
| 10 | 35.802 | 14.815 | 17.003 | 8.518 | 13.064 | 6.710 | 11.334 | 13.233 | 17.477 | 7.571 | 11.3157 | 6.1088 | 11.2058 | 6.0329 |
| Noise Level () | PCM | OI + PCM | OI + DCS | Ours | D-GNC | OI + GNC | Ours + GNC | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ATE (m) | Std | ATE (m) | Std | ATE (m) | Std | ATE (m) | Std | ATE (m) | Std | ATE (m) | Std | ATE (m) | Std | |
| 1 | 113.951 | 53.989 | 17.698 | 8.253 | 12.365 | 5.153 | 13.492 | 6.090 | 43.335 | 13.896 | 4.0235 | 1.8584 | 4.2150 | 1.8826 |
| 2 | 111.403 | 54.106 | 39.964 | 16.652 | 24.664 | 11.707 | 25.571 | 11.958 | 44.859 | 16.985 | 18.9330 | 9.3146 | 18.9429 | 9.3044 |
| 3 | 108.038 | 39.653 | 51.492 | 24.937 | 34.980 | 16.510 | 34.297 | 16.151 | 45.277 | 19.417 | 30.3708 | 14.7687 | 30.3025 | 14.7380 |
| 4 | 98.795 | 38.421 | 62.715 | 30.596 | 40.315 | 18.607 | 38.682 | 17.873 | 46.192 | 20.283 | 36.5794 | 17.4698 | 36.5397 | 17.1571 |
| 5 | 98.909 | 39.586 | 67.526 | 31.298 | 43.420 | 20.053 | 42.361 | 19.1428 | 48.213 | 21.789 | 41.0118 | 19.350 | 41.0852 | 19.1168 |
| 6 | 97.372 | 41.464 | 73.040 | 34.739 | 43.631 | 20.194 | 43.231 | 19.5631 | 49.363 | 22.467 | 42.3226 | 19.8184 | 42.4672 | 19.924 |
| 7 | 88.277 | 38.572 | 72.526 | 35.259 | 45.189 | 20.606 | 44.914 | 20.1161 | 48.016 | 21.909 | 44.4454 | 20.303 | 44.0455 | 20.2566 |
| 8 | 87.086 | 38.354 | 69.034 | 33.882 | 44.554 | 19.711 | 44.291 | 19.262 | 48.614 | 21.774 | 43.6520 | 19.1942 | 43.3634 | 18.9289 |
| 9 | 77.532 | 34.223 | 68.225 | 32.246 | 44.800 | 19.341 | 44.443 | 18.7434 | 47.241 | 21.616 | 43.7138 | 18.7792 | 44.0341 | 18.999 |
| 10 | 73.651 | 32.999 | 66.824 | 33.040 | 45.681 | 19.860 | 45.093 | 19.475 | 46.440 | 20.922 | 44.4772 | 19.0131 | 44.4518 | 19.1225 |
References
- Wang, X.; Fan, X.; Shi, P.; Ni, J.; Zhou, Z. An Overview of Key SLAM Technologies for Underwater Scenes. Remote Sens. 2023, 15, 2496. [Google Scholar] [CrossRef]
- Do, H.; Hong, S.; Kim, J. Robust loop closure method for multi-robot map fusion by integration of consistency and data similarity. IEEE Robot. Autom. Lett. 2020, 5, 5701–5708. [Google Scholar] [CrossRef]
- Dellaert, F.; Kaess, M. Factor graphs for robot perception. Found. Trends® Robot. 2017, 6, 1–139. [Google Scholar] [CrossRef]
- Mangelson, J.G.; Dominic, D.; Eustice, R.M.; Vasudevan, R. Pairwise consistent measurement set maximization for robust multi-robot map merging. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 2916–2923. [Google Scholar]
- Rosen, D.M.; Doherty, K.J.; Terán Espinoza, A.; Leonard, J.J. Advances in Inference and Representation for Simultaneous Localization and Mapping. Annu. Rev. Control. Robot. Auton. Syst. 2021, 4, 215–242. [Google Scholar] [CrossRef]
- Tian, Y.; Chang, Y.; Herrera Arias, F.; Nieto-Granda, C.; How, J.P.; Carlone, L. Kimera-Multi: Robust, Distributed, Dense Metric-Semantic SLAM for Multi-Robot Systems. IEEE Trans. Robot. 2022, 38, 2022–2038. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Latif, Y.; Cadena, C.; Neira, J. Robust loop closing over time for pose graph SLAM. Int. J. Robot. Res. 2013, 32, 1611–1626. [Google Scholar] [CrossRef]
- Huber, P.J. Robust estimation of a location parameter. In Breakthroughs in Statistics; Springer: New York, NY, USA, 1992; pp. 492–518. [Google Scholar]
- Sünderhauf, N.; Protzel, P. Switchable constraints for robust pose graph SLAM. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 1879–1884. [Google Scholar]
- Agarwal, P.; Tipaldi, G.D.; Spinello, L.; Stachniss, C.; Burgard, W. Robust map optimization using dynamic covariance scaling. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 62–69. [Google Scholar]
- Olson, E.; Agarwal, P. Inference on networks of mixtures for robust robot mapping. Int. J. Robot. Res. 2013, 32, 826–840. [Google Scholar] [CrossRef]
- Carlone, L.; Calafiore, G.C. Convex relaxations for pose graph optimization with outliers. IEEE Robot. Autom. Lett. 2018, 3, 1160–1167. [Google Scholar] [CrossRef]
- Lajoie, P.Y.; Hu, S.; Beltrame, G.; Carlone, L. Modeling perceptual aliasing in slam via discrete–continuous graphical models. IEEE Robot. Autom. Lett. 2019, 4, 1232–1239. [Google Scholar] [CrossRef]
- Yang, H.; Antonante, P.; Tzoumas, V.; Carlone, L. Graduated non-convexity for robust spatial perception: From non-minimal solvers to global outlier rejection. IEEE Robot. Autom. Lett. 2020, 5, 1127–1134. [Google Scholar] [CrossRef]
- Dong, J.; Nelson, E.; Indelman, V.; Michael, N.; Dellaert, F. Distributed real-time cooperative localization and mapping using an uncertainty-aware expectation maximization approach. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 5807–5814. [Google Scholar]
- Indelman, V.; Nelson, E.; Dong, J.; Michael, N.; Dellaert, F. Incremental distributed inference from arbitrary poses and unknown data association: Using collaborating robots to establish a common reference. IEEE Control Syst. Mag. 2016, 36, 41–74. [Google Scholar]
- Lajoie, P.Y.; Ramtoula, B.; Chang, Y.; Carlone, L.; Beltrame, G. DOOR-SLAM: Distributed, online, and outlier resilient SLAM for robotic teams. IEEE Robot. Autom. Lett. 2020, 5, 1656–1663. [Google Scholar] [CrossRef]
- Rosinol, A.; Abate, M.; Chang, Y.; Carlone, L. Kimera: An Open-Source Library for Real-Time Metric-Semantic Localization and Mapping. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 1689–1696. [Google Scholar]
- Ebadi, K.; Chang, Y.; Palieri, M.; Stephens, A.; Hatteland, A.; Heiden, E.; Thakur, A.; Funabiki, N.; Morrell, B.; Wood, S.; et al. LAMP: Large-scale autonomous mapping and positioning for exploration of perceptually-degraded subterranean environments. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 80–86. [Google Scholar]
- Chang, Y.; Tian, Y.; How, J.P.; Carlone, L. Kimera-Multi: A system for distributed multi-robot metric-semantic simultaneous localization and mapping. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 11210–11218. [Google Scholar]
- Zheng, S.; Wang, J.; Rizos, C.; Ding, W.; El-Mowafy, A. Simultaneous Localization and Mapping (SLAM) for Autonomous Driving: Concept and Analysis. Remote Sens. 2023, 15, 1156. [Google Scholar] [CrossRef]
- Kim, B.; Kaess, M.; Fletcher, L.; Leonard, J.; Bachrach, A.; Roy, N.; Teller, S. Multiple relative pose graphs for robust cooperative mapping. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 3185–3192. [Google Scholar]
- Carlone, L.; Censi, A.; Dellaert, F. Selecting good measurements via ℓ 1 relaxation: A convex approach for robust estimation over graphs. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 2667–2674. [Google Scholar]
- Smith, R.; Self, M.; Cheeseman, P. Estimating uncertain spatial relationships in robotics. In Autonomous Robot Vehicles; Springer: New York, NY, USA, 1990; pp. 167–193. [Google Scholar]
- Olson, E. Recognizing places using spectrally clustered local matches. Robot. Auton. Syst. 2009, 57, 1157–1172. [Google Scholar] [CrossRef]
- Chu, Y.; Liu, B.; Cai, S.; Luo, C.; You, H. An efficient local search algorithm for solving maximum edge weight clique problem in large graphs. J. Comb. Optim. 2020, 39, 933–954. [Google Scholar] [CrossRef]
- Dellaert, F. Factor Graphs and GTSAM: A Hands-on Introduction; Georgia Institute of Technology: Atlanta, GA, USA, 2012. [Google Scholar]
- MIT-SPARK/Kimera-RPGO: Robust Pose Graph Optimization. Available online: https://github.com/MIT-SPARK/Kimera-RPGO (accessed on 10 May 2023).
- Release 4.2a7 · Borglab/Gtsam. Available online: https://github.com/borglab/gtsam/releases/tag/4.2a7 (accessed on 10 May 2023).


| Noise Level () | O-ini | D-GNC-ini | PCM | DCS | O-lcs | GNC |
|---|---|---|---|---|---|---|
| 1 | 231 | 81 | 1328 | 146 | 2178 | 10,897 |
| 2 | 232 | 101 | 1326 | 103 | 2255 | 17,794 |
| 3 | 233 | 100 | 1348 | 70 | 2224 | 18,191 |
| 4 | 230 | 101 | 1313 | 57 | 2245 | 21,279 |
| 5 | 232 | 115 | 1299 | 56 | 2234 | 26,863 |
| 6 | 230 | 109 | 1294 | 64 | 2202 | 25,744 |
| 7 | 232 | 117 | 1286 | 61 | 2241 | 31,033 |
| 8 | 231 | 117 | 1376 | 53 | 2216 | 30,913 |
| 9 | 232 | 111 | 1405 | 46 | 2271 | 27,632 |
| 10 | 232 | 107 | 1412 | 40 | 2230 | 30,652 |
| Noise Level () | D-GNC | Ours | |||
|---|---|---|---|---|---|
| ATE (m) | Std | ATE (m) | Std | Precision | |
| 1 | 12.420 | 4.125 | 1.501 | 0.796 | 1.00 |
| 2 | 10.708 | 3.772 | 3.634 | 1.858 | 1.00 |
| 3 | 11.160 | 4.153 | 5.387 | 2.726 | 1.00 |
| 4 | 12.447 | 4.796 | 7.036 | 3.591 | 1.00 |
| 5 | 13.686 | 5.525 | 8.556 | 4.358 | 1.00 |
| 6 | 15.155 | 6.025 | 9.822 | 5.042 | 0.98 |
| 7 | 15.022 | 6.382 | 11.008 | 5.654 | 0.96 |
| 8 | 16.631 | 7.159 | 11.838 | 6.128 | 0.95 |
| 9 | 18.919 | 7.915 | 12.604 | 6.491 | 0.93 |
| 10 | 20.422 | 8.181 | 13.267 | 6.763 | 0.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Zhao, J.; Feng, T.; Ye, C.; Xiong, L. Robust Loop Closure Selection Based on Inter-Robot and Intra-Robot Consistency for Multi-Robot Map Fusion. Remote Sens. 2023, 15, 2796. https://doi.org/10.3390/rs15112796
Chen Z, Zhao J, Feng T, Ye C, Xiong L. Robust Loop Closure Selection Based on Inter-Robot and Intra-Robot Consistency for Multi-Robot Map Fusion. Remote Sensing. 2023; 15(11):2796. https://doi.org/10.3390/rs15112796
Chicago/Turabian StyleChen, Zhihong, Junqiao Zhao, Tiantian Feng, Chen Ye, and Lu Xiong. 2023. "Robust Loop Closure Selection Based on Inter-Robot and Intra-Robot Consistency for Multi-Robot Map Fusion" Remote Sensing 15, no. 11: 2796. https://doi.org/10.3390/rs15112796
APA StyleChen, Z., Zhao, J., Feng, T., Ye, C., & Xiong, L. (2023). Robust Loop Closure Selection Based on Inter-Robot and Intra-Robot Consistency for Multi-Robot Map Fusion. Remote Sensing, 15(11), 2796. https://doi.org/10.3390/rs15112796






