3PCD-TP: A 3D Point Cloud Descriptor for Loop Closure Detection with Twice Projection
Abstract
1. Introduction
- A point cloud preprocessing approach has been introduced to weaken the rotational and translational effect of sensors. The origin and primary direction of cloud points have been redefined according to the distribution of point clouds, to render the new point cloud coordinates independent of the sensor coordinate system.
- The design of the 3D global descriptor 3PCD-TP combines semantic information and height information. Thereinto, the abilities of the descriptors in describing and discriminating scenes have been strengthened by using semantic information and equivoluminal multilayer coding schemes.
- A twice-projection-based weighted similarity algorithm has been proposed to measure the similarity between scenes in terms of the weighted sum of the Hamming distance of the side-view projection and the cosine distance of the top-view projection of the descriptors and to reduce the probability of loop closure mismatching.
2. Related Work
2.1. Vision-Based LCD Algorithms
2.2. LiDAR-Based LCD Algorithms
2.3. Motivation of This Work
3. Methods
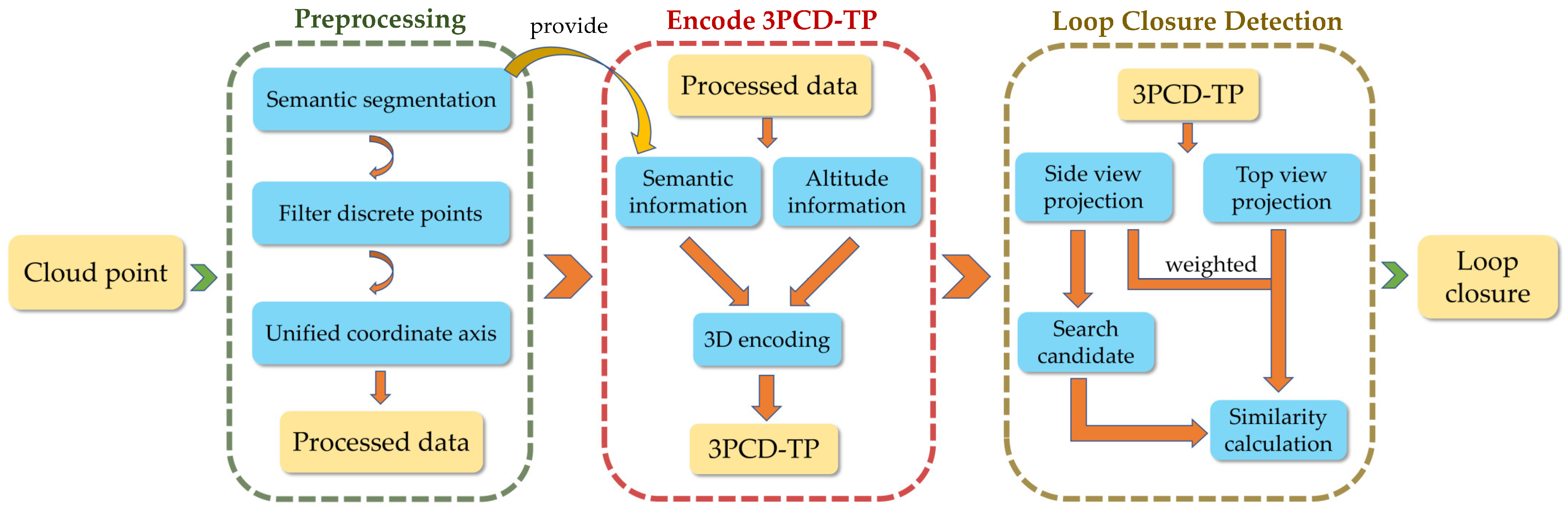
3.1. Algorithm Overview
3.2. Preprocessing of Point Clouds
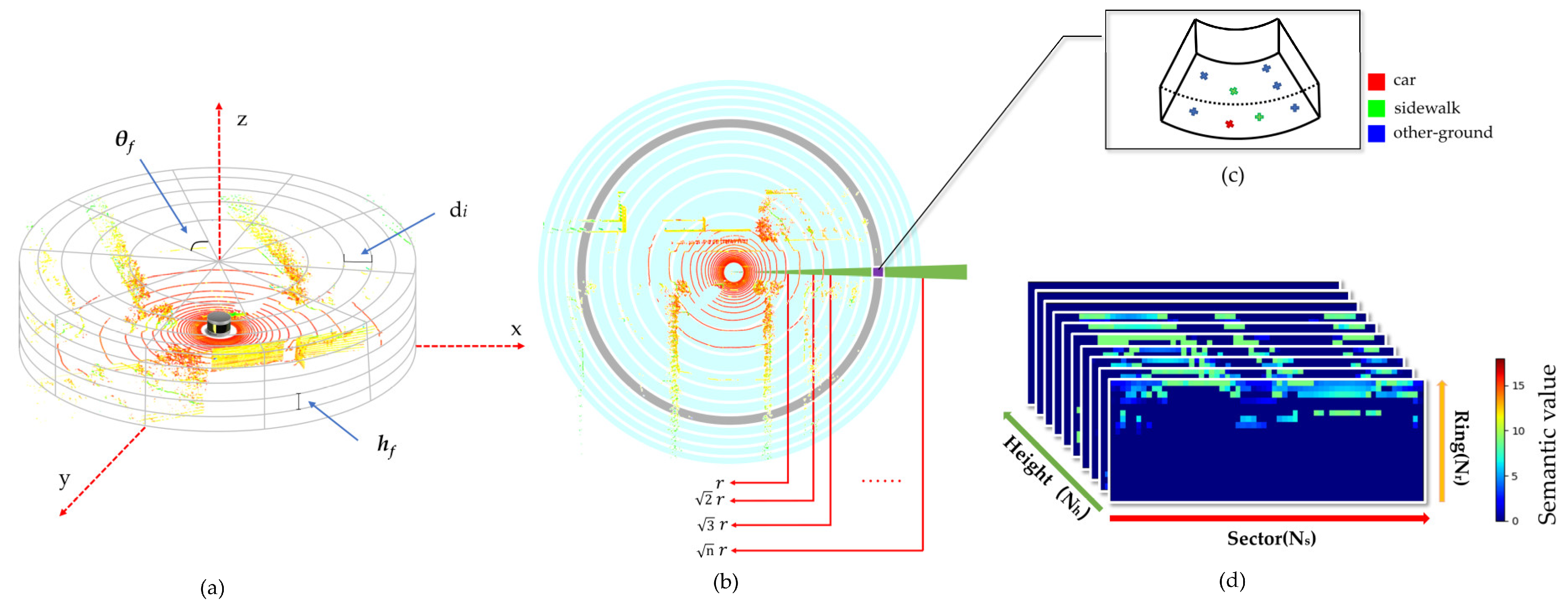
3.2.1. Acquisition of Semantic Information
3.2.2. Unified Coordinate Axis
| Algorithm 1 Preprocessing Algorithm |
| Input: raw point cloud data ; Output: point cloud after preprocessing ; Algorithm:
|
3.3. Construction and Twice Projection of Descriptors
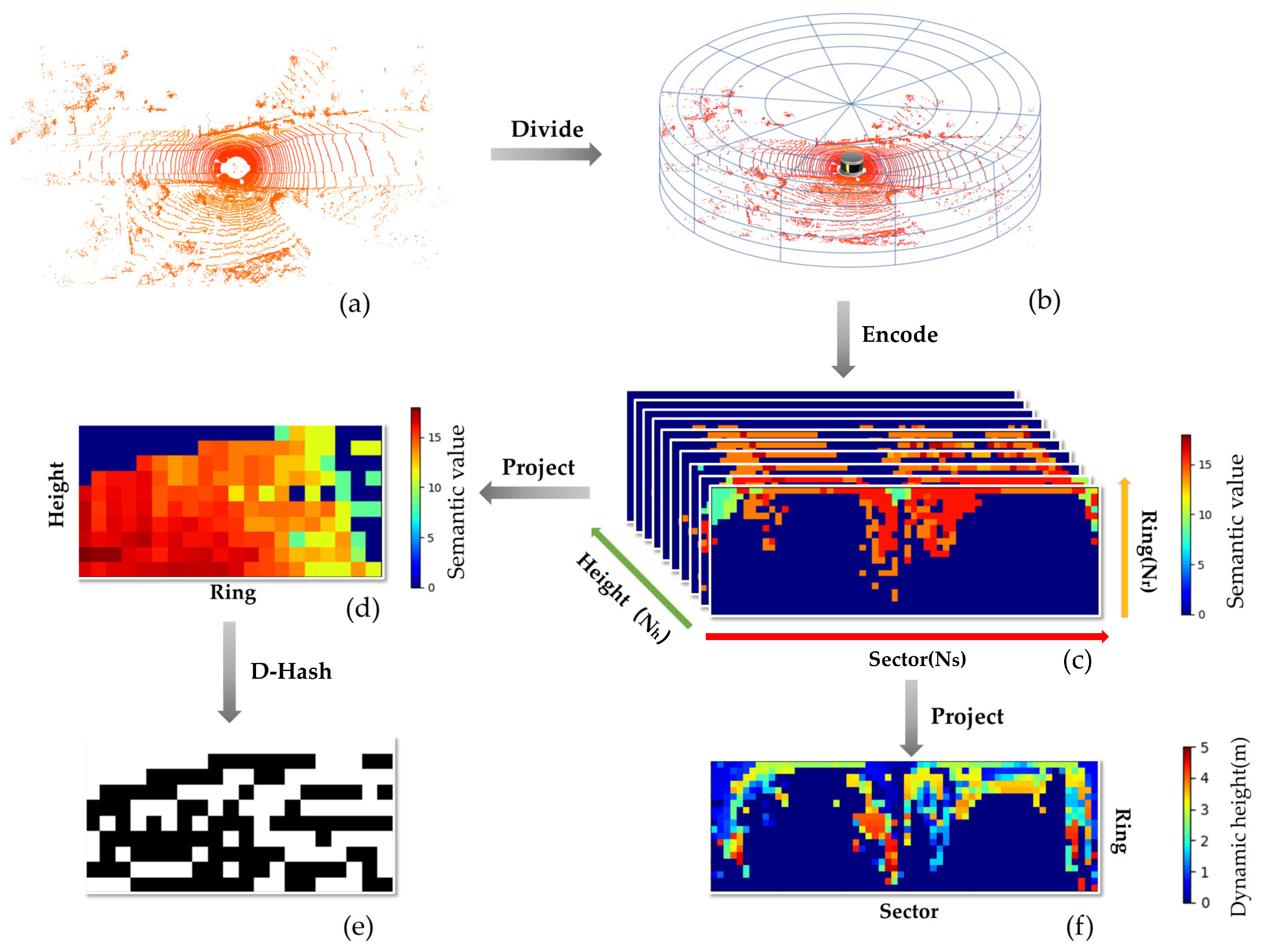
3.3.1. Construction of Descriptors
3.3.2. Twice Projection
3.4. Generation of the Weighted Distance Function
4. Experiments
4.1. Experimental Results over the Public Dataset
4.1.1. Introduction to the Dataset KITTI
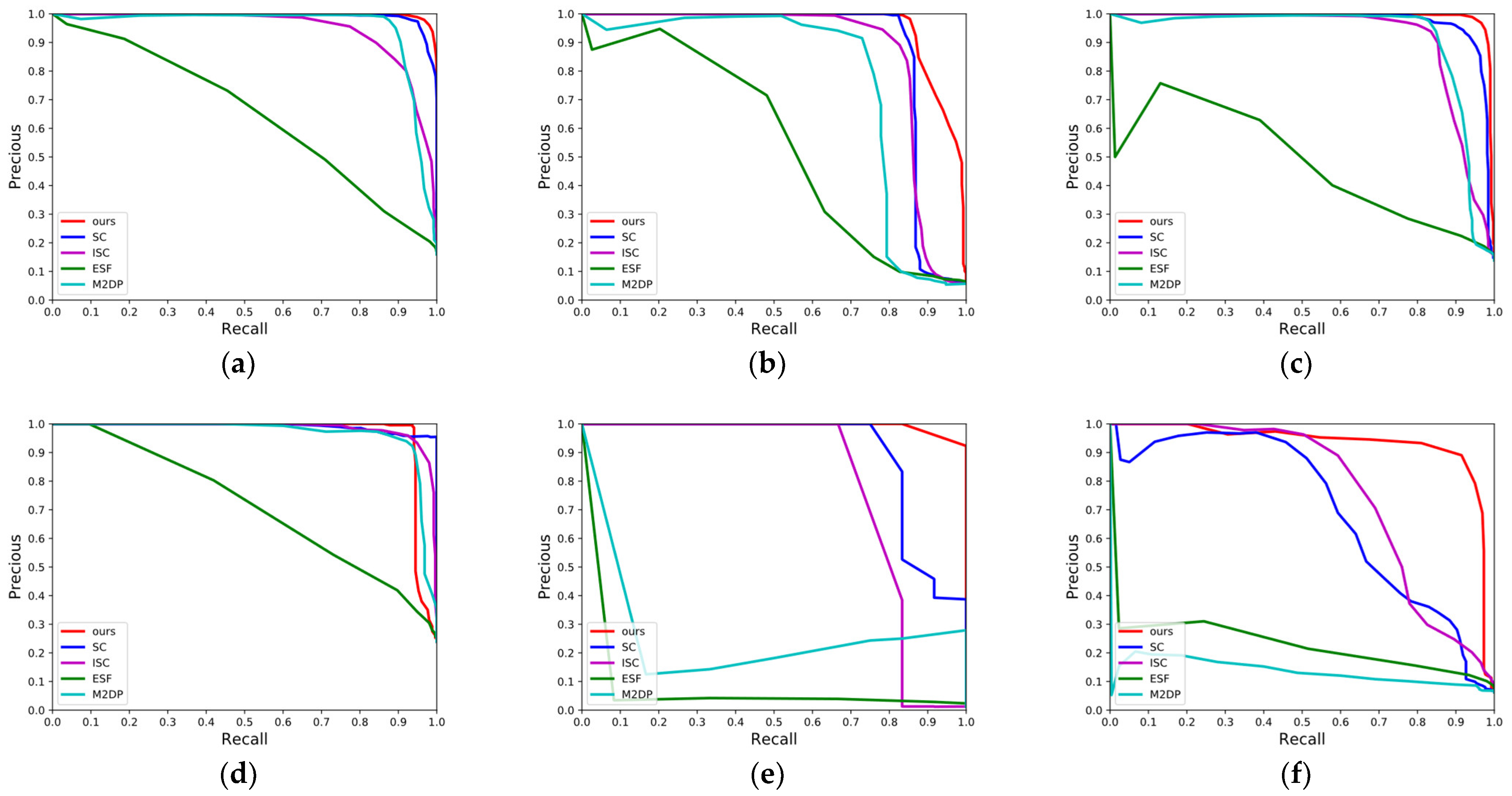
4.1.2. P-R Curves over the Dataset KITTI
4.1.3. Maximum F1-Score and EP Value Results over the Dataset KITTI
4.2. Experimental Results over the Campus Dataset
4.2.1. Introduction to the Campus Dataset
4.2.2. P-R Curves over the Campus Dataset
4.2.3. Evaluation of Maximum F1-Score and EP Value
4.2.4. Rotation-Translation Comparative Experiment
4.2.5. Application of 3PCD-TP in SLAM
4.2.6. Reverse Loop Closure Detection in Real-World Scenes
4.3. Analysis of Computation Time
4.3.1. Time Comparison Experiment
4.3.2. Distance Function Efficiency Comparison
4.4. Effectiveness Evaluation Experiment
4.4.1. Comparison Experiment
4.4.2. Ablation Experiment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Angeli, A.; Filliat, D.; Doncieux, S.; Meyer, J.-A. Fast and incremental method for loop-closure detection using bags of visual words. IEEE Trans. Robot. 2008, 24, 1027–1037. [Google Scholar] [CrossRef]
- Magnusson, M.; Andreasson, H.; Nuchter, A.; Lilienthal, A.J. Automatic Appearance-Based Loop Detection from Three-Dimensional Laser Data Using the Normal Distributions Transform. J. Field Robot. 2009, 26, 892–914. [Google Scholar] [CrossRef]
- Li, S.; Li, L.; Lee, G.; Zhang, H. A hybrid search algorithm for swarm robots searching in an unknown environment. PLoS ONE 2014, 9, e111970. [Google Scholar] [CrossRef] [PubMed]
- Kim, G.; Kim, A. Scan context: Egocentric spatial descriptor for place recognition within 3d point cloud map. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 4802–4809. [Google Scholar]
- Wang, H.; Wang, C.; Xie, L. Intensity scan context: Coding intensity and geometry relations for loop closure detection. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Virtral, 31 August 2020; pp. 2095–2101. [Google Scholar]
- Wang, Y.; Sun, Z.; Xu, C.-Z.; Sarma, S.E.; Yang, J.; Kong, H. Lidar iris for loop-closure detection. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020; pp. 5769–5775. [Google Scholar]
- Geiger, A.; Lenz, P.; Stiller, C.; Urtasun, R. Vision meets robotics: The KITTI dataset. Int. J. Robot. Res. 2013, 32, 1231–1237. [Google Scholar] [CrossRef]
- Gálvez-López, D.; Tardos, J.D.J.I.T.o.R. Bags of binary words for fast place recognition in image sequences. IEEE Trans. Robot. 2012, 28, 1188–1197. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Tardós, J.D. Orb-slam2: An open-source slam system for monocular, stereo, and rgb-d cameras. IEEE Trans. Robot. 2017, 33, 1255–1262. [Google Scholar] [CrossRef]
- Qin, T.; Li, P.L.; Shen, S.J. VINS-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator. IEEE Trans. Robot. 2018, 34, 1004–1020. [Google Scholar] [CrossRef]
- Żywanowski, K.; Banaszczyk, A.; Nowicki, M.R. Comparison of camera-based and 3d lidar-based place recognition across weather conditions. In Proceedings of the 2020 16th International Conference on Control, Automation, Robotics and Vision (ICARCV), Shenzhen, China, 13–15 December 2020; pp. 886–891. [Google Scholar]
- Zhu, Y.; Ma, Y.; Chen, L.; Liu, C.; Ye, M.; Li, L. Gosmatch: Graph-of-semantics matching for detecting loop closures in 3d lidar data. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020; pp. 5151–5157. [Google Scholar]
- Lim, K.; Treitz, P.; Wulder, M.; St-Onge, B.; Flood, M. LiDAR remote sensing of forest structure. Prog. Phys. Geogr. 2003, 27, 88–106. [Google Scholar] [CrossRef]
- Scovanner, P.; Ali, S.; Shah, M. A 3-dimensional sift descriptor and its application to action recognition. In Proceedings of the 15th ACM International Conference on Multimedia, Augsburg, Germany, 25–29 September 2007; pp. 357–360. [Google Scholar]
- Knopp, J.; Prasad, M.; Willems, G.; Timofte, R.; Van Gool, L. Hough transform and 3D SURF for robust three dimensional classification. In Proceedings of the European Conference on Computer Vision, Crete, Greece, 5–11 September 2010; pp. 589–602. [Google Scholar]
- Sivic, J.; Zisserman, A. Video Google: A text retrieval approach to object matching in videos. In Proceedings of the Computer Vision, IEEE International Conference on Computer Vision, Nice, France, 13–16 October 2003; p. 1470. [Google Scholar]
- Salti, S.; Tombari, F.; Di Stefano, L. SHOT: Unique signatures of histograms for surface and texture description. Comput. Vis. Image Underst. 2014, 125, 251–264. [Google Scholar] [CrossRef]
- Prakhya, S.M.; Liu, B.; Lin, W. B-SHOT: A binary feature descriptor for fast and efficient keypoint matching on 3D point clouds. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–3 October 2015; pp. 1929–1934. [Google Scholar]
- Guo, J.; Borges, P.V.; Park, C.; Gawel, A. Local descriptor for robust place recognition using lidar intensity. IEEE Robot. Autom. Lett. 2019, 4, 1470–1477. [Google Scholar] [CrossRef]
- Belongie, S.; Malik, J.; Puzicha, J. Shape matching and object recognition using shape contexts. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 509–522. [Google Scholar] [CrossRef]
- Rusu, R.B.; Blodow, N.; Beetz, M. Fast point feature histograms (FPFH) for 3D registration. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 3212–3217. [Google Scholar]
- Wohlkinger, W.; Vincze, M. Ensemble of shape functions for 3d object classification. In Proceedings of the 2011 IEEE International Conference on Robotics and Biomimetics, Karon Beach, Thailand, 7–11 December 2011; pp. 2987–2992. [Google Scholar]
- He, L.; Wang, X.; Zhang, H. M2DP: A novel 3D point cloud descriptor and its application in loop closure detection. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 231–237. [Google Scholar]
- Dubé, R.; Dugas, D.; Stumm, E.; Nieto, J.; Siegwart, R.; Cadena, C. Segmatch: Segment based place recognition in 3d point clouds. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May 2017; pp. 5266–5272. [Google Scholar]
- Dubé, R.; Cramariuc, A.; Dugas, D.; Nieto, J.; Siegwart, R.; Cadena, C. SegMap: 3d segment mapping using data-driven descriptors. arXiv 2018, arXiv:1804.09557. [Google Scholar]
- Wang, Y.; Dong, L.; Li, Y.; Zhang, H. Multitask feature learning approach for knowledge graph enhanced recommendations with RippleNet. PLoS ONE 2021, 16, e0251162. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.; He, Y.; Tan, U.-X. Seed: A segmentation-based egocentric 3D point cloud descriptor for loop closure detection. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 25–29 October 2020; pp. 5158–5163. [Google Scholar]
- Li, L.; Kong, X.; Zhao, X.R.; Huang, T.X.; Li, W.L.; Wen, F.; Zhang, H.B.; Liu, Y. SSC: Semantic Scan Context for Large-Scale Place Recognition. In Proceedings of the 2021 IEEE/Rsj International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 1 October 2021; pp. 2092–2099. [Google Scholar] [CrossRef]
- Tang, H.; Liu, Z.; Zhao, S.; Lin, Y.; Lin, J.; Wang, H.; Han, S. Searching efficient 3d architectures with sparse point-voxel convolution. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 685–702. [Google Scholar]
- Zhang, Y.; Tian, G.; Shao, X.; Zhang, M.; Liu, S.J.I.T.o.I.E. Semantic Grounding for Long-Term Autonomy of Mobile Robots towards Dynamic Object Search in Home Environments. IEEE Trans. Ind. Electron. 2022, 70, 1655–1665. [Google Scholar] [CrossRef]
- Zhang, Y.; Tian, G.H.; Lu, J.X.; Zhang, M.Y.; Zhang, S.Y. Efficient Dynamic Object Search in Home Environment by Mobile Robot: A Priori Knowledge-Based Approach. IEEE Trans. Veh. Technol. 2019, 68, 9466–9477. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, D.; Frangi, A.F.; Yang, J.-y. Two-dimensional PCA: A new approach to appearance-based face representation and recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 131–137. [Google Scholar] [CrossRef] [PubMed]
- Maćkiewicz, A.; Ratajczak, W. Principal components analysis (PCA). Comput. Geosci. 1993, 19, 303–342. [Google Scholar] [CrossRef]
- Gerbrands, J.J. On the relationships between SVD, KLT and PCA. Pattern Recognit. 1981, 14, 375–381. [Google Scholar] [CrossRef]
- Orfanidis, S. SVD, PCA, KLT, CCA, and All That. Optim. Signal Process. 2007, 332–525. [Google Scholar]
- Sun, Y.X.; Liu, M.; Meng, M.Q.H. Improving RGB-D SLAM in dynamic environments: A motion removal approach. Robot. Auton. Syst. 2017, 89, 110–122. [Google Scholar] [CrossRef]
- Shan, T.; Englot, B.; Meyers, D.; Wang, W.; Ratti, C.; Rus, D. Lio-sam: Tightly-coupled lidar inertial odometry via smoothing and mapping. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020; pp. 5135–5142. [Google Scholar]





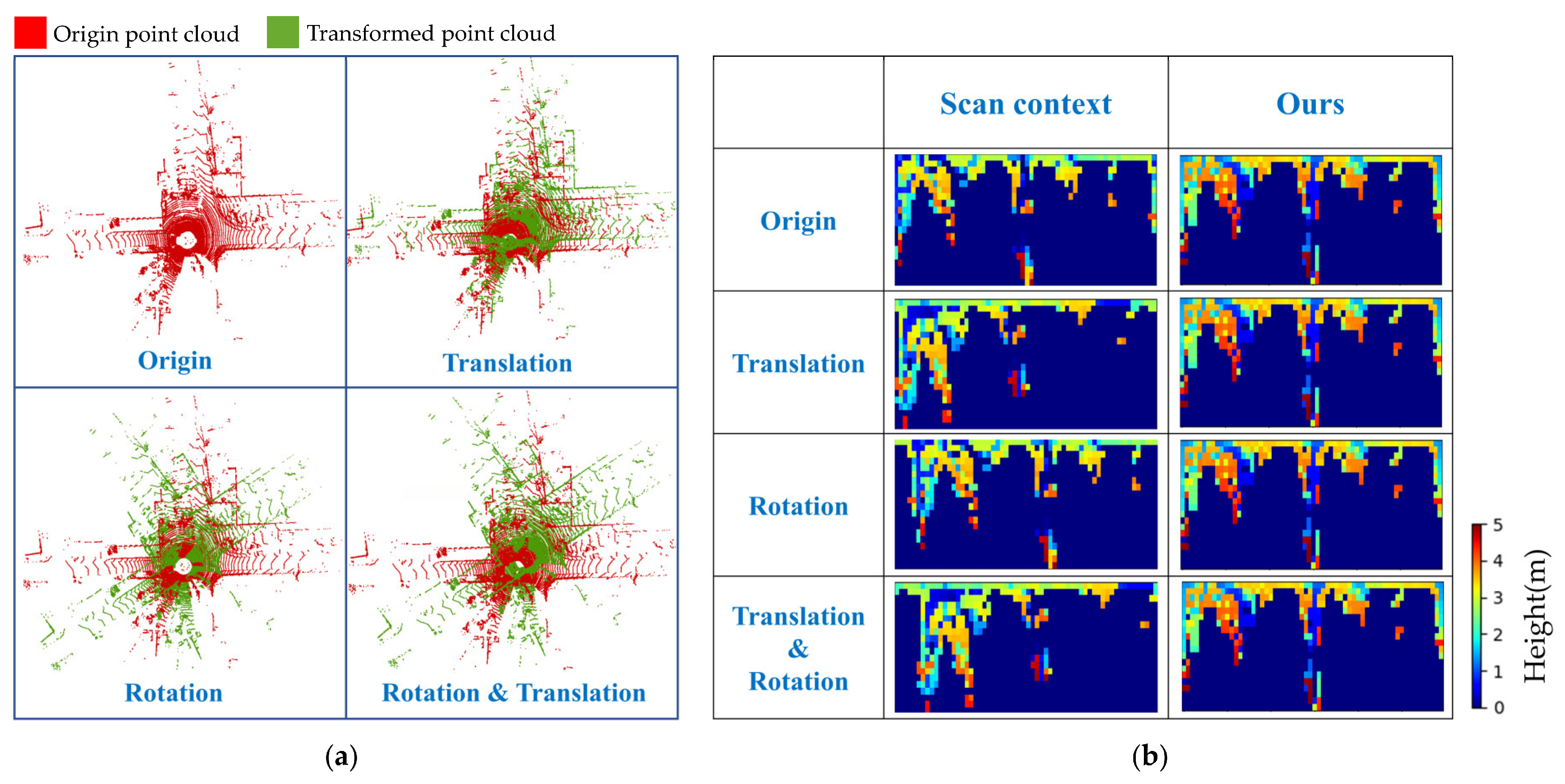
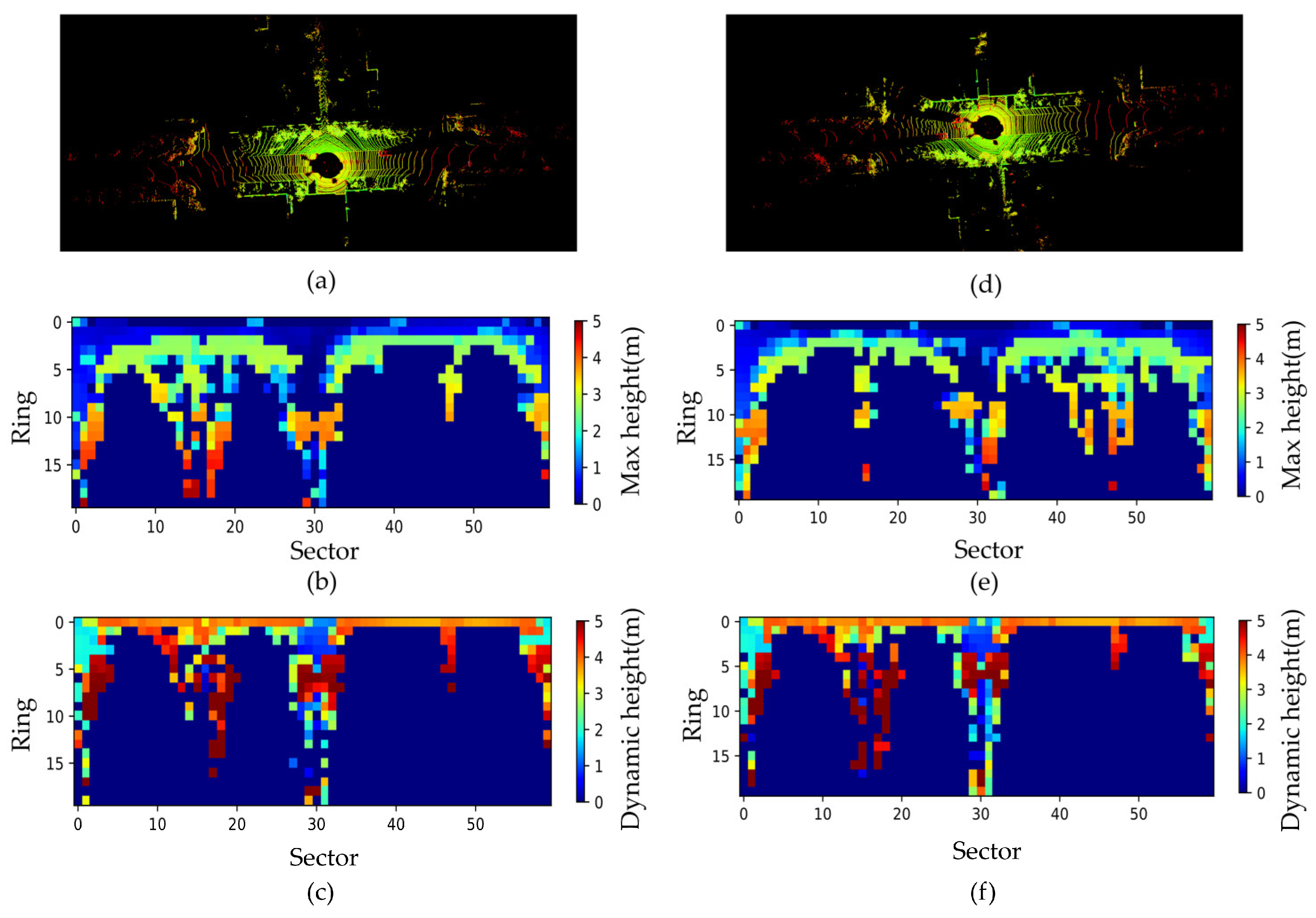




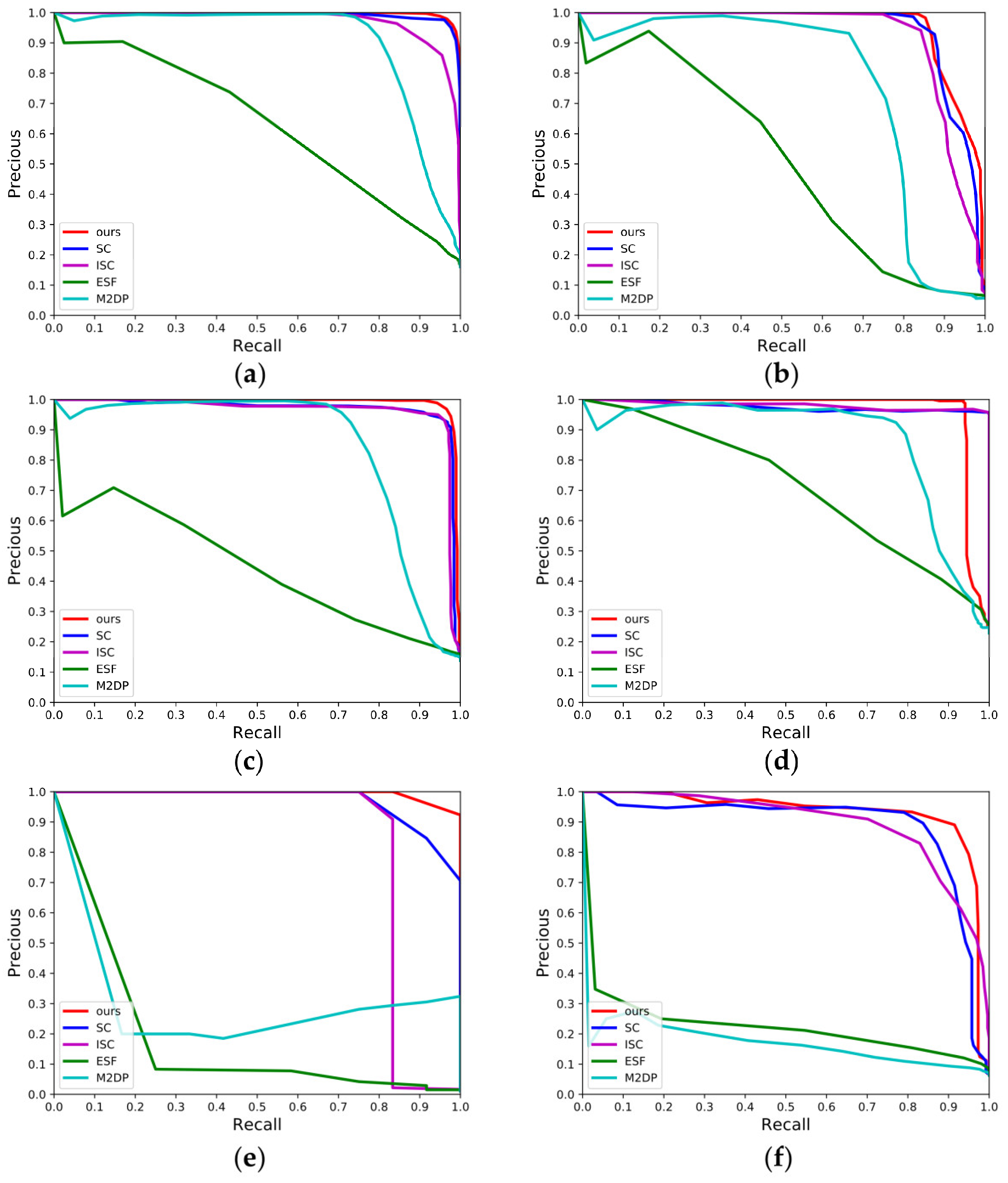
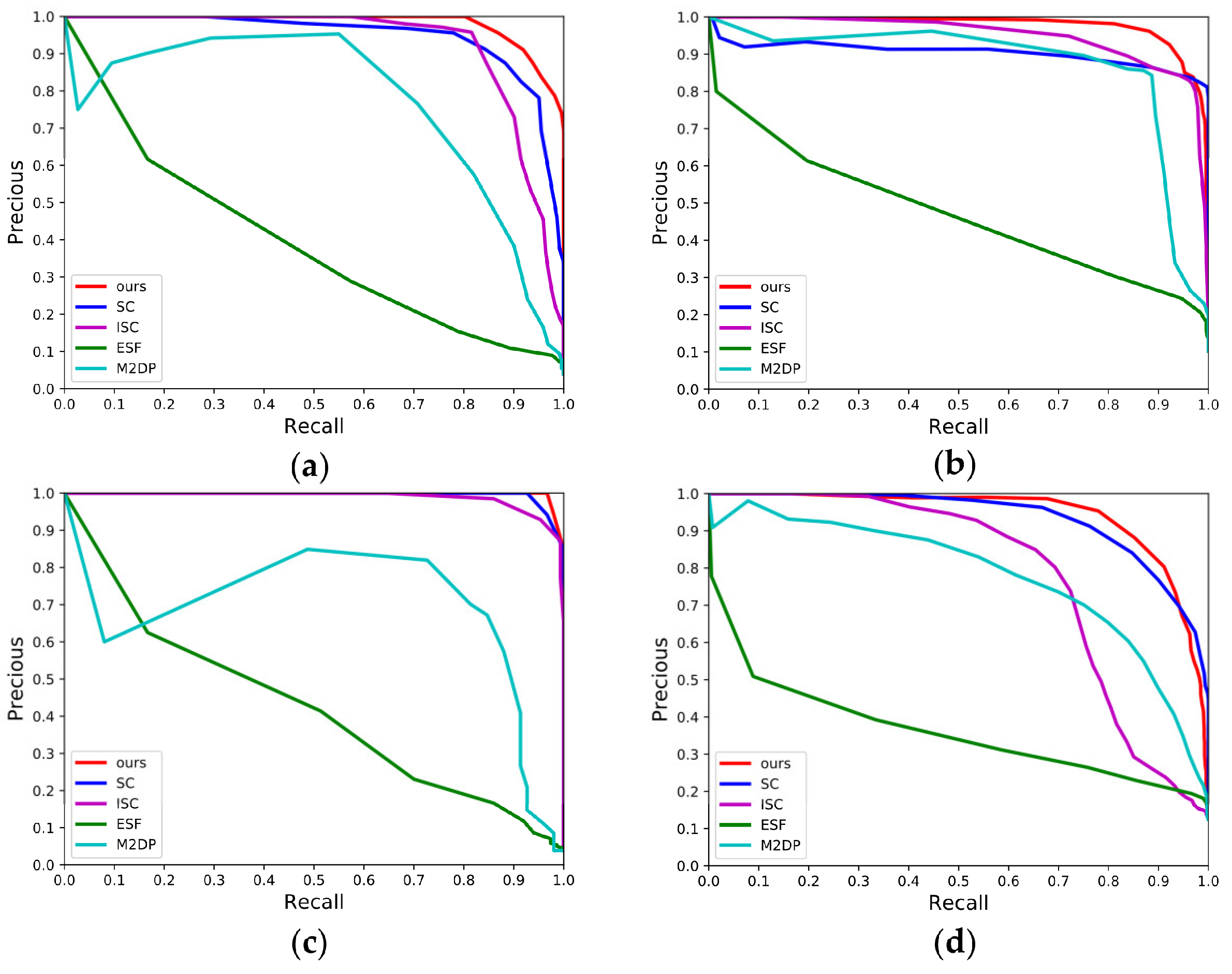

| Methods | M2DP | ESF | SC | ISC | Ours |
|---|---|---|---|---|---|
| 00 | 0.924/0.491 | 0.580/0.482 | 0.961/0.796 | 0.870/0.638 | 0.973/0.906 |
| 02 | 0.812/0.472 | 0.575/0.438 | 0.901/0.892 | 0.857/0.703 | 0.913/0.898 |
| 05 | 0.897/0.484 | 0.481/0.250 | 0.931/0.746 | 0.883/0.647 | 0.967/0.886 |
| 06 | 0.930/0.717 | 0.623/0.547 | 0.976/0.800 | 0.941/0.812 | 0.965/0.931 |
| 07 | 0.436/0.062 | 0.075/0.017 | 0.857/0.875 | 0.800/0.833 | 0.960/0.917 |
| 08 | 0.221/0.026 | 0.303/0.143 | 0.657/0.501 | 0.712/0.614 | 0.902/0.601 |
| Avg | 0.703/0.375 | 0.440/0.313 | 0.881/0.768 | 0.843/0.709 | 0.947/0.857 |
| Methods | M2DP | ESF | SC | ISC | Ours |
|---|---|---|---|---|---|
| School-01 | 0.242/0.441 | 0.365/0.300 | 0.834/0.671 | 0.801/0.671 | 0.915/0.901 |
| School-02 | 0.963/0.453 | 0.337/0.083 | 0.890/0.513 | 0.888/0.572 | 0.924/0.613 |
| School-03 | 0.767/0.243 | 0.470/0.503 | 0.965/0.967 | 0.929/0.820 | 0.983/0.983 |
| School-04 | 0.772/0.508 | 0.391/0.250 | 0.816/0.531 | 0.727/0.602 | 0.867/0.603 |
| Avg | 0.686/0.411 | 0.391/0.284 | 0.876/0.671 | 0.836/0.666 | 0.922/0.775 |
| Methods | Avg Execution Time(s/Query) | ||||
|---|---|---|---|---|---|
| M2DP | ESF | SC | ISC | Ours | |
| KITTI-00 | 0.3655 | 0.0728 | 0.0867 | 0.0697 | 0.0711 |
| KITTI-02 | 0.3871 | 0.0784 | 0.0861 | 0.0687 | 0.0675 |
| KITTI-05 | 0.3869 | 0.0785 | 0.0885 | 0.0678 | 0.0663 |
| KITTI-06 | 0.3827 | 0.0664 | 0.0846 | 0.0656 | 0.0701 |
| KITTI-07 | 0.3451 | 0.0571 | 0.0748 | 0.0608 | 0.0631 |
| KITTI-08 | 0.3628 | 0.0751 | 0.0772 | 0.0640 | 0.0618 |
| School-01 | 0.3427 | 0.0492 | 0.0608 | 0.0530 | 0.0589 |
| School-02 | 0.3468 | 0.0552 | 0.0611 | 0.0537 | 0.0502 |
| School-03 | 0.3431 | 0.0725 | 0.0604 | 0.0533 | 0.0529 |
| School-04 | 0.3455 | 0.0732 | 0.0509 | 0.0482 | 0.0479 |
| Methods | Time (ms) |
|---|---|
| MAD | 0.00480 |
| SAD | 0.00488 |
| SSD | 0.00929 |
| Ours Hamming Distance | 0.000982 |
| Ours D-Hash Generation | 0.00401 |
| Ours Total | 0.00499 |
| Methods | Avg Time (ms/Query) | |||
|---|---|---|---|---|
| MAD | SAD | SSD | Ours (D-Hash) | |
| KITTI-00 | 0.0243 | 0.0247 | 0.0467 | 0.00900 |
| KITTI-02 | 0.0241 | 0.0244 | 0.0463 | 0.00899 |
| KITTI-05 | 0.0240 | 0.0244 | 0.0464 | 0.00897 |
| KITTI-06 | 0.0240 | 0.0243 | 0.0463 | 0.00901 |
| KITTI-07 | 0.0243 | 0.0249 | 0.0468 | 0.00899 |
| KITTI-08 | 0.0239 | 0.0242 | 0.0464 | 0.00900 |
| School-01 | 0.0239 | 0.0244 | 0.0461 | 0.00897 |
| School-02 | 0.0232 | 0.0236 | 0.0467 | 0.00897 |
| School-03 | 0.0239 | 0.0241 | 0.0459 | 0.00899 |
| School-04 | 0.0242 | 0.0250 | 0.0470 | 0.00899 |
| Avg | 0.0240 | 0.0244 | 0.0465 | 0.00899 |
| Methods | M2DP | ESF | SC | ISC | Ours |
|---|---|---|---|---|---|
| KITTI-00 | 0.856/0.487 | 0.570/0.450 | 0.968/0.811 | 0.908/0.810 | 0.973/0.906 |
| KITTI-02 | 0.776/0.455 | 0.527/0.417 | 0.911/0.898 | 0.889/0.729 | 0.913/0.898 |
| KITTI-05 | 0.816/0.469 | 0.460/0.308 | 0.946/0.576 | 0.948/0.623 | 0.967/0.886 |
| KITTI-06 | 0.841/0.450 | 0.615/0.484 | 0.977/0.577 | 0.976/0.524 | 0.965/0.931 |
| KITTI-07 | 0.490/0.100 | 0.137/0.042 | 0.880/0.875 | 0.870/0.875 | 0.960/0.917 |
| KITTI-08 | 0.250/0.080 | 0.305/0.174 | 0.865/0.517 | 0.829/0.562 | 0.902/0.601 |
| School-01 | 0.735/0.375 | 0.385/0.308 | 0.914/0.707 | 0.739/0.554 | 0.915/0.901 |
| School-02 | 0.864/0.468 | 0.487/0.400 | 0.897/0.503 | 0.891/0.572 | 0.924/0.613 |
| School-03 | 0.770/0.300 | 0.458/0.313 | 0.822/0.590 | 0.799/0.507 | 0.983/0.983 |
| School-04 | 0.725/0.455 | 0.406/0.389 | 0.811/0.512 | 0.744/0.604 | 0.867/0.603 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Jiang, X.; Zhou, W.; Chen, Y.; Zhang, H. 3PCD-TP: A 3D Point Cloud Descriptor for Loop Closure Detection with Twice Projection. Remote Sens. 2023, 15, 82. https://doi.org/10.3390/rs15010082
Wang G, Jiang X, Zhou W, Chen Y, Zhang H. 3PCD-TP: A 3D Point Cloud Descriptor for Loop Closure Detection with Twice Projection. Remote Sensing. 2023; 15(1):82. https://doi.org/10.3390/rs15010082
Chicago/Turabian StyleWang, Gang, Xudong Jiang, Wei Zhou, Yu Chen, and Hao Zhang. 2023. "3PCD-TP: A 3D Point Cloud Descriptor for Loop Closure Detection with Twice Projection" Remote Sensing 15, no. 1: 82. https://doi.org/10.3390/rs15010082
APA StyleWang, G., Jiang, X., Zhou, W., Chen, Y., & Zhang, H. (2023). 3PCD-TP: A 3D Point Cloud Descriptor for Loop Closure Detection with Twice Projection. Remote Sensing, 15(1), 82. https://doi.org/10.3390/rs15010082








