CSANet: Cross-Scale Axial Attention Network for Road Segmentation
Abstract
1. Introduction
- A novel deep model is proposed for road segmentation, which adopts a global attention mechanism to exploit the long dependence.
- Our proposed method is able to capture dense contextual information and better combine features at different scales. This results in more accurate road segmentation results.
- The proposed method consumes less computing resources than most other networks.
2. Related Work
2.1. None-Local Network
2.2. Axial Attention
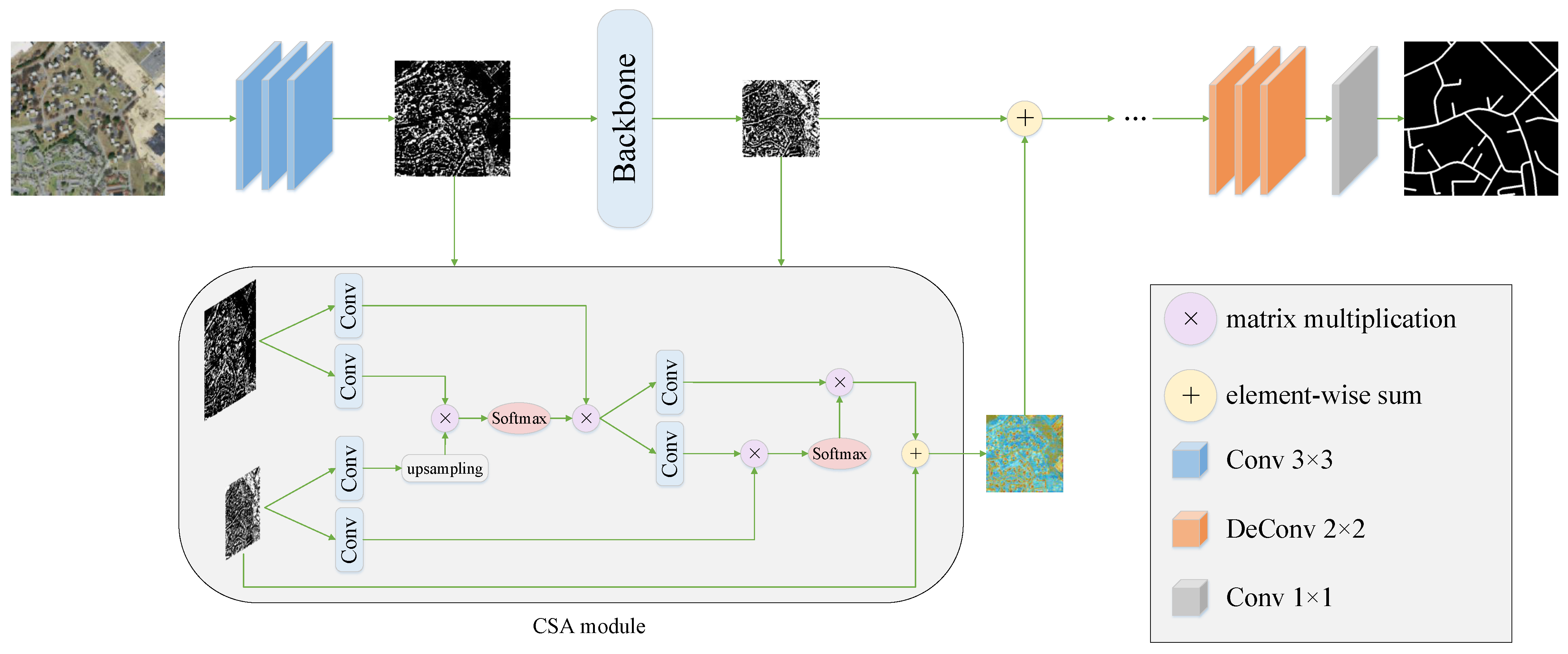
3. Method
3.1. Overall Network Framework
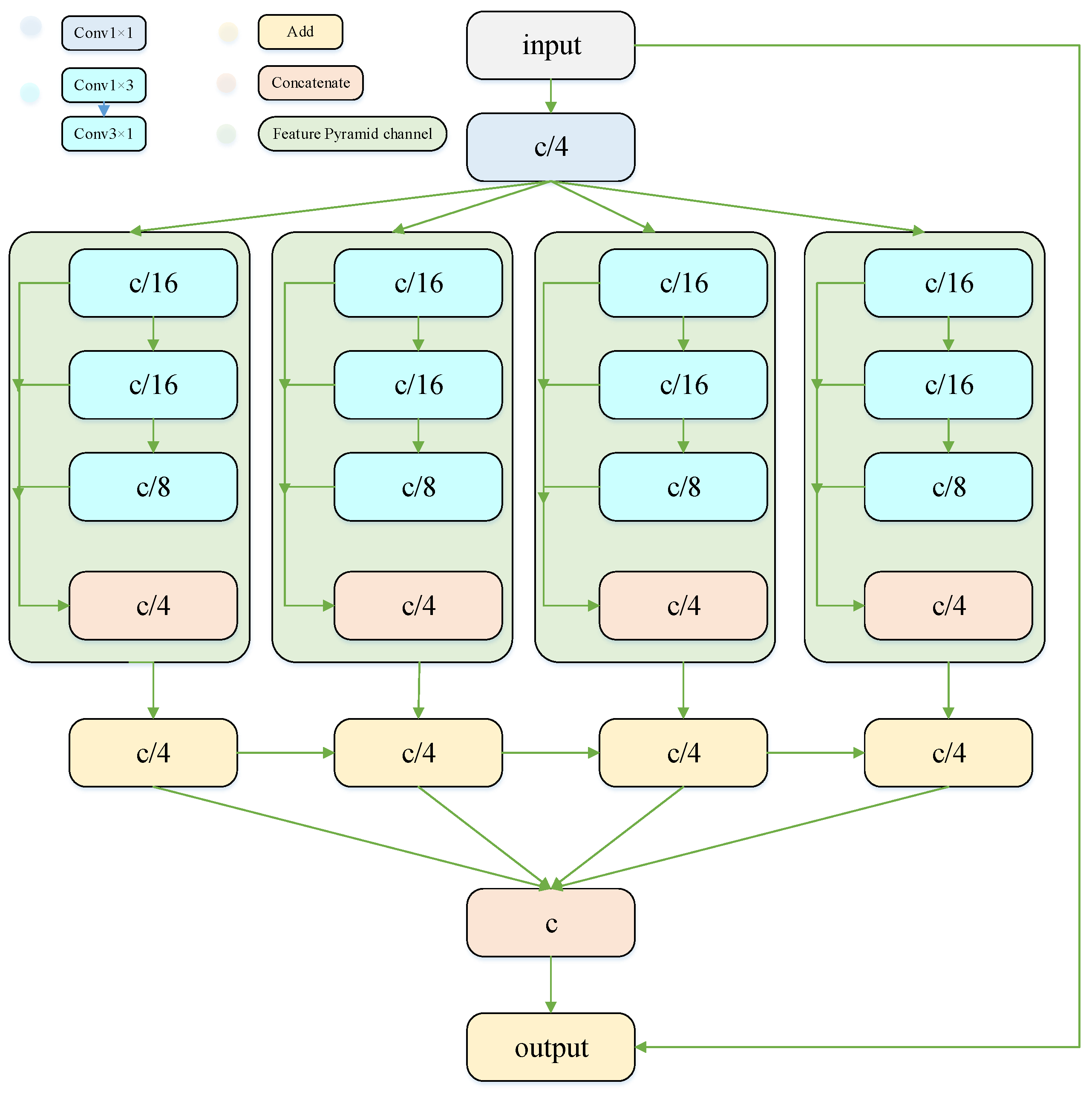
3.2. Backbone
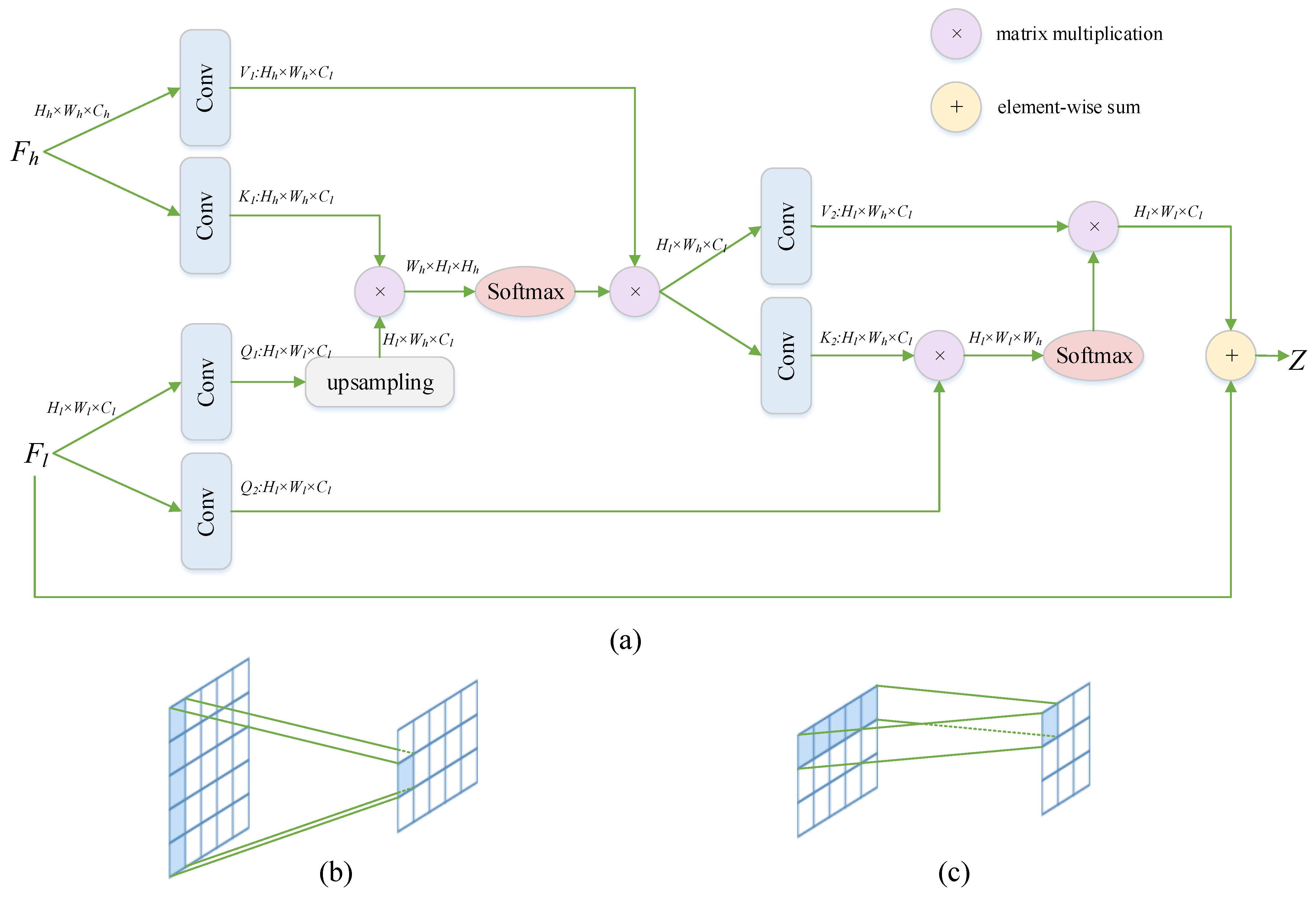
3.3. CSANet
4. Experiments
4.1. Datasets
4.1.1. Massachusetts Roads Dataset
4.1.2. DeepGlobe Dataset
4.2. Implementation Details
4.3. Metrics
5. Results
5.1. Comparison with Other Classic Methods
- 1.
- UNet [42]: This method adopts an encoder–decoder structure and captures local information through small convolution kernels. In the decoder part, the corresponding encoder features and decoder features are concatenated and the resolution is gradually recovered through a deconvolution operation.
- 2.
- SegNet [43]: SegNet captures local information by stacking convolutional layers, and a lot of convolution operations and unpooling are used to restore the resolution in the decoder part.
- 3.
- PSPNet [44]: The PSPNet method is based on multiscale feature fusion and introduces more contextual features through a global mean pooling operation. It downsamples features to different scales and reduces the feature dimension through 1 × 1 convolutional layers.
- 4.
- ENet [45]: ENet increases the receptive field by atrous convolution and reduces information loss effectively by combining downsampling and pooling.
- 5.
- DeepLabv3 [46]: This method captures multiscale information with parallel atrous convolution at different sampling rates through the Atrous Spatial Pyramid Pooling (ASPP) module.
- 6.
- CFPNet [36]: CFPNet expands the receptive field with a small number of parameters through parallel asymmetric atrous convolution.
5.2. Segmentation Results on Massachusetts Roads Dataset
5.3. Segmentation Results on DeepGlobe Dataset
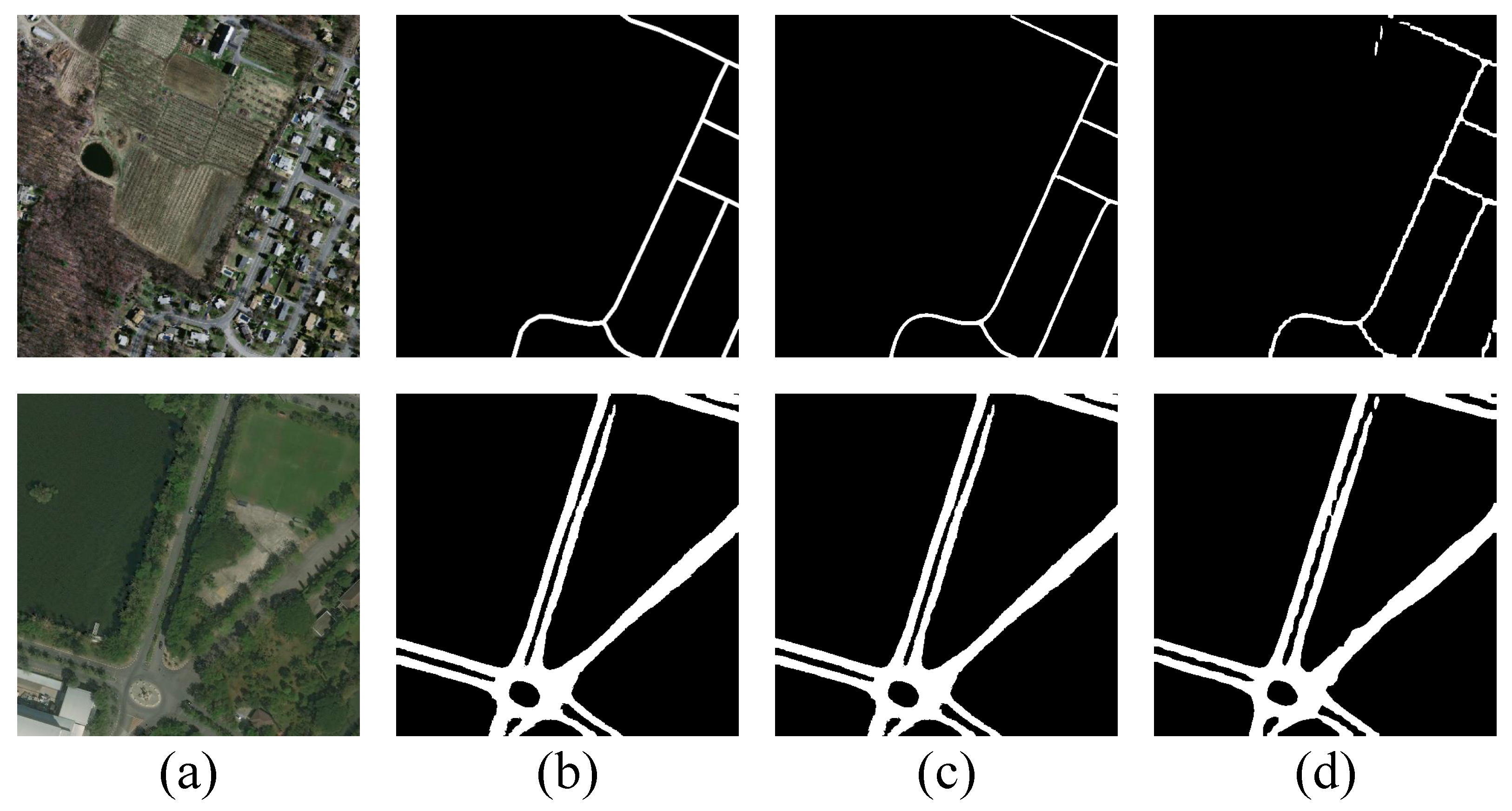
5.4. Segmentation Maps
5.5. Ablation Studies
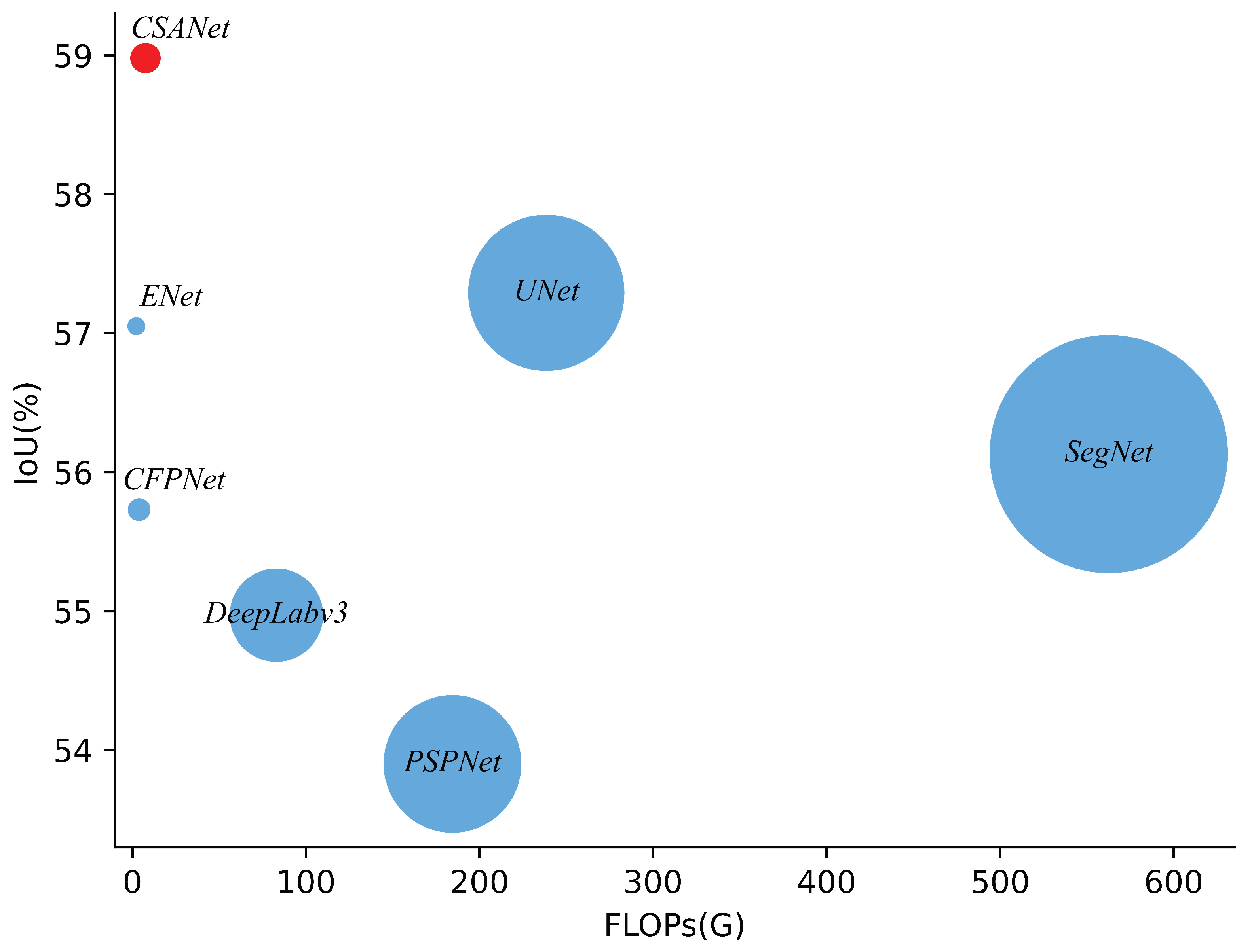
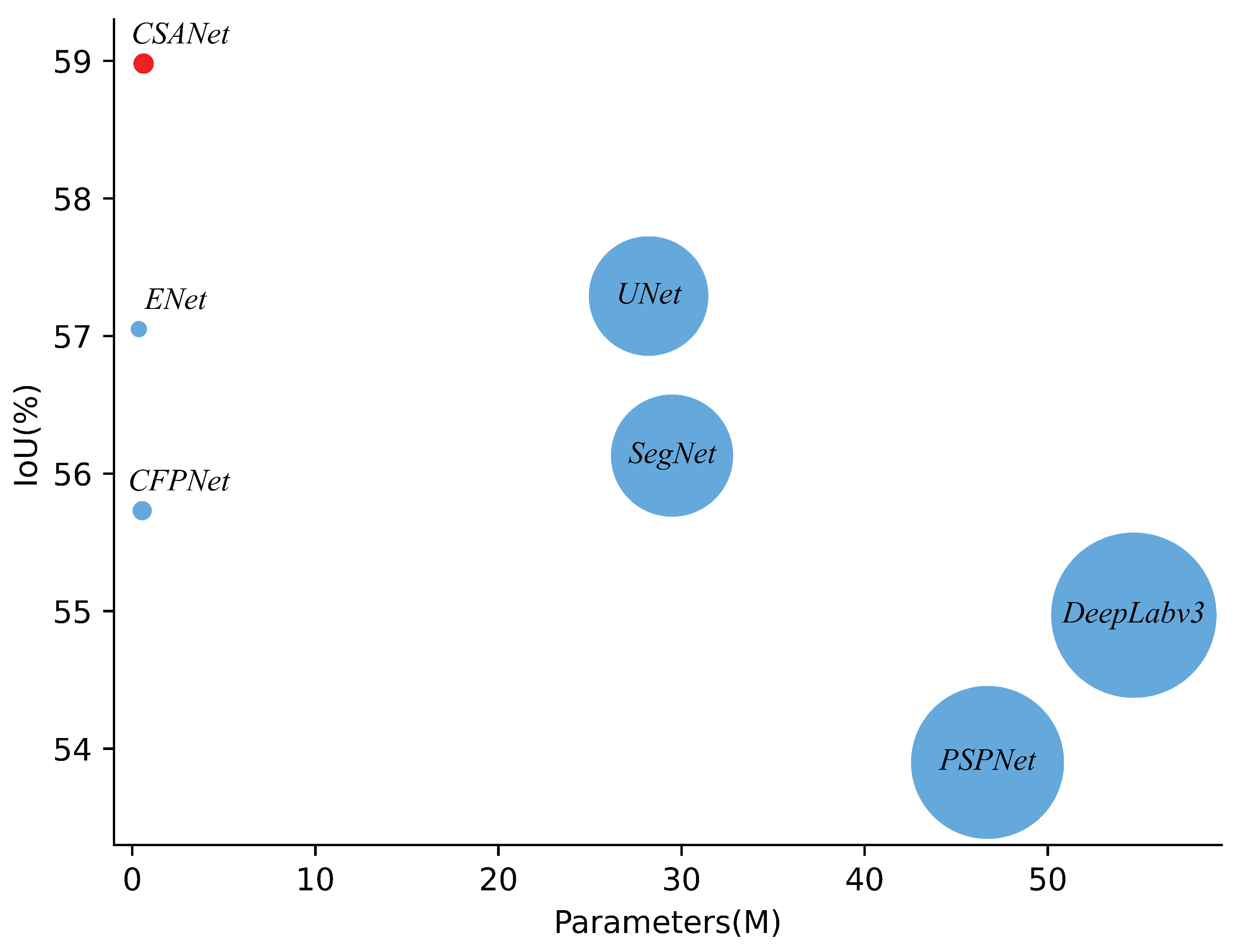
5.6. Computational Complexity Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, Z.; Sun, Y.; Liu, M. icurb: Imitation learning-based detection of road curbs using aerial images for autonomous driving. IEEE Robot. Autom. Lett. 2021, 6, 1097–1104. [Google Scholar] [CrossRef]
- Xu, Z.; Sun, Y.; Liu, M. Topo-boundary: A benchmark dataset on topological road-boundary detection using aerial images for autonomous driving. IEEE Robot. Autom. Lett. 2021, 6, 7248–7255. [Google Scholar] [CrossRef]
- Steger, C.; Glock, C.; Eckstein, W.; Mayer, H.; Radig, B. Model-based road extraction from images. In Automatic Extraction of Man-Made Objects from Aerial and Space Images; Springer: Berlin/Heidelberg, Germany, 1995; pp. 275–284. [Google Scholar]
- Sghaier, M.O.; Lepage, R. Road extraction from very high resolution remote sensing optical images based on texture analysis and beamlet transform. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 9, 1946–1958. [Google Scholar] [CrossRef]
- Máttyus, G.; Luo, W.; Urtasun, R. Deeproadmapper: Extracting road topology from aerial images. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 3438–3446. [Google Scholar]
- Batra, A.; Singh, S.; Pang, G.; Basu, S.; Jawahar, C.; Paluri, M. Improved road connectivity by joint learning of orientation and segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–17 June 2019; pp. 10385–10393. [Google Scholar]
- Mosinska, A.; Marquez-Neila, P.; Koziński, M.; Fua, P. Beyond the pixel-wise loss for topology-aware delineation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3136–3145. [Google Scholar]
- Zhou, G.; Chen, W.; Gui, Q.; Li, X.; Wang, L. Split Depth-wise Separable Graph-Convolution Network for Road Extraction in Complex Environments from High-resolution Remote-Sensing Images. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5614115. [Google Scholar] [CrossRef]
- Lan, M.; Zhang, Y.; Zhang, L.; Du, B. Global context based automatic road segmentation via dilated convolutional neural network. Inf. Sci. 2020, 535, 156–171. [Google Scholar] [CrossRef]
- Tao, C.; Qi, J.; Li, Y.; Wang, H.; Li, H. Spatial information inference net: Road extraction using road-specific contextual information. ISPRS J. Photogramm. Remote Sens. 2019, 158, 155–166. [Google Scholar] [CrossRef]
- Henry, C.; Azimi, S.M.; Merkle, N. Road segmentation in SAR satellite images with deep fully convolutional neural networks. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1867–1871. [Google Scholar] [CrossRef]
- Shamsolmoali, P.; Zareapoor, M.; Zhou, H.; Wang, R.; Yang, J. Road segmentation for remote sensing images using adversarial spatial pyramid networks. IEEE Trans. Geosci. Remote Sens. 2020, 59, 4673–4688. [Google Scholar] [CrossRef]
- Li, Y.; Xu, L.; Rao, J.; Guo, L.; Yan, Z.; Jin, S. A Y-Net deep learning method for road segmentation using high-resolution visible remote sensing images. Remote Sens. Lett. 2019, 10, 381–390. [Google Scholar] [CrossRef]
- Yu, F.; Koltun, V. Multi-scale context aggregation by dilated convolutions. arXiv 2015, arXiv:1511.07122. [Google Scholar]
- Wegner, J.D.; Montoya-Zegarra, J.A.; Schindler, K. A higher-order CRF model for road network extraction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 1698–1705. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 1–11. [Google Scholar]
- Wang, X.; Girshick, R.; Gupta, A.; He, K. Non-local neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7794–7803. [Google Scholar]
- Mnih, V. Machine Learning for Aerial Image Labeling; University of Toronto: Toronto, ON, Canada, 2013. [Google Scholar]
- Demir, I.; Koperski, K.; Lindenbaum, D.; Pang, G.; Huang, J.; Basu, S.; Hughes, F.; Tuia, D.; Raskar, R. Deepglobe 2018: A challenge to parse the earth through satellite images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 172–181. [Google Scholar]
- Hou, S.; Shi, H.; Cao, X.; Zhang, X.; Jiao, L. Hyperspectral Imagery Classification Based on Contrastive Learning. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5521213. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Wang, L.; Li, R.; Zhang, C.; Fang, S.; Duan, C.; Meng, X.; Atkinson, P.M. UNetFormer: A UNet-like transformer for efficient semantic segmentation of remote sensing urban scene imagery. ISPRS J. Photogramm. Remote Sens. 2022, 190, 196–214. [Google Scholar] [CrossRef]
- Fu, J.; Liu, J.; Tian, H.; Li, Y.; Bao, Y.; Fang, Z.; Lu, H. Dual attention network for scene segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3146–3154. [Google Scholar]
- Zhao, H.; Zhang, Y.; Liu, S.; Shi, J.; Loy, C.C.; Lin, D.; Jia, J. Psanet: Point-wise spatial attention network for scene parsing. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 267–283. [Google Scholar]
- Yuan, Y.; Huang, L.; Guo, J.; Zhang, C.; Chen, X.; Wang, J. Ocnet: Object context network for scene parsing. arXiv 2018, arXiv:1809.00916. [Google Scholar]
- Yu, C.; Wang, J.; Peng, C.; Gao, C.; Yu, G.; Sang, N. Learning a discriminative feature network for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1857–1866. [Google Scholar]
- Cao, Y.; Xu, J.; Lin, S.; Wei, F.; Hu, H. Gcnet: Non-local networks meet squeeze-excitation networks and beyond. In Proceedings of the IEEE/CVF International Conference on Computer Vision Workshops, Seoul, Korea, 27–28 October 2019. [Google Scholar]
- Chi, L.; Yuan, Z.; Mu, Y.; Wang, C. Non-local neural networks with grouped bilinear attentional transforms. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11804–11813. [Google Scholar]
- Yin, M.; Yao, Z.; Cao, Y.; Li, X.; Zhang, Z.; Lin, S.; Hu, H. Disentangled non-local neural networks. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 191–207. [Google Scholar]
- Wang, H.; Zhu, Y.; Green, B.; Adam, H.; Yuille, A.; Chen, L.C. Axial-deeplab: Stand-alone axial-attention for panoptic segmentation. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 108–126. [Google Scholar]
- Huang, Z.; Wang, X.; Huang, L.; Huang, C.; Wei, Y.; Liu, W. Ccnet: Criss-cross attention for semantic segmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 603–612. [Google Scholar]
- Hou, Q.; Zhou, D.; Feng, J. Coordinate attention for efficient mobile network design. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 13713–13722. [Google Scholar]
- Luu, H.M.; Park, S.H. Extending nn-UNet for brain tumor segmentation. arXiv 2021, arXiv:2112.04653. [Google Scholar]
- Valanarasu, J.M.J.; Oza, P.; Hacihaliloglu, I.; Patel, V.M. Medical transformer: Gated axial-attention for medical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Strasbourg, France, 27 September–1 October 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 36–46. [Google Scholar]
- Lou, A.; Guan, S.; Loew, M. CaraNet: Context Axial Reverse Attention Network for Segmentation of Small Medical Objects. arXiv 2021, arXiv:2108.07368. [Google Scholar]
- Lou, A.; Loew, M. Cfpnet: Channel-wise feature pyramid for real-time semantic segmentation. In Proceedings of the 2021 IEEE International Conference on Image Processing (ICIP), Virtual, 19–22 September 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1894–1898. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 2818–2826. [Google Scholar]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A.A. Inception-v4, inception-resnet and the impact of residual connections on learning. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Mnih, V.; Hinton, G.E. Learning to label aerial images from noisy data. In Proceedings of the 29th International Conference on Machine Learning (ICML-12), Edinburgh, Scotland, 26 June–1 July 2012; pp. 567–574. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. Segnet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid scene parsing network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2881–2890. [Google Scholar]
- Paszke, A.; Chaurasia, A.; Kim, S.; Culurciello, E. Enet: A deep neural network architecture for real-time semantic segmentation. arXiv 2016, arXiv:1606.02147. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Schroff, F.; Adam, H. Rethinking atrous convolution for semantic image segmentation. arXiv 2017, arXiv:1706.05587. [Google Scholar]



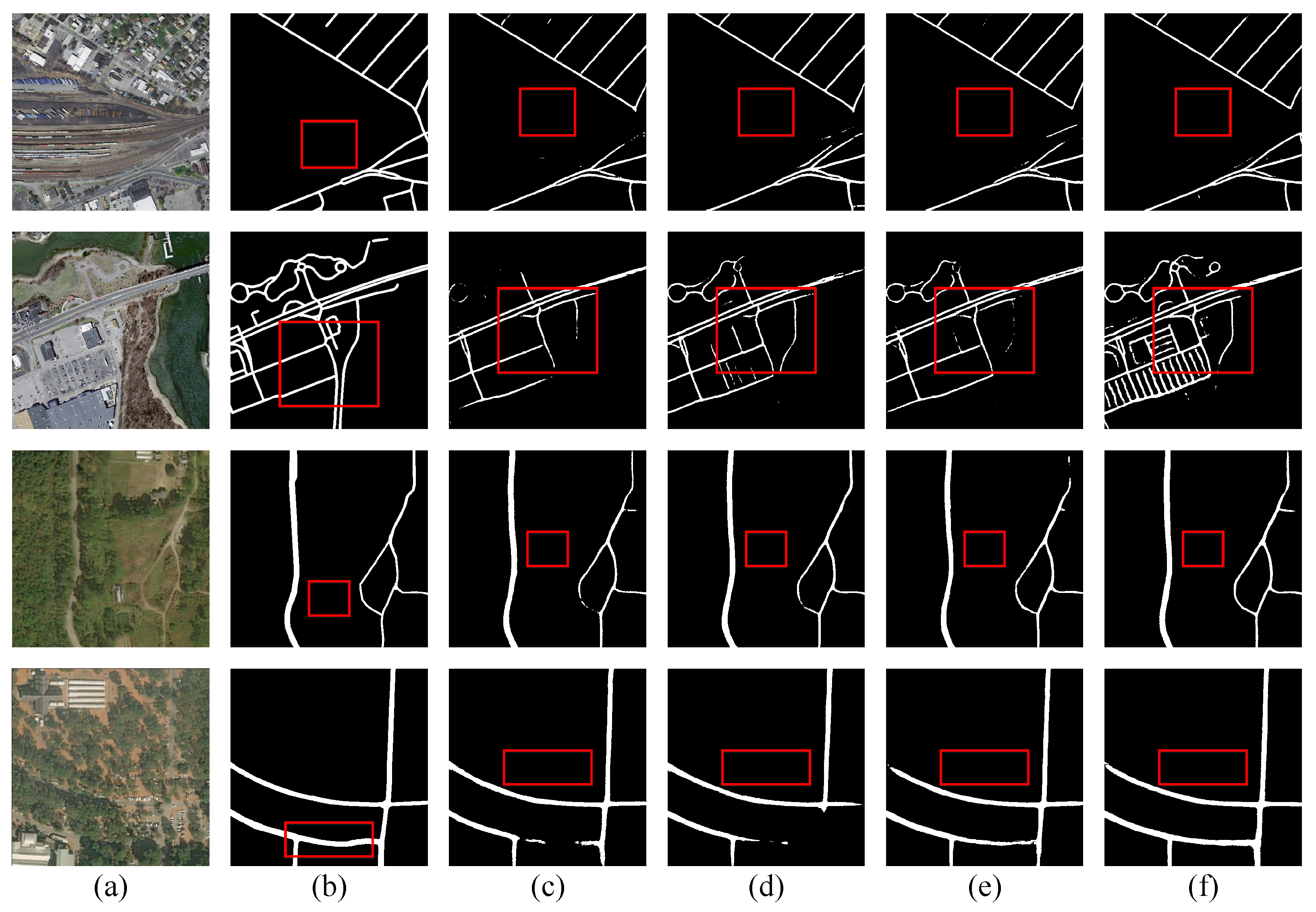
| Method | Recall | Precision | IoU | IoU | Accuracy | F1 |
|---|---|---|---|---|---|---|
| Unet [42] | 68.15 | 78.23 | 57.29 | 84.49 | 98.06 | 72.84 |
| Enet [45] | 66.08 | 80.68 | 57.05 | 84.57 | 97.10 | 72.65 |
| DeepLabv3 [46] | 66.57 | 75.93 | 54.97 | 83.69 | 97.92 | 70.95 |
| CFPNet [36] | 67.73 | 75.89 | 55.73 | 85.10 | 97.94 | 71.57 |
| SegNet [43] | 66.47 | 78.30 | 56.13 | 82.84 | 98.02 | 71.90 |
| PSPNet [44] | 66.19 | 74.37 | 53.90 | 85.14 | 97.84 | 70.04 |
| CSANet | 69.14 | 80.05 | 58.98 | 84.95 | 98.16 | 74.20 |
| Method | Recall | Precision | IoU | IoU | Accuracy | F1 |
|---|---|---|---|---|---|---|
| Unet [42] | 57.23 | 78.15 | 49.33 | 69.15 | 98.48 | 66.07 |
| Enet [45] | 54.50 | 79.09 | 47.64 | 69.35 | 97.43 | 64.53 |
| DeepLabv3 [46] | 76.08 | 78.65 | 63.06 | 83.14 | 98.09 | 77.34 |
| CFPNet [36] | 76.25 | 80.78 | 64.54 | 83.90 | 98.20 | 78.45 |
| SegNet [43] | 61.01 | 74.40 | 50.43 | 67.18 | 97.43 | 67.04 |
| PSPNet [44] | 69.38 | 77.86 | 57.95 | 77.86 | 97.84 | 73.38 |
| CSANet | 75.05 | 83.37 | 65.28 | 84.17 | 98.29 | 78.99 |
| No. | CSA-1 | CSA-2 | Recall | Precision | IoU | F1 |
|---|---|---|---|---|---|---|
| 1 | 67.32 | 79.5 | 57.36 | 72.9 | ||
| 2 | ✓ | 68.67 | 79.96 | 58.59 | 73.89 | |
| 3 | ✓ | 67.86 | 79.85 | 57.94 | 73.37 | |
| 4 | ✓ | ✓ | 69.14 | 80.05 | 58.98 | 74.20 |
| No. | CSA-1 | CSA-2 | Recall | Precision | IoU | F1 |
|---|---|---|---|---|---|---|
| 1 | 73.97 | 83.38 | 64.46 | 78.39 | ||
| 2 | ✓ | 74.54 | 83.49 | 64.96 | 78.76 | |
| 3 | ✓ | 74.06 | 83.28 | 64.48 | 78.40 | |
| 4 | ✓ | ✓ | 75.05 | 83.37 | 65.28 | 78.99 |
| Method | IoU | Param | FLOPs |
|---|---|---|---|
| UNet | 57.29 | 28.2 M | 238.53 G |
| ENet | 57.05 | 0.36 M | 2.25 G |
| DeepLabv3 | 54.97 | 54.7 M | 82.98 G |
| CFPNet | 55.73 | 0.54 M | 3.89 G |
| SegNet | 56.13 | 29.48 M | 562.56 G |
| PSPNet | 53.90 | 46.71 M | 184.44 G |
| CSANet | 58.98 | 0.62 M | 7.55 G |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, X.; Zhang, K.; Jiao, L. CSANet: Cross-Scale Axial Attention Network for Road Segmentation. Remote Sens. 2023, 15, 3. https://doi.org/10.3390/rs15010003
Cao X, Zhang K, Jiao L. CSANet: Cross-Scale Axial Attention Network for Road Segmentation. Remote Sensing. 2023; 15(1):3. https://doi.org/10.3390/rs15010003
Chicago/Turabian StyleCao, Xianghai, Kai Zhang, and Licheng Jiao. 2023. "CSANet: Cross-Scale Axial Attention Network for Road Segmentation" Remote Sensing 15, no. 1: 3. https://doi.org/10.3390/rs15010003
APA StyleCao, X., Zhang, K., & Jiao, L. (2023). CSANet: Cross-Scale Axial Attention Network for Road Segmentation. Remote Sensing, 15(1), 3. https://doi.org/10.3390/rs15010003





