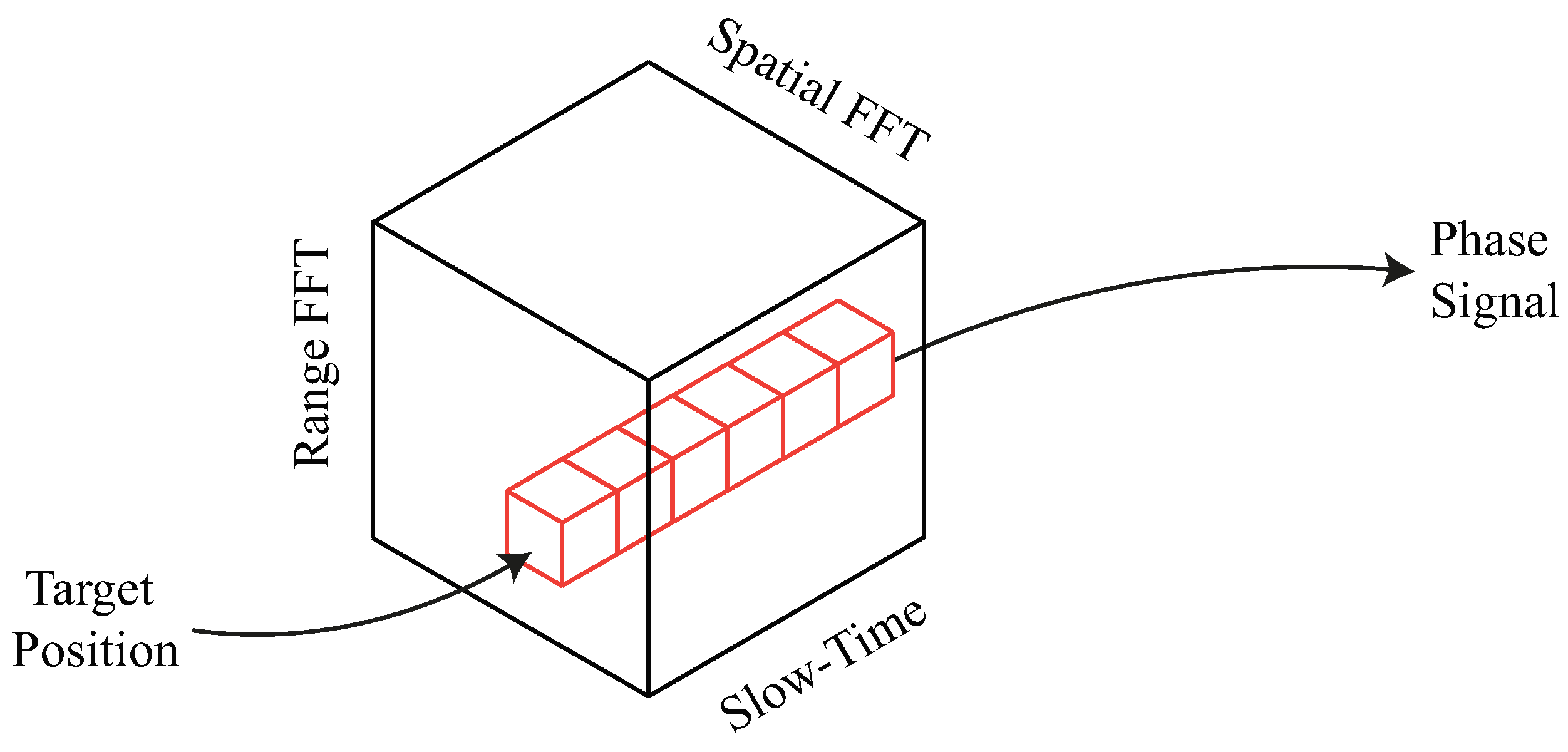
1. Introduction
The industry of drones, also known as Unmanned Aerial Vehicles (UAVs), has rapidly grown in recent years, as drones make various applications easier, such as commercial delivery or mapping search and rescue operations [
1,
2,
3]. UAVs are extensively used also in research, especially in contexts where they can speed up massive data collection and reduce the workload of the research teams. Advances in the field of drone technology, such as efficient algorithms to avoid obstacles and increased battery lifetime, joined with optimized structural design, allow to control the UAV beyond the visual line of sight, enabling the autopilot-based control and navigation functionalities not only in military scenarios but also for civil applications [
4]. Unfortunately, however, as with any other kind of technology, drones may represent a potential threat to the community or the environment because of intentional illicit use or unintentional events that may happen. Ensuring the safety of the air space in the presence of drones is the biggest problem due to the risk of injuries that drones can bring to the general public. The potential use of UAVs for terrorist attacks against infrastructures and soft targets is a growing concern for those in charge of keeping cities and outdoor spaces safe, being drone technology nowadays globally available. On the other hand, even when used for benefit, drone-related accidents may happen: the drone can be a victim of jamming, or someone can try to override the control of the legitimate pilot [
5,
6,
7,
8].
Among the possible methods and techniques to detect drones and gather information about their characteristics and flight dynamics, radar signals can be used both for detection and classification purposes [
9]. By exploiting the radar technology, it is possible not only to measure the drones’ velocity or distance but also to estimate their physical dimensions, for example by measuring their Radar Cross-Section (RCS) [
10,
11]. Additionally, the micro-Doppler component of the radar signal reflected by a drone can be properly extracted and processed to detect and classify different types of UAVs [
12] as well as their characteristics (such as physical dimensions, number and type of drone propellers), eventually supported by the help of Machine Learning (ML) algorithms [
13,
14,
15,
16]. Measuring the propeller’s rotational speed of a radar-detected UAV can provide useful information to better understand the characteristics of the drone being detected. This is a very challenging task, and different approaches have been proposed to solve it. In [
17], the authors present a method based on the analysis of the Doppler produced by the propellers, and they suggest the same technique can also allow us to measure the propeller’s length. The proposed method is very interesting, but the radar system used is a Continuous Wave Radar, and due to the fact that more than one single target can be present in the reference scenario, the approach can be very difficult to use in practical applications. Even in [
18], a technique to measure the propeller’s dimensions and speed is proposed, which is based on the use not of a radar system but of a Lidar system. The problem with this method is the low speed of the propeller under test, which is equal to four rounds per second (corresponding to 240 rounds per minute (RPM)). A different approach is based on optical cameras: the image processing method proposed in [
19] aims to extract the rotational speed of the propellers. In this case, the limitation of the method is related to the maximum allowable distance of the target, which is constrained, in its turn, by the technical characteristics of the camera optical sensor.
Radar-based detection is one of the best options to measure the propellers’ rotational speed if the UAV is far away from the sensor, and recent works developed and extended this approach from a static target to a moving one [
20,
21]. As a matter of fact, for drones equipped with propellers, information about their rotational speed may help in understanding if the UAV is carrying some kind of potentially harmful load. This is an important task if the radar system is employed to monitor the air space and detect any threats, as armed drones can be used in terrorist attacks or military situations. To this aim, in [
15], the authors try to analyze the micro-Doppler effect generated by the propellers’ rotation to understand whether the detected UAV is carrying some weight or payload.
Differently from the mentioned approach, this paper presents a radar-based processing method to indirectly measure the propeller’s speed by analyzing the phase of the beat signal generated by the propeller vibration and propagating to the drone chassis. Laboratory experiments have been carried out to test the proposed approach, and the obtained results are promising.
The rest of the paper is organized as follows.
Section 2 briefly presents how to measure and detect vibrations with a radar sensor, and in
Section 3, the proposed experimental setup and signal processing technique applied to the radar signal are described.
Section 4 and
Section 5 presents the performed experimental activity and the obtained results, and finally,
Section 6 provides some conclusive remarks and highlights possible future research developments.
2. Vibration Detection with Radar
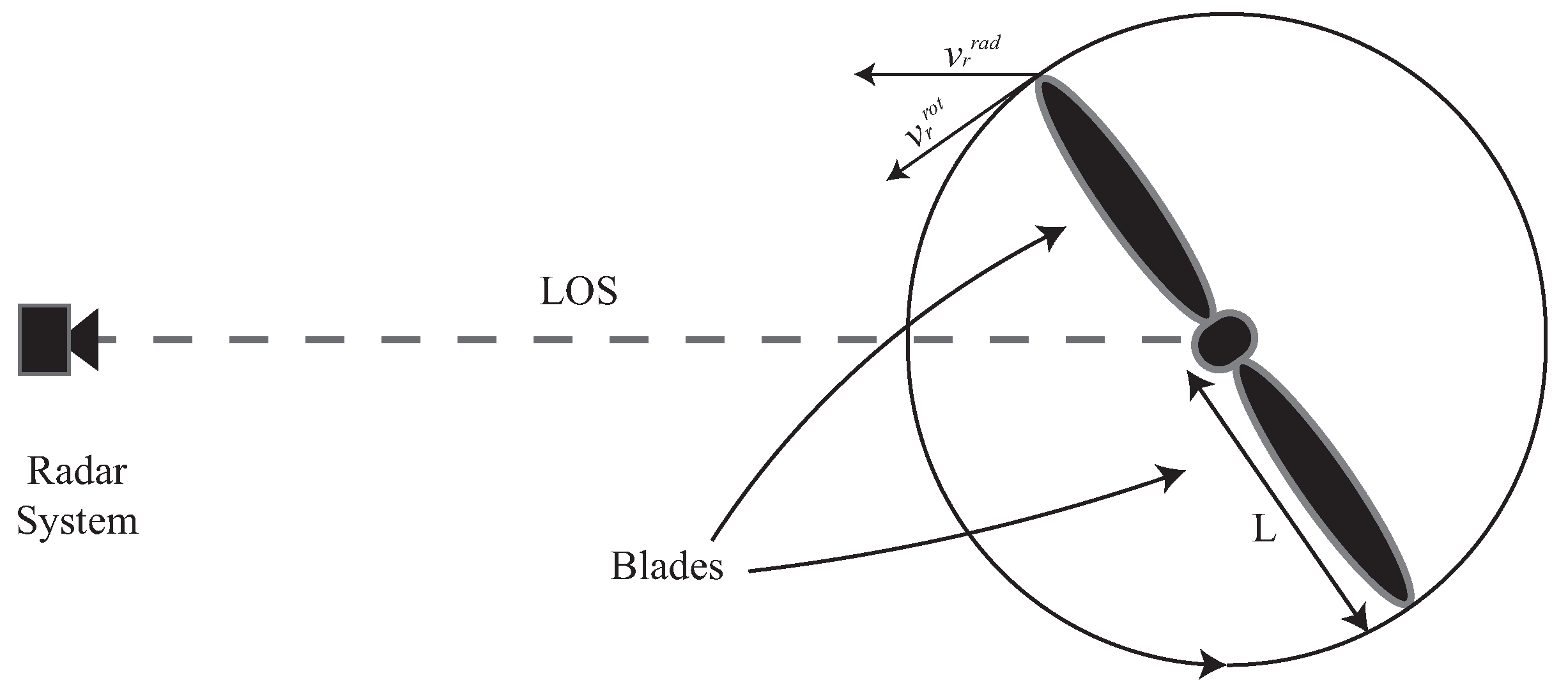
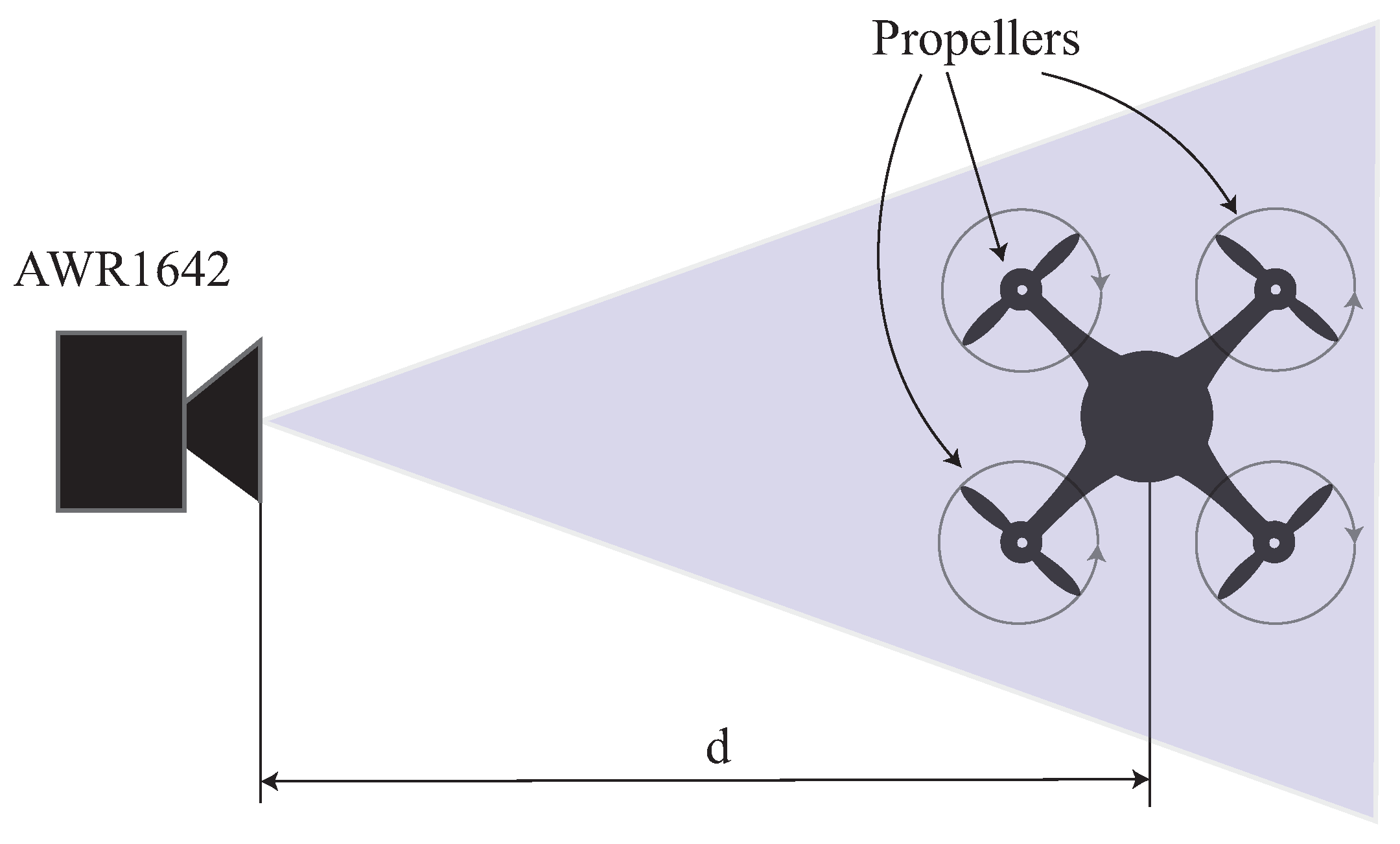
Measuring the rotational speed of a propeller is a very difficult task to perform with the common Doppler approach. A simple scheme of how to implement this operation by exploiting the Doppler effect is depicted in
Figure 1.
Assuming that the propeller merely rotates and does not translate, the only Doppler component produced by the rotation is the micro-Doppler one. The Doppler shift produced by the rotation of the propeller is directly related to the rotational speed; by measuring the former term, it is possible to obtain the latter, but to this aim, the length of the propeller
L is a necessary piece of information [
22]. For a better understanding of radar characteristics that can be exploited to measure the rotational speed, some analyses based on real components of commercial drones can be performed.
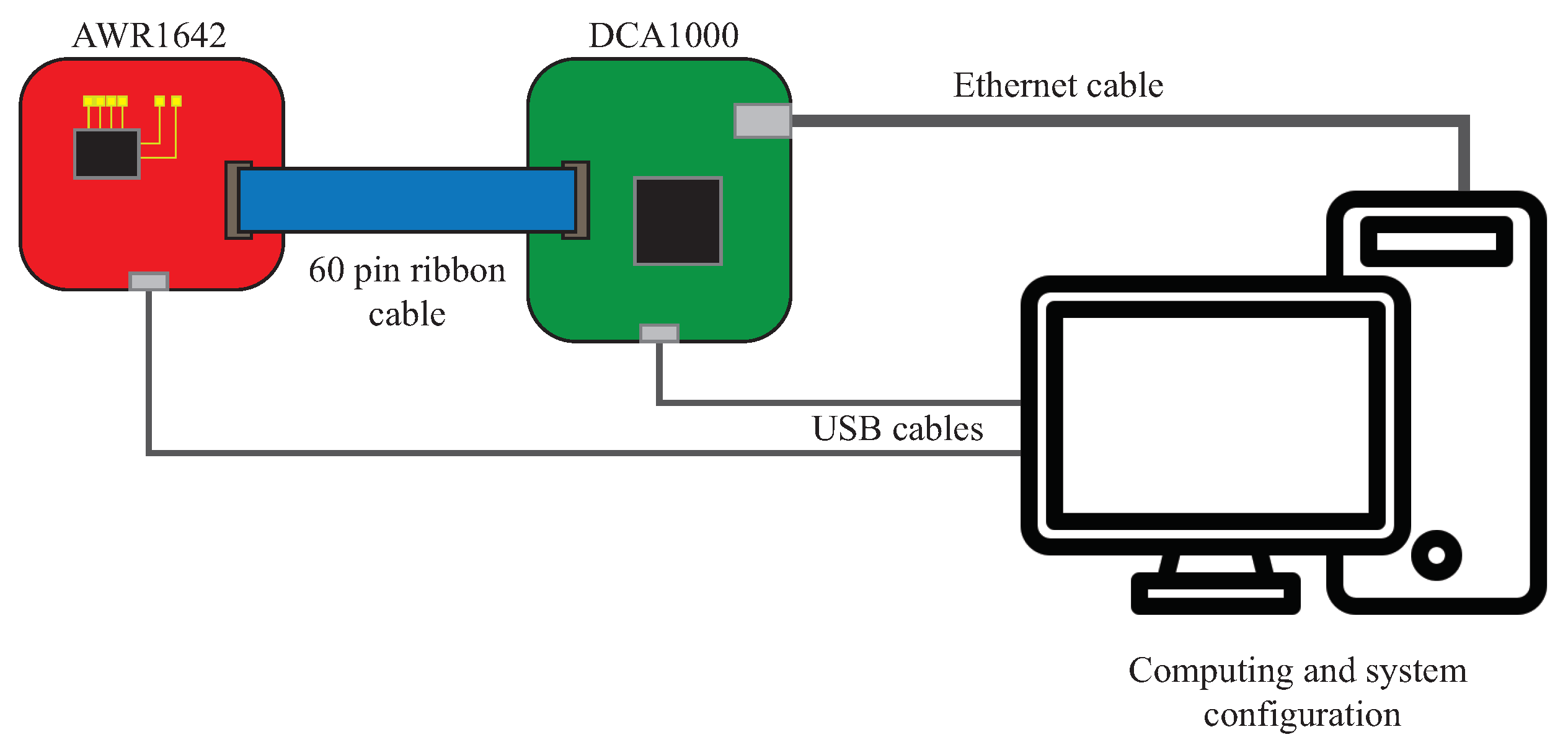
The frame of the drone used in this work has a longitudinal dimension of 45 cm, and the two-blades propellers have a 20 cm long diameter. The drone is equipped with four motors featuring
= 1000 RPM/V, meaning that they can rotate at 1000 Rounds Per Minute (RPM) for each 1 V of supplied battery voltage. In this case, an 11 V battery is used, so a maximum rotational speed of 11,000 RPM can be obtained. From these values, it is possible to compute the maximum Doppler shift generated by the propellers as follows:
where
is the maximum Doppler shift given in Hz,
is the radial velocity measured in m/s,
represents the radar signal wavelength measured in m,
L is half the diameter of the propellers given in m,
c is the speed of light in m/s, and
is the rotational velocity expressed in RPM. For example, if we consider a propeller with a diameter of 20 cm at 11,100 RPM, the Doppler shift is
= 58,100 Hz. To measure this rotational velocity, the radar sensor needs a Pulse Repetition Interval (PRI) shorter than 8.6 ns. This is very difficult to achieve with a commercial system, and it becomes possible only in the case where the propeller rotates at much lower speed [
23].
To reveal and measure the propellers’ rotational speed, it is possible to exploit the effects of vibrations and the features they provide to the radar signals. Monitoring propellers’ vibrations is an important task for a UAV designer; vibrations can be generated by an unbalanced propeller and can affect the performance of the UAV. However, vibrations are not only caused by structural defects, but they are intrinsic to the propeller rotation. For this reason, huge efforts are made to design propellers featuring very small vibrations or advanced control systems that aim to reduce their impact on the drone performance [
24,
25,
26]. The effect of a propeller vibration is depicted in
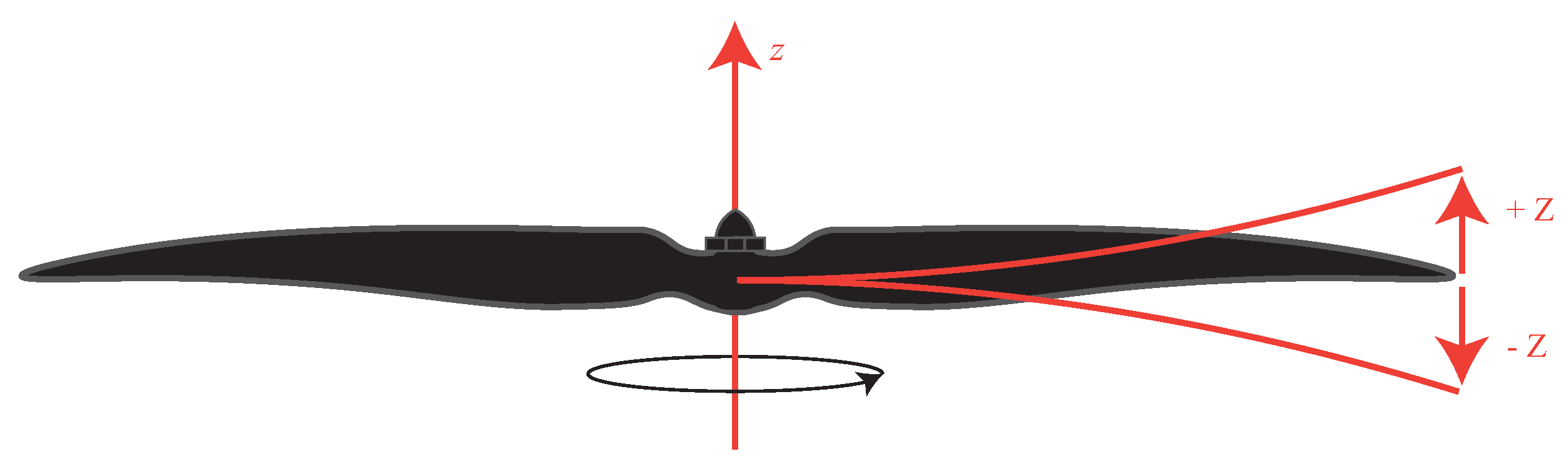
Figure 2, where
z is the reference axis, and
and
is the propeller displacement, due to its vibration along the direction orthogonal to the rotation plane.
Despite being a big problem for drones, from the radar system point of view, the vibration of the propeller is a phenomenon that can be leveraged to indirectly measure the propeller’s rotational speed. In fact, propellers’ vibrations propagate to the whole drone chassis, and it is possible to try to measure its resulting displacement and relate it to the type and number of propellers the drone is equipped with. Assuming that the system is not ideal, the vibration induced by the propeller on the chassis will not only be along the
z-axis (see
Figure 2), but there will be a component also in the direction radial to the pointing direction of the radar system. This component, if detected, can be correlated to the rotation speed of the propellers and consequently used to measure its value.
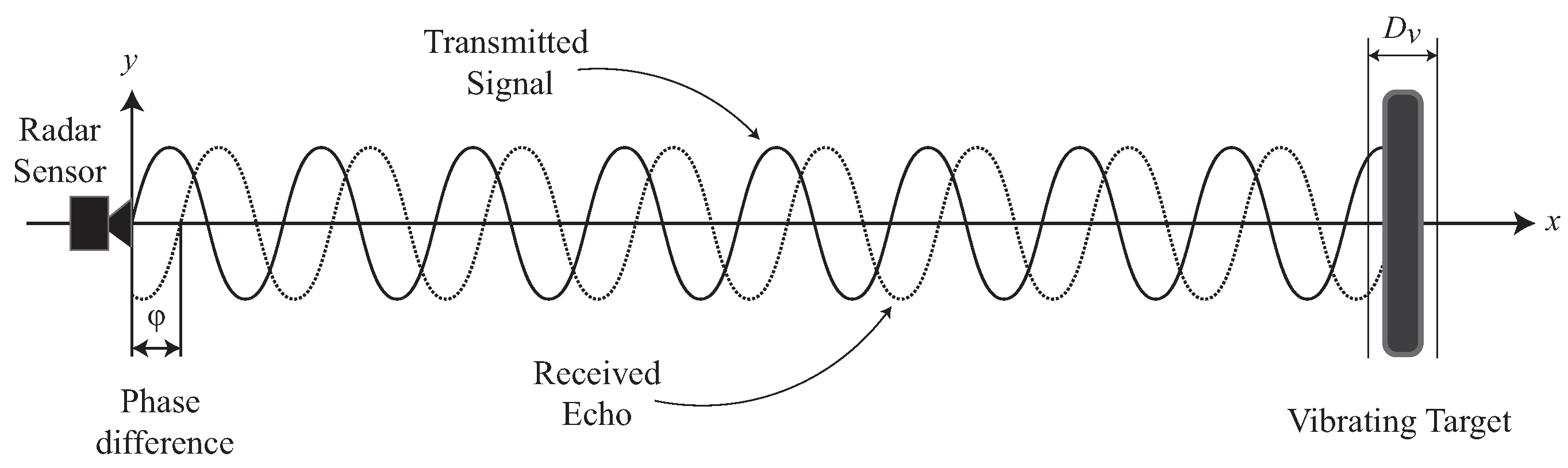
To understand how to perform the process described above with a radar sensor, it is possible to start from a setup where a generic vibrating target is present in the detection field of the radar. In this case, the sensor can not only detect the target but also measure its vibration-related displacement. No matter what type of radar is used, this effect is always present if the target has moving parts, such as the propellers of a UAV, or if the target itself vibrates [
27]. In fact, the micro-Doppler effect is exploited in different application fields from target classification to vibration measurement. For example, it is exploited to measure vital parameters of a person or to monitor the health conditions of a building or infrastructure [
28,
29,
30,
31]. The model of the micro-Doppler effect of a vibrating target can be derived from the classical Doppler formulation: it is presented in [
32,
33,
34] and schematized in
Figure 3.
In general, vibrations of a target take place not only along the radial direction of the radar wave-front, but this is the only direction along which the sensor can detect vibrations. As a consequence, a vibration of the drone chassis generated by one or more propellers can be detected only through its radial component. As such, for the sake of simplicity, only the radial component of the target vibration is considered in the model. Such a component can be identified by two parameters: the main vibration frequency
, and the displacement
. The frequency is composed by several terms, but in order to simplify the model, only a single term will be considered. The evolution of displacement over time can be therefore written as:
By naming the distance between the radar and the target as
, the range distance can vary according to the law
, so the received signal can be written as:
where
is the backscattering coefficient,
is the carrier frequency,
is the wavelength and
is the phase term. For a propeller,
is a very small value, so the radar system needs a specific design to be able to work with such a reduced RCS [
35]. This is an additional reason motivating the development of other methods to measure the propeller speed. The term
can be replaced in Equation (
3), obtaining the resulting
as:
Equation (
4) includes two terms: the main distance
and the displacement vibration of the target. To extract the micro-Doppler effect related to the vibration, it is possible to replace
with
, and the micro-Doppler takes the form:
The generated micro-Doppler vibration frequency can be exploited to detect the propeller’s rotational speed.
4. Experimental Test and Results
Several tests are performed to carry out the measurement of the propellers’ speed. To run the tests, propellers are covered with aluminum tape in order to improve their RCS. This is necessary because the radar system used, specifically designed for automotive applications, is not aimed to detect objects with such a small RCS. The test is conducted at different rotational speeds kept constant, and it is simultaneously measured by a reference digital laser tachometer, namely the DT2234C+ [
49], shown in
Figure 12.
The laser tachometer has a measurement input range of [2.5; 99,999] RPM with a resolution equal to 0.1 RPM in the range [2.5; 999.9] RPM and equal to 1 RPM in the range [1000; 99,999] RPM. The value measured by the laser tachometer does not directly provide the propeller speed: since the blades are covered with the aluminum tape, they are both detected by the device, so to properly convert the measured value of rotational speed (given in RPM) to the frequency measured by the radar (in Hz), the following calculation must be performed:
where
is the rotational frequency,
is the number of blades of the propeller, and
is the value measured by the tachometer.
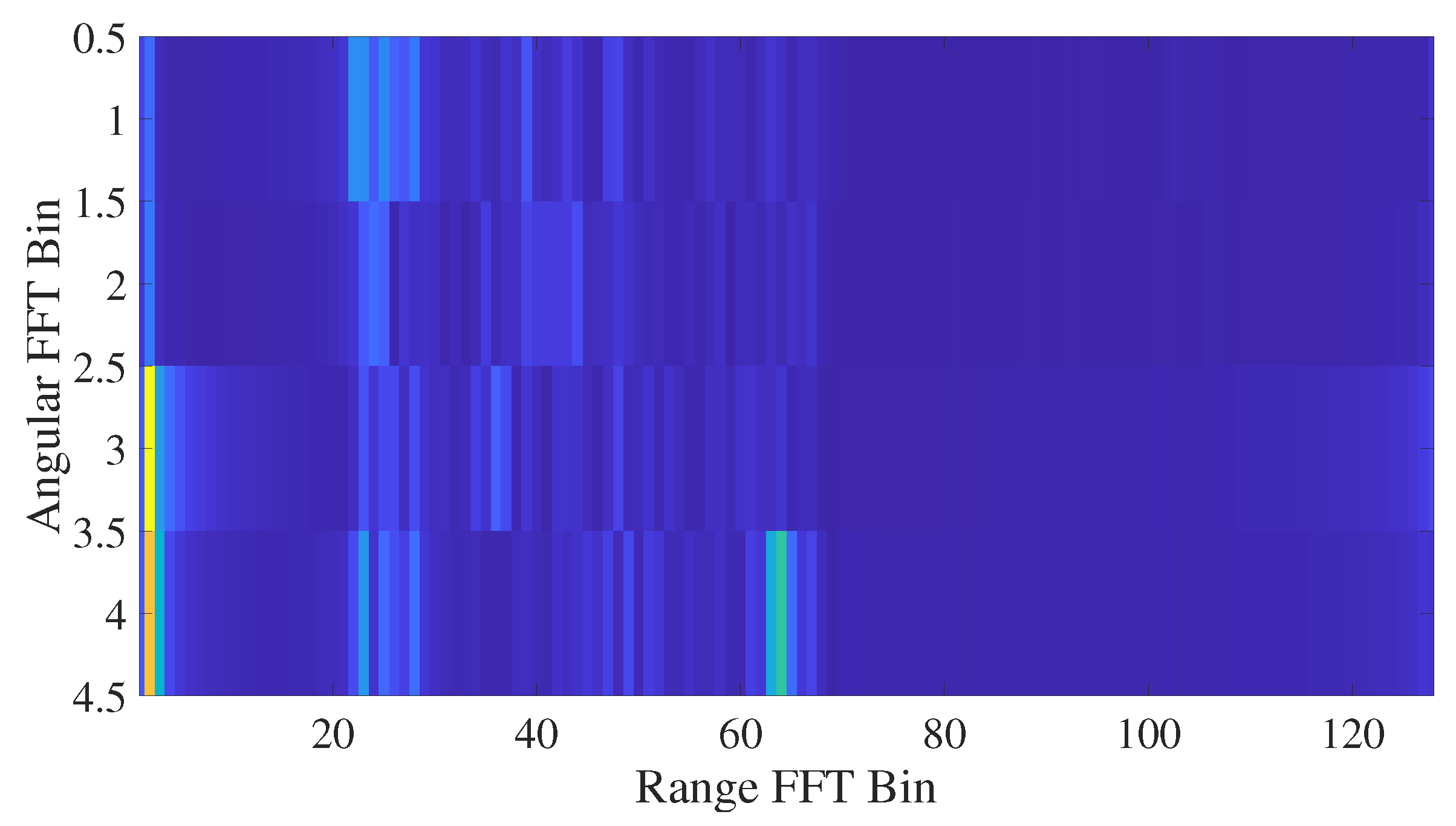
The results obtained with the FFT and MUSIC approaches are reported in
Table 2 and
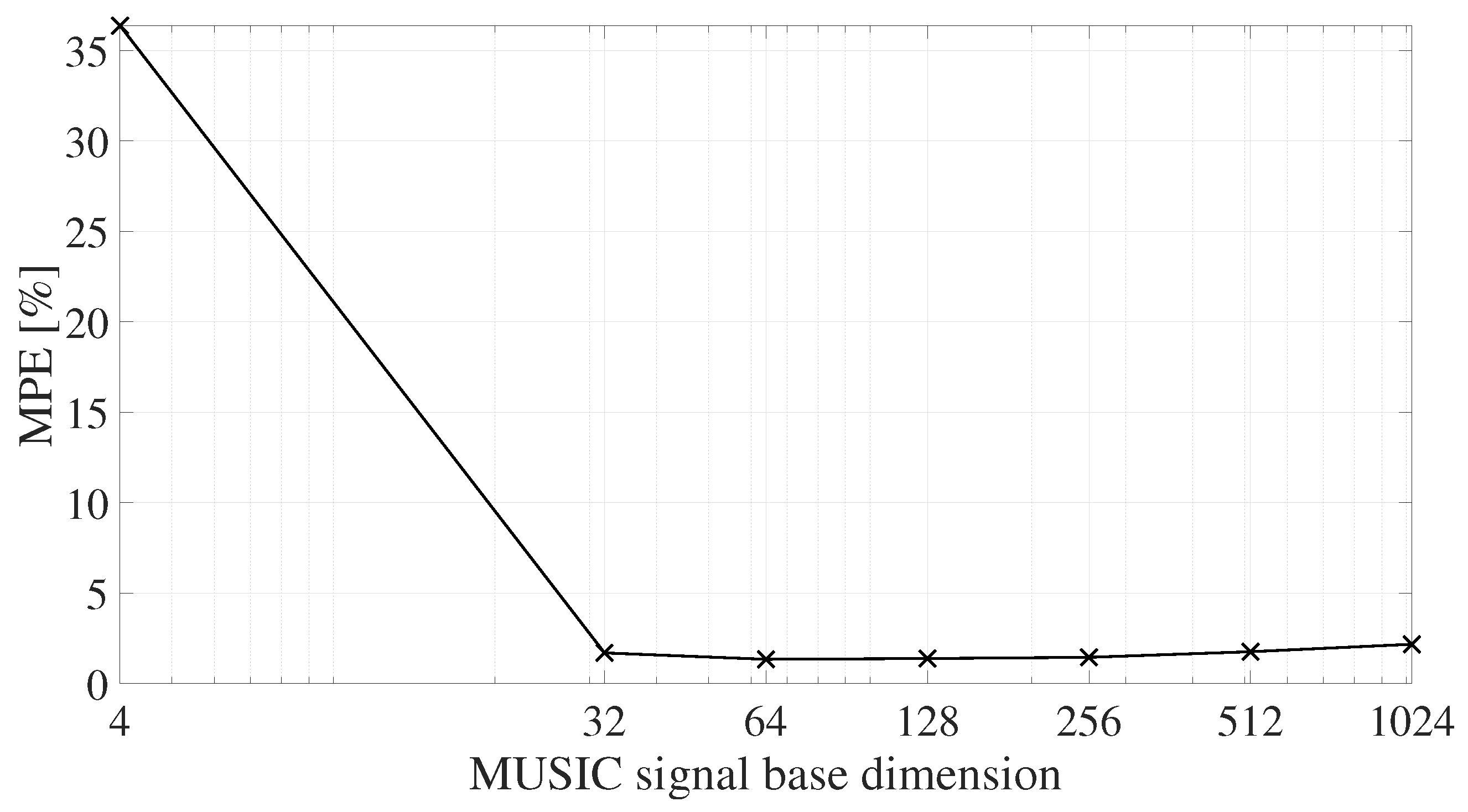
Table 3, respectively. The angular and range bins used to obtain the position of the target are chosen by considering the center of the UAV’s chassis, at angular bin “1” and range bin “25”; the front axis is located at angular bin “1” and range bin “22”; and the rear axis is located at angular bin “1” and range bin “28”. These values are determined by the frontal position of the drone to the radar sensor and by the 45 cm-long wheelbase of the chassis. To be applied, the MUSIC algorithm needs the dimension of the signal subspace as input. This dimension is in general of the same order as the number of main components searched within the original signal. In general, this parameter is very difficult to select, since the number of main signal components cannot be known a priori. For this reason, numerous tests were carried out with different values of the signal base dimension, and the best result in terms of minimum percentage error was obtained with a dimension of sixty-four. All results obtained with the FFT and MUSIC techniques are reported in
Appendix A.
The last rows of
Table 2 and
Table 3 are related to a test in which the drone chassis is tilted in front along the pitch axis. The FFT and the MUSIC computation are made on all the 51,200 samples of the extracted vibration signal. With the configuration parameters chosen, the acquisition has a time duration of 49.971 s. In general, with radar systems, the length of the acquisition window is crucial to provide the extracted information in a short time (ideally, in quasi-real time). In this case, performing the analysis on all the vibration signal samples acquired on a quite long time window has the sole purpose of testing the approach with the maximum possible frequency resolution. Reducing the number of signal samples will provide the rotational speed value in less time but with reduced measurement performance. As an example, if the computation of the FFT is made over all the signal samples, the frequency resolution for the setup chosen is 0.01 Hz, while with fewer samples, for example 5120, collected on a shorter time window, the resolution would amount to 0.1 Hz. This can reduce the accuracy in the evaluation of the calculated peak frequency, which would result in increased uncertainty of the measured propellers’ rotational speed. To mitigate this problem, since one of the goals of this work is to understand the measurement capabilities of the proposed approach, all vibration signal samples are used for computation in the frequency analysis, as the rotational conditions of the propellers are controlled and kept stationary during the acquisition.
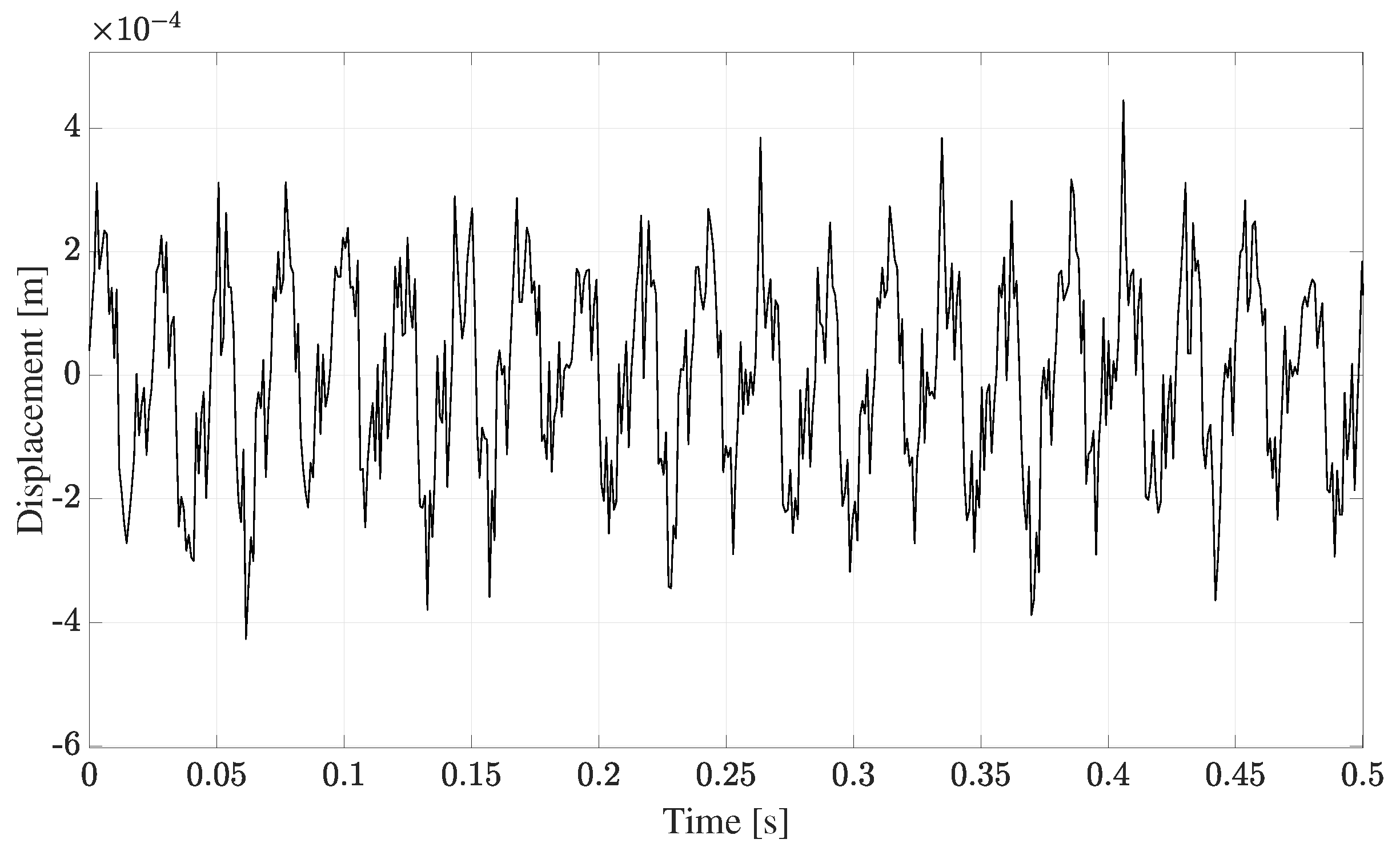
The two highest peaks within the signal spectrum and the signal pseudo-spectrum are selected to obtain the results. An example of the temporal evolution of the vibration displacement signal is illustrated in
Figure 13.
It is possible to quantify the difference between the reference rotational speed provided by the laser tachometer and the proposed radar-based approach by computing the Mean Percentage Error (MPE) [
50] defined as follows:
where
N is the number of measured values. As regards the FFT-based technique, the MPE is 1.08%, and for the MUSIC-based technique, it is 1.34%. The MPE obtained with the MUSIC technique is slightly higher than the MPE obtained with FFT, but in the latter case, the detection of the peaks is more difficult to perform, since the spectrum of the vibration signal is noisier. The variation of the MUSIC MPE obtained for different values of the signal basis dimension is given in
Figure 14.
5. Discussion
In general, the FFT approach can be applied to UAVs with more propellers per axis. To denoise the signal, the application of a proper filter could be considered, but tuning the filter parameters in a specific frequency range, without any information about the UAV, could be extremely difficult. The adoption of the MUSIC algorithm removes much noise from the vibration signal spectrum, thus supporting decisions taken based on the resulting pseudo-spectrum. This approach will preserve the main harmonics of the signal without knowing their frequency in advance, which would be necessary to design a proper filter. While the application of the MUSIC algorithm simplifies detection, it worsens the measurement performance evaluated in terms of the defined MPE. However, this could be an acceptable trade-off considering that in the presence of a very noisy FFT, a peak due to the noise and not to the signal could be selected, thus further worsening performance.
In comparison with the results obtained by other recent approaches, such as those presented in [
51], the proposed method is able to estimate the propellers’ rotational speed even when the range resolution is larger than the length of the propeller’s blade. In fact, as described in
Section 1, the capability of the sensor to measure the displacement is related to the wavelength of the transmitted signal and not to the range resolution. Moreover, the approach proposed in [
51] remains purely theoretical, while the validity of the method proposed in this work is confirmed by experimental tests.