Indoor 3D Point Cloud Segmentation Based on Multi-Constraint Graph Clustering
Abstract
1. Introduction
- The MCGC method based on graph clustering with multi-constraints effectively exploits indoor main structural planes, local surface convexities, and color information of point clouds to partition indoor scenes into object parts. In this way, we can not only completely segment large-scale structural planes, but also perform efficient segmentation with the local details of indoor objects.
- We propose a series of heuristic rules based on the prior knowledge of the indoor scenes to extract horizontal structural planes and achieve the match between surface patches and structural planes by a global energy optimization. This process improves the robustness of the segmentation method to noise, outliers, and clutter.
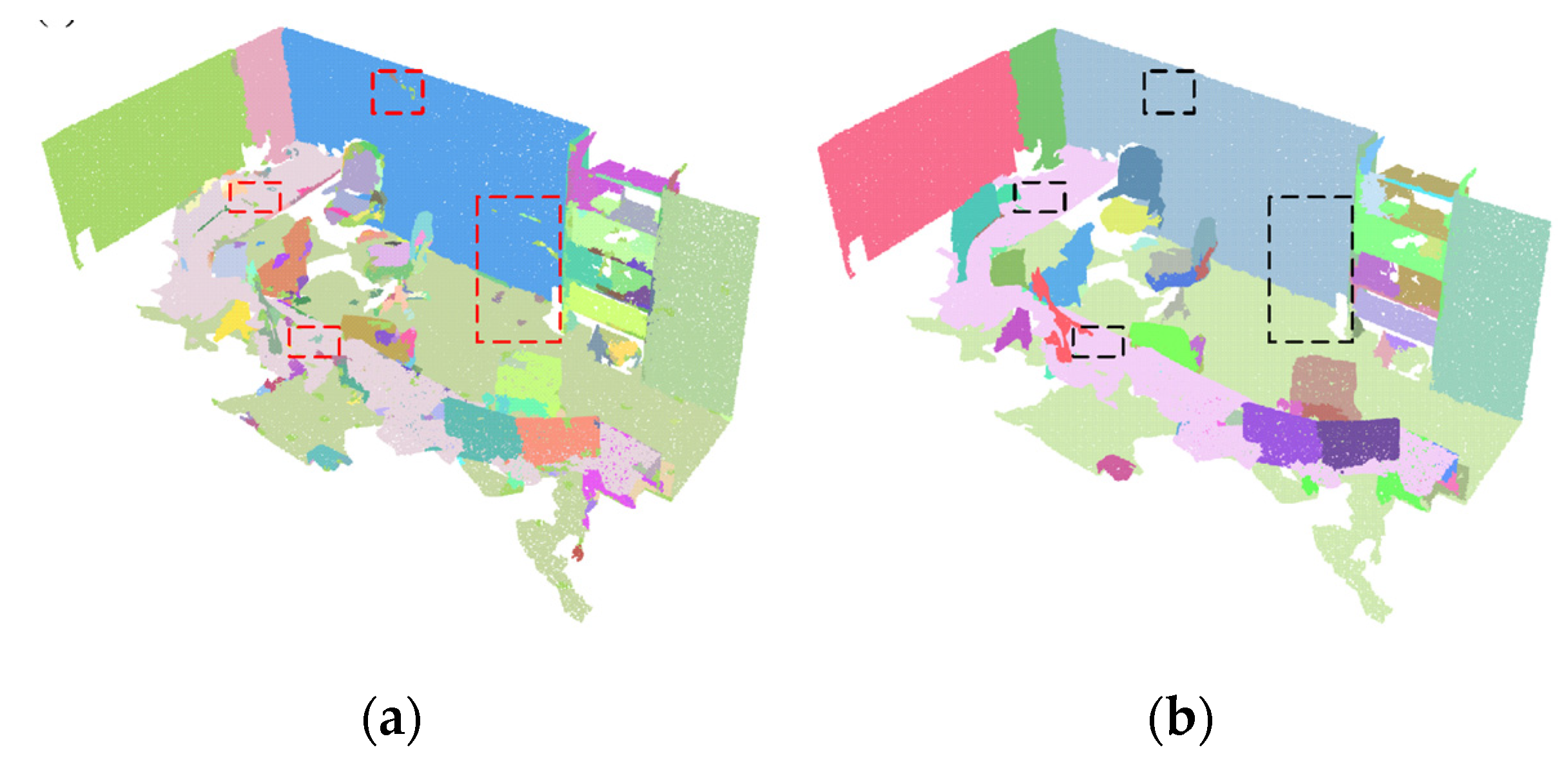
- We design a post-refinement procedure to merge the over-segmented segments from the inaccurate normal estimation of noisy point clouds at boundaries into their neighboring segments and filter out the outliers, improving the accuracy of segmentation.
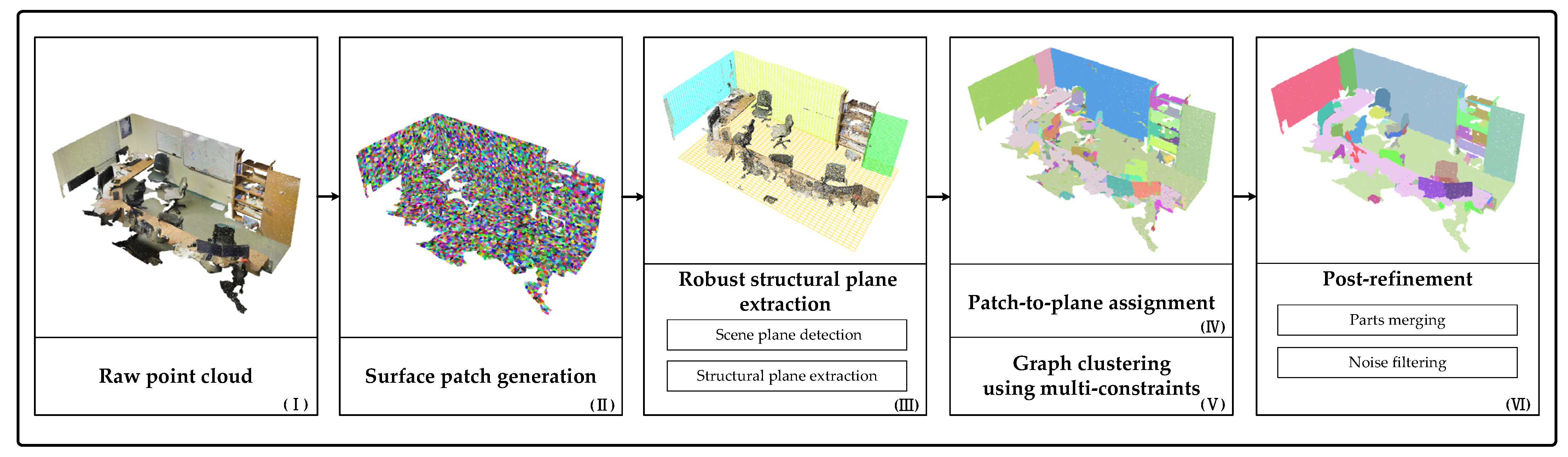
2. Materials and Methods
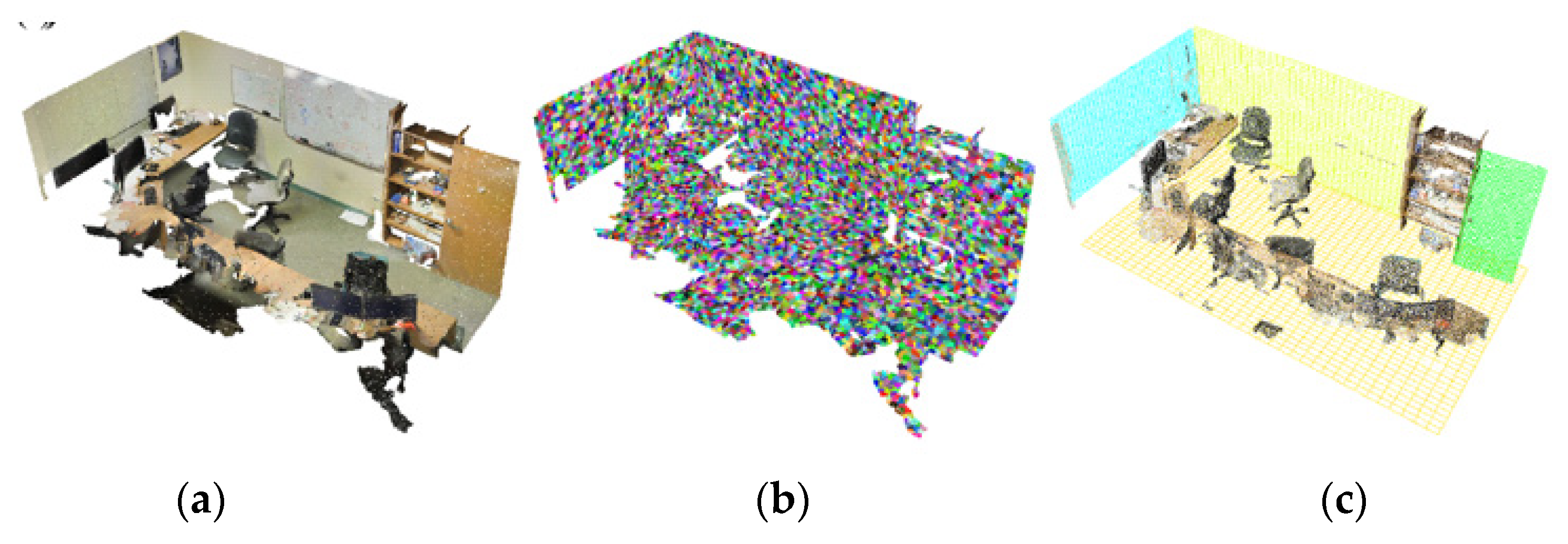
2.1. Surface Patch Generation
2.2. Robust Structural Plane Extraction
2.2.1. Scene Plane Detection
2.2.2. Structural Plane Extraction
2.3. Patch-to-Plane Assignment via Global Energy Optimization
| Algorithm 1. Patch-to-Plane Assignment | |
| Input: : the set of all surface patches of the indoor scene : indoor scene structural planes Output: : assignment variables which indicates surface patch belonging a plane Initialization: iteration , maximum iteration | |
| 1. | while do |
| 2. | calculate the energy of Equation (1) |
| 3. | Repeat |
| 4. | obtain initial assignment variables by minimizing Equation (1) |
| 5. | move the plane label of patch to another plane label |
| 6. | recalculate by Equation (1) via new assignment variables |
| 7. | if then |
| 8. | |
| 9. | |
| 10. | |
| 11. | Else |
| 12. | |
| 13. | end if |
| 14. | end while |
| 15. | Return |
2.4. Graph Clustering Using Multi-Constraints
| Algorithm 2. Multi-Constraint Graph Clustering | |
| Input: | |
| : the set of all surface patches of the indoor scene | |
| : the adjacent graph of the surface patches | |
| : assignment variables which indicates surface patch belonging a plane | |
| Output: | |
| : the set of connected components after edge classification | |
| : the labels of surface patches after segmentation | |
| 1. | for all do |
| 2. | for all do |
| 3. | if then |
| 4. | , |
| 5. | else if && then |
| 6. | , |
| 7. | else if && then |
| 8. | , |
| 9. | for all do |
| 10. | remove |
| 11. | connected components |
| 12. | for all do |
| 13. | the label assigned to |
| 14. | Return |
2.5. Post-Refinement
| Algorithm 3. Segmentation post-refinement | |
| Input: : the set of all surface patches of the indoor scene; : the adjacent graph of the surface patches : the set of connected components after edge classification : the labels of surface patches after segmentation Output: : the final labels of surface patches after post-refinement initialization: , | |
| 1. | for all do |
| 2. | if the number of patches then |
| 3. | for all do |
| 4. | for all do |
| 5. | |
| 6. | if then |
| 7. | |
| 8. | |
| 9. | |
| 10. | for all do |
| 11. | if the number of points then |
| 12. | |
| 13. | Return |
2.5.1. Segments Merging
2.5.2. Noise Filtering
3. Results
3.1. Datasets Description
3.2. Evaluation Metric
3.3. Parameter Settings
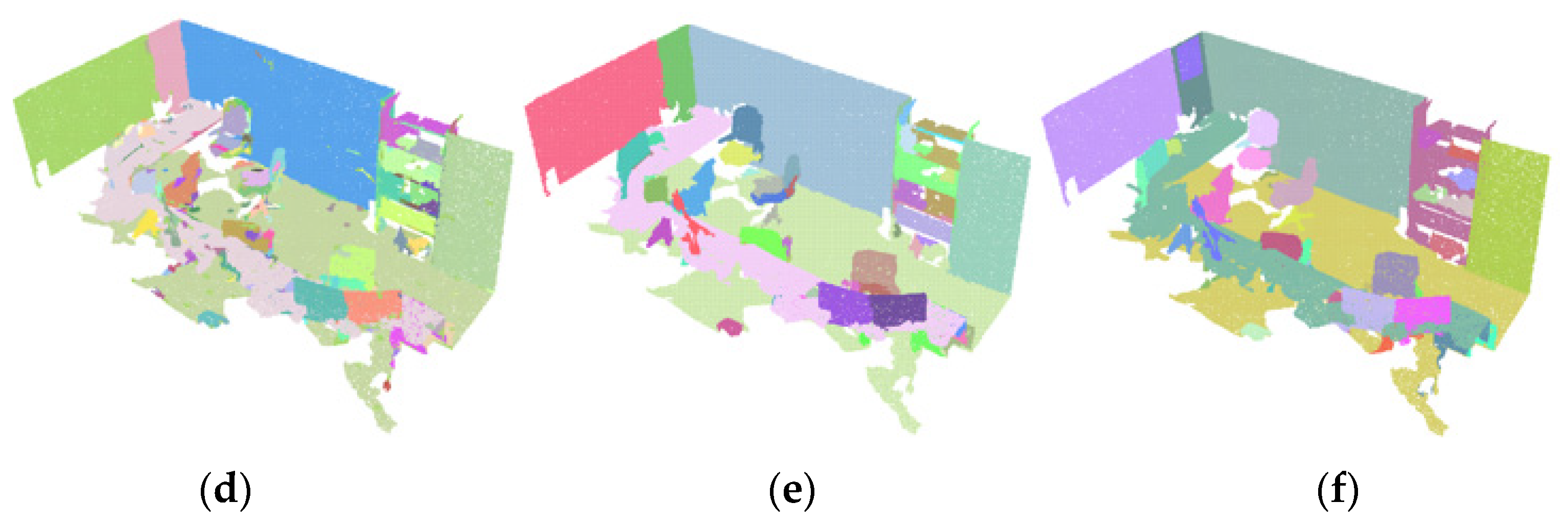
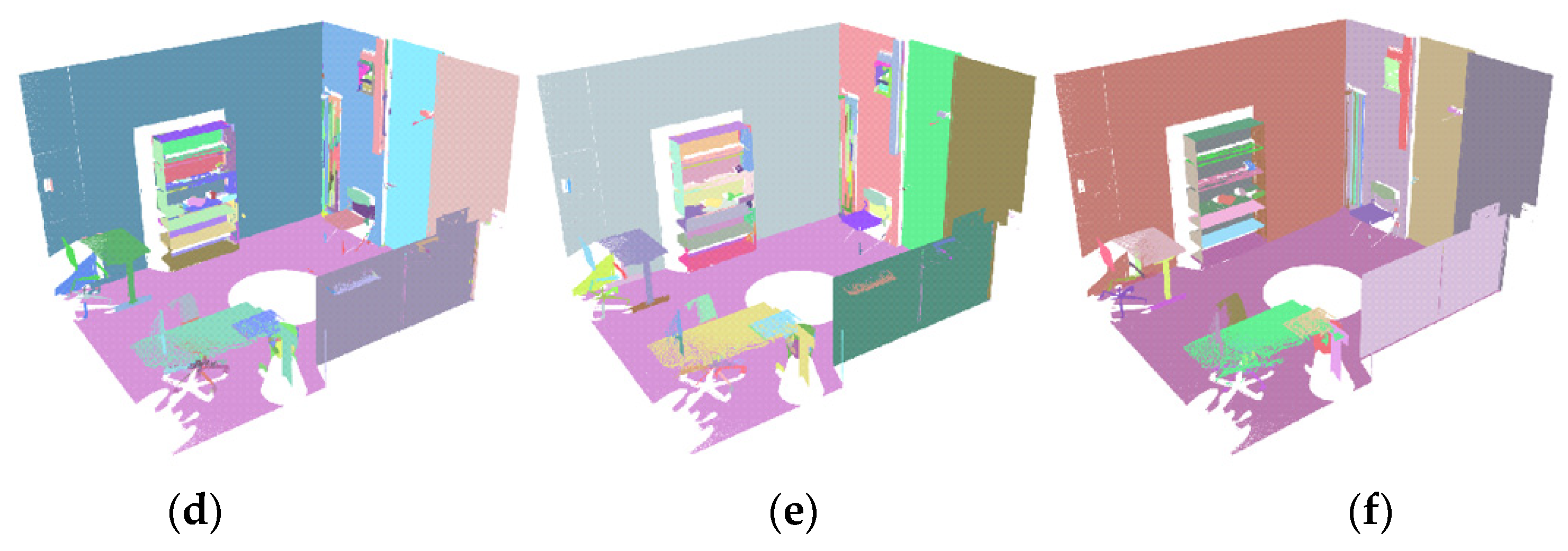
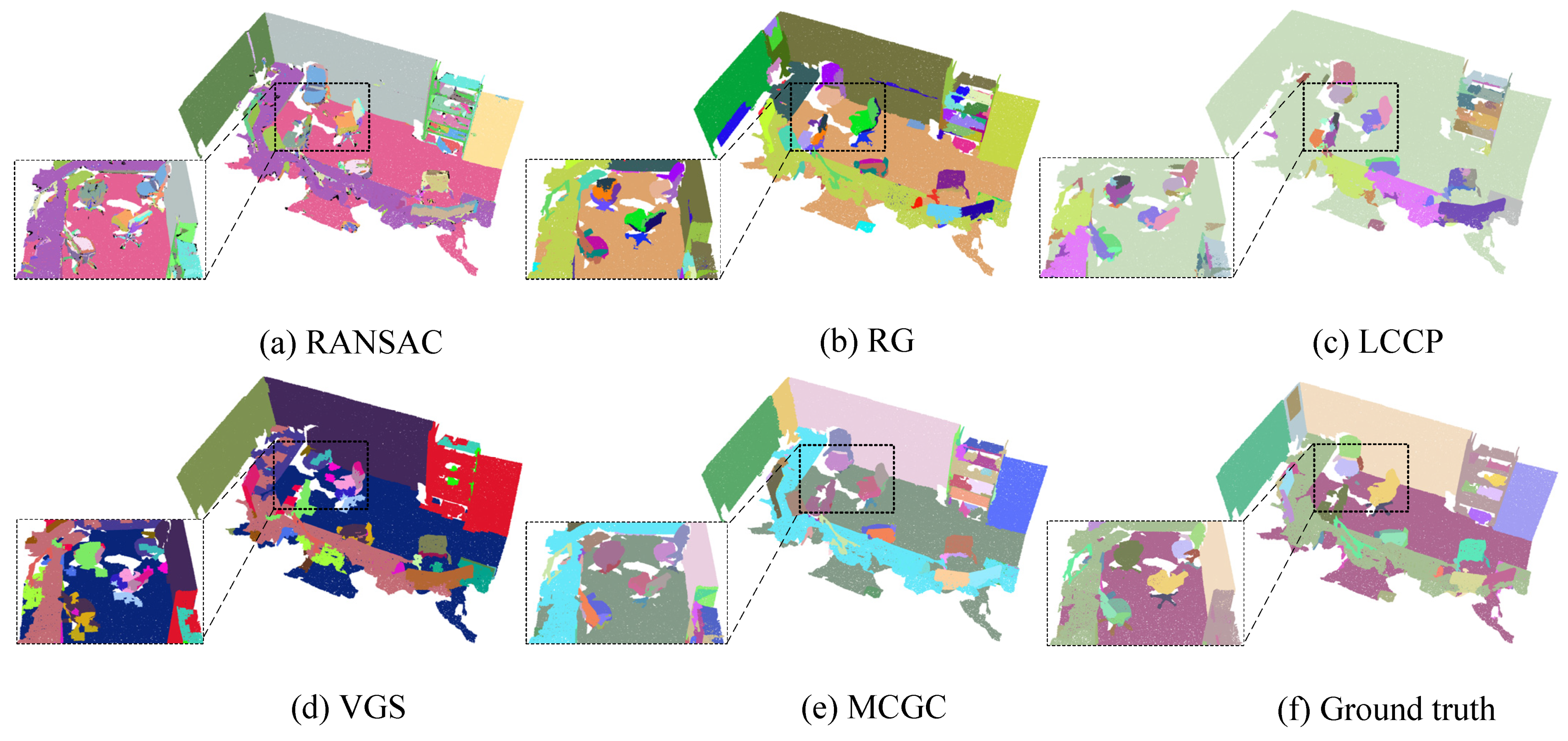
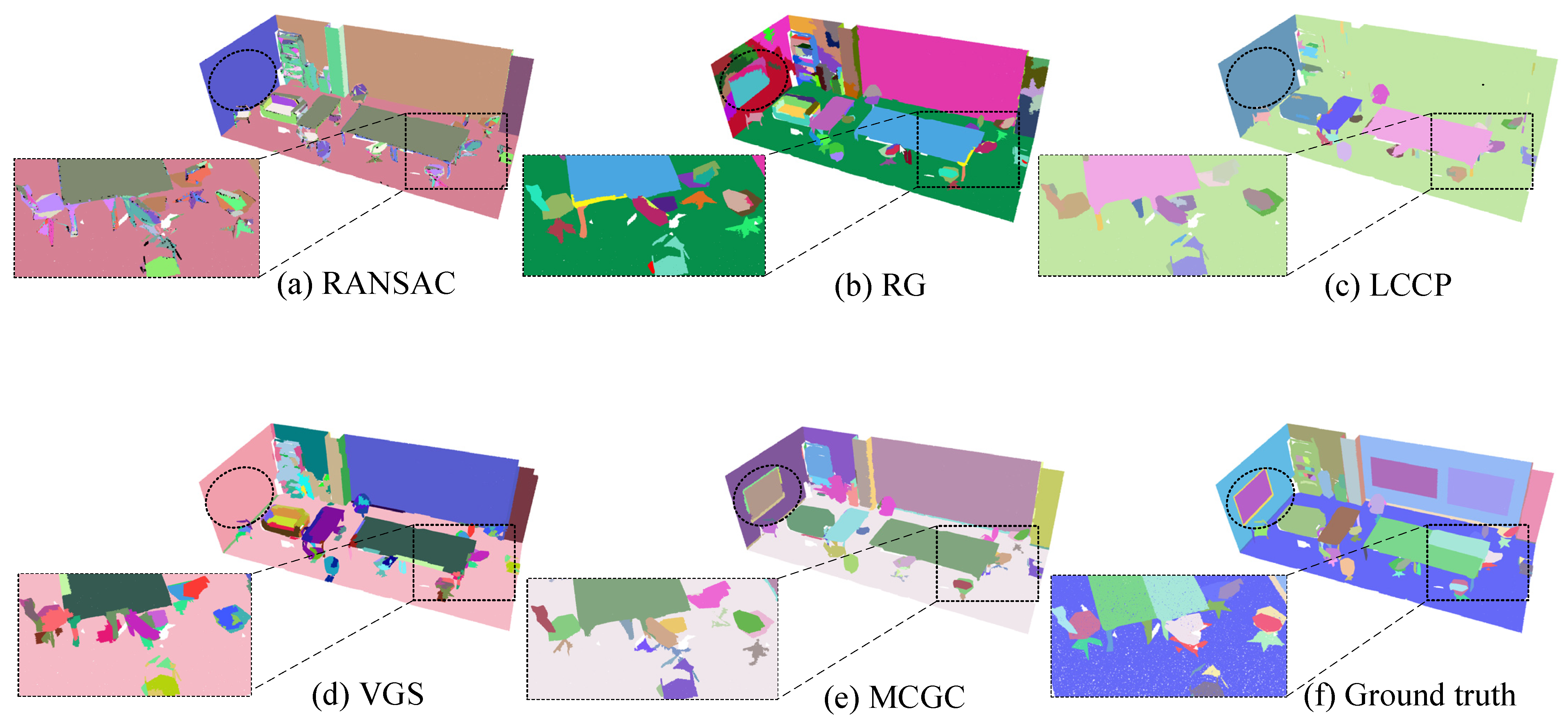
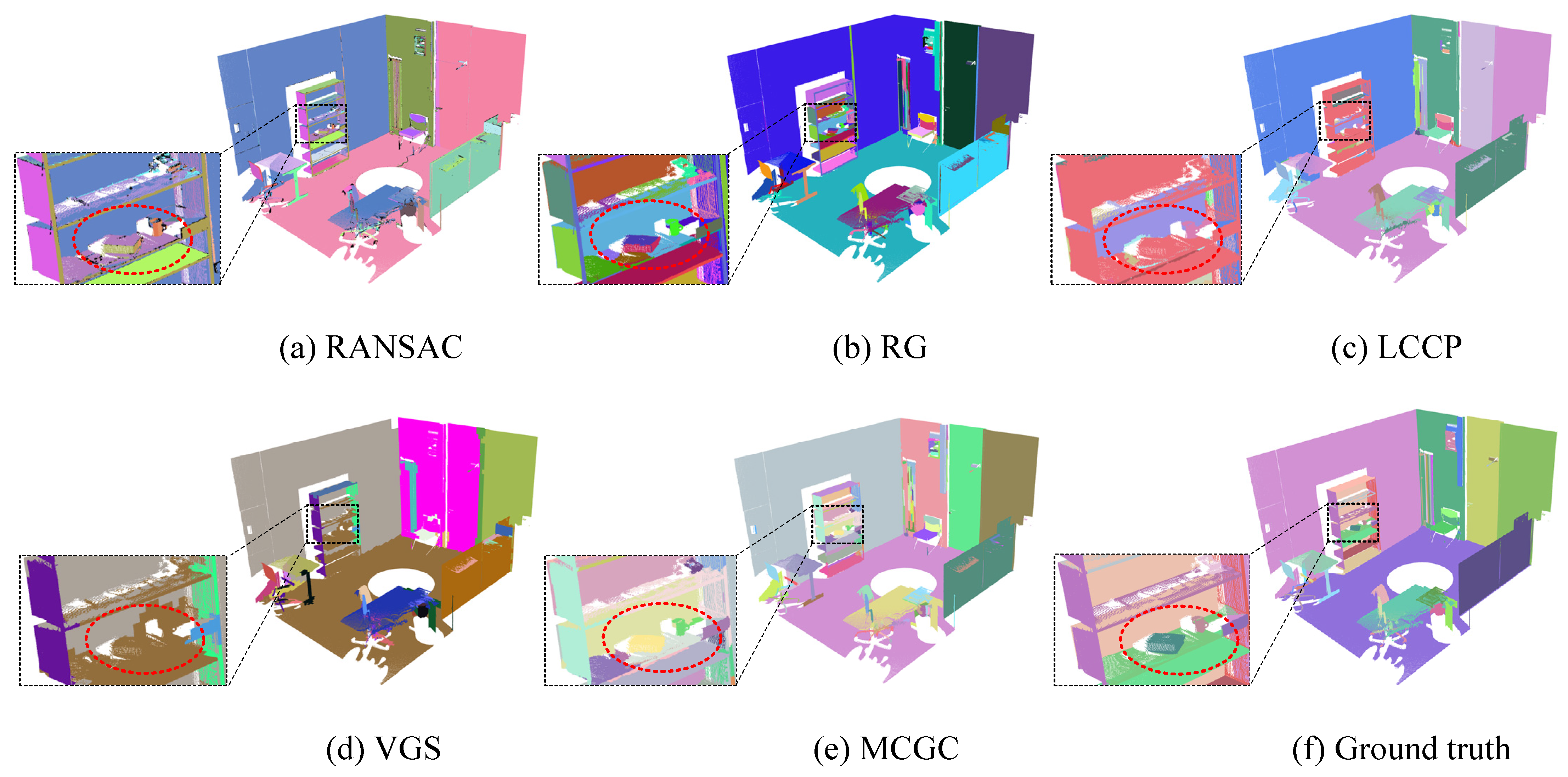
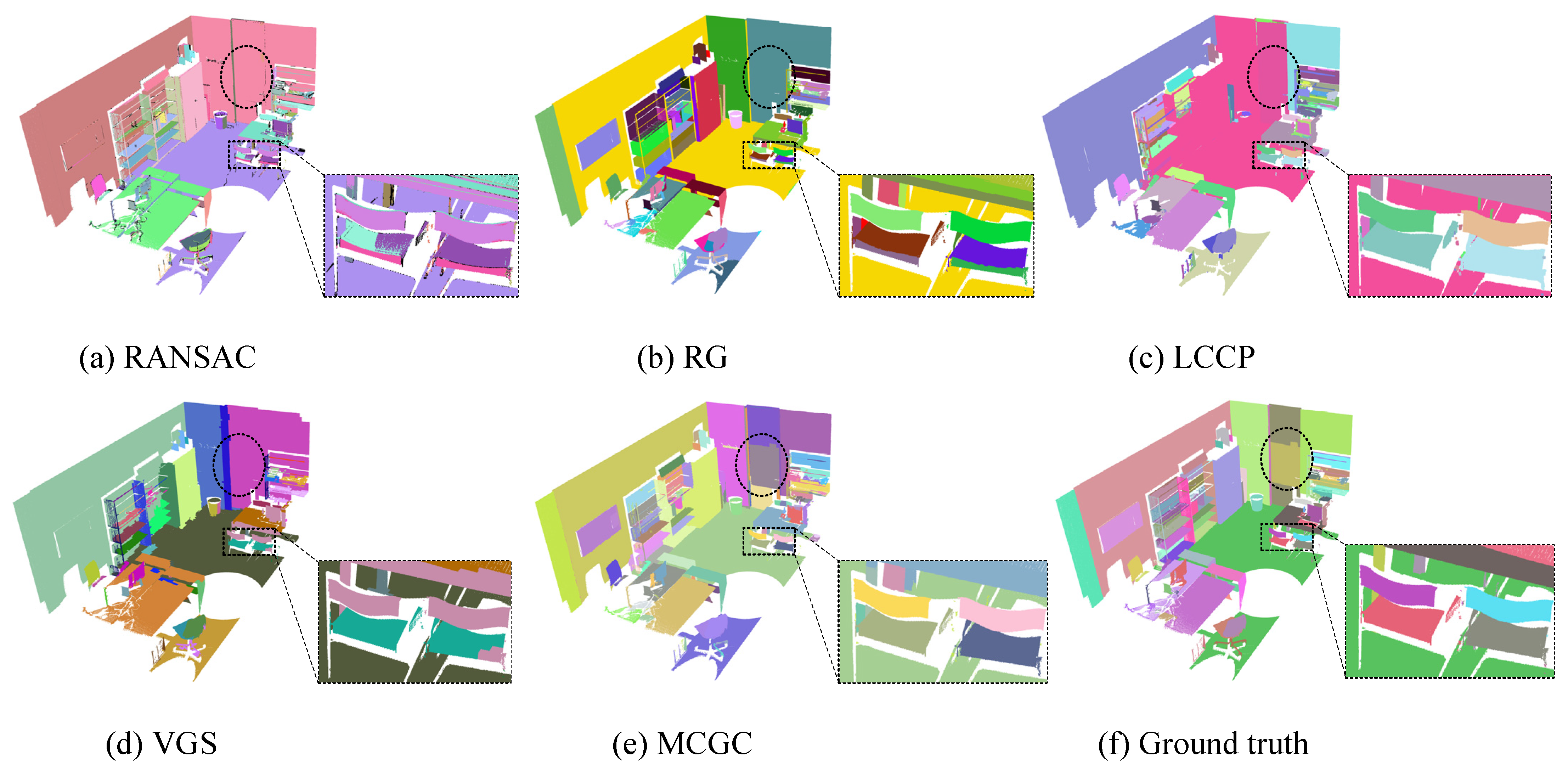
3.4. Qualitative Evaluation
3.5. Quantitative Evaluation
3.6. Effect Analysis
4. Discussion
5. Conclusions
- This paper introduced a novel method (MCGC) based on multi-constraint graph clustering for indoor segmentation, which effectively exploits pluralistic information of 3D indoor scenes. Importantly, we closely integrated extracted structural planes, local surface convexity, and color information of objects for scene segmentation to solve the issues of the model mismatch and the lack of detailed parts in the previous unsupervised segmentation algorithms. In particular, we presented a robust plane extraction method and used global optimization to assign patches to the indoor structural planes. Moreover, we demonstrated how the extracted planes are jointly segmented with local convexity information and color constraint by employing a graph clustering method. In addition, the entire MCGC algorithm is based on surface patches generated from the point cloud, and a post-refinement step is designed to filter the outliers, which significantly improves computation speed and saves computation overhead. The segment precision and recall of experimental results reach 70% on average, at an average processing speed of 724,000 points per second.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, B.; Hua, X.; Yu, K.; Xuan, W.; Chen, X.; Tao, W. Indoor Point Cloud Segmentation Using Iterative Gaussian Mapping and Improved Model Fitting. IEEE Trans. Geosci. Remote Sens. 2020, 58, 7890–7907. [Google Scholar] [CrossRef]
- Macher, H.; Landes, T.; Grussenmeyer, P. From Point Clouds to Building Information Models: 3D Semi-Automatic Reconstruction of Indoors of Existing Buildings. Appl. Sci. 2017, 7, 1030. [Google Scholar] [CrossRef]
- Biglia, A.; Zaman, S.; Gay, P.; Aimonino, D.R.; Comba, L. 3D point cloud density-based segmentation for vine rows detection and localisation. Comput. Electron. Agric. 2022, 199, 107166. [Google Scholar] [CrossRef]
- Maturana, D.; Scherer, S. VoxNet: A 3D Convolutional Neural Network for real-time object recognition. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 922–928. [Google Scholar] [CrossRef]
- Chen, X.; Wu, H.; Lichti, D.; Han, X.; Ban, Y.; Li, P.; Deng, H. Extraction of indoor objects based on the exponential function density clustering model. Inf. Sci. 2022, 607, 1111–1135. [Google Scholar] [CrossRef]
- Xu, Z.; Liang, Y.; Xu, Y.; Fang, Z.; Stilla, U. Geometric Modeling and Surface-Quality Inspection of Prefabricated Concrete Components Using Sliced Point Clouds. J. Constr. Eng. Manag. 2022, 148, 04022087. [Google Scholar] [CrossRef]
- Park, J.; Kim, J.; Lee, D.; Jeong, K.; Lee, J.; Kim, H.; Hong, T. Deep Learning–Based Automation of Scan-to-BIM with Modeling Objects from Occluded Point Clouds. J. Manag. Eng. 2022, 38, 04022025. [Google Scholar] [CrossRef]
- Fan, Y.; Wang, M.; Geng, N.; He, D.; Chang, J.; Zhang, J.J. A self-adaptive segmentation method for a point cloud. Vis. Comput. 2017, 34, 659–673. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, X.; Shi, W.; Song, S.; Tristan, A.C.; Li, K. An Accurate and Robust Region-Growing Algorithm for Plane Segmentation of TLS Point Clouds Using a Multiscale Tensor Voting Method. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4160–4168. [Google Scholar] [CrossRef]
- Saglam, A.; Makineci, H.B.; Baykan, N.A.; Baykan, K. Boundary constrained voxel segmentation for 3D point clouds using local geometric differences. Expert Syst. Appl. 2020, 157, 113439. [Google Scholar] [CrossRef]
- Schnabel, R.; Wahl, R.; Klein, R. Efficient RANSAC for point-cloud shape detection. Comput. Graph. Forum 2007, 26, 214–226. [Google Scholar] [CrossRef]
- Li, L.; Yang, F.; Zhu, H.; Li, D.; Li, Y.; Tang, L. An Improved RANSAC for 3D Point Cloud Plane Segmentation Based on Normal Distribution Transformation Cells. Remote. Sens. 2017, 9, 433. [Google Scholar] [CrossRef]
- Xu, B.; Chen, Z.; Zhu, Q.; Ge, X.; Huang, S.; Zhang, Y.; Liu, T.; Wu, D. Geometrical Segmentation of Multi-Shape Point Clouds Based on Adaptive Shape Prediction and Hybrid Voting RANSAC. Remote Sens. 2022, 14, 2024. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Z.; Zhao, X.; Hong, D.; Li, W.; Cai, W.; Zhan, Y. AF2GNN: Graph convolution with adaptive filters and aggregator fusion for hyperspectral image classification. Inf. Sci. 2022, 602, 201–219. [Google Scholar] [CrossRef]
- Yao, D.; Zhi-Li, Z.; Xiao-Feng, Z.; Wei, C.; Fang, H.; Yao-Ming, C.; Cai, W.-W. Deep hybrid: Multi-graph neural network collaboration for hyperspectral image classification. Def. Technol. 2022, in press. [CrossRef]
- Ding, Y.; Zhao, X.; Zhang, Z.; Cai, W.; Yang, N. Graph Sample and Aggregate-Attention Network for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2021, 19, 5504205. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Z.; Zhao, X.; Hong, D.; Cai, W.; Yu, C.; Yang, N.; Cai, W. Multi-feature fusion: Graph neural network and CNN combining for hyperspectral image classification. Neurocomputing 2022, 501, 246–257. [Google Scholar] [CrossRef]
- Golovinskiy, A.; Funkhouser, T. Min-cut based segmentation of point clouds. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision Workshops, ICCV Workshops, Kyoto, Japan, 27 September–4 October 2009; pp. 39–46. [Google Scholar] [CrossRef]
- Boykov, Y.; Funka-Lea, G. Graph Cuts and Efficient N-D Image Segmentation. Int. J. Comput. Vis. 2006, 70, 109–131. [Google Scholar] [CrossRef]
- Yan, J.; Shan, J.; Jiang, W. A global optimization approach to roof segmentation from airborne lidar point clouds. ISPRS J. Photogramm. Remote Sens. 2014, 94, 183–193. [Google Scholar] [CrossRef]
- Isack, H.; Boykov, Y. Energy-Based Geometric Multi-model Fitting. Int. J. Comput. Vis. 2011, 97, 123–147. [Google Scholar] [CrossRef]
- Yang, H.; Wang, Z.; Lin, L.; Liang, H.; Huang, W.; Xu, F. Two-Layer-Graph Clustering for Real-Time 3D LiDAR Point Cloud Segmentation. Appl. Sci. 2020, 10, 8534. [Google Scholar] [CrossRef]
- Xu, Y.; Tuttas, S.; Hoegner, L.; Stilla, U. Voxel-based segmentation of 3D point clouds from construction sites using a probabilistic connectivity model. Pattern Recognit. Lett. 2018, 102, 67–74. [Google Scholar] [CrossRef]
- Papon, J.; Abramov, A.; Schoeler, M.; Worgotter, F. “Voxel Cloud Connectivity Segmentation Supervoxels for Point Clouds,” in CVPR13. 2013, pp. 2027–2034. Available online: https://openaccess.thecvf.com/content_cvpr_2013/html/Papon_Voxel_Cloud_Connectivity_2013_CVPR_paper.html (accessed on 27 April 2022).
- Lin, Y.; Wang, C.; Zhai, D.; Li, W.; Li, J. Toward better boundary preserved supervoxel segmentation for 3D point clouds. ISPRS J. Photogramm. Remote Sens. 2018, 143, 39–47. [Google Scholar] [CrossRef]
- Li, H.; Liu, Y.; Men, C.; Fang, Y. A novel 3D point cloud segmentation algorithm based on multi-resolution supervoxel and MGS. Int. J. Remote Sens. 2021, 42, 8492–8525. [Google Scholar] [CrossRef]
- Charles, R.Q.; Su, H.; Kaichun, M.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 77–85. [Google Scholar] [CrossRef]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space. arXiv 2017, arXiv:1706.02413. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Z.; Zhao, X.; Cai, W.; Yang, N.; Hu, H.; Huang, X.; Cao, Y.; Cai, W. Unsupervised Self-correlated Learning Smoothy Enhanced Locality Preserving Graph Convolution Embedding Clustering for Hyperspectral Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5536716. [Google Scholar] [CrossRef]
- Ding, Y.; Zhao, X.; Zhang, Z.; Cai, W.; Yang, N.; Zhan, Y. Semi-Supervised Locality Preserving Dense Graph Neural Network with ARMA Filters and Context-Aware Learning for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5511812. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Z.; Zhao, X.; Cai, Y.; Li, S.; Deng, B.; Cai, W. Self-Supervised Locality Preserving Low-Pass Graph Convolutional Embedding for Large-Scale Hyperspectral Image Clustering. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5536016. [Google Scholar] [CrossRef]
- Ding, Y.; Zhao, X.; Zhang, Z.; Cai, W.; Yang, N. Multiscale Graph Sample and Aggregate Network with Context-Aware Learning for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 4561–4572. [Google Scholar] [CrossRef]
- Wan, J.; Xie, Z.; Xu, Y.; Zeng, Z.; Yuan, D.; Qiu, Q. DGANet: A Dilated Graph Attention-Based Network for Local Feature Extraction on 3D Point Clouds. Remote Sens. 2021, 13, 3484. [Google Scholar] [CrossRef]
- Zeng, Z.; Xu, Y.; Xie, Z.; Wan, J.; Wu, W.; Dai, W. RG-GCN: A Random Graph Based on Graph Convolution Network for Point Cloud Semantic Segmentation. Remote. Sens. 2022, 14, 4055. [Google Scholar] [CrossRef]
- Wan, J.; Xu, Y.; Qiu, Q.; Xie, Z. A geometry-aware attention network for semantic segmentation of MLS point clouds. Int. J. Geogr. Inf. Sci. 2022, 37, 138–161. [Google Scholar] [CrossRef]
- Zeng, Z.; Xu, Y.; Xie, Z.; Tang, W.; Wan, J.; Wu, W. LEARD-Net: Semantic segmentation for large-scale point cloud scene. Int. J. Appl. Earth Obs. Geoinf. ITC J. 2022, 112, 102953. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic Graph CNN for Learning on Point Clouds. ACM Trans. Graph. 2019, 38, 146. [Google Scholar] [CrossRef]
- Wang, L.; Huang, Y.; Hou, Y.; Zhang, S.; Shan, J. Graph Attention Convolution for Point Cloud Semantic Segmentation. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 10288–10297. [Google Scholar] [CrossRef]
- Wang, W.; Yu, R.; Huang, Q.; Neumann, U. SGPN: Similarity Group Proposal Network for 3D Point Cloud In-stance Segmentation. arXiv 2019, arXiv:1711.08588. [Google Scholar] [CrossRef]
- Chen, J.; Kira, Z.; Cho, Y.K. LRGNet: Learnable Region Growing for Class-Agnostic Point Cloud Segmentation. IEEE Robot. Autom. Lett. 2021, 6, 2799–2806. [Google Scholar] [CrossRef]
- Yang, B.; Wang, J.; Clark, R.; Hu, Q.; Wang, S.; Markham, A.; Trigoni, N. Learning Object Bounding Boxes for 3D Instance Segmentation on Point Clouds. arXiv 2019, arXiv:1906.01140. [Google Scholar] [CrossRef]
- Oh, S.; Lee, D.; Kim, M.; Kim, T.; Cho, H. Building Component Detection on Unstructured 3D Indoor Point Clouds Using RANSAC-Based Region Growing. Remote Sens. 2021, 13, 161. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Y. Slice-Guided Components Detection and Spatial Semantics Acquisition of Indoor Point Clouds. Sensors 2022, 22, 1121. [Google Scholar] [CrossRef]
- Xu, Y.; Tuttas, S.; Hoegner, L.; Stilla, U. Geometric Primitive Extraction from Point Clouds of Construction Sites Using VGS. IEEE Geosci. Remote Sens. Lett. 2017, 14, 424–428. [Google Scholar] [CrossRef]
- Runz, M.; Buffier, M.; Agapito, L. MaskFusion: Real-Time Recognition, Tracking and Reconstruction of Multiple Moving Objects. In Proceedings of the 2018 IEEE International Symposium on Mixed and Augmented Reality (ISMAR), Munich, Germany, 16–20 October 2018; pp. 10–20. [Google Scholar] [CrossRef]
- Pham, T.T.; Eich, M.; Reid, I.; Wyeth, G. Geometrically consistent plane extraction for dense indoor 3D maps segmentation. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016; pp. 4199–4204. [Google Scholar] [CrossRef]
- Yang, B.; Dong, Z.; Zhao, G.; Dai, W. Hierarchical extraction of urban objects from mobile laser scanning data. ISPRS J. Photogramm. Remote Sens. 2015, 99, 45–57. [Google Scholar] [CrossRef]
- Dong, Z.; Yang, B.; Hu, P.; Scherer, S. An efficient global energy optimization approach for robust 3D plane segmentation of point clouds. ISPRS J. Photogramm. Remote Sens. 2018, 137, 112–133. [Google Scholar] [CrossRef]
- Lin, Y.; Li, J.; Wang, C.; Chen, Z.; Wang, Z.; Li, J. Fast regularity-constrained plane fitting. ISPRS J. Photogramm. Remote Sens. 2020, 161, 208–217. [Google Scholar] [CrossRef]
- Awwad, T.M.; Zhu, Q.; Du, Z.; Zhang, Y. An improved segmentation approach for planar surfaces from unstructured 3D point clouds. Photogramm. Rec. 2010, 25, 5–23. [Google Scholar] [CrossRef]
- Stein, S.C.; Schoeler, M.; Papon, J.; Worgotter, F. Object Partitioning Using Local Convexity. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 304–311. [Google Scholar] [CrossRef]
- Araújo, A.M.C.; Oliveira, M.M. A robust statistics approach for plane detection in unorganized point clouds. Pattern Recognit. 2020, 100, 107115. [Google Scholar] [CrossRef]
- Farid, R. Region-Growing Planar Segmentation for Robot Action Planning. In AI 2015: Advances in Artificial Intelligence; Springer: Cham, Switzerland, 2015; pp. 179–191. [Google Scholar] [CrossRef]
- Limberger, F.A.; Oliveira, M.M. Real-time detection of planar regions in unorganized point clouds. Pattern Recognit. 2015, 48, 2043–2053. [Google Scholar] [CrossRef]
- Vo, A.-V.; Truong-Hong, L.; Laefer, D.F.; Bertolotto, M. Octree-based region growing for point cloud segmentation. ISPRS J. Photogramm. Remote Sens. 2015, 104, 88–100. [Google Scholar] [CrossRef]
- Boykov, Y.; Veksler, O.; Zabih, R. Fast approximate energy minimization via graph cuts. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 23, 1222–1239. [Google Scholar] [CrossRef]
- Armeni, I.; Sener, O.; Zamir, A.R.; Jiang, H.; Brilakis, I.; Fischer, M.; Savarese, S. 3D Semantic Parsing of Large-Scale Indoor Spaces. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1534–1543. [Google Scholar] [CrossRef]
- Su, F.; Zhu, H.; Li, L.; Zhou, G.; Rong, W.; Zuo, X.; Li, W.; Wu, X.; Wang, W.; Yang, F.; et al. Indoor interior segmentation with curved surfaces via global energy optimization. Autom. Constr. 2021, 131, 103886. [Google Scholar] [CrossRef]
- Rabbani, T.; Heuvel, F.A.; Vosselman, G. Segmentation of point clouds using smoothness constraint. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2006, 36, 248–253. [Google Scholar]






| Data | Points | Area | Height | Density | From | |
|---|---|---|---|---|---|---|
| (m2) | (m) | (Points/m3) | ||||
| S3DIS | conference | 1,922,357 | 42.75 | 4.5 | 9993 | Matterport |
| office-1 | 759,861 | 16.8 | 2.7 | 16,752 | Matterport | |
| office-2 | 2,145,926 | 40.7 | 2.8 | 18,831 | Matterport | |
| UZH | Room-L9 | 10,997,024 | 23.4 | 3 | 156,653 | Laser |
| Room-L80 | 10,843,388 | 22.75 | 3 | 158,877 | Laser | |
| Parameter | Descriptor | Value |
|---|---|---|
| The voxel resolution | 0.01 m | |
| The seed resolution | 0.07 m | |
| The distance threshold of the outliers | 0.03 m | |
| The threshold of local convexity constraint | 8 | |
| The threshold of color constraint | 25 | |
| The maximum number of patches of the component to be merged | 3 | |
| The maximum number points of the separated parts to be outliers | 50 |
| Data | (%) | (%) | (%) | (%) | (%) |
|---|---|---|---|---|---|
| Conference | 73.53 | 69.44 | 8.30 | 10.29 | 71.43 |
| Office-1 | 70.91 | 72.22 | 9.26 | 7.27 | 71.56 |
| Office-2 | 79.45 | 66.67 | 10.34 | 8.22 | 72.50 |
| Room-L9 | 77.05 | 87.04 | 11.11 | 3.28 | 81.74 |
| Room-L80 | 74.26 | 80.65 | 4.30 | 2.97 | 77.32 |
| Data | Computing Time (s) | |||||
|---|---|---|---|---|---|---|
| Surface Patch Generation | Robust Structural Plane Extraction | Patch-to-Plane Assignment | Multi-Constraint Graph Clustering | Post-Refinement | Total Time | |
| Conference | 0.762 | 3.04 | 0.002 | 0.17 | 0.266 | 4.24 |
| Office-1 | 0.291 | 1.092 | 0.002 | 0.052 | 0.146 | 1.583 |
| Office-2 | 0.646 | 5.26 | 0.001 | 0.292 | 0.425 | 6.624 |
| Room-L9 | 4.656 | 17.685 | 0.002 | 0.316 | 0.885 | 23.544 |
| Room-L80 | 2.692 | 10.08 | 0.002 | 0.222 | 0.536 | 13.532 |
| Data | (%) | (%) | (%) | (%) | (%) | |
|---|---|---|---|---|---|---|
| Room_L80 | MCGC-1 | 39.67 | 51.61 | 13.98 | 7.44 | 44.86 |
| MCGC-2 | 46.09 | 56.99 | 16.13 | 5.22 | 50.96 | |
| MCGC-3 | 52.73 | 62.37 | 21.51 | 0.9 | 57.15 | |
| MCGC-4 | 71.43 | 75.27 | 4.3 | 6.1 | 73.28 | |
| MCGC-5 | 50.45 | 60.22 | 16.13 | 2.7 | 54.9 | |
| MCGC | 74.26 | 80.65 | 4.3 | 2.97 | 77.32 | |
| Conference | MCGC-1 | 30.95 | 31.33 | 3.61 | 8.33 | 31.13 |
| MCGC-2 | 36.84 | 42.17 | 16.87 | 9.47 | 39.32 | |
| MCGC-3 | 48.84 | 50.6 | 12.05 | 2.33 | 49.71 | |
| MCGC-4 | 68.57 | 57.83 | 7.23 | 12.86 | 62.75 | |
| MCGC-5 | 39.58 | 45.78 | 10.84 | 7.29 | 42.46 | |
| MCGC | 73.53 | 69.44 | 8.3 | 10.29 | 71.43 |
| Data | Method | (%) | (%) | (%) | (%) | (%) | Runtime (s) |
|---|---|---|---|---|---|---|---|
| Conference | Efficient RANSAC | 19.35 | 28.92 | 48.19 | 7.50 | 23.19 | 6.3027 |
| RG | 32.94 | 33.73 | 21.69 | 12.94 | 33.33 | 20.43 | |
| LCCP | 30.95 | 31.33 | 3.61 | 8.33 | 31.13 | 3.47 | |
| VGS | 42.86 | 43.37 | 28.92 | 7.14 | 43.12 | 10.101 | |
| MCGC | 73.53 | 69.44 | 8.30 | 10.29 | 71.43 | 5.771 | |
| Office-1 | Efficient RANSAC | 19.82 | 40.74 | 42.59 | 2.70 | 26.67 | 3.846 |
| RG | 50.00 | 46.30 | 20.37 | 6.00 | 48.10 | 8.352 | |
| LCCP | 31.58 | 44.44 | 9.26 | 10.53 | 36.92 | 1.497 | |
| VGS | 53.66 | 40.72 | 16.67 | 14.63 | 46.31 | 4.752 | |
| MCGC | 70.91 | 72.22 | 9.26 | 7.27 | 71.56 | 2.586 | |
| Office-2 | Efficient RANSAC | 40.23 | 39.77 | 34.48 | 10.23 | 40.00 | 10.138 |
| RG | 20.96 | 40.23 | 43.68 | 3.00 | 27.55 | 78.094 | |
| LCCP | 28.21 | 25.29 | 16.09 | 11.54 | 26.67 | 4.486 | |
| VGS | 33.58 | 45.98 | 36.78 | 7.46 | 38.81 | 9.786 | |
| MCGC | 79.45 | 66.67 | 10.34 | 8.22 | 72.50 | 6.88 | |
| Room-L9 | Efficient RANSAC | 24.36 | 35.19 | 27.78 | 6.41 | 28.83 | 78.450 |
| RG | 34.44 | 57.41 | 35.19 | 5.56 | 43.05 | 266.326 | |
| LCCP | 27.06 | 42.59 | 11.11 | 10.59 | 33.09 | 37.638 | |
| VGS | 65.79 | 46.30 | 9.26 | 10.53 | 54.35 | 46.630 | |
| MCGC | 77.05 | 87.04 | 11.11 | 3.28 | 81.74 | 23.544 | |
| Room-L80 | Efficient RANSAC | 47.62 | 43.00 | 16.13 | 11.90 | 45.16 | 64.287 |
| RG | 42.22 | 61.29 | 9.70 | 2.96 | 50.00 | 155.026 | |
| LCCP | 39.67 | 51.61 | 13.98 | 7.44 | 44.86 | 24.788 | |
| VGS | 64.81 | 37.63 | 9.68 | 14.81 | 47.62 | 33.186 | |
| MCGC | 74.26 | 80.65 | 4.30 | 2.97 | 77.32 | 13.532 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Z.; Xie, Z.; Wan, J.; Zeng, Z.; Liu, L.; Tao, L. Indoor 3D Point Cloud Segmentation Based on Multi-Constraint Graph Clustering. Remote Sens. 2023, 15, 131. https://doi.org/10.3390/rs15010131
Luo Z, Xie Z, Wan J, Zeng Z, Liu L, Tao L. Indoor 3D Point Cloud Segmentation Based on Multi-Constraint Graph Clustering. Remote Sensing. 2023; 15(1):131. https://doi.org/10.3390/rs15010131
Chicago/Turabian StyleLuo, Ziwei, Zhong Xie, Jie Wan, Ziyin Zeng, Lu Liu, and Liufeng Tao. 2023. "Indoor 3D Point Cloud Segmentation Based on Multi-Constraint Graph Clustering" Remote Sensing 15, no. 1: 131. https://doi.org/10.3390/rs15010131
APA StyleLuo, Z., Xie, Z., Wan, J., Zeng, Z., Liu, L., & Tao, L. (2023). Indoor 3D Point Cloud Segmentation Based on Multi-Constraint Graph Clustering. Remote Sensing, 15(1), 131. https://doi.org/10.3390/rs15010131







