Climatological Changes in Soil Moisture during the 21st Century over the Indian Region Using CMIP5 and Satellite Observations
Abstract
:1. Introduction
2. Data and Methodology
- H = depth/height (in m)
- ρw = density of water (in kg/m3)
- V = Volumetric soil moisture (in m3/m3)
- STDobs = Standard deviation of observations (AMSR-E)
3. Results
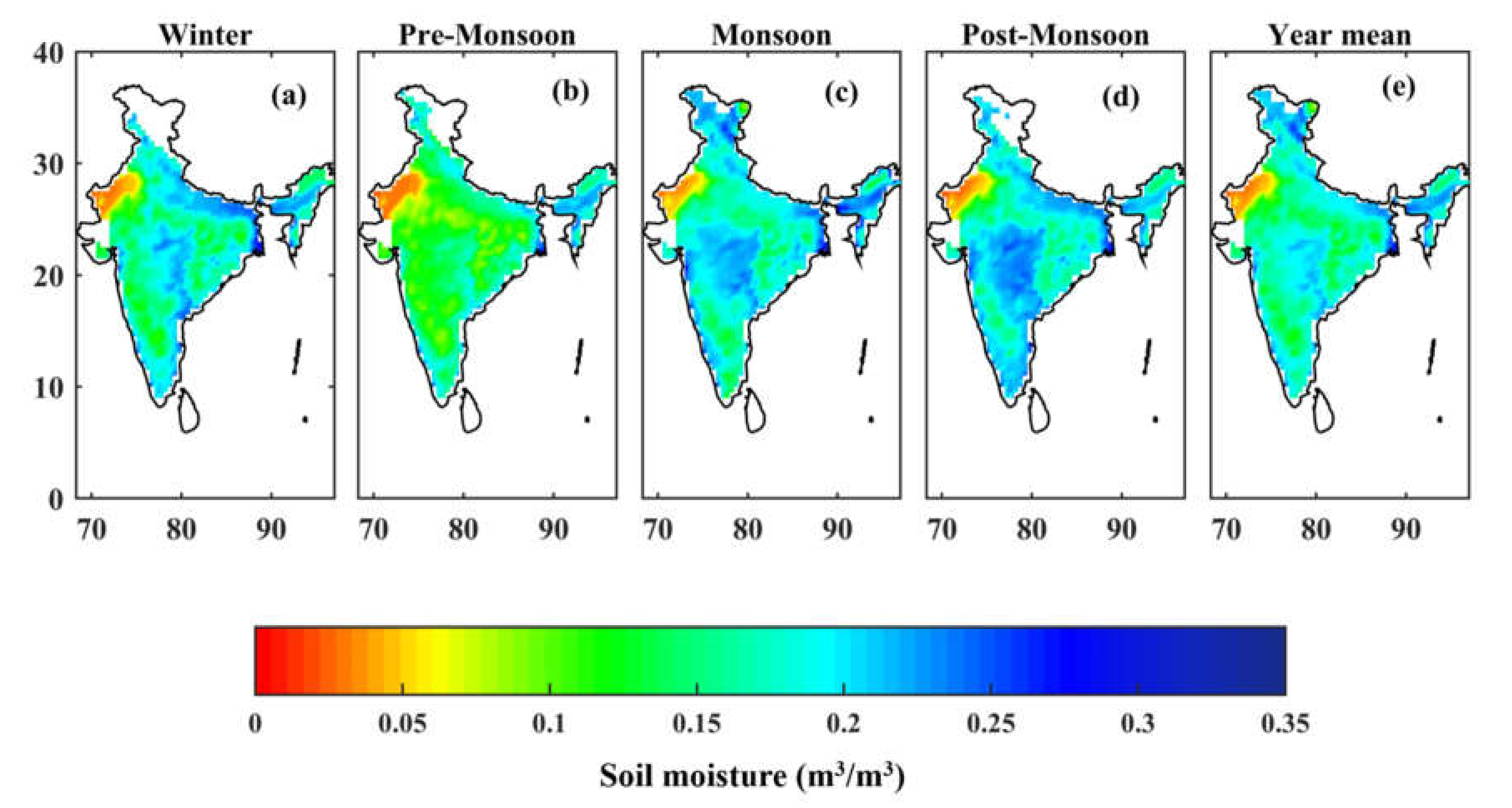
3.1. AMSR-E Seasonal and Annual Climatologies:
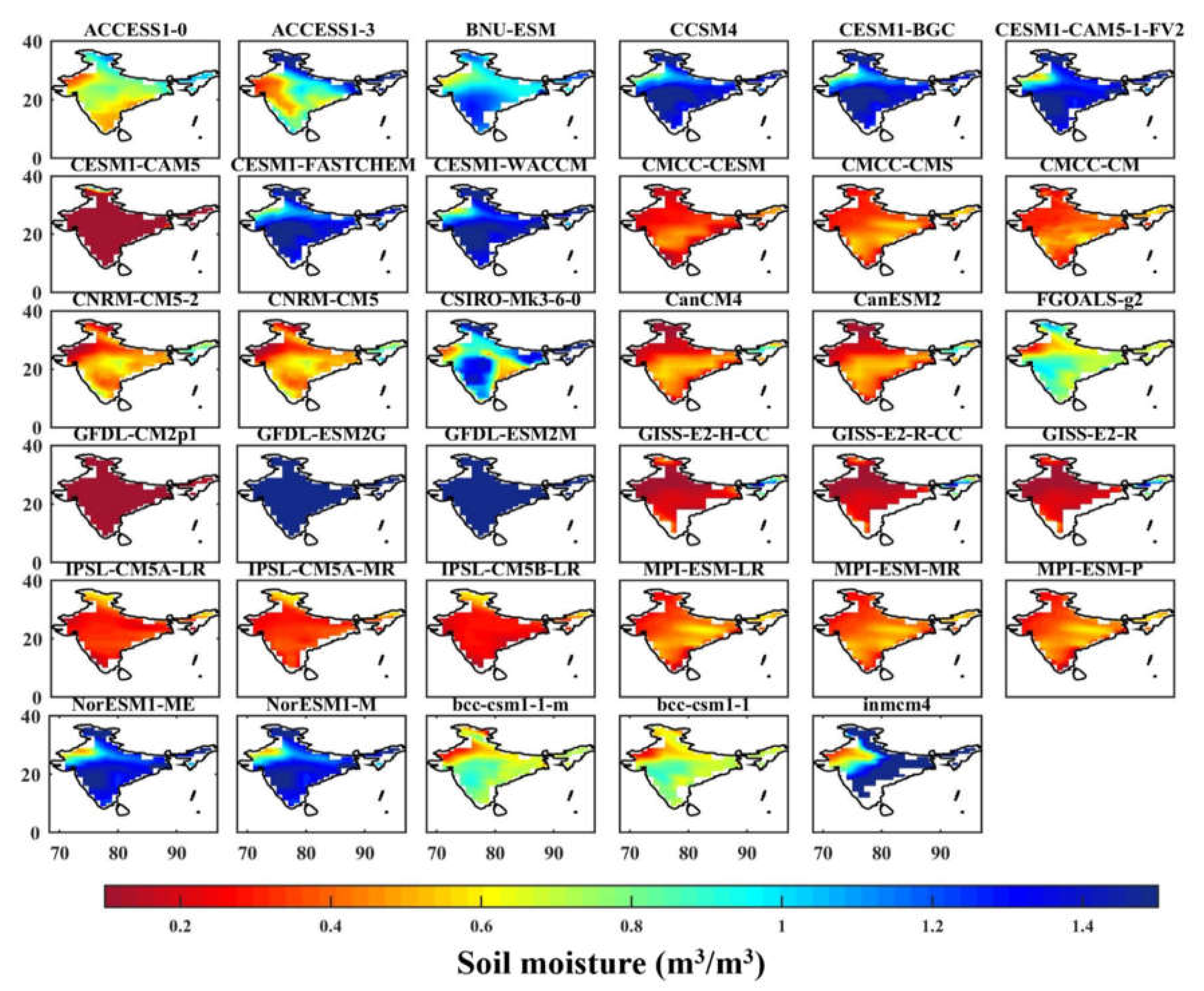
3.2. CMIP5 Historical Seasonal Distributions
3.3. RCP8.5 Seasonal Climatologies
3.4. Statistical Methods
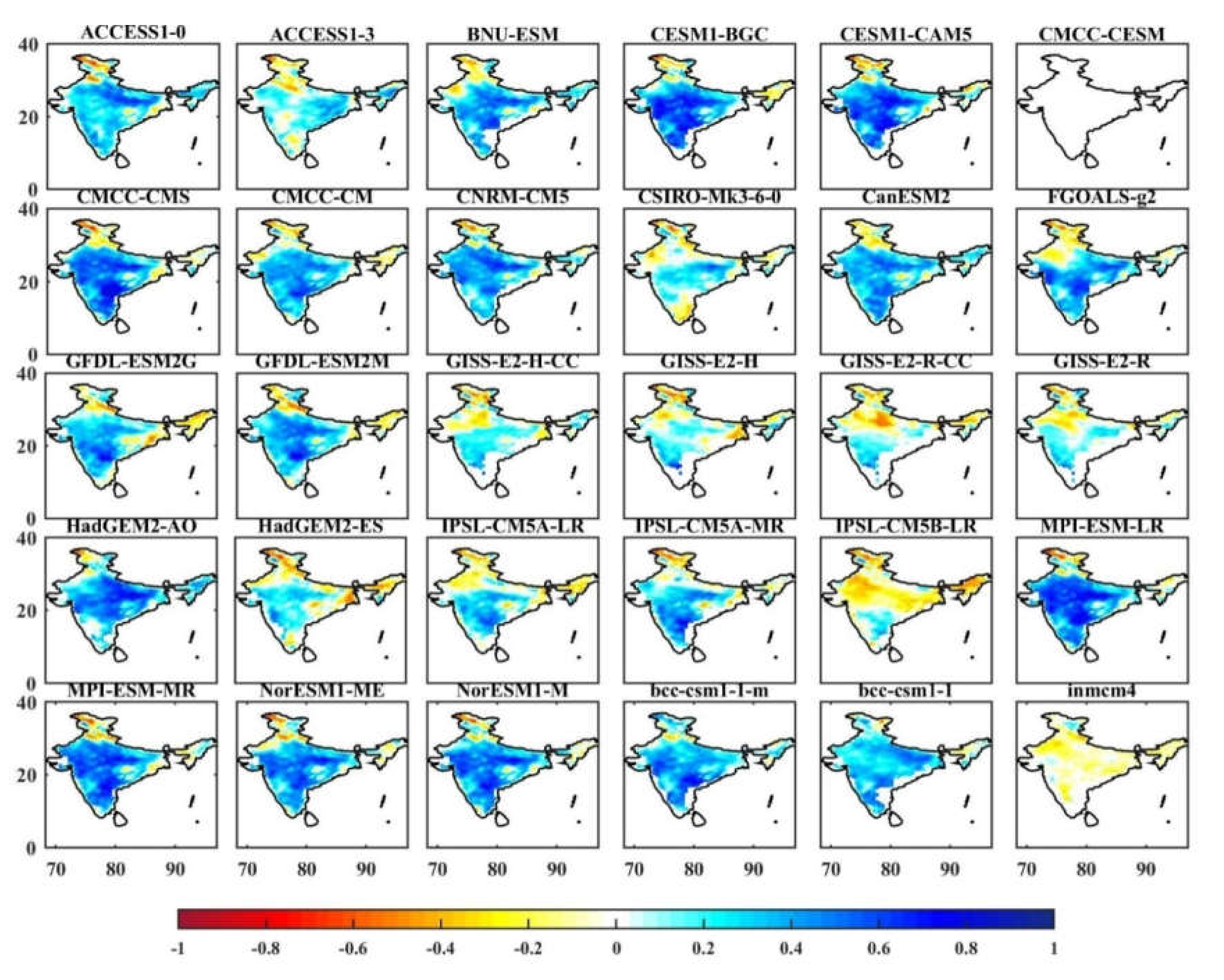
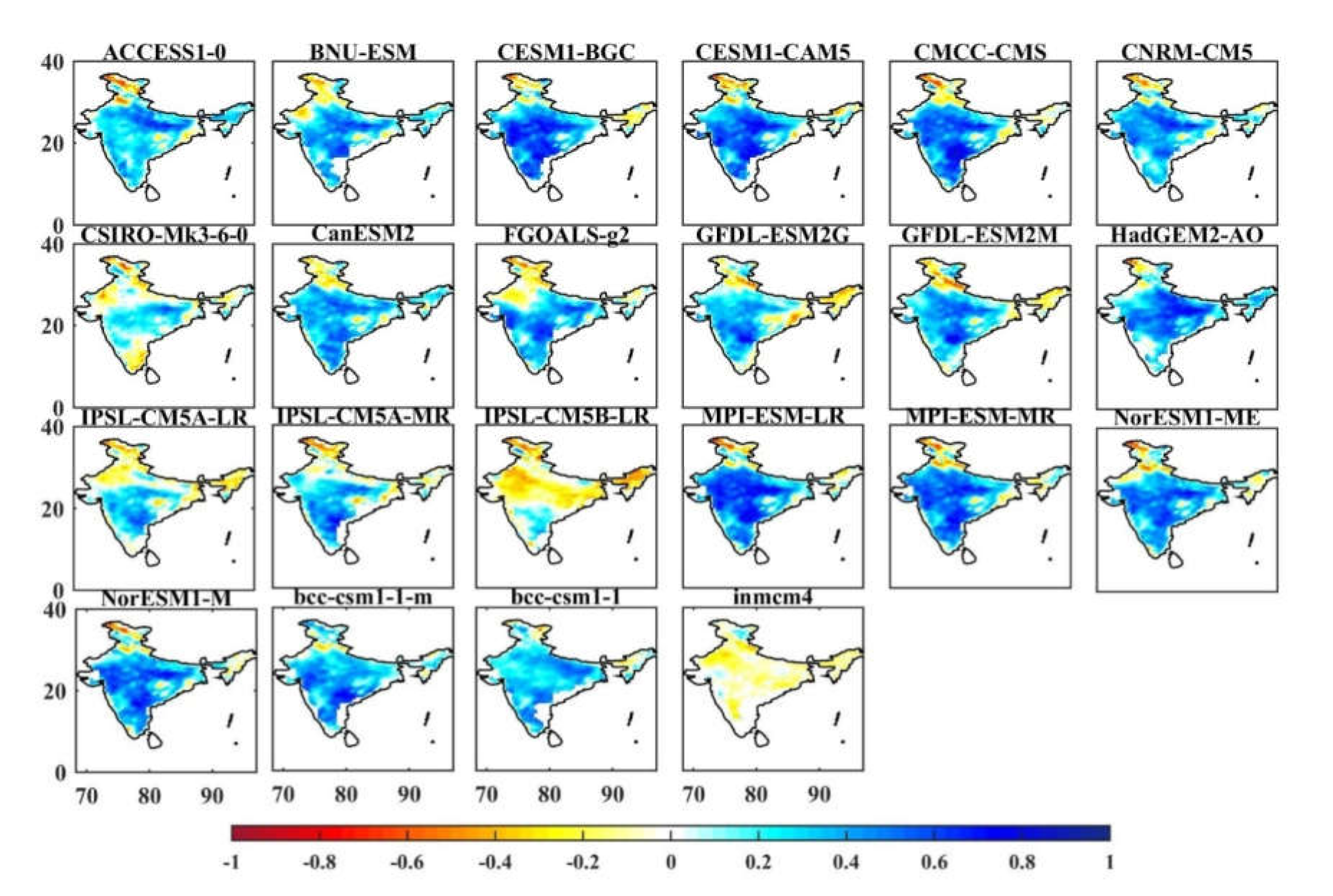
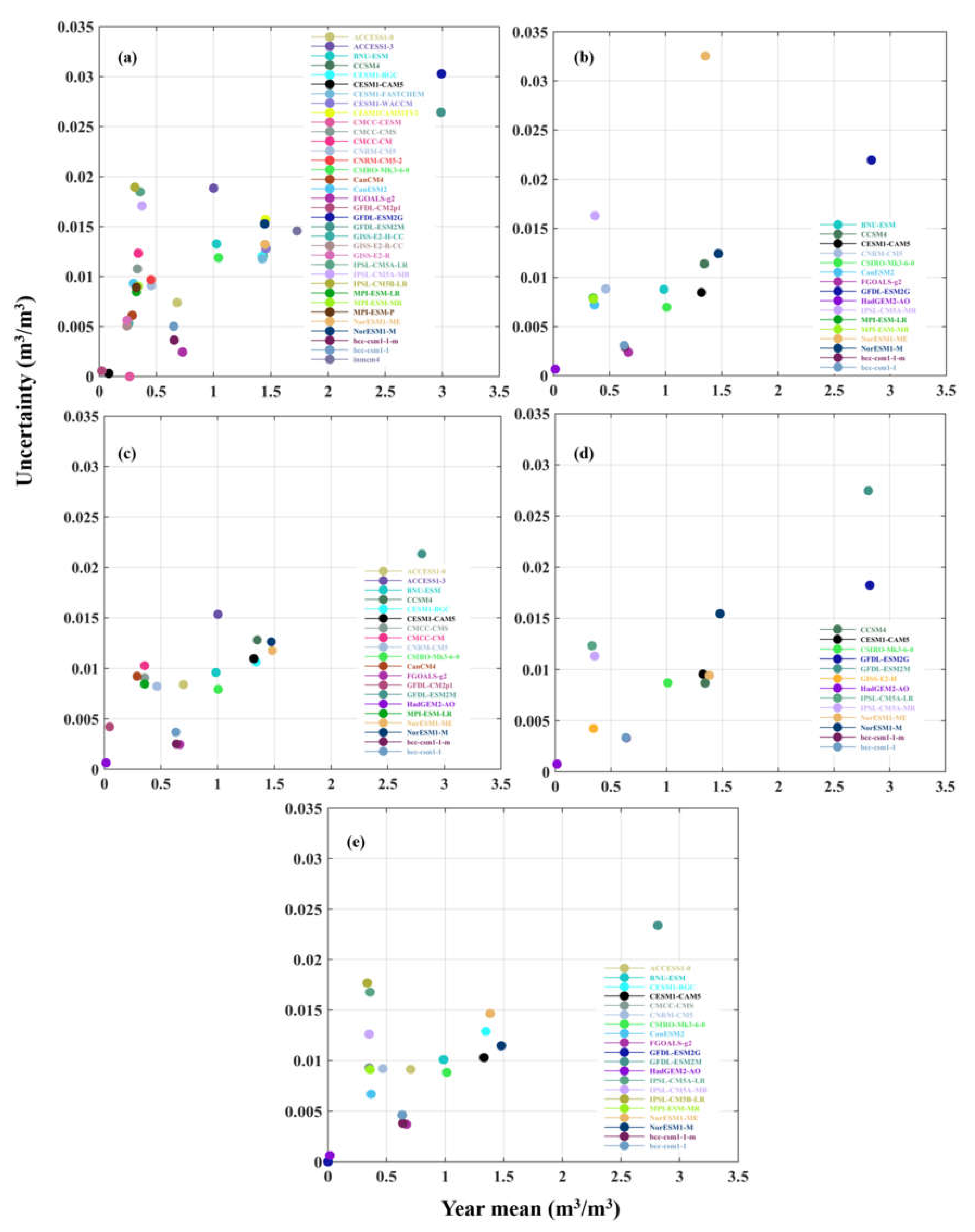
3.4.1. Spatial Correlation Analysis between CMIP5 and AMSR-E
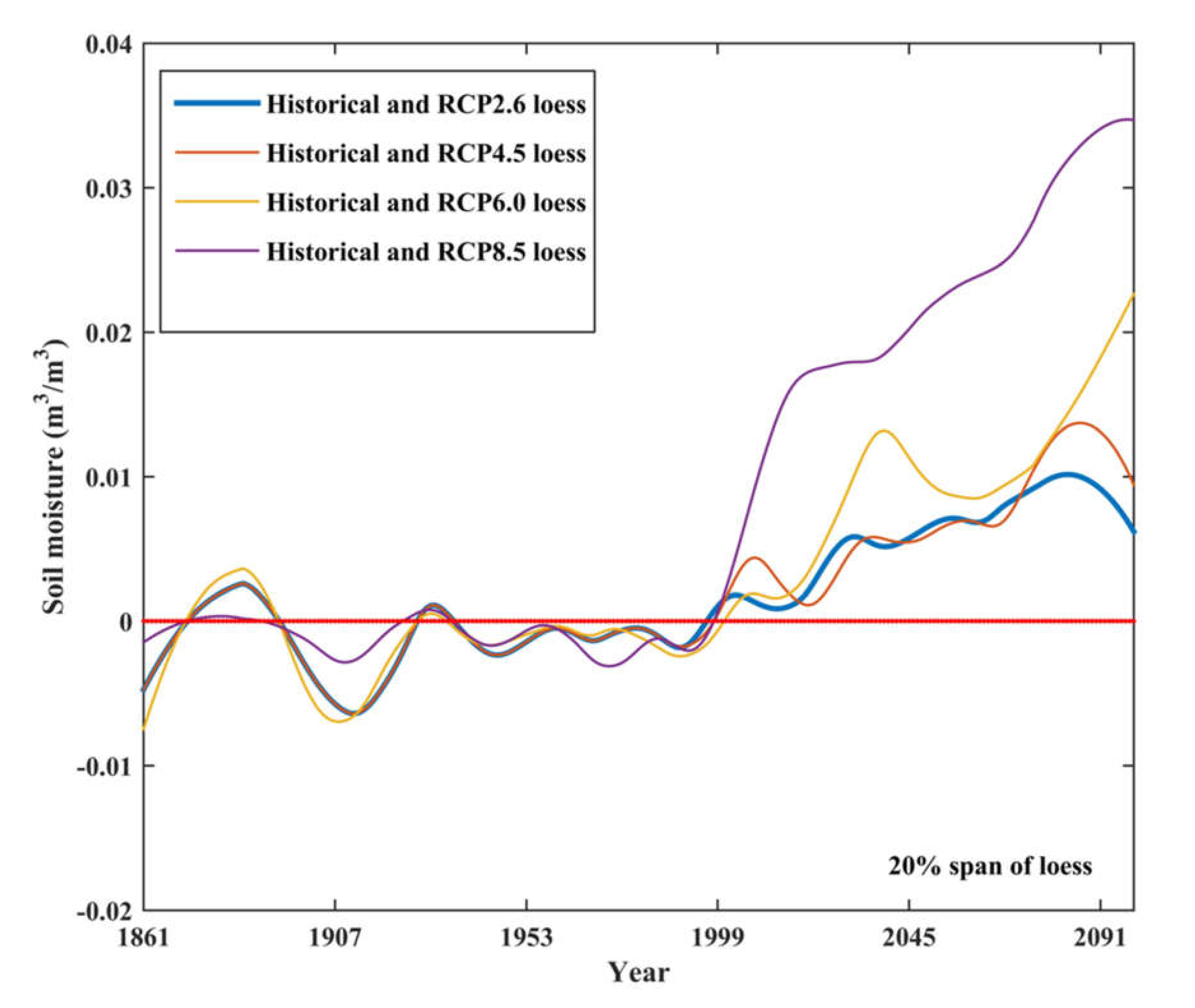
3.4.2. Soil Moisture Anomalies
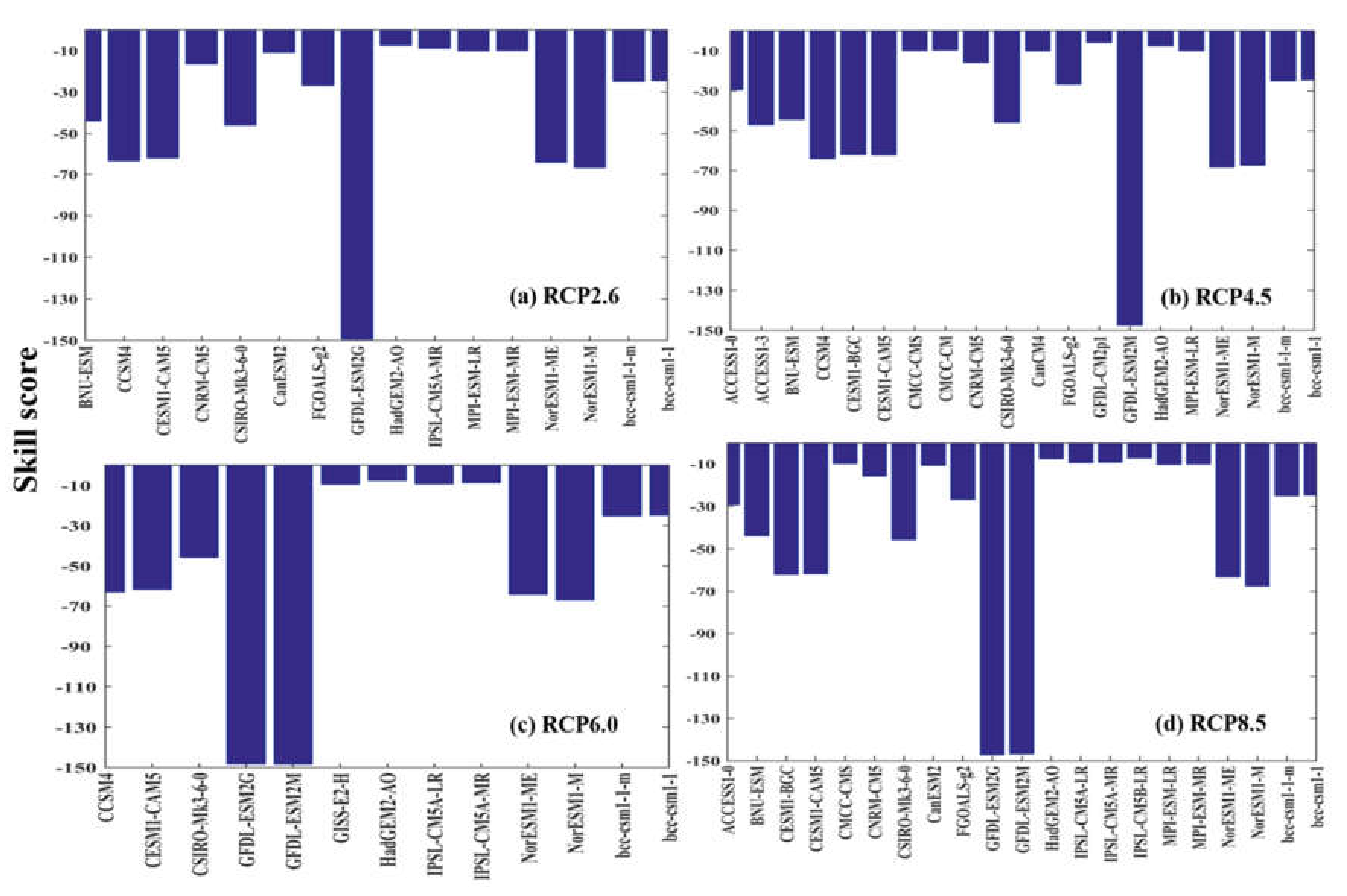
3.4.3. RCP’s Skill Scores
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AMSR-E | Advanced Microwave Scanning Radiometer-Earth observation system |
| CEDA | Centrer for Environmental Data Analysis |
| CMIP3 | Coupled Model Intercomparison Project Phase3 |
| CMIP5 | Coupled Model Intercomparison Project Phase5 |
| CONUS | Contiguous United States |
| ESM | Earth System Models |
| GCMs | General Circulation Models or Global Climate Models |
| GLDAS | Global Land Data Assimilation System |
| IPCC | Intergovernmental Panel on Climate Change (IPCC) |
| JAXA | Japan Aerospace Exploration Agency |
| Loess | Locally Estimated Scatterplot Smoothing |
| NASA | National Aeronautics and Space Administration |
| NSIDC | National Snow and Ice Data Centre |
| PCMDI | Program Climate Model Diagnosis and Intercomparison |
| RCPs | Representative Concentration Pathways |
| RMSE | Root Mean Square Error |
| SM | Soil moisture |
| STDobs | Standard deviation of observation (AMSR-E) |
| UKMO | United Kingdom Meteorological Office |
| USA | United States of America |
| WCRP | World Climate Research Program |
References
- Al-Yaari, A.; Ducharne, A.; Cheruy, F.; Crow, W.T.; Wigneron, J.P. Satellite-based soil moisture provides missing link between summertime precipitation and surface temperature biases in CMIP5 simulations over conterminous United States. Sci. Rep. 2019, 9, 1657. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bai, W.; Gu, X.; Li, S.; Tang, Y.; He, Y.; Gu, X.; Bai, X. The performance of multiple model-simulated soil moisture datasets relative to ECV satellite data in China. Water 2018, 10, 1384. [Google Scholar] [CrossRef] [Green Version]
- Reichle, R.H.; Koster, R.D.; Liu, P.; Mahanama, S.P.P.; Njoku, E.G.; Owe, M. Comparison and assimilation of global soil moisture retrievals from the Advanced Microwave Scanning Radiometer for the Earth Observing System (AMSR-E) and the Scanning Multichannel Microwave Radiometer (SMMR). J. Geophys. Res. 2007, 112, D09108. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, J.; Chen, Y.; Wang, A.; De Maeyer, P. The spatiotemporal response of soil moisture to precipitation and temperature changes in an arid region, China. Remote Sens. 2018, 10, 468. [Google Scholar] [CrossRef] [Green Version]
- Seo, E.; Lee, M.I.; Jeong, J.H.; Koster, R.D.; Schubert, S.D.; Kim, H.M.; Kim, D.; Kang, H.S.; Kim, H.K.; MacLachlan, C.; et al. Impact of soil moisture initialization on boreal summer subseasonal forecasts: Mid-latitude surface air temperature and heat wave events. Clim. Dyn. 2019, 52, 1695–1709. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Wilhelm, M.; Stanelle, T.; Van Den Hurk, B.; Hagemann, S.; Berg, A.; Cheruy, F.; Higgins, M.E.; Meier, A.; Brovkin, V.; et al. Impact of soil moisture-climate feedbacks on CMIP5 projections: First results from the GLACE-CMIP5 experiment. Geophys. Res. Lett. 2013, 40, 5212–5217. [Google Scholar] [CrossRef] [Green Version]
- IPCC. Climate Change: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team, Pachauri, R.K., Meyer, L.A., Eds.; IPCC: Geneva, Switzerland, 2014; p. 151. [Google Scholar]
- Stocker, T.F.; Qin, D.; Plattner, G.K.; Tignor, M.M.B.; Allen, S.K.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, V.; Midgley, P.M. Climate Change 2013 the Physical Science Basis: Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; Volume 9781107057, pp. 1–1535. [Google Scholar] [CrossRef] [Green Version]
- Orlowsky, B.; Seneviratne, S.I. Elusive drought: Uncertainty in observed trends and short- and long-term CMIP5 projections. Hydrol. Earth Syst. Sci. 2013, 17, 1765–1781. [Google Scholar] [CrossRef] [Green Version]
- Roderick, M.L.; Greve, P.; Farquhar, G.D. On the assessment of aridity with changes in atmospheric CO2. Water Resour. Res. 2015, 51, 5450–5463. [Google Scholar] [CrossRef] [Green Version]
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture-climate interactions in a changing climate: A review. Earth Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Dai, A.; Van der Schrier, G.; Jones, P.D.; Barichivich, J.; Briffa, K.R.; Sheffield, J. Global warming and changes in drought. Nat. Clim. Change 2014, 4, 17–22. [Google Scholar] [CrossRef]
- Chen, X.; Hu, Q. Groundwater influences on soil moisture and surface evaporation. J. Hydrol. 2004, 297, 285–300. [Google Scholar] [CrossRef] [Green Version]
- Douville, H. Relevance of soil moisture for seasonal atmospheric predictions: Is it an initial value problem? Clim. Dyn. 2004, 22, 429–446. [Google Scholar] [CrossRef]
- Conil, S.; Douville, H.; Tyteca, S. The relative roles of soil moisture and SST in climate variability explored within ensembles of AMIP-type simulations. Clim. Dyn. 2004, 28, 125–145. [Google Scholar] [CrossRef]
- Du, J.; Kimball, J.S.; Jones, L.A.; Kim, Y.; Glassy, J.; Watts, J.D. A global satellite environmental data record derived from AMSR-E and AMSR2 microwave Earth observations. Earth Syst. Sci. Data 2017, 9, 791–808. [Google Scholar] [CrossRef] [Green Version]
- Nayak, H.P.; Osuri, K.K.; Sinha, P.; Nadimpalli, R.; Mohanty, U.C.; Chen, F.; Rajeevan, M.; Niyogi, D. High-resolution gridded soil moisture and soil temperature datasets for the Indian monsoon region. Sci. Data 2018, 5, 180264. [Google Scholar] [CrossRef] [PubMed]
- Kishore, P.; Velicogna, I.; Geruo, A.; Mohajerani, Y.; Ciracì, E.; Charakola, S.; Basha, G.; Rao, S.V.B. Soil Moisture Variability in India: Relationship of Land Surface–Atmosphere Fields Using Maximum Covariance Analysis. Remote Sens. 2019, 11, 335. [Google Scholar] [CrossRef] [Green Version]
- Zahid, M.; Iqbal, W.; Rasul, G. CMIP5 Projected Soil Moisture Changes over South Asia. Pak. J. Meteoro. 2014, 10, 13–24. [Google Scholar]
- Yuan, S.; Quiring, S.M. Evaluation of soil moisture in CMIP5 simulations over the contiguous United States using in situ and satellite observations. Hydrol. Earth Syst. Sci. 2017, 21, 2203–2218. [Google Scholar] [CrossRef] [Green Version]
- Ruosteenoja, K.; Markkanen, T.; Venäläinen, A.; Räisänen, P.; Peltola, H. Seasonal soil moisture and drought occurrence in Europe in CMIP5 projections for the 21st century. Clim. Dyn. 2018, 50, 1177–1192. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Wang, L.; Ross, K.W.; Liu, C.; Berry, K. Standardized soil moisture index for drought monitoring based on soil moisture active passive observations and 36 years of North American Land Data Assimilation System data: A case study in the Southeast United States. Remote Sens. 2018, 10, 301. [Google Scholar] [CrossRef] [Green Version]
- Xin, X.; Wu, T.; Zhang, J.; Yao, J.; Fang, Y. Comparison of CMIP6 and CMIP5 simulations of precipitation in China and the East Asian summer monsoon. Int. J. Climatol. 2020, 40, 6423–6440. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Frauenfeld, O.W. A comprehensive evaluation of precipitation simulations over China based on CMIP5 multi-model ensemble projections. J. Geophys. Res. Atmos. 2014, 119, 5767–5786. [Google Scholar] [CrossRef]
- Taylor, C.M.; de Jeu, R.A.; Guichard, F.; Harris, P.P.; Dorigo, W.A. Afternoon rain more likely over drier soils. Nature 2012, 489, 423. [Google Scholar] [CrossRef] [Green Version]
- Xin, X.; Wu, T.; Zhang, J. Introduction of CMIP5 experiments carried out with the climate system models of Beijing climate center. Adv. Clim. Chang. Res. 2013, 4, 41–49. [Google Scholar] [CrossRef]
- Ji, D.; Wang, L.; Feng, J.; Wu, Q.; Cheng, H.; Zhang, Q.; Yang, J.; Dong, W.; Dai, Y.; Gong, D.; et al. Description and basic evaluation of Beijing Normal University earth system model (BNU-ESM) version 1. Geosci. Model Dev. 2014, 7, 2039–2064. [Google Scholar] [CrossRef] [Green Version]
- Merryfield, W.J.; Lee, W.; Boer, G.; Kharin, V.; Scinocca, J.; Flato, G.; Ajayamohan, R.; Fyfe, J.; Tang, Y.; Polavarapu, S. The Canadian seasonal to interannual prediction system. Part I: Models and initialization. Mon. Weather Rev. 2013, 141, 2910–2945. [Google Scholar] [CrossRef]
- Arora, V.K.; Scinocca, J.F.; Boer, G.J.; Christian, J.R.; Denman, K.L.; Flato, G.M.; Kharin, V.V.; Lee, W.G.; Merryfield, W.J. Carbon emission limits required to satisfy future representative concentration pathways of greenhouse gases. Geophys. Res. Lett. 2011, 38, L05805. [Google Scholar] [CrossRef]
- Scoccimarro, E.; Gualdi, S.; Bellucci, A.; Sanna, A.; Giuseppe Fogli, P.; Manzini, E.; Vichi, M.; Oddo, P.; Navarra, A. Effects of tropical cyclones on ocean heat transport in a high-resolution coupled general circulation model. J. Clim. 2011, 24, 4368–4384. [Google Scholar] [CrossRef] [Green Version]
- Voldoire, A.; Sanchez-Gomez, E.; Salas y Mélia, D.; Decharme, B.; Cassou, C.; Sénési, S.; Valcke, S.; Beau, I.; Alias, A.; Chevallier, M.; et al. The CNRM-CM5.1 global climate model: Description and basic evaluation. Clim. Dyn. 2013, 40, 2091–2121. [Google Scholar] [CrossRef] [Green Version]
- Bi, D.; Dix, M.; Marsland, S.J.; O’Farrell, S.; Rashid, H.A.; Uotila, P.; Hirst, A.C.; Kowalczyk, E.; Golebiewski, M.; Sullivan, A.; et al. The ACCESS coupled model: Description, control climate and evaluation. Aust. Meteorol. Oceanogr. J. 2013, 63, 41–64. [Google Scholar] [CrossRef]
- Rotstayn, L.D.; Collier, M.A.; Dix, M.R.; Feng, Y.; Gordon, H.; O’Farrell, S.; Smith, I.; Syktus, J. Improved simulation of Australian climate and ENSO-related rainfall variability in a global climate model with an interactive aerosol treatment. Int. J. Climatol. 2010, 30, 1067–1088. [Google Scholar] [CrossRef]
- Volodin, E.M.; Diansky, N.A.; Gusev, A.V. Simulating present-day climate with the INMCM4.0 coupled model of the atmospheric and oceanic general circulations. Izvestiya Atmos. Ocean. Phys. 2010, 46, 414–431. [Google Scholar] [CrossRef]
- Cheruy, F.; Campoy, A.; Dupont, J.-C.; Ducharne, A.; Hourdin, F.; Haeffelin, M.; Chiriaco, M.; Idelkadi, A. Combined influence of atmospheric physics and soil hydrology on the simulated meteorology at the SIRTA atmospheric observatory. Clim. Dynam. 2013, 40, 2251–2269. [Google Scholar] [CrossRef]
- Li, L.; Lin, P.; Yu, Y.; Wang, B.; Zhou, T.; Liu, L.; Liu, J.; Bao, Q.; Xu, S.; Huang, W.; et al. The flexible global ocean-atmosphere-land system model.; grid-point version 2: FGOALS-g2. Adv. Atmos. Sci. 2013, 30, 543–560. [Google Scholar] [CrossRef]
- Zanchettin, D.; Rubino, A.; Matei, D.; Bothe, O.; Jungclaus, J. Multidecadal-to-centennial SST variability in the MPI-ESM simulation ensemble for the last millennium. Clim. Dyn. 2013, 40, 1301–1318. [Google Scholar] [CrossRef]
- Raddatz, T.; Reick, C.; Knorr, W.; Kattge, J.; Roeckner, E.; Schnur, R.; Schnitzler, K.-G.; Wetzel, P.; Jungclaus, J. Will the tropical land biosphere dominate the climate–carbon cycle feedback during the twenty-first century? Clim. Dynam. 2007, 29, 565–574. [Google Scholar] [CrossRef]
- Miller, R.; Schmidt, G.; Nazarenko, L.; Tausnev, N.; Bauer, S.; DelGenio, A.; Kelley, M.; Lo, K.; Ruedy, R.; Shindell, D.; et al. CMIP5 historical simulations (1850–2012) with GISS ModelE2. J. Adv. Model. Earth Syst. 2014, 6, 441–478. [Google Scholar] [CrossRef]
- Gent, P.R.; Danabasoglu, G.; Donner, L.J.; Holland, M.M.; Hunke, E.C.; Jayne, S.R.; Lawrence, D.M.; Neale, R.B.; Rasch, P.J.; Vertenstein, M.; et al. The Community Climate System Model Version 4. J. Clim. 2011, 24, 4973–4991. [Google Scholar] [CrossRef]
- Bentsen, M.; Bethke, I.; Debernard, J.; Iversen, T.; Kirkevåg, A.; Seland, Ø.; Drange, H.; Roelandt, C.; Seierstad, I.; HooseCKristjánsson, J. The Norwegian earth system model, NorESM1-M–Part 1: Description and basic evaluation. Geosci. Model Dev. Discus. 2012, 5, 2843–2931. [Google Scholar] [CrossRef]
- Collins, W.J.; Bellouin, N.; Doutriaux-Boucher, M.; Gedney, N.; Halloran, P.; Hinton, T.; Hughes, J.; Jones, C.D.; Joshi, M.; Liddicoat, S.; et al. Development and evaluation of an earth-system model–HadGEM2. Geosci. Model Dev. 2011, 4, 1051–1075, 2011. [Google Scholar] [CrossRef] [Green Version]
- Dunne, J.; John, J.; Adcroft, A.; Griffies, S.; Hallberg, R.; Shevliakova, E.; Stouffer, R.; Cooke, W.; Dunne, K.; Harrison, M.; et al. GFDL’s ESM2 global coupled climate–carbon earth system models. Part I: Physical formulation and baseline simulation characteristics. J. Clim. 2012, 25, 6646–6665. [Google Scholar] [CrossRef] [Green Version]
- Long, M.; Lindsay, K.; Peacock, S.; Moore, J.K.; Doney, S. Twentieth-century oceanic carbon uptake and storage in CESM1(BGC). J. Clim. 2013, 26, 6775–6800. [Google Scholar] [CrossRef]
- Lamarque, J. CESM1-FASTCHEM Model Output Prepared for CMIP5 Historical, Served by ESGF; WDCC at DKRZ: Hamburg, Germany, 2013. [Google Scholar] [CrossRef]
- Marsh, D.R.; Mills, M.J.; Kinnison, D.E.; Lamarque, J.F.; Calvo, N.; Polvani, L.M. Climate change from 1850 to 2005 simulated in CESM1 (WACCM). J. Clim. 2013, 26, 7372–7390. [Google Scholar] [CrossRef] [Green Version]
- Draper, C.S.; Walker, J.P.; Steinle, P.; De Jeu, R.A.M.; Holmes, T.R.H. An evaluation of AMSR-E derived soil moisture over Australia. Remot. Sen. Environ. 2009, 113, 703–710. [Google Scholar] [CrossRef]
- Cleveland, W.S.; Devlin, S.J. Locally weighted regression: An approach to regression analysis by local fitting. J. Am. Stat. Assoc. 1988, 83, 596–610. [Google Scholar] [CrossRef]
- Kim, H.; Parinussa, R.; Konings, A.G.; Wagner, W.; Cosh, M.H.; Lakshmi, V.; Zohaib, M.; Choi, M. Global-scale assessment and combination of SMAP with ASCAT (active) and AMSR2 (passive) soil moisture products. Remote Sens. Environ. 2018, 204, 260–275. [Google Scholar] [CrossRef]
- Kishore, P.; Jyothi, S.; Basha, G.; Rao, S.V.B.; Rajeevan, M.; Velicogna, I.; Sutterley, T.C. Precipitation climatology over India: Validation with observations and reanalysis datasets and spatial trends. Clim. Dyn. 2016, 46, 541–556. [Google Scholar] [CrossRef] [Green Version]
- Burkey, J. Estimating a Models Skill of Predictability, MATLAB Central File Exchange. Available online: https://www.mathworks.com/matlabcentral/fileexchange/14177-estimating-a-models-skill-of-predictability (accessed on 18 December 2021).
- Unnikrishnan, C.K.; Rajeevan, M.; Vijayabhaskara Rao, S.; Manoj, K. Development of a high resolution land surface dataset for the south Asian monsoon region. Curr. Sci. 2013, 105, 1235–1246. [Google Scholar]
- Mishra, V.; Asoka, A.; Vatta, K.; Lall, U. Groundwater depletion and associated CO2 emissions in India. Earth’s Future 2018, 6, 1672–1681. [Google Scholar] [CrossRef]
- Dirmeyer, P.A.; Jin, Y.; Singh, B.; Yan, X. Trends in Land-Atmosphere Interactions from CMIP5 Simulations. J. Hydrometeoral. 2013, 14, 829–849. [Google Scholar] [CrossRef]
- Zebaze, S.; Jain, S.; Salunke, P.; Shafiq, S.; Mishra, S.K. Assessment of CMIP5 multimodel mean for the historical climate of Africa. Atmos. Sci. Lett. 2019, 20, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Dike, V.N.; Shimizu, M.H.; Diallo, M.; Lin, Z.; Nwofor, O.K.; Chineke, T.C. Modelling present and future African climate using CMIP5 scenarios in HadGEM2-ES. Int. J. Climatol. 2015, 35, 1784–1799. [Google Scholar] [CrossRef]
- Sheffield, J.; Barrett, A.P.; Colle, B.; Fernando, D.N.; Fu, R.; Geil, K.L.; Hu, Q.; Kinter, J.; Kumar, S.; Langenbrunner, B.; et al. North American climate in CMIP5 experiments. Part I: Evaluation of historical simulations of continental and regional climatology. J. Climatol. 2013, 26, 9209–9245. [Google Scholar] [CrossRef] [Green Version]
- Vogel, M.M.; Zscheischler, J.; Seneviratne, S.I. Varying soil moisture-atmosphere feedbacks explain divergent temperature extremes and precipitation projections in central Europe. Earth Syst. Dyn. 2018, 9, 1107–1125. [Google Scholar] [CrossRef] [Green Version]
- Singh, R.; AchutaRao, K. Quantifying uncertainty in twenty-first century climate change over India. Clim. Dyn. 2018, 52, 3905–3928. [Google Scholar] [CrossRef]
- Knutti, R.; Sedláček, J. Robustness and uncertainties in the new CMIP5 climate model projections. Nat. Clim. Chang. 2013, 3, 369–373. [Google Scholar] [CrossRef]
- Zhang, Q.; Xiao, M.; Singh, V.P.; Liu, L.; Xu, C.Y. Observational evidence of summer precipitation deficit-temperature coupling in China. J. Geophys. Res.-Atmos. 2015, 120, 10040–10049. [Google Scholar] [CrossRef] [Green Version]



| S. No | Model Name | Historical | RCP2.6 | RCP4.5 | RCP6.0 | RCP8.5 | References | |
|---|---|---|---|---|---|---|---|---|
| 1 | BCC-csm-1-1 | Y | Y | Y | Y | Y | Xin et al. [26] | |
| 2 | BCC-csm-1-1-m | Y | Y | Y | Y | Y | Xin et al. [26] | |
| 3 | BNU-ESM | Y | Y | Y | N | Y | Ji et al. [27] | |
| 4 | CanCM4 | Y | N | Y | N | N | Merryfield et al. [28] | |
| 5 | CanESM2 | Y | Y | N | N | Y | Arora et al. [29] | |
| 6 | CMCC-CESM | Y | N | N | N | Y | Scoccimarro et al. [30] | |
| 7 | CMCC-CM | Y | N | Y | N | Y | Scoccimarro et al. [30] | |
| 8 | CMCC-CMS | Y | N | Y | N | Y | Scoccimarro et al. [30] | |
| 9 | CNRM-CM5 | Y | Y | Y | N | Y | Scoccimarro et al. [30] | |
| 10 | CNRM-CM5-2 | Y | N | N | N | N | Voldoire et al. [31] | |
| 11 | ACCESS1-0 | Y | N | Y | N | Y | Bi et al. [32] | |
| 12 | ACCESS1-3 | Y | N | Y | N | Y | Bi et al. [32] | |
| 13 | CSIRO-MK3-6.0 | Y | Y | Y | Y | Y | Rotstayn et al. [33] | |
| 14 | INMCM4 | Y | N | Y | N | Y | Volodin et al. [34] | |
| 15 | IPSL-CM5A-LR | Y | N | N | Y | Y | Cheruy et al. [35] | |
| 16 | IPSLCM5A-MR | Y | Y | Y | Y | Y | Cheruy et al. [35] | |
| 17 | IPSLCM5B-LR | Y | N | Y | N | Y | Cheruy et al. [35] | |
| 18 | FGOALS-G2 | Y | Y | Y | N | Y | Li et al. [36] | |
| 19 | MPI-ESM-LR | Y | Y | Y | N | Y | Zanchettin et al. [37] | |
| 20 | MPI-ESM-MR | Y | Y | N | N | Y | Zanchettin et al. [37] | |
| 21 | MPI-ESM-P | Y | N | N | N | N | Raddatz et al. [38] | |
| 22 | GISS-E2-H | N | Y | Y | Y | Y | Miller et al. [39] | |
| 23 | GISS-E2-HCC | Y | N | Y | N | Y | Miller et al. [39] | |
| 24 | GISS-E2-R | Y | Y | Y | Y | Y | Miller et al. [39] | |
| 25 | GISS-E2-R-CC | Y | N | Y | N | Y | Miller et al. [39] | |
| 26 | CCSM4 | Y | Y | Y | Y | N | Gent et al. [40] | |
| 27 | NorESM1-M | Y | Y | Y | Y | Y | Bentsen et al. [41] | |
| 28 | NorESM1-ME | Y | Y | Y | Y | Y | Bentsen et al. [41] | |
| 29 | HadGEM2-AO | N | Y | Y | Y | Y | Collins et al. [42] | |
| 30 | HadGEM2-ES | N | Y | Y | Y | Y | Collins et al. [42] | |
| 31 | GFDL-ESM-2G | Y | Y | N | Y | Y | Dunne et al. [43] | |
| 32 | GFDL-ESM-2M | Y | N | Y | Y | Y | Dunne et al. [43] | |
| 33 | GFDL-CM2p1 | Y | N | Y | N | N | Dunne et al. [43] | |
| 34 | CESM1-BGC | Y | N | Y | N | Y | Long et al. [44] | |
| 35 | CESM1-CAM5 | Y | Y | Y | Y | Y | Long et al. [44] | |
| 36 | CESM1-CAM5-1-FV2 | Y | N | N | N | N | Long et al. [44] | |
| 37 | CESM1-FASTCHEM | Y | N | N | N | N | Lamarque et al. [45] | |
| 38 | CESM1-WACCM | Y | N | N | N | N | Daniel et al. [46] | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sravani, C.; Kishore, P.; Jiang, J.H.; Rao, S.V.B. Climatological Changes in Soil Moisture during the 21st Century over the Indian Region Using CMIP5 and Satellite Observations. Remote Sens. 2022, 14, 2108. https://doi.org/10.3390/rs14092108
Sravani C, Kishore P, Jiang JH, Rao SVB. Climatological Changes in Soil Moisture during the 21st Century over the Indian Region Using CMIP5 and Satellite Observations. Remote Sensing. 2022; 14(9):2108. https://doi.org/10.3390/rs14092108
Chicago/Turabian StyleSravani, Charakola, Pangaluru Kishore, Jonathan H. Jiang, and S. Vijaya Bhaskara Rao. 2022. "Climatological Changes in Soil Moisture during the 21st Century over the Indian Region Using CMIP5 and Satellite Observations" Remote Sensing 14, no. 9: 2108. https://doi.org/10.3390/rs14092108
APA StyleSravani, C., Kishore, P., Jiang, J. H., & Rao, S. V. B. (2022). Climatological Changes in Soil Moisture during the 21st Century over the Indian Region Using CMIP5 and Satellite Observations. Remote Sensing, 14(9), 2108. https://doi.org/10.3390/rs14092108







