1. Introduction
Synthetic Aperture Radar (SAR) images have been used and studied in interferometric analyses for decades to map the elevations and displacements of the earth’s surface [
1]. The temporal decorrelation of SAR image stacks, acquired over repeated orbits, limits interferometric analyses to specific pixels, i.e., persistent scatterers (PSs), since the latter exhibit scattering behaviour that is stable over time. Typically, the selection of valid pixels and the detection of reliable scatterers in each resolution cell is an intense research topic, where the goal is to find as many valid scatterers as possible at the best spatial resolution. With respect to interferometric techniques, SAR Tomography (TomoSAR) has introduced a different strategy for processing a SAR data stack and has supported the evolution of interferometry in three-dimensional (3D) [
2,
3], four-dimensional [
4,
5], and five-dimensional [
6,
7]) applications. In contrast to interferometry, TomoSAR offers the possibility of identifying multiple permanent scatterers superimposed in a single resolution cell, thus significantly increasing the density of detected scatterers.
In analogy to time series interferometry, e.g., PS interferometry [
8], TomoSAR relies on the persistence of the scatterers during the observation period. Although the tomographic model of distributed sources [
9] can mitigate the short-term effects of decorrelating sources, distinguishing between reliable scatterers and false alarms is a daunting task, especially when dealing with data obtained over a long time interval.
The key point in TomoSAR PS detection is to identify and increase the number of detectable stable scatterers in the presence of noise. At the same time, the possibility of signal misinterpretation, i.e., false alarms [
5], needs to be minimized. Currently, efforts are still underway to develop modern and advanced methods to further increase the detection probability of persistent scatterers.
In the framework of SAR tomography, the detection of reliable scatterers can be generally addressed with detection methods that control the false alarm rate (FAR), such as the generalized likelihood ratio test (GLRT). GLRT has been used extensively, not only in tomographic PS recognition but also in various target recognition applications [
10,
11]. Within the GLRT scheme, the detection of individual or single scatterers present in a resolution cell is straightforward [
12,
13]. The critical aspect is to distinguish between multiple scatterers and especially to distinguish between single and double scatterers. Among the different strategies, there are two successful methods commonly used in the literature for characterizing multiple scatterers lying in the same range azimuth pixel: (1) sequential GLRT with cancellation (SGLRTC) [
12] and (2) support GLRT [
13], which is based on estimating the support of the unknown signal that best fits the data. SGLRTC adopts a cancellation strategy that first cancels the dominant scatterer and then evaluates the presence of the secondary scatterer in the residual signal. Support GLRT is a sequential test in which the presence of scatterers is detected first, followed by the discrimination of multiple scatterers. In other words, testing the signal strength in sub-spaces with higher dimensionality is achieved by sequentially adding a single direction, starting with the first one. When comparing the two approaches, SGLRTC is more efficient in terms of computational requirements, while support GLRT has a super-resolution capability that enables the detection of multiple layovered scatterers at distances below the Rayleigh resolution. To improve the computational efficiency of support GLRT, ref. [
14] proposed a fast implementation that is able to maintain the super-resolution capability.
Spatial averaging or multi-looking operations, through the estimation of a second-order data covariance matrix, represent a solid and significant strategy for improving the detection capability of typical GLRT-based methods over the scene and, in particular, over regions characterized by a low signal-to-noise ratio (SNR) [
15,
16]. The use of the covariance matrix of the data can improve the detection probability at the cost of a small reduction in spatial resolution. Indeed, by trading off spatial resolution, undeniable improvements have been reported in the context of SAR tomography for the detection of multiple permanent scatterers. In addition, the potential of polarimetric SAR (PolSAR) data is expected to further improve detection performance. The authors of [
17,
18] have shown that increasing the length of the observation vector as input to support GLRT [
13] using dual polarization data can mitigate the problem of a reduced number of available baselines. To take full advantage of PolSAR data, however, a method has been developed in [
19] (denoted as scattering property-based support GLRT) that incorporates polarimetric information into the detection test. The aim is not only to improve detection performance but also to allow the test to identify PS backscattering mechanisms. Indeed, this method can be considered as a first attempt at the classification of PSs besides the detection and the extraction of their parameters related to the elevation, displacement, or thermal dilation in 3D, 4D, and 5D applications.
This paper presents a comparative study to answer the question of which polarization design for a radar antenna provides the best detection probability. To this end, we introduce an extension of the scattering support GLRT [
19] that takes the dependence on the polarization basis into account. The analysis is based upon the evaluation of the detection performance in all synthesized polarizations obtained from polarimetric measurements on a linear orthonormal basis. The main consequence of the analysis is the complete characterization of the studied scatterers. This allows the selection of the optimal polarization, i.e., the polarization that provides the highest detection probability. The identification of the best polarization basis is, in fact, the main contribution of the proposed method, which consequently leads to an increase in the density of the detected permanent scatterers and provides a better possibility of modeling the three-dimensional structures of the sensed objects and their possible slow deformation and thermal dilation. Additionally, the proposed method paves the way for comprehending the detection performance in TomoSAR data in terms of the transmitted and received polarizations used, thus complementing polarimetric-based PS detection studies.
The paper is organized as follows.
Section 2 begins with the basic principles of SAR polarimetry, while an overview of existing scattering support GLRT is given in
Section 3. After these introductory descriptions, the proposed method is presented in
Section 4. Experimental results using simulated and real data sets from the Experimental SAR System (ESAR) of the German Aerospace Center and Uninhabited Aerial Vehicle SAR (UAVSAR) are presented in
Section 5. The discussion and conclusions regarding the reported results are provided in
Section 6 and
Section 7.
2. SAR Polarimetry
The polarization information in SAR images is related to both the geometrical structure and the orientation of the observed objects [
20]. The characteristic information of any target sensed by a full polarimetric radar sensor can be represented in a
scattering matrix
.
where the complex scattering coefficient
represents the electromagnetic wave emitted through the polarization channel
v and received on channel
h. In the case of interchanging the role of the transmitting and receiving antennas, i.e., with the reciprocity theorem, the scattering matrix is symmetric, i.e.,
. Once the scattering matrix in (
1) is known, a key point is that radar cross-sections can be synthesized for any arbitrary combination of transmit and receive polarizations [
21]. In this study, we will consider this point to determine the optimal transmit and receive polarizations that offer the best PS detection performance.
Let us now consider the geometry of the multi-baseline, multi-temporal polarimetric SAR imaging system that operates at wavelength
and range distance
r. In this geometry, referring to a resolution cell, the stack data vector
, which collects the information from
N polarimetric sensors, can be represented as Equation (
2) [
22,
23]. The data stack is acquired under interferometric conditions and co-registered with respect to a given master image and compensated for atmospheric effects and possible small-scale nonlinear deformations. Each polarimetric sensor is assumed to acquire images in three linear polarization channels (
hh,
hv,
vv) with reciprocal condition. The multi-baseline imaging geometry thus yields
image channels or
, where
represents the set of
complex vectors.
In (
2),
is the
lth realization, i.e., look, of the complex reflectivity vector of
M superimposed scatterers into the resolution cell, which is invariant with respect to the different polarizations. Moreover, the matrix
equals to
with
, where
represents the steering vector of the
mth superimposed scatterer, where
, and
is the parameter vector representing the
mth scatterer position in the elevation direction in the 3D case, or the position and mean deformation velocity in the 4D case, or the position, mean deformation velocity, and thermal dilation coefficient in the 5D case:
In (
3),
,
, and
denote the elevation, velocity, and thermal dilation, respectively, of the
mth scatterer, and the vectors
,
, and
indicate the spatial, temporal, and thermal baselines in multi-baseline multi-temporal acquisition mode. Moreover,
is the incident angle,
is the exponential operator, and
i is the standard imaginary unit. Additionally, the operator ⊗ indicates the Kronecker product, and
is the unitary polarimetric target vector representing the polarimetric backscattering pattern of the
mth scatterer.
From a statistical point of view, the data vector
in (
2) is typically modeled as a zero-mean complex circular Gaussian random vector, with covariance matrix:
where
is the standard deviation of the additive noise
n in (
2),
is a
identity matrix, and
is a diagonal operator. Moreover,
and
E are Hermitian and expectation operators, respectively. Multi-look SAR tomography is generally concerned with reconstructing the backscattering distribution (
) for each resolution cell using the covariance matrix estimated by a set of
L independent and homogeneous looks. Here, the multi-look operation is used, since estimating the covariance matrix of the data with a single look gives a poor estimate.
The estimation of
can be approached in the framework of spectral estimation theory [
24], and beamforming is the simple method that recovers the backscattering distribution from a given scatterer while limiting the other interfering spectral components. Therefore, the recovered power of the filtered signal from the
mth scatterer is given by [
25]:
Since different realizations of an image are usually not available, the actual covariance matrix
R is unknown. It is straightforward, however, to approximate
R by the sample covariance matrix
by spatially averaging
L similar pixels in the images that share statistical similarity.
where
indicates the relative importance of the
lth pixel during averaging. Currently, the developed tomographic reconstruction methods are affected by decorrelating sources and the temporal decoherence of the multi-temporal data. This indeed leads to defocusing and blurring effects in the reconstruction. In such a situation, it is important to distinguish the reliable scatterers and false alarms, e.g., using detection methods such as GLRT. The next section gives an overview of the scattering-based support GLRT.
3. Overview of Scattering-Based Support GLRT
To solve the problem of detecting reliable and genuine scatterers, scattering support GLRT is among the most competitive techniques that allow for the identification of scatterers by controlling the false alarm rate [
13,
19]. According to the signal model in (
2), the multiple hypothesis tests are given as [
19]:
where the hypothesis
assumes the absence of a scatterer, i.e., the observed data
are a circularly symmetric Gaussian random vector with zero mean and covariance matrix
, while
assumes the presence of
m scatterers whose parameters are in the unknown matrix
, while
contains the reflectivity of the
m scatterers and
. Moreover,
is formed by their
m corresponding steering vectors.
If
is rejected in favor of
, then the observed data can be assumed to follow a circularly symmetric Gaussian random vector with zero mean and covariance matrix
R given in (
4). Here, we assume the presence of up to two scatterers per resolution cell, i.e.,
. Although the identification of
m scatterers is generally and theoretically possible, detection of up to two scatterers is challenging in practice due to the limited number and distribution of baselines and may not be feasible, especially when dealing with areas with short buildings and no skyscrapers, such as our study area. With this assumption, the likelihood ratio for the binary test (
,
) equals:
where
f is the joint probability density function of the looks
, e.g., a Gaussian zero-mean model. In (
8),
means that the hypothesis of the absence of the scatterer (
) is rejected and the data stack consists of either one (
) or two (
) scatterers. By substituting the maximum likelihood estimation (MLE) of the unknowns (
) into (
8), the first stage of the scattering property-based support GLRT [
19], which serves as a decision rule for the presence or absence of scatterers, can be written as follows:
where
, in which the matrix
is satisfying the equality
, and obtained by Cholesky decomposition. The threshold
in the above equations can be defined using the FAR approach [
13]. It can be shown that the solution of the maximization in (
9) with respect to
is equivalent to the maximum eigenvalue of the following matrix:
where
and
are, respectively, the maximum eigenvalue and trace of matrix
X,
, and
, and
is a
identity matrix.
The second stage of the scattering support GLRT, instead, operates the decision according to the rule of the presence of single or double scatterers
[
19]:
In analogy to the first stage of scattering support GLRT, Equation (
11) is derived by substituting the unknown parameters into the likelihood ratio of the binary test
. The parameters
and
can be obtained by the MLE approach, and the fast implementation allows decoupled MLEs as:
In [
19], it is shown that the scattering support GLRT (
10) and (
11) outperforms the conventional support GLRT [
18] in the detection of both single and double scatterers. The attempt of the current work is to further improve the detection performance by introducing an extension to the scattering support GLRT method.
4. The Proposed Method
Polarimetric radar systems typically measure complex backscattering of any target on a linear horizontal and vertical orthogonal polarization basis
. This is commonly equivalent to the acquisition of images in the polarization channels
hh,
hv,
vh, and
vv. Therefore, in the case of multi-baseline polarimetric data, the response of a reciprocal medium can be represented by the vector in Equation (
2)
that has
unique elements, where
is the complex backscattering vector from the vertical polarized transmitted signal and the horizontal polarized return in all baselines.
Since any orthogonal set of elliptically polarized states can form a polarization basis, the polarimetric response vector can be represented in any arbitrary orthogonal elliptic basis
, where
q is the orthogonal complement of
p. In this way, a complete characterization of the backscattering of targets can be obtained using the polarization synthesis theorem [
21]. Thus, the multi-baseline polarimetric response vector in Equation (
2) can be transformed from the linear basis
(or polarization channels {
hh,
hv,
vv}) to a desired
basis (or polarization channels {
pp,
pq,
qq}) as [
26]:
where
In (
14),
is a complex polarization ratio that represents the polarization state of an electromagnetic wave with a specific orientation (
) and ellipticity (
) as:
Accordingly, the first stage of the scattering support GLRT in (
10), for any specific polarization basis, can be revised as follows:
while the second stage of the test is re-written as:
In analogy to the scattering-based support GLRT, the threshold
in the proposed method can be calculated using the FAR approach (see [
13]). Note that the sample covariance matrix
is still computed on the basis (
) of the original data set, while the matrix
W is in charge of changing the polarization basis of the original data to any arbitrary transmitted/received wave by radar antenna. The detection tests in (
16) and (
17) are a function of
and the geometrical parameters
and
. Therefore,
and
are estimated with (
12), while the MLEs of
and
are represented as:
6. Discussion
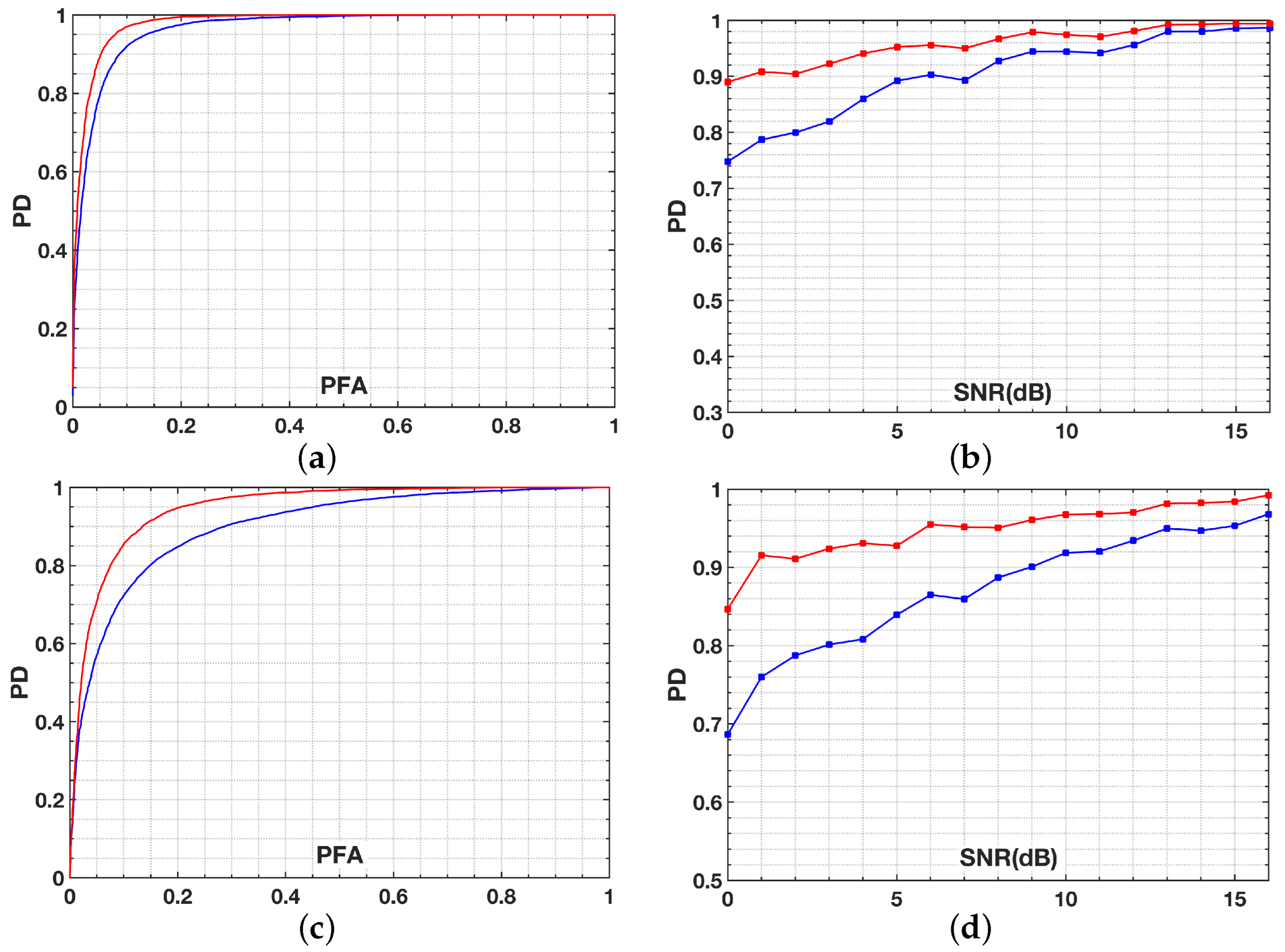
The results and analyses presented in the previous section are discussed here. Based upon the numerical experiments, the proposed method increases the probability of detection of both single and double scatterers compared to the existing scattering support GLRT under the same conditions. The improvement in detection at both stages of the test is mainly related to the optimization of the polarization bases by the proposed method. The detection tests, in general, depend indirectly on the polarization basis of the data stack via the covariance matrix. Our method uses the best combination of transmit and receive polarizations to achieve the best detection performance at a constant false alarm rate.
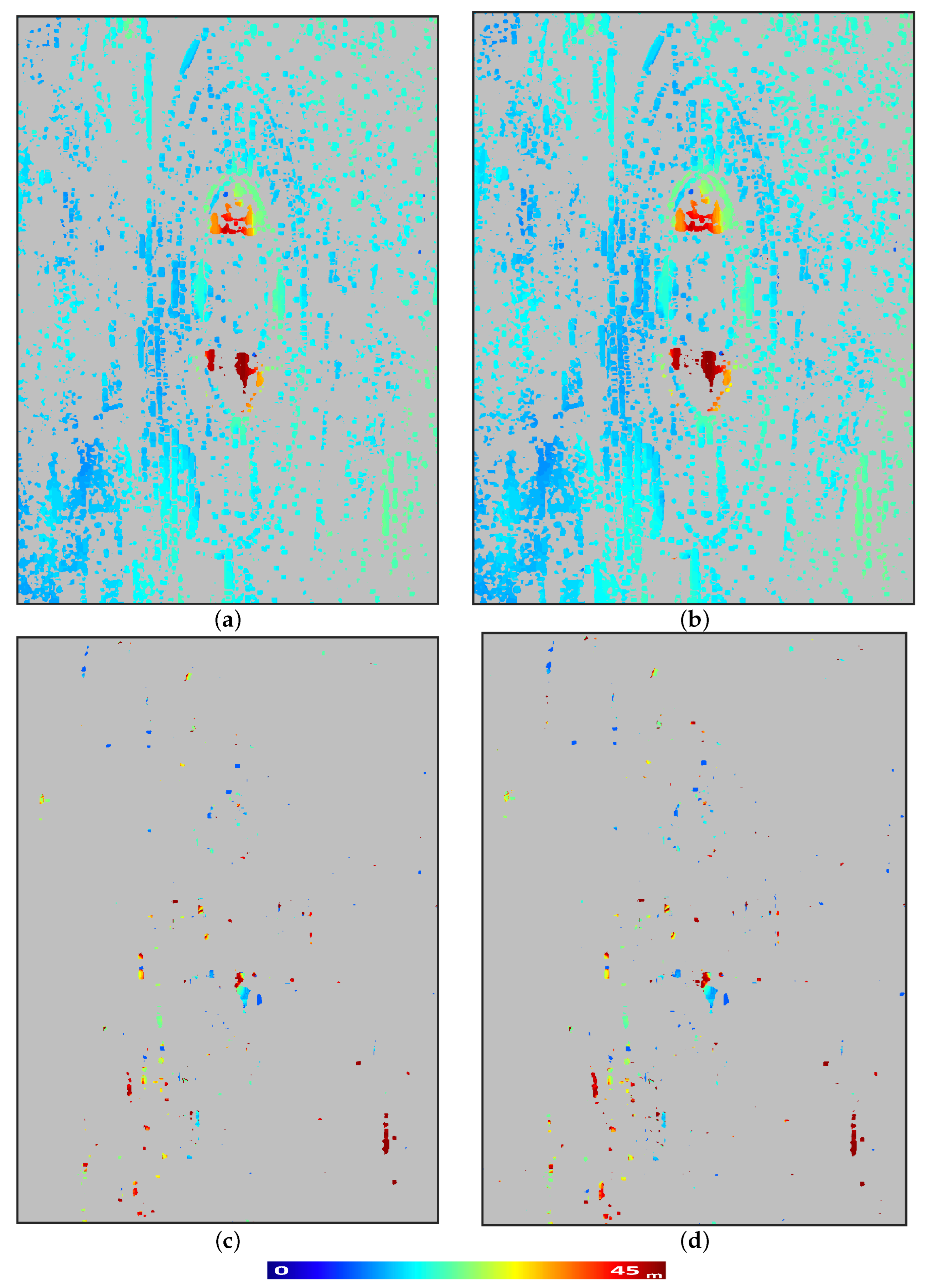
In analogy with the simulated experiments, the results with real data presented in
Figure 3 confirm the performance of the proposed method over the existing scattering support GLRT. The validity and reliability of the GLRT-based techniques, especially the support GLRT and the scattering support GLRT, have been extensively evaluated and confirmed in the literature [
7,
13,
14,
15,
16,
17,
18,
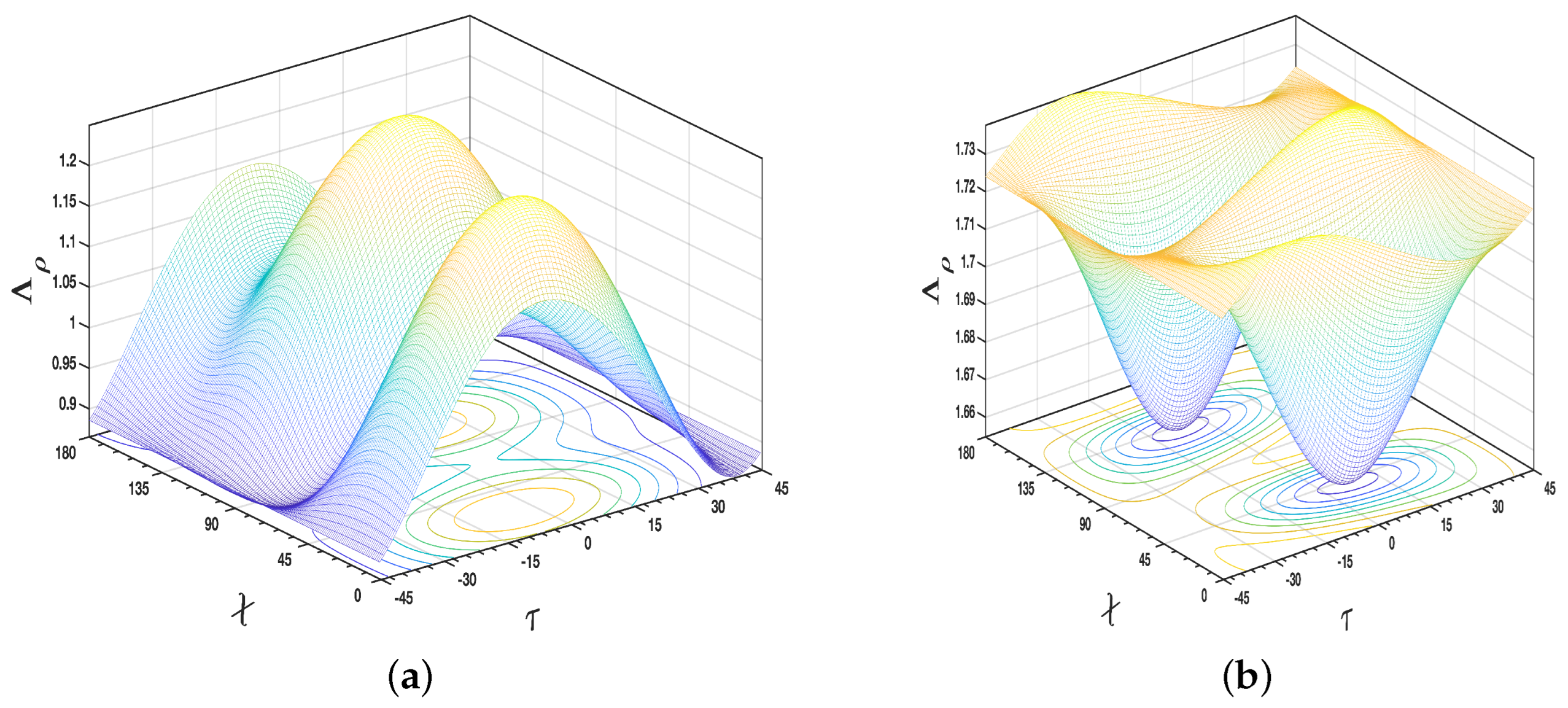
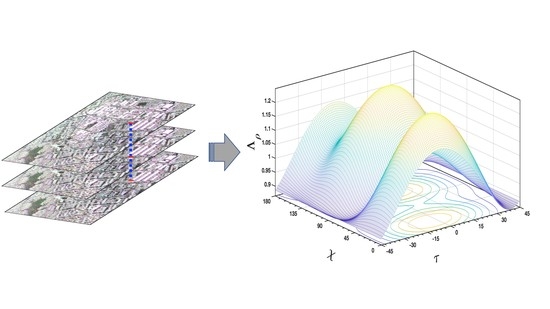
19]. According to the results, and in the context of the multi-look detection process with polarimetric data, it could be more efficient to design the detection test based upon polarization basis optimization rather than relying on the use of the conventional horizontal and vertical transmit and receive polarizations in the radar data. The efficiency of such an optimization is that it provides a higher density of detected PSs. The proposed method provides the possibility of revealing the presence of weaker scatterers by using the optimal polarization basis; these scatterers could not be detected using the detection tests relying only on the use of the conventional horizontal and vertical polarization basis. This is in line with the point that detection performance depends upon the polarization basis used, as shown in
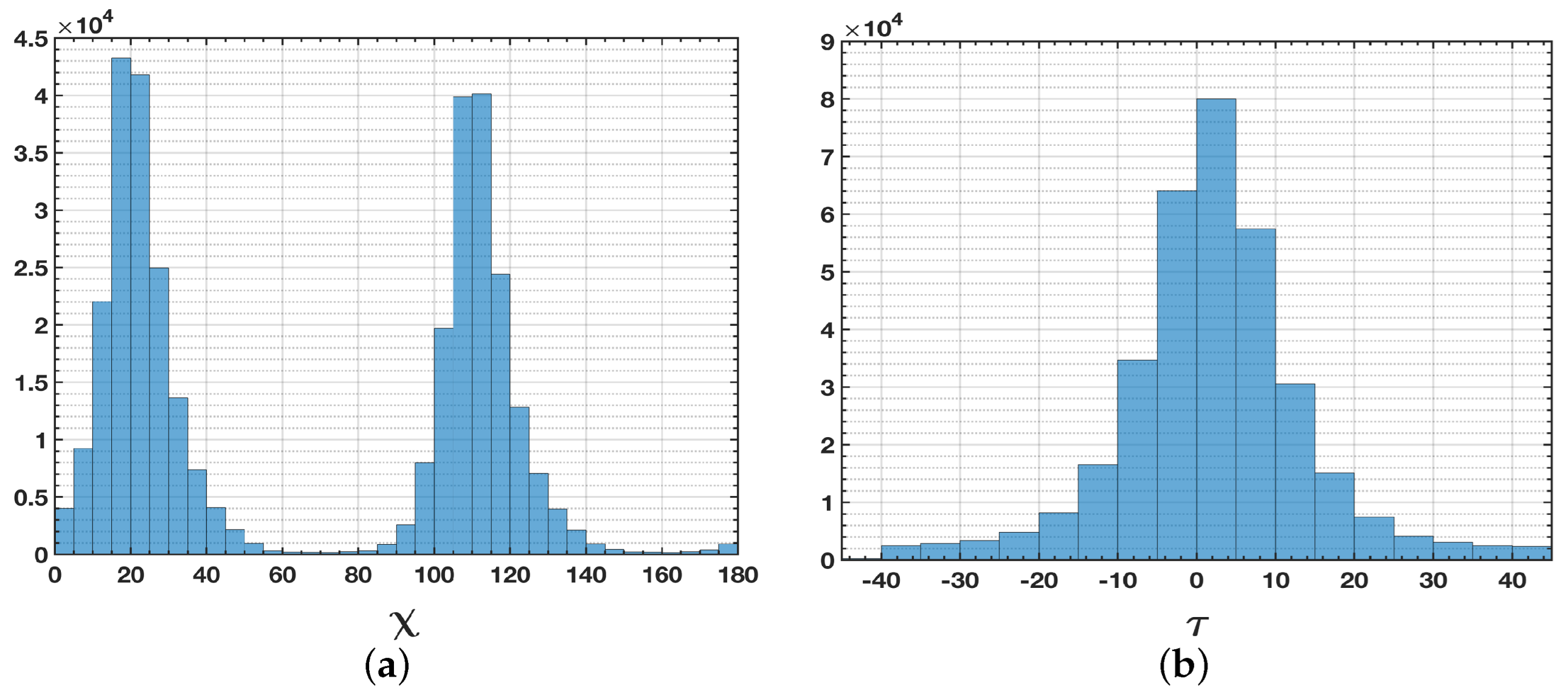
Figure 4 for two sample resolution cells. Typically, the best polarization basis for the detection process will vary from pixel to pixel, and the optimal basis depends mainly upon the sensed target. The statistics of the optimal polarization over different detected PSs, however, can provide important information about the effects of the polarization design of a radar antenna on the probability of scatterer identification. The analysis of the reported histograms using the ESAR data set in
Figure 5 provides an important indication: the linear polarization basis (
) with orientation angles of
and
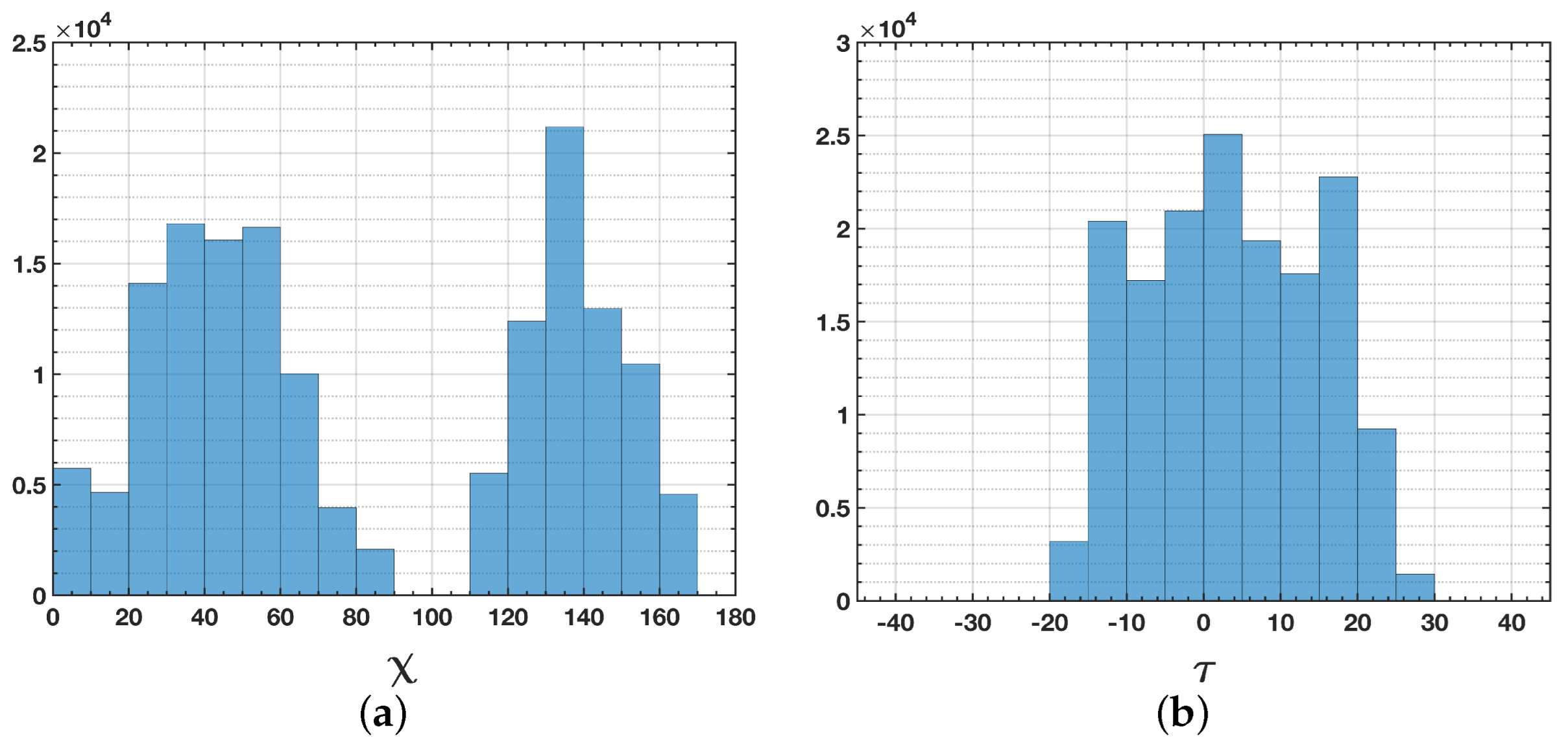
is the optimal polarization for detecting permanent scatterers in the Dresden test area. Similarly, the histograms obtained from the UAVSAR data set in
Figure 8 confirm the capability of the linear polarization basis (
) in the PS detection process. At the Mondah test site, however, linear polarization with orientation angles of
and
is identified as the most optimal polarization basis. Recall that the change in optimal polarization from pixel to pixel and from study area to study area is due to the fact that the optimal polarization basis is a function of the backscattering mechanism of the sensed targets. Therefore, each study area may have a different optimal polarization, depending on the targets presented.
Generally, the use of such polarization bases in both test sites made it possible to detect the presence of additional weaker scatterers that were not detectable with the conventional horizontal-vertical polarization basis.
The efficiency of the implemented methods for processing our real data stack in
Figure 3 is given in terms of processing time. The experiments were performed in the MATLAB environment on a desktop system with a configuration of Intel(R) Core(TM) i7-4510U CPU @ 2.00 GHz and 12 GB RAM. The total runtime for the existing scattering support GLRT is about
h, while the runtime for the proposed method increases to
h. Although this increase in runtime may limit the application of the proposed framework in the tomographic processing of large data sets, some tips can be considered to reduce the processing time. For example, the geometrical parameters (
and
) can be scanned at widely discretized intervals. In addition, the use of Matlab Mex files or parallel computing and Graphics Progressing Units (GPUs) can also significantly reduce running times. Although online processing is an interesting strategy to extend the application of the proposed method, the requirement of the method for large amounts of data to be uploaded as input may limit online processing tools.
Although not examined in this study, the proposed method, like other existing tomographic GLRT-based methods, is expected to be applicable to detecting permanent scatterers in built-up regions with high-rise structures and also for mapping elevations and displacements of the earth’s surface in non-urban regions by detecting PSs from coherent points such as rocks, etc. The performance of the method in such scenarios has yet to be evaluated. In addition, the detection of PSs from single and double scatterers can be extended to additional scatterers (e.g., triple and quadruple scatterers). This calls for the extension of testing to multiple stages. Testing and evaluating the effectiveness of the proposed method with multiple stages in a study area with high-rise skyscrapers will be a future line of research after this study.